机器学习 —— 概率图模型(推理:连续时间模型)
概率图模型在因果推断、不确定性推理、决策分析、贝叶斯网络等领域的应用研究

概率图模型在因果推断、不确定性推理、决策分析、贝叶斯网络等领域的应用研究摘要概率图模型 (Probabilistic Graphical Model, PGM) 是一种强大的工具,用于表示和推理复杂系统中的不确定性关系。
它通过将变量之间的依赖关系以图的形式表示,结合概率论,对现实世界问题进行建模和分析。
本文将重点探讨概率图模型在因果推断、不确定性推理、决策分析、贝叶斯网络等领域的应用研究。
关键词:概率图模型,因果推断,不确定性推理,决策分析,贝叶斯网络1. 引言在现实世界中,我们经常面临着充满不确定性的问题。
概率图模型提供了一种结构化的框架,帮助我们理解和分析这些不确定性。
它将变量之间的依赖关系以图的形式表示,并将概率论融入其中,以进行推断和预测。
概率图模型的应用范围非常广泛,涵盖了机器学习、人工智能、计算机视觉、自然语言处理、生物信息学等多个领域。
本文将重点探讨概率图模型在以下四个领域的应用研究:*因果推断: 识别变量之间的因果关系,并进行因果推断。
*不确定性推理: 在不确定性环境下进行推理和决策。
*决策分析: 利用概率图模型进行决策分析,选择最佳策略。
*贝叶斯网络: 作为概率图模型的一种特殊类型,在各个领域得到了广泛应用。
2. 概率图模型基础概率图模型由两部分组成:图结构和概率分布。
图结构表示变量之间的依赖关系,而概率分布则量化了变量的概率信息。
*图结构: 图结构由节点和边组成。
每个节点表示一个随机变量,边则表示变量之间的依赖关系。
常见的图结构类型包括:o有向图:边表示变量之间的因果关系。
o无向图:边表示变量之间的相关性。
o混合图:包含有向边和无向边。
*概率分布: 概率分布定义了变量的概率信息。
常用的概率分布包括:o离散概率分布:例如,伯努利分布、多项式分布。
o连续概率分布:例如,高斯分布、指数分布。
概率图模型的优点在于:*结构化的表示: 图结构可以直观地表示变量之间的依赖关系,便于理解和分析。
强化学习算法中的概率图模型方法详解(五)

在强化学习算法中,概率图模型是一种常用的方法之一。
概率图模型是指用图来表示随机变量之间的依赖关系的一种模型。
它将变量之间的关系用图的形式表示出来,并通过概率分布来描述这些变量之间的关系。
在强化学习中,概率图模型可以用来表示状态之间的依赖关系,并且可以通过这些关系来进行决策和预测。
在强化学习中,智能体需要根据环境的状态来做出决策,以获得最大的累积奖励。
概率图模型可以帮助智能体对环境的状态进行建模,并且可以通过这些模型来进行决策。
在概率图模型中,有两种常用的表示方法:贝叶斯网络和马尔可夫网络。
贝叶斯网络是一种有向图模型,它用有向边表示变量之间的依赖关系。
在贝叶斯网络中,每个节点表示一个随机变量,有向边表示这个节点依赖于其他节点。
通过这种方式,可以用贝叶斯网络来表示状态之间的依赖关系,并且可以通过这些关系来进行决策和预测。
马尔可夫网络是一种无向图模型,它用无向边表示变量之间的依赖关系。
在马尔可夫网络中,每个节点表示一个随机变量,无向边表示这些节点之间的相关性。
通过这种方式,可以用马尔可夫网络来表示状态之间的依赖关系,并且可以通过这些关系来进行决策和预测。
在强化学习中,概率图模型可以用来表示智能体与环境之间的状态转移关系。
这些状态转移关系可以通过贝叶斯网络或马尔可夫网络来表示,然后可以通过这些网络来进行决策和预测。
通过这种方式,智能体可以更好地理解环境的状态,并且可以更准确地做出决策。
除了表示状态之间的依赖关系,概率图模型还可以用来表示智能体对环境的观测。
在强化学习中,智能体通常不能直接观测环境的状态,而是通过观测来了解环境的状态。
概率图模型可以用来表示智能体观测到的信息,并且可以通过这些信息来进行决策和预测。
通过概率图模型,智能体可以更好地理解环境的状态和观测,并且可以更准确地做出决策。
通过这种方式,概率图模型可以帮助强化学习算法更好地适应不同的环境,并且可以更有效地学习和改进。
总的来说,概率图模型是强化学习算法中一种非常重要的方法。
机器学习知识:机器学习中的知识表示与推理

机器学习知识:机器学习中的知识表示与推理近年来,人工智能技术的快速发展,让机器学习这个领域变得越来越受到关注。
机器学习无疑是实现人工智能的一种重要手段,其核心任务是从样本数据中学习出模型来,使得该模型能够对新的训练数据进行分类、预测等任务。
在机器学习中,知识表示与推理是非常重要的话题。
在本文中,我们将对机器学习中的知识表示与推理展开讨论。
一、知识表示知识表示是指将现实中的问题、概念、判断等抽象成模型,以便计算机能够理解、存储和处理这些信息。
知识表示是机器学习中不可或缺的重要组成部分,因为机器学习需要通过学习提取数据样本的特征,来构造知识模型。
在机器学习中,有三种常用的知识表示方法:符号表示、神经网络表示和贝叶斯网络表示。
1.符号表示符号表示是将实际问题转换为一些规则、公式等符号形式的语言的操作。
符号表示的模型可以提供关于问题的精确和准确的信息,也可以快速生成新的数据。
但是,由于它是基于人类语言和常识的,因此它可能无法处理复杂的问题。
2.神经网络表示神经网络表示是利用具有各种连接强度的神经元构建模型。
神经网络可以处理复杂的非线性问题,但是它无法直接将人类语言转换为符号表示。
3.贝叶斯网络表示贝叶斯网络表示是一种旨在表示变量之间的概率关系的概率图模型。
贝叶斯网络可以处理复杂的不确定性,并可以通过学习数据的统计规律来构建知识模型。
但是,贝叶斯网络的训练和推理可能需要更多的计算资源。
二、知识推理知识推理是一种基于已有知识,来推导新知识的过程。
它往往是指从已知前提出发,推导出新结论的过程。
知识推理是机器学习中的一个重要环节,因为它可以使机器从已有知识中提取新的模式。
在机器学习中,知识推理主要分为以下三种类型:基于规则的推理、基于统计的推理和基于逻辑的推理。
1.基于规则的推理基于规则的推理是一种将先前广泛收集的知识表示为规则的推理方法。
这种方法中,推理是通过匹配输入数据与规则库中的一条或多条规则来完成的。
虽然基于规则的推理可以提供直观的解释,但由于规则复杂的表示和条目有限性,其中存在过拟合和泛化性能差的问题。
高中数学六种概率模型

高中数学六种概率模型在高中数学中,概率是一个重要的概念,在日常生活中也随处可见。
概率模型是用来描述不确定事件发生的可能性的数学模型。
在高中数学中,我们学习了六种常见的概率模型,分别是等可能模型、几何模型、排列模型、组合模型、条件概率模型和贝叶斯模型。
第一种概率模型是等可能模型。
在等可能模型中,我们假设所有的结果是等可能发生的,例如掷硬币、掷骰子等。
在这种情况下,我们可以通过计算事件发生的可能性来求解概率。
例如,抛掷一枚硬币,出现正面的概率和出现反面的概率都是1/2。
第二种概率模型是几何模型。
几何模型适用于一些连续事件,例如抛掷一根棍子,棍子落在某个距离范围内的概率。
这种情况下,我们需要用到几何概率的计算方法,即事件的概率等于事件所占的长度或面积与总长度或面积的比值。
第三种概率模型是排列模型。
排列模型适用于有序事件的概率计算。
例如,从一副扑克牌中抽出三张牌,求得其中一种特定牌型的概率。
这种情况下,我们可以使用排列的计算公式,将事件的可能性与总的可能性进行比较。
第四种概率模型是组合模型。
组合模型适用于无序事件的概率计算。
例如,从一副扑克牌中抽出三张牌,求得其中任意三张牌的概率。
这种情况下,我们可以使用组合的计算公式,将事件的可能性与总的可能性进行比较。
第五种概率模型是条件概率模型。
条件概率模型是指在已知一些信息的情况下,求另外一些信息的概率。
例如,在已知某人生病的情况下,求他感染某种疾病的概率。
在条件概率中,我们需要用到贝叶斯公式来计算概率。
第六种概率模型是贝叶斯模型。
贝叶斯模型是一种用来更新先验概率的模型。
在贝叶斯模型中,我们通过观察到的事实来更新我们对事件发生的概率的估计。
这种模型常常用于统计学和机器学习中。
高中数学中有六种常见的概率模型,分别是等可能模型、几何模型、排列模型、组合模型、条件概率模型和贝叶斯模型。
这些模型可以帮助我们计算事件发生的可能性,对我们理解概率提供了有力的工具。
通过学习这些模型,我们可以更好地理解和应用概率知识,为未来的学习和工作打下坚实的基础。
机器学习——概率图模型(推理:MAP)

机器学习——概率图模型(推理:MAP) MAP 是最⼤后验概率的缩写。
后验概率指的是当有⼀定观测结果的情况下,对其他随机变量进⾏推理。
假设随机变量的集合为X ,观察到的变量为 e, W = X-e , AP = P(W|e). 后验概率和联合概率是不同的两个概念。
事实上,后验概率更接近推理本⾝的“意义”,并且被越来越多的⽤于诊断系统中。
在医疗诊断系统中,存在包括病症,症状等许多随机变量,使⽤VE或者消息传递之类的推理⼿段确实可以获得每个随机变量的概率以及某些随机变量的联合概率(⼀个Scope的概率)。
但实际上,如果⾯对某些很少出现的症状以及对应病症,联合概率密度函数并不合适,⽐如病⼈红细胞减少的概率⾮常⼩,但红细胞减少很⼤⼏率上对应“⽩⾎病”。
如果求联合分布则会得到⼀个较⼩的概率值(因为得⽩⾎病的⼈本来就不多,加上有其他症状⼲扰),但是如果使⽤后验概率,则能排除此⼲扰。
1. 积化和的最⼤化 最⼤后验概率是⼀种推理⼿段。
w = argmax P(W|e)。
W是尚未观测到的随机变量,使得此概率最⼤的意义是在获得某观测后,推断最可能发⽣了什么。
这个公式把MAP变成了⼀个优化问题。
P(X)实际上是⼀系列 P(scope)的乘积。
在取对数的情况下,积就变成了和,对数的底是可以随意选择的。
demo example 如下图所⽰. 如果 PHI_k (Dk) 是链状分解的情况下,可以采⽤变量分离最⼤化的⽅式来求取其最⼤值。
如图所⽰: 由变量边际类⽐可知,还可由消息传递的⽅式来计算最终结果。
实际上这⾥的最⼤值代替了边际。
利⽤消息传递的⽅式计算最⼤后验概率如图所⽰: 最⼤化执⾏完毕后,得到的是各个变量的“势”,以及使得“势”最⼤的变量组合取值。
简⽽⾔之,就是⼀组推断的结果。
2. NP完备的MAP问题2.1 对应问题 对应问题是在⼯程中经常碰到的问题。
例如多⽬视觉中的配准,同⼀个物体被不同像素观测到。
那么我们关⼼的两个不同的像素值各是多少。
机器学习 —— 概率图模型(推理:团树算法)
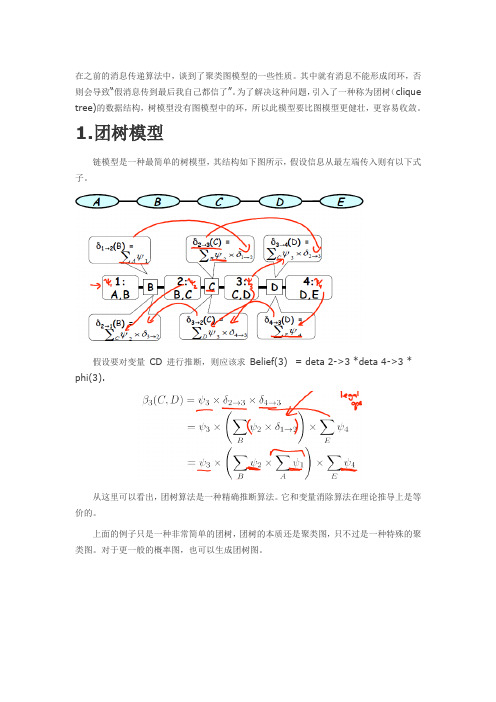
在之前的消息传递算法中,谈到了聚类图模型的一些性质。
其中就有消息不能形成闭环,否则会导致“假消息传到最后我自己都信了”。
为了解决这种问题,引入了一种称为团树(clique tree)的数据结构,树模型没有图模型中的环,所以此模型要比图模型更健壮,更容易收敛。
1.团树模型链模型是一种最简单的树模型,其结构如下图所示,假设信息从最左端传入则有以下式子。
假设要对变量CD 进行推断,则应该求Belief(3) = deta 2->3 *deta 4->3 * phi(3).从这里可以看出,团树算法是一种精确推断算法。
它和变量消除算法在理论推导上是等价的。
上面的例子只是一种非常简单的团树,团树的本质还是聚类图,只不过是一种特殊的聚类图。
对于更一般的概率图,也可以生成团树图。
其中,每个cluster都是变量消除诱导图中的一个最小map。
2.团树模型的计算从上面分析可知,团树模型本质上和变量消除算法还有说不清道不明的关系(团树模型也是精确推理模型)。
但是这个算法的优势在于,它可以利用消息传递机制达到收敛。
之前提过,聚类图模型中的收敛指的是消息不变。
除此之外,聚类图的本质是一种数据结构,它可以储存很多中间计算结果。
如果我们有很多变量ABCDEF,那么我们想知道P(A),则需要执行一次变量消除。
如果要计算P(B)又要执行一次变量消除。
如果中途得到了某个变量的观测,又会对算法全局产生影响。
但是使用团树模型可以巧妙的避免这些问题。
首先,一旦模型迭代收敛之后。
所有的消息都是不变的,每个消息都是可以被读取的。
每个团的belief,实际上就是未归一划的联合概率,要算单个变量的概率,只需要把其他的变量边际掉就行。
这样一来,只需要一次迭代收敛,每个变量的概率都是可算的。
并且算起来方便。
其次,如果对模型引入先验知识比如A = a 时,我们需要对D 的概率进行估计。
按照变量消除的思路又要从头来一次。
但是如果使用团树结构则不用,因为A的取值只影响deta1->2以及左向传递的消息,对右向传递的消息则毫无影响,可以保留原先对右向传递消息的计算值,只重新计算左向传递结果即可。
机器学习

研究现状
传统的研究现 状
大数据环境下 的研究现状
传统机器学习的研究方向主要包括决策树、随机森林、人工神经络、贝叶斯学习等方面的研究。
决策树是机器学习常见的一种方法。20世纪末期,机器学习研究者J.Ross Quinlan将Shannon的信息论引入 到了决策树算法中,提出了ID3算法。1984年I.Kononenko、E.Roskar和I.Bratko在ID3算法的基础上提出了ASSISTANTAlgorithm,这种算法允许类别的取值之间有交集。同年,A.Hart提出了Chi-Squa统计算法,该算法采 用了一种基于属性与类别关联程度的统计量。1984年L.Breiman、C.Ttone、R.Olshen和J.Freidman提出了决策 树剪枝概念,极大地改善了决策树的性能。1993年,Quinlan在ID3算法的基础上提出了一种改进算法,即C4.5 算法。C4.5算法克服了ID3算法属性偏向的问题增加了对连续属性的处理通过剪枝,在一定程度上避免了“过度 适合”现象。但是该算法将连续属性离散化时,需要遍历该属性的所有值,降低了效率,并且要求训练样本集驻 留在内存,不适合处理大规模数据集。2010年Xie提出一种CART算法,该算法是描述给定预测向量X条件分布变量 Y的一个灵活方法,已经在许多领域得到了应用。CART算法可以处理无序的数据,采用基尼系数作为测试属性的 选择标准。CART算法生成的决策树精确度较高,但是当其生成的决策树复杂度超过一定程度后,随着复杂度的提 高,分类精确度会降低,所以该算法建立的决策树不宜太复杂。2007年房祥飞表述了一种叫SLIQ(决策树分类) 算法,这种算法的分类精度与其他决策树算法不相上下,但其执行的速度比其他决策树算法快,它对训练样本集 的样本数量以及属性的数量没有限制。SLIQ算法能够处理大规模的训练样本集,具有较好的伸缩性;执行速度快 而且能生成较小的二叉决策树。SLIQ算法允许多个处理器同时处理属性表,从而实现了并行性。但是SLIQ算法依 然不能摆脱主存容量的限制。
生成式模型 推理式模型-概述说明以及解释

生成式模型推理式模型-概述说明以及解释1.引言1.1 概述在机器学习领域中,生成式模型和推理式模型是两种常见的方法。
它们都是用于描述和处理概率和不确定性的模型。
生成式模型主要关注如何生成样本数据,而推理式模型则着眼于对给定数据进行推理和预测。
生成式模型是一种通过建模随机变量的联合概率分布,从而生成新的样本数据的方法。
它通过观察已知数据的特征,学习生成这些数据的分布规律。
生成式模型的核心思想是通过学习到的分布,来生成具有与训练样本相似的新样本。
生成式模型的一大优势是可以生成新的、不存在的数据样本,从而扩展数据集。
生成式模型常用的方法包括隐马尔可夫模型(HMM)、混合高斯模型(GMM)、变分自编码器(VAE)等。
与之相对,推理式模型则主要关注给定数据后如何进行推理,即通过已知的条件获得目标值的后验分布。
推理式模型用于对已知数据进行分类、回归、聚类等任务,并且可以用于预测未来的结果。
推理式模型更加注重对特征和目标之间的依赖关系建模,以便进行准确的预测。
推理式模型常用的方法包括逻辑回归、支持向量机(SVM)、深度神经网络(DNN)等。
生成式模型和推理式模型在应用领域上也有所差异。
生成式模型常用于自然语言处理、图像生成、语音合成等任务,因为它可以生成符合特定领域规则的新样本。
而推理式模型则广泛应用于文本分类、图像识别、推荐系统等任务,因为它能够对已知数据进行准确的预测和推理。
本文将详细介绍生成式模型和推理式模型的定义、原理和在不同领域的应用。
通过对两种模型的深入理解,有助于我们选择合适的模型用于解决具体问题,并推动机器学习技术的进一步发展。
1.2文章结构文章结构部分的内容如下:文章结构的目的是为读者概述本文的组织方式和内容安排,并给出每个部分的简要介绍。
通过清晰明了的结构,读者可以更好地理解和把握文章全貌,以便在阅读过程中更容易找到所需的信息。
本文主要包含以下几个部分:1. 引言:本部分将对生成式模型和推理式模型进行概述,并介绍文章的结构安排和目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有一种很重要的概率图模型用于SLAM,视觉追踪,识别,传感融合等领域,称为为Template Model. 其特征是每个状态具有多个随机变量,下个状态随机变量的取值受到上个状态的影响。
并且随机变量之间的交互属于复制关系。
如下图所示:
显然,普通的概率图模型的图是确定的,并不会图的结构不会改变,而这种Template Model的图结构会随着时间的改变自行增殖,故此模型的推理算法需要单独讨论。
1、变未知为已知,图的截断
一种简单的思路是在某个时间点对图模型进行截断,将增殖的PGM变为固定的PGM,再在图模型上运行推理算法。
对如图所示结构而言,获得的信息是1~t时间传感器的观测值。
算法目标是推测St
时刻的状态。
定义s(t+1)时刻的“猜测状态为xigma_dot_(t+1),可知,其分布为t时刻
状态的和。
也就是t时刻取值的线性组合。
在给定t+1时刻的观测时,s(t+1)可表达为下式:
s(t+1)真正的值实际上和t+1时刻的观测,对t+1时刻的猜测,以及分母——对t+1时刻观测量的猜测有关。
分母实际上是一个跟状态无关的常数,最后求不同状态S取值比例的时候分母是可以忽略的。
所以重要的是分子。
分子和两个量有关,第一个是观测模型,第二个是t+1时刻状态猜测量。
而状态猜测量是线性组合,每次计算都可以直接带入上次结果。
所以,这种结构的Template Model算起来并不会非常困难。
