概率图模型介绍与计算
概率图模型的推理算法在空间数据分析中的应用(五)

概率图模型的推理算法在空间数据分析中的应用概率图模型是一种用于表示变量之间依赖关系的工具,它可以帮助我们理解变量之间的关系,从而进行推理和预测。
在空间数据分析中,概率图模型的推理算法可以帮助我们更好地理解空间数据的特征和变化规律,为空间数据分析提供了新的方法和思路。
一、概率图模型的基本原理概率图模型是一种用图来表示变量之间概率依赖关系的模型。
它由节点和边组成,节点表示随机变量,边表示变量之间的依赖关系。
概率图模型分为有向图模型和无向图模型两种,分别用于表示变量之间的因果关系和相关关系。
在空间数据分析中,概率图模型可以用来表示空间位置之间的依赖关系,帮助我们理解空间数据的分布规律和变化趋势。
二、概率图模型的推理算法概率图模型的推理算法是指根据模型和观测数据,推导出未知变量的后验分布的算法。
在空间数据分析中,概率图模型的推理算法可以帮助我们从观测数据中推断出空间位置之间的依赖关系和分布规律,为空间数据的预测和模拟提供支持。
常用的概率图模型的推理算法包括变量消除、信念传播、马尔可夫链蒙特卡洛等方法,它们可以帮助我们有效地进行空间数据分析和预测。
三、概率图模型在空间数据模式识别中的应用概率图模型在空间数据模式识别中发挥着重要作用。
通过构建空间变量之间的依赖关系图,可以帮助我们发现空间数据的模式和规律,从而进行空间数据的分类和聚类。
例如,在地理信息系统中,可以利用概率图模型来识别城市的发展模式和规律,为城市规划和发展提供支持。
另外,在环境监测和灾害预警中,概率图模型也可以帮我们发现空间数据中的异常模式和趋势,提高空间数据的监测和预警效果。
四、概率图模型在地图生成和路径规划中的应用概率图模型在地图生成和路径规划中也有着广泛的应用。
通过构建空间位置之间的依赖关系图,可以帮助我们生成更加真实和准确的地图,为地图导航和定位提供支持。
另外,在路径规划中,概率图模型可以帮助我们分析空间位置之间的依赖关系和交通规律,找到最优的路径和规划方案,提高路径规划的准确性和效率。
概率图模型在医学影像分析中的应用指南(九)

概率图模型是一种用来描述随机变量之间关系的数学模型。
在医学影像分析中,概率图模型被广泛应用于解决一些复杂的问题,如图像分割、疾病诊断和治疗效果预测等。
本文将介绍概率图模型在医学影像分析中的应用指南,包括常见的概率图模型类型、数据预处理、模型训练和评估等内容。
一、概率图模型介绍概率图模型是一种用图来描述随机变量之间依赖关系的数学模型。
它分为有向图模型和无向图模型两种类型。
在医学影像分析中,常用的概率图模型包括贝叶斯网络、马尔科夫随机场和条件随机场等。
贝叶斯网络用有向无环图表示变量之间的依赖关系,马尔科夫随机场用无向图表示变量之间的关联,条件随机场用无向图表示标记序列之间的依赖关系。
二、数据预处理在应用概率图模型进行医学影像分析之前,需要对数据进行预处理。
这包括图像采集、去噪、配准、分割和特征提取等步骤。
图像采集是指通过医学影像设备获取患者的影像数据,去噪是指去除图像中的噪声干扰,配准是指将不同时间点或不同模态的图像对齐,分割是指将图像分割成不同的组织或结构,特征提取是指从图像中提取有用的特征用于模型训练和预测。
三、模型训练在进行模型训练时,需要选择合适的概率图模型和相应的学习算法。
对于贝叶斯网络,常用的学习算法包括参数学习和结构学习;对于马尔科夫随机场,常用的学习算法包括逐步逼近和信念传播;对于条件随机场,常用的学习算法包括梯度下降和拟牛顿法。
在模型训练过程中,需要使用标注数据进行监督学习或者无监督学习,通过最大化似然函数或者最小化损失函数来优化模型参数。
四、模型评估在模型训练完成后,需要对模型进行评估。
常用的评估指标包括准确率、召回率、F1分数、ROC曲线和AUC值等。
这些指标可以用来评估模型对于不同疾病或结构的识别能力和预测准确性。
除了定量评估指标,还可以通过可视化分析来观察模型的预测结果和误差情况,从而进一步改进模型的性能。
五、应用示例概率图模型在医学影像分析中有着广泛的应用。
例如,可以利用贝叶斯网络来建立疾病诊断模型,通过学习不同疾病和临床特征之间的关系,实现对患者疾病风险的预测;可以利用马尔科夫随机场来进行图像分割和标记,提取图像中不同组织和结构的区域;可以利用条件随机场来进行疾病预后预测,根据患者的临床信息和影像特征,预测患者治疗效果和生存期。
概率图模型的推理方法详解(Ⅰ)

概率图模型的推理方法详解概率图模型是一种用图来表示随机变量之间依赖关系的数学模型。
它通过图的节点表示随机变量,边表示随机变量之间的依赖关系,可以用来描述各种复杂的现实世界问题。
概率图模型包括了贝叶斯网络和马尔可夫网络两种主要类型,它们都可以用来进行推理,即根据已知的信息来推断未知的变量。
在本文中,将详细介绍概率图模型的推理方法,包括贝叶斯网络和马尔可夫网络的推理算法。
一、概率图模型概率图模型是一种用图来表示随机变量之间依赖关系的数学模型。
它通过图的节点表示随机变量,边表示随机变量之间的依赖关系,可以用来描述各种复杂的现实世界问题。
概率图模型包括了贝叶斯网络和马尔可夫网络两种主要类型。
贝叶斯网络是一种有向图模型,用来表示变量之间的因果关系;马尔可夫网络是一种无向图模型,用来表示变量之间的相关关系。
概率图模型可以用来进行概率推理,即根据已知的信息来推断未知的变量。
二、贝叶斯网络的推理方法在贝叶斯网络中,每个节点表示一个随机变量,每条有向边表示一个因果关系。
贝叶斯网络的推理方法主要分为两种:精确推理和近似推理。
1. 精确推理精确推理是指通过精确的计算来得到准确的推理结果。
常用的精确推理算法包括变量消去算法和团树传播算法。
变量消去算法通过逐步消去变量来计算联合概率分布,但是对于大型网络来说计算复杂度很高。
团树传播算法通过将网络转化为一个树状结构来简化计算,提高了计算效率。
2. 近似推理近似推理是指通过近似的方法来得到推理结果。
常用的近似推理算法包括马尔科夫链蒙特卡洛算法和变分推断算法。
马尔科夫链蒙特卡洛算法通过构建马尔科夫链来进行抽样计算,得到近似的概率分布。
变分推断算法通过将概率分布近似为一个简化的分布来简化计算,得到近似的推理结果。
三、马尔可夫网络的推理方法在马尔可夫网络中,每个节点表示一个随机变量,每条无向边表示两个变量之间的相关关系。
马尔可夫网络的推理方法主要分为两种:精确推理和近似推理。
1. 精确推理精确推理是指通过精确的计算来得到准确的推理结果。
机器学习及应用 第10章 概率图模型

对于一阶马尔科夫模型,系统在时刻t +1的状态仅仅依赖于时刻t 的状态,
而与之前的状态无关。即,如果已知当前时刻的系统状态,那么系统的未
来状态独立于过去的状态。
进一步,假定从 到 的转移概率(Transition Probability)是独立于时间的,
即
ij=P qt1 S j | qt Si 满足 ij ≥ 0 且
10.4 综合案例
def forward(self):
retList = [] # 进行初始化,即第一天的天气状况 theata = self.pai * self.B[:, self.observe_list[0]] max_inx = np.argmax(theata) # 第一天的天气状态(序号) print("theata 1:",theata, self.weather[max_inx]) retList.append(self.weather[max_inx]) lenth = len(self.observe_list) for i in range(1,lenth): # 计算后面几天的天气状况
10.2 马尔科夫过程
10.2.1 马尔科夫过程
马尔科夫过程有如下特性:在已知系统当前状态的条件下,它未来的演变
不依赖于过去的演变。也就是说,一个马尔科夫过程可以表示为系统在状
态转移过程,第t +1次结果只受第t 次结果的影响,即只与当前状态有关,
而与过去状态,即系统的初始状态以及此次转移前的所有状态无关。
theata = (theata.dot(self.A)) # 上一个观察状态序列值到各个隐藏状态的概率值。 theata = theata * ((self.B[:, self.observe_list[i]])) #在x轴上求和,即新的在该状态的 局部概率。 max_inx = np.argmax(theata) # 预测的当天天气状态(序号) print("theata 1:", theata, self.weather[max_inx]) retList.append(self.weather[max_inx]) return retList if __name__ == "__main__": observe_list = [0,1,3] # 观察序列 a = HMM(observe_list) # 创建一个HMM对象 predict_list = a.forward() # 前向计算 print(predict_list)
概率图模型的推理方法详解(七)

概率图模型的推理方法详解概率图模型(Probabilistic Graphical Models,PGMs)是一种用来表示和推断概率分布的工具。
它是通过图的形式来表示变量之间的依赖关系,进而进行推理和预测的。
概率图模型主要分为贝叶斯网络(Bayesian Network)和马尔科夫网络(Markov Network)两种类型。
本文将从推理方法的角度对概率图模型进行详细解析。
1. 参数化概率图模型的推理方法参数化概率图模型是指模型中的概率分布由参数化的形式给出,如高斯分布、伯努利分布等。
对于这种类型的概率图模型,推理的关键是求解潜在的参数,以及根据参数进行概率分布的推断。
常见的方法包括极大似然估计、期望最大化算法和变分推断等。
极大似然估计是一种常用的参数估计方法,它通过最大化观测数据的似然函数来求解模型的参数。
具体来说,对于给定的数据集,我们可以计算出参数θ下观测数据的似然函数L(θ)。
然后求解参数θ使得似然函数最大化,即max L(θ)。
这样得到的参数θ就是在给定数据下最合理的估计。
期望最大化算法(Expectation-Maximization,EM)是一种迭代算法,用于在潜变量模型中求解模型参数。
EM算法的基本思想是通过迭代交替进行两个步骤:E步骤(Expectation),求解潜变量的期望;M步骤(Maximization),根据求得的期望最大化似然函数。
通过反复迭代这两个步骤,最终可以得到模型的参数估计。
变分推断(Variational Inference)是一种近似推断方法,用于在概率图模型中求解后验分布。
变分推断的核心思想是通过在一些指定的分布族中寻找一个最接近真实后验分布的分布来近似求解后验分布。
具体来说,我们可以定义一个变分分布q(θ)来逼近真实的后验分布p(θ|D),然后通过最小化变分分布与真实后验分布的KL散度来求解最优的变分分布。
2. 非参数化概率图模型的推理方法非参数化概率图模型是指模型中的概率分布不是由有限的参数化形式给出,而是通过一些非参数的方式来表示概率分布,如核密度估计、Dirichlet过程等。
概率图模型的推理方法详解(六)

概率图模型的推理方法详解概率图模型是一种用于描述随机变量之间关系的工具,它能够有效地表示变量之间的依赖关系,并且可以用于进行推理和预测。
在实际应用中,概率图模型广泛应用于机器学习、人工智能、自然语言处理等领域。
本文将详细介绍概率图模型的推理方法,包括贝叶斯网络和马尔科夫随机场两种主要类型的概率图模型,以及它们的推理算法。
1. 贝叶斯网络贝叶斯网络是一种用有向无环图表示的概率图模型,它描述了变量之间的因果关系。
在贝叶斯网络中,每个节点表示一个随机变量,节点之间的有向边表示了变量之间的依赖关系。
贝叶斯网络中的概率分布可以由条件概率表来表示,每个节点的条件概率表描述了该节点在给定其父节点的取值情况下的概率分布。
在进行推理时,我们常常需要计算给定一些证据的情况下,某些变量的后验概率分布。
这可以通过贝叶斯网络的条件概率分布和贝叶斯定理来实现。
具体来说,给定一些证据变量的取值,我们可以通过贝叶斯网络的条件概率表计算出其他变量的后验概率分布。
除了基本的推理方法外,贝叶斯网络还可以通过变量消除、置信传播等方法进行推理。
其中,变量消除是一种常用的推理算法,它通过对变量进行消除来计算目标变量的概率分布。
置信传播算法则是一种用于处理概率传播的通用算法,可以有效地进行推理和预测。
2. 马尔科夫随机场马尔科夫随机场是一种用无向图表示的概率图模型,它描述了变量之间的联合概率分布。
在马尔科夫随机场中,每个节点表示一个随机变量,边表示了变量之间的依赖关系。
不同于贝叶斯网络的有向图结构,马尔科夫随机场的无向图结构表示了变量之间的无向关系。
在进行推理时,我们常常需要计算给定一些证据的情况下,某些变量的后验概率分布。
这可以通过马尔科夫随机场的联合概率分布和条件随机场来实现。
具体来说,给定一些证据变量的取值,我们可以通过条件随机场计算出其他变量的后验概率分布。
除了基本的推理方法外,马尔科夫随机场还可以通过信念传播算法进行推理。
信念传播算法是一种用于计算概率分布的通用算法,可以有效地进行推理和预测。
机器学习 —— 概率图模型(推理:连续时间模型)
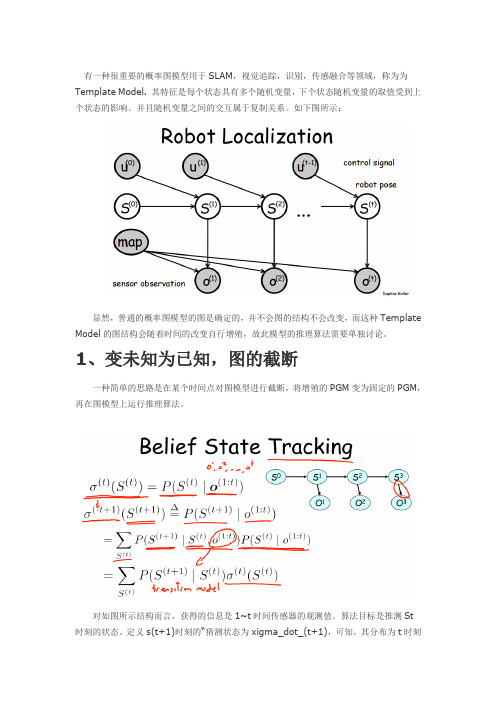
有一种很重要的概率图模型用于SLAM,视觉追踪,识别,传感融合等领域,称为为Template Model. 其特征是每个状态具有多个随机变量,下个状态随机变量的取值受到上个状态的影响。
并且随机变量之间的交互属于复制关系。
如下图所示:
显然,普通的概率图模型的图是确定的,并不会图的结构不会改变,而这种Template Model的图结构会随着时间的改变自行增殖,故此模型的推理算法需要单独讨论。
1、变未知为已知,图的截断
一种简单的思路是在某个时间点对图模型进行截断,将增殖的PGM变为固定的PGM,再在图模型上运行推理算法。
对如图所示结构而言,获得的信息是1~t时间传感器的观测值。
算法目标是推测St
时刻的状态。
定义s(t+1)时刻的“猜测状态为xigma_dot_(t+1),可知,其分布为t时刻
状态的和。
也就是t时刻取值的线性组合。
在给定t+1时刻的观测时,s(t+1)可表达为下式:
s(t+1)真正的值实际上和t+1时刻的观测,对t+1时刻的猜测,以及分母——对t+1时刻观测量的猜测有关。
分母实际上是一个跟状态无关的常数,最后求不同状态S取值比例的时候分母是可以忽略的。
所以重要的是分子。
分子和两个量有关,第一个是观测模型,第二个是t+1时刻状态猜测量。
而状态猜测量是线性组合,每次计算都可以直接带入上次结果。
所以,这种结构的Template Model算起来并不会非常困难。
机器学习 —— 概率图模型(推理:团树算法)
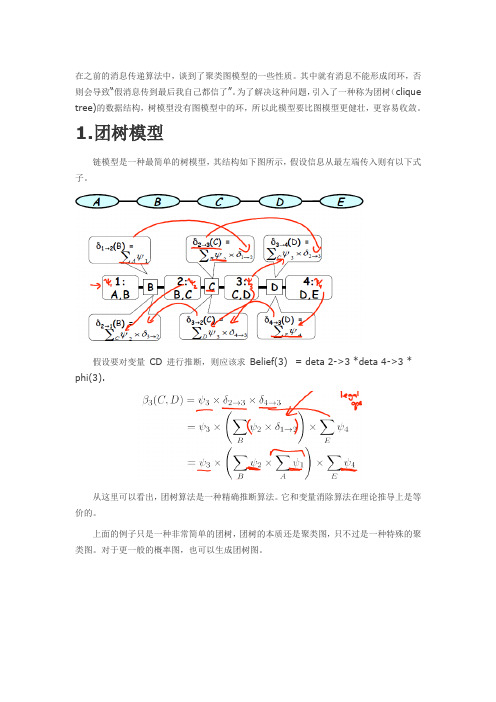
在之前的消息传递算法中,谈到了聚类图模型的一些性质。
其中就有消息不能形成闭环,否则会导致“假消息传到最后我自己都信了”。
为了解决这种问题,引入了一种称为团树(clique tree)的数据结构,树模型没有图模型中的环,所以此模型要比图模型更健壮,更容易收敛。
1.团树模型链模型是一种最简单的树模型,其结构如下图所示,假设信息从最左端传入则有以下式子。
假设要对变量CD 进行推断,则应该求Belief(3) = deta 2->3 *deta 4->3 * phi(3).从这里可以看出,团树算法是一种精确推断算法。
它和变量消除算法在理论推导上是等价的。
上面的例子只是一种非常简单的团树,团树的本质还是聚类图,只不过是一种特殊的聚类图。
对于更一般的概率图,也可以生成团树图。
其中,每个cluster都是变量消除诱导图中的一个最小map。
2.团树模型的计算从上面分析可知,团树模型本质上和变量消除算法还有说不清道不明的关系(团树模型也是精确推理模型)。
但是这个算法的优势在于,它可以利用消息传递机制达到收敛。
之前提过,聚类图模型中的收敛指的是消息不变。
除此之外,聚类图的本质是一种数据结构,它可以储存很多中间计算结果。
如果我们有很多变量ABCDEF,那么我们想知道P(A),则需要执行一次变量消除。
如果要计算P(B)又要执行一次变量消除。
如果中途得到了某个变量的观测,又会对算法全局产生影响。
但是使用团树模型可以巧妙的避免这些问题。
首先,一旦模型迭代收敛之后。
所有的消息都是不变的,每个消息都是可以被读取的。
每个团的belief,实际上就是未归一划的联合概率,要算单个变量的概率,只需要把其他的变量边际掉就行。
这样一来,只需要一次迭代收敛,每个变量的概率都是可算的。
并且算起来方便。
其次,如果对模型引入先验知识比如A = a 时,我们需要对D 的概率进行估计。
按照变量消除的思路又要从头来一次。
但是如果使用团树结构则不用,因为A的取值只影响deta1->2以及左向传递的消息,对右向传递的消息则毫无影响,可以保留原先对右向传递消息的计算值,只重新计算左向传递结果即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率图模型介绍与计算01 简单介绍概率图模型是图论和概率论结合的产物,它的开创者是鼎鼎大名的Judea Pearl,我十分喜欢概率图模型这个工具,它是一个很有力的多变量而且变量关系可视化的建模工具,主要包括两个大方向:无向图模型和有向图模型。
无向图模型又称马氏网络,它的应用很多,有典型的基于马尔科夫随机场的图像处理,图像分割,立体匹配等,也有和机器学习结合求取模型参数的结构化学习方法。
严格的说他们都是在求后验概率:p(y|x),即给定数据判定每种标签y的概率,最后选取最大的后验概率最大的标签作为预测结果。
这个过程也称概率推理(probabilistic inference)。
而有向图的应用也很广,有向图又称贝叶斯网络(bayes networks),说到贝叶斯就足以可以预见这个模型的应用范围咯,比如医疗诊断,绝大多数的机器学习等。
但是它也有一些争议的地方,说到这就回到贝叶斯派和频率派几百年的争议这个大话题上去了,因为贝叶斯派假设了一些先验概率,而频率派认为这个先验有点主观,频率派认为模型的参数是客观存在的,假设先验分布就有点武断,用贝叶斯模型预测的结果就有点“水分”,不适用于比较严格的领域,比如精密制造,法律行业等。
好吧,如果不遵循贝叶斯观点,前面讲的所有机器学习模型都可以dismiss咯,我们就通过大量数据统计先验来弥补这点“缺陷”吧。
无向图和有向图的例子如(图一)所示:图一(a)无向图(隐马尔科夫)(b)有向图概率图模型吸取了图论和概率二者的长处,图论在许多计算领域中扮演着重要角色,比如组合优化,统计物理,经济等。
图的每个节点都可看成一个变量,每个变量有N个状态(取值范围),节点之间的边表示变量之间的关系,它除了可以作为构建模型的语言外,图还可以评价模型的复杂度和可行性,一个算法的运行时间或者错误界限的数量级可以用图的结构性质来分析,这句话说的范围很广,其实工程领域的很多问题都可以用图来表示,最终转换成一个搜索或者查找问题,目标就是快速的定位到目标,试问还有什么问题不是搜索问题?树是图,旅行商问题是基于图,染色问题更是基于图,他们具有不同的图的结构性质。
对于树的时间复杂度我们是可以估算出来的,而概率图模型的一开始的推理求解方法也是利用图的结构性质,把复杂图转换成树(容易处理的图)的形式来求解,这个算法被称为联合树算法(junction tree algorithm)。
联合树算法简单的说就是利用图的条件独立性质把图分解,然后以树的形式组织,最后利用树的良好操作性进行推理求解(消息传递),联合树算法是后续章节的重要的推理算法之一。
但并不是所有的图都能拆分成树的形式,一般只有合适的稀疏边的图才能转成树,因此联合树算法也有一定的限制。
不能构建联合树,那怎么推理求解?好在还有其他几种方法,概率图模型的第二个成分:概率,既然进入了概率空间,那基于蒙特卡洛(MCMC)的采样方法也就可以使用了,反正就是求最大后验概率,MCMC的求解方法也是经常利用的工具,还有一些基于均值场(mean field)以及变分方法(variational method)的求解工具。
这几个求解方法的算法复杂度比较如(图二)所示:(图二) 推理求解算法性能比较(图二)中的几种求解方法也都是概率图模型或者统计机器学习里经常使用的方法,MCMC方法和变分方法都起源于统计物理,最近很火的深度学习也算是概率图模型的一个应用,尽管你要反对,我也要把它划到概率图模型下^.^,RBM,CRBM,DBM都是很特殊的概率图模型,整个思路从建模到求解方法都是围绕着求取图模型节点的最大后验概率来开展的。
MCMC求解方法就不说了,深度学习里已经用的很多咯,而变分方法(variational method)很有吸引力,andrew ng的师傅Michael Jordan认为把变分方法用在统计机器学习中的有希望的方法是把凸分析和极家族分布函数链接起来,既然有凸分析,那么就会伴随着凸松弛(convex relaxtion),因为数据是离散的,具体可以看前面的关于凸松弛的博文介绍。
另外还有一些图模型特有的求解方法,比如beliefpropagation(sum-product algorithm)n或者expectation propagation等求解方法。
上面算是对概率图模型做了个简单的介绍,接下的来的博文就是按照下面的提纲来记录一下学习笔记,在尽量不违背honor code的情况下,用原来Daphne koller教授的作业来做辅助介绍。
一、介绍图模型定义二、利用基于变分方法的极家族和凸分析来求边缘概率三、逼近求解方法,如belief-propagation、expectation-propagation等四、均值场求解方法等各种优化求解方法五、结构化学习02 概率图模型定义翻开Jordan和Wainwright著作的书,正文开始(第二章)就说概率图模型的核心就是:分解(factorization)。
的确是这样的,对于复杂的概率图模型,要在复杂交织的变量中求取某个变量的边缘概率,常规的做法就是套用贝叶斯公式,积分掉其他不相干的变量,假设每个变量的取值状态为N,如果有M个变量,那么一个图模型的配置空间就有N^M,指数增长的哦,就这个配置空间已经让我们吃不消了,不可以在多项式时间内计算完成,求边缘概率就没办法开展下去了。
此时分解就派上用场咯,我们想法找到一些条件独立,使得整个概率图模型分解成一个个的团块,然后求取团块的概率,这样就可以把大区域的指数增长降为小区域的指数增长。
毕竟100^20这样的计算量比25*(4^20)的计算量大多咯。
好了,不说这么抽象了,下面进入正题:(图一)(图二)无向图模型又称马尔科夫随机场(markov random filed)无向图模型的分解就是通过团块(clique)来完成,所谓团块就是全连接的最大子图,如(图二)所示,(a)图的{1,2,3,4},{4,5,6},{6,7}都是全连接的最大子图,假设团块用C表示,为每个团块分配一个兼容函数(compatibility function),它的作用就是把团块取值状态映射到正实值空间,说白了就是给这个团块一个度量,可以是概率,也可以是取值状态和真实标签之间的差值平方和,根据应用而定,这个兼容函数有时又被称为势函数(potential function),有了兼容函数,无向图模型就可以通过(公式二)分解:(公式二)(公式二)中的Z是归一化的常量,学名叫配分函数(partition function),一归一化就成概率了,不归一化不满足概率和为1的性质。
为了能在图模型中直观的看到团块,可以用因子图(factor graph)来表示无向图模型,如(图二)(b)所示,和黑块连接的顶点表示全部互相连接(全连接),一个黑块部分表示一个团块,所以上面分解又多了一个名字:因子分解(factorization)。
上面说了很多枯燥的定义,目标只有一个,引出两种图模型的分解公式:(公式一)和(公式二),那为什么可以分解成那个样子?现在通过两个小例子说明一下:对于有向图模型,如(图三)所示模型,一个人的聪明程度(Intelligence)可以影响他的年级(Grade:痴呆的读高年级的概率低,聪明的一般走的比较远),而且对他的成绩(SAT)也有高低影响。
当我们知道一个人的聪明度后,年级和成绩还有关系吗?二本就根本没有关系,在这里不要想多,其实很简单,给定一个物体后,那么这个物体上的两个属性值就决定了,已经存在的事实,所以二者是独立的。
朴素贝叶斯就是根据这个条件独立做的分解。
(图三)另外注意一下,这里给定的是父亲节点,(公式一)中也强调了这点,如果不给父亲节点,条件独立就变的稍微复杂一些,如(图四)中有一个比(图三)稍微复杂一些的有向图模型:(图四)在(图四)中Difficulty表示试卷难度,Intelligence表示考生聪明度,如果什么都不给,这二者是独立的,因为试卷难度和考生没有关系,所谓的高考很难,但是这跟我有什么关系?我又不参加高考^.^,但是如果一旦给定空考生的年级(grade),情况就变得不一样了,比如考生考到了博士,如果他不聪明,那说明啥?说明卷子不难,水的很,如果卷子很难,考生一定很聪明,所以这中间有个因果推理关系。
这就是Judea peal提出的explain away问题(Even if two hidden causes are independent in the prior, they can become dependent when we observe an effect that they can both influence),在前面的博文《目标检测(ObjectDetection)原理与实现(三)》也解释了这个问题,如果这个例子没有解释清楚,可以看下前面的例子。
对于无向图模型的条件独立就要简单一些,是从图论的可达性(reachability)考虑,也可从图的马尔科夫性入手,如(图五)所示:(图五)(图五)是个标准的隐马尔科夫模型(HMM),当给定X2时,就相当于在X2除切了一刀,在X2前后之间的变量都相互独立。
独立就可以分解了,比如条件概率独立公式:P(A,B|C)=P(A|C)*P(B|C),团块兼容函数也是如此。
如果X1-X5我们都给定,那这个模型分解的团块都是相似的,每个图块都可以用一个通用的标记来表示,因此图模型里又提了一种盘子表示法(plate notation),如(图六)所示:(图六)(图六)不是表示的HMM的盘子模型,而是LDA模型的盘子模型,只是让大家了解一下通用分解模版的表示方法,其实很多时候这个表示方法反而不是那么清晰,南加州大学有一个做机器学习的博士生就在吐槽这个表示方法,有兴趣的可以去看看(链接)。
今天算是了解一下概率图模型的基本定义和两个分解公式,这两个分解公式只是给出了图模型不好求概率的一个解决方法的切入点,下节就来学习一下概率图模型如何通过分解来进行边缘概率推理求解。
03 图模型推理算法这节了解一下概率图模型的推理算法(Inference algorithm),也就是如何求边缘概率(marginalization probability)。
推理算法分两大类,第一类是准确推理(Exact Inference),第二类就是近似推理(Approximate Inference)。
准确推理就是通过把分解的式子中的不相干的变量积分掉(离散的就是求和);由于有向图和无向图都是靠积分不相干变量来完成推理的,准确推理算法不区分有向图和无向图,这点也可以在准确推理算法:和积算法(sum-product)里体现出来,值得一提的是有向图必须是无环的,不然和积算法不好使用。
