第6章 西姆松定理及应用(含答案)
概率论与数理统计课后答案第6章

概率论与数理统计课后答案第6章第6章习题参考答案1.设是取⾃总体X的⼀个样本,在下列情形下,试求总体参数的矩估计与最⼤似然估计:(1),其中未知,;(2),其中未知,。
2.设是取⾃总体X的⼀个样本,其中X服从参数为的泊松分布,其中未知,,求的矩估计与最⼤似然估计,如得到⼀组样本观测值X 0 1 2 3 4频数17 20 10 2 1求的矩估计值与最⼤似然估计值。
3.设是取⾃总体X的⼀个样本,其中X服从区间的均匀分布,其中未知,求的矩估计。
4.设是取⾃总体X的⼀个样本,X的密度函数为其中未知,求的矩估计。
5.设是取⾃总体X的⼀个样本,X的密度函数为其中未知,求的矩估计和最⼤似然估计。
6.设是取⾃总体X的⼀个样本,总体X服从参数为的⼏何分布,即,其中未知,,求的最⼤似然估计。
7. 已知某路⼝车辆经过的时间间隔服从指数分布,其中未知,现在观测到六个时间间隔数据(单位:s):1.8,3.2,4,8,4.5,2.5,试求该路⼝车辆经过的平均时间间隔的矩估计值与最⼤似然估计值。
8.设总体X的密度函数为,其中未知,设是取⾃这个总体的⼀个样本,试求的最⼤似然估计。
9. 在第3题中的矩估计是否是的⽆偏估计?解故的矩估计量是的⽆偏估计。
10.试证第8题中的最⼤似然估计是的⽆偏估计。
11. 设为总体的样本,证明都是总体均值的⽆偏估计,并进⼀步判断哪⼀个估计有效。
12.设是取⾃总体的⼀个样本,其中未知,令,试证是的相合估计。
13.某车间⽣产滚珠,从长期实践中知道,滚珠直径X服从正态分布,从某天⽣产的产品中随机抽取6个,量得直径如下(单位:mm):14.7,15.0,14.9,14.8,15.2,15.1,求的0.9双侧置信区间和0.99双侧置信区间。
14.假定某商店中⼀种商品的⽉销售量服从正态分布,未知。
为了合理的确定对该商品的进货量,需对和作估计,为此随机抽取七个⽉,其销售量分别为:64,57,49,81,76,70,59,试求的双侧0.95置信区间和⽅差的双侧0.9置信区间。
托勒密定理和西姆松定理(一)

【例3】⑵由△ABC外接圆的弧BC上一点P分别向边BC、AC 与AB作垂线PK、PL和PM。 BC AC AB 求证: 求 PK PL PM
3
1
【例1】⑶等腰梯形一条对角线的平方,等于一腰的平方加上 两底之积。已知,梯形ABCD,AD=BC,AB∥ CD,求证: BD2=BC2+AB·CD。
【例2】⑵如图,已知圆的内接正五边形ABCDE,P为 BC 上 的一点,则 的 点,则PA+PABCD中,∠ABC=60°,∠BAD= ∠BCD=90°, ,AB=2,CD=1,对角线AC、BD 交于点O,如图,求sin∠AOB。
【例1】⑴证明 明托勒密定 托勒密定理及其逆定理。 及其逆定 ①四边形ABCD内接于圆, 求证: AC·BD=AD·BC+AB·CD。
(
【例1】⑴证明托勒密定理及其逆定理。 ②四边形ABCD满足, AC·BD=AD·BC+AB·CD,求 证:四边形ABCD 是圆内接四边形。
【例1】⑵如图,已知P为正△ABC外接圆 BC 上一点, 求证: PA=PB+PC
托勒密定理和西姆松定理(一)
托勒密定理 托勒密定 托勒密定理:圆内接四边形两条对角线乘积等于两组对边乘积 圆内接 边形两条对角线乘积等 两组对边乘积 之和。 逆定理:一个凸四边形的两组对边乘积的和等于其对角线的乘 积,那么该四边形内接于一个圆 积,那么该四边形内接于 个圆(或者说该四边形的四个顶点共 圆) 广义定理 对于 般的四边形ABCD,有 广义定理:对于一般的四边形 有AB·CD+ AD·BC≥AC·BD,当且仅当ABCD是圆内接四边形时等号成立。
水力学第六章课后习题答案

7.14虹吸管将A 池中的水输入B 池,已知长度1l =3m ,2l =5m ,直径d =75mm ,两池水面高差H =2m ,最大超高h =1.8m ,沿程摩阻系数λ=0.02,局部损失系数:进口a ζ=0.5,转弯b ζ=0.2,出口c ζ=1,试求流量及管道最大超高断面的真空度。
解: 以下游水面为基准面,从上池水面到下池水面列伯努利方程:22222350.7 1.00.0222220.0752v l v v v v H g d g g g gζλζζ+⎛⎫=+++=++⨯ ⎪⎝⎭b c 进∴ 3.20v ==(m/s )23.200.07514.144Q vA π==⨯⨯=(L/s )从C 过流断面到下池水面列伯努利方程:2222222C C C C Cp v l v v z g g d g gαλζρ++=+ 取1C α= ∵C v v =∴251.8 2.010.02 1.00.0752a C C V p p p vH g g g ρρ-⎛⎫==-=++-⨯- ⎪⎝⎭25 3.203.80.02 3.100.07529.807=-⨯⨯=⨯m答:流量14.14Q =L/s ,管道最大超高断面的真空度为3.10m 。
7.16水从密闭容器A ,沿直径d =25mm ,长l =10m 的管道流入容器B ,已知容器A 水面的相对压强1p =2at ,水面高1H =1m ,2H =5m ,沿程摩阻系数λ=0.025,局部损失系数:阀门v ζ=4.0,弯头b ζ=0.3,试求流量。
解: 以地面为基准面,从A 池面到B 池面列伯努利方程:222111222123222v b p v p v l v H H g g g g d g ααζζζζλρρ⎛⎫++=+++++++ ⎪⎝⎭进出取120v v ==;20p =;0.5ζ=进; 1.0ζ=出,则有121122100.5 1.0 4.030.30.0250.025p g H H g v ρ⎡⎤⎛⎫+-⎢⎥⎪⎝⎭⎢⎥=⎢⎥⎛⎫+++⨯+⨯ ⎪⎢⎥⎝⎭⎣⎦ ()122120516.4g ⨯+-⎡⎤=⎢⎥⎣⎦4.37=(m/s )24.370.025 2.154Q vA π==⨯⨯=(l /s )答:流量 2.15Q =l /7.17水车由一直径d =150mm ,长l =80m 的管道供水,该管道中有两个闸阀和4个90°弯头(λ=0.03,闸阀全开a ζ=0.12,弯头b ζ=0.48)。
大学物理第6章习题参考答案

第六章习题解答6-1 解:首先写出S 点的振动方程 若选向上为正方向,则有:0c o s02.001.0ϕ=- 21cos 0-=ϕ,0s i n 00>-=ϕωυA 0sin 0<ϕ 即 πϕ320-=或π34 初始相位 πϕ320-=则 m t y s )32cos(02.0πω-=再建立如图题6-1(a)所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为: ux t =∆则该波的波动方程为:m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0若坐标原点不选在S 点,如习题6-1图(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为: uL x t -=∆则该波的波方程为:m uL x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0若P 点选在S 点左侧,P 点比S 点超前时间为ux L -,如习题6-1图(c)所示,则⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0u x L t y⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t∴不管P 点在S 点左边还是右边,波动方程为: ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t y6-2 解(1)由习题6-2图可知, 波长 m 8.0=λ 振幅A=0.5m习题6-1图习题6-1图频率 Hz 125Hz 8.0100===λuv周期 s 10813-⨯==vT ππυω2502==(2)平面简谐波标准波动方程为: ⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u xt A y 由图可知,当t=0,x=0时,y=A=0.5m ,故0=ϕ。
将ϕπωω、、、u v A )2(=代入波动方程,得:m )100(250cos 5.0⎥⎦⎤⎢⎣⎡-=x t y π(3) x =0.4m 处质点振动方程.⎥⎦⎤⎢⎣⎡-=)1004.0(250cos 5.0t y π m )250cos(5.0ππ-=t6-3 解(1)由习题6-3图可知,对于O 点,t=0时,y=0,故2πϕ±=再由该列波的传播方向可知,00<υ取 2πϕ=由习题6-3图可知,,40.0m OP ==λ且u=0.08m/s ,则ππλππω52rad/s 40.008.0222====u v rad/s可得O 点振动表达式为:m t y )252cos(04.00ππ+=(2) 已知该波沿x 轴正方向传播,u=0.08m/s,以及O 点振动表达式,波动方程为:m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ(3) 将40.0==λx 代入上式,即为P 点振动方程:m t y y p ⎥⎦⎤⎢⎣⎡+==ππ2152cos 04.00 (4)习题6-3图中虚线为下一时刻波形,由图可知,a 点向下运动,b 点向上运动。
四个重要定理(梅涅劳斯,塞瓦,托勒密,西姆松)

四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是 。
塞瓦(Ceva)定理(塞瓦点)△ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1. 设AD是△ABC的边BC上的中线,直线CF交AD于F。
求证:。
【分析】CEF截△ABD→(梅氏定理)【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。
2. 过△ABC的重心G的直线分别交AB、AC于E、F,交CB于D。
求证:。
【分析】连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→(梅氏定理)DGF截△ACM→(梅氏定理)∴===1【评注】梅氏定理3. D、E、F分别在△ABC的BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅氏定理4. 以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5. 已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6. 已知正七边形A1A2A3A4A5A6A7。
求证:。
(第21届全苏数学竞赛)【分析】【评注】托勒密定理7. △ABC的BC边上的高AD的延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F。
求证:BC·EF=BF·CE+BE·CF。
第六章_分析力学_习题解答

6.1、一长为0l 、质量为m 的匀质棒,斜靠在固定的半球形碗的边缘,一端置于碗内,如图示。
已知碗是光滑的,半径为r ;棒在碗内的长度为(2)l l r <。
用虚功原理证明棒的全长为2204(2)l r l l-=。
6.2、用绳子等距离地在定点O 处悬挂两个相同的匀质球。
两球之上另旋转一相同的球体,如图示。
已知分别悬挂两球的绳长都是l ,用虚功原理求出α角与β角之间的关系。
6.3、用轻质橡皮圈捆扎三个置于光滑水平桌面上的相同球体,捆扎的高度与球心的高度相同。
将第四个同样的球体置于三球之上,由虚功原理求出橡皮圈中的张力。
已知每个球体的重量为P6.4、一弹性绳圈,它的自然长度为0l ,弹性系数为k ,单位长度质量(线密度)为σ。
将此弹性圈套在一半径为0(2)R R l π>的光滑球面上,弹性圈因自重而下滑。
用虚功原理求出平衡时弹性绳圈对球心所张的角度θ应满足的方程。
6.5、一半径为R 的半球形碗内装有两个质量分别为1m 和2m 的球体,它们的半径同为(2)r r R <。
用虚功原理求出这两个球体在碗中平衡时它们的连心线与水平线间的夹角。
6.6、一轻杆长为2l ,一端光滑铰链于固定点O ,另一端点及中点分别焊接有质量为'm 和m 的小球。
杆可在铅直平面内绕固定点摆动。
写出此力学系统的拉格朗日函数,并求出其作微小摆动时的周期。
6.7、一半径为r 、质量为'm 的圆柱形轱辘,其轴线沿水平方向。
轱辘上绕有长为l 的轻绳,绳的自由端系一质量为m 的重物。
初始时绳子完全绕在轱辘上,体系静止。
尔后重物下落带动轱辘转动。
写出此力学系的拉格朗日函数,并求出绳子完全释放时轱辘转动角速度的大小。
6.8、上题中,如果绳子具有弹性,弹性势能为2/2ks ,s 为绳子的伸长。
证明重物m 的运动为维持恒定的加速运动上附加一角频率为ω的振动,其中2('2)/'k m m m m ω=+。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
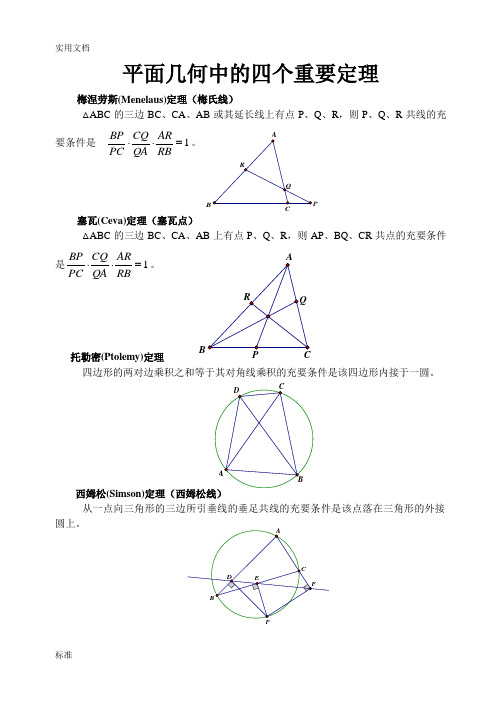
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
数理统计课后答案-第六章
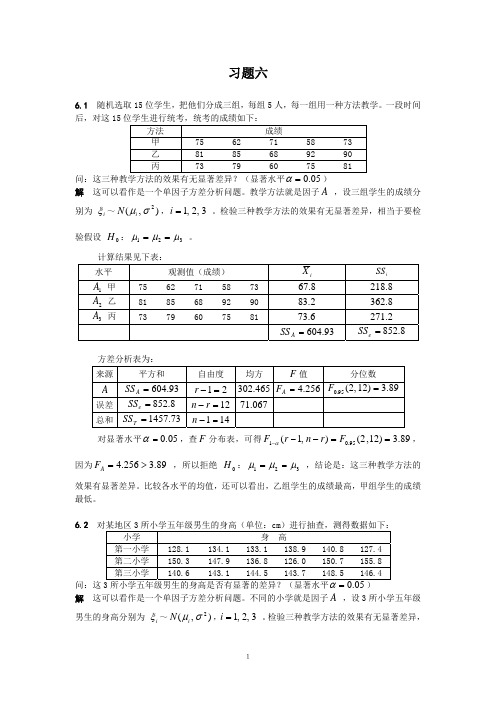
r
,
SST =
∑ j∑ ( i
=1 =1
X ij − X ,SSe =
)
2
∑ j∑ ( i
=1
X ij − X i
)
2
∑ SS i ,SS A =
i =1
ni ( X i ∑ i
r
=1
−X
)
2
可以证明离差分解公式: SST = SS e + SS A ,以及在 H 0 : μ1 = μ2 = ... = μr 成立时有
58 92 75
67.8 83.2 73.6 SS A = 604.93
218.8 362.8 271.2 SS e = 852.8
方差分析表为: 来源 平方和 自由度
A
误差 总和
SS A = 604.93
SS e = 852.8
SS T = 1457.73
r −1 = 2 n − r = 12 71.067 n − 1 = 14
ξ i ~ N ( μ i , σ 2 ) ,i = 1, 2, 3 。 检验三种教学方法的效果有无显著差异,
1
相当于要检验假设 H 0 : μ1 = 计算结果见下表: 水平
μ 2 = μ3 。
Xi
133.7333 144.5833
SS i
观测值(身高) 128.1 134.1 133.1 138.9 140.8 127.4 150.3 147.9 136.8 126.0 150.7 155.8 140.6 143.1 144.5 143.7 148.5 146.4
ξ i j ~ N (μ i j , σ 2 ) , 其中, μi j = μ + αi + β j , i = 1, 2, 3, 4 ,j = 1, 2, 3 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章西姆松定理及应用【基础知识】西姆松定理 过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足点共线(此线常称为西姆松线).证明如图6-1,设P 为ABC △的外接圆上任一点,从P 向三边BC ,CA ,AB 所在直线作垂线,垂足分别为L ,M ,N .连PA ,PC ,由P ,N ,A ,M 四点共圆,有βαγβLMAPBNC图6-1PMN PAN PAB PCB PCL ∠=∠=∠=∠=∠.又P ,M ,C ,L 四点共圆,有PML PCL ∠=∠. 故PMN PML ∠=∠,即L ,N ,M 三点共线. 注 此定理有许多证法.例如,如下证法:如图6-1,连PB ,令PBC α∠=,PCB β∠=, PCM γ∠=,则PAM α∠=,PAN β∠=,PBN γ∠=,且cos BL PB α=⋅,cos LC PC β=⋅,cos CM PC γ=⋅, cos MA PA α=⋅,cos AN PA β=⋅,cos NB PB γ=⋅.对ABC △,有cos cos cos 1cos cos cos BL CM AN PB PC PA LC MA NB PC PA PB αγββαγ⋅⋅⋅⋅⋅=⋅⋅=⋅⋅⋅.故由梅涅劳斯定理之逆定理,知L ,N ,M 三点共线.西姆松定理还可运用托勒密定理、张角定理、斯特瓦尔特定理来证(略).西姆松定理的逆定理 若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上. 证明如图6-1,设点P 在ABC △的三边BC ,CA ,AB 所在直线上的射影分别为L ,M ,N ,且此三点共线.由PN AB ⊥于N ,PM AC ⊥于M ,PL BC ⊥于L ,知P ,B ,L ,N 及P ,N ,A ,M 分别四点共圆,而AB 与LM 相交于N ,则PBC PBL PNM PAM ∠=∠=∠=∠,从而P ,B ,C ,A 四点共圆,即点P 在ABC △的外接圆上. 【典型例题与基本方法】1.找到或作出三角形外接圆上一点在三边上的射影,是应用西姆松定理的关键例1如图6-2,过正ABC △外接圆的AC 上点P 作PD ⊥直线AB 于D ,作PE AC ⊥于E ,作PF BC ⊥于F .求证:111PF PD PE+=.PEFABCD图6-2证明由PD ⊥直线AB 于D ,PE AC ⊥于E ,PF BC ⊥于F ,知A ,E ,P ,D 及E ,F ,C ,P 分别四点共圆,则60DPE BAE ∠=∠=︒,60EPF ECF ∠=∠=︒. 由西姆松定理,知D ,E ,F 三点共线,从而以P 为视点,对PDF △应用张角定理,有sin sin sin DPF DPE EPF PE PF PD ∠∠∠=+,即sin120sin60sin60PE PF PD ︒︒︒=+,故111PF PD PE+=. 例2如图6-3,设AD ,BE ,CF 为ABC △的三条高线,自D 点作DP AB ⊥于P ,DQ BE ⊥于Q ,DR CF ⊥于R ,DS AC ⊥于S ,连PS .求证:Q ,R 在直线PS 上. QHES R ABDCPF 图6-3证明由于BFH △的外接圆为BDHF ,而D 为该圆上一点,且D 在BFH △三边所在直线上的射影分别为P ,Q ,R ,于是,由西姆松定理知P ,Q ,R 三点共线. 同理,可证Q ,R ,S 是HEC △的西姆线上三点.由于直线PQR 与直线QRS 有两个公共点Q ,R ,所以这两直线重合,故Q ,R 在直线PS 上. 例3如图64-,设P 为ABC △外接圆上一点,作PA BC '⊥交圆周于A ',作PB '⊥直线AC 交圆周于B ',作PC AB '⊥交圆周于C '.求证:AA BB CC '''∥∥.L MPNAB C C 'B'A'图6-4证明设PA BC '⊥于L ,PB '上直线AC 于N ,PC AB '⊥于M ,则由西姆松定理知L ,M ,N 三点共线.注意到L ,B ,P ,M 及A ',B ,P ,A 分别四点共圆,连BP ,则 AMN BML BPL BPA BAA ''∠=∠=∠=∠=∠,于是AA LN '∥.同样,注意到A ,B ,P ,B '及A ,M ,P ,N 分别四点共圆,连PA ,则ABB APB APN AMN ''∠=∠=∠=∠,于是BB LN '∥.由A ,P ,C ',C 四点共圆,知180ACC APC ''∠+∠=︒.注意到APC APM ANM CNM '∠=∠=∠=∠,则180ACC CNM '∠+∠=︒,于是CC LM '∥,故AA BB CC '''∥∥.例4如图6-5,设P 为ABC △外接圆上BC 内一点,过P 作PD ⊥BC 于D ,作PF ⊥直线AB 于F ,设H 为ABC △的垂心.延长PD 至P ',使PD P D '=.求证:HP DF '∥.(1979年山西省竞赛题改编) MA'H P'PABCD FE H '图6-5证明连AH 并延长交BC 于A ',交圆于H ',则由HCB BAH BCH ''∠=∠=∠,知HA A H '''=.又由已知PP BC '⊥,且P D DP '=,连PH ',则知PH '与P H '关于BC 对称,从而PH H P HH '''∠=∠. 由于从P 点已向ABC △的两边所在直线AB ,BC 引了垂线PF ,PD ,再过点P 向边AC 所在直线作垂线PE ,垂足为E ,则由西姆松定理,知F ,D ,E 三点共线,设西姆松线EF 与HA '交于M .此时,又由P ,C ,E ,D 四点共圆,有CPE CDE ∠=∠.在Rt PCE △中,CPE ∠与PCE ∠互余;在Rt MDA '△中,A DM CDE '∠=∠与DMA '∠互余.故DMA PCE PCA PH H P HH ''''∠=∠=∠=∠=∠,由此即知HP EF '∥,故HP DF '∥.例5如图66-,设P 为ABC △外接圆上一点,过点P 分别作PL BC ⊥于L ,作PN ⊥直线AB 于N ,直线LN 交BC 边上的高线于K ,设H 为ABC △的垂心.求证:PK LH ∥.FPM HS Q BD G L CA K 图6-6N证明由于从P 点引了ABC △的边BC ,BA 所在直线的垂线,再过P 点作PM AC ⊥于M ,则由西姆松定理,知L ,M ,N 三点共直线,即L ,M ,N ,K 四点共线.设BC 边上的高线为AD ,延长AD 交圆于F ,连PF 交BC 于G ,交西姆松线NL 于Q ,连PH 交西姆松线NL 于S .由P ,C ,L ,M 四点共圆及A ,F ,C ,P 共圆,连PC ,则MLP MCP AFP LPF ∠=∠=∠=∠,从而QP QL =,即Q 为Rt PLG △的斜边PG 的中点.连HG ,由DFC ABC DHC ∠=∠=∠,知HD DF =,有HGD DGF LGP QLG ∠=∠=∠=∠,从而HG ML ∥,即SQ 是PHG △的中位线,亦即HS SP =. 又PL KH ∥,有LPS KHS ∠=∠及PSL HSK ∠=∠,于是PSL HSK △△≌,即有PL KH ∥,亦即四边形PKHL 为平行四边形,故PK LH ∥.注由此例可得,三角形外接圆周上一点P 与垂心H 的连线段PH ,被关于P 点的西姆松线所平分,这是西姆松线的一条重要性质.2.注意发现四点共圆与三点共线的联系,灵活应用西姆松定理及其逆定理例6如图67-,延长凸四边形ABCD 的边AB ,DC 交于E ,延长AD ,BC 交于F .试证:BCE △,CDF △,ADE △,ABF △的四个外接圆共点.EMPRSDB CA 图6-7FQ证明设BCE △与CDF △的两个外接圆除交于点C 外,另一交点为M .设点M 在直线BE ,EC ,BC 上的射影分别为P ,Q ,R ,则由西姆松定理,知P ,Q ,R 三点共线.同样,M 点在直线DC ,CF ,DF 上的射影Q ,R ,S 也三点共线,故P ,Q ,R ,S 四点共线. 在ADE △中,P 在AE 上,Q 在DE 上,S 在边AD 所在直线上,且P ,Q ,S 三点共线,则由西姆松定理的逆定理,知M 点在ADE △的外接圆上.在ABF △中,P 在直线AB 上,R 在BF 上,S 在AF 上,且P ,R ,S 三点共线,由西姆松定理的逆定理,知M 点在ABF △的外接圆上.故BCE △,CDF △,ADE △,ABF △的四个外接圆共点.注此例题的结论实际为宪全四边形ABECFD 的四个三角形AED △、BEC △、CFD △、ABF △的外接圆共点,此点称为密克尔(Miquel )点,直线PQRS 称为完全四边形的西姆松线. 【解题思维策略分析】 1.证明点共线的又一工具例7如图68-,设P 为四边形1234A A A A 外接圆上任一点,点P 在直线12A A ,23A A ,34A A ,41A A ,上的射影分别为1B ,2B ,3B ,4B ,又点P 在直线12B B ,23B B ,34B B ,41B B 上的射影分别为1C ,2C ,3C ,4C .求证:1C ,2C ,3C ,4C 共线.Q PB 1B 4B 3B 2C 4C 3C 2C 1A 2A 3A 4A 1图6-8证明连13A A ,过P 作13A A 的垂线,垂足为Q .从而,点P 关于123A A A △的西姆松线为12B B Q 同样,点P 关于134A A A △的西姆松线为34B QB .由14111A B P AQP A B P ∠=∠=∠,知点P 在14QB B △的外接圆上,由西姆松定理,知点P 在14QB B △三边上的垂足1C ,3C ,4C 共线. 同理,1C ,2C ,4C 三点也共线.故1C ,2C ,3C ,4C 四点共线(此直线称为P 点圆内接四边形关于1234A A A A 的西姆松线). 2.注意西姆松线在转化问题中的媒介作用例8如图69-,设P 为ABC △外接圆周上任一点,P 点关于边BC ,AC 所在直线的对称点分别为1P ,2P .求证:直线12P P 经过ABC △的垂心H .P 2P 1BHLC P图6-9N证明由于1P ,2P 分别为P 点关于直线BC ,AC 的对称点,设1PP 交直线BC 于L ,2PP 变直线AC 于N ,则L ,M 分别为P 点在ABC △的边BC ,CA 所在直线上的射影,且L ,N 分别为线段1PP ,2PP 的中点.由西姆松定理,知LN 为西姆松线,此时2LN PP ∥.又由前面例5知,当H 为ABC △的垂心时,直线LN 平分线段PH .于是,可知H 点在直线12P P 上,即直线12P P 经过H 点.例9如图610-,一条直线L 与圆心为O 的圆不相交,E 是l 上一点,OE l ⊥,M 是l 上任意异于E 的点,从M 作O 的两条切线分别切圆于A 和B ,C 是MA 上的点,使得EC MA ⊥,D 是MB 上的点,使得ED MB ⊥,直线CD 交OE 于F .求证:点F 的位置不依赖于M 的位置.(IMO 35-预选题)图6-10M l E证明令OE a =,O 的半径为R ,连结EA ,EB ,OA ,OB ,OM ,AB ,设AB 交OM 于G ,交OE 于Q ,则,OA MA ⊥,OB MB ⊥,OM ⊥AB .由射影定理,得2OG OM OB ⋅=,又由M ,E ,Q ,G 四点共圆,有22OQ OE OG OM OB R ⋅=⋅==,从而知2R OQ a=,由2OB OQ OE =⋅,有OEB OBQ △∽△,既有BEO OBQ BAO ∠=∠=∠,即123∠=∠=∠.由此得(901)903180MEB MAB ∠+∠=︒+∠+︒-∠=︒(),故A ,B ,E ,M 四点共圆.作EN AB ⊥交AB 的延长线于N ,由西姆松定理,知C ,D ,F ,N 四点共线.注意到A ,N ,E ,C 与A ,O ,E ,M 均四点共圆,有ENF EAM EOM ∠=∠=∠又由EN OM ∥,有ENF NEF ∠=∠,故ENF NEF ∠=∠.在Rt NEQ △中,由上推知F 为EQ 的中点,因此,()2211===222a R EF EQ OE OQ a--.故F 的位置不依赖于M 的位置.例10已知锐角ABC △,CD 是过点C 的高线,M 是边AB 的中点,过M 的直线分别与CA 、CB 交于点K 、L ,且CK CL =.若CKL △的外心为S ,证明:SD SM =.(2003年波兰奥林匹克题)证明如图6-11,作ABC △的外接圆,延长CS 交ABC 于点T ,联结TM ,作TK AC '⊥于点K ',TL BC '⊥于点L '.图6-11L'LSDB MAK 'K C注意到S 为KLC △的外心,且KC LC =,所以CS 为KCL ∠的平分线.于是T 为弧AB 的中点. 又M 为AB 的中点,则TM AB ⊥.由西姆松定理,知K '、M 、L '三点共线.又CT 是K CL ''∠的角平分线,且K '、L '、M 三点共线,则CK CL ''=.即直线K ML ''是过M 与CT 垂直的直线,又直线KML 也是过M 与CS 垂直的直线,从而K '与K 重合,L '与L 重合.即90CKT CLT ∠=∠=︒,亦即知C 、K 、T 、L 四点共圆.故S 为四边形CKTL 的外接圆圆心,即有SC ST =,于是S 为TC 的中点.又CD AB ⊥,则CD MT ∥.故SM SD =. 3.注意西姆松线性质的应用三角形外接圆上一点的西姆松线平分该点与三角形垂心的连线. 此性质已在例5给出一种证法,现另证如下: 如图6-12,设H 为ABC △的垂心,P 为其外接圆上一点,作HBC △的外接圆HBC ,则该圆与ABC 关于BC 对称(参见垂心性质7).P'LHQM PABCN图6-12设点P 的垂足线(即西姆松线)为LMN ,由P 、B 、L 、M 四点共圆,有PLM PBM ∠=∠ 设HBC 与直线PL 交于点P '、Q ,则L 为PP '的中点,连HP ',由LP H QH '∠=的度数PA =的度数PBA PBM PLM =∠=∠=∠,知P H LMN '∥.由此即知PH 被直线LMN 平分. 例11如图613-,由ABC △的顶点A 引另两顶点B 、C 的内、外角平分线的垂线,垂足分别为F 、G 、E 、D ,则F 、G 、E 、D 四点共线,且此线与ABC △的中位线重合.IFGE DBCKLA图6-13证明延长BE 、CD 相交于点K ,设CG 与BE 相交于点I ,则I 为ABC △的内心.由1=2CAI A ∠∠,1119090222CKI CIK B C A ⎛⎫∠=︒-∠=︒-∠+∠=∠ ⎪⎝⎭,知A 、I 、C 、K 四点共圆.对ICK △及点A 应用西姆松定理,知G 、E .D 三点共线.图6-13同理,对BCL △及点A 应用西姆松定理,知F 、G 、E 三点共线. 故F 、G 、E 、D 四点共线.由于C 为ICK △的垂心,则由西姆松线的性质知直线GED 平分AC .同理,直线FGE 平分AB ,故直线FD 与ABC △的中位线重合.注由例11再回过来看例2,在例2中,是由点D 引DEF △另两个顶点E .F 的内、外角平分线的垂线,垂足分别为P 、Q 、R 、S .4.注意西姆松定理与托勒密定理的等价性 可用西姆松定理证明托勒密定理:如图614-,ABCD 为任意圆O 内接凸四边形,连AC ,过D 向ABC △各边作垂线,AB ,AC ,BC 所在直线上的垂足分别为1C ,1B ,1A ,连11C B ,11B A ,由西姆松定理,知111111C B B A C A +=.①图6-14由A ,1C ,1B ,D 四点共圆,且AD 为该圆直径及正弦定理,有111111sin sin C B AD C DB AD C AB =⋅∠=⋅∠,设R 为O 半径,则11sin sin 2BC C AB BAC R ∠=∠=,故 112AD BCC B R⋅=. 同理,112CD AB B A R ⋅=,112AC BDC A R⋅= 于是,由①式有AD BC CD AB AC BD ⋅+⋅=⋅.此即为托勒密定理. 也可用托勒密定理证明西姆松定理:设ABCD 是O 的内接四边形,则由托勒密定理,有 AD BC AB CD AC BD ⋅+⋅=⋅.②作1DC ⊥直线AB 于1C ,作1DB ⊥直线AC 于1B ,则由1A ,1C ,1B ,D 四点共圆,且AD 为该圆直径及正弦定理,有11111111sin sin C B C B AD C DB C AB ==∠∠,即1111sin 2BCC B AD C AB AD R=⋅∠=⋅.(R 为O 半径),亦即112AD BC R C B ⋅=⋅.同理,112AB CD R A B ⋅=⋅,112AC BD R AC ⋅=⋅. 把上述三式代入②式,有111111C B A B AC +=,故1A ,1B ,1C 三点在一条直线上,此即为西姆松定理,因此,在应用中,我们应当注意灵活处置,若应用哪个定理方便,就应用哪个定理.【模拟实战】习题A1.设P 为ABC △外接圆周劣孤BC 上一点,P 在边BC ,CA ,AB 上的射影分别为L ,M ,N , 令PL l =,PM m =,PN n =,BC a =,CA b =,AB c =.求证:mna lnb lmc =+.2.设PA ,PB ,PC 为O 的三条弦,分别以它们为直径作圆两两相交于D ,E .F .求证:D , E ,F 三点共线.3.自ABC △的顶点A 作B ∠的内、外角平分线BE ,BF 的垂线,垂足为E ,F ,再作C ∠的内、外角平分线CG ,CD 的垂线,垂足为G ,D .求证:F ,G ,E ,D 四点共线. 4.求证:正三角形外接圆周上任一点到三边距离的平方和为定值.5.若三圆均经过其三圆心所成的外接圆上任何一点,则此三圆两两相交于三个共线点.习题B1.点P ,Q 是ABC △的外接圆上的两点(异于A ,B ,C ),点P 关于直线BC ,CA ,AB 的对称 点分别是U ,V ,W ,连线QU ,QV ,QW 分别与直线BC ,CA ,AB 交于点D ,E ,F .求证: (Ⅰ)U ,V ,W 三点共线;(Ⅱ)D ,E ,F 三点共线.2.设ABCD 是一个圆内接四边形,点P ,Q 和R 分别是D 到直线BC ,CA 和AB 的射影. 证明:PQ QR =的充要条件是ABC ADC ∠=∠的角平分线的交点在AC 上.(IMO -44试题)3.(卡诺定理)过ABC △外接圆上一点P ,向三边所在直线引斜线分别交BC ,CA ,AB 于点D ,E ,F ,且PDB PEC PFB ∠=∠=∠.求证:D ,E ,F 共线.4.过ABC △的三顶点引互相平行的三直线,它们和ABC △的外接圆的交点分别为A ',B ',C '.在ABC △的外接圆上任取一点P ,设PA ',PB ',PC '与BC ,CA ,AB 或其延长线分别交于D ,E ,F .求证:D ,E ,F 共线. 5.(清宫定理)设P ,Q 为ABC △外接圆上异于A ,B ,C 的任意两点,P 点关于BC ,CA ,AB 的对称点分别为U ,V ,W ,而QU ,QV ,QW 和BC ,CA ,AB 分别交于D ,E ,F .求证:D ,E ,F 共线.6.设P ,Q ,为ABC △外接圆半径OK 或延长线上两点,2OP OQ R ⋅=,其中R 为外接圆半径,P 点关于BC 、CA 、AB 的对称点分别为U ,V ,W ,而QU ,QV ,QW 分别交BC ,CA ,AB 于点D ,E ,F .求证:D ,E ,F 共线.第六章西姆松定理及应用答案习题A1.由西姆松定理,知L ,M ,N 三点共线,注意到P ,L ,N ,B 及P ,M ,C ,L 分别四点共圆,知LPN B ∠=∠,LPM C ∠=∠.又由张角定理,有()sin sin sin B C B CPL PM PN∠+∠∠∠=+,即 sin sin sin mn A ln B lm C ⋅∠=⋅∠+⋅∠再应用正弦定理,得mn a ln b lm c ⋅=⋅+⋅. 2.根据直径所对的圆周角是直角,知90BDP ADP ∠=∠=︒,90BFP CFP ∠=∠=︒,90CEP AEP ∠=∠=︒,即知D ,A ,B ;B ,F ,C ;C ,E ,A 分别三点共线.又PD AB ⊥于D ,PE AC ⊥于E ,PF BC ⊥于F ,P 是ABC △外接圆周上一点,由西姆松定理,知D ,E ,F 三点共线.3.延长BE ,CD 相交于点K ,延长CG ,BF 相交于点L .设CG 与BE 相交于点I ,则I 为ABC △的内心.由12CAI BAC ∠=∠,而()11909022CKI CIK B C BAC ∠=︒-∠=︒-∠+∠=∠,从而A ,I ,C ,K四点共圆.又AD CK ⊥于D ,AE KB ⊥于E ,AG CI ⊥于G ,A 是ICK △外接圆上任一点,由西姆松定理,知D ,E ,G 三点共线.同理,B ,I ,A ,L 四点共圆,AE BI ⊥于E ,AG IL ⊥于G ,AF BL ⊥于F ,由西姆松定理,知E ,G ,F 三点共线.故F ,G ,E ,D 四点共线.4.设正ABC △外接圆弧AB 上任一点P 到边BC ,CA ,AB 的距离分别为a h ,b h ,c h ,其垂足分别为D ,E ,F ,正三角形边长为a .由面积等式可得a b c h h h +-=.此式两边平方,得()2222324a b c a b b c a c h h h h h h h h h a +++--=.由sin sin b a h hPAC PBD PA PB =∠=∠=,有a b h PA h PB ⋅=⋅. 同理,a c h PA h PC ⋅=⋅,故a b h PA h PB k PC ⋅=⋅=⋅.又P ,F ,E ,A 及P ,D ,B ,F 分别四点共圆,有PFD PBD PAC ∠=∠=∠,PDF PBF PCA ∠=∠=∠, 得PFD PAC △△≌,故c h PA a DF =⋅,同理,a h PB a DE =⋅,b hPC a EF=⋅,即 a c b a c bh h h h h h k EF DE EF⋅⋅⋅===由西姆松定理,知D ,E ,F 共线,即DF FE DE +=.于是 £()0a b a c b c hb h h h h h h DE DF EF k ®---=--=⋅,故222234a b c h h h a ++=.5.设以ABC △的三个顶点为圆心的三圆,皆经过同一点M ,而M 在ABC △的外接圆上,A 与B 另交于D ,A 与C 另交于E ,B 与C 另交于F . 注意到A 与B 中,公共弦MD ⊥连心线AB ;A 与C 中,公共弦ME ⊥连心线AC ;B 与C 中,公共弦MF ⊥连心线BC .对ABC △及其外接圆周上一点M ,应用西姆松定理,知D ,E ,F 三点共线.习题B1.(Ⅰ)设从点P 向BC ,CA ,AB 作垂线,垂足分别为X ,Y ,Z .由对称性,知XY 为PUV △的中位线,故UV XY ∥同理,VW YZ ∥,WU XZ ∥.由西姆松定理,知X ,Y ,Z 三点共线,故U ,V ,W 三点共线.(Ⅱ)由P ,C ,A ,B 四点共圆,有PCE ABP ∠=∠.亦有22PCV PCE ABP PBW ∠=∠=∠=∠. 又PCQ PBQ ∠=∠,则PCV PCQ PBW PBQ ∠+∠=∠+∠. 即QCV QBW ∠=∠,从而QCV QBWS CV CQS BQ BW⋅=⋅△△.同理,QAW QCUS AW AQS CQ CU ⋅=⋅△△,1QBU QCV QAW QBU QAV QBW QCU QAVS S S S BQ BU S AQ AV S S S ⋅=∴⋅⋅=⋅△△△△△△△△. 于是,1QBU QCV QAWQCV QAV QBWS S S BD CE AF DC EA FB S S S ⋅⋅=⋅⋅=△△△△△△ 由梅勒劳斯定理的逆定理,知D ,E ,F 三点共线.2.由西姆松定理知P ,Q ,R 三点共线.而90DPC DQC ∠=∠=︒,则D ,P ,C ,Q 四点共圆.于是,DCA DPQ DPR ∠=∠=∠.同理,由D ,Q ,R ,A 共圆,有DAC DRP ∠=∠.故DCA DPR △∽△. 类似地,DAB DQP △∽△,DBC DRQ △∽△,从而//DA DR DB QR BC QP BA DC DP DB PQ BA PQ BC ⋅⋅===⋅⋅,故DA BAPQ QR DC BC=⇔=,而ABC ∠和ADC ∠的角平分线分AC 的比分别为BA BC 和DADC.即可证. 3.设P 在BC ,由PDB PFB PEC PEA ∠=∠=∠=∠,知B ,P ,D ,F 四点共圆,P ,F ,A ,E 四点共圆,从而PFD PBD PBC PAE PFE ∠=∠=∠=∠=∠,故F ,D ,E 共线(当90PBD PEC PFB ∠=∠=∠=︒时,即为西姆松定理). 4.由PCE A '∠=∠及AA BB ''∥,有A BGD '=∠ (G 为PA '与BB '的交点),即PCE BGD ∠=∠.又 CBB CPB ''∠=∠,从而在BGD △和PCE △中,有BDP CEP ∠=∠,即知D ,P ,E ,C 四点共圆,有PDE PCE A '∠=∠=∠,故AA DE '∥.同理,AA DF '∥,所以D ,E ,F 共线(当PA BC '⊥时,即为西姆松定理). 另证设P B '与AB 交于点X .注意到BB CC ''∥,则知B BC C ''为等腰梯形,有B C BC ''=,即有B PC BAC ''∠=∠.从而AXP XAC AXP XPC ∠+∠=∠+∠.于是E F ∠=∠.同理E D ∠=∠,F D ∠=∠.故E D F ∠=∠=∠.由卡诺定理(即上一题)知D 、E 、F 三点共线.5.设Q ,P 顺次在BC 上,由PCE PBA ∠=∠.有PCV PBW ∠=∠.又PCQ PBQ ∠=∠,有 QCV QBW ∠=∠.故QCNQBW S VC QC PC QC S WB QB PB QB⋅⋅==⋅⋅△△. 同理,QAWQCU S PA QA S PC QC ⋅=⋅△△,QBV QAV S PB QB S PA QA⋅=⋅△△. 于是,1QBU QCU QAW QCU QAV QBW S S S BD CE AF PB QB PC QC PA QA DC EA FB S S S PC QC PA QA PB QB⋅⋅⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅⋅△△△△△△ 由梅勒劳斯定理的逆定理,知D ,E ,F 共线(当P ,Q 重合时,即为西姆松定理).6.设K 点在BC 上,连OC ,则2OP OQ OC ⋅=,又POC COQ ∠=∠,则OPC COQ △∽△,有 OCP OQC ∠=∠.又OKC OQC KCQ ∠=∠+∠,OCK OCP KCP ∠=∠+∠,而OKC OCK ∠=∠,O CP OQC ∠=∠,知PCK KCQ ∠=∠,即2QCV KCE ∠=∠. 同理,2QBW KBA ∠=∠.又KCE KBA ∠=∠,则QCV QBW ∠=∠,有 QCVQBW S CV CQ PC QC S QB WB PB QB ⋅⋅==⋅⋅△△.同理QAW QCU S PA QA S PC QC ⋅=⋅△△,QBU QAV S PB QB S PA QA ⋅=⋅△△.故1QBU QCV QAW QCU QAV QBWS S S BD DE AF DZ EA FB S S S ⋅⋅=⋅⋅=△△△△△△,故D ,E ,F 共线[当P (或Q )在圆周上时,即为西姆松定理]。
