Simson定理
平面几何四大神奇定理
【分析】
【评注】对称变换
12. G是△ABC的重心,以AG为弦作圆切BG于G,延长CG交圆于D。求证:AG2=GC·GD。
【分析】
【评注】平移变换
13. C是直径AB=2的⊙O上一点,P在△ABC内,若PA+PB+PC的最小值是 ,求此时△ABC的面积S。
【分析】
【评注】旋转变换
【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。
2.过△ABC的重心G的直线分别交AB、AC于E、F,交CB 于D。
求证: 。
【分析】连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→ (梅氏定理)
DGF截△ACM→ (梅氏定理)
∴ = = =1
【评注】梅氏定理
3.D、E、F分别在△ABC的BC、CA、AB边上,
费马点:已知O是△ABC内一点,∠AOB=∠BOC=∠COA=120°;P是△ABC内任一点,求证:PA+PB+PC≥OA+OB+OC。(O为费马点)
【分析】将C C',O O',P P',连结OO'、PP'。则△B OO'、△B PP'都是正三角形。
∴OO'=OB,PP'=PB。显然△BO'C'≌△BOC,△BP'C'≌△BPC。
,AD、BE、CF交成△LMN。
求S△LMN。
【分析】
【评注】梅氏定理
4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证:AE、BF、CG相交于一点。
【分析】
【评注】塞瓦定理
5. 已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。
simson定理

simson定理(原创版)目录1.引言:介绍 Simson 定理的背景和意义2.Simson 定理的定义:解释 Simson 定理的含义和公式表达式3.Simson 定理的证明:概述证明过程,包括关键的引理和思路4.Simson 定理的应用:探讨在几何、拓扑学等领域的应用案例5.结论:总结 Simson 定理的重要性和影响正文1.引言Simson 定理,又称 Simson 公式,是一种在几何和拓扑学中广泛应用的定理。
该定理在 19 世纪由英国数学家 Robert Simson 发现,它对于研究多面体的性质和结构具有重要意义。
本文将从 Simson 定理的定义、证明和应用等方面进行介绍。
2.Simson 定理的定义Simson 定理是指:对于一个凸多面体,它的体积 V、表面积 S 和所有面的角度之和θ满足以下关系:V = (1/6)Sθ。
其中,凸多面体是指所有面都是凸多边形且所有顶点都在多面体内部的多面体。
3.Simson 定理的证明为了证明 Simson 定理,我们需要引入一个关键的引理:一个凸多面体的所有面的角度之和等于 4π。
接下来,我们将通过这个引理来证明Simson 定理。
证明过程如下:设凸多面体有 n 个面,每个面的角度分别为α1, α2,..., αn。
根据欧拉公式,我们有:V = (1/3)S = (1/3)(α1 + α2 +...+ αn)又因为一个凸多面体的所有面的角度之和等于 4π,即:α1 + α2 +...+ αn = 4π将上述等式代入 V 的表达式中,得:V = (1/3)(4π) = (4/3)π再根据 Simson 定理的公式 V = (1/6)Sθ,我们有:(1/6)Sθ = (4/3)π从而得到:θ = (8/3)π由于凸多面体的所有面都在一个球体内,根据球体的体积公式,我们有:V = (1/3)πR其中,R 为球体的半径。
将 V 的表达式代入上式,得:(1/3)πR = (4/3)π解得:R = 2因此,我们可以得到 Simson 定理的公式:V = (1/6)Sθ =(1/6)S(8/3)π = (4/3)πR = (4/3)π(2) = (32/3)π4.Simson 定理的应用Simson 定理在几何、拓扑学等领域具有广泛的应用。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
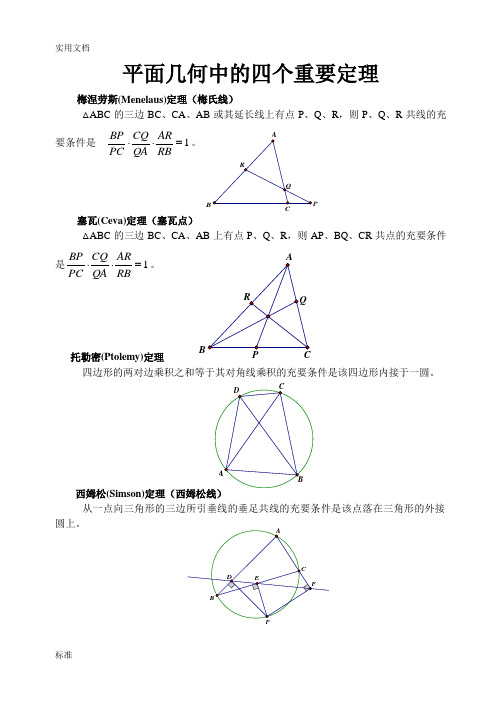
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
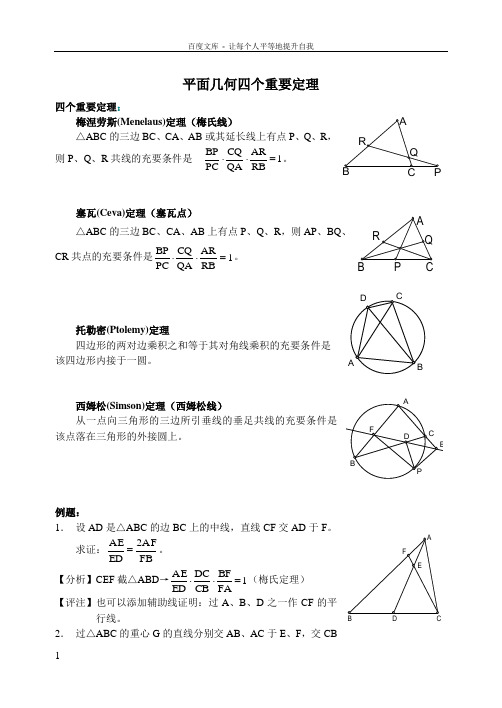
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
数学竞赛常用平面几何名定理

高中数学常用平面几何名定理定理1 Ptolemy定理托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
定理2 Ceva定理定理3 Menelaus定理定理4 蝴蝶定理定理内容:圆O中的弦PQ的中点M,任作两弦AB,CD,弦AD与BC分别交PQ 于X,Y,则M为XY之中点。
定理5 张角定理在△ABC中,D是BC上的一点。
连结AD。
张角定理指出:sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD定理6 Simon line西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
定理7 Eular line:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半定理8 到三角形三定点值和最小的点——费马点已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
定理9 三角形内到三边距离之积最大的点是三角形的重心定理10到三角形三顶点距离的平方和最小的点是三角形的重心在几何里,平面是无限延展的,是无大小的,是不可度量的,是无厚度的,通常画平行四边形来表示平面0、勾股定理,即直角三角形两直角边的平方和等于斜边的平方。
这是平面几何中一个最基本、最重要的定理,国外称为毕达哥拉斯定理。
1、欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半2、九点圆:任意三角形三边的中点.三条高线的垂足.垂心与各顶点连线的中点,这9点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
3、费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
平面几何四大定理

平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏成)△ ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充妥条件是— = loPC QA RB室瓦(Ccva)定理(塞瓦点)A ABC 的三边BC、CA、AB 上有点P、Q、R,则AP、BQ、CR共点的充妥条件是BP CQ ARPC QA RBlo托勒密(Ptolemy)定理四边彩的两对边乘积之和等于其对角线乘积的充妾条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充妄条件是该点落在三角形的外接网上。
例题:1.设AD是二ABC的边BC上的中线,直线XF交AD于F。
a. AE 2AF求'正: LC = 0ED FB【分析】CEF —— = 1 (梅氏定理)ED CB FA【评注】也叮以添加辅助线证明:过A、B、D之一作CF的平行践。
2.过^ABC的重心G的直经分别交AB、AC于E、F,交CB word于Po求证: BE CF —+ —EA FA【分析】连结异延长AG交BC于M,则M为BC的中点Oc 止BE AG DEG 裁zlABM— --------------EA GMCF AGPGF^AACM^--—FA Of 黑=1 (梅氏定理)U D罪=1 (梅氏定理)DC.BE 十CF _GM (DB + DC)_GM 2MD_[ EA+ FA AGMD 2GM MD~ 【评注】梅氏定理3.D、E、F分别在A ABC的BC、CA、AB边上,RD AF CF= 人,AD、BE、CF 交成ALMNoDC FB EA求S_LM*【分析】【评注】梅氏定理4. 以AABC各边为底边向外作相似的等膝zLBCE、ACAF.AABGo求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5.已知ZiABC 中,ZB=2ZCo 求证:AC2=AB2+AB - BCo【分析】过A作BC的平行线交A ABC的外接圆于D,连结BPo 则CD=DA=AB, AC=BDo由,七勒密定理,AC - BP=AD - BC+CD - ABo【评注】托勒密定理6.已知正七边形A|A2A5A4A S A6A7O求证:+—!—o (第21届全苏数学竞赛)A | A 2 A j A j A]Aq【分析】【评注】托勒密定理7. AABC的BC边上的商AD的延长线交外接阅于P,作PE1AB于E,延长ED交AC延长残于F。
平面几何的几个重要定理--西姆松定理答案

平面几何的几个重要定理--西姆松定理答案第一篇:平面几何的几个重要定理--西姆松定理答案《西姆松定理及其应用》西姆松定理:若从∆ABC外接圆上一点P作BC、AB、AC的垂线,垂足分别为D、E、F,则D、E、F三点共线;证明:连接DE、DF,显然,只需证明∠BDE=∠FDC即可;Θ∠BDP=∠BEP=90︒∴B、E、P、D四点共圆,∴∠BDE=∠BPE同理可得:∠FDC=∠PFC又Θ∠BEP=∠PFC=90︒且∠PCF=180︒-∠PBA=∠PBE∴∠BPE=∠FPC∴∠BDE=∠FDC∴D、E、F 三点共线西姆松的逆定理:从一点P向∆ABC的三边(或它们的延长线)作垂线,若其垂足L、M、N在同一直线上,则P在∆ABC的外接圆上;例1.设∆ABC的三条垂线AD、BE、CF的垂足分别为D、E、F;从点D作AB、BE、CF、AC的垂线,其垂足分别为P、Q、R、S,求证P、Q、R、S在同一直线上;证明:设∆ABC的垂心为O,则O、E、C、D四点共圆Θ由西姆松定理有:Q、R、S三点共线又ΘO、F、B、D四点共圆且由西姆松定理有:P、Q、R三点共线∴P、Q、R、S 四点共圆例2.四边形ABCD是圆内接四边形,且∠D是直角,若从B作直线AC、AD的垂线,垂足分别为E、F,则直线EF平分线段BD。
证明:作BG⊥DC,由西姆松定理有:F、E、G共线,又Θ∠BFD=∠FDG=∠DGB=90︒∴四边形BFDG为矩形∴对角线FG平分另一条对角线BD例3.求证:四条直线两两相交所构成的四个三角形的外接圆相交于一点,且由该点向四条直线所作垂线的垂足在一条直线上;证明:如图,设四条直线AB、BC、CD、AD中,AB交CD于点E,BC交AD于点F,圆BCE与圆CDF的另一个交点为G∴∠BGF=∠BGC+∠CGF=∠BEC+∠CDA∴∠BGF+∠A=180︒,即圆ABF 过点G同理圆AED也过点G∴圆BCE、圆CDF、圆ABF、圆AED交于同一点G若点G向AB、BC、CD、DA所作垂线的垂足分别为E、L、M、N、P,由西姆松定理可知L、M、N在一条直线上,M、N、P在一条直线上,故L、M、N、P在同一条直线上例4.设∆ABC的外接圆的任意直径为PQ,则关于P、Q的西姆松线是互相垂直的。
三角形的各个心总结与归纳

三角形的心三角形只有五种心重心:三中线的交点,三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍;垂心:三高的交点;内心:三内角平分线的交点,是三角形的内切圆的圆心的简称;外心:三中垂线的交点;旁心:一条内角平分线与其它二外角平分线的交点.(共有三个.)是三角形的旁切圆的圆心的简称.当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心.1三角形重心重心是三角形三边中线的交点,三线交一可用燕尾定理证明,十分简单。
证明过程又是塞瓦定理的特例。
已知:△ABC中,D为BC中点,E为AC中点,AD与BE交于O,CO延长线交AB于F。
求证:F为AB中点。
证明:根据燕尾定理,S△AOB=S△AOC,又S△AOB=S△BOC,∴S△AOC= S△BOC,再应用燕尾定理即得AF=BF,命题得证。
重心的几条性质:1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+ X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y 1+Y2+Y3)/3 竖坐标:(z1+z2+z3)/35、三角形内到三边距离之积最大的点。
重心三条中线定相交,交点位置真奇巧,交点命名为“重心”,重心性质要明了,重心分割中线段,数段之比听分晓;长短之比二比一,灵活运用掌握好.2三角形垂心的性质设⊿ABC的三条高为AD、BE、CF,其中D、E、F为垂足,垂心为H,角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1、锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.2、三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心;3、垂心H关于三边的对称点,均在△ABC的外接圆上。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)

P 、Q R ,则P 、Q R 共线的充要条件是聖CQ ARj 。
PC QA RBBP CQ AR PC QA RB _ °平面几何中的四个重要定理梅涅劳斯(Menelaus )定理(梅氏线)△ABC 的三边BC CA AB 或其延长线上有点塞瓦(Ceva )定理(塞瓦点)△ABC 的三边 BC CA AB 上有点 P 、Q R ,贝U AP 、BQ CR 共点的充要条件是 托勒密(Ptolemy )定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson )定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接 圆上。
例题:PA 1设AD是MBC的边BC上的中线,直线CF交AD于F。
求证:AE 2AFED。
AE DC RF【分析】CEF截△ARCH — .— .— =1 (梅氏定理)ED CR FA【评注】也可以添加辅助线证明:过A、R、D之一作CF的平行线。
2、过△ARC的重心G的直线分别交AB AC于E、F,交CR于D。
RE CF=1。
求证:EA FADEG截A ARM H REEAAGGMMDDR(梅氏定理)DGF截△ACM H =1 (梅氏定理)FA GM DCRE CF=GM (DR DC)=GM2MDEA FA AG MD 2GM MD【评注】梅氏定理3、D E、F分别在A ARC的RC CA AR边上,RD AFDC FRCEEAAD RE、CF交成△ LMN 求S A LM N O【分析】【评注】梅氏定理4、以A ARC各边为底边向外作相似的等腰A RCE A CAF A ARG 求证:AE、RF、CG相交【分析】连结并延长AG交RC于M,则M为RC的中点。
FLEM N【评注】塞瓦定理5、已知△ABC 中,/ B=2/ G 求证:AC^AB+ABBCo【分析】过A 作BC 的平行线交△ABC 的外接圆于D,连结BD 贝 U CD=DA=AB AC=BD由托勒密定理,AC BD=ADBC+CDAB【评注】托勒密定理求证:1 1 1A !A 2=A !A 3 A !A 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何表示
过三角形外接圆上异于三角形顶点的任意一点作三边的垂线, 则三垂足共线.
□
一阶描述
基本定义:
选定 A,B,C 三点
□
取外接圆上任意一点 P
□
得到三个垂足 D,E,F
□
基本描述:
: A,B,C 三点不共线
西姆松定理
它们的坐标分别为
这三点构成的三角形的外接圆心及半径分别为
P 点的坐标为 .
全部
(x 1,y 1),(x 2,y 2),(x 3,y 3).l 1=AB,l 2=BC,l 3=CA.(u,v),r.(a,b)D(a 1,b 1),E(a 2,b 2),F(a 3,b 3).
91
□
●
: P 在三角形 ABC 的外接圆上
□
●
: P 不同于 A,B,C
□
●
: D 是 P 到 BC 的垂足
□
●
: E 是 P 到 CA 的垂足
□
l 1l 2l 3(l 21=(x 1-x 2)2+(y 1-y 2
)2
[l 22=(x 2-x 3)2+(y 2-y 3)2
[l 23=(x 3-x 1)2+(y 3-y 1
)2[l 1+l 2>l 3[l 2+l 3>l 1[l 3+l 1>
l 2)92^uvr ((x 1-u)2
+(y 1-v)2=r 2
[
(x 2-u)2+(y 2-v)2=r 2[(x 3-u)2
+(y 3-v)2
=r 2
[(u-a)2+(v-b)2=r 2)
93\(a=x 1[b=y 1)[\(a=x 2[b=y 2)[\(a=x 3[b=y 3)
94(a 1-x 2)(b 1-y 3)-(a 1-x 3)(b 1-y 2)=0[(a 1-a)(x 2-x 3)+(b 2-b)(y 2-y 3)=0
95^
●
: F 是 P 到 AB 的垂足
□
●
: D,E,F 三点共线
□
该定理可以表示为:
这是一个复杂的描述.
●逻辑描述是很复杂的
●
将几何性质表示为逻辑公式是可行的 ●
但不适合人工推导
□□
96< (a 1-a 2)(b 1-b 3)-(b 1-b 2)(a 1-a 3)=0]x 1y 1x 2y 2x 3y 3aba 1b 1a 2b 2a 3b 3(91[92[93[94[95[96> < ).。
