反比例函数中K的计算
反比例函数中比例系数k的几何意义

反思小结
在反比例函数 y 10 的图象上,有一系列点A1,A2, x A3…..An,An+1,若A1横坐标为2,且以后每点的 横坐标与它前一个点的横坐标的差都为2. 现分别 过点A1,A2,A3…..An,An+1作X轴与Y轴的垂线 段,构成若干个矩形如图10所示,将图中阴影部 分的面积从左到右依次记为S1、S2、S3、…Sn, 5 5 15 2 5 2 (5 _____, ) 则S1=________, S +S +S =____ S1+S2 2 1 2 3 4 2 5 10 n 2 (5 ) +S3+….+Sn=________________.( 用n的代数式表 n 1 n 1 A 示)
C
S SOAD SABD SBCD SOCD 4 1 4
达标测试
已知几何图形的面积S,求比例系数k
5、如图,已知双曲线 (k>0) 经过矩形OABC边AB的中点F,交BC于点E, 且四边形OEBF的面积为2,则k的值为( B )。
y
y
k x
A 1
所以
B 2
C 4
S OAB 4
O
y
已知几何图形的面积S,求比例系数k k y 变式、如图,已知双曲线 x ( k>0 )经
B
D
C E A
x
而
SOAB SOBC SOAC
即
S ODE 1 S OAB 1 4 k 3 2
1 k 2
相似三角形的面积比 等于相似比的平方 k 4;
k 0 k 4
k 0 k 4
4 y x
达标测试
4、如图,在平面直角坐标系中, 点O为原点,菱形OABC的对角线 OB在x轴上,顶点A在反比例函数 2 的图像上,求菱形的面积。 y B
反比例函数中K的几何意义课件

k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
反比例函数k几何意义模型大全

反比例函数k几何意义模型大全摘要:一、反比例函数的概念与基本性质二、反比例函数的几何意义1.反比例函数与坐标轴的交点2.反比例函数图象上的点与k的关系3.反比例函数图象的缩放与翻转三、反比例函数的应用1.实际问题中的反比例关系2.数学模型中的反比例函数应用四、反比例函数的计算与分析1.反比例函数的求解2.反比例函数的图像分析五、总结与拓展正文:一、反比例函数的概念与基本性质反比例函数是数学中一种重要的函数类型,其一般形式为y = k/x,其中k 为常数且k≠0。
反比例函数具有以下基本性质:1.当x>0时,y>0;当x<0时,y<0。
2.当x增大时,y减小;当x减小时,y增大。
3.反比例函数的图象为双曲线,且两条分支分别位于第一、第三象限。
二、反比例函数的几何意义1.反比例函数与坐标轴的交点:反比例函数y = k/x与x轴、y轴的交点分别为(0,k)和(k,0)。
2.反比例函数图象上的点与k的关系:反比例函数图象上的点(x,y)满足xy = k。
3.反比例函数图象的缩放与翻转:反比例函数图象随着k的变化而缩放,k增大时图象变得更瘦,k减小时图象变得更胖。
同时,反比例函数图象可以沿x轴或y轴翻转。
三、反比例函数的应用1.实际问题中的反比例关系:许多实际问题中存在反比例关系,如速度与时间、面积与边长等。
通过建立反比例函数模型,可以更好地描述这些关系。
2.数学模型中的反比例函数应用:反比例函数在数学模型中有广泛应用,如电阻与电流、电压的关系、物流配送中的距离与时间关系等。
四、反比例函数的计算与分析1.反比例函数的求解:当给出反比例函数的形式,可以通过代入法、图像法等方法求解k值。
2.反比例函数的图像分析:通过对反比例函数图象的分析,可以了解其性质、变化趋势等。
五、总结与拓展反比例函数是数学中的重要概念,掌握其基本性质、几何意义及应用有助于解决实际问题和数学模型。
同时,反比例函数也是进一步学习其他数学知识的基础,如微积分、三角函数等。
反比例函数计算公式

反比例函数计算公式
1、y=k/x 其中X是自变量,Y是X的函数
2、y=k/x=k·1/x
3、xy=k
4、y=k·x^-1
5、① k ≠ 0 ②一般情况下,自变量 x 的取值范围是 x ≠ 0 的一切实数③函数 y 的取值范围也是一切非零实数 .
两种有关联的量,一种量随另一种量变化而变化,但这两种量的积一定是个常数,这时,这两种量是成反比例的量,它们的关系叫做反比例关系。
一般用来x的变化规律来表示y的变化规律。
反比例量涵盖三个量,一个定量和两个变量。
研究两个变量的膨胀(或减少)之间的关系。
一个量的变化导致另一个量的相反变化。
这两个量是成反比的,它们的关系是成反比的。
形如 y/x=k(一定)(k不等于0)的函数叫做反比例函数,k叫做反比例系数。
(一定),这是求反比例的公式。
用字母表示反比例的关系式k(一定)=yx。
反比例,指的是两种有关联的变量,一种量变化,另一种量也随着变化,假设这两种量中相对应的两个数的乘积一定,既然如此那,他们就叫做成反比例的量,他们的关系叫做反比例关系。
比例(proportion)是一个数学术语,表示两个或多个比相等的式子。
在一个比例中,两个外项的积等于两个内项的积,叫做比例的基本性质。
反比例函数知识点总结,比例系数k的几何意义和七大常考模型
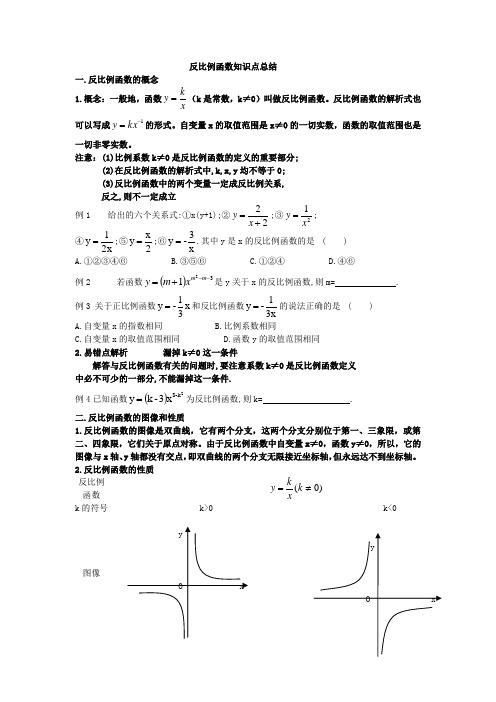
反比例函数知识点总结一.反比例函数的概念1.概念:一般地,函数x k y =(k 是常数,k ≠0)叫做反比例函数。
反比例函数的解析式也可以写成1-=kx y 的形式。
自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数。
注意:(1)比例系数k ≠0是反比例函数的定义的重要部分;(2)在反比例函数的解析式中,k,x,y 均不等于0;(3)反比例函数中的两个变量一定成反比例关系,反之,则不一定成立例1 给出的六个关系式:①x(y+1);②22+=x y ;③21x y =; ④x 21y =;⑤2x y =;⑥x3-y =.其中y 是x 的反比例函数的是 ( ) A.①②③④⑥ B.③⑤⑥ C.①②④ D.④⑥ 例2 若函数()321--+=m m x m y 是y 关于x 的反比例函数,则m= .例3 关于正比例函数x 31-y =和反比例函数x31-y =的说法正确的是 ( ) A.自变量x 的指数相同 B.比例系数相同C.自变量x 的取值范围相同D.函数y 的取值范围相同2.易错点解析 漏掉k ≠0这一条件解答与反比例函数有关的问题时,要注意系数k ≠0是反比例函数定义中必不可少的一部分,不能漏掉这一条件.例4已知函数()2k -8x 3-k y =为反比例函数,则k= .二.反比例函数的图像和性质1.反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
2.反比例函数的性质反比例函数 )0(≠=k xk y k 的符号 k>0 k<0图像性质 ①x 的取值范围是x ≠0, y 的取值范围是y ≠0; ②当k>0时,函数图像的两个分支分别 在第一、三象限。
在每个象限内,y 随x 的增大而减小。
浅谈反比例函数中的k值法解题

浅谈反比例函数中的“K ”值法解题摘 要:随着新课程标准的推进,近几年,在中考试题中关于反比例函数方面的试题出现了不少新题型。
而反比例函数的“K ”值是一个最关键的因素,可以说是反比例函数的精髓所在。
接下来,让我们一起探讨一下反比例函数中利用“K ”值法解题的问题。
关键词:反比例函数 “K ”值 象限 图像所谓“K ”值法解题,就是通过反比例函数特有的“K ”值的一些性质进行分析解题。
结合近几年中考题,“K ”值主导的反比例函数习题越来越多。
这里就反比例函数的“K ”值的意义来解决问题进行例析。
以下是利用“K ”值求解关于面积、反比例函数性质、反比例函数图像及反比例函数和正比例函数相结合等方面的解法淡析。
一、“K ”值的几何意义及利用其求相关图形面积研究函数问题要透视函数的本质特征。
所以,我们先从“K ”值的本质出发对其进行精确剖析。
下面就是反比例函数的几何意义。
反比例函数y=x k (k ≠0)中,比例系数k 有一个很重要的几何意义。
那就是:过反比例函数y=xk (k ≠0)的图像上任意一点P 作x 轴,y 轴的垂线PM 、PN ,垂足为M 、N (如图1-1所示),则矩形PMON 的面积S=PM ·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x 轴、y 轴的垂线,它们与x 轴、y 轴所围成的矩形面积为常数k 。
从而有PNO S ∆=PMO S ∆=k 21。
在解有关反比例函数的问题时,若能灵活运用反比例函数中k 的几何意义,会给解题带来很多方便。
现举例说明。
例1.已知点C 为反比例函数6y x=-上的一点,过点C 向坐标轴引垂线,垂足分别为A 、B ,那么四边形AOBC 的面积为 。
解析:因为四边形AOBC 的面积S=CA ·CB=xy x y =∙,又因为6y x=-,所以xy k =, 即S=6-=6,故四边形AOBC 的面积为6。
例2.(03年全国初中数学联赛试题)若函数kx y =(k >0)与函数1y x=的图象相交于A 、C 两点,AB 垂直x 轴于B ,则△ABC 的面积为( )。
反比例函数中K值的几何意义及其应用

反比例函数中K值的几何意义及其应用当考虑反比例函数时,我们可以将其视为一种特殊的函数关系,其中两个变量之间存在着反比关系。
反比例函数的一般形式可以表示为y=k/x,其中k是一个常数,x和y是函数的自变量和因变量。
在反比例函数中,K值是一个常数,它代表了反比例函数的特定特性。
K值的几何意义是直线y=k/x在平面中的位置和特点。
为了更好地理解K值的几何意义,我们可以思考以下问题:1.K值的符号:当K值为正数时,反比例函数图像位于第一和第三象限,当K值为负数时,图像位于第二和第四象限。
2.K值的绝对值:绝对值越小,曲线越陡峭;绝对值越大,曲线越平滑。
这是因为K值的绝对值代表了x和y之间的反比关系的强度。
3.K值对函数图像的平移效果:当K增大时,函数图像会沿着y轴缩小,而当K减小时,函数图像会沿着y轴放大。
这是因为反比例函数的图像是关于y轴对称的。
应用方面,反比例函数在科学、工程和经济学等领域有广泛的应用。
下面列举了几个常见的应用:1.物理学–比如在牛顿第二定律中,质量(m)与加速度(a)是反比例关系,即F=k/m,其中F是力,k是常数。
当应用这个反比例关系时,我们可以利用K值计算质量和加速度之间的强度关系。
2.经济学–比如供需关系中,商品价格(P)与需求量(D)也遵循反比例关系,即P=k/D,其中k是一个常数。
通过K值,我们可以了解价格和需求之间的关系,从而调整市场供需平衡。
3.化学–比如在浓度计算中,溶液中溶质的浓度(C)与溶液体积(V)是反比例关系,即C=k/V,其中k是一个常数。
通过K值,我们可以计算溶液中的溶质浓度和体积之间的关系。
4.网络传输–在计算机网络中,带宽(B)和数据传输速率(R)也存在反比例关系,即R=k/B,其中k是一个常数。
通过K值,我们可以确定数据传输速率和带宽之间的关系,从而优化网络性能。
5.金融学–比如货币价值与通货膨胀之间存在反比例关系,即货币价值(V)=k/通货膨胀(I),其中k是一个常数。
反比例函数整章知识点复习

在生物学中,反比例函数可用于描述种群数量与资 源之间的关系,如食物与捕食者数量等。
03
反比例函数的图像与性质
反比例函数的图像绘制
通过选择适当的x值,计算对应的y值 ,在坐标系上标出对应的点,连接各 点绘制出反比例函数的图像。
100%
经济问题
在经济学中,反比例函数可以用 来描述成本与产量的关系、供需 关系等。
80%
生态问题
在生态学中,反比例函数可以用 来描述种群数量与环境容量的关 系等。
05
反比例函数习题解析
基础题目解析
01
02
03
题目
已知点$P(x, y)$在反比例 函数$y = frac{k}{x}$的图 象上,若$x$与$y$的乘积 为$2k$,则$k$的值为 ____.
竞赛题目解析
01
k、a、b 的值;
02
k、a、b 的值;
03
k、a、b 的值;
04
k、a、b 的值;
THANK YOU
感谢聆听
反比例函数的计算方法
01
对于反比例函数
$f(x)
=
frac{k}{x}$,求值时只需将 $x$ 值
代入函数中即可。
02
若需要求 $f(x)$ 的导数或积分, 则需使用相应的微积分法则进行 计算。
反比例函数在实际问题中的应用
在物理学中,反比例函数可用于描述两个物理量之 间的反比关系,如电荷与电场强度、电流与电阻等 。
反比例函数的图像
图像特点
双曲线,分布在两个象限内,随着k的正负变化而分别分布在第一 、三象限或第二、四象限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数中K的计算
反比例函数是数学中的一种特殊函数形式,其形式可以表示为y=k/x,其中y和x分别为函数的因变量和自变量,k为比例常数。
反比例函数中
的比例常数k是一个关键参数,它决定了函数的形状和性质。
在本篇文章中,将详细介绍如何计算反比例函数中的比例常数k。
首先,我们需要明确的一点是,反比例函数中的比例常数k并非固定
的数值,而是与函数的具体形式有关。
在反比例函数y=k/x中,k可以是
任意实数,只要它不等于零。
下面给出一种计算反比例函数中的比例常数k的方法:
1.已知两个具体的点(x1,y1)和(x2,y2)在反比例函数上,我们可以利
用这两个点的坐标来计算比例常数k。
2.将已知的点坐标代入反比例函数的表达式y=k/x中,得到以下两个
方程:
-k=x1*y1
-k=x2*y2
x1*y1=x2*y2
3.现在我们可以解这个方程来计算比例常数k。
这个方程可能需要进
行乘法、除法和求解根的操作,具体的步骤如下:
a.将方程变形为k=x1*y1/x2*y2、根据乘法和除法的运算法则,我们
可以将x1和x2分别除以y1和y2,得到:
k=(x1/y1)*(y1/x2)*x2*y2
b.化简这个表达式,得到k=x1*x2
c.代入已知的点坐标,并计算出k的具体数值。
注意,在计算过程中,需要注意小数点的精确性,以确保结果的准确性。
以上就是计算反比例函数中比例常数k的一种方法。
这个方法基于已
知的点坐标,通过联立方程,解出比例常数k的具体数值。
在实际计算中,可以使用计算器或计算软件来简化繁琐的计算过程,以提高计算的准确性
和效率。
需要注意的是,反比例函数中的比例常数k不能为零。
如果k为零,
那么函数将无法定义,因为除数不能为零。
因此,在计算反比例函数中的
比例常数k时,需要确保k的数值不为零。
总结起来,计算反比例函数中的比例常数k的方法是利用已知的点坐标,通过联立方程解出k的具体数值。
这个过程可以借助计算器或计算软
件来简化和加快计算速度。
同时,需要注意保持计算的精确性,以得到准
确的结果。
