医学统计学分析计算题_与解析
医学统计学样题及答案解析
1、某市1974年为了解该地居民发汞的基础水平，调查了留住该第一年以上，无明显肝、肾疾病，无汞作业接触史的居民238人的发汞含量如下：发汞值 1.5～ 3.5～ 5.5～7.5～9.5～11.5～13.5～15.5～17.5～19.5～21.5（ mol/kg）:人数20 66 60 48 18 16 6 1 0 3（1）说明此频数分布的特征。
（2）选用何种指标描述其集中趋势和离散趋势？（3）估计该地居民发汞值的95%参考值范围？答：（1）偏态分布（2）选用中位数描述集中趋势，四分位间距描述离散趋势（3）频数相对频数累积频数累积相对频数1.5～20 0.08403361 200.0840343.5～66 0.27731092 860.3613455.5～60 0.25210084 1460.6134457.5～48 0.2016806194 0.815127 69.5～18 0.07563025 2120.89075611.5～16 0.06722689 2280.95798313.5～ 6 0.02521008 2340.98319315.5～ 1 0.00420168 2350.98739517.5～0 0 235 0.98739519.5～21.5 3 0.01260504 238 1合计238P2.5=1.5+(238×2.5%-0)×2/20=2.095P97.5=13.5+(238×97.5%－228)×2/6=14.85所以估计该地居民发汞值的95%参考值范围（2.095，14.85）2、某市场出售一批番茄汁罐头，罐头内vc平均含量（mg/100g）是未知的。
今从中抽取16个罐头，经测定含量如下：16，22，21，23，21，19，15，13，23，17，20，29，18，22，16，25计算：（1）试问这批罐头内vc平均含量及95%区间估计？（2）假如另一批罐头vc平均含量为22mg/100g，试问这两批罐头vc含量是否相同？答：（1）样本平均值＝20 样本标准差＝4.115 16开方＝420－2.131×4.115/4=17.820＋2.131×4.115/4=22.192(17.8, 22.192)(2) 22∈(17.8, 22.192)所以含量相同3、某药厂为了解其生产的某药物（同一批）之有效成分含量是否符合国家规定的标准，随机抽取了该药10片，得其样本均数为103.0mg，标准差2.22mg，试估计该批药物有效成分的平均含量？答：该批药物有效成分的平均含量的95%可信区间为：（样本均值-1.96标准误，样本均值+1.96标准误）即：（101.6，104.4）4、为了观察寒冷对动物鸟中17-KS排出量的影响，实验安排了营养正常组的大白鼠在寒冷前与寒冷后分别测定尿中17-KS排出量，请问这个实验设计的模型是什麽？答：这个实验设计的模型是配对设计资料的t检验5、男性四组人群营养实验中胡罗卜素春、夏、秋、冬四季之比较春夏秋冬∑X 13373.10 13313.00 11739.20 7063.00N 137 179 135 123x97.61 74.37 86.96 57.42∑X2 1454669.21 1133189.22 1174964.10 481172.32（1）试检验四季之间胡萝卜素存留量（毫克）有无显著差别？（2）如有显著差别，应如何确定？（一）1. 假设和和确定检验水准H0 ：四季之间胡萝卜素存留量的总体均数相等，μ1=μ2=μ3=μ4H1 ：四季之间胡萝卜素存留量总体均数不全相等α=0.05检验统计量F值∑X ＝13373.10+13313.10+11739.20+7063.00＝45488.30 N ＝137+179+135+123＝574 ∑X2＝4243994.85C=（∑X ）2/N=(45488.30)2/574=3604852.68∑∑=-=-=-=740.86050.33079.416)22C x x x SS ij （总＝4243994.85－3604852.68＝639142.17ν总 = N-1 = 574-1=573091.4505.330107.18106.24100.25106.46)x ()(SS 22222ij 2=-+++=-=-=∑∑∑C nx x n ii 组间 ＝（13373.10）2/137 ＋ （13313.00）2/179 ＋ （11739.20）2/135＋（7063.00）2/123－3604852.68＝117075.46ν组间 = k-1 =4-1 =3SS 组内=∑-2)(i ijx x=S 总- SS 组间 =639142.17-117075.46=522066.71ν组内= N-k =574-4=570MS 组间 = SS 组间/ν组间 =117075.46/3=39025.15MS 组内= SS 组内/ν组内=522066.71/570=915.91F= MS 组间/MS 组内=39025.15/915.91=42.61方差分析结果表变异来源SS νMS F P 总639142.17 573组间117075.46 3 39025.15 42.61 <0.01组内522066.71 570 915.913.确定P值和作出推断结论以ν1（ν组间）=3及ν2（ν组内）=570，查F界值表得P<0.01，按 =0.05水准拒绝H0，接受H1，故可以认为四季之间胡萝卜素存留量（毫克）差别有统计学意义。
医学统计学部分试题及答案解析
第一章绪论1.下列关于概率的说法，错误的是A. 通常用P表示B. 大小在0%与100%之间C. 某事件发生的频率即概率D. 在实际工作中，概率是难以获得的E. 某事件发生的概率很小，在单次研究或观察中时，称为小概率事件[参考答案] C. 某事件发生的频率即概率2.下列有关个人基本信息的指标中，属于有序分类变量的是A. 学历B. 民族C. 血型D. 职业E. 身高[参考答案] A. 学历3.下列有关个人基本信息的指标，其中属于定量变量的是A. 性别B. 民族C. 职业D. 血型E. 身高[参考答案] E. 身高4.下列关于总体和样本的说法，不正确的是A. 个体间的同质性是构成总体的必备条件B. 总体是根据研究目的所确定的观察单位的集合C. 总体通常有无限总体和有限总体之分D. 一般而言，参数难以测定，仅能根据样本估计E. 从总体中抽取的样本一定能代表该总体[参考答案] E. 从总体中抽取的样本一定能代表该总体5.在有关2007年成都市居民糖尿病患病率的调查研究中，总体是A. 所有糖尿病患者B. 所有成都市居民C. 2007年所有成都市居民D. 2007年成都市居民中的糖尿病患者E. 2007年成都市居民中的非糖尿病患者[参考答案] C. 2007年所有成都市居民6.简述小概率事件原理。
答：当某事件发生的概率很小，习惯上认为小于或等于0.05时，统计学上称该事件为小概率事件，其含义是该事件发生的可能性很小，进而认为它在一次抽样中不可能发生，这就是所谓小概率事件原理，它是进行统计推断的重要基础。
7.举例说明参数和统计量的概念答：某项研究通常想知道关于总体的某些数值特征，这些数值特征称为参数，如整个城市的高血压患病率。
根据样本算得的某些数值特征称为统计量，如根据几百人的抽样调查数据所算得的样本人群高血压患病率。
统计量是研究人员能够知道的，而参数是他们想知道的。
一般情况下，这些参数是难以测定的，仅能根据样本估计。
医学统计学分析计算题-答案(1)
第二单元 计量资料的统计推断分析计算题某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数标准差 标准值*红细胞数/1012·L -1 男 360女 255 血红蛋白/g ·L -1 男 360女255请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大 (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同） 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
该地女性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
医学统计学分析计算题-答案
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别例 数 均 数 标准差 标准值* 红细胞数/1012·L -1男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
医学统计学分析计算题答案
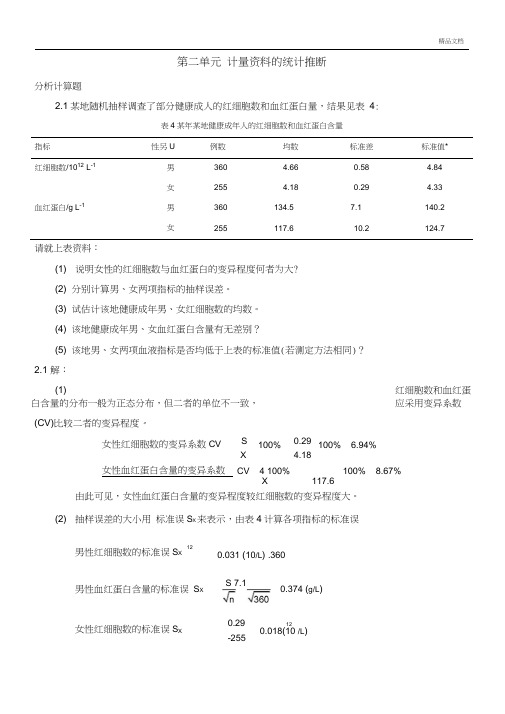
第二单元计量资料的统计推断分析计算题2.1某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4:表4某年某地健康成年人的红细胞数和血红蛋白含量指标性另U例数均数标准差标准值*红细胞数/1012L-1男360 4.660.58 4.84女255 4.180.29 4.33血红蛋白/g L-1男360134.57.1140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大?(2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值(若测定方法相同)？2.1 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。
女性红细胞数的变异系数CV S100%0.29100% 6.94%X 4.18女性血红蛋白含量的变异系数CV 4 100%100% 8.67%X117.6由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误S X来表示，由表4计算各项指标的标准误120.031 (10/L) .360男性红细胞数的标准误S X男性血红蛋白含量的标准误S X0.374 (g/L)女性红细胞数的标准误S X 0.29-255120.018(10 /L) S 7.1(3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100,可视为大样本 未知，但n 足够大，故总体均数的区间估计按(X u /2S X ,X u /2S X )计算。
该地男性红细胞数总体均数的 95%可信区间为:(4.66- 1.96 @031 , 4.66+ 1.96 @031),即(4.60,4.72)10%。
该地女性红细胞数总体均数的 95%可信区间为：(4.18 - 1.96 0.018,4.18+ 1.96 0.018), 即卩(4.14,4.22)1012/L 。
医学统计学分析计算题-答案 (1)
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
《医学统计学》计算题答案
《医学统计学》计算分析题参考答案孙振球主编. 医学统计学.第3版. 北京：人民卫生出版社，2010第二章计量资料的统计描述计算分析题（P26）1. 根据某单位的体检资料，116名正常成年女子的血清甘油三酯测量结果如下，请据此资料：（1）描述集中趋势应选择何指标？并计算之。
（2）描述离散趋势应选择何指标？并计算之。
（3）求该地正常成年女子血清甘油三酯的95%参考值范围。
（4）试估计该地正常成年女子血清甘油三脂在0.8mmol/L以下者及1.5mmol/L者各占正常成年女子总人数的百分比？表2-1某单位116名正常成年女子的血清甘油三酯（mmol/L）测量结果组段频数0.6~ 10.7~ 30.8~ 90.9~ 131.0~ 191.1~ 251.2~ 181.3~ 131.4~ 91.5~ 51.6~1.7 1合计116（1）数据文件数值变量名：组段，频数；用Compute产生新变量“组中值”（也可直接输入组中值）。
（2）操作步骤Analyze èData èWeight Cases ；Weight Cases by 频数。
Analyze èDescriptives èDescriptives ；将“组中值”选入V ariable 框中；单击OK 。
（3）结果解释表2-1显示某单位116名正常成年女子的血清甘油三酯测量结果呈正态分布，故选择均数描述集中趋势，选择标准差描述离散趋势。
某单位116名正常成年女子的血清甘油三酯测量结果的均数为1.16（mmol/L ），标准差为0.20（mmol/L ）；该地正常成年女子血清甘油三酯的95%参考值范围是（0.77，1.55）mmol/L 。
计算过程根据公式s x 96.1±，即1.16±1.96×0.20。
该单位正常成年女子血清甘油三酯在0.8 mmol/L 以下者估计占总人数的3.59％，1.5 mmol/L 以下者估计占总人数的95.54％。
医学统计学分析计算题-答案 (1)
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯= 由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
医学专业医学统计学试题(答案见标注)
医学专业医学统计学试题（答案见标注）姓名学号得分一．名词解释（请各举一例进行说明）（4分×4）1、概率2、抽样误差3、标准误4、可信区间二、单项选择题（2分×10）1．在对两个变量x与y进行直线相关分析后发现：相关系数r的值近似为0，经检验，得p>0.9。
下专业结论时，正确的表述应该是（）A、x与y之间呈直线关系B、x与y之间呈曲线关系C、x与y之间没有直线关系D、x与y之间毫无关系2．为了直观地比较化疗后相同时间点上一组乳腺癌患者血清肌酐和血液尿素氮两项指标观察值的变异程度的大小可选用的变异指标是（）A、标准差B、标准误C、变异系数D、算术平均数3．各观察值均加（或减）同一数后，（）A、均数不变，标准差改变B、均数改变，标准差不变C、两者均改变D、两者均不变4．为了解两种治疗方法对原发性肝癌的疗效，随机把病人分成两组，一组用5-氟尿嘧啶+辅助治疗，另一组用安慰剂+辅助治疗。
治疗结果按缓解、死亡划分。
第一组12人，7人缓解、5人死亡；第二组11人，4人缓解、7人死亡，要分析两种疗法的治疗效果之间的差别有无显著性意义，应选用的统计方法是：（）A x2检验B Fisher的精确概率C t 检验D 秩和检验5．正态分布曲线下，横轴上，从均数u到u+1.96σ的面积为：（）A、47.5%B、95%C、45%D、97.5%6.两样本均数的t检验，按0.05的检验水准拒绝H0，若此时推断有误，其错误的概率为（）（A）0.05 （B）>0.05 （C）<0.05 （D）不一定7．下列分布中，均数与方差相等的分布是（）A、Poisson分布B、正态分布C、t分布D、二项分布8．计算麻疹疫苗接种后血清检查的阳转率，分母为（）A、麻疹易感儿数B、麻疹患儿人数C、麻疹疫苗接种人数D、麻疹疫苗接种后的阳转人数9 .四个样本率作比较，2)3(05.02χχ>，可认为______。
医学统计学习题及答案
医学统计学习题及答案医学统计学是一门应用广泛的学科，它在医学研究和临床实践中扮演着重要的角色。
以下是一些医学统计学的基础习题及答案，供学习者参考。
习题一：描述性统计问题：某医院对100名患者的体重进行了测量，测得的平均体重为70公斤，标准差为10公斤。
请计算该组数据的变异系数。
答案：变异系数（Coefficient of Variation, CV）的计算公式为：\[ CV = \frac{标准差}{平均值} \times 100\% \]代入数据得：\[ CV = \frac{10}{70} \times 100\% \approx 14.29\% \]习题二：概率分布问题：假设某疾病的发病率为0.01，即每1000人中有1人患病。
如果随机抽取100人，求至少有1人患病的概率。
答案：使用二项分布的补数原理，计算没有人患病的概率，然后求其补数。
没有人患病的概率为：\[ P(0) = (1 - 0.01)^{100} \]至少有1人患病的概率为：\[ P(\geq 1) = 1 - P(0) \]习题三：假设检验问题：某药物对降低血压有显著效果。
在一项研究中，研究人员将100名高血压患者随机分为两组，每组50人。
一组接受药物治疗，另一组接受安慰剂。
治疗后，药物治疗组的平均血压降低了10毫米汞柱，而安慰剂组的平均血压降低了2毫米汞柱。
假设两组的血压降低量服从正态分布，标准差均为5毫米汞柱。
请问药物治疗是否显著优于安慰剂？答案：使用独立样本t检验来比较两组的血压降低量。
首先计算t值：\[ t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s^2}{n_1} +\frac{s^2}{n_2}}} \]其中，\(\bar{X}_1\) 和 \(\bar{X}_2\) 分别是两组的平均血压降低量，\(s\) 是标准差，\(n_1\) 和 \(n_2\) 是样本大小。
代入数据得：\[ t = \frac{10 - 2}{\sqrt{\frac{5^2}{50} + \frac{5^2}{50}}} \]计算t值后，与t分布的临界值进行比较，如果t值大于临界值，则拒绝原假设，认为药物治疗显著优于安慰剂。
(完整版)医学统计学试题及答案
第一套试卷及参考答案一、选择题（40分）1、根据某医院对急性白血病患者构成调查所获得的资料应绘制（ B ）A 条图B 百分条图或圆图C线图D直方图2、均数和标准差可全面描述 D 资料的特征A 所有分布形式Ｂ负偏态分布Ｃ正偏态分布Ｄ正态分布和近似正态分布3、要评价某市一名5岁男孩的身高是否偏高或偏矮，其统计方法是（A ）A 用该市五岁男孩的身高的95%或99%正常值范围来评价B 用身高差别的假设检验来评价C 用身高均数的95%或99%的可信区间来评价D 不能作评价4、比较身高与体重两组数据变异大小宜采用（A ）A 变异系数B 方差C 标准差D 四分位间距5、产生均数有抽样误差的根本原因是（ A ）A.个体差异B. 群体差异C. 样本均数不同D. 总体均数不同6. 男性吸烟率是女性的10倍，该指标为（A ）（A）相对比（B）构成比（C）定基比（D）率7、统计推断的内容为（ D ）A.用样本指标估计相应的总体指标B.检验统计上的“检验假设”C. A和B均不是D. A和B均是8、两样本均数比较用t检验，其目的是检验（ C ）A两样本均数是否不同B两总体均数是否不同C两个总体均数是否相同D两个样本均数是否相同9、有两个独立随机的样本，样本含量分别为n1和n2，在进行成组设计资料的t检验时，自由度是（D ）（A）n1+ n2（B）n1+ n2–1 （C）n1+ n2 +1 （D）n1+ n2 -210、标准误反映（A ）A 抽样误差的大小 B总体参数的波动大小 C 重复实验准确度的高低 D 数据的离散程度11、最小二乘法是指各实测点到回归直线的(C)Ａ垂直距离的平方和最小Ｂ垂直距离最小Ｃ纵向距离的平方和最小Ｄ纵向距离最小12、对含有两个随机变量的同一批资料,既作直线回归分析,又作直线相关分析。
令对相关系数检验的t值为t r，对回归系数检验的t值为t b，二者之间具有什么关系？（C）A t r>t bB t r<t bC t r= t b D二者大小关系不能肯定13、设配对资料的变量值为x1和x2，则配对资料的秩和检验（D ）A分别按x1和x2从小到大编秩B把x1和x2综合从小到大编秩C把x1和x2综合按绝对值从小到大编秩D把x1和x2的差数按绝对值从小到大编秩14、四个样本率作比较，χ2>χ20.05,ν可认为（ A ）A各总体率不同或不全相同 B各总体率均不相同C各样本率均不相同 D各样本率不同或不全相同15、某学院抽样调查两个年级学生的乙型肝炎表面抗原，其中甲年级调查35人，阳性人数4人；乙年级调查40人，阳性人数8人。
医学统计学试题(卷)与答案解析
第一套试卷及参考答案一、选择题（40分）1、根据某医院对急性白血病患者构成调查所获得的资料应绘制（ B ）A 条图B 百分条图或圆图 C线图 D直方图2、均数和标准差可全面描述 D 资料的特征A 所有分布形式Ｂ负偏态分布Ｃ正偏态分布Ｄ正态分布和近似正态分布3、要评价某市一名5岁男孩的身高是否偏高或偏矮，其统计方法是（ A ）A 用该市五岁男孩的身高的95%或99%正常值范围来评价B 用身高差别的假设检验来评价C 用身高均数的95%或99%的可信区间来评价D 不能作评价4、比较身高与体重两组数据变异大小宜采用（ A ）A 变异系数B 方差C 标准差D 四分位间距5、产生均数有抽样误差的根本原因是（ A ）A.个体差异B. 群体差异C. 样本均数不同D. 总体均数不同6. 男性吸烟率是女性的10倍，该指标为（ A ）（A）相对比（B）构成比（C）定基比（D）率7、统计推断的内容为（ D ）A.用样本指标估计相应的总体指标B.检验统计上的“检验假设”C. A和B均不是D. A和B均是8、两样本均数比较用t检验，其目的是检验（ C ）A两样本均数是否不同B两总体均数是否不同C两个总体均数是否相同 D两个样本均数是否相同9、有两个独立随机的样本，样本含量分别为n1和n2，在进行成组设计资料的t检验时，自由度是（ D ）（A）n1+ n2（B）n1+ n2–1 （C）n1+ n2 +1 （D） n1+ n2 -210、标准误反映（ A ）A 抽样误差的大小B总体参数的波动大小 C 重复实验准确度的高低 D 数据的离散程度11、最小二乘法是指各实测点到回归直线的 (C)Ａ垂直距离的平方和最小Ｂ垂直距离最小Ｃ纵向距离的平方和最小Ｄ纵向距离最小12、对含有两个随机变量的同一批资料,既作直线回归分析,又作直线相关分析。
令对相关系数检验的t值为t r，对回归系数检验的t值为t b，二者之间具有什么关系？（C）A t r>t bB t r<t bC t r= t b D二者大小关系不能肯定13、设配对资料的变量值为x1和x2，则配对资料的秩和检验（D ）A分别按x1和x2从小到大编秩B把x1和x2综合从小到大编秩C把x1和x2综合按绝对值从小到大编秩D把x1和x2的差数按绝对值从小到大编秩14、四个样本率作比较，χ2>χ20.05,ν可认为（ A ）A各总体率不同或不全相同B各总体率均不相同 C各样本率均不相同D各样本率不同或不全相同15、某学院抽样调查两个年级学生的乙型肝炎表面抗原，其中甲年级调查35人，阳性人数4人；乙年级调查40人，阳性人数8人。
医学统计学分析计算题_答案与解析
WORD文档下载可编辑第二单元计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数/1012·L-1男360 4.66 0.58 4.84女255 4.18 0.29 4.33血红蛋白/g·L-1男360 134.5 7.1 140.2女255 117.6 10.2 124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？(2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18SCVX=⨯=⨯=女性血红蛋白含量的变异系数10.2100%100%8.67%117.6SCVX=⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
(完整版)医学统计学试题及答案
第一套试卷及参考答案一、选择题（40分）1、根据某医院对急性白血病患者构成调查所获得的资料应绘制（ B ）A 条图B 百分条图或圆图C线图D直方图2、均数和标准差可全面描述 D 资料的特征A 所有分布形式Ｂ负偏态分布Ｃ正偏态分布Ｄ正态分布和近似正态分布3、要评价某市一名5岁男孩的身高是否偏高或偏矮，其统计方法是（A ）A 用该市五岁男孩的身高的95%或99%正常值范围来评价B 用身高差别的假设检验来评价C 用身高均数的95%或99%的可信区间来评价D 不能作评价4、比较身高与体重两组数据变异大小宜采用（A ）A 变异系数B 方差C 标准差D 四分位间距5、产生均数有抽样误差的根本原因是（ A ）A.个体差异B. 群体差异C. 样本均数不同D. 总体均数不同6. 男性吸烟率是女性的10倍，该指标为（A ）（A）相对比（B）构成比（C）定基比（D）率7、统计推断的内容为（ D ）A.用样本指标估计相应的总体指标B.检验统计上的“检验假设”C. A和B均不是D. A和B均是8、两样本均数比较用t检验，其目的是检验（ C ）A两样本均数是否不同B两总体均数是否不同C两个总体均数是否相同D两个样本均数是否相同9、有两个独立随机的样本，样本含量分别为n1和n2，在进行成组设计资料的t检验时，自由度是（D ）（A）n1+ n2（B）n1+ n2–1 （C）n1+ n2 +1 （D）n1+ n2 -210、标准误反映（A ）A 抽样误差的大小 B总体参数的波动大小 C 重复实验准确度的高低 D 数据的离散程度11、最小二乘法是指各实测点到回归直线的(C)Ａ垂直距离的平方和最小Ｂ垂直距离最小Ｃ纵向距离的平方和最小Ｄ纵向距离最小12、对含有两个随机变量的同一批资料,既作直线回归分析,又作直线相关分析。
令对相关系数检验的t值为t r，对回归系数检验的t值为t b，二者之间具有什么关系？（C）A t r>t bB t r<t bC t r= t b D二者大小关系不能肯定13、设配对资料的变量值为x1和x2，则配对资料的秩和检验（D ）A分别按x1和x2从小到大编秩B把x1和x2综合从小到大编秩C把x1和x2综合按绝对值从小到大编秩D把x1和x2的差数按绝对值从小到大编秩14、四个样本率作比较，χ2>χ20.05,ν可认为（ A ）A各总体率不同或不全相同 B各总体率均不相同C各样本率均不相同 D各样本率不同或不全相同15、某学院抽样调查两个年级学生的乙型肝炎表面抗原，其中甲年级调查35人，阳性人数4人；乙年级调查40人，阳性人数8人。
医学统计学分析计算题_答案与解析
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标 性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯= 由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
《医学统计学》计算题答案
《医学统计学》计算分析题参考答案孙振球主编. 医学统计学.第3版. 北京：人民卫生出版社，2010第二章计量资料的统计描述计算分析题（P26）1. 根据某单位的体检资料，116名正常成年女子的血清甘油三酯测量结果如下，请据此资料：（1）描述集中趋势应选择何指标？并计算之。
（2）描述离散趋势应选择何指标？并计算之。
（3）求该地正常成年女子血清甘油三酯的95%参考值范围。
（4）试估计该地正常成年女子血清甘油三脂在0.8mmol/L以下者及1.5mmol/L者各占正常成年女子总人数的百分比？表2-1某单位116名正常成年女子的血清甘油三酯（mmol/L）测量结果组段频数0.6~ 10.7~ 30.8~ 90.9~ 131.0~ 191.1~ 251.2~ 181.3~ 131.4~ 91.5~ 51.6~1.7 1合计116（1）数据文件数值变量名：组段，频数；用Compute产生新变量“组中值”（也可直接输入组中值）。
（2）操作步骤Analyze èData èWeight Cases ；Weight Cases by 频数。
Analyze èDescriptives èDescriptives ；将“组中值”选入V ariable 框中；单击OK 。
（3）结果解释表2-1显示某单位116名正常成年女子的血清甘油三酯测量结果呈正态分布，故选择均数描述集中趋势，选择标准差描述离散趋势。
某单位116名正常成年女子的血清甘油三酯测量结果的均数为1.16（mmol/L ），标准差为0.20（mmol/L ）；该地正常成年女子血清甘油三酯的95%参考值范围是（0.77，1.55）mmol/L 。
计算过程根据公式s x 96.1±，即1.16±1.96×0.20。
该单位正常成年女子血清甘油三酯在0.8 mmol/L 以下者估计占总人数的3.59％，1.5 mmol/L 以下者估计占总人数的95.54％。
医学统计学分析计算题答案
医学统计学分析计算题答案第⼆单元计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成⼈的红细胞数和⾎红蛋⽩量，结果见表4：表4 某年某地健康成年⼈的红细胞数和⾎红蛋⽩含量指标性别例数均数标准差标准值*红细胞数/1012·L-1男360 4.660.58 4.84⼥255 4.180.29 4.33⾎红蛋⽩/g·L-1男360134.57.1140.2⼥255117.610.2124.7请就上表资料：(1) 说明⼥性的红细胞数与⾎红蛋⽩的变异程度何者为⼤？(2) 分别计算男、⼥两项指标的抽样误差。
(3) 试估计该地健康成年男、⼥红细胞数的均数。
(4) 该地健康成年男、⼥⾎红蛋⽩含量有⽆差别？(5) 该地男、⼥两项⾎液指标是否均低于上表的标准值（若测定⽅法相同）？ 2.1解：(1) 红细胞数和⾎红蛋⽩含量的分布⼀般为正态分布，但⼆者的单位不⼀致，应采⽤变异系数(CV )⽐较⼆者的变异程度。
⼥性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X === ⼥性⾎红蛋⽩含量的变异系数10.2100%100%8.67%117.6S CV X === 由此可见，⼥性⾎红蛋⽩含量的变异程度较红细胞数的变异程度⼤。
(2) 抽样误差的⼤⼩⽤标准误X S 来表⽰，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L) 男性⾎红蛋⽩含量的标准误0.374X S ===(g/L) ⼥性红细胞数的标准误0.018X S ===(1210/L) ⼥性⾎红蛋⽩含量的标准误0.639X S ===(g/L) (3) 本题采⽤区间估计法估计男、⼥红细胞数的均数。
样本含量均超过100，可视为⼤样本。
σ未知，但n ⾜够⼤，故总体均数的区间估计按(/2/2X X X u S X u S αα-+ ,)计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标 性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
该地女性红细胞数总体均数的95%可信区间为：(4.18－1.96×0.018 , 4.18＋1.96×0.018)，即(4.14 , 4.22)1210/L 。
(4) 两成组大样本均数的比较，用u 检验。
1) 建立检验假设，确定检验水准H 0：12μμ=，即该地健康成年男、女血红蛋白含量均数无差别 H 1：12μμ≠，即该地健康成年男、女血红蛋白含量均数有差别0.05α=2) 计算检验统计量22.829X X u ===3) 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地健康成年男、女的血红蛋白含量均数不同，男性高于女性。
(5) 样本均数与已知总体均数的比较，因样本含量较大，均作近似u 检验。
1) 男性红细胞数与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地男性红细胞数的均数等于标准值H 1：0μμ<，即该地男性红细胞数的均数低于标准值 单侧0.05α= ② 计算检验统计量0 4.66 4.845.8060.031X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性红细胞数的均数低于标准值。
2) 男性血红蛋白含量与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地男性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地男性血红蛋白含量的均数低于标准值 单侧0.05α= ② 计算检验统计量0134.5140.215.2410.374X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性血红蛋白含量的均数低于标准值。
3) 女性红细胞数与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地女性红细胞数的均数等于标准值 H 1：0μμ<，即该地女性红细胞数的均数低于标准值 单侧0.05α= ② 计算检验统计量0 4.18 4.338.3330.018X X t S μ--===-③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性红细胞数的均数低于标准值。
4) 女性血红蛋白含量与标准值的比较 ① 建立检验假设，确定检验水准H 0：0μμ=，即该地女性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地女性血红蛋白含量的均数低于标准值 单侧0.05α= ② 计算检验统计量0117.6124.711.1110.639X X t S μ--===- ③ 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性血红蛋白含量的均数低于标准值。
2.2 为了解某高寒地区小学生血红蛋白含量的平均水平，某人于1993年6月随机抽取了该地小学生708名，算得其血红蛋白均数为103.5g/L ，标准差为1.59g/L 。
试求该地小学生血红蛋白均数的95%可信区间。
2.2解：σ未知，n 足够大时，总体均数的区间估计可用(/2/2X X X u S X u S αα-+ , )。
该地小学生血红蛋白含量均数的95％可信区间为：(103.5 1.96103.5 1.96-+, )，即(103.38 , 103.62)g/L 。
2.3 一药厂为了解其生产的某药物（同一批次）之有效成分含量是否符合国家规定的标准，随机抽取了该药10片，得其样本均数为103.0mg ，标准差为2.22mg 。
试估计该批药剂有效成分的平均含量。
2.3解：该批药剂有效成分的平均含量的点值估计为103.0 mg 。
σ未知且n 很小时，总体均数的区间估计可用()/2,/2,X X X t S X t S αναν-+ , 估计。
查t 界值表得t 0.05/2,9=2.262，该批药剂有效成分的平均含量的95％可信区间为：(103.0 2.262103.0 2.262-+, ，即(101.41 , 104.59)mg 。
2.4 152例麻疹患儿病后血清抗体滴度倒数的分布如表5，试作总体几何均数的点值估计和95%区间估计。
表5 152例麻疹患儿病后血清抗体滴度倒数的分布滴度倒数 1 2 4 8 16 32 64 128 256 512 1024 合计 人 数171031334224311522.4解：将原始数据取常用对数后记为X ，则152 1.85970.44250.0359X n X S S ====，，，，用(/2/2X X X u S X u S αα-+，)估计，则滴度倒数对数值的总体均数的95％可信区间为：(1.8597 1.960.0359 1.8597 1.960.0359-⨯+⨯ , )，即(1.7893 , 1.9301)。
所以滴度倒数的总体几何均数的点估计值为： 1.8597101072.39X ==，滴度倒数的总体几何均数的95%区间估计为( 1.7893 1.93011010, )，即(61.56 , 85.13)。
SPSS 操作 数据录入：打开SPSS Data Editor 窗口，点击Variable View 标签，定义要输入的变量x 和f ；再点击Data View 标签，录入数据（见图2.4.1，图2.4.2）。
图2..4.1 Variable View窗口内定义要输入的变量x和f图2.4.2 Data View窗口内录入数据分析：Transform Compute…Target Variable：键入 logxNumeric Expression： LG10(x) 将原始数据取对数值OKData Weight Cases…Weight cases by Frequency Variable： f 权重为fOKAnalyze Descriptive Statistics Explore… 探索性分析Dependent list：logx 分析变量logx Display： StatisticsS tatistics…：Descriptives 统计描述注：最后得到结果是原始数据对数值的均数及其95%可信区间。
2.5 某口腔医生欲比较“个别取模器龈下取模技术”与“传统硅橡胶取模方法”两种取模技术精度的差异，在12名病人口中分别用两种方法制取印模，在体视显微镜下测量标志点到龈沟底的距离，结果如表6，问两种取模方法结果有无差异？表6 12个病人口腔某测量标志点到龈沟底的距离/cm病例号个别取模器龈下取模技术传统硅橡胶取模方法1 0.626 0.6142 0.627 0.6263 0.670 0.6544 0.548 0.5495 0.590 0.5746 0.603 0.5877 0.605 0.6028 0.347 0.3389 0.768 0.75910 0.576 0.57211 0.330 0.31812 0.233 0.2192.5解：本题为配对设计的两样本均数的比较，采用配对t检验。
表2.5.1 12个病人口腔某测量标志点到龈沟底的距离/cm(1) 建立检验假设，确定检验水准H 0：0d μ=，即两种取模方法结果无差异 H 1：0d μ≠，即两种取模方法结果有差异0.05α=(2) 计算检验统计量两种取模方法结果的差值d 的计算见表2.5.1。
120.00930.00610.0018d d n d S S ====， ，， 00.00935.1670.0018d d t S -=== 112111n ν=-=-=(3) 确定P 值，作出统计推断查t 界值表得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为两种取模方法结果有差异，个别取模器龈下取模法标志点到龈沟底的距离略高于传统硅胶取模法。
病例号 个别取模器龈下取模1d 传统硅橡胶取模法2d12d d d =-1 0.626 0.614 0.012 2 0.627 0.626 0.0013 0.670 0.654 0.016 4 0.548 0.549 -0.0015 0.590 0.574 0.016 6 0.603 0.587 0.016 7 0.605 0.602 0.0038 0.347 0.338 0.009 9 0.768 0.759 0.009 10 0.576 0.572 0.004 11 0.330 0.318 0.012 120.2330.2190.014SPSS操作数据录入：打开SPSS Data Editor窗口，点击Variable View标签，定义要输入的变量x1和x2；再点击Data View标签，录入数据（见图2.5.1，图2.5.2）。