医学统计学分析计算题-答案(1)
医学统计学习题答案1
习题答案第一章思考题答案1.某医生收治200名患者，随机分成2组，每组100人。
一组用A药，另一组用B药。
经过2个月的治疗，A药组治愈了90人，B组治愈了85名患者，请根据现有结果评议下列说法是否正确，为什么a)A药组的疗效高于B药组。
(对,但不提倡这样说,原因是容易被误解)b)A药的疗效高于B药。
(不对,这是针对总体而言的)2.某校同一年级的A班和B班用同一试卷进行一次数学测验。
经过盲态改卷后，公布成绩：A班的平均成绩为80分，B班的平均成绩为81分，请评议下列说法是否正确，为什么a)可以称A班的这次考试的平均成绩低于B班，不存在抽样误差。
(对)b)通过这次考试的平均成绩，说明B班的数学平均水平高于A班。
(不对,一次考试只是一次抽样的结果)c)对于评价两个班级的数学平均水平而言，这次考试成绩只是一次抽样观察结果，所以存在抽样误差，不能仅凭这次考试的平均分差异推断两个班级的平均水平的高低。
(对)d)对于研究两个班级的这次考试成绩而言，A班所有学生的这次考试成绩构成了一个总体A，B班所有学生的这次考试成绩构成了一个总体B。
(对)：3. 请根据变量和资料分类的定义，评议下列说法是否正确，为什么a)如果变量取值中含有小数点，则该变量为连续型变量。
(不对,离散型变量取值也可以定义为取值含有小数点)b)如果资料为离散型变量的取值，则该资料一定为分类资料。
(不对,如白细胞计数,这是离散型的资料,但不具有分类性质)c)某研究者观察某个患者的24小时的心电图，发现该患者在这24小时中共有90个早博，并记为90个早博/24小时，故该资料也有量纲。
根据定义，应认为该资料为计量资料。
(本质上这是个体计数资料,但因为不具有分类意义,所以通常按计数资料进行统计分析)第二章习题的答案1. 是非题(1) 不论数据呈什么分布，都可以用算术均数和中位数表示其平均水平。
（错）(2) 少数几个数据比大多数数据大几百倍，一般不宜用算术均数表示其平均水平。
医学统计学分析计算题答案
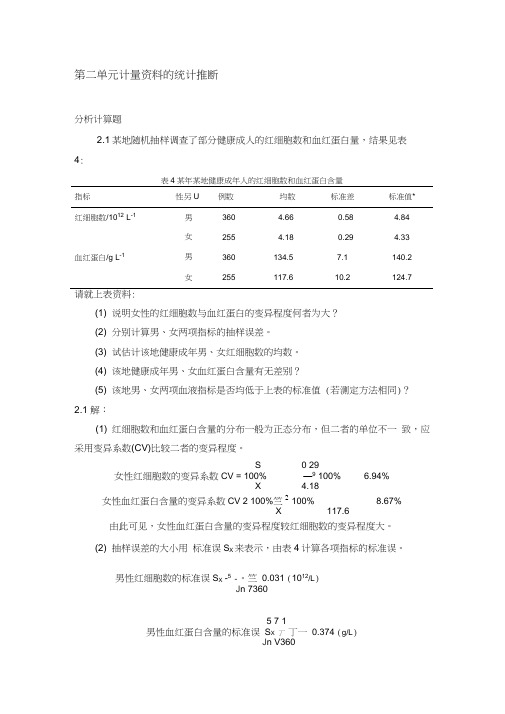
第二单元计量资料的统计推断分析计算题2.1某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4:表4某年某地健康成年人的红细胞数和血红蛋白含量指标性另U例数均数标准差标准值*红细胞数/1012L-1男360 4.660.58 4.84女255 4.180.29 4.33血红蛋白/g L-1男360134.57.1140.2女255117.610.2124.7请就上表资料:(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？(2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值 (若测定方法相同)？2.1 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。
S 0 29女性红细胞数的变异系数CV = 100% —9 100% 6.94%X 4.18女性血红蛋白含量的变异系数CV 2 100%竺2100% 8.67%X 117.6由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误S X来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误S X -5-。
竺0.031 (1012/L)J n 73605 7 1男性血红蛋白含量的标准误S X丁丁一0.374 (g/L)J n V360可视为大样本。
未知，但n 足够大，故总体均数的区间估计按该地男性红细胞数总体均数的 95%可信区间为:(4.66— 1.96 0.031 , 4.66+ 1.96 E .031),即(4.60,4.72)1012/L 。
该地女性红细胞数总体均数的 95%可信区间为：(4.18— 1.96 0.018,4.18+ 1.96 0.018), 即(4.14,4.22)1012/L 。
医学统计学分析计算题-答案(1)
第二单元 计量资料的统计推断分析计算题某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数标准差 标准值*红细胞数/1012·L -1 男 360女 255 血红蛋白/g ·L -1 男 360女255请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大 (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同） 解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
该地女性红细胞数总体均数的95%可信区间为：－× , ＋×，即 , 1210/L 。
医学统计学分析计算题-答案
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别例 数 均 数 标准差 标准值* 红细胞数/1012·L -1男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
医学统计学练习(一)
---------------------------------------------------------------最新资料推荐------------------------------------------------------医学统计学练习(一)联系要求：1、将答案写在答题纸上，下次上课上交。
2、计算题只写出分析方法，不需要进行计算。
医学统计学练习题（一）第六章方差分析 1．方差分析的基本思想？ 2．方差分析的条件？ 3．简述随机区组设计、拉丁方设计、交叉设计、析因设计、正交设计的主要设计要点及其变异度分解方法。
4．简述重复测量数据方差分析的应用条件。
5．有 3 组进食高脂饮食的家兔，接受不同处理后，测定其血清肾素血管紧张素转化酶（ACE）浓度，试比较三组家兔的血清 ACE 浓度。
3 组家兔的血清 ACE 浓度对照组 61.24 58.65 46.79 37.43 66.54 59.27 A 降脂药 82.35 56.47 61.57 48.79 62.54 60.87 B 降脂药 26.23 46.87 24.36 38.54 42.16 30.33 6．为研究注射不同剂量植物雌激素大豆异黄酮单体对大白鼠子宫重量的影响，取 5 窝不同种系的大白鼠，每窝 3 只，随机地分配到 3 个组内接受不同剂量大豆异黄酮单体的注射，然后测定其子宫重量，结果见下表。
问注射不同剂量的大豆异黄酮单体对大白鼠子宫重量是否有影响?3 组大白鼠子宫重量大白鼠种系大豆异黄酮单体剂量(g/100g)0.25 0.5 0.751 102 117 1452 56 68 118 3 67 96 1364 73 89 1245 53 68 102 7．某中医院研究中药复方（A 药）治疗高血压的疗效，以传1 / 5统的抗高血压卡托普利（B 药）作对照。
同时还考虑个体差异与给药 A、B 顺序对收缩压的影响。
通过交叉设计进行临床研究，记录患者服用 A、B 两种药物结果见下表。
医学统计学分析计算题-答案 (1)
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
医学统计学试题及答案
医学统计学试题及答案一、选择题（每题2分，共20分）1. 医学统计学中的“总体”是指：A. 所有可能的样本B. 所有可能的个体C. 研究中所关注的全部个体D. 研究中实际测量到的个体答案：C2. 以下哪个是参数估计的常用方法？A. 描述性统计B. 假设检验C. 点估计D. 方差分析答案：C3. 以下哪个是描述数据离散程度的统计量？A. 平均数B. 中位数C. 标准差D. 众数答案：C4. 医学统计学中的“样本”是指：A. 研究中实际测量到的个体B. 所有可能的个体C. 研究中所关注的全部个体D. 所有可能的样本答案：A5. 以下哪个是医学统计学中的“误差”？A. 抽样误差B. 系统误差C. 随机误差D. 所有选项都是答案：D6. 以下哪个是正态分布的特点？A. 均数、中位数、众数相等B. 均数大于中位数C. 中位数大于众数D. 众数大于均数答案：A7. 以下哪个是相关系数的取值范围？A. -1到1B. 0到1C. -∞到∞D. 1到∞答案：A8. 以下哪个是医学统计学中常用的非参数检验方法？A. t检验B. 方差分析C. 卡方检验D. 秩和检验答案：D9. 以下哪个是医学统计学中的“效应量”？A. 样本量B. 效应大小C. 标准差D. 信度答案：B10. 以下哪个是医学统计学中的“混杂因素”？A. 研究设计中的变量B. 研究中的误差来源C. 影响研究结果的外部因素D. 研究中的随机误差答案：C二、简答题（每题5分，共20分）1. 简述医学统计学中的“假设检验”。
答案：假设检验是统计学中用于检验研究假设是否成立的一个过程。
它通常包括零假设（H0）和备择假设（H1）。
通过收集数据并进行统计分析，我们可以决定是接受零假设还是拒绝零假设，从而支持或反对研究假设。
2. 解释什么是“置信区间”。
答案：置信区间是参数估计中用来表示估计值的可信程度的一个范围。
它给出了一个区间，在这个区间内，我们相信参数的真实值有一定概率（如95%）会落在这个范围内。
《医学统计学》计算题答案
《医学统计学》计算分析题参考答案孙振球主编. 医学统计学.第3版. 北京：人民卫生出版社，2010第二章计量资料的统计描述计算分析题（P26）1. 根据某单位的体检资料，116名正常成年女子的血清甘油三酯测量结果如下，请据此资料：（1）描述集中趋势应选择何指标？并计算之。
（2）描述离散趋势应选择何指标？并计算之。
（3）求该地正常成年女子血清甘油三酯的95%参考值范围。
（4）试估计该地正常成年女子血清甘油三脂在0.8mmol/L以下者及1.5mmol/L者各占正常成年女子总人数的百分比？表2-1某单位116名正常成年女子的血清甘油三酯（mmol/L）测量结果组段频数0.6~ 10.7~ 30.8~ 90.9~ 131.0~ 191.1~ 251.2~ 181.3~ 131.4~ 91.5~ 51.6~1.7 1合计116（1）数据文件数值变量名：组段，频数；用Compute产生新变量“组中值”（也可直接输入组中值）。
（2）操作步骤Analyze èData èWeight Cases ；Weight Cases by 频数。
Analyze èDescriptives èDescriptives ；将“组中值”选入V ariable 框中；单击OK 。
（3）结果解释表2-1显示某单位116名正常成年女子的血清甘油三酯测量结果呈正态分布，故选择均数描述集中趋势，选择标准差描述离散趋势。
某单位116名正常成年女子的血清甘油三酯测量结果的均数为1.16（mmol/L ），标准差为0.20（mmol/L ）；该地正常成年女子血清甘油三酯的95%参考值范围是（0.77，1.55）mmol/L 。
计算过程根据公式s x 96.1±，即1.16±1.96×0.20。
该单位正常成年女子血清甘油三酯在0.8 mmol/L 以下者估计占总人数的3.59％，1.5 mmol/L 以下者估计占总人数的95.54％。
（完整版）医学统计学试题和答案
（一）单项选择题3．抽样的目的是（ b ）。
A．研究样本统计量 B. 由样本统计量推断总体参数C．研究典型案例研究误差 D. 研究总体统计量4．参数是指（b ）。
A．参与个体数 B. 总体的统计指标C．样本的统计指标 D. 样本的总和5．关于随机抽样，下列那一项说法是正确的（ a ）。
A．抽样时应使得总体中的每一个个体都有同等的机会被抽取B．研究者在抽样时应精心挑选个体，以使样本更能代表总体C．随机抽样即随意抽取个体D．为确保样本具有更好的代表性，样本量应越大越好6.各观察值均加（或减）同一数后（ b ）。
A.均数不变，标准差改变B.均数改变，标准差不变C.两者均不变D.两者均改变7.比较身高和体重两组数据变异度大小宜采用（ a ）。
A.变异系数B.差C.极差D.标准差8.以下指标中（d）可用来描述计量资料的离散程度。
A.算术均数B.几何均数C.中位数D.标准差9.偏态分布宜用（c）描述其分布的集中趋势。
A.算术均数B.标准差C.中位数D.四分位数间距10.各观察值同乘以一个不等于0的常数后，（b）不变。
A．算术均数 B.标准差C.几何均数D.中位数11.（ a ）分布的资料，均数等于中位数。
A.对称B.左偏态C.右偏态D.偏态12.对数正态分布是一种（ c ）分布。
A.正态B.近似正态C.左偏态D.右偏态13.最小组段无下限或最大组段无上限的频数分布资料，可用（ c ）描述其集中趋势。
A.均数B.标准差C.中位数D.四分位数间距14.（ c ）小，表示用该样本均数估计总体均数的可靠性大。
A. 变异系数B.标准差C. 标准误D.极差15.血清学滴度资料最常用来表示其平均水平的指标是（ c ）。
A. 算术平均数B.中位数C.几何均数D. 平均数16.变异系数CV的数值（ c ）。
A. 一定大于 1B.一定小于 1C. 可大于1，也可小于 1D.一定比标准差小17.数列8、-3、5、0、1、4、-1的中位数是（ b ）。
卫生统计学考试试题及答案
卫生统计学试题及答案（一）1.用某地6〜16岁学生近视情况的调查资料制作统计图，以反映患者的年龄分布，可用图形种类为.A.普通线图B.半对数线图C.直方图D.直条图E.复式直条图【答案】C （6——16岁为连续变量，得到的是连续变量的频数分布）直方图（适用于数值变量，连续性资料的频数表变量）直条图（适用于彼此独立的资料）2.为了反映某地区五年期间鼻咽癌死亡病例的年龄分布，可采用.A.直方图B.普通线图C.半对数线图D.直条图E.复式直条图（一个检测指标，两个分组变量）【答案】E3.为了反映某地区2000~1974年男性肺癌年龄别死亡率的变化情况，可采用.A.直方图B.普通线图（适用于随时间变化的连续性资料，用线段的升降表示某事物在时间上的发展变化趋势）C.半对数线图（适用于随时间变化的连续性资料，尤其比较数值相差悬殊的多组资料时采用，线段的升降用来表示某事物的发展速度）D.直条图E.复式直条图【答案】E4.调查某疫苗在儿童中接种后的预防效果，在某地全部1000名易感儿童中进行接种，经一定时间后从中随机抽取300名儿童做效果测定，得阳性人数228名。
若要研究该疫苗在该地儿童中的接种效果，则 .A.该研究的样本是1000名易感儿童B.该研究的样本是228名阳性儿童C.该研究的总体是300名易感儿童D.该研究的总体是1000名易感儿童E.该研究的总体是228名阳性儿童【答案】D5.若要通过样本作统计推断，样本应是.A.总体中典型的一部分B.总体中任一部分C.总体中随机抽取的一部分D.总体中选取的有意义的一部分E.总体中信息明确的一部分6.下面关于均数的正确的说法是.A.当样本含量增大时，均数也增大B.均数总大于中位数C.均数总大于标准差D.均数是所有观察值的平均值E.均数是最大和最小值的平均值【答案】D7.某地易感儿童注射乙肝疫苗后，从中随机抽取100名儿童测量其乙肝表面抗体滴度水平，欲描述其平均水平，宜采用 .A.均数B.几何均数C.中位数D.方差E.四分位数间距【答案】B几何均数（geometric mean是用于反映一组经对数转换后呈对称分布的变量值在数量上的平均水平，在医学研究中常适用于免疫学的指标。
医学统计学试题及答案
第一套试卷及参考答案一、选择题(40分）1、根据某医院对急性白血病患者构成调查所获得的资料应绘制( B ）A 条图B 百分条图或圆图C线图D直方图2、均数和标准差可全面描述 D 资料的特征A 所有分布形式Ｂ负偏态分布Ｃ正偏态分布Ｄ正态分布和近似正态分布3、要评价某市一名5岁男孩的身高是否偏高或偏矮，其统计方法是（A ）A 用该市五岁男孩的身高的95％或99％正常值范围来评价B 用身高差别的假设检验来评价C 用身高均数的95％或99％的可信区间来评价D 不能作评价4、比较身高与体重两组数据变异大小宜采用（A ）A 变异系数B 方差C 标准差D 四分位间距5、产生均数有抽样误差的根本原因是（ A ）A。
个体差异 B. 群体差异 C. 样本均数不同D。
总体均数不同6. 男性吸烟率是女性的10倍,该指标为( A )（A）相对比（B）构成比（C）定基比（D）率7、统计推断的内容为( D ）A.用样本指标估计相应的总体指标B.检验统计上的“检验假设"C. A和B均不是 D。
A和B均是8、两样本均数比较用t检验,其目的是检验（ C )A两样本均数是否不同B两总体均数是否不同C两个总体均数是否相同D两个样本均数是否相同9、有两个独立随机的样本，样本含量分别为n1和n2，在进行成组设计资料的t检验时,自由度是（D ）(A）n1+ n2（B）n1+ n2–1 (C）n1+ n2 +1 （D）n1+ n2—210、标准误反映（A )A 抽样误差的大小 B总体参数的波动大小 C 重复实验准确度的高低 D 数据的离散程度11、最小二乘法是指各实测点到回归直线的(C)Ａ垂直距离的平方和最小Ｂ垂直距离最小Ｃ纵向距离的平方和最小Ｄ纵向距离最小12、对含有两个随机变量的同一批资料,既作直线回归分析,又作直线相关分析。
令对相关系数检验的t值为t r，对回归系数检验的t值为t b，二者之间具有什么关系？（C)A t r〉t bB t r〈t bC t r= t b D二者大小关系不能肯定13、设配对资料的变量值为x1和x2，则配对资料的秩和检验（D )A分别按x1和x2从小到大编秩B把x1和x2综合从小到大编秩C把x1和x2综合按绝对值从小到大编秩D把x1和x2的差数按绝对值从小到大编秩14、四个样本率作比较,χ2〉χ20。
医学统计学分析计算题-答案 (1)
第二单元 计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性 别 例 数 均 数 标准差 标准值* 红细胞数/1012·L -1 男 360 4.66 0.58 4.84女 255 4.18 0.29 4.33 血红蛋白/g ·L -1 男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯= 由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
医学专业医学统计学试题(答案见标注)
医学专业医学统计学试题（答案见标注）姓名学号得分一．名词解释（请各举一例进行说明）（4分×4）1、概率2、抽样误差3、标准误4、可信区间二、单项选择题（2分×10）1．在对两个变量x与y进行直线相关分析后发现：相关系数r的值近似为0，经检验，得p>0.9。
下专业结论时，正确的表述应该是（）A、x与y之间呈直线关系B、x与y之间呈曲线关系C、x与y之间没有直线关系D、x与y之间毫无关系2．为了直观地比较化疗后相同时间点上一组乳腺癌患者血清肌酐和血液尿素氮两项指标观察值的变异程度的大小可选用的变异指标是（）A、标准差B、标准误C、变异系数D、算术平均数3．各观察值均加（或减）同一数后，（）A、均数不变，标准差改变B、均数改变，标准差不变C、两者均改变D、两者均不变4．为了解两种治疗方法对原发性肝癌的疗效，随机把病人分成两组，一组用5-氟尿嘧啶+辅助治疗，另一组用安慰剂+辅助治疗。
治疗结果按缓解、死亡划分。
第一组12人，7人缓解、5人死亡；第二组11人，4人缓解、7人死亡，要分析两种疗法的治疗效果之间的差别有无显著性意义，应选用的统计方法是：（）A x2检验B Fisher的精确概率C t 检验D 秩和检验5．正态分布曲线下，横轴上，从均数u到u+1.96σ的面积为：（）A、47.5%B、95%C、45%D、97.5%6.两样本均数的t检验，按0.05的检验水准拒绝H0，若此时推断有误，其错误的概率为（）（A）0.05 （B）>0.05 （C）<0.05 （D）不一定7．下列分布中，均数与方差相等的分布是（）A、Poisson分布B、正态分布C、t分布D、二项分布8．计算麻疹疫苗接种后血清检查的阳转率，分母为（）A、麻疹易感儿数B、麻疹患儿人数C、麻疹疫苗接种人数D、麻疹疫苗接种后的阳转人数9 .四个样本率作比较，2)3(05.02χχ>，可认为______。
医学统计学习题及答案
医学统计学习题及答案医学统计学是一门应用广泛的学科，它在医学研究和临床实践中扮演着重要的角色。
以下是一些医学统计学的基础习题及答案，供学习者参考。
习题一：描述性统计问题：某医院对100名患者的体重进行了测量，测得的平均体重为70公斤，标准差为10公斤。
请计算该组数据的变异系数。
答案：变异系数（Coefficient of Variation, CV）的计算公式为：\[ CV = \frac{标准差}{平均值} \times 100\% \]代入数据得：\[ CV = \frac{10}{70} \times 100\% \approx 14.29\% \]习题二：概率分布问题：假设某疾病的发病率为0.01，即每1000人中有1人患病。
如果随机抽取100人，求至少有1人患病的概率。
答案：使用二项分布的补数原理，计算没有人患病的概率，然后求其补数。
没有人患病的概率为：\[ P(0) = (1 - 0.01)^{100} \]至少有1人患病的概率为：\[ P(\geq 1) = 1 - P(0) \]习题三：假设检验问题：某药物对降低血压有显著效果。
在一项研究中，研究人员将100名高血压患者随机分为两组，每组50人。
一组接受药物治疗，另一组接受安慰剂。
治疗后，药物治疗组的平均血压降低了10毫米汞柱，而安慰剂组的平均血压降低了2毫米汞柱。
假设两组的血压降低量服从正态分布，标准差均为5毫米汞柱。
请问药物治疗是否显著优于安慰剂？答案：使用独立样本t检验来比较两组的血压降低量。
首先计算t值：\[ t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s^2}{n_1} +\frac{s^2}{n_2}}} \]其中，\(\bar{X}_1\) 和 \(\bar{X}_2\) 分别是两组的平均血压降低量，\(s\) 是标准差，\(n_1\) 和 \(n_2\) 是样本大小。
代入数据得：\[ t = \frac{10 - 2}{\sqrt{\frac{5^2}{50} + \frac{5^2}{50}}} \]计算t值后，与t分布的临界值进行比较，如果t值大于临界值，则拒绝原假设，认为药物治疗显著优于安慰剂。
卫生统计学试题与答案1
卫⽣统计学试题与答案1⼀、选择题1.对两个定量变量同时进⾏了直线相关和直线回归分析，r有统计学意义（P<0.05），则_____.A.b⽆统计学意义B.b有⾼度统计学意义C.b有统计学意义D.不能肯定b有⽆统计学意义E.a有统计学意义【答案】C2.关于基于秩次的⾮参数检验，下列说法错误的是_____.A.符号秩和检验中，差值为零不参加编秩B.两样本⽐较的秩和检验⽅法中的正态近似法为参数检验C.当符合正态假定时，⾮参数检验犯II类错误的概率较参数检验⼤D.当样本⾜够⼤时，秩和分布近似正态E.秩和检验适⽤于检验等级资料、可排序资料和分布不明资料的差异【答案】B3.随机事件的概率为______.B.P=0C.P=－0.5D.0≤P≤1E.－0.5< p="">【答案】D4.两样本均数⽐较，经t检验得出差别有统计学意义的结论时，P越⼩，说明______.A.两样本均数差别越⼤B.两总体均数差别越⼤C.越有理由认为两总体均数不同D.越有理由认为两样本均数不同E.越有理由认为两总体均数相同【答案】C5.为研究缺氧对正常⼈⼼率的影响，有50名志愿者参加试验，分别测得试验前后的⼼率，应⽤何种统计检验⽅法来较好地分析此数据_____.A.配对t检验B.成组t检验C.成组秩和检验D.配对秩和检验E.两组⽅差齐性检验【答案】A6.作符号秩和检验时，记统计量T为较⼩的秩和，则正确的是_____.A.T值越⼤P值越⼩B.T值越⼤越有理由拒绝H0C.P值与T值毫⽆联系D.T值越⼩P值越⼩E.以上都不对【答案】D7.⽅差分析中要求______.A.各个样本均数相等B.各个总体⽅差相等C.各个总体均数相等D.两样本⽅差相等E.两个样本来⾃同⼀总体【答案】B8.⽐较⾮典型肺炎和普通肺炎患者的⽩细胞计数⽔平，若，可作单侧检验。
A.已知⼆组患者的⽩细胞计数均降低B.已知⼆组患者的⽩细胞计数均升⾼C.不清楚哪⼀组的⽩细胞计数⽔平有变化D.已知⾮典型肺炎患者的⽩细胞计数不⾼于普通肺炎E.两组⽩细胞计数值的总体⽅差不相等【答案】D9.计算某地⼉童肺炎的发病率，现求得男、⼥童肺炎发病率分别为21.2%和19.1%，可认为______.A.男童的肺炎发病率⾼于⼥童B.应进⾏标准化后再做⽐较C.资料不具可⽐性，不能直接作⽐D.应进⾏假设检验后再下结论E.以上都不对【答案】D10.⽐较两个率时，不需要进⾏率的标准化的情况有______.A.内部构成不同B.内部构成相同C.未知各年龄别⼈⼝数D.缺乏各年龄别死亡⼈数E.不易寻找标准⼈⼝构成【答案】B11.四格表资料在哪种情况下作χ2检验不必校正______.A.T>1且n>40B.T>5或n>40C.T>5且n>40D.1< p="">E.T>5且n<40【答案】C12.欲⽐较三种药物的疗效（⽆效、好转、显效、痊愈）孰优孰劣，最好选择______.A.t检验B.⽅差分析C.χ2检验D.秩和检验E.u检验【答案】D13.下⾯说法中不正确的是_____.A.没有个体差异就不会有抽样误差B.抽样误差的⼤⼩⼀般⽤标准误来表⽰C.好的抽样设计⽅法，可避免抽样误差的产⽣D.医学统计资料主要来⾃统计报表、医疗⼯作记录、专题调查或实验等E.抽样误差是由抽样造成的样本统计量与总体参数间的差别及样本统计量间的差别【答案】C14.实验设计和调查设计的根本区别是_____.A.实验设计以动物为对象B.调查设计以⼈为对象C.调查设计可随机分组D.实验设计可⼈为设置处理因素E.以上都不对【答案】D15.在下述抽样调查⽅法中，在样本量相同的前提下，抽样误差最⼩的是_____.A.简单随机抽样B.系统抽样C.分层抽样D.整群抽样E.多阶段整群抽样【答案】C16.对两个变量进⾏直线相关分析，r=0.46，P>0.05，说明两变量之间______.A.有相关关系B.⽆任何关系C.⽆直线相关关系D.⽆因果关系E.有伴随关系【答案】C17.某医师研究丹参预防冠⼼病的作⽤，实验组⽤丹参，对照组⽆任何处理，这种对照属于______.A.实验对照B.空⽩对照C.相互对照D.标准对照E.历史对照【答案】B18.在两独⽴样本⽐较的秩和检验中，实验组的观察值为0，0，7，14，32，40，对照组的观察值为0，1，2，4，4，8.编秩中零值的秩应分别编为______.A.2，3；1B.1.5，1.5；3C.2，2；2D.2.5，2.5；1E.不参加编秩【答案】C19.两样本⽐较的秩和检验（两组样本例数相等），如果假设成⽴，则对样本来说：______.A.两组秩和相等B.两组秩和的绝对值相等C.两组秩和相差很⼤D.两组秩和相差⼀般不会很⼤E.两组秩和的差值相等【答案】D20.在简单线性回归分析中，得到回归系数为-0.30，经检验有统计学意义，说明______.A.X对Y的影响占Y变异的30%B.X增加⼀个单位，Y平均减少30%C.X增加⼀个单位，Y平均减少0.30个单位D.Y增加⼀个单位，X平均减少30%E.Y增加⼀个单位，X平均减少0.30个单位【答案】C⼆、多选题在A、B、C、D和E中选出⼀个最佳答案，将答案的字母填在相应下划线的空格⾥。
医学统计学习题答案1[精品文档]
![医学统计学习题答案1[精品文档]](https://img.taocdn.com/s3/m/ab324ae976eeaeaad0f3300c.png)
习题答案第一章思考题答案1.某医生收治200名患者，随机分成2组，每组100人。
一组用A药，另一组用B药。
经过2个月的治疗，A药组治愈了90人，B组治愈了85名患者，请根据现有结果评议下列说法是否正确，为什么？a)A药组的疗效高于B药组。
(对,但不提倡这样说,原因是容易被误解)b)A药的疗效高于B药。
(不对,这是针对总体而言的)2.某校同一年级的A班和B班用同一试卷进行一次数学测验。
经过盲态改卷后，公布成绩：A班的平均成绩为80分，B班的平均成绩为81分，请评议下列说法是否正确，为什么？a)可以称A班的这次考试的平均成绩低于B班，不存在抽样误差。
(对)b)通过这次考试的平均成绩，说明B班的数学平均水平高于A班。
(不对,一次考试只是一次抽样的结果)c)对于评价两个班级的数学平均水平而言，这次考试成绩只是一次抽样观察结果，所以存在抽样误差，不能仅凭这次考试的平均分差异推断两个班级的平均水平的高低。
(对) d)对于研究两个班级的这次考试成绩而言，A班所有学生的这次考试成绩构成了一个总体A，B班所有学生的这次考试成绩构成了一个总体B。
(对)3. 请根据变量和资料分类的定义，评议下列说法是否正确，为什么？a)如果变量取值中含有小数点，则该变量为连续型变量。
(不对,离散型变量取值也可以定义为取值含有小数点)b)如果资料为离散型变量的取值，则该资料一定为分类资料。
(不对,如白细胞计数,这是离散型的资料,但不具有分类性质)c)某研究者观察某个患者的24小时的心电图，发现该患者在这24小时中共有90个早博，并记为90个早博/24小时，故该资料也有量纲。
根据定义，应认为该资料为计量资料。
(本质上这是个体计数资料,但因为不具有分类意义,所以通常按计数资料进行统计分析)第二章习题的答案1. 是非题(1) 不论数据呈什么分布，都可以用算术均数和中位数表示其平均水平。
（错）(2) 少数几个数据比大多数数据大几百倍，一般不宜用算术均数表示其平均水平。
医学统计学分析计算题_答案与解析
WORD文档下载可编辑第二单元计量资料的统计推断分析计算题2.1 某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数/1012·L-1男360 4.66 0.58 4.84女255 4.18 0.29 4.33血红蛋白/g·L-1男360 134.5 7.1 140.2女255 117.6 10.2 124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？(2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？(5) 该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV)比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18SCVX=⨯=⨯=女性血红蛋白含量的变异系数10.2100%100%8.67%117.6SCVX=⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L )男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
卫生统计学考试试题及答案(附解释)
卫生统计学试题及答案（一）1.用某地6～16岁学生近视情况的调查资料制作统计图，以反映患者的年龄分布，可用图形种类为______.A.普通线图B.半对数线图C.直方图D.直条图E.复式直条图【答案】C（6——16岁为连续变量，得到的是连续变量的频数分布）直方图（适用于数值变量，连续性资料的频数表变量）直条图（适用于彼此独立的资料）2.为了反映某地区五年期间鼻咽癌死亡病例的年龄分布，可采用______.A.直方图B.普通线图C.半对数线图D.直条图E.复式直条图(一个检测指标，两个分组变量)【答案】E? 3.为了反映某地区2000~1974年男性肺癌年龄别死亡率的变化情况，可采用______.A.直方图B.普通线图（适用于随时间变化的连续性资料，用线段的升降表示某事物在时间上的发展变化趋势）C.半对数线图（适用于随时间变化的连续性资料，尤其比较数值相差悬殊的多组资料时采用，线段的升降用来表示某事物的发展速度）D.直条图E.复式直条图【答案】E4.调查某疫苗在儿童中接种后的预防效果，在某地全部1000名易感儿童中进行接种，经一定时间后从中随机抽取300名儿童做效果测定，得阳性人数228名。
若要研究该疫苗在该地儿童中的接种效果，则______.A.该研究的样本是1000名易感儿童B.该研究的样本是228名阳性儿童C.该研究的总体是300名易感儿童D.该研究的总体是1000名易感儿童E.该研究的总体是228名阳性儿童【答案】D5.若要通过样本作统计推断，样本应是__________.A.总体中典型的一部分B.总体中任一部分C.总体中随机抽取的一部分D.总体中选取的有意义的一部分E.总体中信息明确的一部分【答案】C6.下面关于均数的正确的说法是______.A.当样本含量增大时，均数也增大B.均数总大于中位数C.均数总大于标准差D.均数是所有观察值的平均值E.均数是最大和最小值的平均值【答案】D7.某地易感儿童注射乙肝疫苗后，从中随机抽取100名儿童测量其乙肝表面抗体滴度水平，欲描述其平均水平，宜采用______.A.均数B.几何均数C.中位数D.方差E.四分位数间距【答案】B几何均数（geometric mean）是用于反映一组经对数转换后呈对称分布的变量值在数量上的平均水平，在医学研究中常适用于免疫学的指标。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二单元 计量资料的统计推断分析计算题2.1某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量，结果见表4：表4 某年某地健康成年人的红细胞数和血红蛋白含量指 标性别 例数 均数 标准差 标准值* 红细胞数/1012·L-1男 360 4.66 0.58 4.84女255 4.18 0.29 4.33 血红蛋白/g ·L -1男 360 134.5 7.1 140.2女255117.610.2124.7请就上表资料：(1) 说明女性的红细胞数与血红蛋白的变异程度何者为大？ (2) 分别计算男、女两项指标的抽样误差。
(3) 试估计该地健康成年男、女红细胞数的均数。
(4) 该地健康成年男、女血红蛋白含量有无差别？ (5)该地男、女两项血液指标是否均低于上表的标准值（若测定方法相同）？ 2.1解：(1) 红细胞数和血红蛋白含量的分布一般为正态分布，但二者的单位不一致，应采用变异系数(CV )比较二者的变异程度。
女性红细胞数的变异系数0.29100%100% 6.94%4.18S CV X =⨯=⨯= 女性血红蛋白含量的变异系数10.2100%100%8.67%117.6S CV X =⨯=⨯=由此可见，女性血红蛋白含量的变异程度较红细胞数的变异程度大。
(2) 抽样误差的大小用标准误X S 来表示，由表4计算各项指标的标准误。
男性红细胞数的标准误0.031X S ===(1210/L ) 男性血红蛋白含量的标准误0.374X S ===(g/L )女性红细胞数的标准误0.018X S ===(1210/L )女性血红蛋白含量的标准误0.639X S ===(g/L ) (3) 本题采用区间估计法估计男、女红细胞数的均数。
样本含量均超过100，可视为大样本。
σ未知，但n 足够大 ，故总体均数的区间估计按(/2/2X X X u S X u S αα-+, )计算。
该地男性红细胞数总体均数的95%可信区间为：(4.66－1.96×0.031 , 4.66＋1.96×0.031)，即(4.60 , 4.72)1210/L 。
该地女性红细胞数总体均数的95%可信区间为：(4.18－1.96×0.018 , 4.18＋1.96×0.018)，即(4.14 , 4.22)1210/L 。
(4) 两成组大样本均数的比较，用u 检验。
1) 建立检验假设，确定检验水准H 0：12μμ=，即该地健康成年男、女血红蛋白含量均数无差别 H 1：12μμ≠，即该地健康成年男、女血红蛋白含量均数有差别0.05α=2) 计算检验统计量22.829X X u ===3) 确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地健康成年男、女的血红蛋白含量均数不同，男性高于女性。
(5) 样本均数与已知总体均数的比较，因样本含量较大，均作近似u 检验。
1) 男性红细胞数与标准值的比较 ①建立检验假设，确定检验水准H 0：0μμ=，即该地男性红细胞数的均数等于标准值H 1：0μμ<，即该地男性红细胞数的均数低于标准值 单侧0.05α= ②计算检验统计量0 4.66 4.845.8060.031X X t S μ--===- ③确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性红细胞数的均数低于标准值。
2) 男性血红蛋白含量与标准值的比较 ①建立检验假设，确定检验水准H 0：0μμ=，即该地男性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地男性血红蛋白含量的均数低于标准值 单侧0.05α= ②计算检验统计量0134.5140.215.2410.374X X t S μ--===- ③确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地男性血红蛋白含量的均数低于标准值。
3) 女性红细胞数与标准值的比较 ①建立检验假设，确定检验水准H 0：0μμ=，即该地女性红细胞数的均数等于标准值 H 1：0μμ<，即该地女性红细胞数的均数低于标准值 单侧0.05α= ②计算检验统计量0 4.18 4.338.3330.018X X t S μ--===-③确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性红细胞数的均数低于标准值。
4) 女性血红蛋白含量与标准值的比较 ①建立检验假设，确定检验水准H 0：0μμ=，即该地女性血红蛋白含量的均数等于标准值 H 1：0μμ<，即该地女性血红蛋白含量的均数低于标准值 单侧0.05α= ②计算检验统计量0117.6124.711.1110.639X X t S μ--===- ③确定P 值，作出统计推断查t 界值表(ν＝∞时)得P <0.0005，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为该地女性血红蛋白含量的均数低于标准值。
2.2 为了解某高寒地区小学生血红蛋白含量的平均水平，某人于1993年6月随机抽取了该地小学生708名，算得其血红蛋白均数为103.5g/L ，标准差为1.59g/L 。
试求该地小学生血红蛋白均数的95%可信区间。
2.2解：σ未知，n 足够大时，总体均数的区间估计可用(/2/2X X X u S X u S αα-+ , )。
该地小学生血红蛋白含量均数的95％可信区间为：(103.5 1.96103.5 1.96-+, )，即(103.38 , 103.62)g/L 。
2.3 一药厂为了解其生产的某药物（同一批次）之有效成分含量是否符合国家规定的标准，随机抽取了该药10片，得其样本均数为103.0mg ，标准差为2.22mg 。
试估计该批药剂有效成分的平均含量。
2.3解：该批药剂有效成分的平均含量的点值估计为103.0 mg 。
σ未知且n 很小时，总体均数的区间估计可用()/2,/2,X X X t S X t S αναν-+ , 估计。
查t 界值表得t 0.05/2,9=2.262，该批药剂有效成分的平均含量的95％可信区间为：(103.0 2.262103.0 2.262-+, ，即(101.41 , 104.59)mg 。
2.4152例麻疹患儿病后血清抗体滴度倒数的分布如表5，试作总体几何均数的点值估计和95%区间估计。
表5152例麻疹患儿病后血清抗体滴度倒数的分布滴度倒数 1 2 4 8 16 32 64 128 256 512 1024 合计 人 数171031334224311522.4解：将原始数据取常用对数后记为X ，则152 1.85970.44250.0359X n X S S ====，，，，用(/2/2X X X u S X u S αα-+，)估计，则滴度倒数对数值的总体均数的95％可信区间为：(1.8597 1.960.0359 1.8597 1.960.0359-⨯+⨯ , )，即(1.7893 , 1.9301)。
所以滴度倒数的总体几何均数的点估计值为： 1.8597101072.39X ==，滴度倒数的总体几何均数的95%区间估计为( 1.7893 1.93011010, )，即(61.56 , 85.13)。
SPSS 操作 数据录入：打开SPSS Data Editor 窗口，点击Variable View 标签，定义要输入的变量x 和f ；再点击Data View 标签，录入数据（见图2.4.1，图2.4.2）。
图2..4.1 Variable View 窗口内定义要输入的变量x 和f图2.4.2 Data View窗口内录入数据分析：Compute…TransformTarget Variable：键入logxNumeric Expression：LG10(x)将原始数据取对数值DataWeight Case s…Frequency Variable：f 权重为fWeight cases byExplore… 探索性分析Descriptive StatisticsAnalyzeDependent list：logx 分析变量logxDisplay：StatisticsDescriptives统计描述注：最后得到结果是原始数据对数值的均数及其95%可信区间。
2.5 某口腔医生欲比较“个别取模器龈下取模技术”与“传统硅橡胶取模方法”两种取模技术精度的差异，在12名病人口中分别用两种方法制取印模，在体视显微镜下测量标志点到龈沟底的距离，结果如表6，问两种取模方法结果有无差异？表6 12个病人口腔某测量标志点到龈沟底的距离/cm2.5解：本题为配对设计的两样本均数的比较，采用配对t 检验。
表2.5.1 12个病人口腔某测量标志点到龈沟底的距离/cm(1)建立检验假设，确定检验水准H 0：0d μ=，即两种取模方法结果无差异病例号 个别取模器龈下取模技术传统硅橡胶取模方法1 0.626 0.6142 0.627 0.6263 0.670 0.654 4 0.548 0.5495 0.590 0.5746 0.603 0.587 7 0.605 0.6028 0.347 0.3389 0.768 0.759 10 0.576 0.572 11 0.330 0.318 120.2330.219病例号 个别取模器龈下取模1d传统硅橡胶取模法2d12d d d =-1 0.626 0.614 0.012 2 0.627 0.626 0.0013 0.670 0.654 0.016 4 0.548 0.549 -0.0015 0.590 0.574 0.016 6 0.603 0.587 0.016 7 0.605 0.602 0.0038 0.347 0.338 0.009 9 0.768 0.759 0.009 10 0.576 0.572 0.004 11 0.330 0.318 0.012 120.2330.2190.014H 1：0d μ≠，即两种取模方法结果有差异0.05α=(2)计算检验统计量两种取模方法结果的差值d 的计算见表2.5.1。
120.00930.00610.0018d d n d S S ====， ，， 00.00935.1670.0018d d t S -=== 112111n ν=-=-=(3)确定P 值，作出统计推断查t 界值表得P <0.001，按0.05α=水准，拒绝H 0，接受H 1，差别有统计学意义，可以认为两种取模方法结果有差异，个别取模器龈下取模法标志点到龈沟底的距离略高于传统硅胶取模法。