测试技术与信号处理课后答案
信号处理与测试技术习题及答案
第一章习题：一、填空题1、电量分为和，如电流、电压、电场强度和电功率属于；而描述电路和波形的参数，如电阻、电容、电感、频率、相位则属于。
2、传感器输出的经过加工处理后，才能进—步输送到记录装置和分析仪器中。
3、现代科学认为，、、是物质世界的三大支柱。
4、与三大支柱相对应，现代科技形成了三大基本技术，即、、。
5、传感技术是人的的扩展和延伸；通信技术是人的的扩展和延伸；计算机技术是人的的延伸。
6、、、技术构成了信息技术的核心。
二、简答题1、举例说明信号测试系统的组成结构和系统框图。
2、举例说明传感技术与信息技术的关系。
3、分析计算机技术的发展对传感测控技术发展的作用。
4、分析说明信号检测与信号处理的相互关系。
三、参考答案（－）填空题1、电能量、电参量、电能量、电参量2、电信号、信号调理电路3、物质、能量、信息4、新材料技术、新能源技术和信息技术5、感官（视觉、触觉）功能、信息传输系统(神经系统)、信息处理器官(大脑)功能6、传感、通信和计算机第二章习题：一、填空题1、确定性信号可分为和两类。
2、信号的有效值又称为，它反映信号的。
3、概率密度函数是在域，相关函数是在域，功率谱密度是在域上描述随机信号。
4、周期信号在时域上可用、和参数来描述。
5、自相关函数和互相关函数图形的主要区别是。
6、因为正弦信号的自相关函数是同频率的，因此在随机噪声中含有时，则其自相关函数中也必然含有，这是利用自相关函数检测随机噪声中含有的根据。
7、周期信号的频谱具有以下三个特点：_________、________、_________。
8、描述周期信号的数学工具是__________；描述非周期信号的数学工具是________。
9、同频的正弦信号和余弦信号,其相互相关函数是的。
10、信号经典分析方法是和。
11、均值E[x(t)]表示集合平均值或数学期望，反映了信号变化的，均方值反映信号的。
12、奇函数的傅立叶级数是，偶函数的傅立叶级数是。
机械测试技术与信号分析简答题及答案
一、问答题(每题8分，共40分)1．在系统特性测量中常用白噪声信号作为输入信号，然后测量系统的输出，并将输出信号的频谱作为系统频率特性。
请用卷积分定理解释这样做的道理。
答：白噪声是指功率谱密度在整个频域内均匀分布的噪声，所有频率具有相同能量的随机噪声称为白噪声。
在其频谱上是一条直线。
系统频率特性：传递函数的一种特殊情况，是定义在复平面虚轴上的传递函数。
时域卷积分定理：两个时间函数的卷积的频谱等于各个时间函数的乘积，即在时域中两信号的卷积等效于在频域中频谱相乘。
频域卷积分定理：两个时间函数的频谱的卷积等效于时域中两个时间函数的乘积。
y(t)=h(t)*x(t),对y(t)作付式变换，转到相应的频域下Y(f)=H(f)X(f)，由于x(t)是白噪声，付式变换转到频域下为一定值，假定X(f)=1，则有Y(f)=H(f)，此时就是传递函数。
2．用1000Hz的采样频率对200Hz的正弦信号和周期三角波信号进行采样，请问两个信号采样后是否产生混叠？为什么？3．什么是能量泄露和栅栏效应？能量泄漏与栅栏效应之间有何关系？能量泄漏：将截断信号的谱XT(ω)与原始信号的谱X（ω）相比较可知，它已不是原来的两条谱线，而是两段振荡的连续谱．这表明原来的信号被截断以后，其频谱发生了畸变，原来集中在f0处的能量被分散到两个较宽的频带中去了，这种现象称之为频谱能量泄漏（Leakage）。
栅栏效应：对采样信号的频谱,为提高计算效率,通常采用FFT算法进行计算,设数据点数为N = T/dt = T.fs则计算得到的离散频率点为Xs(fi) , fi = i.fs/N , i = 0,1,2,…,N/2。
这就相当于透过栅栏观赏风景,只能看到频谱的一部分,而其它频率点看不见,因此很可能使一部分有用的频率成分被漏掉,此种现象被称为栅栏效应。
频谱的离散取样造成了栅栏效应，谱峰越尖锐，产生误差的可能性就越大。
例如，余弦信号的频谱为线谱。
《测试技术》课后习题答案
第一章1答：测试技术是实验科学的一部分，主要研究各种物理量的测量原理和测量信号分析处理方法，是进行各种科学实验研究和生产过程参数测量必不可少的手段，起着人的感官的作用。
2答：测试系统由传感器、中间变换装置和显示记录装置三部分组成。
传感器将被测物理量检出并转换为电量，中间变换装置对接收到的电信号用硬件电路进行分析处理或经A/D变换后用软件进行信号分析，显示记录装置则测量结果显示出来，提供给观察者或其它自动控制装置。
3答：在工程领域，科学实验、产品开发、生产监督、质量控制等，都离不开测试技术。
测试技术应用涉及到航天、机械、电力、石化和海洋运输等每一个工程领域。
4答：例如：全自动洗衣机中用到如下传感器：衣物重量传感器，衣质传感器，水温传感器，水质传感器，透光率光传感器(洗净度) 液位传感器，电阻传感器(衣物烘干检测)。
第二章1答：信号波形是指被测信号幅度随时间的变化历程。
2答：从信号描述上分为：确定性信号与非确定性信号；从信号的幅值和能量上分为：能量信号与功率信号；从分析域上分为：时域与频域；从连续性分为：连续时间信号与离散时间信号；从可实现性分为：物理可实现信号与物理不可实现信号。
3答：可以用明确数学关系式描述的信号称为确定性信号。
不能用数学关系式描述的信号称为非确定性信号。
4答：在所分析的区间（-∞，∞），能量为有限值的信号称为能量信号，能量不是有限值的信号称为功率信号。
5答：周期信号的自相关函数仍然是同频率的周期信号，但不保留原信号的相位信息。
6答：信号频域分析是采用傅立叶变换将时域信号x(t)变换为频域信号X(f)。
时域分析只能反映信号的幅值随时间的变化情况，除单频率分量的简谐波外，很难明确揭示信号的频率组成和各频率分量大小。
信号频谱X(f)代表了信号在不同频率分量成分的大小，能够提供比时域信号波形更直观，丰富的信息。
7答：周期函数展开为傅立叶级数的物理意义: 把一个比较复杂的周期信号看成是许多不同频率的简谐信号的叠加。
测试技术课程课后习题答案
（2）当ξ=0.7时可解得A（400）=0.975；φ （400）=-43.03°
即幅值比为：A（400）=0.975；相位移为43.03°。
2-11 一个可视为二阶系统的装置输入一个单位 阶跃函数后，测得其响应的第一个超调量峰值 为0.15，振荡周期为6.23s。已知该装置的静态 增益为3，试求该装置的传递函数和该装置在无 阻尼固有频率处的频率响应。
0.2%
不能，这个变化量是太小。
3-6 一个电容测微仪其传感器的圆形极板的半径r=4mm，工 作初始间隙δ=0.3mm，问：1）工作时，如果传感器与工件的 间隙变化量∆δ=±0.1μn时，电容变化量是多少？2）如果测量 电路的灵敏度S1=100V/pF，读数仪表的灵敏度S2=5格/mV， 当 ∆δ=±0.1μn时，读数仪表的指示值变化多少格？
1
1 2
A()
1
0.414
1 0.35 2 12
2
1 T
幅值误差为：1-0.414=0.586
2-3 求周期信号x（t）=0.5cos10t+0.2cos （100t-45°），通过传递函数为 H(s) 1
0.005s 1
的装置后得到的稳态响应。
解： x(t) x1(t) x2 (t)
第二章习题
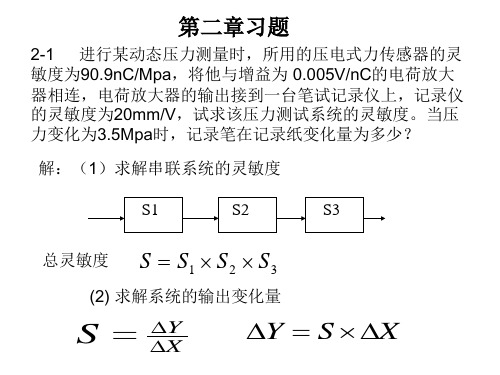
2-1 进行某动态压力测量时，所用的压电式力传感器的灵 敏度为90.9nC/Mpa，将他与增益为 0.005V/nC的电荷放大 器相连，电荷放大器的输出接到一台笔试记录仪上，记录仪 的灵敏度为20mm/V，试求该压力测试系统的灵敏度。当压 力变化为3.5Mpa时，记录笔在记录纸变化量为多少？
2-5 用一个一阶系统作100Hz正弦信号的测 量，如果要求限制振幅误差在5％以内，则时 间常数应取多少？若用该系统测量50Hz的正 弦信号，问此时振幅误差和相角差是多少？
测试技术（2-6章）（李迪张春华著）华南理工大学教材供应中心课后答案
第二章 测量结果的数据处理及误差分析√2-3 用标准测力机检定材料试验机，若材料试验机的示值为5.000MN ，标准测力仪输出力值为4.980MN ，试问材料机在5.000MN 检定点的示值误差、示值的相对误差各为多少?解：示值误差=，020.0000.5980.4−=−示值的相对误差=%04.0000.5020.0−=−√2-8 设间接测量量z x y =+，在测量x 和时是一对一对同时读数的。
测量数据如下表。
试求的标准测量序号y z 偏差。
1 2 3 4 5 6 78 9 10 x 读数100 104 1029810310199101105102 y 读数51 51 5450515250505351解：101.5x =，51.3y =，0.42y σ=，0.687x σ=152.8z x y =+=z x y =+，1,1z z x y∂∂∴==∂∂ 由于10(,)()(0.55iix y x x y y ρ−−∴==∑0.98z σ∴=。
1m 距离的标准偏差为0.2mm 。
如何表示间的函数式？求测此10m 距离的标准差。
见书P27-28页的内容。
5.033，25.039，25.034mm 。
如不计其他不确定度来源，最佳值及其标准不确定度。
见书P36页例题2.8√2-9 用米尺逐段丈量一段10m 的距离，设丈量接测量解：参√2-14 用千分尺重复测量某小轴工件直径10次，得到的测量数据为25.031，25.037，25.034，25.036，25.038，25.037，25.036，2试估计解：参答案网 w w w .h k s h p .c n第三章 信号描述与分析-3 求指数函数的频谱。
√解：()e (00)atx t A a t −=>≥，3dt e Ae dt e t x X t j at t j ∫∫+∞−−+∞∞−−==0)()(ωωω220)()ωωωωω+−=+=+−=+∞+−a j a A j a A e j a Ata j （3-4 求被截断的余弦函数0cos t ω0cos ||()0 ||t t x t t Tω<⎧=⎨≥T解：⎩(题图3-4 )的傅里叶变换。
测试技术(第二版)课后复习题答案_贾民平
测试技术与信号处理习题解答授课教师：陈杰来第一章习题（P29）1-1府轉质个职躺切齢肆帥静!耶个职臨号！饷腮i 普各狀啊酿?解：（1） 瞬变信号-指数衰减振荡信号，其频谱具有连续性和衰减性。
（2） 准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散性。
（3） 周期信号，因为各简谐成分的频率比为有理数，其频谱具有离散性、 谐波性和收敛性。
1-2求信号x （t ）=sm 2^1的有效值（均方根值）畑二J 討:工“）曲.解：x （t ）=sin2 f °t 的有效值（均方根值）：J 丄：。
(1 cos 4 f o t) dt 2T o o［丄(T o -^si n4 f o T o )：2T o4 f oxrms1'■■,'TTox 2 (t)dtT oTosin 2 2 f o t dtu1------ sin 4 f o t 4 f 0T 0)1-3聽I呵抽三斛擁开拥腓师开丸耦茫触他1加般认胖離礼解：周期三角波的时域数学描述如下：T o2 x(t)0 tT 0 2T o x(t nT o )(1)傅里叶级数的三角函数展开：b n 1 T o/2T oT o / 2 T o /2 T o T o /2 4 T o /2 T o4 2 n 2 52 T o /2(1 T o /2a。
an 2n 2x(t)dt 2 T o /2T 00(1—t)dt T o x(t)cos n o t dt 2t)cos n o t dt T on 1,3,5, T o则x(t)sin n x(t)sin n o t dt n 2,4,6,，式中由于x(t)是偶函数，sinn o t 是奇函数，o t 也是奇函数，而奇函数在上下限对称区间上的积分等于o 。
故b n 0。
因此，其三角函数展开式如下:x(t)12 cos n n 1 nt41匕 2sin(n o t n 1 n2)(n=1,3, 5,…)其频谱如下图所示：A())1■2()」4 22・ 41 2 3 49 24 25 213 0 5 00 3 0 5 0单边幅频谱单边相频谱(2)复指数展开式复指数与三角函数展开式之间的关系如下：1 21 V a ! b ：4 I m C nR e C nC 0 IA onarctg3oI m C nR e C n1 2 A 1arctg (电)a n故有I nC N =-b n /21 A1A n = an 2 2 arctg ( “) a nR e C N =31/22. 2 n 2 sin 2222 2n 0n 1,3,5, n 2,4,6,a o C n-5 0-3 0 - 0 0------------------------ ko 3 o 5 o实频谱j i R e C n1 2 222 9 225 22 25 2-5 0-3 o - o 0虚频谱o 3 o 5 o双边幅频谱t|Cn2 25 22 9 2 225 2-5 o -3 o - o o双边相频谱1-4求三角形窗函数｛图J22）的频谱［井作频谱Kkt用傅里叶变换求频谱。
测试技术_课后答案
w ww .kh d a w.c o m信号及其描述习题1.1求周期方波（图1-4）的傅立叶级数（复指数函数形式）。
画出频谱图|C n |—ω ；φn —ω 图并与表1-1对比。
解：傅立叶级数的复指数形式表达式：⋅⋅⋅±±±==∑+∞−∞=,3,2,1,0;)(0n eC t x n tjn nω式中： []()⎪⎩⎪⎨⎧⋅⋅⋅±±±=⋅⋅⋅±±±=−=−−=+×+−=⎥⎦⎤⎢⎣⎡−+⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤+⎢⎣⎡−==−−−−−−−−−∫∫∫,6,4,2;0,5,3,1;2cos 12111)(1)(1200002002002022000000000000n n n A j n n A j e e n jA n jA e jn A T e jn A T dt Ae dt e A T dt e t x T C jn jn T t jn T t jn T t jn T t jn T T t jn n πππππωωππωωωωω所以： ⋅⋅⋅±±±±=⎟⎠⎞⎜⎝⎛−=∑+∞−∞=,7,5,3,1;2)(0n en A j t x t jn n ωπ幅值频谱：⋅⋅⋅±±±==+=,5,3,1;222n n A C C C nI nR n π相位频谱：立叶级数的复指数形式的幅值频谱图和相位频谱都是双边频谱图。
求正弦信x s求指数函数的频谱。
）和单位阶跃函数（题图）的频谱 ⎪⎩⎪⎨⎧⋅⋅⋅−−−=⋅⋅⋅=−=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛−==,5,3,1;2,5,3,1;202n n n A arctg C C arctg nR nI n πππϕ傅 号的绝对均值和均方根值1.2 x (t )=x 0sin ωt μ| |x rm 解： ωππωμ2;2sin 1)(lim 0000000====∫∫∞→T x tdt x T dt t x T T T x 式中：()2sin 1)(10020002000x dt dt x T dt t x T x T T rms ===∫∫ω1.3 解：00;Ae x ;()(≥>=−t t t αα)f j A dt e Ae dt e t x f X ft j t ft j παπαπ2)()(022+=⋅==∫∫∞+−−∞+∞−−1.41-1a 1-1b .求符号函数（题图w ww .kh d a w.c o m解:1) 符号函数的频谱:令: fj dt e e dt e e dt e t x f X t x e t x ft j tft j t ft j t ππαπααπαα1)1(lim )()(;)(lim )(0220021101=⎟⎠⎞⎜⎝⎛+−===∫∫∫∞+−−−∞−−→−−→2)单位阶跃函数的频谱: fj dt e e dt e t x f X t x e t x ft j t ft j tππααπαα21lim )()(;)(lim )(02022202=⎟⎠⎞⎜⎝⎛===∫∫∞+−−→−−→1.5求被截断的余弦函数cos ω0t （题图1-2）的傅立叶变换。
测试技术课后题部分答案
1.1简述测量仪器的组成与各组成部分的作用答：感受件、中间件和效用件。
感受件直接与被测对象发生联系，感知被测参数的变化，同时对外界发出相应的信号;中间件将传感器的输出信号经处理后传给效用件，放大、变换、运算;效用件的功能是将被测信号显示出来。
1.2测量仪器的主要性能指标及各项指标的含义是什么答：精确度、恒定度、灵敏度、灵敏度阻滞、指示滞后时间等。
精确度表示测量结果与真值一致的程度;恒定度为仪器多次重复测量时，指示值的稳定程度；灵敏度以仪器指针的线位移或角位移与引起这些位移的被测量的变化值之间的比例表示；灵敏度阻滞又称感量，是足以引起仪器指针从静止到做微小移动的被测量的变化值；指示滞后时间为从被测参数发生改变到仪器指示出该变化值所需时间,或称时滞。
2.3试述常用的一、二阶测量仪器的传递函数及它的实例答:一阶测量仪器如热电偶；二阶测量仪器如测振仪.2。
4试述测量系统的动态响应的含义、研究方法及评价指标。
答：测量系统的动态响应是用来评价系统正确传递和显示输入信号的指标.研究方法是对系统输入简单的瞬变信号研究动态特性或输入不同频率的正弦信号研究频率响应.评价指标为时间常数τ（一阶）、稳定时间t s和最大过冲量A d（二阶)等。
2.6试说明二阶测量系统通常取阻尼比ξ=0.6~0。
8范围的原因答：二阶测量系统在ξ=0.6~0。
8时可使系统具有较好的稳定性，而且此时提高系统的固有频率ωn会使响应速率变得更快。
3.1测量误差有哪几类?各类误差的主要特点是什么？答：系统误差、随机误差和过失误差。
系统误差是规律性的，影响程度由确定的因素引起的，在测量结果中可以被修正；随机误差是由许多未知的或微小因素综合影响的结果，出现与否和影响程度难以确定,无法在测量中加以控制和排除,但随着测量次数的增加，其算术平均值逐渐接近零；过失误差是一种显然与事实不符的误差.3。
2试述系统误差产生的原因及消除方法答：仪器误差，安装误差，环境误差,方法误差，操作误差(人为误差），动态误差。
测试技术与信息处理第章习题与答案
一、判断题(本题共10分，对则打“√”，不对则打“×”)1．压电传感器的电压灵敏度及电荷灵敏度不受外电路的影响。
(√) 2．将传感器做成差动式可以提高灵敏度、改善非线性、实现某些补偿。
(√) 3．压电式传感器在后接电荷放大器时，可基本消除电缆电容的影响，而且可以实现对变化缓慢的被测量的测量。
(√) 4．只要保证两组相对桥臂阻抗大小之积相等这一条件，就可使直流电桥及交流电桥达到平衡。
(×) 5．磁电式传感器由于存在运动部分，因此不能用于高频测量。
(×) 6．测量小应变时，应选用灵敏度高的金属应变片；测量大应变时，应选用灵敏度低的半导体应变片。
(√) 7．由于霍尔式传感器输出的霍尔电势与控制电流及所处的磁场强度的乘积成正比，因此可用作乘法器。
(√) 8．压电式传感器的电荷灵敏度与外电路（连接电缆、前置放大器）无关，电压灵敏度则受外电路的影响。
(√) 9．用差动变压器式电感传感器测量位移时，直接根据其输出就能辨别被测位移的正负极性。
(×) 10．半导体应变片的灵敏度比金属应变片高，线性和稳定性也比后者好。
(×) 11．差动螺管式自感传感器与差动变压器式互感传感器的结构相似，都是把被测位移的变化转换成输出电压的变化。
(×) 12．由于线圈可以做得比较轻巧，因此动圈式磁电传感器可以用来测量变化比较快的被测量，而动铁式磁电传感器则不能。
(×) 13．压电式传感器的电荷灵敏度只取决于压电材料本身，而电压灵敏度则还与外电路的电气特性有关。
(√) 14．测量小应变时，应选用金属丝应变片，测量大应变时，应选用半导体应变片。
( × )15．测量小应变时，应选用灵敏度高的金属丝应变片，测量大应变时，应选用灵敏度低的半导体应变片。
(√) 16．作为温度补偿的应变片应和工作应变片作相邻桥臂且分别贴在与被测试件相同的置于同一温度场的材料上。
(√) 17．交流电桥可测静态应变，也可测动态应变。
《测试技术与信号处理》习题答案-华科版
《测试技术与信号处理》习题答案第二章 信号分析基础1、请判断下列信号是功率信号还是能量信号： （1）)()(10cos 2∞<<-∞=t e t x t π （2）)()(||10∞<<-∞=-t et x t【解】（1）该信号为周期信号，其能量无穷大，但一个周期内的平均功率有限，属功率信号。
（2）信号能量：⎰∞∞-==101)(2dt t x E ，属于能量信号。
2、请判断下列序列是否具有周期性，若是周期性的，请求其周期。
)8()(π-=n j e n x【解】设周期为N ，则有：8)88()()(N jNn j en x e N n x ⋅==+-+π若满足)()(n x N n x =+，则有1)8/sin()8/cos(8/=-=-N j N ejN即：k N π28/=，k N π16=，k = 0，1，2，3，… N 不是有理数，故序列不是周期性的。
3、已知矩形单脉冲信号x 0(t)的频谱为X 0(ω)=A τsinc(ωτ/2) ，试求图示三脉冲信号的频谱。
【解】三脉冲信号的时域表达式为：)()()()(000T t x t x T t x t x -+++=根据Fourier 变换的时移特性和叠加特性，可得其频谱：)]cos(21)[2(sin )()()()(000T c A e X X e X X T j T j ωωττωωωωωω+=++=-4、请求周期性三角波（周期为T ，幅值为0—A ）的概率分布函数F(x)与概率密度函数p(x) 。
【解】在一个周期T 内，变量x (t )小于某一特定值x 的时间间隔平均值为：T Ax t i =∆ 取n 个周期计算平均值，当∞→n 时，可有概率分布函数：AxnT t n x F i n =∆=∞→lim)( 概率密度函数：Adx x dF x p 1)()(==5、请求周期性方波的自相关函数。
（设周期为T ，幅值为0—A ）t-T【解】对周期函数，可取一个周期求自相关函数，但由于函数的不连续性，必须分段积分，如图：当2/0T ≤≤τ时（图a ）])()()()([1)()(1)(222020⎰⎰⎰⎰⎰----⋅-+-⋅-+-⋅+⋅=+=T T T T TT T Tx Adt A dt A A dt A A Adt A T dt t x t x T R ττττττ 即：)41()(2TA R x ττ-=当T T ≤≤τ2/时（图b ）])()()()([1)(23232/2/0⎰⎰⎰⎰-----⋅-+⋅-+⋅+-⋅=T T TT T T T x dt A A Adt A Adt A dt A A T R τττττ即：)43()(2TA R x ττ--=第三章 信息论基础知识1、某装置的正常工作温度保持在35—40℃之间。
测试技术基础课后习题答案
第2章习题及解答1.判断正误(1)凡频谱是离散的信号必然是周期信号。
( × )准周期信号(2)任何周期信号都由频率不同，但成整倍数比的离散的谐波叠加而成。
( × )(3)周期信号的频谱是离散的，非周期信号的频谱也是离散的。
( × )(4)周期单位脉冲序列的频谱仍为周期单位脉冲序列。
( √ )(5)非周期变化的信号就是随机信号。
( × )准周期信号(6)非周期信号的幅值谱表示的是其幅值谱密度与时间的函数关系。
( × )(7)信号在时域上波形有所变化，必然引起频谱的相应变化。
( × )(8)各态历经随机过程是平稳随机过程。
( √ )(9)平稳随机过程的时间平均统计特征等于该过程的集合平均统计特征。
( √ )(10)非周期信号的频谱都是连续的。
( × ) 准周期信号(11)单位脉冲信号的频谱是无限带宽谱（√）(12)直流信号的频谱是冲击谱（√）2.选择正确答案填空(1)描述周期信号的数学工具是(B )。
A.相关函数B. 傅里叶级数C. 拉普拉斯变换D. 傅里叶变换(2)描述非周期信号的数学工具是( C )。
A.三角函数B. 拉普拉斯变换C. 傅里叶变换D. 傅里叶级数(3)将时域信号进行时移，则频域信号将会( D )A.扩展B. 压缩C. 不变D. 仅有相移(4) 瞬变信号的傅里叶变换的模的平方的意义为( C )A.信号的一个频率分量的能量B. 在f 处的微笑频宽内，频率分量的能量与频宽之比C. 在f 处单位频宽中所具有的功率(5) 概率密度函数是在（C ）域，相关函数是在（A ）域，功率谱密度函数是在（ D ）域描述随机信号。
A.时间B. 空间C. 幅值D. 频率(6) 白噪声信号的自相关函数是（C ）A.相关函数B. 奇函数C. 偶函数D. 不存在3．已知方波信号傅里叶级数，请描述式中各常数相的物理意义，并绘出频谱图。
见书中例题4．已知锯齿波信号傅里叶级数，请描述式中各常数相的物理意义，并绘出频谱图。
(完整版)测试技术部分课后习题参考答案
第1章 测试技术基础知识1.4 常用的测量结果的表达方式有哪3种？对某量进行了8次测量，测得值分别为：82.40、82.43、82.50、82.48、82.45、82.38、82.42、82.46。
试用3种表达方式表示其测量结果。
解：常用的测量结果的表达方式有基于极限误差的表达方式、基于t 分布的表达方式和基于不确定度的表达方式等3种1）基于极限误差的表达方式可以表示为0max x x δ=±均值为8118i x x ==∑82.44因为最大测量值为82.50，最小测量值为82.38，所以本次测量的最大误差为0.06。
极限误差max δ取为最大误差的两倍，所以082.4420.0682.440.12x =±⨯=±2）基于t 分布的表达方式可以表示为x t x x ∧±=σβ0标准偏差为s ==0.04样本平均值x 的标准偏差的无偏估计值为ˆx σ==0.014 自由度817ν=-=，置信概率0.95β=，查表得t 分布值 2.365t β=，所以082.44 2.3650.01482.440.033x =±⨯=±3）基于不确定度的表达方式可以表示为0x x x x σ∧=±=±所以082.440.014x =±解题思路：1）给出公式；2）分别计算公式里面的各分项的值；3）将值代入公式，算出结果。
第2章 信号的描述与分析2.2 一个周期信号的傅立叶级数展开为12ππ120ππ()4(cos sin )104304n n n n n y t t t ∞==++∑（t 的单位是秒） 求：1）基频0ω；2）信号的周期；3）信号的均值；4）将傅立叶级数表示成只含有正弦项的形式。
解：基波分量为12ππ120ππ()|cos sin 104304n y t t t ==+ 所以：1）基频0π(/)4rad s ω=2）信号的周期02π8()T s ω==3）信号的均值42a = 4）已知 2π120π,1030n n n n a b ==，所以4.0050n A n π=== 120π30arctan arctan arctan 202π10n n nn bn a ϕ=-=-=-所以有0011()cos()4 4.0050cos(arctan 20)24n n n n a n y t A n t n t πωϕπ∞∞===++=+-∑∑2.3某振荡器的位移以100Hz 的频率在2至5mm 之间变化。
测试技术与信号处理复习题(客观题)
测试技术与信号处理复习题（客观题）第1、3 章一、判断题. 1. 对多次测量的数据取算数平均值，就可以减少随机误差的影响。
（√ ）2. 传感器的线性范围越宽，表明其工作量程越大。
（√ ）3. 一台仪器的重复性很好，但测得的结果并不准确，这是由于存在随机误差的缘故。
（√ ）4. 一台仪器的重复性很好，但其静态测量结果也可能存在很大的误差。
（√ ）5. 频率不变性原理是指任何测试装置的输出信号的频率总等于输入信号的频率。
（√ ）6. 固有频率f n = 600 Hz 的振动子测量600Hz 的谐波信号，输出不会失真。
（× ）7. 若振动子的固有频率f n = 400 Hz，则其工作频率范围为0 ~ 400 Hz。
（× ）8. 测试系统的幅频特性在工作频带内通常是频率的线性函数，而线性测量系统的灵敏度是时间的线性函数。
（× ）9. 线性测量系统的灵敏度是时间的线性函数。
（× ）10. 测量系统的固有频率越高，其灵敏度也越高。
（× ）11. 一般来说，测试系统的灵敏度越高，则其测试范围越窄。
（√ ）12. 同一测量系统，测量有效频带不同的信号时肯定表现出不同的幅频特性。
（× ）13. 一阶系统的时间常数τ 越小越好。
（√ ）14. 一般的机械系统都可近似看成是二阶的“质量-弹簧-阻尼”系统。
（√ ）15. 在线性时不变系统中，当初始条件为零时，系统输出量与输入量之比的拉氏变换称为传递函数。
（√ ）16. 当输入信号x(t) 一定时，系统的输出y(t) 将完全取决于传递函数H (t) ,而与系统的物理模型无关。
（√ ）17. 测试装置的灵敏度越高，其测量范围就越大。
（× ）18. 随机误差不可能被修正，但在了解其统计规律之后，还是可以控制和减少它们对测量结果的影响。
（√ ）19. 实际测试系统的输出与输入之间保持严格的线性关系（× ）20. 测试装置的相频特性表示了信号各频率分量的初相位和频率间的函数关系。
测试技术基础答案 第五章 信号处理初步
第五章信号处理初步一、知识要点及要求(1)了解信号处理的目的和分类，及数字信号处理的基本步骤；(2)掌握模拟信号数字化出现的问题、原因和措施；(3)掌握信号的相关分析及其应用；(4)掌握信号的功率谱分析及其应用。
二、重点内容及难点(一)信号处理1、信号处理的目的(1)分离信号和噪声，提高信噪比；(2)从信号中提取有用的特征信号；(3)修正测试系统的某些误差，如传感器的线性误差、温度影响等。
2、信号处理的分类模拟信号处理：对模拟信号进行处理，由一系列能实现模拟运算的电路来实现。
数字信号处理：对数字信号进行处理，可以在通用计算机上借助程序来实现，或由专用数字信号处理机（DSP芯片）来实现。
(二)数字信号处理的基本步骤1、(1)电压幅值调整；(2)必要的滤波；(3)隔直；(4)解调。
2、A/D转换的作用：把模拟信号转换为数字信号，以便能用数字方法进行处理。
(1)采样：时间离散；(2)量化：幅值离散；(3)截断。
3、计算机或数字信号处理器的作用对数字化之后的信号进行处理。
(三)模拟信号的数字化1、时域采样和混叠时域采样，就是等时间间隔地取点。
从数学处理上看，就是乘以采样函数，时域相乘相当于频域作卷积，就相当于频谱的周期延拓，即频谱的搬移。
在频域中，如果频谱的搬移距离过小，搬移后的频谱就会有一部分相互交叠，从而使新合成的频谱与原频谱不一致，无法准确地恢复原时域信号，这种现象称为混叠。
2、时域截断和泄漏时域截断，就是取有限长的信号。
从数学处理上看，就是乘以有限宽矩形窗函数。
时域相乘相当于频域作卷积，就相当于频谱的周期延拓，即频谱的搬移。
在频域中，由于矩形窗函数的频谱是一个无限带宽的sinc函数，即使原模拟信号是有限带宽的，截断后也必然成为无限带宽的，这种信号的能量在频率轴分布扩展的现象称为泄漏。
3、频域采样和栅栏效应频域采样，就是在频率轴上等间隔地取点，使频率离散化。
从数学处理上看，就是乘以频率采样函数。
频域相乘相当于时域作卷积，就相当于时域波形的周期延拓，即频域波形的搬移。
测试技术章节习题(附答案)
各章节习题(后附答案)第一章 信号及其描述（一）填空题1、 测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。
这些物理量就是 ，其中目前应用最广泛的是电信号。
2、 信号的时域描述，以 为独立变量；而信号的频域描述，以 为独立变量。
3、 周期信号的频谱具有三个特点： ， ， 。
4、 非周期信号包括 信号和 信号。
5、 描述随机信号的时域特征参数有 、 、 。
6、 对信号的双边谱而b ，实频谱（幅频谱）总是 对称，虚频谱（相频谱）总是 对称。
（二）判断对错题（用√或×表示）1、 各态历经随机过程一定是平稳随机过程。
（ ）2、 信号的时域描述与频域描述包含相同的信息量。
（ ）3、 非周期信号的频谱一定是连续的。
（ ）4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。
（ ）5、 随机信号的频域描述为功率谱。
（ ）（三）简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。
2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ，均方值2x ψ，和概率密度函数p(x)。
3、 求指数函数)0,0()(≥>=-t a Ae t x at的频谱。
4、 求被截断的余弦函数⎩⎨⎧≥<=Tt T t t t x ||0||cos )(0ω的傅立叶变换。
5、 求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x atω的频谱。
第二章测试装置的基本特性（一）填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ，输入信号2sin)(tt x =，则输出信号)(t y 的频率为=ω ，幅值=y ，相位=φ 。
2、 试求传递函数分别为5.05.35.1+s 和2224.141nn n s s ωωω++的两个环节串联后组成的系统的总灵敏度。
3、 为了获得测试信号的频谱，常用的信号分析方法有 、和 。
测试技术课后答案
作业一1、欲使测量结果具有普遍科学意义的条件是什么？答：①用来做比较的标准必须是精确已知的，得到公认的；②进行比较的测量系统必须是工作稳定的，经得起检验的。
2、非电量电测法的基本思想是什么？答：基本思想：首先要将输入物理量转换为电量，然后再进行必要的调节、转换、运算，最后以适当的形式输出。
3、什么是国际单位制？其基本量及其单位是什么？答：国际单位制是国际计量会议为了统一各国的计量单位而建立的统一国际单位制，简称SI，SI制由SI单位和SI单位的倍数单位组成。
基本量为长度、质量、时间、电流强度、热力学温度、发光强度，其单位分别为米、千克、秒、安培、开尔文、坎德拉、摩尔。
4、一般测量系统的组成分几个环节？分别说明其作用？答：一般测量系统的组成分为传感器、信号调理和测量电路、指示仪器、记录仪器、数据处理仪器及打印机等外部设备。
传感器是整个测试系统实现测试与自动控制的首要关键环节，作用是将被测非电量转换成便于放大、记录的电量；中间变换（信号调理）与测量电路依测量任务的不同而有很大的伸缩性，在简单的测量中可完全省略，将传感器的输出直接进行显示或记录；信号的转换（放大、滤波、调制和解调）；显示和记录仪器的作用是将中间变换与测量电路出来的电压或电流信号不失真地显示和记录出来；数据处理仪器、打印机、绘图仪是上述测试系统的延伸部分，它们能对测试系统输出的信号作进一步处理，以便使所需的信号更为明确。
5、举例说明直接测量和间接测量的主要区别是什么？答：无需经过函数关系的计算，直接通过测量仪器得到被测量值的测量为直接测量，可分为直接比较和间接比较两种。
直接将被测量和标准量进行比较的测量方法称为直接比较；利用仪器仪表把原始形态的待测物理量的变化变换成与之保持已知函数关系的另一种物理量的变化，并以人的感官所能接收的形式，在测量系统的输出端显示出来，弹簧测力。
间接测量是在直接测量的基础上，根据已知的函数关系，计算出所要测量的物理量的大小。
测试技术与信号处理课后答案
机械工程测试技术基础习题解答教材：机械工程测试技术基础，熊诗波 黄长艺主编，机械工业，2006年9月第3版第二次印刷。
第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出||–ω和φn –ω图，并与表1-1对比。
解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取（-T/2，T/2）00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn tn n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ21,3,,(1cos )00,2,4,6,n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ 1,3,5,2arctan1,3,5,200,2,4,6,nI n nRπn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩图1-4 周期方波信号波形图没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。
解答：00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰222200rms0000111cos 2()d sin d d 22T T Tx x ωtx x t t x ωt t t T T T-====⎰⎰⎰1-3 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。
测试技术与信号处理课程习题解答
Chapter 0 绪论0－1．举例说明什么是测试？答：(1) 测试例子：为了确定一端固定的悬臂梁的固有频率，我们可以采用锤击法对梁进行激振，再利用压电传感器、电荷放大器、波形记录器记录信号波形，由衰减的振荡波形便可以计算出悬臂梁的固有频率。
（2）结论：由本例可知：测试是指确定被测对象悬臂梁的属性—固有频率的全部操作，是通过一定的技术手段—激振、拾振、记录、数据处理等，获取悬臂梁固有频率的信息的过程。
0－2. 测试技术的任务是什么？答：测试技术的任务主要有:通过模型试验或现场实测，提高产品质量；通过测试，进行设备强度校验，提高产量和质量；监测环境振动和噪声，找振源，以便采取减振、防噪措施；通过测试，发现新的定律、公式等；通过测试和数据采集，实现对设备的状态监测、质量控制和故障诊断。
0－3. 以方框图的形式说明测试系统的组成，简述主要部分的作用。
答：（1）测试系统方框图如下。
（2）各部分的作用如下：●传感器是将被测信息转换成某种电信号的器件；●信号的调理是把来自传感器的信号转换成适合传输和处理的形式；●信号处理环节可对来自信号调理环节的信号，进行各种运算、滤波和分析；●信号显示、记录环节将来自信号处理环节的信号显示或存贮。
●模数（A/D）转换和数模（D/A）转换是进行模拟信号与数字信号相互转换，以便用计算机处理。
0－4．测试技术的发展动向是什么?传感器向新型、微型、智能型方向发展；测试仪器向高精度、多功能、小型化、在线监测、性能标准化和低价格发展；参数测量与数据处理向计算机为核心发展。
Chapter 1 信号分类与表述1－1．求周期方波的傅立叶级数（复指数函数形式），画出|cn|-ω和ϕ-ω图。
解：(1)方波的时域描述为：(2) 从而：1－2．求正弦信号的绝对均值和均方根值。
解(1)(2)1－3．求符号函数和单位阶跃函数的频谱。
解：(1)因为不满足绝对可积条件，因此，可以把符合函数看作为双边指数衰减函数：其傅里叶变换为：(2)阶跃函数：Chapter 2 信号分析与处理2－1．已知信号的自相关函数，求该信号的均方值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
测试技术与信号处理课后答案机械工程测试技术基础习题解答教材：机械工程测试技术基础，熊诗波 黄长艺主编，机械工业出版社，2006年9月第3版第二次印刷。
第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。
解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取（-T/2，T/2）000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )L T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±L 。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩L ππ图1-4 周期方波21,3,,(1cos)00,2,4,6,nAnAc n nnn⎧=±±±⎪==-=⎨⎪=±±±⎩LLπππ1,3,5,2arctan1,3,5,200,2,4,6,nInnRπncπφncn⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩LLL没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sinx t xωt=的绝对均值xμ和均方根值rms x。
解答：00002200000224211()d sin d sin d cosT TT Txx x x x μx t t xωt tωt tωtT T T TωTωπ====-==⎰⎰⎰rmsx====1-3 求指数函数()(0,0)atx t Ae a t-=>≥的频谱。
解答：(2)22022(2)()()(2)2(2)a j f tj f t at j f te A A a j fX f x t e dt Ae e dt Aa j f a j f a f-+∞∞---∞-∞-=====-+++⎰⎰πππππππ()X f=π/20ω00幅频图相频图周期方波复指数函数形式频谱图πωω0ω0Im ()2()arctanarctanRe ()X f ff X f a==-πϕ1-4 求符号函数(见图1-25a)和单位阶跃函数(见图1-25b)的频谱。
a)符号函数的频谱10()sgn()10t x t t t +>⎧==⎨-<⎩t =0处可不予定义，或规定sgn(0)=0。
该信号不满足绝对可积条件，不能直接求解，但傅里叶变换存在。
可以借助于双边指数衰减信号与符号函数相乘，这样单边指数衰减信号频谱图 f|X (f )|Aφ(f ) fπ/2-π/2 tsgn(t ) 0 1 -1 tu (t )0 1图1-25 题1-4图a)符号函数 b)阶跃函数便满足傅里叶变换的条件。
先求此乘积信号x 1(t)的频谱，然后取极限得出符号函数x (t )的频谱。
10()sgn()0atatate t x t et et --⎧>==⎨-<⎩10()sgn()lim ()a x t t x t →==22211224()()(2)j f t at j f t at j f t f X f x t e dt e e dt e e dt ja f ∞∞-----∞-∞==-+=-+⎰⎰⎰πππππ[]101()sgn()lim ()a X f t X f jf→===-πF1()X f fπ=02()02f f f πϕπ⎧<⎪⎪=⎨⎪->⎪⎩b)阶跃函数频谱10()00t u t t >⎧=⎨<⎩在跳变点t =0处函数值未定义，或规定u (0)=1/2。
阶跃信号不满足绝对可积条件，但却存在傅里叶变1()sgn()at x t e t -=符号函数tx 1(t )0 1-符号函数频谱f φ(f )0 π/2 0f|X (f )|-π/2换。
由于不满足绝对可积条件，不能直接求其傅里叶变换，可采用如下方法求解。
解法1：利用符号函数11()sgn()22u t t =+ [][]1111111()()sgn()()()22222U f u t t f j f j f f ⎛⎫⎡⎤⎡⎤==+=+-=- ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦δδππF F F()2211()()2U f f f δπ=+结果表明，单位阶跃信号u (t )的频谱在f =0处存在一个冲激分量，这是因为u (t )含有直流分量，在预料之中。
同时，由于u (t )不是纯直流信号，在t =0处有跳变，因此在频谱中还包含其它频率分量。
解法2：利用冲激函数10()()d 00tt u t t δττ-∞>⎧==⎨<⎩⎰时时根据傅里叶变换的积分特性1111()()d ()(0)()()222t U f f f f j j f f δττδδππ-∞⎡⎤⎡⎤==∆+∆=-⎢⎥⎢⎥⎣⎦⎣⎦⎰F1-5 求被截断的余弦函数0cos ωt (见图1-26)的傅里叶变换。
单位阶跃信号频谱f |U (f )|(1/2f φ(f )0 π/2 -π/20cos ()0ωt t T x t t T⎧<⎪=⎨≥⎪⎩解：0()()cos(2)x t w t f t =π w (t )为矩形脉冲信号 ()2sinc(2)W f T Tf =π()002201cos(2)2j f t j f tf t e e πππ-=+所以002211()()()22j f tj f t x t w t ew t e -=+ππ根据频移特性和叠加性得： 000011()()()22sinc[2()]sinc[2()]X f W f f W f f T T f f T T f f =-++=-++ππ可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二，各向左右移动f 0，同时谱线高度减小一半。
也说明，单一频率的简谐信号由于截断导致频谱变得无限宽。
1-6 求指数衰减信号0()sin atx t eωt-=的频谱fX (f )Tf-f 0被截断的余弦函数频谱 图1-26 被截断的余弦函数t tT -TT -Tx (t )w (t )10 01-解答：()0001sin()2j t j tt e e j-=-ωωω 所以()001()2j t j tatx t ee e j--=-ωω单边指数衰减信号1()(0,0)atx t ea t -=>≥的频谱密度函数为 11221()()j t at j t a j X f x t e dt e e dt a j a ∞∞----∞-====++⎰⎰ωωωωω根据频移特性和叠加性得：[]001010222200222000222222220000()()11()()()22()()[()]2[()][()][()][()]a j a j X X X j j a a a a ja a a a ⎡⎤---+=--+=-⎢⎥+-++⎣⎦--=-+-+++-++ωωωωωωωωωωωωωωωωωωωωωωωωωω指数衰减信号1-7 设有一时间函数f (t )及其频谱如图1-27所示。
现乘以余弦型振荡0cos ()m ωt ωω>。
在这个关系中，函数f (t )叫做调制信号，余弦振荡0cos ωt 叫做载波。
试求调幅信号0()cos f t ωt的傅里叶变换，示意画出调幅信号及其频谱。
又问：若0mωω<时将会出现什么情况？解：0()()cos()x t f t t =ω()[()]F f t =ωF()0001cos()2j t j tt e e -=+ωωω所以0011()()()22j tj t x t f t ef t e -=+ωω根据频移特性和叠加性得：11()()()22X f F F =-++ωωωω 可见调幅信号的频谱等于将调制信号的频谱一分为二，各向左右移动载频ω0，同时谱线高度减小一半。
图1-27 题1-7图ωF (ω)f(t) 0t-ωω若0mωω<将发生混叠。
1-8 求正弦信号0()sin()x t x ωt φ=+的均值xμ、均方值2xψ和概率密度函数p (x )。
解答： (1)000011lim()d sin()d 0T T xT μx ttx ωt φt T T →∞==+=⎰⎰，式中02πTω=—正弦信号周期 (2)22222200000111cos 2()lim ()d sin ()d d 22T T T x T x x ωt φψx t t x ωt φt t T T T →∞-+==+==⎰⎰⎰(3)在一个周期内12ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T t P x x t x x T T T →∞<≤+===22Δ0Δ0000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x πx x →→<≤+====-fX (f )ω0 -ω0矩形调幅信号频谱正弦信号第二章 测试装置的基本特性2-1 进行某动态压力测量时，所采用的压电式力传感器的灵敏度为90.9nC/MPa ，将它与增益为0.005V/nC 的电荷放大器相连，而电荷放大器的输出接到一台笔式记录仪上，记录仪的灵敏度为20mm/V 。
试计算这个测量系统的总灵敏度。
当压力变化为3.5MPa 时，记录笔在记录纸上的偏移量是多少？解：若不考虑负载效应，则各装置串联后总的灵敏度等于各装置灵敏度相乘，即S =90.9(nC/MPa)⨯0.005(V/nC)⨯20(mm/V)=9.09mm/M Pa 。
偏移量：y =S ⨯3.5=9.09⨯3.5=31.815mm 。
2-2 用一个时间常数为0.35s 的一阶装置去测量周期分别为1s 、2s 和5s 的正弦信号，问稳态响应幅值误差将是多少？解：设一阶系统1()1H s s τ=+，1()1H j ωτω=+()()A H ωω===，T 是输入的正弦信号的周期稳态响应相对幅值误差()1100%A δω=-⨯，将已知周期代入得58.6%1s32.7%2s8.5%5s T T T δ=⎧⎪≈=⎨⎪=⎩2-3 求周期信号x (t )=0.5cos10t +0.2cos(100t −45︒)通过传递函数为H (s )=1/(0.005s +1)的装置后得到的稳态响应。