人教版九年级上册期中检测题
人教版2024-2025学年九年级数学上册期中检测考试试卷[含答案]
![人教版2024-2025学年九年级数学上册期中检测考试试卷[含答案]](https://uimg.taocdn.com/bfdd7c88185f312b3169a45177232f60dccce771.webp)
2024-2025学年人教版九年级数学上册期中检测考试试卷同学,你好!答题前请认真阅读以下内容:1.本卷为物理卷,全卷共4页,满分150分,答题时长120分钟,考试形式为闭卷.2.请在答题卡相应位置作答,在试卷上答题视为无效.3.不得使用计算器.一、选择题(每题3分,共计36分,每题只有唯一选项正确,请把正确答案填入答题卡指定位置)1.下列图形中,不属于中心对称图形的是( )A .B .C .D .2.若一元二次方程2440mx x ++=没有实数根,则m 的取值范围是( )A .1m < B .1m <-C .1m ³-D .1m >3.抛物线()21112y x =-+-的顶点坐标为( )A .()1,1--B .()1,1C .()1,1-D .()1,1-4.已知1x ,2x 是方程2440x x ++=的两个根,则12x x +的值为( )A .4-B .4C .2-D .25.如图,在Rt ABC △中,已知9030BAC C Ð=°Ð=°,,将ABC V 绕点A 顺时针旋转70°得到AB C ¢¢△,则CAC ¢Ð的度数是( )A .60°B .70°C .80°D .90°6.二次函数()20y ax bx a =+¹的图象如图所示,则关于x 的一元二次方程20ax bx +=的根的情况是( ) A .有两个相等的实数根B .有两个不相等的实数根C .只有一个实数根D .没有实数根7.若二次函数2y ax =的图象经过()2,4P -,则该图象必经过点( )A .()2,4B .()2,4--C .()4,2--D .()4,2-8.电影《志愿军》不仅讲述了中国人民志愿军抗美援朝的故事,更是通过鲜活生动的人物塑造,让观众体会到历史事件背后的人性和情感,一上映就获得全国人民的追捧.某地第一天票房约3亿元,若以后每天票房按相同的增长率增长,三天后票房收入累计达18亿元,若把增长率记作x ,则方程可以列为( )A .()3118x +=B .()23118x +=C .()233118x +=+D .()()23313118x x +++=+9.为方便市民进行垃圾分类投放,某环保公司第一个月投放1000个垃圾桶,计划第三个月投放垃圾桶y 个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x ,那么y 与x 的函数关系是( )A .()210001y x =+B .()210001y x =-C .()211000y x =-+D .21000y x =+10.若方程20x px q -++=的一个根大于1,另一根小于1,则p q +的值( )A .不大于1B .大于1C .小于1D .不小于111.函数2y x bx c =++与y x =的图象如图所示,有以下结论:①240b c ->;②1b c +=-;③360b c ++=;④当13x <<时,()210x b x c +-+<,其中正确的个数是( )A .1B .2C .3D .412.如图,在ABC V 中,90BAC Ð=°,AB AC =,2BC =.点D 在BC 上,且13BD CD =∶∶.连接AD ,将线段AD 绕点A 顺时针旋转90°得到线段AE ,连接BE ,DE .则BDE V 的面积是( )A .14B .38C .34D .32二、填空题(每题4分,共计24分,把答案填在答题卡指定位置上)13.一元二次方程260x x m -+=有两个实数根1x ,2x .若12x =,则2x 的值为 14.若二次函数()232y x =-+,则此二次函数图象的对称轴是 .15.若点(),1A a -关于原点对称的点为()5,B b ,则点(),C a b 关于y 轴对称的点D 的坐标为.16.已知,a b 是一元二次方程2310x x -+=的两个根.则22ba b a b-+=+.17.小明推铅球,铅球行进高度()m y (与水平距离()m x 之间的关系式为()21184105y x =--+,当铅球行进的高度为16m 5时,铅球行进的水平距离x = .18.如图,在Rt ABC △中,90ACB Ð=°,30B Ð=°,AC =P 是BC 边上一动点,连接AP ,把线段AP 绕点A 逆时针旋转60°到线段AQ ,连接CQ ,则线段CQ 的最小值为.三、解答题(19、20、21题每题10分;22-26题每题12分,共计90分;请在答题卡指定位置作答,并写出别要的解答过程和步骤才给分)19.解方程(1)()22250x --=;(2)2520x x +-=.20.如图,在平面直角坐标系中,已知ABC V 的三个顶点的坐标分别为()()()5,4,0,3,2,1A B C .(1)画出ABC V 关于原点成中心对称的111A B C △,并写出点1C 的坐标;(2)画出将111A B C △绕点1C 按顺时针方向旋转90°所得到的221A B C △.21.已知关于x 的一元二次方程()()21360x m x m ---+=.(1)利用判别式判断方程实数根的情况;(2)若该方程只有一个根小于2,求m 的取值范围.22.如图,在ABC V 中,点E 在BC 边上,AE AB =,将线段AC 绕A 点旋转到AF 的位置,使得CAF BAE Ð=Ð,连接EF ,EF 与AC 交于点G .(1)求证:EF BC =;(2)若63ABC Ð=°,25ACB Ð=°,求FGC Ð的度数.23.已知抛物线2y ax bx c =++经过()2,0A -、()4,0B 、()2,8C 三点.(1)求抛物线的解析式,并写出抛物线的顶点M 的坐标;(2)该抛物线经过平移后得到新抛物线241y x x =-++,求原抛物线平移的方向和距离.24.近年来,湖北省某地致力打造特色乡村旅游,发展以“农家乐”“高端民宿”为代表的旅游度假区.为迎接旅游旺季的到来,某民宿准备重新调整房间价格,已知该民宿有20个房间,当每个房间每天的定价为500元时,所有房间全部住满;当每个房间每天的定价每增加50元时,就会有一个房间无人入住,如果有游客居住房间,民宿每天需要对每个房间各支出100元的其他费用.设每个房间每天的定价增加x 个50元(020x ££,且x 为整数),该民宿每天游客居住的房间数量为y 间,所获利润为W 元.为吸引游客,该地物价部门要求民宿尽最大可能让利游客.(1)分别求出y 与x ,W 与x 之间的函数关系式;(2)当定价为多少元时,民宿每天获得的利润可以达到9600元;(3)求当每个房间的定价为多少元时,民宿每天获得的利润最大,最大利润是多少?25.素材一:秦、汉时期是中国古代桥梁的创建发展时期,此时期创造了以砖石为材料主体的拱券结构,为后来拱桥的出现创造了先决条件.如图(1)是位于某市中心的一座大桥,已知该桥的桥拱呈抛物线形.在正常水位时测得桥拱处水面宽度OB 为40米,桥拱最高点到水面的距离为10米.素材二:在正常水位时,一艘货船在水面上航行,已知货船的宽DE 为16米,露出水面的高DG 为7米.四边形DEFG 为矩形,OD BE =.现以点O 为原点,以OB 所在直线为x 轴建立如图(2)所示的平面直角坐标系,将桥拱抽象为一条抛物线.(1)求此抛物线的解析式.(2)这艘货船能否安全过桥?(3)受天气影响,水位上升0.5米,若货船露出水面的高度不变,此时该货船能否安全过桥?26.如图①,在直角三角形纸片ABC 中,90BAC Ð=°,6AB =,8AC =.【数学活动】将三角形纸片ABC 进行以下操作:①折叠三角形纸片ABC ,使点C 与点A 重合,得到折痕DE ,然后展开铺平;②将DEC V 绕点D 顺时针方向旋转得到DFG V ,点E ,C 的对应点分别是点F ,G ,直线GF 与边AC 交于点M (点M 不与点A 重合),与边AB 交于点N .【数学思考】(1)折痕DE 的长为______;(2)在DEC V 绕点D 旋转的过程中,试判断MF 与ME 的数量关系,并证明你的结论;【数学探究】;(3)如图②,在DEC V 绕点D 旋转的过程中,当直线GF 经过点B 时,求AM 的长;【问题延伸】;(4)在DEC V 绕点D 旋转的过程中,连接AF ,则AF 的取值范围是______.【分析】本题主要考查了中心对称图形,解题的关键是找出对称中心.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.根据定义逐一判断即可.【详解】解:A .是中心对称图形,故本选项不合题意;B .不是中心对称图形,故本选项符合题意;C .是中心对称图形,故本选项不合题意;D .是中心对称图形,故本选项不合题意.故选:B .2.D【分析】本题主要考查根的判别式,熟练掌握一元二次方程的根与判别式间的关系是解题的关键.由方程无实数根即240b ac D =-<,从而得出关于m 的不等式,解之可得.【详解】解:∵关于x 的一元二次方程2440mx x ++=无实数根,22444416160b ac m m \D =-=-´=-<,解得:1m >.故选:D .3.A【分析】本题考查的是二次函数的性质,根据()2y a x h k =-+的顶点式(),h k 即可得到答案,熟练掌握二次函数的顶点式是解题的关键.【详解】解:抛物线()21112y x =-+-的顶点坐标为()1,1--,故选:A 4.A【分析】本题主要考查了根与系数的关系,1x ,2x 是一元二次方程200ax bx c a ++=¹()的两根时,12bx x a +=-.利用一元二次方程根与系数的关系求解即可.【详解】解:∵1x ,2x 是方程2440x x ++=的两个实数根,∴12441x x +=-=-.故选:A .【分析】本题主要考查了旋转的性质,熟知旋转的性质是解题的关键.【详解】解:∵将ABC V 绕点A 顺时针旋转70°得到AB C ¢¢△,∴70CAC ¢Ð=°,故选:B .6.B【分析】本题考查二次函数与一元二次方程的关系,解答本题的关键是掌握二次函数的性质;一元二次方程210ax bx ++=的根即为二次函数20y ax bx a +=¹()的图像与x 轴的交点的横坐标,结合图像即可得到答案.【详解】解:一元二次方程20 ax bx +=的根即为二次函数()20y ax bx a =+¹的图像与直线x轴的交点的横坐标,结合图像,可知二次函数20y ax bx a +=¹()的图像与x 轴有两个不同的交点,即方程20 ax bx +=有两个不相等的实数根,故选:B .7.A【分析】本题考查了二次函数图象与性质,主要利用了二次函数图象的对称性,确定出函数图象的对称轴为y 轴是解题的关键.先确定出二次函数图象的对称轴为y 轴,再根据二次函数的对称性解答.【详解】解:Q 二次函数2y ax =的对称轴为y 轴,且图象经过()2,4P -,\该图象必经过点()2,4,故选:A .8.D【分析】本题考查了增长率问题(一元二次方程的应用),根据题意求出第二天和第三天的票房即可求解.【详解】解:由题意得:第二天的票房为()31x +亿元,第三天的票房为()231x +亿元,∴()()23313118x x ++++=故选:D .【分析】本题主要考查了列二次函数关系式,根据题意可得,第二个月投放垃圾桶数量为()10001x +个,则第三个月投放垃圾桶数量为()210001x +个,据此可得答案.【详解】解:由题意得,()210001y x =+,故选:A .10.B【分析】本题考查的是一元二次方程根与系数的关系,由题意可设20x px q -++=的两个根分别为12,x x ,结合题意设11x >,21x <,12x x p +=,12x x q =-,可得()()12110x x --<,再进一步解得可得答案.【详解】解:设20x px q -++=的两个根分别为12,x x ,结合题意设11x >,21x <,12x x p +=,12x x q =-,∴()()12110x x --<,∴()121210x x x x -++<,∴10q p --+<,∴1p q +>.故选:B .11.B【分析】利用判别式的意义对①进行判断;利用x =1,1y =可对②进行判断;利用3x =,3y =对③进行判断;根据13x <<时,2x bx c x ++<可对④进行判断.本题考查了二次函数与不等式,二次函数图象与系数的关系,利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.【详解】解:Q 抛物线与x 轴没有公共点,240b c \D =-<,故①不符合题意;1x =Q ,1y =,11b c \++=,即0b c +=,故②不符合题意;3x =Q ,3y =,933b c \++=,360b c \++=,故③不符合题意;13x <<Q 时,2x bx c x ++<,()210x b x c \+-+<的解集为13x <<,故④不符合题意;故选:B .12.B【分析】本题考查了全等三角形的判定与性质,等腰直角三角形,根据SAS 证明EAB DAC △≌△是解题的关键.据旋转的性质得出,90AD AE DAE =Ð=°,再根据SAS 证明EAB DAC △≌△得出45C ABE Ð=Ð=°,CD BE =,得出90EBC Ð=°,再根据三角形的面积公式即可求解.【详解】解:90BAC Ð=°Q ,AB AC =,45ABC C \Ð=Ð=°,90BAD CAD Ð+Ð=°.由旋转得AD AE =,90BAD BAE DAE Ð+Ð=Ð=°,CAD BAE \Ð=Ð.在ADC △和AEB V 中,AD AE CAD BAE AC AB =ìïÐ=Ðíï=î()SAS ADC AEB \V V ≌,BE CD \=,45ABEC Ð=Ð=°.90EBD ABE ABC \Ð=Ð+Ð=°.2BC =Q ,13BD CD =::,11242BD \=´=, 33242BE CD ==´=,BDE \V 的面积是1113322228BD BE ×=´´=.故答案为:B .13.4【分析】本题考查了一元二次方程根与系数的关系,熟练掌握和运用一元二次方程根与系数的关系是解决本题的关键.根据一元二次方程根与系数的关系,即可求得答案.【详解】解:∵260x x m -+=有两个实数根1x ,2x ,12x =,∴126x x +=,∴24x =;故答案为:4.14.直线2x =-【分析】本题主要考查了二次函数对称轴.根据二次函数的顶点式写出对称轴即可.【详解】解:二次函数()232y x =-+,图象的对称轴是直线2x =-,故答案为:直线2x =-.15.()5,1【分析】本题考查平面直角坐标系中任意一点(),P x y ,关于原点的对称点是(),x y --,即关于原点的对称点,横纵坐标都变成相反数,得出a ,b 的值,根据关于y 轴对称的点横坐标互为相反数,纵坐标相等,即可得出答案.【详解】解:关于原点的对称点,横纵坐标都变成相反数,∴5a =-,1b =,即点C 为()5,1-,根据关于y 轴对称的点横坐标互为相反数,纵坐标相等,∴点(),C a b 关于y 轴对称的点D 的坐标为()5,1,故答案为:()5,1.16.73##123【分析】本题考查了一元二次方程的根与系数的关系,分式的化简,完全平方公式的化简计算,熟练掌握知识点是解题的关键.由题意得,3a b +=,1ab =,故()222927332b a b a b a b a b ab +---+===++.【详解】解:由题意得,3a b +=,1ab =∵22222222b a b b a b a b a b a b a b-++-+==+++,而()2222a b a b ab +=+-,∴()222927332b a b a b a b a b ab +---+===++,故答案为:73.17.2或6【分析】本题考查了二次函数的应用中函数式中自变量与函数表达的实际意义,把165y =代入函数解析式求解即可。
人教版2023-2024学年九年级上册期中数学质量检测试题(含解析)

人教版2023-2024学年九年级上册期中数学质量检测试题一.选择题(共12小题,满分36分,每小题3分)1.已知关于x的方程(m+1)x2+2x﹣3=0是一元二次方程,则m的取值范围是()A.m>﹣1B.m≠0C.m≤﹣1D.m≠﹣12.在平面直角坐标系中,点A(3,﹣4)与点B关于原点对称,则点B的位置()A.第一象限B.第二象限C.第三象限D.第四象限3.若n(n≠0)是关于x的方程x2+mx+n=0的根,则m+n的值为()A.0B.1C.﹣1D.﹣24.在下列方程中,满足两个实数根的和等于2的方程是()A.x2﹣2x+4=0B.x2+2x﹣4=0C.x2+2x+4=0D.x2﹣2x﹣4=0 5.一元二次方程x2+2020=0的根的情况是()A.有两个相等的实根B.有两个不等的实根C.只有一个实根D.无实数根6.如图,要为一幅长为29cm,宽为22cm的照片配一个相框,要求相框的四条边宽度相等,且相框所占面积为照片面积的四分之一,相框边的宽度为xcm,则可列方程为()A.(29﹣2x)(22﹣2x)=×29×22B.(29﹣2x)(22﹣2x)=×29×22C.(29﹣x)(22﹣x)=×29×22D.(29﹣x)(22﹣x)=×29×227.二次函数y=x2+3x﹣2的图象是()A.B.C.D.8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=﹣1,则下列四个结论错误的是()A.a﹣b+c<0B.2a+b=0C.4a﹣2b+c=0D.am2+b(m+1)≥a9.已知抛物线y=a(x﹣h)2+k与x轴有两个交点A(﹣1,0),B(3,0),抛物线y=a (x﹣h﹣m)2+k与x轴的一个交点是(4,0),则m的值是()A.5B.﹣1C.5或1D.﹣5或﹣1 10.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是()A.柱子OA的高度为3mB.喷出的水流距柱子1m处达到最大高度C.喷出的水流距水平面的最大高度是3mD.水池的半径至少要3m才能使喷出的水流不至于落在池外11.汽车在行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素,某车的刹车距离s(m)与车速x(km/h)之间有下列关系:s=0.01x+0.01x2,在一个限速40km/h的弯道上的刹车距离不能超过()A.15.8m B.16.4m C.14.8m D.17.4m12.如图,将△ABD绕顶点B顺时针旋转40°得到△CBE,且点C刚好落在线段AD上,若∠CBD=32°,则∠E的度数是()A.32°B.34°C.36°D.38°二.填空题(共6小题,满分24分,每小题4分)13.已知方程(a﹣3)x|a|﹣1+3x+3a=0是关于x的一元二次方程,则a=.14.设m,n是方程x2﹣x﹣2=0的两根,则m2+n+mn=.15.要将函数y=ax2+bx+c的图象向右平移3个单位长度.再向上平移2个单位长度得到的二次函数为y=2x2﹣4x+3,那么a+b+c=.16.若函数y=x2﹣4x+b的图象与坐标轴只有两个交点,则b的值是.17.如图,在喷水池的中心A处竖直安装一根水管AB,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线的表达式为y=﹣(x﹣1)2+3(0≤x≤3),则选取点D为坐标原点时的抛物线表达式为,其中自变量的取值范围是,水管AB的长为m.18.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=63°,∠E=71°,且AD⊥BC,则∠BAC的度数为.三.解答题(共8小题,满分90分)19.解下列方程:(1)(2x+1)2=9;(2)x2﹣2x﹣1=0;(3)(x﹣3)2=4(3﹣x).20.已知关于x的一元二次方程mx2+nx﹣2=0.(1)当n=m﹣2时,证明方程有两个实数根;(2)若方程有两个不相等的实数根,写出一组满足条件的m,n的值,并求出此时方程的根.21.二次函数f(x)=ax2+bx+c的自变量x的取值与函数y的值列表如下:(1)根据表中的信息求二次函数的解析式,并用配方法求出顶点的坐标;(2)请你写出两种平移的方法,使平移后二次函数图象的顶点落在直线y=x上,并写出平移后二次函数的解析式.22.如图,抛物线与直线交于点A(﹣4,﹣1)和点B(﹣2,3),抛物线顶点为A,直线与y轴交于点C.(1)求抛物线和直线的解析式;(2)若y轴上存在点P使△PAB的面积为9,求点P的坐标.23.在乐善中学组织的体育测试中,小壮掷出的实心球的高度y(m)与水平距离x(m)之间的关系式是y=﹣(x﹣3)2+,求小壮此次实心球推出的水平距离.24.如图,在一个边长为32cm的正方形的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计),且折成的长方体盒子的表面积是864cm2,求剪去小正方形的边长.25.利用对称性可设计出美丽的图案,在边长为1的方格中,有如图所示的四边形(顶点都在格点上)(1)先作该四边形关于直线l成轴对称图形.(2)再作出你所作图形连同原四边形绕O点按顺时针方向旋转90°后的图形.(3)完成上述设计后,求整个图案的面积.26.如图,已知二次函数的图象过点O(0,0),A(8,4),与x轴交于另一点B,且对称轴是直线x=3.(1)求该二次函数的解析式;(2)若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求M的坐标.参考答案与试题解析一.选择题(共12小题,满分36分,每小题3分)1.解:由题意得:m+1≠0,解得:m≠﹣1,故选:D.2.解:点A的坐标是(3,﹣4),若点A与点B关于原点对称,则点B的坐标为(﹣3,4),位于第二象限.故选:B.3.解:把x=n代入方程x2+mx+n=0得n2+mn+n=0,∵n≠0,∴n+m+1=0,即m+n=﹣1.故选:C.4.解:A、Δ=b2﹣4ac=(﹣2)2﹣4×1×4=﹣12<0,方程没有实数根,所以A选项不符合题意;B、x1+x2=﹣2,所以B选项不符合题意;C、Δ=b2﹣4ac=4﹣4×4<0,方程没有实数根,所以C选项不符合题意;D、x1+x2=2,所以D故选:D.5.解:∵a=1,b=0,c=2020,∴Δ=b2﹣4ac=02﹣4×1×2020=﹣8080<0,∴一元二次方程x2+2020=0的根的情况是无实数根.故选:D.6.解:设相框边的宽度为xcm,则可列方程为:(29﹣2x)(22﹣2x)=×29×22.故选:B.7.解:∵y=x2+3x﹣2=(x+)2﹣,∴抛物线的开口向上,顶点坐标为(﹣,﹣),对称轴为直线x=﹣故选:B.8.解:由抛物线可得当x=﹣1时,y<0,故a﹣b+c<0,故结论A正确;抛物线可得对称轴为x=﹣=﹣1,故2a﹣b=0,故结论B错误.由抛物线经过原点,对称轴为直线x=﹣1可知,当x=﹣2时,y=0,故4a﹣2b+c=0,故结论C正确;当x=﹣1时,该函数取得最小值,则am2+bm+c≥a﹣b+c,即am2+b(m+1)≥a,故结论D正确;故选:B.9.解:∵抛物线y=a(x﹣h)2+k的对称轴为直线x=h,抛物线y=a(x﹣h﹣m)2+k的对称轴为直线x=h+m,∴当点A(﹣1,0)平移后的对应点为(4,0),则m=4﹣(﹣1)=5;当点B(3,0)平移后的对应点为(4,0),则m=4﹣3=1,即m的值为5或1.故选:C.10.解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴当x=0时,y=3,即OA=3m,故A选项正确,当x=1时,y取得最大值,此时y=4,故B选项正确,C选项错误,当y=0时,x=3或x=﹣1D选项正确,故选:C.11.解:将x=40代入s=0.01x+0.01x2得,s=0.01×40+0.01×402=16.4,即刹车距离不能超过16.4m.故选:B.12.解:∵将△ABD绕点B顺时针旋转40°得到△CBE,∴CB=AB,∠ABC=40°,∠D=∠E,∴∠A=∠ACB=(180°﹣40°)=70°,∵∠CBD=32°,∴∠ABD=∠ABC+∠CBD=40°+32°=72°,∴∠D=∠E=180°﹣∠A﹣∠ABD=180°﹣70°﹣72°=38°.故选:D.二.填空题(共6小题,满分24分,每小题4分)13.解:∵(a﹣3)x|a|﹣1+3x+3a=0是关于x的一元二次方程,∴a﹣3≠0且|a|﹣1=2,解得a=﹣3,故答案为:﹣3.14.解:∵m是方程x2﹣x﹣2=0的根,∴m2﹣m﹣2=0,∴m2=m+2,∴m2+n+mn=m+2+n+mn=m+n+mn+2,∵m,n是方程x2﹣x﹣2=0的两根,∴m+n=1,mn=﹣2,∴m2+n+mn=1﹣2+2=1.故答案为:1.15.解:y=2x2﹣4x+3=2(x﹣1)2+1,把抛物线y=2(x﹣1)2+1向左平移3个单位长度,向下平移2个单位长度得到抛物线的解析式为y=2(x﹣1+3)2+1﹣2=2x2+8x+7,所以a=2,b=8,c=7,所以,a+b+c=17,故答案为17.16.解:令y=0,则x2﹣4x+b=0,当函数y=x2﹣4x+b的图象与坐标轴只有两个交点时有两种情况:①Δ=0,且函数图象不过原点∴△=(﹣4)2﹣4b=0解得:b=4;②Δ>0,且函数y=x2﹣4x+b的图象过原点,∴b=0故答案为:0或4.17.解:以池中心A为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.抛物线的解析式为,当选取点D为坐标原点时,相当于将原图象向左平移3个单位,故平移后的抛物线表达式为:(﹣3≤x≤0);令x=﹣3,则y=﹣+3=2.25.故水管AB的长为2.25m.故答案为:y=﹣(x+2)2+3,﹣3≤x≤0,2.25.18.解:由旋转性质得:∠C=∠E=71°,∠BAD=∠CAE=63°,∵AD⊥BC,∴∠CAD=90°﹣∠C=90°﹣71°=19°,∴∠BAC=∠BAD+∠CAD=63°+19°=82°,故答案为:82°.三.解答题(共8小题,满分90分)19.解:(1)(2x+1)2=9,开方得:2x+1=±3,解得:x1=1,x2=﹣2;(2)x2﹣2x﹣1=0,x2﹣2x=1,x2﹣2x+1=1+1,(x﹣1)2=2,开方得:x﹣1=,x1=1+,x2=1﹣;(3)(x﹣3)2=4(3﹣x),(x﹣3)2+4(x﹣3)=0,(x﹣3)(x﹣3+4)=0,x﹣3=0,x﹣3+4=0x1=3,x2=﹣1.20.(1)证明:当n=m﹣2时,Δ=n2﹣4×m×(﹣2)=(m﹣2)2﹣4×m×(﹣2)=m2﹣4m+4+8m=m2+4m+4=(m+2)2≥0,∴当n=m﹣2时,方程有两个实数根.(2)解:∵方程有两个不相等的实数根,∴Δ=n2﹣4×m×(﹣2)=n2+8m>0,∴符合题意.当m=n=1时,原方程为x2+x﹣2=0,即(x﹣1)(x+2)=0,解得:x1=1,x2=﹣2.21.解:(1)把(﹣1,0),(0,3),(3,0)分别代入y=ax2+bx+c(a≠0)中,得.解得.则该二次函数的解析式为:y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点的坐标为(1,4);(2)∵二次函数f(x)=ax2+bx+c的顶点坐标(1,4);∴二次函数图象向右平移3个单位后抛物线的顶点为(4,4)或向下平移3个单位后抛物线的顶点为(1,1)落在直线y =x 上,则此时抛物线的解析式为:y =﹣(x ﹣4)2+4或y =﹣(x ﹣1)2+1.22.解:(1)由抛物线的顶点A (﹣4,﹣1)设二次函数为y =a (x +4)2﹣1,将B (﹣2,3)代入得,3=a (﹣2+4)2﹣1,解得a =1,∴二次函数为y =(x +4)2﹣1(或y =x 2+8x +15),设一次函数的解析式为y =kx +b ,将A (﹣4,﹣1)和B (﹣2,3)代入得,解得,∴一次函数的解析式为y =2x +7;(2)由直线y =2x +7可知C (0,7),设P (0,n ),∴PC =|n ﹣7|,∴S △PAB =S △PAC ﹣S △BPC =(4﹣2)•|n ﹣7|=9,∴|n ﹣7|=9,∴n =﹣2或16,∴P (0,﹣2)或P (0,16).23.解:令y =0,则﹣(x ﹣3)2+=0,解得:x 1=8,x 2=﹣2(舍去),故小壮此次实心球推出的水平距离为:8米.24.解:设剪去小正方形的边长为xcm ,则折成的长方体盒子的底面的长为(32﹣2x )cm ,宽为=(16﹣x )(cm ),由题意得:2x (16﹣x )+2(16﹣x )(32﹣2x )+2x (32﹣2x )=864,整理得:x 2+16x ﹣80=0,解得:x =4或x =﹣20(不符合题意,舍去),答:剪去小正方形的边长为4cm.25.解:(1)图形如图所示;(2)图形如图所示;(3)整个图案的面积=4××2×5=20.26.解:(1)∵抛物线过原点,对称轴是直线x=3,∴B点坐标为(6,0),设抛物线解析式为y=ax(x﹣6),把A(8,4)代入得a•8×2=4,解得a=,∴抛物线解析式为y=x(x﹣6),即y=x2﹣x;(2)设M(t,0),易得直线OA的解析式为y=x,设直线AB的解析式为y=kx+b,把B(6,0),A(8,4)代入得,解得,∴直线AB的解析式为y=2x﹣12,∵MN∥AB,∴设直线MN的解析式为y=2x+n,把M(t,0)代入得2t+n=0,解得n=﹣2t,∴直线MN的解析式为y=2x﹣2t,解方程组得,则N (t ,t ),∴S △AMN =S △AOM ﹣S △NOM=•4•t ﹣•t •t=﹣t 2+2t=﹣(t ﹣3)2+3,当t =3时,S △AMN 有最大值3,此时M 点坐标为(3,0).。
人教版九年级语文上册期中考试卷及答案

人教版九年级语文上册期中考试卷及答案班级:姓名:得分:一、语文积累与综合运用(30分)1.默写古诗文中的名句。
(10分)(1)补全下列名句中的上句或下句。
(6分)①山舞银蛇,(毛泽东《沁园春·雪》)②,将登太行雪满山。
(李白《行路难》)③,枳花明驿墙。
(温庭筠《商山早行》)④野芳发而幽香,。
(欧阳修《醉翁亭记》)⑤露从今夜白,。
(杜甫《月夜忆舍弟》)⑥,湘水无情吊岂知?(刘长卿《长沙过贾谊宅》)(2)根据提示默写出相应的名句。
(4分)①韩愈《左迁至蓝关示侄孙湘》中坦陈心志、不惜残年、忠君之弥坚的句子是“,。
”②苏轼《水调歌头·明月几时有》中道出千古离共同人心愿的句子是“,。
”【答案】(1)①原驰蜡象②欲渡黄河冰塞川③槲叶落山路④佳木秀而繁阴⑤月是故乡明⑥汉文有道恩犹薄(2)①欲为圣明除弊事肯将衰朽惜残年②但愿人长久千里共婵娟(每空一分,出现错字、漏字、别字现象,该空不得分。
)【解析】本题考查学生对古诗文名句的识记能力。
解答此类题目,我们需要在平时的学习中,做好积累,根据提示语句写成相应的句子,尤其要注意不能出现错别字。
第(1)小题是直接默写,第(2)小题是理解性识记,注意结合语境填充。
注意“驰”“塞”“槲”“弊”“衰”“婵”等字的写法。
2.阅读下面的文字,完成(1)~(4)小题。
(9分)喜欢一个人的文字,可以不需要理由,就像眼前读简祯的文字,不曾móu()面,却感觉她就在眼前,如一个老朋友,在轻轻诉说着旧事新愁。
读简祯散文,如看一路山水,目不遐接,叮当作响;如闻满街市声,不乏情趣;如参一路禅.()意,静心益智;还可兼想一路心事,自有独处的妙境。
我喜欢一个人静静地阅读,夜深人静,她的文字就是月,可以赏,可以读,可以通心。
我的心因她的文字而开朗,如一股清泉,沁月而出,因美而陶醉。
而此时的夜因了她的字更加wú()媚。
“若有眠,枕的是月”,而此时,我若有眠,枕的自然是她的文字。
2024年最新人教版九年级数学(上册)期中考卷及答案(各版本)

2024年最新人教版九年级数学(上册)期中考卷一、选择题(每题3分,共30分)1. 若一个数的立方根是±2,则这个数是()A. 4B. 8C. 16D. 322. 下列各数中,不是有理数的是()A. 2B. 0.5C. 3/4D. √23. 下列等式中,正确的是()A. 3x + 4y = 7B. 2x 3y = 5C. 4x + 5y = 9D. 5x 6y = 84. 下列各式中,正确的是()A. a^2 + b^2 = c^2B. a^2 b^2 = c^2C. a^2 + b^2 = c^2D. a^2 b^2 = c^25. 下列各式中,正确的是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a b)^2 = a^2 2ab +b^2 C. (a + b)^2 = a^2 2ab + b^2 D. (a b)^2 = a^2 + 2ab +b^26. 下列各式中,正确的是()A. (a + b)(c + d) = ac + ad + bc + bdB. (a b)(c d) =ac ad bc + bd C. (a + b)(c d) = ac + ad bc bd D. (ab)(c + d) = ac ad + bc bd7. 下列各式中,正确的是()A. a^3 + b^3 = (a + b)(a^2 ab + b^2)B. a^3 b^3 = (a b)(a^2 + ab + b^2)C. a^3 + b^3 = (a b)(a^2 ab + b^2)D.a^3 b^3 = (a + b)(a^2 + ab + b^2)8. 下列各式中,正确的是()A. a^4 b^4 = (a + b)(a^2 ab + b^2)B. a^4 b^4 = (a b)(a^2 + ab + b^2)C. a^4 b^4 = (a + b)(a^2 + ab + b^2)D. a^4 b^4 = (a b)(a^2 ab + b^2)9. 下列各式中,正确的是()A. (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3B. (a b)^3 =a^3 3a^2b + 3ab^2 b^3 C. (a + b)^3 = a^3 3a^2b + 3ab^2 + b^3 D. (a b)^3 = a^3 + 3a^2b 3ab^2 b^310. 下列各式中,正确的是()A. (a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4B. (a b)^4 = a^4 4a^3b + 6a^2b^2 4ab^3 + b^4C. (a + b)^4 = a^4 4a^3b + 6a^2b^2 + 4ab^3 + b^4D. (a b)^4 = a^4 + 4a^3b6a^2b^2 4ab^3 + b^4二、填空题(每题4分,共40分)11. 若一个数的平方根是±3,则这个数是_________。
人教版九年级上册数学期中考试试卷含答案
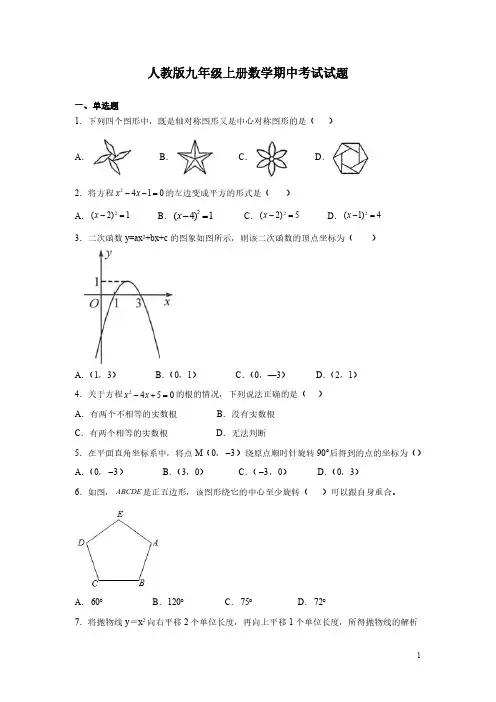
人教版九年级上册数学期中考试试题一、单选题1.下列四个图形中,既是轴对称图形又是中心对称图形的是()A .B .C .D .2.将方程2410x x --=的左边变成平方的形式是()A .2(2)1x -=B .2(4)1x -=C .2(2)5x -=D .2(1)4x -=3.二次函数y=ax 2+bx+c 的图象如图所示,则该二次函数的顶点坐标为()A .(1,3)B .(0,1)C .(0,—3)D .(2,1)4.关于方程2450x x -+=的根的情况,下列说法正确的是()A .有两个不相等的实数根B .没有实数根C .有两个相等的实数根D .无法判断5.在平面直角坐标系中,将点M (0,3-)绕原点顺时针旋转90°后得到的点的坐标为()A .(0,3-)B .(3,0)C .(3-,0)D .(0,3)6.如图,ABCDE 是正五边形,该图形绕它的中心至少旋转()可以跟自身重合。
A .60︒B .120︒C .75︒D .72︒7.将抛物线y =x 2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的解析式是()A .y =(x +2)2+1B .y =(x -2)2+1C .y =(x +2)2-1D .y =(x -2)2-18.关于x 的一元二次方程x 2+px +q =0的两根同为负数,则()A .p >0且q >0B .p >0且q <0C .p <0且q >0D .p <0且q <09.在同一坐标系内,一次函数y ax b =+与二次函数28y ax x b =++的图象可能是A .B .C .D .10.如图,已知△ABC 的顶点坐标分别为A(0,2),B(1,0),C(2,1).若二次函数y=x 2+bx+1的图像与阴影部分(含边界)一定有公共点,则实数b 的取值范围是()A .b≤-2B .b<-2C .b≥-2D .b>-2二、填空题11.已知点(2,1)在抛物线y=ax 2上,则此函数的开口方向___________12.若关于x 的一元二次方程(m ﹣2)x 2+x+m 2﹣4=0的一个根为0,则m 值是_____.13.在平面直角坐标系中,点P (—10,a )与点Q (b ,b+1)关于原点对称,则a+b=____14.二次函数y=ax 2+bx+c (a≠0)图象上部分点的坐标(x ,y )对应值列表如下:x…-3-2-101…y…-4-3-4-7-12…则该图象的对称轴是___________15.如图,在等腰直角三角形△ABC中,∠C=90°,AC=,将△ABC绕点B顺时针旋转60°得到△DBE,连接DC,则线段DC=_____________cm.三、解答题16.抛物线y=-x2+bx+c的部分图象如图所示,若y≥0,则x的取值范围是___________17.解方程(1)x2+2x—8=0(2)2x2+3x+1=018.在正方形网格中建立平面直角坐标系xOy,△ABC的三个顶点均在格点上,(1)画出△ABC关于点O的中心对称图形△A1B1C1(2)线段AC与线段A1C1的位置关系是______________19.王师傅开了一家商店,七月份盈利2500元,九月份盈利3600元,且每个月盈利的平均增长率都相等,求每月盈利的平均增长率.20.已知关于x的方程x2+5x﹣p2=0.(1)求证:无论p取何值,方程总有两个不相等的实数根;(2)设方程的两个实数根为x1、x2,当x1+x2=x1x2时,求p的值.21.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.(1)求此抛物线的解析式;(2)求△BCD的面积.22.如图,P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A 逆时针旋转后,得到△P AB(1)点P与点P’之间的距离;(2)∠APB的度数.23.已知某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售的单价每降低1元,每天就多卖5件,但要求销售单价不得低于成本.(1)设降价x元,求出每天的销售利润y(元)与x(元)之间的函数关系式;(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元时,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)24.如图,△ABC是边长为4的等边三角形,点D是线段BC的中点,∠EDF=120°,把∠EDF绕点D旋转,使∠EDF的两边分别与线段AB、AC交于点E、F.(1)当DF⊥AC时,求证:BE=CF;(2)在旋转过程中,BE+CF是否为定值?若是,求出这个定值;若不是,请说明理由;(3)在旋转过程中,连接EF,设BE=x,△DEF的面积为S,求S与x之间的函数解析式,并求S的最小值.25.已知:抛物线l1:y=—x2+bx+3交x轴于点A、B,(点A在点B的左侧),交y轴于点C,其对称轴为直线x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,5—2)(1)求抛物线2l 的函数表达式;(2)P 为直线1x =上一动点,连接PA ,PC ,当PA PC =时,求点P 的坐标;(3)M 为抛物线2l 上一动点,过点M 作直线//MN y 轴,交抛物线1l 于点N ,求点M 自点A 运动至点E 的过程中,线段MN 长度的最大值.参考答案1.C【详解】解:A 、是中心对称图形,不是轴对称图形,故选项错误;B 、是轴对称图形,不是中心对称图形,故选项错误;C 、既是轴对称图形,又是中心对称图形,故选项正确;D 、是中心对称图形,不是轴对称图形,故选项错误.故选C.2.C【详解】2410x x --=2445x x +=-()225x -=故答案为:C .【点睛】本题考查了一元二次方程的转换问题,掌握配方法是解题的关键.3.D【解析】【分析】根据抛物线与x 轴的两个交点坐标确定对称轴后即可确定顶点坐标.【详解】解:观察图象发现图象与x 轴交于点(1,0)和(3,0),∴对称轴为2x =,∴顶点坐标为(2,1),故选:D .【点睛】本题考查了二次函数的性质及二次函数的图象的知识,解题的关键是根据交点坐标确定对称轴,难度不大.4.B【解析】【分析】根据一元二次方程根的判别式直接判断即可.【详解】解:关于方程2450x x -+=,∵1,4,5a b c ==-=,∴224(4)41540b ac -=--⨯⨯=-<,∴方程2450x x -+=没有实数根,故选:B .【点睛】本题主要考查一元二次方程根的判别式,熟知240b ac ->,有两个不相等的实数根;240b ac -=,有两个相等的实数根;24<0b ac -,没有实数根;是解题的关键.5.C【解析】【分析】根据旋转的性质即可确定点坐标.【详解】解:点(0,3)M -绕原点O 顺时针旋转90︒,得到的点的坐标为(3,0)-,故选:C .【点睛】本题考查了坐标与图形变化-旋转,解题的关键是掌握图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45︒,60︒,90︒,180︒.6.D【解析】【分析】根据正五边形的每个中心角相等且其和为360°即可得到结论.【详解】根据正五边形的性质,每个中心角的相等,则每个中心角的度数为360°÷5=72°,故该图形绕它的中心至少旋转72度可以跟自身重合.故选:D .【点睛】本题考查了图形的旋转及正多边形的性质,关键是抓住正多边形的中心角相等这一性质,问题即解决.7.B【解析】【分析】根据抛物线的平移规律“上加下减,左加右减”解答即可.【详解】将抛物线y =x 2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的解析式是y =(x -2)2+1.故选B.本题考查了抛物线的平移规律,熟记抛物线的平移规律“上加下减,左加右减”是解决问题的关键.8.A【解析】【详解】试题解析:设x1,x2是该方程的两个负数根,则有x1+x2<0,x1x2>0,∵x1+x2=-p,x1x2=q∴-p<0,q>0∴p>0,q>0.故选A.9.C【解析】【分析】x=0,求出两个函数图象在y轴上相交于同一点,再根据抛物线开口方向向上确定出a>0,然后确定出一次函数图象经过第一、三象限,从而得解.【详解】x=0时,两个函数的函数值y=b,所以,两个函数图象与y轴相交于同一点,故B、D选项错误;由A、C选项可知,抛物线开口方向向上,所以,a>0,所以,一次函数y=ax+b经过第一三象限,所以,A选项错误,C选项正确.故选C.【点睛】=+在不同情况下所在本题考查了二次函数图象,一次函数的图象,应该熟记一次函数y kx b的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.10.C【解析】根据y=x 2+bx+1与y 轴交于点(0,1),且与点C 关于x=1对称,则对称轴x≤1时,二次函数y=x 2+bx+1与阴影部分一定有交点,据此可求出b 的取值范围.【详解】当二次函数y=x 2+bx+1的图象经过点B (1,0)时,1+b+1=0.解得b=-2,故排除B 、D ;因为y=x 2+bx+1与y 轴交于点(0,1),所以(0,1)与点C 关于直线x=1对称,当对称轴x≤1时,二次函数y=x 2+bx+1与阴影部分一定有交点,所以-2b ≤1,解得b≥-2,故选C.【点睛】本题考查二次函数图象,解题的关键是利用特殊值法进行求解.11.向上【解析】【分析】根据二次函数图象上点的坐标特征,将点(2,1)代入抛物线方程,然后解关于a 的方程,求得a 的值,从而可以确定抛物线方程的二次项系数,即可以判断这条抛物线的开口方向.【详解】解:∵点(2,1)在抛物线y=ax 2上,∴点(2,1)满足抛物线方程y=ax 2,∴1=4a ,解得a =14;∴抛物线方程y =14x 2的二次项系数a =14>0,∴这条抛物线的开口方向向上.故答案是:向上.【点睛】本题考查了二次函数图象上点的坐标特征.经过图象上的某点时,该点一定满足该函数的关系式.12.-2【解析】【分析】根据一元二次方程的解的定义把x=0代入方法解得m=±2,然后根据一元二次方程的定义确定m 的值.【详解】把x=0代入方程(m-2)x 2+(2m-1)x+m 2-4=0得m 2-4=0,解得m=2或m=-2,而m-2≠0,所以m=-2.故答案为-2.【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.13.1-【解析】【分析】根据两个点关于原点对称时,它们的坐标符号相反可得10b =,11a =-,进而可得a b +的值.【详解】解: 点(10,)P a -与点(,1)Q b b +关于原点对称,10b ∴=,111a b =--=-,11101a b ∴+=-+=-,故答案为:1-.【点睛】本题主要考查了两个点关于原点对称,解题的关键是掌握点的坐标的变化规律:点关于原点对称时,它们的坐标符号相反.14.2x =-【解析】【分析】根据二次函数的图象具有对称性和表格中的数据,可以计算出该函数图象的对称轴.【详解】解:由表格可得,当x 取-3和-1时,y 值相等,该函数图象的对称轴为直线3(1)22-+-==-x ,【点睛】本题考查二次函数的性质、二次函数图象上点的坐标特征,解题的关键是明确题意,利用二次函数的对称性解答.15.2##2-+【解析】【分析】连接CE,延长DC交AB于H,先证明CH⊥AB,由直角三角形的性质可求解.【详解】如图,连接CE,延长DC交AB于H,∵将△ABC绕点B顺时针旋转60°得到△DBE,∴∠ABD=∠CBE=60°,BC=BE=AC=DE,∠ACB=∠DEB=90°,∴△BCE是等边三角形,∠EDB=45°,∴CE=BC,∠CEB=60°,∴CE=DE,∠DEC=30°,∴∠EDC=∠ECD=75°,∴∠BDH=∠EDC−∠EDB=30°,∵∠BDH+∠DBA=90°,∴CH⊥AB,又∵∠ACB=90°,BC=AC=2cm,∴AB AC=4(cm),CH=AH=BH=2(cm),∵CH⊥AB,BH=2cm,∠BDH=30°,∴BD=2BH=4cm,=(cm),)(cm),∴DC=DH−CH=(【点睛】本题考查了旋转的性质,等边三角形的性质,等腰直角三角形的性质,直角三角形的性质,灵活运用这些性质解决问题是本题的关键.16.−3≤x≤1【解析】【分析】函数的对称轴为:x=−1,与x轴的一个交点坐标为(1,0),则另外一个交点坐标为:(−3,0),即可求解.【详解】解:函数的对称轴为:x=−1,与x轴的一个交点坐标为(1,0),则另外一个交点坐标为:(−3,0),故:y≥0时,−3≤x≤1,故答案为:−3≤x≤1.【点睛】本题考查的是抛物线与x轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点,及这些点代表的意义及函数特征.17.(1)x1=2,x2=-4(2)x1=-1,x2=-1.2【解析】【分析】(1)利用因式分解法即可求解;(2)利用因式分解法即可求解.【详解】(1)x2+2x—8=0(x-2)(x+4)=0∴x-2=0或x+4=0∴x1=2,x2=-4(2)2x2+3x+1=0(2x+1)(x+1)=0∴2x+1=0或x+1=0∴x1=-12,x2=-1.【点睛】此题主要考查一元二次方程的求解,解题的关键是熟知因式分解法的运用.18.(1)见解析;(2)平行【解析】【分析】(1)分别作出三顶点关于原点的对称点,再顺次连接即可得;(2)根据中心对称的性质,即可得出平行且相等的关系.【详解】A B C即为所求.解:(1)如图所示,△111(2)由中心对称的性质可知:线段AC与线段A1C1平行且相等,线段AC与线段A1C1的位置关系是平行,故答案是:平行.【点睛】本题考查了利用旋转变换作图、中心对称图形,解题的关键是熟练掌握网格结构准确找出对应点的位置.19.20%【解析】【分析】设从七月到九月,每月盈利的平均增长率为x,根据该商店七月份及九月份的盈利额,即可得出关于x 的一元二次方程,解之取其正值即可得出结论.【详解】解:设从七月到九月,每月盈利的平均增长率为x ,依题意,得:22500(1)3600x +=,解得:10.220%x ==,2 2.2x =-(不合题意,舍去).答:从从七月到九月,每月盈利的平均增长率为20%.【点睛】本题考查了一元二次方程的应用,解题的关键是找准等量关系,正确列出一元二次方程.20.(1)证明见解析;(2)p =【解析】【分析】(1)求出根的判别式△=25+p 2,根据判别式的意义即可得出无论p 取何值,方程总有两个不相等的实数根;(2)根据根与系数的关系求出两根和与两根积,再代入x 1+x 2=x 1x 2,得到一个关于p 的一元二次方程,解方程即可.【详解】(1)证明:△=52﹣4(﹣p 2)=25+4p 2,∵无论p 取何值时,总有p 2≥0,∴25+4p 2>0,∴无论p 取何值时,方程总有两个不相等的实数根;(2)解:由题意可得,x 1+x 2=﹣5,x 1x 2=﹣p 2,∵x 1+x 2=x 1x 2,∴﹣5=﹣p 2,∴p =【点睛】本题考查了根的判别式和根与系数的关系,注意熟记以下知识点:(1)一元二次方程ax 2+bx+c =0(a≠0)的根与△=b 2﹣4ac 有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0时,方程有两个相等的实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.(2)一元二次方程ax 2+bx+c =0(a≠0)的两实数根分别为x 1,x 2,则有x 1+x 2=﹣a b ,x 1•x 2=c a.21.(1)2(1)4y x =--+;(2)6【解析】【分析】(1)设抛物线顶点式解析式2(1)4y a x =-+,然后把点B 的坐标代入求出a 的值,即可得解;(2)令0y =,解方程得出点C ,D 坐标,再用三角形面积公式即可得出结论.【详解】解:(1) 抛物线的顶点为(1,4)A ,∴设抛物线的解析式2(1)4y a x =-+,把点(0,3)B 代入得,43a +=,解得1a =-,∴抛物线的解析式为2(1)4y x =--+;(2)由(1)知,抛物线的解析式为2(1)4y x =--+;令0y =,则20(1)4x =--+,1x ∴=-或3x =,(1,0)C ∴-,(3,0)D ;4CD ∴=,11||43622BCD B S CD y ∆∴=⨯=⨯⨯=.【点睛】本题二次函数综合题,主要考查了待定系数法,坐标轴上点的特点,三角形的面积公式,解本题的关键是求出抛物线解析式,是一道比较简单的中考常考题.22.(1)6;(2)150︒【解析】【分析】(1)由已知PAC ∆绕点A 逆时针旋转后,得到△P AB ',可得PAC ∆≅△P AB ',PA P A =',旋转角60P AP BAC ∠'=∠=︒,所以APP ∆'为等边三角形,即可求得PP ';(2)由APP ∆'为等边三角形,得60APP ∠'=︒,在△PP B '中,已知三边,用勾股定理逆定理证出直角三角形,得出90P PB ∠'=︒,可求APB ∠的度数.【详解】解:(1)连接PP ',由题意可知10BP PC '==,AP AP '=,PAC P AB ∠=∠',而60PAC BAP ∠+∠=︒,所以60PAP ∠'=度.故APP ∆'为等边三角形,所以6PP AP AP '=='=;(2)利用勾股定理的逆定理可知:222PP BP BP '+=',所以∆'BPP 为直角三角形,且90BPP ∠'=︒可求9060150APB ∠=︒+︒=︒.【点睛】本题考查旋转的性质,旋转变化前后,对应线段、对应角分别相等,解题的关键是你掌握旋转的图形的大小、形状都不改变.23.(1)252002500,(050)y x x x =-++≤≤;(2)销售单价为80元时,每天的销售利润最大,最大利润是4500元;(3)销售单价应该控制在82元至90元之间【解析】【分析】(1)根据“利润=(售价-成本)⨯销售量”列出方程;(2)把(1)中的二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答;(3)每天的销售利润不低于4000元,根据二次函数与不等式的关系求出x 的取值范围,再根据每天的总成本不超过7000元,以及50100100x ≤-≤,列不等式组即可.【详解】解:(1)由题意得:(10050)(505)y x x =--+,(50)(505)x x =-+,252002500,(050)x x x =-++≤≤,所以252002500,(050)y x x x =-++≤≤;(2)22520025005(20)4500y x x x =-++=--+ ,50a =-< ,∴抛物线开口向下.050x ≤≤Q ,对称轴是直线20x =,∴当20x =时,即销售单价是80元,每天的销售利润最大,最大利润是4500y =最大值;即销售单价为80元时,每天的销售利润最大,最大利润是4500元;(3)当4000y =时,2400052002500x x =-++,解得:110x =,230x =,∴当1030x ≤≤时,即销售单价在7010090x ≤-≤,每天的销售利润不低于4000元,由每天的总成本不超过7000元,得50(550)7000x + ,解得:18x ≤,82100x ∴≤-,50100100x ≤-≤Q ,∴销售单价应该控制在82元至90元之间.【点睛】本题主要考查二次函数的实际应用,解题的关键是弄清题意,列出相应等式,借助二次函数解决实际问题.24.(1)见解析;(2)BE+CF =2,是为定值;(3)S x ﹣1)2,当x =1时,S最小值为4.【解析】【分析】(1)根据四边形内角和为360°,可求∠DEA =90°,根据“AAS”可判定△BDE ≌△CDF ,即可证BE =CF ;(2)过点D 作DM ⊥AB 于M ,作DN ⊥AC 于N ,如图2,易证△MBD ≌△NCD ,则有BM =CN ,DM =DN ,进而可证到△EMD ≌△FND ,则有EM =FN ,就可得到BE+CF =BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=12BC=2;(3)过点F作FG⊥AB,由题意可得S△DEF=S△ABC﹣S△AEF﹣S△BDE﹣S△BCF,则可求S与x 之间的函数解析式,根据二次函数最值的求法,可求S的最小值.【详解】(1)∵△ABC是边长为4的等边三角形,点D是线段BC的中点,∴∠B=∠C=60°,BD=CD,∵DF⊥AC,∴∠DFA=90°,∵∠A+∠EDF+∠AFD+∠AED=180°,∴∠AED=90°,∴∠DEB=∠DFC,且∠B=∠C=60°,BD=DC,∴△BDE≌△CDF(AAS)(2)过点D作DM⊥AB于M,作DN⊥AC于N,则有∠AMD=∠BMD=∠AND=∠CND=90°.∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.∵∠EDF=120°,∴∠MDE=∠NDF.在△MBD和△NCD中,BMD CNDB CBD DC∠=∠⎧⎪∠∠⎨⎪⎩==∴△MBD≌△NCD(AAS)BM=CN,DM=DN.在△EMD 和△FND 中,EMD FND DM DN MDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△EMD ≌△FND (ASA )∴EM =FN ,∴BE+CF =BM+EM+CF =BM+FN+CF =BM+CN=2BM =2BD×cos60°=BD =12BC =2(3)过点F 作FG ⊥AB ,垂足为G,∵BE =x∴AE =4﹣x ,CF =2﹣x ,∴AF =2+x ,∵S △DEF =S △ABC ﹣S △AEF ﹣S △BDE ﹣S △BCF ,∴S =12BC×AB×sin60°﹣12AE×AF×sin60°﹣12BE×BD×sin60°﹣12CF×CD×sin60°=12×(4﹣x )×(2+x )1212×(2﹣x )∴Sx ﹣1)2(∴当x =1时,S【点睛】本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,通过证明三角形全等得到BM =CN ,DM =DN ,EM =FN 是解决本题的关键.25.(1)215222y x x =--;(2)(1,1);(3)12【解析】【分析】(1)由对称轴可求得b ,可求得1l 的解析式,令0y =可求得A 点坐标,再利用待定系数法可求得2l 的表达式;(2)设P 点坐标为(1,)y ,由勾股定理可表示出2PC 和2PA ,由条件可得到关于y 的方程可求得y ,可求得P 点坐标;(3)可分别设出M 、N 的坐标,可表示出MN ,再根据函数的性质可求得MN 的最大值.【详解】解:(1) 抛物线21:3l y x bx =-++的对称轴为1x =,12b∴-=-,解得2b =,∴抛物线1l 的解析式为2y x 2x 3=-++,令0y =,可得2230x x -++=,解得1x =-或3x =,A ∴点坐标为(1,0)-,抛物线2l 经过点A 、E 两点,∴可设抛物线2l 解析式为(1)(5)y a x x =+-,又 抛物线2l 交y 轴于点(20,5)D -,552a ∴-=-,解得12a =,2115(1)(5)2222y x x x x ∴=+-=--,∴抛物线2l 的函数表达式为215222y x x =--;(2)设P 点坐标为(1,)y ,由(1)可得C 点坐标为(0,3),22221(3)610PC y y y ∴=+-=-+,2222[1(1)]4PA y y =--+=+,PC PA = ,226104y y y ∴-+=+,解得1y =,P ∴点坐标为(1,1);(3)由题意可设215(,2)22M x x x --,//MN y 轴,2(,23)N x x x ∴-++,令221523222x x x x -++=--,可解得1x =-或113x =,①当1113x -< 时,2222153113449(23)(2)4()2222236MN x x x x x x x =-++---=-++=--+,显然411133-< ,∴当43x =时,MN 有最大值496;②当1153x < 时,2222153113449(2)(23)4()2222236MN x x x x x x x =----++=--=--,显然当43x >时,MN 随x 的增大而增大,∴当5x =时,MN 有最大值,23449(512236⨯--=;综上可知在点M 自点A 运动至点E 的过程中,线段MN 长度的最大值为12.【点睛】本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理等知识点,在(1)中求得A 点的坐标是解题的关键,在(2)中用P 点的坐标分别表示出PA 、PC 是解题的关键,在(3)中用M 、N 的坐标分别表示出MN 的长是解题的关键,注意分类讨论.。
人教版九年级上册数学期中考试试题含答案

人教版九年级上册数学期中考试试卷一、单选题1.下列图案中,不是轴对称图形的是()A .B .C .D .2.用配方法解方程x 2+2x ﹣1=0,原方程应变形为()A .(x+1)2=0B .(x ﹣1)2=2C .(x+1)2=2D .(x ﹣1)2=53.若方程x 2+kx ﹣2=0的一个根是﹣2,则k 的值是()A .﹣1B .1C .2D .﹣24.顶点(﹣5,﹣1),且开口方向、形状与函数y =13x 2的图象相同的抛物线是()A .2153y x =-B .21(5)13y x =-+C .21(5)13y x =--D .21(5)13y x =+-5.菱形ABCD 的一条对角线长为6,边AB 的长是方程x 2﹣7x+12=0的一个根,则菱形ABCD 的周长为()A .16B .12C .16或12D .246.新能源汽车越来越受消费者喜爱,我国新能源汽车近几年销量逐年增加,2018年销量为95万辆,到2020年销量为120万辆,设年平均增长率为x ,可列方程为()A .952(1)x -=120B .952(1)x +=120C .1202(1)x -=95D .95(1+2x )=1207.抛物线y =x 2+4x ﹣m 2+2(m 是常数)与坐标轴交点的个数为()A .0B .1C .3D .2或38.如图,将Rt ∆ABC 以直角顶点C 为旋转中心顺时针旋转使点A 刚好落在AB 上(即:点A’),若∠A=55︒则图中∠1=()A .110︒B .102︒C .105︒D .125︒9.已知二次函数y =ax 2+bx+c (a≠0)图象上部分点的坐标(x ,y)的对应值如表所示,则方程ax 2+bx+2.32=0的根是()A .0或4B .1或5C 4D 210.如图,二次函数y =ax 2+bx 的图象经过点P ,若点P 的横坐标为﹣1,则一次函数y =(a ﹣b )x+b 的图象大致是()A .B .C .D .二、填空题11.已知坐标系中点()2,A a -和点(),3B b 关于原点中心对称,则a b +=__________.12.将二次函数y =﹣(x ﹣1)2的图象沿x 轴向左平移2个单位,得到的函数表达式为___.13.若关于x 的方程(k ﹣1)x 2+2x ﹣1=0有两个实数根,则k 的取值范围是___.14.已知抛物线y =x 2+bx+c 的部分图象如图所示,当y >0时,x 的取值范围是___.15.将边长为3的正方形ABCD 绕点C 顺时针方向旋转45°到FECG 的位置(如图),EF与AD相交于点H,则HD的长为___.(结果保留根号)16.已知矩形的周长为18cm,绕它的一边旋转成一个圆柱,则旋转成的圆柱的最大侧面积为___m2.17.如图,抛物线y=ax2+bx+c(a≠0)经过点(2,0),对称轴为直线x=﹣1.下列结论:①abc>0;②8a+c=0;③对于任意实数m,总有a(m2﹣1)+b(m+1)≥0;④对于a的每一个确定值,若一元二次方程ax2+bx+c=P(P为常数,且P>0)的根为整数,则P的值有且只有三个,其中正确的结论是___.三、解答题18.解方程:2x2﹣5x+1=019.已知二次函数y=x2﹣2mx+m2+2(m是常数).(1)求证:不论m为何值,该函数的图象与x轴没有公共点;(2)把该函数的图象沿y轴向下平移个单位长度后,得到的函数的图象与x轴只有一个公共点.20.在正方形网格中,建立如图所示的平面直角坐标系xOy, ABC的三个顶点都在格点上,点A的坐标(4,4),若将 ABC绕点O逆时针旋转90°.(1)画出旋转后的 111A B C;(2)点1A坐标为,1B坐标为,1C坐标为.21.甲、乙两人同解方程组515410ax yx by+=⎧⎨-=-⎩①②,由于甲看错了方程①中的a,得到方程组的解为31xy=-⎧⎨=⎩,乙看错了方程②中的b,得到方程组的解为54xy=⎧⎨=-⎩.(1)求a,b的值;(2)若关于x的一元二次方程a2x﹣bx+m=0两实数根为1x,2x,且满足71x﹣2x=6,求实数m的值.22.观察下列两个三位数的乘积,其中百位上的数字都是901×999,902×998,903×997,……,998×902,999×901.解决以下问题:(1)根据上面的规律填空,912×;(2)若某个三位数中,十位上的数字与个位上的数字组成的两位数为x,则这个三位数可以表示为,当x取何值时,以上两个三位数的乘积最大.23.如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=﹣16x2+bx+c表示.(1)求抛物线的函数关系式和拱顶D到地面OA的距离;(2)一辆货运汽车载集装箱后高为6m,宽为4m,若隧道内设双向行车道,那么这辆货车能否安全通过?24.某经销商销售一种产品,这种产品的成本价为10元/千克,物价部门规定这种产品的销售价不高于18元/千克,同时公司要保证获得的利润不低于20%,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?(3)当售价为多少时,公司能获得最大利润,最大利润是多少?25.已知抛物线y=ax2+bx+c(a≠0)经过A(4,0)、B(﹣1,0)、C(0,4)三点.(1)求抛物线的函数解析式;(2)如图1,点D是直线AC上方的抛物线的一点,DN⊥AC于点D,DM//y轴交AC于点M ,求 DMN 周长的最大值及此时点D 的坐标;(3)如图2,点P 为抛物线第一象限上的点,连接OP 与直线AC 相交于点Q ,若:COQ AOQ S S △△=3:5,求点P 的坐标.参考答案1.C 【详解】试题分析:A 、是轴对称图形,故错误;B 、是轴对称图形,故错误;C 、不是轴对称图形,故正确;D 、是轴对称图形,故错误.故选C .考点:轴对称图形.2.C 【分析】方程移项后,利用完全平方公式配方得到结果,即可作出判断.【详解】解:方程移项得:x 2+2x =1,配方得:x 2+2x+1=2,则方程变形为(x+1)2=2.故选:C .3.B 【解析】将x =﹣2代入方程即可求出k 的值.【详解】解:将x =﹣2代入x 2+kx ﹣2=0,∴4﹣2k ﹣2=0,∴k =1,故选:B .4.D 【分析】根据抛物线的顶点和开口方向、形状与函数y =13x 2的图象相同,可得出抛物线解析式为21(5)13y x =+-.【详解】解:∵抛物线的顶点为(﹣5,﹣1),∴抛物线解析式为2(5)1y a x =+-;∵开口方向、形状与函数y =13x 2的图象相同,∴13a =,抛物线解析式为:21(5)13y x =+-;故选:D .5.A 【分析】先利用因式分解法解方程得到x 1=3,x 2=4,再根据菱形的性质可确定边AB 的长是4,然后计算菱形的周长.【详解】(x ﹣3)(x ﹣4)=0,x ﹣3=0或x ﹣4=0,所以x 1=3,x 2=4,∵菱形ABCD 的一条对角线长为6,∴边AB的长是4,∴菱形ABCD的周长为16.故选A.6.B【分析】根据平均增长率问题列出方程即可.【详解】∵2018年销量为95万辆,到2020年销量为120万辆,年平均增长率为x,(1)x+=120∴952故选B.7.D【解析】先计算判别式的值可判断抛物线与x轴的交点个数,而抛物线与y轴一定有一个交点,于是可判断抛物线y=x2+4x﹣m2+2的图象与坐标轴的交点个数.【详解】解:y=x2+4x﹣m2+2∵△=42−4×(﹣m2+2)=4m2+8>0,∴抛物线与x轴有2个公共点,∵x=0时,y=x2+4x﹣m2+2=﹣m2+2,∴抛物线与y轴的交点为(0,﹣m2+2),当﹣m2+2=0时,即m=时,抛物线与坐标轴交于原点,此时抛物线y=x2+4x﹣m2+2(m 是常数)与坐标轴交点的个数为2个,∴抛物线y=x2+4x﹣m2+2的图象与坐标轴的交点个数为3或2个.故选:D.【点睛】本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),Δ=b2−4ac决定抛物线与x轴的交点个数:Δ=b2−4ac>0时,抛物线与x轴有2个交点;Δ=b2−4ac=0时,抛物线与x轴有1个交点;Δ=b2−4ac<0时,抛物线与x轴没有交点.8.C解:根据旋转图形可得:AC=A′C ,则∠CA′A=∠A=55°,则∠A′CA=70°,即选择的角度为70°,所以∠BCB′=70°,根据∠ACB=90°,∠A=55°可得∠B=35°,根据旋转可得:∠B′=∠B=35°,根据三角形外角的性质可得:∠1=∠B′+∠BCB′=35°+70°=105°.故选C 9.C 【解析】【分析】利用抛物线经过点(0,0.32)得到0.32c =,根据抛物线的对称性得到抛物线的对称轴为直线2x =,抛物线经过点2)-,由于方程2 2.320ax bx ++=变形为20.322ax bx ++=-,则方程2 2.320ax bx ++=的根理解为函数值为2-所对应的自变量的值,所以方程2 2.320ax bx ++=的根为1x =,24x =【详解】解:由抛物线经过点(0,0.32)得到0.32c =,所以二次函数解析式为20.32y ax bx =++,因为抛物线经过点(0,0.32)、(4,0.32),所以抛物线的对称轴为直线2x =,而抛物线经过点2)-,所以抛物线经过点(42)-,方程2 2.320ax bx ++=变形为20.322ax bx ++=-,所以方程20.322ax bx ++=-的根理解为函数值为2-所对应的自变量的值,所以方程2 2.320ax bx ++=的根为1x =24x =故选:C .【点睛】本题考查了抛物线与x 轴的交点:把求二次函数2(y ax bx c a =++,b ,c 是常数,0)a ≠与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质.10.D 【解析】先求出a <0,b <0,再求出a ﹣b <0,最后判断函数图象即可.【详解】解:由二次函数的图象可知,a <0,b <0,当x =﹣1时,y =a ﹣b <0,∴y =(a ﹣b )x+b 的图象在第二、三、四象限,故选:D .【点睛】本题主要考查二次函数图象上点的坐标特征,一次函数的图象和性质,由二次函数图象得出a ﹣b <0是解题的关键.11.-1【解析】【分析】直接利用关于原点对称点的性质,得出a ,b 的值,即可得出答案.【详解】解:∵坐标系中点A (-2,a )和点B (b ,3)关于原点中心对称,∴b=2,a=-3,则a+b=2-3=-1.故答案为:-1.【点睛】此题主要考查了关于原点对称点的性质,正确掌握横纵坐标的符号关系是解题关键.12.y =﹣2(1)x +【解析】【分析】根据平移的规律左加右减计算即可.【详解】∵二次函数y =﹣2(1)x -的图象沿x 轴向左平移2个单位,∴得到的函数表达式为y =﹣2(12)x -+即y =﹣2(1)x +.故答案为:y =﹣2(1)x .【点睛】本题考查了二次函数的平移问题,熟练掌握平移规律是解题的关键.13.k≥0且k≠1【解析】【分析】由关于x 的方程(k−1)x 2+2x−1=0有两个实数根,知22−4×(k−1)×(−1)≥0且k−1≠0,解之即可.【详解】解:∵关于x 的方程(k−1)x 2+2x−1=0有两个实数根,∴22−4×(k−1)×(−1)≥0且k−1≠0,解得k≥0且k≠1,故答案为:k≥0且k≠1.【点睛】本题主要考查根的判别式和一元二次方程的定义,一元二次方程ax 2+bx +c =0(a≠0)的根与△=b 2−4ac 有如下关系:①当Δ>0时,方程有两个不相等的实数根;②当Δ=0时,方程有两个相等的实数根;③当Δ<0时,方程无实数根.14.x <﹣1或x >3##x >3或x <﹣1【解析】【分析】根据函数图象和二次函数的性质,可以得到该抛物线与x 轴的另一个交点,从而可以得到当y >0时,x 的取值范围.【详解】解:由图象可得,该抛物线的对称轴为直线x =1,与x 轴的一个交点为(﹣1,0),故抛物线与x 轴的另一个交点为(3,0),故当y >0时,x 的取值范围是x <﹣1或x >3,故答案为:x <﹣1或x >3.【点睛】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.15.﹣3【解析】【分析】先根据正方形的性质得到CD=3,∠CDA=90°,再利用旋转的性质得CF=,根据正方形的性质得∠CFE=45°,则可判断△DFH为等腰直角三角形,从而计算CF﹣CD即可得出答案.【详解】解:∵四边形ABCD为正方形,∴CD=3,∠CDA=90°,∵边长为3的正方形ABCD绕点C按顺时针方向旋转到FECG的位置,使得点D落在对角线CF上,∴CF=,∠CFE=45°,∴△DFH为等腰直角三角形,∴DH=DF=CF﹣CD=﹣3.故答案为:﹣3.【点睛】本题考查了旋转的性质,正方形的性质,熟练掌握旋转的性质是解题的关键.16.812π##40.5π【解析】【分析】设矩形的长是a,宽为9-a,旋转形成的圆柱侧面积得到关于a的二次函数,根据二次函数的性质确定最大值即可.【详解】解:设矩形的长为a,宽为9-a,∵旋转形成的圆柱侧面积是S=2πa(9﹣a)=﹣2π(a﹣92)2+812π,∴当a=92时,侧面积有最大值为812π,故答案为:81 2π【点睛】本题考查了二次函数的应用,熟练列出二次函数并掌握求二次函数最值的方法是解题的关键.17.①②③④【解析】【分析】由抛物线y=ax2+bx+c(a≠0)经过点(2,0),对称轴为直线x=﹣1,可得28b ac a=⎧⎨=-⎩,由图可知a<0,即有b=2a<0,c=﹣8a>0,可判断①;由c=﹣8a可判断②;把a(m2﹣1)+b(m+1)变形为a(m+1)2,可判断③;根据抛物线y=ax2+bx+c与直线y=p(P为常数,且p>0)交点横坐标为整数,对称轴是x=﹣1,且抛物线y=ax2+bx+c(a≠0)经过点(2,0),可判断④.【详解】解:∵抛物线y=ax2+bx+c(a≠0)经过点(2,0),对称轴为直线x=﹣1,∴04212a b cba=++⎧⎪⎨=-⎪⎩,解得28b ac a=⎧⎨=-⎩,∴抛物线y=ax2+bx+c为y=ax2+2ax﹣8a,由图可知:a<0,∴b=2a<0,c=﹣8a>0,∴abc>0,故①正确;由c=﹣8a得8a+c=0,故②正确;∵a(m2﹣1)+b(m+1)=a(m2﹣1)+2a(m+1)=a(m+1)(m﹣1)+2a(m+1)=a(m+1)(m﹣1+2)=a(m+1)2,且a<0,(m+1)2≥0,∴a(m+1)2≤0,即a(m2﹣1)+b(m+1)≤0,故③正确;∵抛物线y =ax 2+bx+c 与直线y =p (p 为常数,且p >0)交点横坐标为整数,对称轴是x =﹣1,且抛物线y =ax 2+bx+c (a≠0)经过点(2,0),∴交点横坐标可能是﹣1,0或﹣2,1或﹣3,∴P 的值有且只有三个,故④正确;故答案为:①②③④.【点睛】本题考查二次函数图象的性质的综合应用,涉及图象上点坐标的特征、函数与方程的关系等知识,解题的关键是掌握二次函数的图象性质,利用数形结合解决问题.18.【解析】【分析】将常数项移到右边后把二次项系数化为1,再两边配上一次项系数一半的平方求解可得.【详解】解:∵2x 2-5x=-1,∴25122x x -=-,∴2525125216216x x -+=-+,即2517()416x -=,则54x -=,∴.19.(1)证明见解析,(2)2【解析】(1)计算判别式的值得到△=﹣8,然后根据判别式的意义得到结论;(2)设抛物线沿y 轴向下平移k (k >0)个单位长度后得到的函数图象与x 轴只有一个公共点,利用抛物线的平移规律得到平移后的抛物线解析式为y =x 2﹣2mx+m 2+2﹣k ,然后根据判别式的意义得到△=(﹣2m )2﹣4(m 2+1﹣k )=0,从而解关于k 的方程即可.【详解】解:(1)证明:△=(﹣2m )2﹣4(m 2+2)所以不论m为何值,该函数图象与x轴没有公共点;(2)设抛物线沿y轴向下平移k(k>0)个单位长度后得到的函数图象与x轴只有一个公共点,则平移后的抛物线解析式为y=x2﹣2mx+m2+2﹣k,△=(﹣2m)2﹣4(m2+2﹣k)=0,解得k=2,即把该函数图象沿y轴向下平移2个单位长度后得到的函数图象与x轴只有一个公共点.故答案为:2.20.(1)见解析;(2)1A(-4,4),,1B(-1,1),1C(-1,3).【分析】(1)分解坐标,构造全等三角形即可;(2)根据全等三角形的性质,得到线段长,根据点所在象限,确定坐标即可.【详解】解:(1)画图如下:(2)根据作图,得1A(-4,4),,1B(-1,1),1C(-1,3).【点睛】本题考查了旋转,坐标的确定,三角形的全等,熟练掌握旋转的性质,灵活运用三角形的全等是解题的关键.21.1)a=7,b=-2;(2)-5.【分析】(1)根据题意,-12-b=-10是正确的,5a-20=15是正确的,求解即可;(2)代入a ,b 的值得到72x +2x+m =0,运用根与系数关系定理,综合计算即可.【详解】(1)∵甲看错了方程①中的a ,得到方程组的解为31x y =-⎧⎨=⎩,乙看错了方程②中的b ,得到方程组的解为54x y =⎧⎨=-⎩,∴-12-b=-10是正确的,5a-20=15是正确的,解得a=7,b=-2;(2)把a=7,b=-2代入一元二次方程a 2x ﹣bx+m =0得到72x +2x+m =0,∵一元二次方程a 2x ﹣bx+m =0两实数根为1x ,2x ,∴1x +2x =27-即71x +72x =-2,1x 2x =7m 即m=71x ×2x ,∵71x ﹣2x =6,∴71x =6+2x ,∴6+2x +72x =-2,解得2x =-1,71x =5,∴m=-5.【点睛】本题考查了二元一次方程组的解,一元二次方程根与系数关系定理,正确理解方程组的解,灵活运用根与系数关系定理是解题的关键.22.(1)988;(2)900x +;50x =【解析】【分析】(1)根据已知数据可得两个数的后两位数字加起来是100,即可得解;(2)根据三位数的表示方法计算即可;【详解】(1)由题可得:两个数的后两位数字加起来是100,∴1001288-=,∴912988⨯,故答案是:988.(2)某个三位数中,十位上的数字与个位上的数字组成的两位数为x ,则这个三位数可以表示为900x +,则第二个两位数的后两位是100x -,第二个数是900100x +-,设两个三位数的乘积为y ,则,()()()290090010050902500y x x x =++-=--+,∵0a <,∴50x =时,y 有最大值,∴当50x =时,1001005050x -=-=,∴950950⨯最大.故答案是900x +.【点睛】本题主要考查了数字规律和二次函数的应用,准确计算是解题的关键.23.(1)y =﹣16x 2+2x+4,拱顶D 到地面OA 的距离为10m ;(2)能安全通过;【解析】【分析】(1)根据题意得出点B (0,4)、C (12,4),再利用待定系数法求解可得;(2)根据题意求出x =6﹣4=2时的函数值,比较可得;【详解】解:(1)根据题意将点B (0,4)、C (12,4)代入解析式得:411441246c b c =⎧⎪⎨-⨯++=⎪⎩,解得:24b c =⎧⎨=⎩,∴y =﹣16x 2+2x+4=﹣16(x ﹣6)2+10,∴拱顶D 到地面OA 的距离为10m ;(2)∵隧道内设双向行车道,故每条车到宽6m ,货运汽车宽为4m ,x=6﹣4=2,代入解析式得y=﹣16(2﹣6)2+10=﹣16×16+10=223>6,∴如果隧道内设双向行车道,那么这辆货车能安全通过;【点睛】本题考查了二次函数的应用:构建二次函数模型解决实际问题,利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.24.(1)y与x之间的函数关系式y=−2x+60(10≤x≤18);(2)该经销商想要每天获得150元的销售利润,销售价应定为15元;(3)当销售价为18元时,每天的销售利润最大,最大利润是192元.【解析】【分析】(1)设函数关系式y=kx+b,把(10,40),(18,24)代入求出k和b即可,由成本价为10元/千克,销售价不高于18元/千克,得出自变量x的取值范围;(2)根据销售利润=销售量×每一件的销售利润,找出等量关系列一元二次方程求出x,再根据x的取值范围即可确定x的值;(3)根据销售利润=销售量×每一件的销售利润,得到w和x的关系,利用二次函数的性质得最值即可.【详解】解:(1)设函数关系式y=kx+b,把(10,40),(18,24)代入得:1040 1824k bk b+=⎧⎨+=⎩,解得:260 kb=-⎧⎨=⎩,∴y与x之间的函数关系式y=−2x+60(10≤x≤18);(2)由题意知:(x−10)(−2x+60)=150,整理得:−2x2+80x−600=150,解得:x1=15,x2=25(不合题意,舍去)答:该经销商想要每天获得150元的销售利润,销售价应定为15元.(3)W=(x−10)(−2x+60)=−2x 2+80x−600=−2(x−20)2+200,对称轴x =20,在对称轴的左侧W 随着x 的增大而增大,∵10≤x≤18,∴当x =18时,W 最大,最大为192.即当销售价为18元时,每天的销售利润最大,最大利润是192元.【点睛】本题考查了二次函数的应用,得到每天的销售利润的关系式是解决本题的关键,结合实际情况利用二次函数的性质解决问题.25.(1)234y x x =-++;(2)DMN周长的最大值为,(2,6)D ;(3)P ⎝⎭【解析】【分析】将(4,0)A 、(1,0)B -、(0,4)C 代入2y ax bx c =++中,建立方程组求解即可;(2)延长DM 交x 轴于点H ,通过分析证明DMN是等腰直角三角形,得到1)DMN C DM =△,用待定系数法求得直线AC 的解析式,设2(,34)D m m m -++,点4(),M m m -+,求得DM 的表达式,配方求得DM 最大值,分析得到周长的最大值和点D 的坐标;(3)过点Q 作QE x ⊥轴于点E ,由面积比求得35CQ AQ =,由平行线段分线段成比例得到35OE CQ AE AQ ==,从而知道点Q 的横坐标,代入直线AC 求得纵坐标,用待定系数法求得直线OQ 的解析式,与抛物线建立方程组即可求得点P 的坐标.【详解】解:(1)∵抛物线2(0)y ax bx c a =++≠经过A(4,0)、B(﹣1,0)、C(0,4)三点∴将(4,0)A 、(1,0)B -、(0,4)C 代入2y ax bx c =++中得:164004a b c a b c c ++=⎧⎪-+=⎨⎪=⎩解得:134a b c =-⎧⎪=⎨⎪=⎩∴抛物线的解析式为:234y x x =-++(2)如图1,延长DM 交x 轴于点H ∵(4,0)A 、(0,4)C ∴4OA OC ==又∵90AOC ∠= ,∴45OCA OAC ∠=∠=∵//DM y 轴∴90AHM ∠= ,45AMH ACO ∠=∠= ∴=45DMN AMH ∠=∠∵DN AC⊥∴90DNM ∠=∴45NDM ∠=∴DMN 是等腰直角三角形∴=2DN MN =设直线AC 的解析式为(0)y kx b k =+≠将(4,0)A 、(0,4)C 两点坐标代入得:404k b b +=⎧⎨=⎩解得:14k b =-⎧⎨=⎩∴直线AC 的解析式为:4y x =-+设2(,34)D m m m -++,则点4(),M m m -+∴()22234(4)424DM m m m m m m =-++--+=-+=--+∴当2m =时,DM 取的最大值2,此时(2,6)D ∵DMN 为等腰直角三角形∴1)22DMN C DN MN DM DM DM DM DM=++++=+△∴DMN 周长的最大值为:1)+=,此时(2,6)D (3)如图2:过点Q 作QE x ⊥轴于点E∵:=3:5COQ AOQ S S △△∴35CQ AQ =∵QE x ⊥轴∴90AQE ∠=o又∵90ACO ∠=∴//QE CO ∴35OECQAE AQ ==又∵4OA =∴32OE =,即32Q x =∵点Q 在直线AC 上∴35+4=22Q y =-∴35(,)22Q 设直线OQ 的解析式为:(0y mx m =≠)将点Q 代入得:53m =∴直线OQ 的解析式为:53y x =又∵点P 是直线OQ 与抛物线的交点∴25334y x y x x ⎧=⎪⎨⎪=-++⎩∴234120x x --=234120x x --=即()60x -=或20x +=解得:122,33x x -==又∵P 为抛物线第一象限上的点∴点P的横坐标为:=3P x∴510=339P y +⨯=∴P ⎝⎭【点睛】本题考查待定系数法求一次函数和二次函数解析式、等腰直角三角形性质、相似三角形的判定和性质,二次函数的最值求法等知识点,能够数形结合分析是解题关键.。
人教版九年级上册数学期中考试试题含答案
人教版九年级上册数学期中考试试题一、选择题。
(每小题只有一个正确答案)1.在以下“绿色食品、响应环保、可回收物、节水”四个标志图案中,是中心对称图形的是A .B .C .D .2.将方程23610x x -+=化成一元二次方程的一般形式,其中二次项系数、一次项系数和常数项分别是()A .3,6,1-B .3,6,1C .3,16-D .3,1,63.抛物线()221y x =--的顶点坐标是()A .()2,1-B .()2,1--C .()2,1D .()2,1-4.关于x 的方程2420x x m -++=有一个根为1,-则另一个根为()A .2B .2-C .5D .5-5.将二次函数213y x =的图象向右平移1个单位,再向上平移3个单位,所得图象的解析式为()A .()21133y x =-+B .()21133y x =++C .()21y x 133=--D .()21133y x =+-6.“双十一”即指每年的11月11日,是指由电子商务代表的在全中国范围内兴起的大型购物促销狂欢日.2017年双十一淘宝销售额达到1682亿元.2019年双十一淘宝交易额达2684亿元,设2017年到2019年淘宝双十一销售额年平均增长率为,x 则下列方程正确的是A .()168212684x +=B .()1682122684x +=C .()2168212684x +=D .()()216821168212684x x +++=7.如图,ABC 中,90,40ACB ABC ︒︒∠=∠=.将ABC 绕点B 逆时针旋转得到A BC ''△,使点C 的对应点C '恰好落在边AB 上,则CAA '∠的度数是()A .50︒B .70︒C .110︒D .120︒8.若无论x 取何值,代数式()()13x m x m +--的值恒为非负数,则m 的值为()A .0B .12C .13D .19.已知二次函数2(,,y ax bx c a b c =++是实数,且0a ≠)的图象的对称轴是直线2x =,点()11,A x y 和点2(),z B x y 为其图象上的两点,且12y y <()A .若120,x x -<则1240x x +-<B .若120,x x -<则1240x x +->C .若120,x x ->则()1240a x x +->D .若120,x x ->则()1240a x x +-<10.关于x 的二次函数22(81)8y mx m x m =+++的图像与x 轴有交点,则m 的范围是()A .116m <-B .116m ≥-且0m ≠C .116m =-D .116m >-且0m ≠二、填空题11.点(1,4)M -关于原点对称的点的坐标是_______________________.12.若关于x 的一元二次方程2320x x m -+=有两个相等的实数根;则m 的值为__________.13.如图,四边形ABCE 是О 的内接四边形,D 是CB 延长线上的一点,40,ABD ∠=︒那么AOC ∠的度数为_______________________o14.如图,把小圆形场地的半径增加6m 得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为________________________.m 15.已知二次函数2(,,y ax bx c a b c =++为常数,0,0a c ≠>)上有五点()()1,01,(),p t n -、、()()2,3,0t 、;有下列结论:①0b >;②关于x 的方程20ax bx c ++=的两个根是1-和3;③20p t +<;④()(4m am b a c m +≤--为任意实数).其中正确的结论_______________(填序号即可).16.如图,四边形ABCD 的两条对角线,AC BD 所成的锐角为60,10AC BD += ,则四边形ABCD 的面积最大值为_______________________.三、解答题17.解方程:260x x +-=.18.10月11日,2020中国女超联赛在昆明海堙基地落幕,最终武汉车都江大队夺得冠军.本赛季共有x 支球队参加了第一阶段的比赛,每两队之间进行一场比赛,第一阶段共进行了45场比赛,求x 的值.19.如图,AD=CB ,求证:AB=CD .20.如图,已知,,A B C 均在O 上,请用无刻度的直尺作图.(1)如图1,若点D 是AC 的中点,试画出B Ð的平分线;(2)若42A ∠= ,点D 在弦BC 上,在图2中画出一个含48 角的直角三角形.21.已知二次函数243y x x =-+-(1)若33x -≤≤,则y 的取值范围为_(直接写出结果);(2)若83y -≤≤-,则x 的取值范围为(直接写出结果);(3)若()()12,,1,A m y B m y +两点都在该函数的图象上,试比较1y 与2y 的大小.22.某公司经过市场调查,整理出某种商品在某个月的第天的售价与销量的相关信息如下表:第x 天售价(元件)日销售量(件)130x ≤≤60x +30010x-已知该商品的进价为40元/件.设销售该商品的日销售利润为y 元.(1)求y 与x 的函数关系式;(2)问销售该商品第几天时,日销售利润最大,最大日销售利润为多少元?(3)问在当月有多少天的日销售利润不低于5440元.请直接写出结果.23.如图,已知格点ABC 和点O .(1)A B C '''V 和ABC 关于点O 成中心对称,请在方格纸中画出A B C '''V (2)试探究,以点A ,O ,C ',D 为顶点的四边形为平行四边形的D 点有__________个.24.(问题背景)(1)如图1,Р是正三角形ABC 外一点,30APB ∠= ,则222PA PB PC +=小明为了证明这个结论,将PAB ∆绕点A 逆时针旋转60,请帮助小明完成他的作图;(迁移应用)(2)如图2,在等腰Rt ABC ∆中,,90BA BC ABC =∠= ,点P 在ABC ∆外部,使得45BPC ∠= ,若 4.5PAC S = ,求PC ;(拓展创新)(3)如图3,在四边形ABCD 中,//,AD BC 点E 在四边形ABCD 内部.且,DE EC =90,DEC ∠= 135AEB ∠=︒,3,4,AD BC ==直接写出AB 的长.25.已知抛物线()2:0C y ax bx c a =++>,顶点为()0,0.(1)求,b c 的值;(2)如图1,若1,a P =为y 轴右侧抛物线C 上一动点,过P 作直线PN x ⊥轴交x 轴于点,N 交直线1:22l y x =+于点M ,设点P 的横坐标为m ,当2PM PN =时,求m 的值;(3)如图2,点()00,P x y 为y 轴正半轴上一定点,点,A B 均为y 轴右侧抛物线C 上两动点,若APO BPy ∠=∠,求证:直线AB 经过一个定点.参考答案1.B 【分析】根据中心对称图形的概念解答即可.【详解】解:A 、不是中心对称图形.故错误;B 、是中心对称图形.故正确;C 、不是中心对称图形.故错误;D 、不是中心对称图形.故错误.故选:B .【点睛】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.2.A 【分析】根据一元二次方程的定义判断即可;【详解】∵方程23610x x -+=,∴二次项系数为3,一次项系数为-6,常数项为1;故答案选A .【点睛】本题主要考查了一元二次方程的一般形式,准确分析判断是解题的关键.3.D 【分析】根据抛物线的解析式即可得.【详解】抛物线()221y x =--的顶点坐标是()2,1-,故选:D .【点睛】本题考查了求二次函数的顶点坐标,熟练掌握二次函数的顶点坐标的求法是解题关键.4.C 【分析】根据一元二次方程根与系数的关系求解.【详解】解:设原方程的另一根为x ,则:4141x --+=-=,∴x=4+1=5,故选C .【点睛】本题考查一元二次方程的应用,根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题关键.5.A 【分析】根据函数图象的平移方法判断即可;【详解】二次函数213y x =的图象向右平移1个单位,再向上平移3个单位,可得:()21133y x =-+;故答案选A .【点睛】本题主要考查了二次函数图象的平移,准确分析判断是解题的关键.6.C 【分析】根据一元二次方程增长率问题模型()1na xb +=列式即可.【详解】由题意,增长前为1682a =,增长后2684b =,连续增长2年,代入得()2168212684x +=;故选:C .【点睛】本题考查了一元二次方程在增长率问题中的应用,熟练掌握基本模型,理解公式,找准各数量是解决问题的关键.7.D 【分析】由余角的性质,求出∠CAB=50°,由旋转的性质,得到40ABA '∠=︒,AB A B '=,然后求出BAA '∠,即可得到答案.【详解】解:在ABC 中,90,40ACB ABC ︒︒∠=∠=,∴∠CAB=50°,由旋转的性质,则40ABA '∠=︒,AB A B '=,∴1(18040)702BAA '∠=⨯︒-︒=︒,∴''50+70=120CAA CAB BAA ∠=∠+∠=︒︒︒;故选:D .【点睛】本题考查了旋转的性质,三角形的内角和定理,以及余角的性质,解题的关键是掌握所学的性质,正确求出70BAA '∠=︒.8.B 【分析】先利用多项式乘多项式的法则展开,再根据代数式(x +1−3m )(x−m )的值为非负数时△≤0以及平方的非负性即可求解.【详解】解:(x +1−3m )(x−m )=x 2+(1−4m )x +3m 2−m ,∵无论x 取何值,代数式(x +1−3m )(x−m )的值恒为非负数,∴△=(1−4m )2−4(3m 2−m )=(1−2m )2≤0,又∵(1−2m )2≥0,∴1−2m =0,∴m =12.故选:B .【点睛】本题考查了多项式乘多项式,二次函数与一元二次方程的关系,偶次方非负数的性质,根据题意得出(x +1−3m )(x−m )的值为非负数时△≤0是解题的关键.9.D 【分析】根据二次函数的性质和题目中的条件,可以判断选项中的式子是否正确;【详解】∵二次函数2(,,y ax bx c a b c =++是实数,且0a ≠)的图象的对称轴是直线2x =,点()11,A x y 和点2(),z B x y 为其图象上的两点,且12y y <,∴若a >0,1x <2<2x ,则可能出现124+-x x >0,故A 错误;若a <0,122x x <<,则1240x x +-<,故B 错误;若0a >,12x x >,则1240x x +-<,则()1240a x x +-<,故C 错误;若0a >,12x x >,则1240x x +-<,则()1240a x x +-<,若0a <,12x x >,则1240x x +->,则()1240a x x +-<,故D 正确;故答案选D .【点睛】本题主要考查了二次函数的性质,二次函数图象上点的坐标特征,准确分析计算是关键.10.B 【详解】试题分析:二次函数图象与x 轴有交点,则△=b 2-4ac≥0,且m≠0,列出不等式则可.由题意得2(81)8800m m m m ⎧+-⨯≥⎨≠⎩,解得116m ≥-且0m ≠,故选B.考点:该题考查函数图象与坐标轴的交点判断点评:当△=b 2-4ac >0时图象与x 轴有两个交点;当△=b 2-4ac=0时图象与x 轴有一个交点;当△=b 2-4ac <0时图象与x 轴没有交点.同时要密切注意11.()1,4-【分析】由关于原点对称的点的坐标特征可以得到解答.【详解】解:∵关于原点对称的点的坐标特征为:x x y y =-⎧⎨=-''⎩,由题意得:x=1,y=-4,∴14x y -''=⎧⎨=⎩,∴点M(1,−4)关于原点对称的点的坐标是(-1,4),故答案为(-1,4).【点睛】本题考查图形变换的坐标表示,熟练掌握关于原点对称的点的坐标特征是解题关键.12.13【分析】根据关于x 的一元二次方程2320x x m -+=有两个相等的实数根,得出关于m 的方程,求解即可.【详解】解:∵关于x 的一元二次方程2320x x m -+=有两个相等的实数根,∴△=b 2-4ac=(-2)2-4×3m=0,解得m=13,故答案为:13.【点睛】本题考查了根的判别式,掌握知识点是解题关键.13.80【分析】先根据补角的性质求出∠ABC 的度数,再由圆内接四边形的性质求出∠AEC 的度数,由圆周角定理即可得出∠AOC 的度数.【详解】解:∵∠ABD =40°,∴∠ABC =180°−∠ABD =180°−40°=140°,∵四边形ABCE 为⊙O 的内接四边形,∴∠AEC =180°−∠ABC =180°−140°=40°,∴∠AOC =2∠AEC =2×40°=80°.故答案为:80.【点睛】本题考查的是圆周角定理及圆内接四边形的性质,掌握圆内接四边形的性质和圆周角定理是解答此题的关键.14.6【分析】根据等量关系“大圆的面积=2×小圆的面积”可列方程求解;【详解】设小圆的半径为xm ,则大圆的半径为()6x m +,根据题意得:()2262x x ππ+=,即2212362x x x ++=,解得:16x =+,26x =-(舍去);故答案是:6.【点睛】本题主要考查了一元二次方程的应用,准确分析计算是解题的关键.15.①②④【分析】由抛物线的对称性可知对称轴为0212x +==,可得0p =,即1x =-,3x =是方程20ax bx c ++=的两个根,再根据题目当中给出的条件,代入解析式判断求解即可;【详解】当0x =和2x =时,y t =,∴对称轴为0212x +==,∴当1x =-,3x =时,y 的值相等,∴0p =,∴1x =-,3x =是方程20ax bx c ++=的两个根,故②正确;∵当0x =时,y t =,且c >0,∴t c =>0,∴202p t t +=+>0,故③错误;∵2x =,y t =>0,3x =,0y =,∴在对称轴的右边,y 随x 的增大而减小,∴a <0,∵12bx a =-=,∴2b a =->0,故①正确;∵当3x =时,0y =,∴930a b c ++=,∴30a c +=,∴3c a =-,∴443a c a a a --=-+=-,∵顶点坐标为()1,n ,a <0,∴2am bm c a b c ++≤++,∴2am bm a b +≤+,∴2am bm a +≤-,∴24am bm a c +≤--,故④正确;综上所述:结论正确的是①②④;故答案是:①②④.【点睛】本题主要考查了二次函数图象性质,熟练掌握二次函数图像上点的特征是解题的关键.16.4【分析】根据四边形面积公式,S =12AC×BD×sin60°,根据sin60°=2得出S =12x (10−x )×2,再利用二次函数最值求出即可.【详解】解:∵AC 与BD 所成的锐角为60°,∴根据四边形面积公式,得四边形ABCD 的面积S =12AC×BD×sin60°,设AC =x ,则BD =10−x ,所以S =12x (10−x )×32=34-(x−5)2+2534,所以当x =5,S 有最大值4.【点睛】此题主要考查了四边形面积公式以及二次函数最值,利用二次函数最值求出四边形的面积最大值是解决问题的关键.17.12x =,23x =-【分析】利用因式分解法解方程.【详解】解:()()230x x -+=∴20x -=或30x +=,∴12x =,23x =-.【点睛】本题考查一元二次方程的解法,选择合适的解法是关键.18.10【分析】因为每两队之间进行一场比赛,所以x 支球队之间共进行()112x x -场比赛,由此建立等式计算即可.【详解】()11452x x -=解得10x =或9-0,x > 10,x ∴=答:x 的值为10.【点睛】本题考查了一元二次方程的应用,解题关键在于读懂题意,得出总场数与球队数之间的关系.19.证明见解析.【详解】试题分析:由在同圆中,弦相等,则所对的弧相等和等量加等量还是等量求解.试题解析:∵AD =BC ,,AD BC= ,AD BDBC BD +=+∴ ,AD CD=∴AB =CD .20.(1)见解析;(2)见解析【分析】(1)根据题意连接OD 并延长交劣弧AC 于E 即可得解;(2)延长AD 交圆于M ,连接BO 并延长交圆于N ,即可得到;【详解】解:()1连接OD 并延长交劣弧AC 于E ,连接EB 即为所求:()2延长AD 交圆于,M 连接BO 并延长交圆于,N 连接;,,MN MB BMN ∆即为所求;.【点睛】本题主要考查了利用圆周角定理、垂径定理作图,准确分析判断是解题的关键.21.(1)241y -≤≤;(2)10x -≤≤或45x ≤≤;(3)32m >时21y y <,32m =时21y y =,32m <时21y y >【分析】(1)根据题意得出二次函数的对称轴,再利用已知的x 的取值范围计算即可;(2)分别令3y =-和8y =-,计算即可;(3)分别表示出1y 和2y ,分别令21y y -的取值计算即可;【详解】解:(1)∵243y x x =-+-,33x -≤≤,∴二次函数的对称轴22bx a =-=,∴最小值:当3x =-时,24y =-,最大值:当2x =时,1y =;故:241y -≤≤.(2)∵243y x x =-+-,83y -≤≤-,令3y =-,得0x =或4;令8y =-,得-1x =或5;∴10x -≤≤或45x ≤≤.()3A B 、两点都在该函数图象上,2143y m m ∴=-+-,()()22214132y m m m m =-+++-=-+,2132y y m -=-,令210y y ->,即21y y >,此时32m <,令210y y -=,即21y y =,此时32m =,令210y y -<,即21y y <,此时32m >,综上32m >时21y y <,32m =时21y y =,32m <时21y y >.【点睛】本题主要考查了二次函数的性质,准确分析计算是解题的关键.22.(1)y=2101006000x x -++;(2)第五天日销售利润最大,最大日销售利润为6250元;(3)14天【分析】(1)根据日销售利润等于单件利润乘以销售量即可得解;(2)化二次函数一般式为顶点式,即可判断求解;(3)根据题意列不等式求解即可;【详解】解:(1)()()604030010=+--y x x ,2101006000x x =-++;(2)当130x ≤≤时,2101006000=-++y x x ()21056250=--+x ,∵10a =-<0,∴二次函数开口向下,由题可知:函数对称轴为5x =,∴当5x =时,最大值为6250;答:第五天日销售利润最大,最大日销售利润为6250元.(3)∵2101006000=-++y x x ()21056250=--+x ,当5400y ≥时,()210562505400--+≥x ,解得:414x -≤≤,∵130x ≤≤,∴共有14天.【点睛】本题主要考查了二次函数的应用,准确分析计算是解题的关键.23.(1)见解析;(2)3【分析】(1)根据中心对称的作法,找出对称点,即可画出图形;(2)根据平行四边形的判定,画出使以点A 、O 、C′、D 为顶点的四边形是平行四边形的点即可.【详解】解:(1)作射线AO,BO,CO,在射线上截取A′O=AO,B′O=BO,C′O=CO,顺次连接'''''',A B B C C A,,'''为所求,如图所示△A B C(2)平行四边形AOC′D1,平行四边形AOD2C′,平行四边形AD3OC′∴以点A,O,C',D为顶点的四边形为平行四边形的D点有3个故答案为:3【点睛】此题考查了作图-旋转变换,用到的知识点是中心对称、平行四边形的判定,关键是掌握中心对称的作法,作平行四边形时注意画出所有符合要求的图形.24.(1)见解析;(2)3;(3)5【分析】(1)根据旋转的定义和性质解答;(2)由题意可以得到PBC MBA ∆≅∆,由此可得90AMP ∠= 和PC=AM ,最后由△PAC 的面积等于4.5可以求得PC 的值;(3)根据三角形的性质解答.【详解】(1)如图,作60PAP AP AP ∠=︒'=',,连结P C ',则P AC '△即为所求作的图形:(2)作线段BM 垂直于BP 交PC 延长线于点.M 连接,AM 45,90BPM PBM ∠=︒∠=BPM △为等腰直角三角形,,BP BM ∴=90ABM MBC ABC PBM PBC MBC∠+∠=∠==∠=∠+∠,PBC ABM ∴∠=∠在PBC ∆与MBA ∆中:PB BMPBC ABM BC BA=⎧⎪∠=∠⎨⎪=⎩()PBC MBA SAS ∴∆≅∆90AMP =∴∠21122PAC S PC AM PC ∆∴=⋅=3PC ∴=(3)5.证明如下:如图,将AED 顺时针旋转90︒至FEC ,则ADE FCE ∠=∠,AD FC =,//,90AD BC DEC ∠=︒ ,90ADE BCE ∴∠+∠=︒,即90FCE BCE FCB ∠+∠=∠=︒FCB ∴△为直角三角形,其中3FC AD ==,4BC =,由勾股定理得5BF =,又 旋转角为90︒,即90AEF ∠=︒,则360135BEF AEB AEF ∠=︒-∠-∠=︒,即AEB FEB ∠=∠,在AEB △与FEB 中,AE AFAEB FEB BE BE=⎧⎪∠=∠⎨⎪=⎩∴()AEB FEB SAS △△≌5AB BF ∴==【点睛】本题考查三角形的应用,熟练掌握三角形全等的判定和性质、旋转的意义和性质、等腰三角形和直角三角形的性质是解题关键.25.(1)0,0b c ==;(2)1712m +=或43;(3)见解析【分析】(1)利用二次函数顶点式,代入顶点即可求解;(2)利用二次函数解析式和一次函数解析式,用m 去表示P 、M 点的纵坐标,再利用2PM PN =列出等量关系式即可求解m ;(3)作A 点关于二次函数对称轴的对称点M ,设()2,A p ap 则()2,M p ap -,由已知和中垂线定理可得MPO OPA BPy ∠=∠=∠,即可得M 、P 、B 再同一条直线上,设:PM y kx b =+,代入P 、M 坐标求PM 解析式,再联立抛物线解析式,可表示B 、M 坐标,同理的求直线AB 解析式,根据一次函数解析式可知AB 恒过()00,y .【详解】()1解:设()2y a x h k=-+0,0h k == 代入上式2y ax ∴=0,0b c ∴==()2P Q 在抛物线上,M 在直线上()21,,,22P m m M m m ⎛⎫∴+ ⎪⎝⎭2,PM PN = 2211222m m m ∴+-=解得12m =或43或1-P 为y 轴右侧抛物线C 上一动点0,m ∴>综上1712m =或43()3取A 点关于y 轴的对称点M ,抛物线关于y 轴对称M ∴点在抛物线上.连,MP 设()2,A p ap ,则()2,M p ap -MPO OPA BPy∠=∠=∠ M P B ∴、、三点共线()00,P y 设:PM y kx b=+20ap pk by b⎧=-+⎨=⎩解得200y ap y x y p -=+联立直线BM 与抛物线C ,得:22000ap y ax x y p -+-=2B M ap yx x ap-∴+=-,M x p =- 0B y x ap∴=代入抛物线002,y y B ap ap ⎛⎫ ⎪⎝⎭同理可求200:y ap BA y x y p+=-恒经过定点()00,y -【点睛】本题主要考查一次函数与二次函数综合、一次函数的图像性质、图形对称、等腰三角形三线合一等.本题综合性较强,对各涉及知识点掌握要求较高.特别注意两函数交点需满足各函数解析式.。
人教版九年级上册数学期中考试试卷附答案
人教版九年级上册数学期中考试试题一、选择题。
(每小题只有一个正确答案)1.下列图形是中心对称图形的是()A.B.C.D.2.⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是A.相切B.相交C.相离D.不能确定3.下列一元二次方程中,有两个不相等实数根的是()A.x2+6x+9=0B.x2=x C.x2+3=2x D.(x﹣1)2+1=0 4.S型电视机经过连续两次降价,每台售价由原来的1500元降到了980元.设平均每次降价的百分率为x,则下列方程中正确的是A.1500(1+x)2=980B.980(1+x)2=1500C.1500(1-x)2=980D.980(1-x)2="1500"5.如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是()A.40°B.50°C.70°D.80°6.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是()A.55°B.60°C.65°D.70°7.如图,在△ABC中,AB=AC=2,以AB为直径的⊙O与BC交于点D,点E在 ⊙O上,且∠DEA=30°,则CD的长为()A 3B .3C .3D .28.二次函数=B 2+B 的图象如图,若一元二次方程B 2+B +=0有实数根,则m 的最大值为()A .-3B .3C .5D .99.如图,已知矩形ABCD 中,AB =4cm ,BC =8cm .动点P 在边BC 上从点B 向C 运动,速度为1cm /s ;同时动点Q 从点C 出发,沿折线C →D →A 运动,速度为2cm /s .当一个点到达终点时,另一个点随之停止运动。
设点P 运动的时间为t (s ),△BPQ 的面积为S (cm 2),则描述S (cm 2)与时间t (s )的函数关系的图象大致是()A .B .C .D .10.已知二次函数2y ax c =+,当1x =时,42y -≤≤-,当2x =时,12y -≤≤,则当3x=时,y的取值范围为()A.2123y≤≤B.2103y≤≤C.293y≤≤D.19y≤≤二、填空题11.如果点P(4,﹣5)和点Q关于原点对称,则点Q的坐标为_____.12.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线的函数关系式为_____________.13.已知关于x方程x2﹣3x+a=0有一个根为1,则方程的另一个根为_____.14.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m.15.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C 旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.三、解答题16.解方程:(1)3x2+6x﹣5=0(2)x2+2x﹣24=017.如图,图中每个小方格都是边长为1个单位长度的正方形,△ABC在方格纸中的位置如图所示.(1)请在图中建立平面直角坐标系,使得A,B两点的坐标分别为A(2,﹣1),B(1,﹣4),并写出C点坐标;(2)在图中作出△ABC绕坐标原点旋转180°后的△A1B1C1,并写出A1,B1,C1的坐标;(3)在图中作出△ABC绕坐标原点顺时针旋转90°后的△A2B2C2,并写出A2,B2,C2的坐标.18.已知二次函数y=﹣12x2+3x﹣52(1)用配方法求出函数图象的顶点坐标和对称轴方程;(2)用描点法在如图所示的平面直角坐标系中画出该函数的图象;(3)根据图象,直接写出y的值小于0时,x的取值范围.19.如图,在△ABC中,AB=AC,以AB为直径的 ⊙O分别交AC于点D,交BC于点E,连接ED.(1)求证:ED=EC;(2)填空:①设CD的中点为P,连接EP,则EP与⊙O的位置关系是;②连接OD,当∠B的度数为时,四边OBED是菱形.20.如图,E点是正方形ABCD的边BC上一点,AB=12,BE=5,△ABE逆时针旋转后能够与△ADF重合.(1)旋转中心是,旋转角为度;(2)△AEF是三角形;(3)求EF的长.21.河北内丘柿饼加工精细,色泽洁白,肉质柔韧,品位甘甜,在国际市场上颇具竞争力.上市时,外商王经理按市场价格10元/千克在内丘收购了2000千克柿饼存放入冷库中.据预测,柿饼的市场价格每天每千克将上涨0.5元,但冷库存放这批柿饼时每天需要支出各种费用合计320元,而且柿饼在冷库中最多保存80天,同时,平均每天有8千克的柿饼损坏不能出售.(1)若存放x天后,将这批柿饼一次性出售,设这批柿饼的销售总金额为y元,试写出y与x之间的函数关系式;(2)王经理想获得利润20000元,需将这批柿饼存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)(3)王经理将这批柿饼存放多少天后出售可获得最大利润?最大利润是多少?22.在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.(1)求抛物线C1的表达式;(2)直接用含t的代数式表达线段MN的长;(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.23.已知:如图,在⊙O中,弦AB与半径OE、OF交于点C、D,AC=BD,求证:(1)OC=OD:(2)A EB F.24.问题情境:如图①,P是⊙O外的一点,直线PO分别交⊙O于点A、B,可以发现P A 是点P到⊙O上的点的最短距离.(1)直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是.(2)构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N 是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C 长度的最小值.(3)综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于.参考答案1.B【分析】由中心对称图形的定义判断即可.【详解】A、C、D中图形都不是中心对称图形,是轴对称图形,B中图形是中心对称图形,故选:B.【点睛】本题考查了中心对称图形的概念,理解中心对称图形的概念,能找到对称中心是解答的关键.2.B【分析】根据圆O的半径和圆心O到直线L的距离的大小,相交:d<r;相切:d=r;相离:d>r;即可选出答案.【详解】∵⊙O的半径为8,圆心O到直线L的距离为4,∵8>4,即:d<r,∴直线L与⊙O的位置关系是相交.故选B.3.B【详解】分析:根据一元二次方程根的判别式判断即可.详解:A、x2+6x+9=0.△=62-4×9=36-36=0,方程有两个相等实数根;B、x2=x.x2-x=0.△=(-1)2-4×1×0=1>0.方程有两个不相等实数根;C、x2+3=2x.x2-2x+3=0.△=(-2)2-4×1×3=-8<0,方程无实根;D、(x-1)2+1=0.(x-1)2=-1,则方程无实根;故选B.点睛:本题考查的是一元二次方程根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0时,方程有两个相等的实数根;③当△<0时,方程无实数根.4.C【解析】解:依题意得:第一次降价的售价为:1500(1-x),则第二次降价后的售价为:1500(1-x)(1-x)=1500(1-x)2,∴1500(1-x)2=980.故选C.5.D【解析】【分析】根据圆周角定理得出∠AOC=40°,进而利用垂径定理得出∠AOB=80°即可.【详解】∵∠ABC=20°,∴∠AOC=40°,∵AB是⊙O的弦,OC⊥AB,∴∠AOC=∠BOC=40°,∴∠AOB=80°,故选:D.【点睛】此题考查圆周角定理,关键是根据圆周角定理得出∠AOC=40°.6.C【分析】根据旋转的性质和三角形内角和解答即可.【详解】∵将△ABC绕点C顺时针旋转90°得到△EDC.∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,∴∠ACD=90°-20°=70°,∵点A,D,E在同一条直线上,∴∠ADC+∠EDC=180°,∵∠EDC+∠E+∠DCE=180°,∴∠ADC=∠E+20°,∵∠ACE=90°,AC=CE∴∠DAC+∠E=90°,∠E=∠DAC=45°在△ADC中,∠ADC+∠DAC+∠DCA=180°,即45°+70°+∠ADC=180°,解得:∠ADC=65°,故选C.【点睛】此题考查旋转的性质,关键是根据旋转的性质和三角形内角和解答.7.A【分析】连接AD,根据圆周角定理和含30°的直角三角形的性质解答即可.【详解】连接AD,∵∠DEA=30°,∴∠B=30°,∵AB是直径,∴∠ADB=90°,∵AB=2,∴BD ,∵AC =BA ,∠ADB =90°,∴CD =DB 故选:A .【点睛】考核知识点:圆周角定理.作好辅助线,利用圆周角定理和直角三角形性质解决问题是关键.8.B【解析】∵抛物线的开口向上,顶点纵坐标为-3,∴a >0,−24=-3,即b 2=12a ,∵一元二次方程ax 2+bx+m=0有实数根,∴△=b 2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3,∴m 的最大值为3.故选B.9.A【分析】先求出点P 在BC 边运动的时间,再求出Q 点在CD 边和AD 边运动的时间,然后分Q 点在CD 边运动和在AD 边运动两种情况分别计算出△BPQ 的面积即可得出图象.【详解】点P 在BC 边运动的时间为818()s ÷=Q 点在CD 边运动的时间为422()s ÷=,在AD 边运动的时间824()s ÷=当Q 点在CD 边运动时,即02t <≤时,211222BPQ S BP CQ t t t === 当Q 点在AD 边运动时,即26t <≤时,114222BPQ S BP CD t t === 则根据S (cm 2)与时间t (s )的函数关系式可知图象为A故选A【点睛】本题主要考查矩形中的动点问题,能够找到面积与时间之间的函数关系式是解题的关键.10.A【分析】由当x =1时,-4≤y ≤-2,当x =2时,-1≤y ≤2,将y =ax 2+c 代入得到关于a 、c 的两个不等式组,再设x =3时y =9a +c =m (a +c )+n (4a +c ),求出m 、n 的值,代入计算即可.【详解】解:由x =1时,-4≤y ≤-2得,-4≤a +c ≤-2…①,由x =2时,-1≤y ≤2得,-1≤4a +c ≤2…②,当x =3时,y =9a +c =m (a +c )+n (4a +c ),得491m n m n +=⎧⎨+=⎩,解得5383m n ⎧=-⎪⎪⎨⎪=⎪⎩,故10520()333a c ≤-+≤,8816(4)333a c -≤+≤,∴2123y ≤≤,故选:A .【点睛】本题考查了二元一次方程组的应用,以及二次函数性质的运用,熟练解不等式组是解答本题的关键.11.(﹣4,5)【分析】根据关于原点对称的点的坐标的性质即可作答.即:坐标符号都变.【详解】∵点P (4,﹣5)和点Q 关于原点对称,∴点Q 的坐标为(﹣4,5).故答案为:(﹣4,5).【点睛】考核知识点:关于原点对称的点的坐标.理解关于原点对称的点的坐标的特点是关键.12.25(1)1y x =-+-【分析】先确定出原抛物线的顶点坐标为(0,0),然后根据向左平移横坐标加,向下平移纵坐标减,求出新抛物线的顶点坐标,然后写出即可.【详解】抛物线251y x =-+的顶点坐标为(0,0),∵向左平移1个单位长度后,向下平移2个单位长度,∴新抛物线的顶点坐标为(-1,-2),∴所得抛物线的解析式是()2511y x =-+-.故答案为()2511y x =-+-.【点睛】本题主要考查的是函数图象的平移,根据平移规律“左加右减,上加下减”利用顶点的变化确定图形的变化是解题的关键.13.2【解析】分析:设方程的另一个根为m ,根据两根之和等于-b a ,即可得出关于m 的一元一次方程,解之即可得出结论.详解:设方程的另一个根为m ,根据题意得:1+m=3,解得:m=2.故答案为2.点睛:本题考查了根与系数的关系,牢记两根之和等于-b a是解题的关键.14.-4【分析】根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把2y =-代入抛物线解析式得出水面宽度,即可得出答案.【详解】建立平面直角坐标系,设横轴x 通过AB ,纵轴y 通过AB 中点O 且通过C 点,则通过画图可得知O 为原点,抛物线以y 轴为对称轴,且经过A ,B 两点,OA 和OB 可求出为AB 的一半2米,抛物线顶点C 坐标为()0,2.通过以上条件可设顶点式22y ax =+,其中a 可通过代入A 点坐标()2,0.-代入到抛物线解析式得出:0.5a =-,所以抛物线解析式为20.52y x =-+,当水面下降2米,通过抛物线在图上的观察可转化为:当2y =-时,对应的抛物线上两点之间的距离,也就是直线2y =-与抛物线相交的两点之间的距离,可以通过把2y =-代入抛物线解析式得出:220.52x -=-+,解得:22x =±,所以水面宽度增加到42米,比原先的宽度当然是增加了42 4.故答案是:42 4.-【点睛】考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.15.4【分析】连接OE ,延长EO 交CD 于点G ,作OH ⊥B ′C ,由旋转性质知∠B ′=∠B ′CD ′=90°、AB =CD =5、BC =B ′C =4,从而得出四边形OEB ′H 和四边形EB ′CG 都是矩形且OE =OD =OC =2.5,继而求得CG =B ′E =OH 22222.5 1.5OC CH -=-=2,根据垂径定理可得CF的长.【详解】连接OE ,延长EO 交CD 于点G ,作OH ⊥B ′C 于点H ,A ′B ′与⊙O 相切,则∠OEB ′=∠OHB ′=90°,∵矩形ABCD 绕点C 旋转所得矩形为A ′B ′C ′D ′,∴∠B ′=∠B ′CD ′=90°,AB =CD =5、BC =B ′C =4,∴四边形OEB ′H 和四边形EB ′CG 都是矩形,OE =OD =OC =2.5,∴B ′H =OE =2.5,∴CH =B ′C ﹣B ′H =1.5,∴CG =B ′E =OH ===2,∵四边形EB ′CG 是矩形,∴∠OGC =90°,即OG ⊥CD ′,∴CF =2CG =4,故答案为:4.【点睛】考核知识点:旋转、切线性质、垂径定理.作好辅助线,利用垂径定理和勾股定理解决问题是关键.16.(1)x 1=﹣1+3,x 2=﹣1﹣3;(2)x 1=﹣6,x 2=4【分析】(1)用一元二次方程的求根公式求出方程的根.(2)用十字相乘法因式分解求出方程的根.【详解】(1)3x 2+6x ﹣5=0∵a =3,b =6,c =﹣5.△=36+60=96∴x =6966-∴x 1=﹣1+3,x 2=﹣1﹣3.(2)(x +6)(x ﹣4)=0∴x +6=0或x ﹣4=0∴x 1=﹣6,x 2=4.【点睛】考核知识点:解一元二次方程.掌握公式法和提公因式法是关键.17.(1)图形见解析,C (3,﹣3);(2)图形见解析,A 1(﹣2,1),B 1(﹣1,4),C 1(﹣3,3);(3)图形见解析,A 2(﹣1,﹣2),B 2(﹣4,﹣1),C 2(﹣3,﹣3)【分析】(1)根据已知点的坐标,画出坐标系,由坐标系确定C 点坐标;(2)由关于原点中心对称性画△A 1B 1C 1,可确定写出A 1,B 1,C 1的坐标;(3)根据网格结构找出点A 、B 、C 绕点O 顺时针旋转90°的对应点A 2,B 2,C 2的位置,画△A 2B 2C 2,可确定写出A 2,B 2,C 2的坐标.【详解】解:(1)坐标系如图所示,C (3,﹣3);(2)△A 1B 1C 1如图所示,A 1(﹣2,1),B 1(﹣1,4),C 1(﹣3,3);(3)△A 2B 2C 2如图所示,A 2(﹣1,﹣2),B 2(﹣4,﹣1),C 2(﹣3,﹣3).【点睛】考核知识点:画中心对称图形.理解中心对称图形的定义,利用中心对称性质进行画图是关键.18.(1)函数图象的顶点坐标是(3,2),对称轴是直线x=3;(2)见解析;(3)x<1或x >5【分析】(1)根据配方法可以将题目中的函数解析式化为顶点式,从而可以写出顶点坐标和对称轴方程;(2)根据题目中函数解析式可以画出相应的函数图象;(3)根据(2)中的函数图象可以写出y的值小于0时,x的取值范围.【详解】(1)∵二次函数y=﹣12x2+3x﹣52=21(3)22x--+,∴该函数图象的顶点坐标是(3,2),对称轴是直线x=3;(2)当y=0时,得x1=1,x2=5,当x=0和x=6时,y=5 2 -,函数图象如图所示;(3)由图象可知,y的值小于0时,x的取值范围是x<1或x>5.【点睛】考核知识点:求二次函数的顶点坐标.理解二次函数的性质,画出二次函数图象是关键. 19.(1)见解析;(2)①相切;②60°【分析】(1)根据等腰三角形的性质和圆内接四边形的性质解答即可;(2)①如图,连接AE,OE,根据圆周角定理得到AE⊥BC,根据三角形的中位线定理得到OE∥AC,根据平行线的性质得到OE⊥PE,于是得到结论;②根据已知条件得到△OBE是等边三角形,求得OB=BE,同理OD=DE,根据菱形的判定定理即可得到结论.【详解】解:(1)∵AB=AC,∴∠B=∠C,∵∠CDE=∠B,∴∠CDE=∠C,∴CE=DE;(2)①相切;理由:如图,连接AE,OE,∵AB是⊙O的直径,∴AE⊥BC,∵AB=AC,∴BE=CE,∵BO=OA,∴OE∥AC,∵DE=CE,PD=CP,∴PE⊥AC,∴OE⊥PE,∴EP与⊙O的位置关系是相切;②当∠B的度数为60°时,四边OBED是菱形,∵OB=OE,∠B=60°,∴△OBE是等边三角形,∴OB=BE,同理OD=DE,∴OD=DE=BE=OB,∴四边OBED是菱形.故答案为:相切;60°.【点睛】考核知识点:切线的判定和性质.作好辅助线,充分利用圆的性质和菱形性质解决问题是关键.20.(1)点A ,90°;(2)等腰直角;(3)132【分析】(1)根据图形和已知即可得出答案.(2)根据旋转得出全等,根据全等三角形的性质得出∠BAE=∠DAF ,AE=AF ,求出∠EAF=∠BAD ,即可得出答案.(3)求出AE ,求出AF ,根据勾股定理求出EF 即可.【详解】解:(1)从图形和已知可知:旋转中心是点A ,旋转角的度数等于∠BAD 的度数,是90°,故答案为:点A ,90;(2)等腰直角三角形,理由是:∵四边形ABCD 是正方形,∴∠BAD=90°,∵△ABE 逆时针旋转后能够与△ADF 重合,∴△ABE ≌△ADF ,∴∠BAE=∠DAF ,AE=AF ,∴∠FAE=∠FAD+∠DAE=∠BAE+∠DAE=∠BAD=90°,∴△AEF 是等腰直角三角形,故答案为:等腰直角.(3)由旋转可知∠EAF=90°,△ABE ≌△ADF ,∴AE=AF ,△EAF 是等腰直角三角形在Rt △ABE 中,∵AB=12,BE=5∴222212513AE AB BE =+=+∴222213132EF AE AF =+=+【点睛】本题考查了旋转的性质,勾股定理,全等三角形的性质的应用,注意:旋转后得出的图形和原图形全等.21.(1)y==﹣4x2+920x+20000(1≤x≤80,且x为整数);(2)王经理想获得利润20000元,需将这批柿饼存放50天后出售;(3)存放75天后出售这批柿饼可获得最大利润22500元【分析】(1)根据等量关系“销售总金额=(市场价格+0.5×存放天数)×(原购入量﹣8×存放天数)”列出函数关系式;(2)根据等量关系“利润=销售总金额﹣收购成本﹣各种费用”列出方程求出即可;(3)根据等量关系“利润=销售总金额﹣收购成本﹣各种费用”列出函数关系式并求最大值.【详解】(1)由题意y与x之间的函数关系式为:y=(10+0.5x)(2000﹣8x)=﹣4x2+920x+20000(1≤x≤80,且x为整数);(2)根据题意可得:20000=﹣4x2+920x+20000﹣10×2000﹣320x,解得:x1=100(不合题意舍去),x2=50,答:王经理想获得利润20000元,需将这批柿饼存放50天后出售.(3)设利润为w,由题意得w=﹣4x2+920x+20000﹣10×2000﹣320x=﹣4(x﹣75)2+22500,∵a=﹣4<0,∴抛物线开口方向向下,∵柿饼在冷库中最多保存75天,=22500元.∴x=75时,w最大答:存放75天后出售这批柿饼可获得最大利润22500元.【点睛】考核知识点:二次函数的应用.理解利润关系,列出二次函数,求函数最值是关键. 22.(1)y=x2+x﹣1;(2)MN=t2+2;(3)t=0或1【分析】(1)将点A、B的坐标代入抛物线表达式,即可求解;(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t-1),即可求解;(3)分∠ANM=90°、∠AMN=90°两种情况,分别求解即可.【详解】解:(1)将点A、B的坐标代入抛物线表达式得:421111a ba b--=⎧⎨--=-⎩,解得:11ab=⎧⎨=⎩,故抛物线C1的表达式为:y=x2+x﹣1;(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t﹣1),则MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2;(3)①当∠ANM=90°时,AN=MN,AN=t﹣(﹣2)=t+2,MN=t2+2,t=t2+2,解得:t=0或1(舍去0),故t=1;②当∠AMN=90°时,AM=MN,AM=t+2=MN=t2+2,解得:t=0或1(舍去1),故t=1;综上,t=0或1.【点睛】本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形的性质等,其中(3),要注意分类求解,避免遗漏.23.(1)见解析;(2)见解析【分析】(1)证明:连接OA,OB,证明△OAC≌△OBD(SAS)即可得到结论;(2)根据△OAC≌△OBD,得到∠AOC=∠BOD,即可得到结论.【详解】(1)证明:连接OA,OB,∵OA=OB,∴∠OAC=∠OBD.在△OAC与△OBD中,∵OA OBOAC OBD AC BD=⎧⎪∠=∠⎨⎪=⎩,∴△OAC≌△OBD(SAS).∴OC=OD.(2)∵△OAC≌△OBD,∴∠AOC=∠BOD,∴A EB F..【点睛】此题考查同圆的半径相等的性质,全等三角形的判定及性质,等腰三角形等边对等角的性质,相等的圆心角所对的弧相等的性质,正确引出辅助线证明△OAC≌△OBD是解题的关键.24.(11;(2)﹣4;(3﹣3【分析】(1)先确定出AP最小时点P的位置,如图1中的P'的位置,即可得出结论;(2)先判断出A'M=AM=MD,再构造出直角三角形,利用锐角三角函数求出DH,MH,进而用用勾股定理求出CM,即可得出结论;(3)利用对称性确定出点B关于x轴的对称点B',即可求出结论.【详解】(1)如图1,取BC的中点E,连接AE,交半圆于P',在半圆上取一点P,连接AP,EP,在△AEP中,AP+EP>AE,即:AP'是AP的最小值,∵AE P'E=1,∴AP'1;1;(2)如图2,由折叠知,A'M=AM,∵M是AD的中点,∴A'M=AM=MD,∴以点A'在以AD为直径的圆上,∴当点A'在CM上时,A'C的长度取得最小值,过点M作MH⊥CD于H,在Rt△MDH中,DH=DM•cos∠HDM=2,MH=DM•sin∠HDM=在Rt△CHM中,CM,∴A'C=CM﹣A'M=﹣4;(3)如图3,作⊙B关于x轴的对称圆⊙B',连接AB'交x轴于P,∵B(3,4),∴B'(3,﹣4),∵A(﹣2,3),∴AB'=∴PM+PN的最小值=AB'﹣AM﹣B'N'=AB'﹣AM﹣BN﹣3.﹣3.【点睛】考核知识点:圆,三角函数.根据题意画出图形,构造直角三角形,运用三角函数定义解决问题是关键.。
人教版九年级数学上册试卷 期中检测题
期中检测题(时间:100分钟满分:120分)一、选择题(每小题3分,共30分)1.(2020·黔东南州)已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是( A )A.-7 B.7 C.3 D.-32.(2020·怀化)已知一元二次方程x2-kx+4=0有两个相等的实数根,则k的值为( C ) A.k=4 B.k=-4 C.k=±4 D.k=±23.(宜宾中考)一元二次方程x2-2x+b=0的两根分别为x1和x2,则x1+x2为( C ) A.-2 B.b C.2 D.-b4.(襄阳中考)已知二次函数y=x2-x+14m-1的图象与x轴有交点,则m的取值范围是( A )A.m≤5 B.m≥2 C.m<5 D.m>25.(2020·衢州)某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( B )A.180(1-x)2=461B.180(1+x)2=461C.368(1-x)2=442D.368(1+x)2=4426.(百色中考)抛物线y=x2+6x+7可由抛物线y=x2如何平移得到的( A )A.先向左平移3个单位,再向下平移2个单位B.先向左平移6个单位,再向上平移7个单位C.先向上平移2个单位,再向左平移3个单位D.先回右平移3个单位,再向上平移2个单位7.(2020·株洲)二次函数y=ax2+bx+c,若ab<0,a-b2>0,点A(x1,y1),B(x2,y2)在该二次函数的图象上,其中x1<x2,x1+x2=0,则( B )A.y1=-y2B.y1>y2C.y1<y2D.y1,y2的大小无法确定8.(达州中考)某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5,6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( D )A.2500(1+x)2=9100 B.2500(1+x%)2=9100C.2500(1+x)+2500(1+x)2=9100 D.2500+2500(1+x)+2500(1+x)2=9100 9.(湖州中考)已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( D )10.(2020·宜宾 )函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点(2,0),顶点坐标为(-1,n ),其中n >0.以下结论正确的是( C )①abc >0;②函数y =ax 2+bx +c (a ≠0)在x =1和x =-2处的函数值相等;③函数y =kx +1的图象与y =ax 2+bx +c (a ≠0)的函数图象总有两个不同交点;④函数y =ax 2+bx +c (a ≠0)在-3≤x ≤3内既有最大值又有最小值.A .①③B .①②③C .①④D .②③④解析:根据待定系数法,方程根与系数的关系等知识和数形结合能力仔细分析即可解. 依照题意,画出图形如图,∵函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点(2,0),顶点坐标为(-1,n ),其中n>0.∴a <0,c >0,对称轴为直线x =-b 2a=-1,∴b =2a <0,∴abc >0,故①正确;∵对称轴为直线x =-1,∴x =1与x =-3的函数值是相等的,故②错误;∵顶点为(-1,n ),∴抛物线解析式为y =a (x +1)2+n =ax 2+2ax +a +n ,联立方程组可得:⎩⎪⎨⎪⎧y =kx +1,y =ax 2+2ax +a +n ,可得ax 2+(2a -k )x +a +n -1=0,∴Δ=(2a -k )2-4a (a +n -1)=k 2-4ak +4a -4an ,∵无法判断Δ是否大于0,∴无法判断函数y =kx +1的图象与y =ax 2+bx +c (a ≠0)的函数图象的交点个数,故③错误;当-3≤x ≤3时,当x =-1时,y 有最大值为n ,当x =3时,y 有最小值为16a +n ,故④正确,故选:C二、填空题(每小题3分,共15分)11.(2020·吉林 )一元二次方程x 2+3x -1=0根的判别式的值为__13__.12.(2020·淮安)二次函数y =-x 2-2x +3的图象的顶点坐标为__(-1,4)__.13.(2020·毕节)关于x 的一元二次方程(k +2)x 2+6x +k 2+k -2=0有一个根是0,则k 的值是__1__.14.(襄阳中考)如图,若被击打的小球飞行高度h (单位:m)与飞行时间t (单位:s)之间具有的关系为h =20t -5t 2,则小球从飞出到落地所用的时间为__4__s.第14题图第15题图15.(2020·益阳)某公司新产品上市30天全部售完,图①表示产品的市场日销售量与上市时间之间的关系,图②表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是__1800__元.三、解答题(共75分)16.(8分)用适当的方法解方程:(1)x2-2x-3=0; (2)(2x-1)2=x(3x+2)-7.解:x1=3,x2=-1 解:x1=2,x2=417.(9分)如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A,B两点.(1)求A,B两点的坐标;(2)若y1>y2,请直接写出x的取值范围.解:(1)A(-1,0),B(0,2)(2)-1<x<018.(9分)(衡阳中考)关于x的一元二次方程x2-3x+k=0有实数根.(1)求k的取值范围;(2)如果k是符合条件的最大整数,且一元二次方程(m-1)x2+x+m-3=0与方程x2-3x+k=0有一个相同的根,求此时m的值.解:(1)根据题意得Δ=(-3)2-4k≥0,解得k≤94(2)k的最大整数为2,方程x2-3x+k=0变形为x2-3x+2=0,解得x1=1,x2=2,∵一元二次方程(m-1)x2+x+m-3=0与方程x2-3x+k=0有一个相同的根,∴当x=1时,m-1+1+m-3=0,解得m=3 2;当x=2时,4(m-1)+2+m-3=0,解得m=1,而m-1≠0,∴m的值为3 219.(9分)如图,已知抛物线y =ax 2+bx +c 与x 轴交于点A (1,0),B (3,0),且过点C (0,-3).(1)求抛物线的解析式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y =-x 上,并写出平移后抛物线的解析式.解:(1)抛物线解析式为y =-x 2+4x -3,即y =-(x -2)2+1,∴顶点坐标为(2,1) (2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y =-x 2,平移后抛物线的顶点为(0,0)落在直线y =-x 上20.(9分)(贺州中考)2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?解:(1)设该贫困户2016年到2018年家庭年人均纯收入的年平均增长率为x ,依题意,得2500(1+x )2=3600,解得x 1=0.2=20%,x 2=-2.2(舍去).答:该贫困户2016年到2018年家庭年人均纯收入的年平均增长率为20% (2)3600×(1+20%)=4320(元),4320>4200.答:2019年该贫困户的家庭年人均纯收入能达到4200元21.(10分)(2020·陕西)如图,抛物线y =x 2+bx +c 经过点(3,12)和(-2,-3),与两坐标轴的交点分别为A ,B ,C ,它的对称轴为直线l .(1)求该抛物线的解析式;(2)P 是该抛物线上的点,过点P 作l 的垂线,垂足为D ,E 是l 上的点.要使以P ,D ,E 为顶点的三角形与△AOC 全等,求满足条件的点P ,点E 的坐标.解:(1)将点(3,12)和(-2,-3)代入抛物线解析式得⎩⎪⎨⎪⎧12=9+3b +c ,-3=4-2b +c , 解得⎩⎪⎨⎪⎧b =2,c =-3, 故抛物线的解析式为y =x 2+2x -3 (2)抛物线的对称轴为直线x =-1,令y =0,则x =-3或1,令x =0,则y =-3,故点A ,B 的坐标分别为(-3,0),(1,0),点C (0,-3),故OA =OC =3,∵∠PDE =∠AOC =90°,∴当PD =DE =3时,以P ,D ,E 为顶点的三角形与△AOC 全等,设点P (m ,n ),当点P 在抛物线对称轴右侧时,m -(-1)=3,解得m =2,故n =22+2×2-3=5,故点P (2,5),故点E (-1,2)或(-1,8);当点P 在抛物线对称轴的左侧时,由抛物线的对称性可得,点P (-4,5),此时点E 坐标同上,综上,点P 的坐标为(2,5)或(-4,5);点E 的坐标为(-1,2)或(-1,8)22.(10分)(2020·随州)2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格p (元/只)和销量q (只)与第x 天的关系如下表:1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q (只)与第x 天的关系为q =-2x 2+80x -200 (6≤x ≤30,且x 为整数),已知该型号口罩的进货价格为0.5元/只.(1)直接写出该药店该月前5天的销售价格p 与x 和销量q 与x 之间的函数解析式;(2)求该药店该月销售该型号口罩获得的利润W (元)与x 的函数解析式,并判断第几天的利润最大;(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m 倍的罚款,若罚款金额不低于2000元,则m 的取值范围为__m ≥85__. 解:(1)根据表格数据可知:前5天的某型号口罩销售价格p (元/只)和销量q (只)与第x 天的关系为p =x +1,1≤x ≤5且x 为整数;q =5x +65,1≤x ≤5且x 为整数 (2)当1≤x ≤5且x 为整数时,W =(x +1-0.5)(5x +65)=5x 2+1352 x +652;当6≤x ≤30且x 为整数时,W =(1-0.5)(-2x 2+80x -200)=-x 2+40x -100.即有W =⎩⎪⎨⎪⎧5x 2+1352x +652,1≤x ≤5且x 为整数,-x 2+40x -100,6≤x ≤30且x 为整数,当1≤x ≤5且x 为整数时,售价,销量均随x 的增大而增大,故当x =5时,W 有最大值为495元;当6≤x ≤30且x 为整数时,W =-x 2+40x -100=-(x -20)2+300,故当x =20时,W 有最大值为300元;由495>300,可知:第5天的利润最大为495元 (3)根据题意可知:获得的正常利润之外的非法所得部分为:(2-1)×70+(3-1)×75+(4-1)×80+(5-1)×85+(6-1)×90=1250(元),∴1250m ≥2000,解得m ≥85 .则m 的取值范围为m ≥85 .故答案为:m ≥8523.(11分)(辽阳中考)如图,在平面直角坐标系中,Rt △ABC 的边BC 在x 轴上,∠ABC =90°,以A 为顶点的抛物线y =-x 2+bx +c 经过点C (3,0),交y 轴于点E (0,3),动点P 在对称轴上.(1)求抛物线解析式;(2)若点P 从A 点出发,沿A →B 方向以1个单位/秒的速度匀速运动到点B 停止,设运动时间为t 秒,过点P 作PD ⊥AB 交AC 于点D ,过点D 平行于y 轴的直线l 交抛物线于点Q ,连接AQ ,CQ ,当t 为何值时,△ACQ 的面积最大?最大值是多少?(3)若点M 是平面内的任意一点,在x 轴上方是否存在点P ,使得以点P ,M ,E ,C 为顶点的四边形是菱形,若存在,请直接写出符合条件的M 点坐标;若不存在,请说明理由.解:(1)将点C ,E 的坐标代入二次函数表达式得:⎩⎪⎨⎪⎧-9+3b +c =0,c =3, 解得⎩⎪⎨⎪⎧b =2,c =3, 故抛物线的解析式为:y =-x 2+2x +3 (2)∵y =-x 2+2x +3=-(x -1)2+4,∴A (1,4),将点A ,C 的坐标代入一次函数解析式,可得直线AC 的解析式为:y =-2x +6,点P (1,4-t ),则点D (t +22 ,4-t ),点Q (t +22 ,4-t 24 ),S △ACQ =12 DQ ·BC =-14 t 2+t =-14(t -2)2+1,∵-14<0,故S △ACQ 有最大值,当t =2时,其最大值为1 (3)设点P (1,m ),点M (x ,y ),①当EC 是菱形一条边时,当点M 在点P 右方时,点E 向右平移3个单位、向下平移3个单位得到C ,则点P 向右平移3个单位、向下平移3个单位得到M ,则1+3=x ,m -3=y ,∴x =4,y =m -3即为M (4,m -3),而MP =EP 得:1+(m -3)2=(4-1)2+(m -3-m )2,解得:m =3+17 ,∴y =m -3=17 ,故点M (4,17 );当点M 在点P 左方时,同理可得:点M (-2,3+14 );②当EC 是菱形一对角线时,则EC 中点即为PM 中点,则x +1=3,y +m =3,而PE =PC ,即1+(m -3)2=4+(m -0)2,解得:m =1,故x =2,y =3-m =3-1=2,故点M (2,2);综上,点M (4,17 )或(-2,3+14 )或M (2,2)。
人教版九年级上册数学期中考试试卷含答案解析
人教版九年级上册数学期中考试试题一、选择题。
(每小题只有一个正确答案)1.已知方程2430x x -+=,它的二次项系数、一次项系数、常数项分别是()A .0、4、3B .1、4、3C .1、4-、3D .0、4-、32.已知一元二次方程2230x x b +-=的一个根是1,则b =()A .3B .0C .1D .53.一元二次方程2310x x -+=的两根之和为()A .13B .2C .3-D .34.对于抛物线221y x x =--,下列说法中错误的是()A .顶点坐标为()12,-B .对称轴是直线1x =C .当1x >时,y 随x 的增大减小D .抛物线开口向上5.抛物线2(1)2y x =-+可以由抛物线2x y =平移而得到,下列平移正确的是()A .先向左平移1个单位,再向上平移2个单位B .先向左平移1个单位,再向下平移2个单位C .先向右平移1个单位,再向上平移2个单位D .先向右平移1个单位,再向下平移2个单位6.右图所示,已知二次函数2y ax bx c =++的图象如图所示,则a 、b 、c 满足()A .0a <,0b >,0c >B .0a >,0b <,0c >C .0a <,0b <,0c <D .0a <,0b <,0c >7.如图,已知⊙O 是△ABD 的外接圆,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD=58°,则∠BCD 等于()A .116°B .32°C .58°D .64°8.如图,AB 是O 的弦,半径OC AB ⊥于点D ,且8cm AB =,5cm OC =,则DC 的长是()A .3cmB .2.5cmC .2cmD .1cm9.如图,四边形ABCD 内接于O ,F 是 CD上一点,且 DF BC =,连接CF 并延长交AD 的延长线于点E ,连接AC ,若105ABC ∠=︒,25BAC ∠=︒,则E ∠的度数为()A .60︒B .45︒C .50︒D .30°10.如图,在平面直角坐标系中,已知抛物线2y ax bx =+的对称轴为34x =,且经过点A (2,1),点P 是抛物线上的动点,P 的横坐标为()02m m <<,过点P 作PB x ⊥轴,垂足为B ,PB 交OA 于点C ,点O 关于直线PB 的对称点为D ,连接CD ,AD ,过点A 作AE ⊥x 轴,垂足为E ,则当m =()时,ACD ∆的周长最小.A .1B .1.5C .2D .2.5二、填空题11.一元二次方程x 2﹣4=0的解是_________.12.二次函数()2214y x =+-,当x =________时,y 的最小值是_______.13.若二次函数228y x x c =++的图像上有()11,A y -,()24,B y ,()31,C y 三点,则1y ,2y ,3y 的大小关系是______.14.如图,二次函数y =ax 2+bx +3的图象经过点A (﹣1,0),B (3,0),那么一元二次方程ax 2+bx+3=0的根是_____.15.如图A ,B ,C 是圆O 上的3点,且四边形OABC 是菱形,若点D 是圆上异于A ,B ,C 的另一点,则ADC ∠的度数是_______.16.如图,在⊙O 中,直径AB =6,BC 是弦,∠ABC =30°,点P 在BC 上,点Q 在⊙O 上,且OP ⊥PQ ,当点P 在BC 上移动时,则PQ 长的最大值为__________.17.二次函数y =ax 2+bx +c(a≠0)的图象如图所示,根据图象解答下列问题:(1)方程ax 2+bx +c =0的两个根为____________;(2)不等式ax 2+bx +c>0的解集为________;(3)y 随x 的增大而减小的自变量x 的取值范围为________;(4)若方程ax 2+bx +c =k 有两个不相等的实数根,则k 的取值范围为________.三、解答题18.解方程:(1)24x x=(2)23100x x --=19.如图,已知抛物线2122y x =-+与直线222y x =+交于A ,B 两点,(1)求A ,B 两点的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版九年级上册期中检测题
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分) 1.方程2x 2=3x 的解为( ) A .0 B .32 C .-32 D .0,3
2
2.抛物线y =(x -1)2+2的顶点坐标是( )
A .(-1,2)
B .(-1,-2)
C .(1,-2)
D .(1,2)
3.若x =-2是关于x 的一元二次方程x 2+3
2ax -a 2=0的一个根,则a 的值为( )
A .-1或4
B .-1或-4
C .1或-4
D .1或4
4.若关于x 的一元二次方程(k -1)x 2+4x +1=0有两个不相等的实数根,则k 的取值范围是( )
A .k <5
B .k <5且k≠1
C .k≤5且k≠1
D .k >5
5.某同学在用描点法画二次函数y =ax 2+bx +c 的图象时,列出了下面的表格:
A .-11
B .-2
C .1
D .-5
6.若A(-6,y 1),B(-3,y 2),C(1,y 3)为二次函数y =x 2+4x -5图象上的三点,则y 1,y 2,y 3的大小关系是( )
A .y 1<y 2<y 3
B .y 2<y 3<y 1
C .y 3<y 1<y 2
D .y 2<y 1<y 3
7.定义运算:a b =a(1-b).若a ,b 是方程x 2-x +1
4m =0(m <0)的两根,则b
b -a a 的值为( )
A .0
B .1
C .2
D .与m 有关 8.学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x 个球队参赛.根据题意,下面所列方程正确的是( )
A .x 2=21
B .12x(x -1)=21
C .1
2
x 2=21 D .x(x -1)=21
9.如图,有一块边长为6 cm 的正三角形纸板,在它的三个角处分别截去一个彼此全等
的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A . 3 cm 2
B .32 3 cm 2
C .92 3 cm 2
D .27
2 3 cm 2
在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若
足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a-b>0;①a<-1
60;①
-1
60<a<0;①0<b<-12a.其中正确的结论是()
A.①① B.①① C.①① D.①①
二、填空题(每小题3分,共24分)
11.已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=________.12.若一元二次方程x2+4x+c=0有两个不相等的实数根,则c的值可以是________(写
出一个即可).
13.用一条长40 cm的绳子围成一个面积为64 cm2的矩形.设矩形的一边长为x cm,则可列方程为____________________.
14.将抛物线y=x2-4x向上平移3个单位,再向右平移4个单位得到的抛物线是____________.
15.设一元二次方程x2-3x-1=0的两根分别是x1,x2,则x1+x2(x22-3x2)=________.16.若抛物线y=x2+bx+c与x轴只有一个交点,且过点A(m,n),B(m+6,n),则n=______.
17.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC①x 轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为________.18.设x1,x2是方程x2-x-2 017=0的两实数根,则x13+2 018 x2-2 017=________.
三、解答题(共66分)
19.(6分)用适当的方法解下列方程.
(1)(2x+3)2-16=0; (2)2x2=3(2x+1).
20.(8分)关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
21.(8分)已知抛物线y=-1
2x2-x+4.
(1)用配方法确定它的顶点坐标和对称轴;
(2)x取何值时,y随x的增大而减小?
(3)x取何值时,抛物线在x轴上方?
22.(8分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是____________斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
23.(8分)小区要用篱笆围成一个四边形花坛,花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米,围成的花坛是如图所示的四边形ABCD,其中①ABC=①BCD =90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式;(不要求写出自变量x的取值范围)
(2)当x是多少时,四边形ABCD的面积S最大?最大面积是多少?
24.(8分)已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2的图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
25.(10分)近几年城市建设快速发展,对花木的需求逐年提高,某园林专业户计划投资15万元种植花卉和树木.根据市场调查与预测,种植树木的利润y1(万元)与投资量x(万元)成正比例关系:y1=2x;种植花卉的利润y2(万元)与投资量x(万元)的函数关系如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB①x轴).
(1)写出种植花卉的利润y2关于投资量x的函数关系式;
(2)求此专业户种植花卉和树木获取的总利润W(万元)关于投入种植花卉的资金t(万元)之间的函数关系式;
(3)此专业户投入种植花卉的资金为多少万元时,才能使获取的总利润最大,最大利润是多少万元?
26.(10分)在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图①,在x轴上找一点E,使得①CDE的周长最小,求点E的坐标;
(3)如图①,F为直线AC上的动点,在抛物线上是否存在点P,使得①AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.。
