2004年长郡中学初三数学函数及其图象单元测试及答案b卷整理
长沙市长郡双语实验学校数学初中九年级一次函数易错题压轴难题综合训练
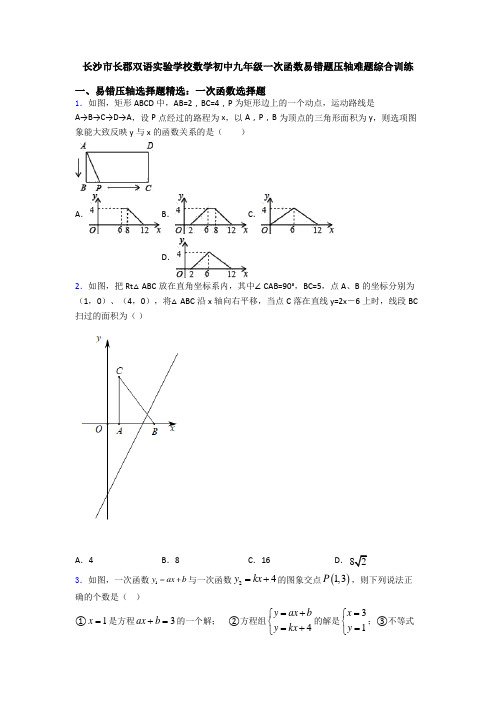
长沙市长郡双语实验学校数学初中九年级一次函数易错题压轴难题综合训练一、易错压轴选择题精选:一次函数选择题1.如图,矩形ABCD 中,AB=2,BC=4,P 为矩形边上的一个动点,运动路线是A→B→C→D→A ,设P 点经过的路程为x ,以A ,P ,B 为顶点的三角形面积为y ,则选项图象能大致反映y 与x 的函数关系的是( )A .B .C .D .2.如图,把Rt △ABC 放在直角坐标系内,其中∠CAB=90°,BC=5,点A 、B 的坐标分别为(1,0)、(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y=2x -6上时,线段BC 扫过的面积为( )A .4B .8C .16D .823.如图,一次函数1y ax b 与一次函数24y kx =+的图象交点()1,3P ,则下列说法正确的个数是( )①1x =是方程3ax b +=的一个解; ②方程组4y ax b y kx =+⎧⎨=+⎩的解是31x y =⎧⎨=⎩;③不等式4ax b kx +>+的解集是1x >; ④不等式44ax b kx +<+<的解集是01x <<.A .1B .2C .3D .4 4.下列函数中y 随x 的增大而增大,且图象与x 轴交点在y 轴左侧的是( )A .21y x =-B .21y x =+C .21y x =-+D .21y x =-- 5.直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示,则关于x 的不等式21k x k x b <+的解集为( )A .0x >B .0x <C .1x >-D .1x <- 6.函数y=kx+b (k 、b 为常数,k≠0)的图象如图,则关于x 的不等式kx+b >0的解集为( )A .x >0B .x <0C .x <2D .x >27.一个有进水管与出水管的容器,从某时刻开始的4min 内只进水不出水,在随后的8min 内既进水又出水,每min 的进水量和出水量是两个常数.容器内的水量y (单位:L )与时间x (单位:min )之间的关系如图所示.根据图象提供的信息,则下列结论错误的是( )A .第4min 时,容器内的水量为20LB .每min 进水量为5LC .每min 出水量为1.25LD .第8min 时,容器内的水量为25L8.一次函数y kx b =+的图象如图所示,则下列说法:①0kb >;②若点(2,)A m -与(3,)B n 都在直线y kx b =+上,则m n >;③当0x >时,y b >.其中正确的说法是( )A .①②B .①③C .②③D .①②③9.已知直线y 1=kx+1(k <0)与直线y 2=mx (m >0)的交点坐标为(12,12m ),则不等式组mx ﹣2<kx+1<mx 的解集为( )A .x>12B .12<x<32C .x<32D .0<x<3210.如图,在矩形ABCD 中,动点P 从点B 出发,沿BC ,CD ,DA 运动到点A 停止,设点P 运动路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图(2)所示,则矩形ABCD 的面积是( )A .10B .16C .20D .3611.在平面直角坐标系中,一次函数y =kx ﹣6(k <0)的图象大致是( )A .B .C .D .12.如图,在平面直角坐标系中,边长为1的正方形ABCD 中,AD 边的中点处有一动点P ,动点P 沿P→D→C→B→A→P 运动一周,则P 点的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )A .B .C .D .13.如图,函数3y x b =+和3y ax =-的图像交于点(2,5)P --,则根据图像可得不等式33x b ax +>-的解集是( )A .5x >-B .3x >-C .2x >-D .2x <-14.如图①,正方形ABCD 中,点P 以恒定的速度从点A 出发,沿AB →BC 的路径运动,到点C 停止.过点P 作PQ ∥BD ,PQ 与边AD (或边CD )交于点Q ,PQ 的长度y ( cm )与点P 的运动时间x (秒)的函数图象如图②所示.当点P 运动3秒时,△APQ 的面积为( )A .6cm 2B .4cm 2C .262cmD .42cm 215.某公司市场营销部的个人收入y (元)与其每月的销售量x (万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )A .1000B .2000C .3000D .400016.在平面直角坐标系中,一次函数1y x =-的图象是( )A .B .C .D .17.已知直线2y x =与y x b =-+的交点的坐标为(1,a ),则方程组2y x y x b =⎧⎨=-+⎩的解是( )A .12x y =⎧⎨=⎩B .21x y =⎧⎨=⎩C .23x y =⎧⎨=⎩D .13x y =⎧⎨=⎩ 18.甲、乙两车从A 城出发匀速行驶至B 城.在整个行驶过程中,甲、乙两车离A 城的距离y (千米)与甲车行驶的时间t (小时)之间的函数关系如图所示.则下列结论: ①,A B 两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,51544t =或 其中正确的结论有( )A .1个B .2个C .3个D .4个 19.下列函数的图象不经过第三象限,且y 随x 的增大而减小的是( ) A .31y x =-+ B .31y x =-- C .31y x D .31y x =-20.下列各图象中,y 不是..x 的函数的是( )A .B .C .D .【参考答案】***试卷处理标记,请不要删除一、易错压轴选择题精选:一次函数选择题1.B【分析】根据题意可以分别表示出各段的函数解析式,从而可以根据各段对应的函数图象判断选项的正误即可.【详解】由题意可得,点P 到A→B 的过程中,y=0(0≤x≤2),故选项C 错误,点P 到B→C 的过程中,y=12⨯2(x-2)=x-2(2<x≤6),故选项A 错误, 点P 到C→D 的过程中,y=12⨯2⨯4=4(6<x≤8),故选项D 错误, 点P 到D→A 的过程中,y=12⨯2(12-x)=12-x(8<x ≤12), 由以上各段函数解析式可知,选项B 正确,故选B.【点睛】本题考查动点问题的函数图象,明确题意,写出各段函数对应的函数解析式,明确各段的函数图象是解题关键. 2.C【解析】试题分析:∵点A 、B 的坐标分别为(1,0)、(4,0),∴AB=3,BC=5,∵∠CAB=90°,∴AC=4,∴点C 的坐标为(1,4),当点C 落在直线y=2x ﹣6上时,∴令y=4,得到4=2x ﹣6,解得x=5,∴平移的距离为5﹣1=4,∴线段BC 扫过的面积为4×4=16,故选C .考点:1.一次函数综合题;2.一次函数图象上点的坐标特征;3.平行四边形的性质;4.平移的性质.3.C【分析】根据函数图象上点的特征和方程及不等式的关系可以直接作出判断.【详解】解:①如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则点(1,3)P 位于直线1y ax b 上,所以1x =是方程3ax b +=的一个解,故①说法正确. ②如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则方程组4y ax b y kx =+⎧⎨=+⎩的解是13x y =⎧⎨=⎩,故②说法错误.③如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则不等式4ax b kx +>+的解集是1x >,故③说法正确.④如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,且直线24y kx =+与y 轴的交点是(0,4),则不等式44ax b kx +<+<的解集是01x <<,故④说法正确.综上所述,说法正确的个数是3,故选:C .【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y kx b =+的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y kx b =+在x 轴上(或下)方部分所有的点的横坐标所构成的集合.4.B【分析】根据一次函数的性质和各个选项中的函数解析式,可以判断哪个选项中的函数y 随x 的增大而增大,且图象与x 轴交点在y 轴左侧,本题得以解决.【详解】解:函数y=2x-1,y 随x 的增大而增大,与x 轴的交点是(0.5,0),在y 轴右侧,故选项A 不符题意;函数y=2x+1,y 随x 的增大而增大,与x 轴的交点是(-0.5,0),在y 轴左侧,故选项B 符题意;函数y=-2x+1,y 随x 的增大而减小,与x 轴的交点是(0.5,0),在y 轴右侧,故选项C 不符题意;函数y=-2x-1,y 随x 的增大而减小,与x 轴的交点是(-0.5,0),在y 轴左侧,故选项D 不符题意;故选:B .【点睛】本题考查了一次函数的性质,解题的关键是明确题意,利用一次函数的性质解答. 5.C【分析】由图象可以知道,当x=-1时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式k 2x <k 1x+b 解集.【详解】两条直线的交点坐标为(-1,2),且当x >-1时,直线l 2在直线l 1的下方,故不等式k 2x <k 1x+b 的解集为x >-1.故选:C .【点睛】此题考查一次函数的图象,解一元一次不等式,解题关键在于掌握两个图象的“交点”是两个函数值大小关系的“分界点”,在“分界点”处函数值的大小发生了改变.6.C【详解】根据图象可知y=kx+b 与x 轴交于(2,0),图像在交点的左侧部分满足不等式kx+b >0 ,故解集为x<2,故选C.7.C【分析】根据选项依次求解,由图可知,第4min 时,对应的容器内的水量为20L ,从某时刻开始的4min 内只进水不出水,在随后的8min 内既进水又出水,可确定两段函数的关系式,即可求出每min 进水量为5L ,第8min 时容器内的水量为25L ,最后根据图像每分钟出水的量为3.75L .【详解】A 项,由图可知,第4min 时,对应的容器内的水量y 为20L ,A 不符合题意;B 项,由题意可知,从某时刻开始的4min 内只进水不出水,0~4min 时的直线方程为:y =kx (k ≠0),通过图像过(4,20),解得k =5,所以每min 进水量为5L ,B 不符合题意;C 项,由B 项可知:每min 进水量为5L ,每分钟出水量=[(12-4)×5-(30-20)]÷(12-4)=3.75L ,C 符合题意;D 项,由题意可知,从某时刻开始的4min 内只进水不出水,0~4min 时的直线方程为:y =kx+b (k ≠0,k 、b 为常数),通过图像过(4,20),(12,30),解得k =54,b =15,所以第8min 时,容器内的水量为25L ,D 不符合题意;故选C .【点睛】此题考查了一次函数的实际应用和识图能力,解题时首先应正确理解题意,然后根据图像的坐标,利用待定系数法确定函数解析式,接着利用函数的性质即可解决问题. 8.B【分析】由图象经过第一,二,三象限,可得k >0,b>0,可判断A ①,根据增减性,可判断②,由图象可直接判断③【详解】解:∵图象过第一,第二,第三象限,∴k >0,b>0,∴0kb >,①正确, y 随x 增大而增大,∵-2<3∴m <n ,②错误,又∵一次函数y kx b =+的图象与y 轴交于点(0,b ), 当0x >时,图像在第一象限,都在点(0,b )的上方,又是增函数,∴这部分图像的纵坐标y>b ,③正确,故①③正确故选:B .【点睛】本题考查一次函数图象上点的坐标特征,一次函数图象的性质,解题关键是灵活运用一次函数图象的性质.9.B【分析】由mx﹣2<(m﹣2)x+1,即可得到x<32;由(m﹣2)x+1<mx,即可得到x>12,进而得出不等式组mx﹣2<kx+1<mx的解集为12<x<32.【详解】把(12,12m)代入y1=kx+1,可得1 2m=12k+1,解得k=m﹣2,∴y1=(m﹣2)x+1,令y3=mx﹣2,则当y3<y1时,mx﹣2<(m﹣2)x+1,解得x<32;当kx+1<mx时,(m﹣2)x+1<mx,解得x>12,∴不等式组mx﹣2<kx+1<mx的解集为12<x<32,故选B.【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.10.C【分析】点P从点B运动到点C的过程中,y与x的关系是一个一次函数,运动路程为4时,面积发生了变化,说明BC的长为4,当点P在CD上运动时,三角形ABP的面积保持不变,就是矩形ABCD面积的一半,并且动路程由4到9,说明CD的长为5,然后求出矩形的面积.【详解】解:∵当4≤x≤9时,y的值不变即△ABP的面积不变,P在CD上运动当x=4时,P点在C点上所以BC=4当x=9时,P点在D点上∴BC+CD=9∴CD=9-4=5∴△ABC的面积S=12AB•BC=12×4×5=10∴矩形ABCD的面积=2S=20故选C.【点睛】本题考查的是动点问题的函数图象,根据矩形中三角形ABP的面积和函数图象,求出BC 和CD的长,再用矩形面积公式求出矩形的面积.11.B【分析】一次函数y=kx+b中,k的符号决定了直线的方向,b的符号决定了直线与y轴的交点位置,据此判断即可.【详解】∵一次函数y=kx﹣6中,k<0∴直线从左往右下降又∵常数项﹣6<0∴直线与y轴交于负半轴∴直线经过第二、三、四象限故选:B.【点睛】本题考查了一次函数的图象问题,掌握一次函数图象的性质是解题的关键.12.D【解析】试题解析:动点P运动过程中:①当0≤s≤时,动点P在线段PD上运动,此时y=2保持不变;②当<s≤时,动点P在线段DC上运动,此时y由2到1逐渐减少;③当<s≤时,动点P在线段CB上运动,此时y=1保持不变;④当<s≤时,动点P在线段BA上运动,此时y由1到2逐渐增大;⑤当<s≤4时,动点P在线段AP上运动,此时y=2保持不变.结合函数图象,只有D选项符合要求.故选D.考点:动点问题的函数图象.13.C【分析】根据一次函数的图象和两函数的交点坐标即可得出答案【详解】解:从图象得到,当x >-2时,3y x b =+的图象在函数y=ax-3的图象上∴不等式3x+b>ax-3的解集是x>-2,故选:C【点睛】此题考查一次函数和一元一次不等式的应用,解题关键在于看懂函数图象14.A【分析】先由图象得出BD 的长及点P 从点A 运动到点B 的时间,再由正方形的性质得出其边长,然后由速度恒定及图象可得当点P 运动3秒时所处的位置,根据AP'Q'的面积等于正方形ABCD 的面积减去△ADQ'、△CP'Q'和△ABP'的面积,列式计算即可.【详解】解:由图象可知:①当PQ 运动到BD 时,PQ 的值最大,即y 最大,故BD=42;②点P 从点A 到点B 运动了2秒;∵四边形ABCD 是正方形,∴AB=AD=BC=CD ,∠DAB=90°.∴AB 2+AD 2=BD 2,即2AB 2=(42)2,解得AB=4.∴AB=AD=BC=CD=4cm .∵点P 的速度恒定,∴当点P 运动3秒时,点P 在BC 的中点处,如图所示:∵P'Q'∥BD ,∴∠CQ'P'=∠CDB=∠CBD=∠CP'Q'.∴CQ'=CP'=12BC=12CD . ∴AP'Q'的面积等于正方形ABCD 的面积减去△ADQ'、△CP'Q'和△ABP'的面积,即: 4×4-12×4×2-12×2×2-12×4×2=6(cm 2). 故选:A .【点睛】本题考查了动点问题的函数图象,读懂图象中的信息并对照几何图形来分析是解题的关键.15.B【分析】根据图像可得出:一次函数经过点(1,7000)和(2,12000),利用待定系数法求出一次函数的表达式,再把0x =代入求解即可.【详解】解:由图可得:一次函数经过点(1,7000)和(2,12000)∴设一次函数的解析式为:y kx b =+,把点(1,7000)和(2,12000)代入得:7000212000k b k b +=⎧⎨+=⎩解得:50002000k b =⎧⎨=⎩∴50002000y x =+∴把0x =代入得:2000y =故答案选B【点睛】本题主要考查了一次函数的图像应用,利用待定系数法求一次函数的解析式是解题的关键.16.A【分析】先确定一次函数解析式中k 与b 的符号,然后再利用一次函数图象及性质即可解答.【详解】解:一次函数y=1-x其中k=-1,b=1其图象为:.故选:A .【点睛】本题考查了一次函数的图象,掌握一次函数的图象与性质是解答本题的关键. 17.A【解析】将交点(1,a)代入两直线:得:a=2,a=-1+b ,因此有a=2,b=a+1=3,即交点为(1,2),而交点就是两直线组成的方程组2y xy x b=⎧⎨=-+⎩的解,即解为x=1,y=2,故选A.18.B【分析】观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.【详解】解:由图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且乙用时3小时,即比甲早到1小时,故①②都正确;设甲车离开A城的距离y与t的关系式为y甲=kt,把(5,300)代入可求得k=60,∴y甲=60t,设乙车离开A城的距离y与t的关系式为y乙=mt+n,把(1,0)和(4,300)代入可得4300m nm n+=⎧⎨+=⎩,解得100100mn=⎧⎨=-⎩,∴y乙=100t-100,令y甲=y乙可得:60t=100t-100,解得t=2.5,即甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;令|y甲-y乙|=50,可得|60t-100t+100|=50,即|100-40t|=50,当100-40t=50时,可解得t=54,当100-40t=-50时,可解得t=154,令y甲=50,解得t=56,令y甲=250,解得t=256,∴当t=56时,y甲=50,此时乙还没出发,此时相距50千米,当t=256时,乙在B城,此时相距50千米,综上可知当t的值为54或154或56或256时,两车相距50千米,故④错误;综上可知正确的有①②共两个,故选:B.【点睛】本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,学会构建一次函数,利用方程组求两个函数的交点坐标,属于中考常考题型.19.A【分析】由一次函数的图象与系数的关系可得出:当k<0,b>0时,一次函数y=kx+b的图象经过第一、二、四象限.再对照四个选项即可得出结论.【详解】∵一次函数的图象不经过第三象限,且y随x的增大而减小,∴k<0,b>0,故选A.【点睛】此题主要考查了一次函数图象与系数的关系,找出图象不经过第三象限情况是解题的关键.20.B【分析】对于自变量x的每一个确定的值y都有唯一的确定值与其对应,则y是x的函数,根据函数的定义解答即可.【详解】根据函数的定义,选项A、C、D图象表示y是x的函数,B图象中对于x的一个值y有两个值对应,故B中y不是x的函数,故选:B.【点睛】此题考查函数的定义,函数图象,结合函数图象正确理解函数的定义是解题的关键.。
长郡初三数学统考试卷答案

一、选择题(每题5分,共50分)1. 若a、b、c是等差数列,且a+c=10,b=6,则该等差数列的公差是()A. 2B. 3C. 4D. 5答案:B解析:由等差数列的性质可知,a+c=2b,代入已知条件得2b=10,解得b=5。
又因为b=6,所以公差d=5-6=-1,故选B。
2. 若函数f(x)=x^2-4x+4在区间[1,3]上的最大值为M,最小值为m,则M+m的值为()A. 8B. 10C. 12D. 14答案:A解析:函数f(x)是一个开口向上的二次函数,其对称轴为x=2。
在区间[1,3]上,当x=2时,函数取得最小值m=0。
又因为f(1)=f(3)=0,所以最大值M=0。
因此,M+m=0+0=8,故选A。
3. 在△ABC中,若a=3,b=4,c=5,则△ABC是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 梯形答案:A解析:根据勾股定理,若a^2+b^2=c^2,则△ABC是直角三角形。
代入已知条件得3^2+4^2=5^2,所以△ABC是直角三角形,故选A。
4. 已知函数f(x)=2x-1,若f(2x+1)=3,则x的值为()A. 1B. 2C. 3D. 4答案:C解析:将2x+1代入函数f(x)得f(2x+1)=2(2x+1)-1=4x+1。
由题意得4x+1=3,解得x=1/2。
因此,x的值为1/2,故选C。
5. 若x、y是方程x^2-2x-3=0的两个实数根,则x+y的值为()A. -3B. 3C. 4D. 6答案:C解析:根据韦达定理,方程x^2-2x-3=0的两个实数根x、y满足x+y=2。
因此,x+y的值为2,故选C。
二、填空题(每题5分,共50分)6. 若等差数列{an}的第一项a1=2,公差d=3,则第10项an的值为______。
答案:31解析:由等差数列的通项公式an=a1+(n-1)d,代入已知条件得an=2+(10-1)×3=31。
7. 若函数f(x)=ax^2+bx+c在x=1时取得最小值,则a、b、c的关系是______。
长郡中学初三期末数学试卷

一、选择题(每题5分,共50分)1. 若a,b是方程x²-3x+2=0的两根,则a+b的值为()A. 1B. 2C. 3D. 42. 下列函数中,是反比例函数的是()A. y=x²B. y=2x+3C. y=3/xD. y=2x²3. 在△ABC中,∠A=60°,∠B=45°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°4. 若|a|=3,则a的值为()A. 3或-3B. 3C. -3D. 05. 下列各数中,有最小正整数解的是()A. x²-3x+2=0B. x²+3x+2=0C. x²-2x+1=0D. x²-5x+6=06. 已知一元二次方程x²-4x+3=0,则方程x²-2x+3=0的解为()A. x=1或x=3B. x=2或x=1C. x=1或x=4D. x=3或x=27. 下列各式中,等式成立的是()A. a²+b²=(a+b)²B. a²+b²=(a-b)²C. (a+b)²=a²+b²+2abD. (a-b)²=a²+b²-2ab8. 在平面直角坐标系中,点P(2,3)关于y轴的对称点为()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)9. 下列各数中,有最小正整数解的是()A. x²-3x+2=0B. x²+3x+2=0C. x²-2x+1=0D. x²-5x+6=010. 若一个长方形的长是宽的2倍,则长方形的周长与面积的关系式为()A. 2(2a+b)=abB. 2(a+b)=abC. 2a+2b=abD. 2a+b=ab二、填空题(每题5分,共50分)11. 若a,b是方程x²-3x+2=0的两根,则ab的值为______。
初三函数测试题目及答案

初三函数测试题目及答案一、选择题(每题3分,共30分)1. 下列哪个选项是一次函数的图象?A. 一条直线B. 一个圆C. 一个椭圆D. 一个抛物线答案:A2. 函数y=2x+3的斜率是多少?A. 2B. 3C. -2D. -3答案:A3. 如果一个函数的图象经过点(2,5),那么这个点一定在函数的:A. 定义域内B. 值域内C. 函数图象上D. 函数图象外答案:C4. 函数y=x^2的反函数是:A. y=√xB. y=x^2C. y=1/xD. y=-x^2答案:A5. 函数y=1/x的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:D6. 函数y=3x-2的零点是多少?A. 0.5B. 1C. 2D. 3答案:B7. 函数y=2x+1的图象与y轴的交点坐标是:A. (0, 1)B. (0, 2)C. (1, 0)D. (1, 2)答案:A8. 函数y=x^2-4x+3的最大值是多少?A. -1B. 0C. 1D. 3答案:B9. 函数y=|x|的图象是:A. 一条直线B. 一个V形C. 一个W形D. 一个倒V形答案:B10. 如果函数y=f(x)是奇函数,那么f(-x)等于:A. f(x)B. -f(x)C. xD. -x答案:B二、填空题(每题4分,共20分)11. 函数y=3x+5的图象与x轴的交点坐标是________。
答案:(-5/3, 0)12. 函数y=x^2-6x+9的最小值是________。
答案:013. 函数y=1/x的图象在x=2处的斜率是________。
答案:1/414. 函数y=x^3-3x^2+3x-1的零点是________。
答案:115. 函数y=2x^2-4x+1的顶点坐标是________。
答案:(1, -1)三、解答题(每题10分,共50分)16. 已知函数y=2x^2-4x+3,求该函数的顶点坐标。
答案:顶点坐标为(1, 1)。
长郡中学初三期末数学试卷

一、选择题(每题4分,共40分)1. 已知二次函数y=ax^2+bx+c的图象开口向上,且顶点坐标为(1,2),则下列选项中正确的是()A. a>0,b>0,c>0B. a>0,b<0,c>0C. a<0,b>0,c>0D. a<0,b<0,c<02. 在△ABC中,∠A=45°,∠B=60°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°3. 已知等差数列{an}的前三项分别为1,3,5,则该数列的公差是()A. 1B. 2C. 3D. 44. 若函数f(x)=x^2-2x+1在区间[1,3]上单调递增,则下列选项中正确的是()A. f(2)>f(1)B. f(2)<f(1)C. f(2)=f(1)D. 无法确定5. 已知一次函数y=kx+b的图象与x轴、y轴分别交于点A、B,且OA=OB,则k与b的关系是()A. k=0,b≠0B. k≠0,b=0C. k=0,b=0D. k≠0,b≠06. 已知一元二次方程x^2-4x+3=0的两个实数根为α、β,则α+β的值为()A. 4B. 3C. 2D. 17. 若直角三角形ABC中,∠A=90°,∠B=30°,则BC的长度是AC长度的()A. 2倍B. √3倍C. 1/2倍D. 1/√3倍8. 已知一元二次方程ax^2+bx+c=0(a≠0)的两个实数根为x1、x2,则x1+x2的值是()A. -b/aB. b/aC. c/aD. √(b^2-4ac)/a9. 在△ABC中,若AB=AC,则下列选项中正确的是()A. ∠A=∠BB. ∠A=∠CC. ∠B=∠CD. ∠A=∠B=∠C10. 已知函数f(x)=2x-3,则f(2x+1)的值为()A. 4x-1B. 2x-5C. 4x-5D. 2x+5二、填空题(每题5分,共50分)11. 若等差数列{an}的前三项分别为2,5,8,则该数列的公差是______。
九年级数学函数图像练习题及答案

九年级数学函数图像练习题及答案练习题一:函数图像综合练习1. 给出函数 y = x^2 的图像,请写出下列函数图像的方程和图像的特点:(1) y = -x^2(2) y = (x + 1)^2(3) y = -(x - 2)^22. 给出函数 y = |x| 的图像,请写出下列函数图像的方程和图像的特点:(1) y = |x - 1|(2) y = -|x + 2|(3) y = 2|x|练习题二:函数图像的平移与伸缩1. 给出函数 y = x^3 的图像,请写出下列函数图像的方程和图像的特点:(1) y = (x - 1)^3(2) y = (x + 2)^3(3) y = -2(x - 2)^32. 给出函数 y = |x| 的图像,请写出下列函数图像的方程和图像的特点:(1) y = |x - 1|(2) y = 2|x + 2|(3) y = -0.5|x|答案:练习题一:1. (1) y = -x^2,图像特点:开口向下的抛物线,顶点在原点。
(2) y = (x + 1)^2,图像特点:开口向上的抛物线,顶点在 (-1, 0) 处。
(3) y = -(x - 2)^2,图像特点:开口向下的抛物线,顶点在 (2, 0) 处。
2. (1) y = |x - 1|,图像特点:折线,折点在 (1, 0) 处。
(2) y = -|x + 2|,图像特点:折线,折点在 (-2, 0) 处。
(3) y = 2|x|,图像特点:折线,折点在原点。
练习题二:1. (1) y = (x - 1)^3,图像特点:开口向上的尖顶抛物线,顶点在 (1, 0) 处。
(2) y = (x + 2)^3,图像特点:开口向上的钝顶抛物线,顶点在 (-2, 0) 处。
(3) y = -2(x - 2)^3,图像特点:开口向下的尖顶抛物线,顶点在 (2, 0) 处。
2. (1) y = |x - 1|,图像特点:折线,折点在 (1, 0) 处。
九年级函数专题试卷及答案

九年级函数专题试卷及答案专业课原理概述部分一、选择题(每题1分,共5分)1. 下列函数中,哪个是正比例函数?A. y = 2x + 3B. y = 3x 2C. y = x^2 + 1D. y = 1/x2. 如果函数y = kx + b的图像是一条经过原点的直线,那么k和b的关系是?A. k = 0, b ≠ 0B. k ≠ 0, b = 0C. k = 0, b = 0D. k ≠ 0, b ≠ 03. 下列函数中,哪个是反比例函数?A. y = 2/xB. y = x^2C. y = 3x + 1D. y = 1/x^24. 如果函数y = kx的图像是一条经过原点的直线,那么k的值是?A. k = 0B. k > 0C. k < 0D. k ≠ 05. 下列函数中,哪个是一次函数?A. y = x^2B. y = 2/xC. y = 3x + 1D. y = 1/x^2二、判断题(每题1分,共5分)1. 正比例函数的图像是一条经过原点的直线。
()2. 反比例函数的图像是一条经过原点的直线。
()3. 一次函数的图像是一条直线。
()4. 二次函数的图像是一条抛物线。
()5. 函数y = kx + b是一次函数当且仅当b = 0。
()三、填空题(每题1分,共5分)1. 如果函数y = kx的图像是一条经过原点的直线,那么k的值是______。
2. 如果函数y = kx + b的图像是一条经过原点的直线,那么b的值是______。
3. 反比例函数的一般形式是______。
4. 二次函数的一般形式是______。
5. 一次函数的图像是一条______。
四、简答题(每题2分,共10分)1. 请简述正比例函数的定义。
2. 请简述反比例函数的定义。
3. 请简述一次函数的定义。
4. 请简述二次函数的定义。
5. 请简述函数图像的斜率是什么。
五、应用题(每题2分,共10分)1. 如果函数y = 2x的图像是一条经过原点的直线,那么当x = 3时,y的值是多少?2. 如果函数y = 3/x的图像是一条经过原点的直线,那么当x = 2时,y的值是多少?3. 如果函数y = kx + b的图像是一条经过原点的直线,那么当x = 1时,y的值是多少?4. 如果函数y = x^2的图像是一条抛物线,那么当x = 2时,y的值是多少?5. 如果函数y = 1/x^2的图像是一条经过原点的直线,那么当x = 3时,y的值是多少?六、分析题(每题5分,共10分)1. 请分析一次函数和二次函数的图像有什么不同。
长郡中学初三数学期末试卷

1. 若a、b是方程x²-5x+6=0的两根,则a+b的值为:A. 2B. 3C. 4D. 52. 下列函数中,y=2x+1是一次函数的是:A. y=x²-2B. y=3x+5C. y=√xD. y=5/x3. 已知三角形ABC的三个内角A、B、C的正弦值分别为1/2、√3/2、1/2,则三角形ABC的形状是:A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形4. 下列数列中,第10项是100的是:A. 1, 3, 5, 7, ...B. 2, 4, 8, 16, ...C. 1, 4, 9, 16, ...D. 1, 2, 4, 8, ...5. 已知正方形的对角线长度为10cm,则该正方形的面积为:A. 25cm²B. 50cm²C. 100cm²D. 200cm²6. 若等腰三角形ABC的底边BC=6cm,腰AB=AC=8cm,则三角形ABC的面积是:A. 24cm²B. 30cm²C. 36cm²D. 40cm²7. 在直角坐标系中,点A(2,3)关于原点O的对称点是:A. (2,3)B. (-2,-3)C. (3,2)D. (-3,-2)8. 下列不等式中,正确的是:A. 3x > 2xB. 3x < 2xC. 3x ≤ 2xD. 3x ≥ 2x9. 若|a| < b,且a > 0,则下列不等式中正确的是:A. a < bB. a > bC. a = bD. a ≥ b10. 下列各式中,完全平方公式是:A. (a+b)² = a² + 2ab + b²B. (a-b)² = a² - 2ab + b²C. (a+b)² = a² - 2ab + b²D. (a-b)² = a² + 2ab - b²11. 已知一元二次方程x²-5x+6=0的两个根是x₁和x₂,则x₁+x₂=______,x₁x₂=______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数及其图象测试
班级___________ 姓名________________
1填空:(13X 2分)
(1) 已知点p(2,-4) 到x轴距离为__________ ,到y轴距离为_________ 。
(2) ____________________________________ 如果点M(a,b)在第二象限,那么a ____________________________________ 0, b _______ 0;
(3) 已知M(0,a)点,N(b,0)点,则点M在 _________ 由上,点N在______ 由上。
(4) _____________________________________________________________ 已知点A的坐标是(4,-5),那么点A关于x轴对称的点的坐标为
_______________________________________________________________________ ,
(5) 矩形的一边长为6,矩形的面积S,与另一边长x之间的函数关系式是―
(6) 已知水池的容量为50米3,每小时灌水量为m (米3),灌满水池所需时间为t
(小时),那么t与m之间的函数关系式是_________________ 。
)
(7) ____________________________ 函数丿一",当a=
_______________________________ 寸,它是正比例函数;当a= _______ 时, 它是反比例函数。
(8) 函数y= •. 2x -4的自变量x的取值范围是____________
(9) 反比例函数的图象过点(-1,2),那么它的解析式为__________ 。
(10) 已知一次函数- 1_' 1 '的图象与y轴的交点坐标为(0,-2),那么
这个一次函数的解析式为________ 。
(11) 函数y=x2+ 2x —4的顶点坐标是, 对称轴是________
(12) 函数y=—2(x+3) 2的顶点坐标是_____________
4
(13) 函数y=-4的图象在第 ___________ 象限,在每一象限内,y随x的
x
增大而________
2•选择题:(10X3分)
(1) 已知x轴上的点P到y轴的距离为3,则点P的坐标为__________
(A) (3,0) (B) (0,3) (C) (3,0)或(-3,0) (D) (0,3)或(0,-3)
(2) 抛物线—淇* 1与x轴交点的个数是________________
(A) 0 (B) 1 (C) 2 (D) 3
(3) _______________________________________________________ 如果k>0, b>0,那么一次函数的W +占图象不经过_________________________ o
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
(4) _________________________________________________ 已知点P(x, x-
2)在第四象限,贝U x的取值范围是 __________________________
(A) x>0 (B) x>2 (C) x<2 (D) 0<x<2
(5) _________________________________ 在下列函数中,正比例函数是o
1
(A) ' 一( B) -"■ (C) 丁二(D)
(6) 如果丫二@ +Ux是正比例函数,那么a的值是__________________ 。
(A) -1 (B) 2 ( C) -1 或2 ( D) 0 或1
2
(7) 如果a<0,b>0,c<0,那么二次函数丿二炉+bx -^-c的图象为 ____________ (
(8) _____________________________________________________________ 已
知抛物线V二塔的顶点在x轴上,则b的值一定为
______________________________________________________________________
<
•解答题:(6分+6分+10分+10分)
1 •已知直线-""1 2和两坐标轴相交所围成的三角形面积为24,
(C)+取](D) + IC
(10).在函数y =中,自变
量
B. x >-1
C. x>-1 且x 工1
D. x >-1 且x 工1
(9)二次函数'
「…八一与一次函数一八
x的取值范围是(
2. 已知直线L 与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点 的纵坐标为1,求直线L 的解析式。
3. —次函数■ '与正比例函数二 "■:
的图象都经过点(2,
1)
(1)
分别求出这两个函数的解析式。
3
2)作出两个函数的图象
3
⑶ 求这两个函数图象与Y 轴围成的三角形面积。
4
4. 在生产中,为了节约原材料,加工某些零件时常利用一些边角废料,如图所 示,△ ABC 为锐角三角形废料板,其中 BO 12 cm, BC 边上的高AD= 8血。
在厶 ABC 上截取矩形PQMN 使 QM 边与BC 边重合,PN 交AD 于 F,设PQ 长为x( cm ),矩 形PQM 的面积为y( cm 2)
⑴ 用含x 的代数式表示AF: AD 的值和PN 的长, 4 分
(2)
求y 与x 的函数关系式; 2 分
分
分分
(3)当x为多少时y取最大值?求出它的最大值,求出此时矩形的长和宽,并判断此时P落在AB边上的位置。
4 分
A
四•综合题:(3分+2分+3分+4分)
已知一个二次函数的图象经过A(-2, 5)、B(0,--)和C(1,-2)三点。
2 2
(1)求出这个二次函数的解析式;(2)通过配方,求函数的顶点P的坐标;(3)作出函数的图象;(4)若函数的图象与x轴相交于点E、F,(E在F的左边)求四边形EBPF的面积及cosF的值
函数及其图象测试答案
1. y=3x+12,或y=-3x+12=
2. y=4x-3
3. ① y=2.5x-4, y=0.5x ②略③ 4/5
4. ⑴AF:AD=(8-X)/8 PN=3(8-X)/2
⑶y最大值为24,此时长为6,宽为4,
2
四.① y=0.5x -x-1.5 ② y=0.5(x-1)
J2
③略④4.5, ——
2
2
⑵ y=-1.5x +12x 为AB的中点
2
-2 p(1,-2)。
