光学习题答案
光学练习题答案

一、判断题1. 光程是光在介质中传播的几何路程。
(× )2. 光在折射率为n 的介质中传播距离为d 时,光程也为d 。
( × )3. 在劈尖干涉实验中,若劈尖角变大,其他条件不变,则干涉条纹间隔会变大。
( × )4. 在杨氏双缝干涉实验中,减小狭缝之间的距离,其他条件不变,则接收屏上的条纹间隔会变大(√)5. 在单缝衍射实验中,增大单缝的宽度,则接收屏上的条纹间隔会变小。
( √ )6. 根据光的偏振理论,经过偏振片后有消光现象的入射光一定是线偏振光。
( √ )7. 在单缝夫琅和费衍射实验中,按“半波带”法分析,就是将缝宽按入射光波长的一半来划分,若缝宽为半波长的偶数倍,则相应级次的条纹为明条纹。
( × ) 8. 自然光一定不是单色光,而线偏振光一定是单色光。
( × ) 9. 若两束光的频率相等,则两束光相遇就可以产生干涉。
( × ) 10. 将牛顿环装置放入水中,则观察到牛顿环将向中心收缩。
( √ ) 11. 光学仪器的分辨本领与光学仪器的口径成正比。
( √ ) 12. 在单缝衍射中,越远离屏幕中心的条纹亮度越暗。
( √ ) 13. 空气牛顿环的反射光线干涉图像中心一定是一个暗斑。
( √ ) 14. 当自然光以布儒斯特角入射到介质表面时,反射光线和折射光线都是线偏振光。
( × ) 二、填空题1.波长为λ的单色光在折射率为n 的介质中,由a 点传播到b 点相位变化了8π,则a 、b 两点之间的几何距离为4nλ。
2. 真空中波长为λ的单色光,在折射率23=n 的介质中传播,若由S 点传到P 点时,相位变化为π,则S、P 间的几何路程为2nλ;光程为2λ。
3.在杨氏双缝干涉实验中,如果屏幕向狭缝靠近,干涉条纹变__密__ ___,若缝距变小,干涉条纹变____疏__。
(填“疏”或“密”)4. 一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜的最小厚度为4nλ。
大学物理光学习题附答案
[
]
33.5649:在如图所示的夫琅禾费衍射装置中,将单缝宽
度 a 稍稍变窄,同时使会聚透镜 L 沿 y 轴正方向作微小平移(单缝与
屏幕位置不动),则屏幕 C 上的中央衍射条纹将
(A) 变宽,同时向上移动
(B) 变宽,同时向下移动
(C) 变宽,不移动
(D)
变窄,同时向上移动
(E) 变窄,不移动
[
]
34.5650:在如图所示的单缝夫琅禾费衍射装置中,设中央明
的部分
(A) 凸起,且高度为 / 4
(B) 凸起,且高度为 / 2
(C) 凹陷,且深度为 / 2
(D) 凹陷,且深度为 / 4 [
]
平玻璃
空气劈尖
工件
O
n=1.68
n=1.60 n=1.58
O
3507 图
14.3507:如图所示,平板玻璃和凸透镜构成牛顿环装置,全 部浸入 n=1.60 的液体中,凸透镜可沿 OO 移动,用波长=500 nm(1nm=109m)的单色光垂直入射。 从上向下观察,看到中心是一个暗斑,此时凸透镜顶点距平板玻璃 的距离最少是
(C) 向棱边方向平移,条纹间隔不变
(D) 向远离棱边的方向平移,条纹间隔不变
(E)
向远离棱边的方向平移,条纹间隔变小
[
]
19.5326:两块平玻璃构成空气劈形膜,左边为棱边,用单色
平行光垂直入射。若上面的平玻璃以棱边为轴,沿逆时针方向作微
小转动,则干涉条纹的
(A) 间隔变小,并向棱边方向平移
(B) 间隔变大,并向远离棱边方向平移
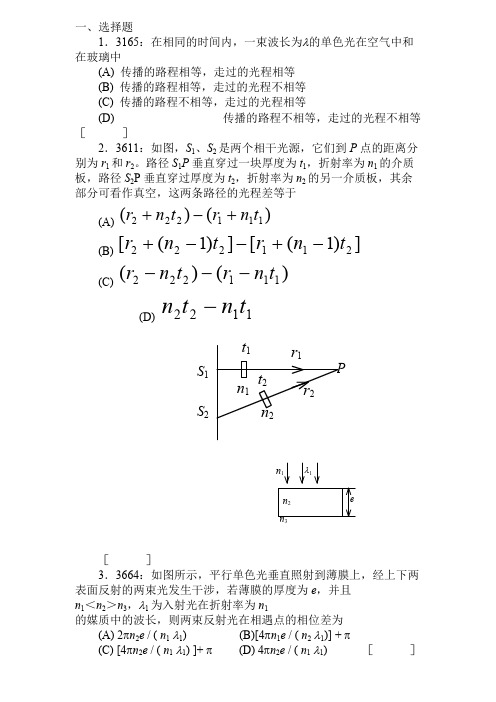
一、选择题 1.3165:在相同的时间内,一束波长为的单色光在空气中和
在玻璃中
初二物理光学练习题及答案

初二物理光学练习题及答案1. 题目:以下哪一项不属于光的性质?A. 折射B. 反射C. 吸收D. 发射答案:D. 发射2. 题目:光的传播速度在以下哪种介质中最快?A. 真空B. 水C. 空气D. 玻璃答案:A. 真空3. 题目:以下哪种材料具有最强的折射能力?A. 金属B. 木材C. 玻璃D. 塑料答案:C. 玻璃4. 题目:以下哪种现象是由光的反射引起的?A. 彩虹B. 折射C. 投影D. 色散答案:C. 投影5. 题目:以下哪种现象是由光的折射引起的?A. 眩光B. 绕射C. 反射D. 极化答案:B. 绕射6. 题目:光的颜色是由什么决定的?A. 光的频率B. 光的波长C. 光的幅度D. 光的速度答案:B. 光的波长7. 题目:以下哪个现象是光的干涉现象?A. 色散B. 极化C. 衍射D. 反射答案:C. 衍射8. 题目:以下哪个现象是光的偏振现象?A. 光的干涉B. 光的反射C. 光的折射D. 光的吸收答案:D. 光的吸收9. 题目:平面镜的特点是什么?A. 只有一面能反射光B. 反射光具有色散现象C. 反射光没有方向性D. 只有特定角度可以观察到镜中的物体答案:A. 只有一面能反射光10. 题目:以下哪个光学器件利用了光的折射原理?A. 凸透镜B. 凹透镜C. 平面镜D. 磨凸镜答案:A. 凸透镜总结:物理光学是初中物理课程中的一个重要内容,通过学习光的性质、传播规律以及光学现象等知识,我们可以更好地理解光的行为和光学器件的工作原理。
本文给出了一些初二物理光学的练习题及答案,希望能帮助同学们复习和巩固相关知识。
通过解答这些问题,同学们可以检验自己对物理光学的理解程度,加深对光学知识的记忆和理解。
在学习过程中,同学们还可以通过查阅教科书和其他资料,对光学知识进行更深入的学习和拓展。
《光学》(崔滨宏)课后习题答案

10.4如图,以光线射入镜面间并反射n 次,最后沿入射时的光路返回,试写出i θ与α间的关系表达式。
解:最后的反射之后,其对另一镜的入射角应为0。
最后(第n 次)的反射角为αθ=n ,第n-1次的反射角为αθ21=-n 。
相邻的两次反射间,有关系式,απθπθ-=-+-2/)2/(1m m ,即αθθ+=-m m 1。
则ααθαθθn n m n m =+-=+-=)1()1(1。
10.5证明:当一条光线通过平板玻璃时,出射光线方向不变,只产生侧向平移。
当入射角1i 很小时,位移t i nn x 11-=∆。
其中,n 为玻璃的折射率,t 为玻璃板的厚度。
证:如图,由于上下两面平行,且两侧折射率相等,所以在下表面的入射角等于上表面的折射角,下表面的折射角等于上表面的入射角。
出射光线保持平行。
2212121221cos /)sin cos cos (sin )sin()cos /()sin(i i i i i t i i i t i i AB BC x -=-=-==∆)cos sin cos (sin 2111i n i i i t -=,在小角度时,有11sin i i ≈,211)2(1cos i i -≈,222)2(1cos i i -≈则)1(])2(1)2(1[)cos sin cos (sin 1222112111-≈---≈-n n ti i in n ti i n i i i t ,即t i n n x 11-=∆ 10.19cm nvf R v u R v u 5.22,2,,211===+∞==+ 10.23 n=210.32 题目有误 9cm 改为9m1.3, 在玻璃中z 方向上传播的单色平面波的波函数为)]}65.0(10[exp{10),(152czt i t P E -⨯-=π 式中c 为真空中的光速,时间以s 为单位,电场强度以V/m 为单位,距离以m 为单位,试求:(1)光波的振幅和时间频率;(2)玻璃的折射率;(3)z 方向的空间频率;(4)在xz 平面内与x 轴成450角方向上的空间频率。
光学原理习题答案

光学原理习题答案1. 一束光线从空气射入玻璃,发生折射现象。
如果光线的入射角为30°,玻璃的折射率为1.5,求折射后光线的折射角。
解,根据折射定律可知,入射角 i、折射角 r 和介质折射率 n 之间的关系为n=sin(i)/sin(r)。
代入已知数据,得到sin(30°)/sin(r)=1.5,解得sin(r)=sin(30°)/1.5,r=arcsin(sin(30°)/1.5),计算得到 r≈20°。
2. 一束光线从水中射入空气,发生折射现象。
如果光线的入射角为45°,水的折射率为1.33,求折射后光线的折射角。
解,同样根据折射定律可知,入射角 i、折射角 r 和介质折射率 n 之间的关系为 n=sin(i)/sin(r)。
代入已知数据,得到 sin(45°)/sin(r)=1.33,解得sin(r)=sin(45°)/1.33,r=arcsin(sin(45°)/1.33),计算得到 r≈33.75°。
3. 一束光线从空气射入玻璃,发生全反射现象。
如果光线的入射角为45°,玻璃的折射率为1.5,求临界角。
解,根据全反射的条件,当入射角大于临界角时,光线发生全反射。
临界角可以通过折射定律的反推得到,即 sin(c)=1/n,代入已知数据,得到 sin(c)=1/1.5,c=arcsin(1/1.5),计算得到 c≈41.81°。
4. 一束光线从玻璃射入水,发生折射现象。
如果光线的入射角为60°,水的折射率为1.33,求折射后光线的折射角。
解,根据折射定律可知,入射角 i、折射角 r 和介质折射率 n 之间的关系为n=sin(i)/sin(r)。
代入已知数据,得到 sin(60°)/sin(r)=1.33,解得sin(r)=sin(60°)/1.33,r=arcsin(sin(60°)/1.33),计算得到 r≈43.3°。
蔡履中-《光学》课后习题答案

第五章习题解答5-2解:a sin E E O = a c o s E E e =a t a n =eoE E 在晶体内:a 22tan )(e o e o n n I I = 出了晶体以后:a 2tan =e o I I 13202.t a n ==a eo I I5-3解:由于光轴与入射面垂直,所以在入射面内各方向折射率相同,由折射定律:解:由于光轴与入射面垂直,所以在入射面内各方向折射率相同,由折射定律: o o i n sin sin =060 04831.=o i e e i n sin sin =060 06435.=e i0164.=D i mm h d 0514********0.).tan .(tan =-=D5-4解:最小偏向角公式解:最小偏向角公式 22a q a sin sinmn +=α为顶角为顶角76250305251260260000.sin .sin sin ===+n m q 006849260.=+m q2239373900¢==.m q 4791.=e n 7395026030479100.sinsin .=+=mq2235373500¢==.m q 04=D m q5-12解:2502pp lp d -=-===.)(d n n e o c α=450时E O =E e 为右旋圆偏振光为右旋圆偏振光α=-450时E O =E e 为左旋圆偏振光为左旋圆偏振光α=300时E O ≠E e为右旋正椭圆偏振光为右旋正椭圆偏振光5-13解:设晶体光轴与P 1夹角为α (1)当α= 0= 0,,π/2/2,,π,3π/2 /2 时,时,时,I=0 I=0 I=0 所以出现所以出现4次消光。
次消光。
当α=π/4/4,,3π/4/4,,5π/4/4,,7π/4 /4 时,时,时,I I 出现极大值,出现极大值, 所以出现4次极大和极小。
次极大和极小。
光学练习题(含答案)

《光学》练习题(2010 年)一、单项选择和填空题C1.将扬氏双缝干涉实验装置放入折射率为n 的介质中,其条纹间隔是空气中的CA 1倍B n 倍 C1倍 D n 倍n nB2 .在菲涅耳圆屏衍射的几何阴影中心处BA永远是个亮点,其强度只与入射光强有关B永远是个亮点,其强度随着圆屏的大小而变C有时是亮点,有时是暗点。
C3.光具组的入射光瞳、有效光阑,出射光瞳之间的关系一般为CA入射光瞳和有效光阑对整个光具组共轭。
B出射光瞳和有效光阑对整个光具组共轭。
C入射光瞳和出射光瞳对整个光具组共轭。
B4 .通过一块二表面平行的玻璃板去看一个点光源,则这个点光源显得离观察者BA 远了B 近了C 原来位置。
C5.使一条不平行主轴的光线,无偏折(即传播方向不变)的通过厚透镜,满足的条件是入射光线必须通过A 光心B 物方焦点C 物方节点D 象方焦点B6.一薄透镜由折射率为 1.5 的玻璃制成,将此薄透镜放在折射率为4/3 的水中。
则此透镜的焦距数值就变成原来在空气中焦距数值的:A2倍B3倍C4倍D 1.5/1.333倍D7. 光线由折射率为n1的媒质入射到折射率为n2的媒质,布儒斯特角i p满足:A . sin i p= n1 / n2B 、 sin i p= n2 / n1C、 tg i p= n1 / n2D、 tgi p= n2 / n1A8 .用迈克耳逊干涉仪观察单色光的干涉,当反射镜M 1移动 0.1mm 时,瞄准点的干涉条纹移过了400 条,那么所用波长为A 5000?B 4987?C 2500?D 三个数据都不对D9 .一波长为 5000? 的单色平行光,垂直射到 0.02cm 宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为 3mm,则所用透镜的焦距为A 60mmB 60cmC 30mmD 30cm.B10. 光电效应中的红限依赖于:A 、入射光的强度B、入射光的频率C、金属的逸出功D、入射光的颜色B11. 用劈尖干涉检测二件的表面,当波长为λ的单色光垂直入射时,观察到干涉条纹如图,图中每一条纹弯曲部分的顶点恰与右边相邻的直线部分的连续相切,由图可见二件表面:A 、有一凹陷的槽,深为4B、有一凹陷的槽,深为2C、有一凸起的埂,高为4D、有一凸起的埂,高为2A12. 随着辐射黑体温度的升高,对应于最大单色光发射本领的波长将:A、向短波方向移动B、向长波方向移动C、先向短波方向,后向长短方向移动D、先向长波方向,后向短波方向移动B13.用单色光观察牛顿环,测得某一亮环直径为 3mm,在它外边第 5 个亮环直径为 4.6mm,用平凸透镜的凸面曲率半径为 1.0m,则此单色光的波长为A 5903 ?B 6080 ?C 7600 ?D三个数据都不对C14. 一束自然光以布儒斯特角入射于平板玻璃,则:A、反射光束偏振面垂直于入射面,而透射光束偏振面平行于入射面并为完全线偏振光B、反射光束偏振面平行偏振于入射面,而透射光束是部分偏振光C、反射光束偏振面是垂直于入射面,而透射光束是部分偏振光D、反射光束和透射光束都是部分偏振光B15.仅用检偏器观察一束光时,强度有一最大但无消光位置,在检偏器前置一4片,使其光轴与上述强度为最大的位置平行,通过检偏器观察时有一消光位置,这束光是:A 、部分偏振光B、椭园偏振光C、线偏振光D、园偏振光B16.要使金属发生光电效应,则应:A、尽可能增大入射光的强度B、选用波长较红限波长更短的光波为入射光C、选用波长较红限波长更长的光波为入射光波D、增加光照的时间;B17. 下列说法正确的是A、利用不同折射率的凸凹透镜相配,可以完全消除去球差和色差;B、近视眼需用凹透镜校正;C、扩大照相景深的方法是调大光圈;D 、天文望远镜的作用是使遥远的星体成像在近处,使得人们能看清楚;D18. 将折射率1的有机玻璃浸没在油中。
光学习题及答案

光学习题及答案练习二十二 光的相干性 双缝干涉 光程一.选择题1. 有三种装置(1) 完全相同的两盏钠光灯 ,发出相同波长的光 ,照射到屏上;(2) 同一盏钠光灯 ,用黑纸盖住其中部将钠光灯分成上下两部分同时照射到屏上; (3) 用一盏钠光灯照亮一狭缝 ,此亮缝再照亮与它平行间距很小的两条狭缝 ,此二亮缝的 光照射到屏上 .以上三种装置 ,能在屏上形成稳定干涉花样的是(A) 装置 (3). (B) 装置 (2). (C) 装置 (1)(3). (D) 装置 (2)(3).2. 在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是 (A) 使屏靠近双缝 .(B) 把两个缝的宽度稍微调窄 . (C) 使两缝的间距变小 . (D) 改用波长较小的单色光源 .3. 如图所示 ,设 s 1、s 2 为两相干光源发出波长为的单色光 ,分别通过两种介质 (折射率分别为 n1和 n 2,且 n 1>n 2)射到介质的分界面上的 P 点,己知 s 1P = s 2P = r,则这两条光的几何路程 r, 在刻有双缝一边的箱子外边时 ,在箱子的对面壁上产生干涉条纹 这箱子时 ,条纹的间隔将会发生什么变化答(A) 保持不变 . (B) 条纹间隔增加 . (C) 条纹间隔有可能增加 . (D) 条纹间隔减小 .5. 用白光 (波长为 4000~ 7600)垂直照射间距为 a=的双缝 ,距缝 50cm 处放屏幕 ,则观察到 的第一级彩色条纹和第五级彩色条纹的宽度分别是 (A) × 104m ,× 104m (B) ×104m , × 103m (C) ×104m , ×104m(D) × 104m ,× 104m 光程差 和相位差分别为(A) r = 0 , = 0 , = 0.(B) r= (n 1- n 2 ) r , =( n 1-n 2) r , =2 (n 1- n 2) r/ (C) r= 0 , =( n 1 -n 2) r , =2 (n 1- n 2) r/ . (D) r =0 , =( n 1- n 2) r , =2 (n 1- n 2) r.,当把一个钠光灯照亮的狭缝放.如果把透明的油缓慢地灌入 4. 如图所示,在一个空长方形箱子的一边刻上一个双缝 图.填空题1. 在双缝干涉实验中 ,两缝分别被折射率为 n 1和 n 2 的透明薄膜遮盖 ,二者的厚度均为 e ,波长为的平行单色光垂直照射到双缝上 ,在屏中央处 ,两束相干光的相位差 =2. 如图所示 , s 1、、s 2为双缝 , s 是单色缝光源 ,当 s 沿平行于 s1、和 s 2 的连线向上作微小移动时 , 中央明条纹将向 s s1移动;若 s 不动 ,而在 s 1后加一很薄的云母片 ,中央 s 2明条纹将向 移动 .(2) 如果用厚度 e=× 102mm,折射率 n=的透明薄膜覆盖在图中的明条纹的坐标 x .练习二十三 薄膜干涉 劈尖.选择题1. 如图 所示 , 薄膜的折射率为 n 2, 入射介质的折射率为 n 1,透 射介质为 n 3,且 n 1< n 2< n 3, 入射光线在两介质交界面的反射光线分 别为 (1)和(2), 则产生半波损失的情况是(A) (1)光产生半波损失 , (2)光不产生半波损失 (B) (1)光 (2)光都产生半波损失 . (C) (1)光 (2)光都不产生半波损失 .(D) (1)光不产生半波损失 , (2)光产生半波损失2. 波长为的单色光垂直入射到厚度为 e 的平行膜上 ,如图 ,若反射光消失 ,则当 n 1<n 2<n 3时,应满足条件 (1); 当 n 1<n 2>n 3时应满足条件 (2). 条件 (1),条件(2) 分别是(A) (1)2ne = k, (2) 2ne = k.3. 如图所示 ,在劳埃镜干涉装置中, 若光源 s 离屏的距离为 D, s 离平面镜的垂直距离为 a(a 很小).则平面镜与屏交界处 A 的 干涉条纹应为 条纹;设入射光波长为,则相邻条纹 中心间的距离为 . 三. 计算题1. 在双缝干涉实验中 ,单色光源 s 到两缝 s 1和 s 2的距离 分别为 l 1 和 l 2,并且 l 1-l 2=3, 为入射光的波长 ,双缝之间的距 离为d, 双缝到屏幕的距离为 D,如图 ,求(1) 零级明纹到屏幕中央 O 点的距离; (2) 相邻明条纹间的距离 . 2. 双缝干涉实验装置如图所示, 双缝与屏之间的距离D=120cm, 两缝之间的距离 d=,用波长 =5000 的单色光垂直照射双缝.(1) 求原点 O(零级明条纹所在处 )上方的第五级明条纹的 坐标 .ds s 12屏xs 1缝后面 ,求上述第五级A图(B) (1)2ne = k + /2,(C) (1)2ne = k -/2, (D) (1)2ne = k,3. 由两块玻璃片( n 1 = )所形成的空气劈尖 ,其一端厚度为零,另一端厚度为,现用波(2) 2ne = k+/2. (2) 2ne = k. (2) 2ne = k -/2.长为 7000 的单色平行光,从入射角为 30 角的方向射在劈尖的表面,则形成的干涉条纹数(A) 27. (B) 56. (C) 40. (D) 100.4. 空气劈尖干涉实验中 , (A) 干涉条纹是垂直于棱边的直条纹(B) 干涉条纹是垂直于棱边的直条纹(C) 干涉条纹是平行于棱边的直条纹 , 劈尖夹角变小时 , 劈尖夹角变小时 , 劈尖夹角变小时 , 劈尖夹角变小时 ,条纹变稀 ,从中心向两边扩展 . ,条纹变密 ,从两边向中心靠拢 . ,条纹变疏 ,条纹背向棱边扩展 .,条纹变密 ,条纹向棱边靠拢 .5. 一束波长为的单色光由空气入射到折射率为 则薄膜的最小厚度应为(A) /2.(B)/2n . (C) /4.(D)/4n ..填空题1. 如图所示 ,波长为的平行单色光垂直照射到两个劈尖上 ,两劈尖角分别为 1 和 2 ,折射率分别为 n 1 和 n 2 ,若二者形成干涉条纹的间距相等 , 则 1 , 2 , n 1 和 n 2 之间的关系是.2. 一束白光垂直照射厚度为 m 的玻璃片 ,玻璃的折射率为 ,在反射光中看见光的波长 是,在透射光中看到的光的波长是.3. 空气劈尖干涉实验中 ,如将劈尖中充水 ,条纹变化的情况是,如将一片玻璃平行的拉开 , 条纹变化的情况是 . 三. 计算题1. 波长为的单色光垂直照射到折射率为 n 2 的劈尖薄膜上 n 1<n 2< n 3,如图所示 ,观察反射光形成的条纹 .(1) 从劈尖顶部 O 开始向右数第五条暗纹中心所对应的 薄膜厚度 e 5 是多少(2) 相邻的二明纹所对应的薄膜厚度之差是多少2. 在折射率 n=的玻璃上 ,镀上 n=的透明介质薄膜 ,入射光垂直于介质膜表面照射 ,观察反n 的透明薄膜上 ,要使透射光得到加强图射光的干涉 ,发现对 1=6000的光干涉相消 ,对2=7000的光波干涉相长 ,且在 6000 ~ 7000之间没 有别的波长的光波最大限度相消或相长的情况 ,求所镀介质膜的厚度 .练习二十四 牛顿环 迈克耳逊干涉仪 衍射现象.选择题1. 严格地说 ,空气的折射率大于 1,因此在牛顿环实验中 ,若将玻璃夹层中的空气逐渐抽去时 ,干涉圆环的半径将(A) 变小 . (B) 不变 . (C) 变大 . (D) 消失 .2. 在图所示三种透明材料构成的牛顿环装置中 涉条纹 ,则在接触点 P 处形成的圆斑为(A) 全明 . (B) 全暗 .(C) 右半部明 ,左半部暗 . (D) 右半部暗 ,左半部明 .3. 在一块平玻璃片 B 上,端正地放一个顶角接近于 ,但小于的圆锥形平凸透镜 A,在 A 、B间形成空气薄层 ,如图所示 ,当用单色光垂直照射平凸透镜时 ,从玻璃片的下面可观察到干涉 条纹 ,其特点是4.把观察牛顿环装置中的平凸透镜换成半径很大的半圆柱面透镜 , 用单色光垂直照射 半圆柱面的平凸透镜时 ,观察到的干涉条纹的特点是(A) 间隔不等的与圆柱面母线平行的干涉直条纹 ,中间密 ,两边稀 . (B) 间隔不等的与圆柱面母线平行的干涉直条纹 ,中间稀 ,两边密 . (C) 间隔相等的与圆柱面母线平行的干涉直条纹 . (D) 间隔相等的与圆柱面母线垂直的干涉直条纹 .5. 在迈克尔逊干涉仪的一条光路中放入一个折射率为 n,厚度为 d 的透明片后 ,这条光路的光程增加了(A) 2(n - 1)d. (B) 2nd.,用单色光垂直照射 ,在反射光中看到干(A) 中心暗的同心圆环状条纹 ,中心密 ,四周疏 . (B) 中心明的同心圆环状条纹 ,中心疏 ,四周密 . (C) 中心暗的同心圆环状条纹 ,环间距相等(D) 中心明的同心圆环状条纹 ,环间距相等(C) (n-1)d.(D) nd..填空题1. 用= 6000 的单色光垂直照射牛顿环装置时,从中央向外数第 4 个暗环(中央暗斑为第 1 个暗环)对应的空气膜厚度为m.2. 光强均为I0 的两束相干光相遇而发生干涉时, 在相遇区域内有可能出现的最大光强是.3. 惠更斯-菲涅耳原理的基本内容是:波阵面上各个面积元上,所发出的子波在观察点P 的, 决定了P 点的合振动及光强.三. 计算题1. 图所示为一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R=400cm, 用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第 5 个明环的半径是.(1) 求入射光的波长(2) 设图中OA=,求在半径为范围内可观察到的明环数目.2. 在如图所示的牛顿环装置玻璃平凸透镜和平面玻璃( 设玻璃折射图中率 n1=之间的空气(n2=改换成水(n2 = ),求第k 个暗环半径的相对改变量(r k-r k ) / r k.练习二十五单缝衍射圆孔衍射光学仪器的分辨率一.选择题1. 对杨氏双缝干涉的理解应为(A) 杨氏双缝干涉是两狭缝衍射光的干涉,因此干涉条纹的分布受单缝衍射因子的调制(B) 杨氏双缝干涉完全是两束相干光的干涉.(C) 杨氏双缝干涉是两条单缝的衍射,无干涉.(D) 杨氏双缝干涉是双光束干涉与单缝衍射的迭加.2. 关于半波带正确的理解是(A) 将单狭缝分成许多条带,相邻条带的对应点到达屏上会聚点的距离之差为入射光波长的1/2.(B) 将能透过单狭缝的波阵面分成许多条带, 相邻条带的对应点的衍射光到达屏上会聚点的光程差为入射光波长的1/2.(C) 将能透过单狭缝的波阵面分成条带,各条带的宽度为入射光波长的1/2.(D) 将单狭缝透光部分分成条带,各条带的宽度为入射光波长的1/2.3. 波长= 5000 的单色光垂直照射到宽度 a = mm 的单缝上,单缝后面放置一凸透镜在凸透镜的焦面上放置一屏幕,用以观测衍射条纹,今测得屏幕上中央条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为 d = 12 mm ,则凸透镜的焦距为(A) 2m. (B) 1m. (C) . (D) . (E) .4. 单色光垂直入射到单狭缝上 ,对应于某一衍射角 到屏上会聚点 A 的光程差为 = 2 , 则(A) 透过此单狭缝的波阵面所分成的半波带数目为二个(B) 透过此单狭缝的波阵面所分成的半波带数目为二个 (C) 透过此单狭缝的波阵面所分成的半波带数目为四个(D) 透过此单狭缝的波阵面所分成的半波带数目为四个5. 一直径为 2mm 的 He - Ne 激光束从地球上发出投射于月球表面 ,己知月球和地面的距离为 376×103km, He -Ne 激光的波长为 6328,则月球得到的光斑直径为(A) × 130m. (B) . × 13 0m. (C) 290× 130 m(D) 29× 130 m..填空题1. 在单缝夫琅和费衍射实验中,设第一级暗纹的衍射角很小,若用钠黄光(1≈ 5890 )照射单缝得到中央明纹的宽度为 , 则用 2=4420 的蓝紫色光照射单缝得到的中央明纹宽度 为.2. 波长为 5000 ~ 6000 的复合光平行地垂直照射在 a=的单狭缝上 ,缝后凸透镜的焦距为,则此 二波 长光零级明纹 的中心间隔为 ,一级明 纹的中 心间 隔为.3. 己知天空中两颗星相对于一望远镜的角距离为× 107rad,它们发出的光波波长按 5500计算 ,要分辨出这两颗星 ,望远镜的口镜至少要为 .三. 计算题1. 用波长 = 6328 的平行光垂直照射单缝 ,缝宽 a = ,缝后用凸透镜把衍射光会聚在焦平面上 ,测得第二级与第三级暗条纹之间的距离为 ,求此透镜的焦距 .2. 在某个单缝衍射实验中 ,光源发出的光含有两种波长 1 和 2,并垂直入射于单缝上 ,假如1的第一级衍射极小与 2 的第二级衍射极小相重合 ,试问(1) 这两种波长之间有何关系(2) 在这两种波长的光所形成的衍射图样中 ,是否还有其它极小相重合练习二十二 光的相干性 双缝干涉.选择题 A C C D B二. 填空题, 此单狭缝两边缘衍射光通过透镜,屏上 A 点为明点 . ,屏上 A 点为暗点 . ,屏上 A 点为明点 .,屏上 A 点为暗点 .1. 2(n1n2)e/.2. 下, 上.3. 暗, x=D/(2 a) .三.计算题1. 光程差=(l2+r2)(l1+r1)=(l2l1)+(r2r1)= l2l1+xd/D=3+xd/D(1)零级明纹=0 有x=3D/d(2)明纹=k=3+x k d/D 有x k=(3k)D/dx=x k+1-x k=D/d2.(1)光程差=r2r1=xd/D=kx k=kD/d因k=5 有x5=6mm(2)光程差=r2-(r1-e+ne)=r2-r1-(n-1)e=x'd/D -(n-1)e=k 有x'=[k+(n-1)e]D/d因k=5,有x'5=练习二十三薄膜干涉劈尖一.选择题B C A C B二.填空题1. n11= n22.2. m; m, m.3. 依然平行等间距直条纹,但条纹变密;依然平行等间距直条纹,条纹间距不变,但条纹平行向棱边移动.三.计算题1.(1)因n1<n2<n 3,所以光程差=2n2e暗纹中心膜厚应满足k=2n2e k=(2k+1)/2 e k=(2k+1)/(4n2)对于第五条暗纹,因从尖端数起第一条暗纹=/2,即k=0,所以第五条暗纹的k=4,故e4=9/(4 n2)(2)相邻明纹对应膜厚差e=e k+1-e k=/(2n2)2.因n1<n2<n3 所以光程差=2n2e1 相消干涉,有=2n2e=(2k1+1)1/22 相长干涉,有=2n2e=2k22/2因 2>1,且中间无其他相消干涉与相长干涉,有k1=k2=k,故(2k+1)1/2=2k2/2 k=1/[2( 2-1)]=3 得e=k2/(2n2)=10-4mm练习二十四牛顿环迈克耳逊干涉仪.选择题 C D D B A二.填空题1. .2. 4I0 .3. 干涉(或相干叠加).三. 计算题1. (1) 明环半径r=[(2k1)R/2]1/2=2r2/[(2 k1)R]=5000 (2) (2k1)=2r2/(R)=100k= 故在OA范围内可观察到50 个明环( 51 个暗环)2. 暗环半径r k kRλ n2r k kRλ n2r k r k kRλn2 kRλ n2r k kRλ n21 n2 1 n21n2 1 n2 n2 13.6%练习二十五单缝圆孔分辨率.选择题 A B B D C二.填空题1. .2. 0, 15mm.3. .三. 计算题1. 单缝衍射暗纹角坐标满足asin k=k线坐标满足x k=ftan≈fsin=f k/ax=x k x k-1f/afax/ =400mm= ;2.(1) 单缝衍射暗纹角坐标满足asin1=1 asin2=22因重合有asin2=asin1,所以1=22(2) asin1=k11 = k122 asin2=k22asin1= asin2得k 2=2k1故当k2=2k1 时,相应的暗纹重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P1:用费马原理证明光的反射定律
1.有一双胶合物镜,其结构参数为:
n 1=1
r 1=83.220
d 1=2 n 2=1.6199
r 2=26.271
d 2=6 n 3=1.5302
r 3=-87.123
n 4=1
(1)计算两条实际光线的光路,入射光线的坐标分别为:
L 1=-300; U 1=-2 °
L 1= ∞ ; h=10 (2)用近轴光路公式计算透镜组的像方焦点和
像方主平面位置及与 近轴像点位置。
P2:r/mm d/mm
26.67
189.67 5.2
-49.66 7.95 25.47 1.6 72.11 6.7 -35.00 2.8
1.614
1
1.6475
1.614
l 1=-300 的物点对应的
2. 有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反光镜反射以后成像在投影物平面上。
光源长为10mm,投影物高为40mm ,要求光源像等于投影物高;反光镜离投影物平面距离为600mm ,求该反光镜的曲率半径等于多少?
6. 已知照相物镜的焦距f′=75mm,被摄景物位于距离x=- ∞ ,-10,-8,-6,-4,-2m 处,试求照相
底片应分别放在离物镜的像方焦面多远的地方
9. 已知航空照相机物镜的焦距f′=500mm ,飞机飞行高度为6000m,相机的幅面为300× 300mm2,问每幅照片拍摄的地面面积。
10. 由一个正透镜组和一个负透镜组构成的摄远系统,前组正透镜的焦距f1′=100 ,后组负透镜的焦距f2 ′ =-50,要求由第一组透镜到组合系统像方焦点的距离与系统的组合焦距之比为1∶1.5,求二透镜组之间的间隔 d 应为多少? 组合焦距等于多少?
11. 如果将上述系统用来对10m 远的物平面成像,用移动第二组透镜的方法,使像平面位于移动前组合系统的像方焦平面上,问透镜组移动的方向和移动距离。
12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距为f1 ′,第二组透镜的焦距为f2′,物平面位于第一组透镜的物方焦面上,求该倒像系统的垂轴放大率。
13. 由两个同心的反射球面(二球面球心重合)构成的光学系统,按照光线反射的顺序第一个反射球面是凹的,第二个反射球面是凸的,要求系统的像方焦恰好位于第一个反射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d 之间的关系。
15. 电影放映机镜头的焦距f′ =120mm ,影片画面的尺寸为22×16mm2 ,银幕大小为 6.6 × 4.8m2,问电影机应放在离银幕多远的地方?如果把放映机移到离银幕50m 远处,要改用多大焦距的镜头?
3. 照相物镜的焦距等于75mm ,底片尺寸为55 55mm 2,求视场光阑位在何处?该照相物镜的最大视场角等于多少?
6.有一薄透镜焦距为50mm ,通光口径为40mm,在透镜左侧30mm 处放置一个直径为20mm 的圆孔光阑,一轴上物点位于光阑左方200mm 处,求:
1)限制光束口径的是圆孔光阑还是透镜框?
2)此时该薄透镜的相对孔径多大?
3)出瞳离开透镜多远,出瞳直径多大?
4.照相机光圈数取
多大光圈数?
1
8,曝光时间用s ,为了拍摄运动目标,将曝光时间改
为
1
500
s,问应取
5.用于跟踪天空飞行目标的电视摄像机,摄像管要求最低的像面光照度为20 lx ,假定天空的光亮度为2500cd/m 2 ,光学系统的透过率等于0.7,问要求使用多大相对孔径的摄影物镜?
1. 周视瞄准的出瞳直径为4mm,视放大率为 3.7 ,求周视瞄准镜的分辨率。
2. 有一照相物镜,相对径孔为1:2,问该照相物镜的目视分辨率多大?
3. 有一架显微镜,视放大率为45 ,出瞳直径为2mm,问该显微镜的理想分辨率多大?(假定波长为555nm)
4. 检验实际光学系统成像质量的常用方法有哪几种?
5. 在光学系统设计阶段评价成像质量的方法有哪几种?
6. 什么叫理想光学系统的分辨率?它具有什么实际意义?理想光学系统的分辨率是怎样确定的?
7. 目前世界上最大的天文望远镜通光口径为5m ,求能被它分辨的双星的最小夹角(=555nm ),与人眼相比,分辨率提高了多少倍?。
