实验一谐波分析实验
S参数和谐波平衡仿真分析 实验报告

实验报告课程名称: ADS射频电路设计基础与典型应用实验项目名称: S参数和谐波平衡仿真分析学院:工学院专业班级:11信息工程姓名:学号:1195111016指导教师:唐加能预习报告一、实验目的本节实验课程将通过给出一个放大器S参数仿真历程的原理图与谐波平衡仿真历程的原理图,并将其电路通过仿真来实现,从而帮助大家对这两种模型有进一步的理解与认识。
二、实验仪器PC,ADS仿真软件三、实验原理S参数仿真中各项需要用到的模型介绍(1)放大器模型Motorola_PAS参数仿真原理图SP1.dsn中的放大器是一个电路模型。
Motorola_PA是这个电路模型的符号。
图1 Motorola_PA 电路模型Motorola_PA符号有子电路,它的特性是由子电路来决定,查看子电路的具体步骤如下:在原理同SP1.dsn中,单击按钮,再单击Motorola_PA电路模型。
其中的Motorola_Mosfet_Model也有子电路,可以通过相同方法进入查看。
图2 Motorola_Mosfet_Model电路模型(2)终端负载Term在S参数仿真中,各个端口都要加载终端负载Term。
(在本次S参数仿真中,电路输入端口没有加源,而在输入端口采用终端负载Term。
)图3 Term电路模型(3)直流电压源在SP1.dsn原理图中,有两个直流电压源V_DC,他们给放大电路提供静态工作点。
图4 直流电压源的电路模型(4)S参数仿真控制器SP1,.dsn原理图中,S参数的仿真控制器S-PARAMETERS用于设置所用到的参数,双击可以进入设置界面图5 仿真控制器的电路模型图6 仿真控制器的设置界面其中部分参数按如下要求设置:扫描的起始值为:800MHz扫描的终止值为:900MHz扫描间隔为:1MHZ谐波平衡仿真各项需要用到的模型介绍BJT晶体管原理图中,BJT_NPN晶体管没有子电路,他的参数主要有电路旁边的晶体管模型BJT_Model设定。
示波器谐波分析实验报告

(1)从信号发生器输出一个正弦信号到CH1,设好信号的输出幅度及频率,调节示波器Time/div按钮,使波形显示幅度合适、显示一两个稳定的正弦波,记下频率f和峰值电压Vp-p.
(2)利用网格线测出正弦波的波峰到波谷的垂直距离dy,并记录Vol/div的值
(3)计算Vp-p=a*dy
五、数据处理:
次数
dy
V/div
Vpp
1
5.2cm
0.2V/cm
1.04V
2
2.1cm
0.5V/cm
1.05V
次数
dx
T/div
T
1
1.9cm
5ms/cm
9.5ms
2
3.8cm
2.5ms/cm
9.5ms
fx(Hz)
fy(Hz)
图形
nx
ny
fx:fy
nx:ny
1
100
100
1
1
1:1
1:1
2
100
200
2、双踪示波器的原理:电子开关使两个待测电压信号YCH1和YCH2周期性地轮流作用在Y偏转板,这样在荧光屏上忽而显示YCH1信号波形,忽而显示YCH2信号波形。由于荧光屏荧光物质的余辉及人眼视觉滞留效应,荧光屏上看到的是两个波形。当扫描信号的周期与被测信号的周期一致或是整数倍,屏上一般会显示出完整周期的正弦波形。
3.将两信号分别接入CH1和CH2,对应做好记录。将示波器的屏幕显示波形,选择列表里,选中CH1,CH2下的X-Y。
4.不能;同步旋钮是使每次扫描都扫描同一个起始相位,使一个示波器内只有一个稳定的图形,但从李萨如图形的形成原理来看,调同步旋钮式不能使它稳定下来的。应该是调频率。
实验报告《谐波电流发射测量不确定度评定报告》

谐波电流发射测量不确定度评定报告版本号:第1/0版1.目的和范围ISO/IEC 17025:2017《检测和校准实验室能力的通用要求》中条款7.6.3指出:开展检测的实验室应评定测量不确定度。
由于检测方法的原因难以严格测量不确定度时,实验室应基于对理论原理的理解或使用该方法的实践经验进行评估。
为了保证检验结果的高可靠性,有必要对测量仪器中涉及的不确定度来源进行确认,并以此评定测量不确定度,从而验证检测结果的水平是否符合要求,为提高检测工作的质量提供重要依据。
本报告从测量设备和设施方面,对于谐波电流发射进行测量不确定度评定。
2.参考标准对于EMC试验项目的测量不确定度评定,主要参考以下标准和规范:●Electromagnetic compatibility (EMC) –Part 3-2: Limits – Limits for harmonic currentemissions (equipment input current ≤ 16 A per phase)●ISO/IEC 17025:2017《检测和校准实验室能力的通用要求》●CISPR 16-4-2 (2014) Specification for radio disturbance and immunity measuringapparatus and methods – Uncertainty in EMC measurements●JJF 1059.1-2012《测量不确定度评定与表示》●CNAS-CL07《测量不确定度的要求》●CNAS-GL07《EMC检测领域不确定度的评估指南》●IEC/TR 61000-1-6:2012《电磁兼容1-6部分:综述测量不确定度评估指南》●UKAS,M3003,Edition 2:2007测量中的不确定度和置信度表示●ISO/IEC Guide 98-3:2008 测量不确定度第3部分:测量中的不确定度表示指南3.基本说明1)概率分布函数的确定标准不确定度()ix u 可通过将i x 的不确定度的值除以包含因子k 来计算,这个包含因子依赖于ix 不确定度的概率分布和与其相应的置信概率。
SPWM多重化及其谐波分析1

2. PWM多重化(MPWM)(续)
2.2.2 数字仿真
三角载波频率 1kHz 直流调制比 0.7 单重与四重(n=4)比较
2.3 结论
PWM n 重化后,其输出波形 的等效载波频率为多重化前载 波频率的 n 倍,而在等效载频 上的谐波幅值降为多重化前载 波频率上谐波幅值的 1/n 。 PWM n 重化后,其谐波分布 只取 n 重化前谐波分布的 kn 次载频谐波,其余各次谐波均 降为零。
3. SPWM多重化(MSPWM)(续)
3.2.2 输出移相方式
调制频率、等效载频、等效载波比、及重数 n 均相同时, 与载波移相方式进行对照比较。
不易消除低次谐波。 当载波比 D 较小时,基波损失较大。 载波比 D 较大时,二者比较接近。
调制频率 fm=100Hz 等效载频 fec=4000Hz 等效载波比 De=40
1. 载波频率 fc=2000Hz 载波比 D=20 重数 n=2
1. 载波频率 fc=1000Hz
载波比 D=10 重数 n=4 2. 载波频率 fc=250Hz 载波比 D=2.5 重数 n=16
3. SPWM多重化(MSPWM)(续)
3.3 结论
载波比 D 较小时,载波移相方式明显优于输出移相方式。 载波比 D 较大时,二者比较接近。 载波移相方式:
3.1.2 输出移相方式
先产生一路 SPWM 波形 u1 n 重化时,使 u2,u3,…,un 依次滞后 1/n 个载波周期,与 u1 一 起构成一个 n 相对称系统。 多重化复合。 优缺点 控制电路结构简单, 可能易于实现。 不易消除低次谐波。 当载波比 D 较小时, 基波损失较大。
3. SPWM多重化(MSPWM)(续)
Uk ∝1 k,
谐波分析实验报告
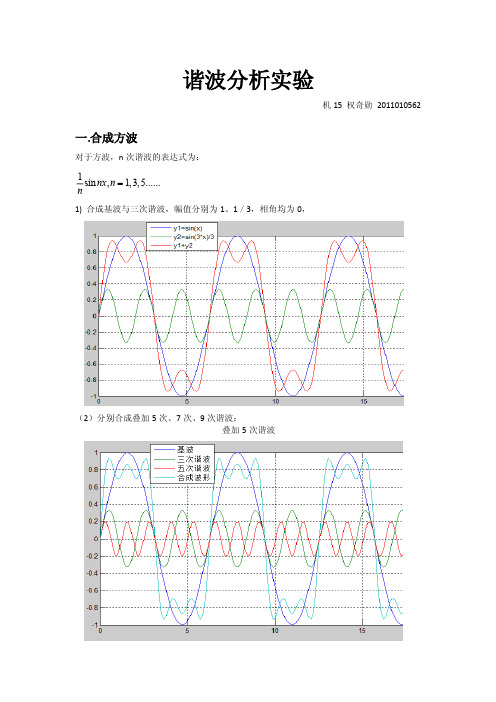
谐波分析实验机15 权奇勋2011010562一.合成方波对于方波,n次谐波的表达式为:1sin nx,n=1,3,5......n1) 合成基波与三次谐波,幅值分别为1、1/3,相角均为0,(2)分别合成叠加5次、7次、9次谐波:叠加5次谐波叠加7次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于方波。
(3)分别改变3、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响将3次谐波的初相角改为-π/2将5次谐波的初相角改为-π/2分析结论:改变谐波与基波间的相角,会使合成波形与方波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
(4)分别改变3、5次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响3次谐波幅值改为(1/3)×2=2/35次谐波幅值改为(1/5)×2=2/5分析结论:改变谐波的幅值,会使合成波形与方波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
二.合成锯齿波(最高谐波次数选为9)对于锯齿波,n次谐波的表达式为:π1nx+p),n=1,2,3......1)合成波的形状与谐波次数的关系叠加2次谐波叠加4次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于锯齿波。
(2)分别改变2、4次谐波与基波间的幅值比例关系2次谐波的幅值改为(1/2)×2=14次谐波的幅值改为(1/4×2)=1/2分析结论:改变谐波的幅值,会使合成波形与锯齿波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
(3)分别改变2、4次谐波与基波间的相角2次谐波的初相角改为pi+pi/2=3pi/24次谐波的初相角改为pi+pi/2=3pi/2分析结论:改变谐波与基波间的相角,会使合成波形与锯齿波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
三.合成三角波(最高谐波次数选为9)对于三角波,n次谐波的表达式为:π×π1nx,n=1,3,5......1)合成波的形状与谐波次数的关系叠加3次谐波叠加5次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于三角波。
谐波分析实验

b、将3次谐波的相角改为+π/2:
c、将5次谐波的相角改为-π/2:
d、将5次谐波的相角改为+π/2:
分析结论:改变谐波与基波的相角会使合成波形与理想状态相比有较大变形失真。
(4)改变3、5次谐波与基波幅值比例关系:
a、3次谐波幅值为1/18:
b、3次谐波幅值为2/9:
(3)锯齿波仅保留偶次谐波后输出波形图:
由波形图可见,此时输出的波的频率变为关闭奇次谐波之前的2倍,在本次实验中为4π。
分析结论:改变谐波与基波的相角会使合成波形与理想状态相比有较大变形失真。
(4)改变3、5次谐波与基波幅值比例关系:
a、3次谐波幅值为1/6:
b、3次谐波幅值为2/3:
c、5次谐波幅值为1/10:
d、5次谐波幅值为2/5:
分析结论:改变谐波的幅值会使合成波形产生失真。
可见与前述方波相比,锯齿波谐波幅值不变为1/n(反比例逐次减小),但包含有偶次谐波,且相角都为π。
方波:
锯齿波:
三角波:
三种波形的相频图(最高9次谐波):
方波:
锯齿波:
三角波:
二、问题讨论
(1)由“一、1、(3)(4)”的分析结论可见,相角对波形影响大。对于“一、1、”中的方波,改变相角会使整个波形产生较大变形失真,但改变幅值只会对波峰波谷处的波形有较大影响。
(2)用正弦波表合成“一、3、”中三角波时,由三角变换关系可知此种情况下相角相对“一、1、”中方波为π/2(见下图),即三种波都用正弦波叠加而成时,若方波相角为0,则锯齿波相角为π,三角波为π/2。
c、5次谐波幅值为1/50:
d、5次谐波幅值为2/25:
分析结论:改变谐波的幅值会使合成波形产生较小失真。
谐波实验报告

实验一 谐波分析实验一、实验目的1)了解分解、合成非正弦周期信号的物理过程2)观察合成某一确定的周期信号时,所必须保持的合理的频率结构,正确的幅值比例和初始相位关系。
二、实验原理本实验主要运用傅立叶分解的方式对方波、锯齿波以及三角波进行分解与合成。
下面就对这三种波形的傅立叶分解原理进行介绍。
傅立叶分解原理对某一个非正弦周期信号X(t)(在有限区间上满足狄里赫利条件的函数),若其周期为T 、频率为f ,则可以分解为无穷项谐波之和。
即010100122()(cos sin )22sin()2sin(2)2n n n n n n n n n a n n x t a t b t T T a n A t T a A f t πππφπφ∞=∞=∞==++ =++ =++∑∑∑ 上式表明,各次谐波的频率分别是基波频率0f 的整数倍。
只要选择符合要求的不同频率成分和相应幅值比例及相位关系的谐波,便可近似地合成相应的方波、三角波等非正弦周期波形,以及任何在有限区间上满足狄里赫利条件的函数。
三、实验内容(一)方波1)方波的谐波分析,右图的一个方波(),022()0,2()()E T x t t T x t t T x t nT x t ⎧=≤≤⎪⎪⎪= ≤≤ ⎨⎪+=⎪⎪⎩进行谐波分析可知:00n a a ==/20/22()sin (1cos )2,1,3,5...0,2,4,6...T n T b x t n tdt T En n En n n ωπππ-= =-⎧ =⎪ =⎨⎪ =⎩⎰ 所以 000211()(sin sin 3sin 5...)35Ex t t t t ωωωπ=+++ 根据实验要求取基波的幅值为1,即212E E ππ=⇒=为了方便,可以取01ω=即方波可以展开成傅立叶级数为:11()(sin sin 3sin 5...)35x t t t t =+++2)合成方波根据讲义的讲解,编写以下程序实现功能要求 a 、一次谐波、三次谐波合成 x=0:4*pi/100:4*pi; y1=sin(x); y2=sin(3*x)/3;plot(x,y1,x,y2,x,y1+y2); grid onb 、一次谐波、三次谐波、五次谐波合成 x=0:4*pi/100:4*pi;y1=sin(x);y2=sin(3*x)/3;y3=sin(5*x)/5;plot(x,y1,x,y2,x,y3,x,y1+y2+y3);grid on之后的谐波合成类似,省略程序,得到的合成方波分别如图所示一次谐波、三次谐波、五次谐波、七次谐波合成方波一次谐波、三次谐波、五次谐波、七次谐波、九次谐波合成方波总结:方波可以通过谐波的叠加得到,叠加的谐波级次越高,方波的失真越小。
谐波反应法的原理及应用

谐波反应法的原理及应用1. 原理概述谐波反应法是一种用于测量催化剂表面酸性或碱性中心浓度和强度的方法。
该方法基于反应物吸附在催化剂表面上并发生谐波反应的特性。
谐波反应是指当入射光频率与物体的共振频率相匹配时,物体会表现出非线性的光学效应。
催化剂表面的酸性或碱性中心会对入射光产生非线性的光学响应,从而可以测量酸性或碱性中心的浓度和强度。
2. 实验步骤使用谐波反应法进行酸性或碱性中心的测量通常需要以下步骤:1.准备样品:将待测催化剂样品制备成适当的形状和尺寸,并确保表面干净无杂质。
2.构建实验装置:将待测样品放置在光源和光探测器之间,确保光源能够提供足够的光强,并将光探测器与计算机或数据采集系统连接以记录测量结果。
3.设置光源频率:根据待测催化剂表面酸性或碱性中心的共振频率,选择适当的光源频率。
使用实验装置中的频率调节器调整光源频率。
4.测量谐波反应信号:通过光探测器测量样品表面反应产生的谐波反应信号,并记录下光强的变化。
5.分析数据:将测得的光强数据与光源频率之间的关系进行分析,通过拟合曲线等方法得到酸性或碱性中心的浓度和强度。
3. 应用领域谐波反应法在酸性或碱性中心的测量方面具有广泛的应用。
以下是一些应用领域的示例:3.1 催化剂开发谐波反应法可以用于催化剂开发过程中对酸性或碱性中心的测量。
通过测量不同催化剂样品的酸性或碱性中心浓度和强度,可以评估催化剂的催化活性和选择性,并优化催化剂的配方和制备方法。
3.2 催化反应机制研究谐波反应法可以用于研究催化反应的机理。
通过测定催化剂表面酸性或碱性中心在不同反应条件下的变化,可以揭示催化反应发生的方式和过程,为催化反应机理的研究提供重要的实验数据。
3.3 催化剂失活机制研究谐波反应法还可以应用于催化剂失活机制的研究。
通过测量催化剂使用一定时间后酸性或碱性中心的变化,可以揭示催化剂失活的原因,进而改进催化剂的稳定性和使用寿命。
3.4 其他领域的应用谐波反应法还可以在其他领域中得到应用,例如环境监测、生物医学研究等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 谐波分析实验 2011010541 机14 林志杭一、实验目的1. 了解分解、合成非正弦周期信号的物理过程。
2. 观察合成某一确定的周期信号时,所必须保持的合理的频率结构,正确的幅值比例和初始相位关系。
二、实验原理对某一个非正弦周期信号x(t),若其周期为T 、频率为f ,则可以分解为无穷项谐波之和。
即010012()sin()sin(2)n n n n n n nx t a A t Ta A nf t πϕπϕ∞=∞==++=++∑∑ 上式表明,各次谐波的频率分别是基波频率f 0的整数倍。
如果f(t)是一个锯齿波,其波形如图1所示,其数学表达式为:(), 02()()E Ex t t t TT x t nT x t =-≤≤+=-E/2E/2-T Ttx(t)图1对f(t)进行谐波分析可知00, , 2n n Ea A nφππ=== 所以101002()sin()2 sin(2)21 {sin(2)sin[2(2)]...}22n n E nx t t n TEnf t n E f t f t πππππππππππ∞=∞==+=+=++++∑∑即锯齿波可以分解成为基波的一次、二次•••n 次•••无数项谐波之和,其幅值分别为基波幅值的1n ,且各次谐波之间初始相角差为零(基波幅值为2E π)。
反过来,用上述这些谐波可以合成为一个锯齿波。
同理,只要选择符合要求的不同频率成份和相应的幅值比例及相位关系的谐波,便可近似地合成相应的方波、三角波等非正弦周期波形。
三、实验内容及操作步骤 1 合成方波周期方波信号x(t)在一个周期中的表达式为:1, 02() 1, 02T t x t T t ⎧--<<⎪⎪=⎨⎪<<⎪⎩波形如图2所示图2 方波波形傅立叶级数为:4, 1,3,5...0, b , 0(1,3,5...)0, 2,4,6...n n n n a n n n φπ⎧=⎪====⎨⎪=⎩展开成傅里叶级数表达式为:411()(sin sin 3sin 5...)35x t t t t π=+++ ①观察基波与三次谐波幅值分别为1、1/3,相位差为零时的合成波波形,如图3所示。
Matlab程序为x=0:4*pi/100:4*pi;>> y1=sin(x);>> y2=sin(3*x)/3;>> plot(x,y1,x,y2,x,y1+y2);>> grid on;图3基波、3次谐波及合成波形②再分别将5次、7次、9次…谐波叠加进去,观察并记录合成波的波形,找出合成波的形状与谐波次数之间有何关系1)将5次谐波叠加进去,如图4所示Matlab程序x=0:4*pi/100:4*pi;>> y1=sin(x);>> y2=sin(3*x)/3;>> y3=sin(5*x)/5;>> plot(x,y1,x,y2,x,y3,x,y1+y2+y3);>> grid on;图4基波、3次谐波、5次谐波及合成波形2)将7次谐波叠加进去,如图5所示程序类似图5基波、3次谐波、5次谐波、7次谐波及合成波形3)将9次谐波叠加进去,如图6所示图6 基波、3次谐波、5次谐波、7次谐波、9次谐波及合成波形总结:a随着叠加谐波次数的增加,合成的谐波的次数越多,合成的波形与方波越接近;方波失真越小,而方波的失真主要体现在波峰波谷处。
b合成波幅值接近于方波的幅值,且在方波幅值上下波动c方波与基波具有相同的零点③分别改变3次、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响,并记录波形。
1)3次谐波相角分别改变60度,90度,120度,180度,270度330度,改变60度的程序x=0:4*pi/100:4*pi;>> y1=sin(x);>> y2=sin(3*x-pi/3)/3;>> plot(x,y1,x,y2,x,y1+y2);>> grid on其余类似如图8所示图8 改变3次谐波相角2)5次谐波相角分别改变60度、90度,120度,180度270度330度,如图9所示图9 改变5次谐波相角分析:(1)改变谐波的相角,合成波形出现了失真,在0~180°失真逐渐加大,180°到达极致,之后又逐渐减少。
(2) 改变三次谐波的相角对合成波形的影响比改变五次谐波相角要大,依次推断,改变低次谐波的相角对合成波形的影响比改变高次谐波相角更大。
④分别改变3次、5次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响,并记录波形。
1)改变3次谐波幅值与基波幅值比分别为1:8、1:1,程序:x=0:4*pi/100:4*pi;y1=sin(x);y2=sin(x*3)/3;y3=sin(x*5)/5;y4=sin(x*3);y5=sin(x*3)/8;plot(x,y1+y2+y3,x,y1+y4+y3,x,y1+y5+y3);grid on如图10所示图10 改变3次谐波与基波间幅值比2)改变5次谐波幅值与基波幅值比分别为1:8、1:1,如图11所示图11 改变5次谐波与基波间幅值比分析:(1)改变谐波幅值,波形出现了失真,且幅值改变越大,对方比合成影响越大(2)不同级次的谐波幅值改变相同的比例,级次越低,方波失真越小2 合成锯齿波锯齿波信号x(t)在一个周期中的表达式为:波形如图13所示:图13 锯齿波波形展开成傅里叶级数表达式为:001()sin()sin(2)...22Ax t t t ωπωππ⎡⎤=-++++⎢⎥⎣⎦①观察基波与2次、3次谐波,幅值满足傅立叶级数表达式,相位差为零时的合成波波形,如图14所示程序:x=0:4*pi/100:4*pi;y1=-sin(x);y2=-sin(2*x)/2;y3=-sin(3*x)/3;plot(x,y1,x,y2,x,y3,x, y1+y2+y3);grid on;图14 基波、2次谐波、3次谐波及合成波形②分别将4次、5次、6次…9次谐波叠加进去,观察并记录合成波的波形,找出合成波的形状与谐波次数之间有何关系),如图15所示图15 各次谐波及合成波形分析:(1)谐波次数越高,合成波的形状越来越接近锯齿波波形,失真越小(2)方波与基波具有相同的零点。
③分别改变3次、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响,并记录波形。
1)3次谐波相角分别改变90度、180度,如图16所示图16 改变3次谐波相角改变2)5次谐波相角分别改变90度、180度,如图17所示图17 5次谐波相角改变结论:(1)对于同一次谐波,180度内,相位改变越大,对合成波影响越大(2)改变三次谐波的相角对合成波形的影响比改变五次谐波相角要大,依次推断,改变低次谐波的相角比改变高次谐波相角对合成波形的影响更大。
④分别改变3次、5次、7次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响,并记录波形1) 改变3次谐波幅值与基波幅值比分别为1:8、1:1,如图18所示图18 3次谐波幅值改变2)改变5次谐波幅值与基波幅值比分别为1:8、1:1,如图19所示图19 5次谐波幅值改变3)改变7次谐波幅值与基波幅值比分别为1:8、1:1,如图20所示图20 7次谐波幅值改变分析:(1)改变谐波幅值,波形出现了失真,且幅值改变越大,合成波形偏离方波越严重(2)越高次谐波幅值增大对于波形失真的影响越严重,低次谐波幅值减小对于合成波形影响较大,而高次谐波幅值减小对波形影响较小3.2.5锯齿波与方波的比较:对于方波和锯齿波,用傅立叶分析的方法合成波形都能很好的近似,锯齿波的傅里叶展开有n次项,即n次谐波,而方波只有奇次项,在近似时,同样的次数叠加,锯齿波的波形更为相近;改变相角和幅值对于合成波形的影响基本一致。
3.3 合成三角波三角波信号x(t)在一个周期中的表达式为:(1)波形如图21所示:图21 三角波波形展开成傅里叶级数表达式为:①观察基波与三次谐波幅值分别为1、1/9,相位差为零时的合成波波形,程序x=0:4*pi/100:4*pi;>> y1=cos(x);>> y2=cos(3*x)/9;>> plot(x,y1,x,y2,x,y1+y2);grid on;如图22所示图22 基波、三次谐波和合成波形3.3.2分别将5次、7次、9次谐波叠加进去,观察并记录合成波的波形,找出合成波的形状与谐波次数之间有何关系),如图23所示图23 五次、七次、九次谐波及合成波形分析:(1)随着谐波次数的增加,合成波的形状越来越接近三角波波形,由于三角波形状与三角函数相似,所以按傅立叶级数合成后波形非常接近三角波(2)基波与方波具有相同的零点。
(3)各次谐波的幅度都不会超过三角波的幅度3.3.3分别改变3次、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响,并记录波形。
1)3次谐波相角分别改变90度、180度,如图24所示图24 改变3次谐波相角2)5次谐波相角分别改变90度、180度,如图25所示图25 改变5次谐波相角2)9次谐波相角分别改变90度、180度,如图25所示图25 改变9次谐波相角分析:(1)改变谐波的相角,合成波形出现了失真(2)改变3次谐波的相角对合成波形的影响较大,而改变9次谐波相角对波形影响甚小,依次推断,低次谐波的相角改变对合成波形的影响比改变高次谐波相角更大。
3.3.4分别改变3次、5次、9次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响,并记录波形。
1)改变3次谐波幅值与基波幅值比分别为1:36、1:1,如图26所示图26 改变三次谐波幅值2)改变5次谐波幅值与基波幅值比分别为1:100、4:25,如图27所示图27 改变5次谐波幅值3)改变9次谐波幅值与基波幅值比分别为1:324、1:9,如图18所示图28 改变9次谐波幅值分析:(1)改变谐波幅值,波形出现了失真,且幅值改变越大,合成波形偏离越严重(2 低次谐波幅值改变比同比例改变高次谐波幅值对于合成波形影响大得多,除基波外增大谐波幅值比减少谐波幅值对合成波形影响大。
3.3.5 三角波与方波、锯齿波的比较:由分析可知,用傅立叶分析方法对于三种波形都有很好的近似,谐波级数越高,合成波形越接近真实波形;对于三种波形,改变谐波与基波间相位和幅值对于合成波的波形、幅值的影响大致相同;三角波与方波相同,只具有奇数次谐波,但三角波初始相位与方波相差2 ;与方波、锯齿波不同,三角波各次谐波幅值为基波幅值的21n,所以高次谐波对与三角波的影响最小;三角波在较低级次谐波叠加下波形就能很好的近似,这是因为三角波波形和余弦函数相似,而方波和锯齿波只有在高级次谐波叠加下波形才近似相同。
