《建筑力学》第5章计算题教程文件
建筑力学(5章)

M eB 0.95kN m
M eC 1.27kN m
M eD 1.59kN m
第5章 扭转杆的强度计算
(2)计算扭矩 1 1 2 2
截面1-1:
Mx 0
T2 WP2 14 106 MPa 71.3MPa π 1003 16
比较上述结果,该轴最大切应力位于BC段内任一截面的 边缘各点处,即该轴最大切应力为τmax=71.3MPa。
第5章 扭转杆的强度计算
圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力 圆轴的扭转试件可分别用Q235钢、铸铁等材料做成, 扭转破坏试验是在扭转试验机上进行。试件在两端外力偶
T1 M eB 0
T1 M eB 0.95kN m
截面2-2:
Mx 0
T1
T2 M eB M eA 0
T2 M eA M eB 2.87kN m
T2
第5章 扭转杆的强度计算
3
截面3-3:
Mx 0
T3 M eD 0
3
T3 M eD 1.59kN m
式中:[σC]为材料的许用挤压应力,可查有关设计手册。
注意:若两个相互挤压构件的材料不同,应对挤压强度 小的构件进行计算。
第5章 扭转杆的强度计算
挤压强度条件在工程中同样可以解决三类问题。 但工程中构件产生单纯挤压变形的情况较少,挤压强
度的计算问题往往是和剪切强度计算同时进行。
第5章 扭转杆的强度计算
第5章 扭转杆的强度计算
当挤压面为平面时,挤压计算面积与挤压面面积相等。
最新完美版建筑力学第五章杆件的内力

目录
第五章 杆件的内力\杆件拉(压)时的内力
解 (1)求支座反 A 力。由杆AD的平衡 x 方程∑Fx=0,可求得 支座反力FD=18 kN。 (2)求横截面1-1、2-2、3-3上的轴力。由于在横截 面B和C上作用有外力,须将杆分为AB、BC、CD三段。
应用截面法,假想地沿1 -1横截面把杆截开,取受力 较简单的右段为研究对象(如图),列出平衡方程 ∑Fx=0,F1-FN1=0 得 FN1= F1 =20 kN
目录
第五章 杆件的内力\杆件拉(压)时的内力
若取右段为研究对象,同样可求得轴力F = FN (如 图),但其方向与用左段求出的轴力方向相反。
为了使两种算法得到的同一截面上的轴力不仅数值相 等,符号相同,规定轴力的正负号如下:当轴力的方向与 横截面的外法线方向一致时,杆件受拉伸长,轴力为正; 反之,杆件受压缩短,轴力为负。 在计算轴力时,通常未知轴力按正向假设。若计算结 果为正,则表示轴力的实际指向与所设指向相同,轴力为 拉力;若计算结果为负,则表示轴力的实际指向与所设指 向相反,轴力为压力。
目录
第五章 杆件的内力\杆件拉(压)时的内力
同理,取2-2横 截面的右段为研究对 象,列出平衡方程
x
得
∑Fx=0,F1+ F2 -FN2=0 FN2= F1-F2=8 kN ∑Fx=0,FN3+ FD =0 FN3= -FD= - 18 kN
取3-3横截面的左段为研究对象,列出平衡方程 得
式中,FN3为负值,说明FN3的指向与假设的方向相反,即 FN3为压力。
5-2-1 外力偶矩的计算
工程中作用于传动轴上的外力偶矩往往不是直接给 出的,而是给出轴所传递的功率和轴的转速。它们之间的 换算关系为 {Me}N· m=9549
《建筑力学》第5章计算题课件
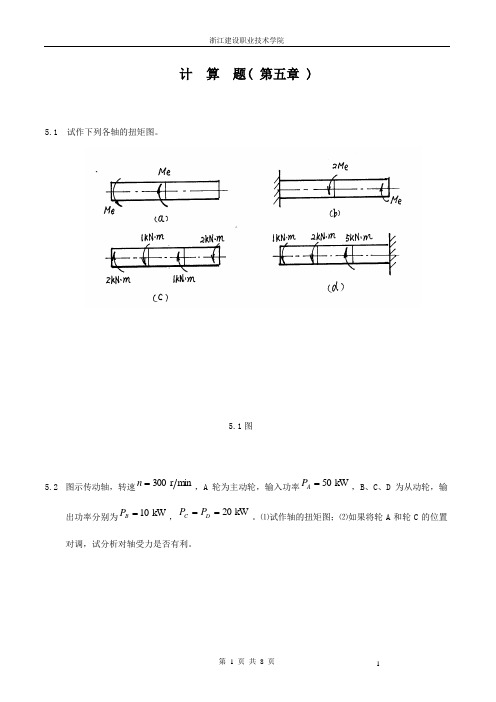
计 算 题( 第五章 )5.1 试作下列各轴的扭矩图。
5.1图5.2 图示传动轴,转速min r 300=n ,A 轮为主动轮,输入功率kW 50=A P ,B 、C 、D 为从动轮,输出功率分别为kW 10=B P ,kW 20==D CP P 。
⑴试作轴的扭矩图;⑵如果将轮A 和轮C 的位置对调,试分析对轴受力是否有利。
题5.2图 题5.3图5.3 T 为圆轴横截面上的扭矩,试画出截面上与T 对应的切应力分布图。
5.4 图示圆截面空心轴,外径mm 40=D ,内径mm 20=d ,扭矩m kN 1⋅=T ,试计算mm 15=ρ的A 点处的扭转切应力A τ以及横截面上的最大和最小的扭转切应力。
题5.4图5.5 一直径为mm 90的圆截面轴,其转速为min r 45,设横截面上的最大切应力为MPa 50,试求所传递的功率。
5.6 将直径mm 2=d ,长m 4=l 的钢丝一端嵌紧,另一端扭转一整圈,已知切变模量GPa 80=G ,求此时钢丝内的最大切应力max τ。
5.7 某钢轴直径mm 80=d ,扭矩m kN 4.2⋅=T ,材料的许用切应力[]MPa 45=τ,单位长度许用扭转角[]m )(5.0 =θ,切变模量GPa 80=G ,试校核此轴的强度和刚度。
5.8 阶梯形圆轴直径分别为d1=40mm ,d2=70mm ,轴上装有三个皮带轮,如图所示。
已知由轮3输入的功率为N3=3kW ,轮1输出的功率为N1=13kW ,轴作匀速转动,转速n=200r/min ,材料的许用切应力[]MPa 60=τ,GPa 80=G ,许用扭转角[]m 2=θ=。
试校核轴的强度和刚度。
题5.8图5.9 一钢轴受扭矩m kN 2.1⋅=T ,许用切应力[]MPa 50=τ,许用扭转角[]m 5.0 =θ,切变模量GPa 80=G ,试选择轴的直径。
5.10 桥式起重机题 5.10图所示。
若传动轴传递的力偶矩m kN M e ⋅=08.1,材料的许用切应力[]MPa 40=τ,GPa 80=G ,同时规定=][θ0.5°/m 。
建筑力学课件:第5章重心和形心

重心和形心
1
第5章 重心和形心
§5-1 重心和形心的坐标公式
§5-2 确定重心和形心位置的 具体方法
力学教程电子教案
重心和形心
2
地球表面或表面附近的物体都会受到地心引力。
任一物体事实上都可看成由无数个微元体组成,这些
微元体的体积小至可看成是质点。任一微元体所受重
力(即地球的吸引力)ΔPi ,其作用点的坐标xi、yi、
x A
的读数为1500 N。试算出机床
重心的坐标。
力学教程电子教案
重心和形心
20
作业 5-4
边长为a的均质等厚正方形板 ABCD,被截去等 腰三角形AEB。试求点E的极限位置 ymax以保证剩余 部分AEBCD的重心仍在该部分范围内。yDa来自CaE A
ymax
B
x
力学教程电子教案
重心和形心
21
作业 5-4
1. 重心坐标的一般公式
z
右图认为是一个空间力系,则
C1
C Ci
P=∑ΔPi
ΔP1
P ΔPi
合力的作用线通过物体的重
心,由合力矩定理
x
o
z1 zC zi
y1 yyiC x1 xC
xi
y
My (P) My (Δ Pi )
P xC Δ Pi xi
xC
Δ Pi xi P
同理有
yC
Δ Pi yi P
xi
y
力学教程电子教案
重心和形心
4
重心位置的确定在实际中有许多的应用。例如,
电机、汽车、船舶、飞机以及许多旋转机械的设计、
制造、试验和使用时,都常需要计算或测定其重心
《建筑力学(上下册)》电子教案 第五章

1. 均匀连续性假设
假设物体在整个体积内都毫无空隙地充满着物质,是密实、连续的, 且任何部分都具有相同的力学性质。
有了这一假设,就可以从被研究物体中取出任一部分来进行研究,它 具有与材料整体相同的性质。还因为假定了材料是密实、连续的,材 料内部在变形前和变形后都不存在任何空隙,也不允许产生重叠,故 在材料发生破坏之前,其变形必须满足几何协调(相容)条件。
若上述理想的变形体的变形局限在弹性范围内,称其为理想弹性体。
上一页 返回
5.3 变形固体的几何分类
按照几何特征,变形固体构件可分为杆、板、壳和实体四大类。 杆的几何特征为长条形,长度尺寸远大于其他两个方向的尺寸(横截
面两个方向的尺寸)。杆横截面中心的连线称为轴线,轴线为直线的 杆称为直杆;轴线为曲线的杆称为曲杆。所有横截面的形状、大小均 相同者称为等截面杆。 板壳的厚度尺寸远小于其他两个方向的尺寸(长度和宽度),板的几 何特征为平面形,壳的几何特征为曲面形。 实体的几何特征为块体,其长、宽、高三个方向的尺寸大体相近,内 部大多为实体。 在本课程中,取等截面弹性直杆为主要研究对象。
下一页 返回
5.1变形固体的概念及变形固体静力学研 究的内容
5.1.2 变形固体静力学研究的内容
变形固体静力学研究的内容为,用变形固体制造成的结构构件或机械 零件(弹性杆件)的静力学响应——内力、应力、变形、变形能;以 及变形固体材料的宏观力学行为——变形、失效等。
上一页 返回
5.2 变形固体的基本假设
下一页 返回
5.4 变形固体的外力、内力及应力的概 念
要研究内力,要确定是变形体内部那部分对相邻部分的内力,最好的 办法是用一个面将这两部分分开,留下一部分研究,将内力暴露出来, 这种方法叫截面法。假想用一截面将如图5-1所示四个力作用下处于 平衡状态的变形固体体从指定截面出截开,分成两部分,若制造变形 固体的材料是均匀连续的,则在截开处的截面上,存在一分布内力系 (若制造变形固体的材料不是均匀连续的,如钢筋混凝土构件,则在 截开处的截面上,仍然存在一内力系,但此内力系就有可能不是分布 内力系)。这一分布内力系可看成上半部分施加给下半部分截面的力。
建筑力学教材课件第五章 静定结构的内力分析

1kW = 1000N· m/s = 1.36PS(马力)
二、扭转内力—扭矩T 以图示圆轴扭转的力学模型为例,用截面法,以m-m截面将轴截分为两段。 取其左段列力偶平衡方程可得 m Me Me Mx(F)=0: T-Me=0 T=Me A B m T为截面的内力偶矩,称为扭 Me T 矩。同理,也可取右段求出截面 A 扭矩。 Mx(F)=0: Me-T' =0 T'=Me 图d为截面扭矩的正负规定。 Me T
解:1、计算各段的轴力。 Fx 0 AB段
FN 1 F1 0 FN 1 10KN
BC段
F
x
0
FN 2 F2 F1 0 FN 2 10KN
CD段
F
x
0
FN3
F4 FN 3 0 FN 3 25kN
F4
2、绘制轴力图。
FN kN
产生轴向拉伸或压缩的杆件称为轴向拉杆或压杆。
轴向拉压的受力特点:外力的作用线与杆的轴线重合。
轴向拉压的变形特点:沿轴线方向伸长或缩短。
力学模型如图
F
轴向拉伸,对应的力称为拉力。
F
F
轴向压缩,对应的力称为压力。
F
如图所示屋架中的弦杆、牵引桥的拉索和桥塔等均为拉 压杆。
工程实例一
轴向压缩构件
工程实例二
1. 轴向拉伸和压缩
2. 剪切 3. 扭转 4. 弯曲
1. 轴向拉伸和压缩
如果在直杆的两端各受到一个外力F的作用, 且二者的大小相等、方向相反、作用线与杆件的轴 线重合,那么杆的变形主要是沿轴线方向的伸长或
缩短,这种变形称为轴向拉伸或压缩。
2. 剪切
如果直杆上受到一对大小相等、方向相反、作
建筑力学 第五章(最终)

dA 2 y dz 2 R2 Z 2dz
于是求得
Sy
z dA
A
R
z
O
2
R2 z2 dz 2 R3 3
2R3
zc
Sy A
3 πR2
4R 3π
2
图5-6
5. 2. 3 组合图形的面积矩计算
当图形是由若干个简单图形(如矩形、圆形和三角形等)组合而成时, 这类图形称为组合图形。由于简单图形的面积及其形心位置均为已知,而且 由面积矩的定义可知,组合图形对某一轴的面积矩等于其各简单图形对该轴 面积矩的代数和,即
5.1.2 物体重心的坐标公式
1. 重心坐标的一般公式
设有一物体,如图5-1所示。重心 c 坐 标为(xc,yc,zc),物体的容重为 γ,总体积 为V。将物体分割成许多微小体积 ΔVi,每 个微小体积所受的重力 PGi Vi , 其作 用点坐标(xi,yi,zi)。整个物体所受的重力
为 PG PGi 。
n
xc
A1x1c A2x2c An xnc A1 A2 An
Ai xic
i 1 n
Ai
i 1
n
yc
A1 y1c A2 y2c An ync A1 A2 An
Ai yic
i 1 n
Ai
i 1
(5-6)
【例5-1】试求图5-2 所示 Z 形平面图形的形心。
解:将Z 形图形视为由三个矩形图形组合而成,以 c1 、c2 、c3 分别表示 这些矩形的形心。取坐标系如图5-2 所示,各矩形的面积和形心坐标为
5. 2. 2 面积矩与形心的关系
由平面图形的形心坐标公式 (5-4) 和面积矩的定义可得
yc
A
建筑力学第五章

从静力学方面探讨:
一、几何可变体系 对于几何可变体系,在任意荷载作用下一般不能
维持平衡而发生运动,因此无静力学解答。
11kN
A
B
二、几何不变体系 A、有多余约束的几何不变体系
q
X1
X2
X3
X4
结论: 有多余约束的几何不变体系 ——超静定结构的几何组成特征。
几何不变体系: 不考虑材料应变条件下,体系受到任意荷载作用 其位置、几何形状保持不变。
二、 瞬变体系
瞬变体系:某一瞬时可以产生微小运动,然后就不能继续运 动的体系。
瞬变体系
5.2 平面体系的自由度、联系的概念
一、自由度 自由度: 确定体系空间位置所需的独立坐标数,
或体系运动时可以独立改变的几何参数的数目。
A
B
(a)
附属部分
基本部分
(b)
附属部分
基本部分
(c)
例题:分析体系的几何组成
加二元体 减二元体
(a)
(b)
(c)
例题:分析体系的几何组成
EF
C
D
C
C
D
A
B
A
BA
B
EF
C
D
A
B
例题:分析体系的几何组成
C
B
D
I
II
A
III
利用规则进行几何组成分析的注意事项:
(1)体系只用三根不全交于一点也不全平行的支座链杆与基础 相连,只需对体系本身作几何组成分析。
其中:m---刚片数; h ---单铰数; r ---支座链杆数 如遇复铰:相当于(n-1)个单铰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题( 第五章 ) 5.1 试作下列各轴的扭矩图。
5.1图
5.2图示传动轴,转速
m in
r
300
=
n,A轮为主动轮,输入功率kW
50
=
A
P,B、C、D为从动轮,输
出功率分别为
kW
10
=
B
P,kW
20
=
=
D
C
P
P。
⑴试作轴的扭矩图;⑵如果将轮A和轮C的位置
对调,试分析对轴受力是否有利。
题5.2图 题5.3图
5.3 T 为圆轴横截面上的扭矩,试画出截面上与T 对应的切应力分布图。
5.4 图示圆截面空心轴,外径mm 40=D ,内径mm 20=d ,扭矩m kN 1⋅=T ,
试计算mm 15=ρ的A 点处的扭转切应力A τ以
及横截面上的最大和最小的扭转切应力。
题5.4图
5.5 一直径为mm 90的圆截面轴,其转速为m in r 45,设横截面上的最大切应力为MPa 50,试求所传递的功率。
5.6 将直径mm 2=d ,长m 4=l 的钢丝一端嵌紧,另一端扭转一整圈,已知切变模量GPa 80=G ,求此时钢丝内的最大切应力
m ax τ。
5.7 某钢轴直径mm 80=d ,扭矩m kN 4.2⋅=T ,材料的许用切应力[]MPa 45=τ,单位长度许用扭
转角[]m )(5.0 =θ,切变模量GPa 80=G ,试校核此轴的强度和刚度。
5.8 阶梯形圆轴直径分别为d1=40mm ,d2=70mm ,轴上装有三个皮带轮,如图所示。
已知由轮3输入的功率为N3=3kW ,轮1输出的功率为N1=13kW ,轴作匀速转动,转速n=200r/min ,材料的许用切应力[]MPa 60=τ,GPa 80=G ,许用扭转角[]m 2
=θ=。
试校核轴的强度和刚度。
题5.8图
5.9 一钢轴受扭矩m kN 2.1⋅=T ,许用切应力[]MPa 50=τ,许用扭转角[]5
.0 =θ,切变模量
GPa 80=G ,试选择轴的直径。
5.10 桥式起重机题 5.10图所示。
若传动轴传递的力偶矩
m kN M e ⋅=08.1,材料的许用切应力
[]MPa 40=τ,GPa 80=G ,同时规定
=][θ0.5°/m 。
试设计轴的直径。
题5.10图
5.11 某空心钢轴,内外径之比8.0=α,转速m in r 250=n ,传递功率kW 60=N ,已知许用切应力[]MPa 40=τ,许用扭转角[]m )
(8.0 =θ,切变模量GPa 80=G ,试设计钢轴的内径和外径。
5.12 某传动轴,横截面上的最大扭矩m kN 5.1⋅=T ,许用切应力[]MPa 50=τ,试按下列两种方案确定截面直径:⑴横截面为实心圆截面;⑵横截面为9.0=α的空心圆截面。
5.13 横截面面积相等的实心轴和空心轴,两轴材料相同,受同样的扭矩T 作用,已知实心轴直径m m 301=d ,空心轴内外径之比值8.0==D d α。
试求二者最大切应力之比及单位长度扭转角之比。
5.14 钢质实心轴和铝质空心轴(内外径比值
6.0=α)的横截面面积相等,钢轴许用应力[]MPa 801=τ,铝轴许用应力[]MPa 502=τ,若仅从强度条件考虑,哪一根轴能承受较大的扭矩?
5.15 实心轴和空心轴通过牙嵌式离合器连接在一起,已知轴的转速m in r 100=n ,传递功率kW 5.7=N ,材料的许用切应力[]MPa 40=τ,试选择实心轴直径1d 和内外径比值5.0=α的空心轴外径2D 。
题5.15图
5.16 已知传动轴的功率分别为kW 300=A N ,kW 200=B N ,kW 500=C N ,若AB 段和BC 段轴的
最大切应力相同,试求此两段轴的直径之比及两段轴的扭转角之比。
题5.16图
5.17 已知轴的许用切应力[]MPa 21=τ,切变模量GPa 80=G ,许用单位扭转角[]m )(3.0 =θ,试
问此轴的直径d 达到多大时,轴的直径应由强度条件决定,而刚度条件总可满足。
5.18 长度、材料、外力偶矩相同的两根圆轴,一根是实心轴,直径为1d ,另一根为空心轴,内外径之比8.022==D d α,试求两轴具有相等强度时的重量比和刚度比。
5.19 图示圆轴承受集度为m 的均匀分布的扭力矩作用,已知轴的抗扭刚度
p GI 和长度l ,试求B 截面的
扭转角B ϕ。
题5.18图 题5.19图
5.20 传动轴外径mm 50=D ,长度mm 510=l ,1l 段内径m m 251=d ,2l 段内径m m 382=d ,欲使轴两段扭转角相等,则2l 应是多长。
5.21图5.21所示一圆轴,直径D=110mm ,力偶矩Me=14kN.m ,材料的许用切应力MPa 70][=τ,试校核轴的强度。
(安全)
题5.21图
部分参考答案
5.1~5.3略
5.4 MPa A 7.63=τ,MPa 9.84max =τ,MPa 4.42min =τ
5.5 kW P 7.33=
5.6 MPa 126max =τ
5.7 MPa 9.23max =τ,m /)(43.0 =θ
5.8 ][4.48max ττ<=MPa AC ,][9.20max ττ<=MPa DB ,
][/74.10max θθ
<=m ,安全 5.9 mm d 7.64=
5.10 mm D 63=
5.11 mm D 79=,mm d 63=
5.12 mm d 541=,mm D 762=,mm d 7.682=
5.13 实心轴与空心轴最大切应力之比为2.733, 实心轴与空心轴单位长度转角之比为4.56,
5.14 0
6.1T /=钢铝T
5.15 45m m d 1≥,46m m D 2≥
5.16 18
6.1d /d 21=,2121/843.0/ =ϕϕ
5.17 100mm d ≥
5.18 重量比为0.51或1.96,刚度之比为1.18或0.85 5.19 P
B GI M 22
=ϕ 5.20 mm 2122=。
