五年级上册组合图形面积计算练习
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
小学五年级组合图形面积练习题
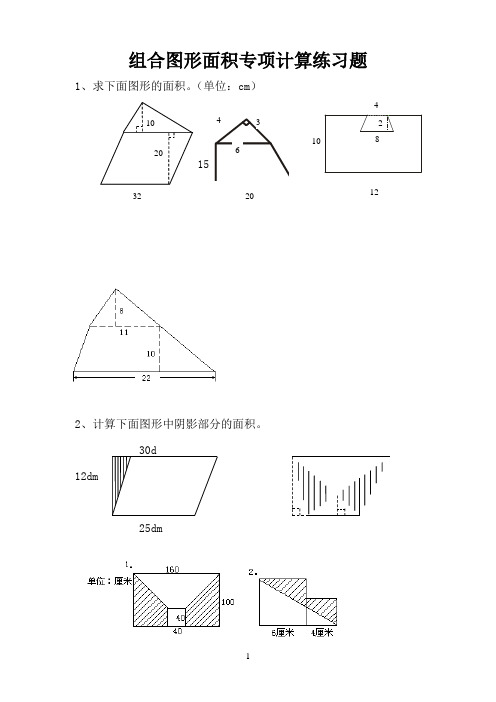
组合图形面积专项计算练习题1、求下面图形的面积。
(单位:cm )2、计算下面图形中阴影部分的面积。
30d12dm25dm3、求下列阴影部分的面积。
②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)16cm12cm 8dm8dm5、“实践操作”显身手:6、如右图所示,平行四边形的面积是48平方厘米,求阴影部分的面积。
7、如右图所示,梯形中阴影部分的面积是150平方厘米,求梯形的面积16cm2、求下面图形的面积。
25组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法,可将复杂问题变得简单。
一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积。
(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图长方形ABCD的面积(单位:厘米)。
四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
小学五年级组合图形面积练习题
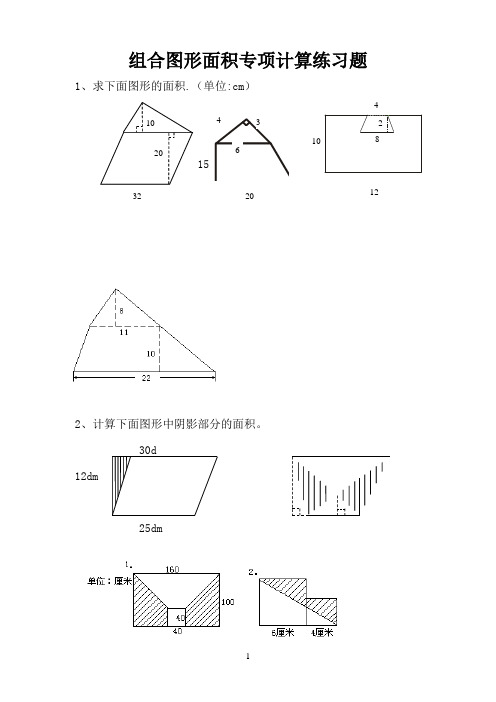
组合图形面积专项计算练习题1、求下面图形的面积.(单位:cm )152、计算下面图形中阴影部分的面积。
30d12dm25dm2010643482 1032 20123、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴.③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)13cm16cm12cm 7cm8dm8dm3dm5、“实践操作"显身手:6、如右图所示,平行四边形的面积是48平方厘米,求阴影部分的面积。
7、如右图所示,梯形中阴影部分的面积是150平方厘米,求梯形的面积16cm2、求下面图形的面积。
25组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合.由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法,可将复杂问题变得简单。
一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积.(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积.3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍.求中间长方形的面积。
1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积.2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图长方形ABCD的面积(单位:厘米).四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
最新苏教版五年级数学上册组合图形的面积专项练习

组合图形的面积专项练习[基础巩固]1.平行四边形的面积公式是(),用字母表示为()。
2.三角形的面积公式是(),用字母表示为()。
3.梯形的面积公式是(),用字母表示为()。
[学以致用]一、选一选。
1.两个()的三角形一定能拼成一个平行四边形。
A.底相等B.面积相等C.等底等高D.完全相同2.一个三角形的高扩大到原来的2倍,底扩大到原来的4倍,面积扩大到原来的( )倍。
A.2B.4C.6D.83.将一些练习本擦成一个长方体,再将它均匀地斜放,如图,这时从正面看到的图形是一个近似的平行四边形,比较两图从正面看到的图形,( )。
A.周长相等,面积不等B.周长不等,面积相等C.周长、面积都相等D.周长、面积都不相等4.李大爷用同样长的篱笆靠墙围了两个养鸡场,这两个养鸡场的面积相比( )。
A.①号大B.②号大C.同样大D.无法确定二、填一填。
1.在括号里填合适的单位。
(1)无锡太湖广场的面积约是67( )。
(2)地球面积约5.1亿()。
(3)港珠澳大桥沉管隧道长度约为5664( )。
(4)中央大厅的面积约3600( )。
2.39公顷=( )平方米 4800公顷=( )平方千米540000平方米=( )公顷 36平方千米=( )平方米3.一个三角形底是16厘米,面积是40平方厘米,这条底边上的高是( )厘米。
4.在一个底是8厘米,高是4厘米的平行四边形中画一个最大的三角形,这个三角形的面积是( )平方厘米。
5.一个平行四边形与一个三角形等底等高,三角形的面积是32平方厘米,平行四边形的面积是( )平方厘米。
6.一个三角形和一个平行四边形的高和面积均相等,如果平行四边形的底是8米,那么三角形的底是( )米;如果三角形的底是4米,那么平行四边形的底是( )米。
7.一个梯形和一个三角形的高相等,面积也相等。
已知梯形的上、下底分别是5分米和7分米,这个三角形的底是( )分米。
8.一个直角梯形的周长是64分米,它的两条腰分别长13分米、15分米,这个直角梯形的面积是( )平方分米。
(完整版)五年级上册数学组合图形面积练习题

五上数学组合图形拓展练习题姓名学号1,已知正方形ABCD的边长是7 厘米,求正方形EFGH的面积。
2、小两个正方形组成下图所示的组合图形厘米,求阴影部分的面积。
3、如图,已知四条线段的长分别是:AB=2厘米,厘米,并且有两个直角。
求四边形ABCD 的面积。
CE=6厘米,CD=5厘米,AF=47、如图:正方形ABCD的边长为 6 厘米,三角形ABE,三角形ADF与四边形AECF的面积彼此相等。
求三角形AEF的面积8、cm)4102012 9、计算下面图形中阴影部分的面积。
12dm10、求下列阴影部分的面积16cm ②已知S 平=48dm2,求S阴。
8dm③已知:阴影部分的面积为24 平方厘米,求梯形的面积7cm 12cm 8dm4dm11、求下面各图形的面积单位:分米)12、“实践操作”显身手:10分1、求下面图形中阴影部分的面积。
13、已知右面的两个正方形边长分别为 6 分米和4 分米,求图中阴影部分的面积。
④求S 阴14、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
单位:厘米)15、如图,这个长方形的长是9厘米,宽是8厘米,A 和B是宽的中点,求长方形内阴影部分的面积。
24 米,宽16 米,中间有一条宽为2 米17、右图是一块长方形公园绿地,绿地长的道路,求草地(阴影部分)的面积。
18、如图,三角形ABC 的面积是24 平方厘米,且BC 的中点,那么阴影部分的面积是多少?如图,三角形 ABC 的面积是 90 平方厘米, EF 平行于 BC ,AB=3AE ,那么九 如图, ABCD 是一个长 12 厘米, 宽 5 厘米的长方形, 阴影部分三角形 ACE 的面积。
十 已知正方形甲的边长是 8 厘米,正方形乙的面积是36 平方厘米,那么图中阴影部分的面积是多少? 三角形甲、乙、丙的面积各是多少平方厘米?20、 如图长方形,长 18厘米,宽 12厘米, AE 、AF 两条线段把长方形面积三等 分,求三角形 AEF 的面积。
五年级数学上册期末常考应用解答题:组合图形面积

五上常考题:组合图形面积1.计算下边图形的面积。
(单位:厘米)解:10×3+(10+15)×(10-3)÷2=30+25×7÷2=30+87.5=117.5(平方厘米)答:这个图形的面积是117.5平方厘米。
2.求出下面方格中图形的面积。
(小方格的边长为1cm。
)解:如图所示:把这个图形分成了两个三角形和一个梯形,它的面积是:7×2÷2+5×1÷2+(5+7)×5÷2=7×2÷2+5×1÷2+12×5÷2=14÷2+5÷2+60÷2=7+2.5+30=9.5+30=39.5(cm²)3.一张长方形纸如图折叠,求阴影面积。
解:8-3=5(厘米)5×10÷2=50÷2=25(平方厘米)10×8-25×2=80-50=30(平方厘米)4.下图是两个正方形,求阴影部分的面积。
解:6×6+4×4=36+16=52(平方厘米)6×6÷2=36÷2=18(平方厘米)4+6=10(厘米)10×4÷2=40÷2=20(平方厘米)52-18-20=34-20=14(平方厘米)5.如图,将这个图形贴满彩纸,买这些彩纸一共用去25.92元钱,这种彩纸的价格是每平方米多少元?解:2.4×1.5+2.4×1.5÷2=3.6+3.6÷2=3.6+1.8=5.4(平方米)25.92÷5.4=4.8(元)答:这种彩纸的价格是每平方米4.8元。
6.选择合适条件计算下面每个图形的面积。
(1)(2)(3)(1)解:15×8=120(平方米)(2)解:(4+7)×8÷2=11×8÷2=88÷2=44(平方分米)(3)解:12×16+20×9÷2=192+180÷2=192+90=282(平方厘米)7.计算下面图形的面积。
五年级组合图形面积练习题
组合图形面积专项计算练习题1、求下面图形的面积.(单位:cm)152、计算下面图形中阴影部分的面积.30d12dm25dm3、求下列阴影部分的面积.201064 34821032 20 12①②已知S平=48dm2.求S阴.③已知:阴影部分的面积为24 ④求S阴.平方厘米.求梯形的面积.4、求下面各图形的面积.(单位:分米)13cm16cm12cm7cm 8dm8dm3dm5、“实践操作”显身手:6、如右图所示.平行四边形的面积是48平方厘米.求阴影部分的面积.7、如右图所示.梯形中阴影部分的面积是150平方厘米.求梯形的面积16cm12cm14cm 24m10m8m1、求下面图形中阴影部分的面积.2、求下面图形的面积.5625组合图形是由两个或两个以上的简单的几何图形组合而成的.组合的形式分为两种:一是拼合组合.二是重叠组合.由于组合图形具有条件相等的特点.往往使得问题的解决无从下手.要正确解答组合图形的面积.应该注意以下几点:1.切实掌握有关简单图形的概念、公式.牢固建立空间观念;2.仔细观察.认真思考.看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法.可将复杂问题变得简单.一个等腰直角三角形.最长的边是12厘米.这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积.(单位:厘米)2.已知正方形ABCD的边长是7厘米.求正方形EFGH的面积.3.有一个梯形.它的上底是5厘米.下底7厘米.如果只把上底增加3厘米.那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形.正方形的边长是12厘米.长方形的四个角的顶点把正方形的四条边各分成两段.其中长的一段是短的2倍.求中间长方形的面积.1.(如下图)已知大正方形的边长是12厘米.求中间最小正方形的面积.2.正图长方形ABCD的面积是16平方厘米.E、F都是所在边的中点.求三角形AEF 的面积.3.求下图长方形ABCD的面积(单位:厘米).四边形ABCD和四边形DEFG都是正方形.已知三角形AFH的面积是7平方厘米.三角形CDH的面积是多少平方厘米?1.图中两个正方形的边长分别是6厘米和4厘米.求阴影部分的面积.2.下图中两个完全一样的三角形重叠在一起.求阴影部分的面积.(单位:厘米)3.下图中.甲三角形的面积比乙三角形的面积大多少平方厘米?下图中正方形的边长为8厘米.CE为20厘米.梯形BCDF的面积是多少平方厘米?1.如下图.正方形ABCD中.AB=4厘米.EC=10厘米.求阴影部分的面积.2.在一个直角三角形铁皮上剪下一块正方形.并使正方形面积尽可能大.正方形的面积是多少?(单位:厘米)3.图中BC=10厘米.EC=8厘米.且阴影部分面积比三角形EFG的面积大10平方厘米.求平行四边形的面积.图中ABCD是长方形.三角形EFD的面积比三角形ABF的面积大6平方厘米.求ED的长.1.如图.平行四边形BCEF中.BC=8厘米.直角三角形中.AC=10厘米.阴影部分面积比三角形ADH的面积大8平方厘米.求AH长多少厘米?2.图中三个正方形的边长是1厘米、2厘米和3厘米.求图中阴影部分的面积. 3.正方形的边长是2(a+b).已知图中阴影部分B的面积是7平方厘米.求阴影部分A和C的和是多少平方厘米?。
小学五年级数学组合图形的面积试题及答案
小学五年级数学组合图形的面积试题及答案集团档案编码:[YTTR-YTPT28-YTNTL98-UYTYNN08]五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷212×3÷2=20×8.5÷2=36÷2=170÷2=18(cm2)=85(cm2)图形面积=梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+正方形面积(2×2)图形面积=长方形面积-梯形面积6×(5-2)+2×210×6–[(3+6)×2÷2]=6×3+4=60-[9×2÷2]=18+4=60-9=22(m2)=51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高=49÷(6+8)×2直角三角形面积=6×7÷2=49÷14×2=42÷2=3.5×2=21(dm2)=7(dm2)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2=45÷12×2=17×7.5÷2=3.75×2=127.5÷2=7.5(cm2)=63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75-45=18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2=40÷10×2=16×8÷2=4×2=128÷2=8(m2)=64(m2)空白部分面积=梯形面积–阴影部分面积:64–40=24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
五年级数学上册组合图形面积计算练习题
1. 一只蜗牛被困在一口深10米的井中,在井底它努力地向上爬呀爬。
它白天向上爬4米,晚上下滑3米。
这只蜗牛第几天能够爬出去?2.长方形的广告牌长为15米,宽为10米,A、B、C、D分别在四条边上,并且C比A低4米,D在B的右边7米,则四边形ABCD的面积是______平方米.3. 如图,折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分.点E在矩形的边上,使得线段AE也平分矩形的面积.已知线段AB=30,BC=24,CD=10,求DE的长.4.如图,三个大小相同的正方形重叠地放在一个大的正方形ABCD内,已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD的边长是______厘米.5. 平行四边形ABCD的边BC长10厘米,直角三角形的直角边EC长8厘米。
已知阴影部分的面积比三角形EGF的面积大9平方厘米。
求CF的长。
6. 边长分别为8cm和6cm的两个正方形ABCD与BEFG如图并排放在一起.连接DE交BG于P,则图中阴影部分APEG的面积是多少?7. 如图中阴影甲的面积比阴影乙的面积大多少()A. 6(平方厘米)B. 8(平方厘米)C. 4(平方厘米)D. 10(平方厘米)8.平行四边形的面积是255平方厘米,求阴影部分的面积.(单位:厘米)9. 为了美化校园,学校在一块梯形空地上种植了3种花,同时为了便于同学们观赏,修建了两条2米宽的小路,如图.种花的面积是多少?如果种每平方米花约要25元,那么种花一共需要多少元?10. 41.如图,将四条长为16cm,宽为2cm的长方形垂直相交平放在桌面上,则桌面被盖住的面积是()A. 72cm 2B. 128cm 2C. 20cm 2D. 112cm 211. 在一长方形草地里有一条宽1米的曲折小路,如图所示,小路的面积是()平方米.A. 10B. 20C. 30D. 2212. (2015•长沙)如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是 __________平方厘米.13.答案解析1、【答案解析】【点拨】白天向上爬4米,晚上下滑3米,所以1天向上爬1米,但最后一天向上爬4米就可以爬出去,因此用井深减去4米,看剩下的每天爬1米可以爬几天,再加上最后爬4米的1天,就求出这只蜗牛第几天能够爬出去了。
数学五年级上册《组合图形的面积》同步训练(含答案)
第六单元《多边形的面积》第4课时组合图形的面积一.选择题1.(2012•碑林区校级自主招生)如图,三角形ADF与三角形ABE、四边形AFCE的面积相等,9BC=厘米,6CD=厘米,求阴影部分的面积()A.5(平方厘米)B.25(平方厘米)C.15(平方厘米)D.10(平方厘米)2.(2012•康县)如图中,两三角形的面积之和占长方形面积的()A.12B.13C.14D.163.(2012•常熟市自主招生)如图所示,甲和乙两幅图的面积相等,其阴影面积相比,下列说法正确的是()A.甲>乙B.甲<乙C.甲=乙4.(2019秋•大兴区期末)如图所示,把一个长方形分成一个梯形和一个三角形.已知梯形的面积比三角形的面积大18厘米2,那么梯形的上底长为()厘米.A.2B.3C.4D.65.如图ABCD是长方形,已知4AB=厘米,6BC=厘米,三角形EFD的面积比三角形ABF的面积大6平方厘米,求(ED=)厘米.A.9B.7C.8D.6二.填空题6.(2019春•海淀区月考)如图,有一块长方形场地,长62=,从A、B两处入口的小路宽都AD mAB m=,宽41是1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为2m.7.(2019春•静安区月考)如图的三角形分成两部分,甲的面积是210cm,乙的面积是2cm.8.(2019•徐州)如图中,阴影部分的面积占大长方形的.9.(2019春•湖北月考)如图,梯形的面积是.10.(2019•长沙县)如图,D是BC的三等分点,E是AC的四等分点,三角形ABC的面积是三角形ADE的面积的 倍.11.(2019春•杨浦区月考)如图,已知AE EC =,:2:3BD DC =,AFE ∆的面积比BFD ∆的面积多2,则ABC ∆的面积是12.(1999•广州自主招生)一个宽是3厘米的长方形,如果将长和宽都增加3厘米,那么面积增加81平方厘米;如果将长和宽都减少2厘米,那么面积减少 平方厘米.三.判断题13.如图所示,梯形的上底长等于下底长的一半,空白面积也等于阴影部分面积的一半. (判断对错)四.计算题14.(2018秋•环江县期末)计算下面图中阴影部分的面积.(单位:分米)15.(2019•武侯区)计算下面图形的面积.(单位:)cm16.(2017•西安模拟)求图中阴影部分的面积(单位:厘米) 17.(2015秋•徐州月考)求下列各图形面积18.(2017秋•栖霞区校级期中)求阴影部分面积.19.(2016秋•贵州月考)计算如图各图形的面积.20.计算下面图形中阴影部分的面积.(单位:分米)五.应用题21.(2019春•无棣县期末)在一块长方形地上,种上三种不同的蔬菜,如图.(1)黄瓜地的周长是多少米?(2)西红柿地的面积是多少?22.(2017•武汉模拟)如图,在直角三角形ABC里面裁剪一个正方形CDEF,剩下两个三角形,已知=,则图中阴影部分的面积是多少平方厘米?BE cm=,43AE cm23.(2017秋•巴南区期中)有一块长方形的地如图,中间有两条2m宽的水泥小路,其余部分为草坪,求草坪的面积?24.实验小学评比“卫生文明班级”需要制作一些流动红旗(如图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形的面积专项练习
(北师大版数学第九册)
一、填空。
1.两个完全一样的三角形都能拼成一个()形。
2.一个平行四边形的面积是4.5平方米,底边上的高是1.5米,底长是()米。
3.两个完全一样的直角梯形能拼成一个()形,也能拼成一个()形。
4.一个三角形的面积是2.5平方米,与它等底等高的平行四边形的面积是()平方米。
5.一个直角三角形的两条直角边分别是3分米、4分米,这个三角形的面积是()平方分米。
6.一个梯形的高是1.2米,上下底的和是3.6米,这个梯形的面积是()平方米。
7.一个平行四边形的面积是9平方分米,底扩大4倍,高不变,它的面积是()平方分米。
8.一个等腰直角三角形,腰长16厘米,面积是()平方厘米。
9.如图,平行四边形的面积24.8平方厘米,阴影部分的面积是()平方厘米。
二、判断,正确的在括号里画“√”、错误的画“×”。
1.一个三角形底长8厘米,高5厘米,它的面积是40平方厘米。
()
2.下面三个三角形的面积都相等。
()
3.任意两个三角形都可以拼成一个平行四边形。
()
4.任意一个梯形都能分成两个一样的平行四边形。
()
5.如果两个三角形的形状不同,它们面积一定不相等。
()
三、选择符合要求的答案,把字母填在括号里。
1.一个三角形的底扩大3倍,高不变,它的面积()。
A.扩大3倍 B.不变、 C.扩大6倍
2.用木条钉成一个长方形,沿对角线拉成一个平行四边形。
这个平行四边形与原来的长方形相比:平行四边形的周长(),平行四边形的面积()。
A.不变 B.变大 C.变小
3.三角形的底和高都扩大2倍,它的面积扩大()。
A.2倍 B.4倍 C.8倍
4.下面第()组中的两个图形不能拼成平行四边形。
5.图中,甲、乙两个三角形的面积比较,()。
A.甲比乙大 B.甲比乙小 C.甲乙面积相等
6.一堆钢管,最上层4根,最下层10根,相邻两层均相差1根,这堆钢管共() A.35根 B.42根 C.49根
四、画出下面各图形底边上的高。
五、计算下面各图形的面积。
六、解决问题。
1.一张长方形的铁板,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角。
求剩下图形的面积是多少?2.一块铁板的形状如下图。
在这块铁板的两面涂上油漆,涂油漆的面积是多少?(单位:
分米)
3、小丽家装修需要30块木板,木板的形状如下图。
(1)一块木板的面积是多少?(用两种方法计算)
(2)如果每块木板需要15元,那么小丽需要花多少钱?
4、估计下面图形的面积。
(每个小方格的面积表示1cm2)
面积约为()面积约为()面积约为()
30cm
48cm
72cm
60cm。
