初中数学找规律题
初中数学找规律练习题(有答案)
精心整理一、简答题1、已知a、b互为相反数，c、d互为倒数，m的倒数等于它本身，则的值是多少？（4分）2、先阅读,再解题:因为,?,?……所以.参照上述解法计算:3、目前市场上有一种数码照相机，售价为3800元/架，预计今后几年内平均每年比上一年降价4%．3年后这种数码相机的售价估计为每架多少元（精确到1元）？4、已知a、b互为相反数，m、n互为倒数，x绝对值为2，求的值5、如果规定符号“﹡”的意义是﹡=，求2﹡﹡4的值。
6、某商店营业员每月的基本工资为300元，奖金制度是：每月完成规定指标10000元营业额的，发奖金300元；若营业额超过规定指标，另奖超额部分营业额的5%，该商店的一名营业员九月份完成营业额13200元，问他九月份的收入为多少元？7、王叔叔家的装修工程接近尾声，油漆工程结束了，经统计，油漆工共做50工时，用了150升油漆，已知油漆每升128元，共粉刷120平方米，在结算工钱时，有以下几种结算方案：(1)按工时算，每6工时300元。
(2)按油漆费用来算，油漆费用的15%为工钱；(3)按粉刷面积来算，每6平方米132元。
请你帮王叔叔算一下，用哪种方案最省钱？8、定义一种新的运算：观察下列式子1⊙3=1×4+3=7；3⊙（-1）=3×4+（-1）=11；5⊙4=5×4+4=24；4⊙（-3）=4×4+（-3）=13．⑴请你想一想：a⊙b=??????????;⑵请你判断a⊙b??????b⊙a(填入“=”或“≠”）???⑶若a=-2，b=-4,求（2a-b)⊙（a-2b)的值.9、阅读下列材料：1×2＝(1×2×3－0×1×2)，2×3＝(2×3×4－1×2×3)，3×4＝(3×4×5－2×3×4)，由以上三个等式相加，可得1×2＋2×3＋3×4＝×3×4×5＝20.读完以上材料，请你计算下列各题：(1)1×2＋2×3＋3×4＋…＋10×11(写出过程)；(2)1×2＋2×3＋3×4＋…＋n×(n＋1)＝________；(3)1×2×3＋2×3×4＋3×4×5＝________.10、从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策：安装“一户一表”的居民用户，按所抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价，收费标准如下：月用电量不超过50千瓦时的部分超过50千瓦时不超过200千瓦时的部分超过200千瓦时的部分收费标准（元/千瓦时）0.53 0.56 0.63 ????例：若某户月用电300千瓦时，需交电费为????（元）（1）若10月份许老师家用电量为130千瓦时，则10月份许老师家应付电费多少元？?（2）已知许老师家10月份的用电量为千瓦时，请完成下列填空（用代数式表示）：①若千瓦时，则10月份许老师家应付电费为?????????????元；②若千瓦时，则10月份许老师家应付电费为???????元；③若千瓦时，则10月份许老师家应付电费为??????????元。
(完整版)七年级找规律经典题汇总带答案
……一、数字排列规律题1、观察下列各算式： 1+3=4=22，1+3+5=9=23，1+3+5+7=16=24… 按此规律 （1）试猜想：1+3+5+7+…+2005+2007的值 ？（2）推广： 1+3+5+7+9+…+（2n-1)+（2n+1)的和是多少 ？2、下面数列后两位应该填上什么数字呢？ 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个（ ）二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球，○是空心球)：●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止，共有实心球 个．2、观察下列图形排列规律（其中△是三角形，□是正方形，○是圆），□○△□□○△□○△□□○△□┅┅，若第一个图形是正方形，则第2008个图形是 （填图形名称）.三、数、式计算规律题 1、已知下列等式：① 13＝12； ② 13＋23＝32； ③ 13＋23＋33＝62； ④ 13＋23＋33＋43＝102 ；由此规律知，第⑤个等式是 ． 2、观察下面的几个算式： 1+2+1=4， 1+2+3+2+1=9， 1+2+3+4+3+2+1=16， 1+2+3+4+5+4+3+2+1=25，… 根据你所发现的规律，请你直接写出下面式子的结果： 1+2+3+…+99+100+99+…+3+2+1=____.3、，，，，已知：24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律，，若…21010 规律发现专题训练1．用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案：第(4)个图案中有黑色地砖4块；那么第(n )个图案中有白色．．地砖 块。
初中数学找规律
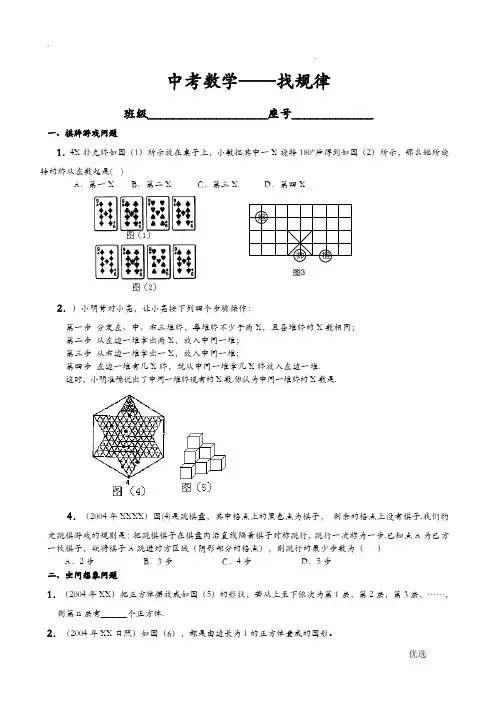
中考数学——找规律班级___________________座号_____________一、棋牌游戏问题1．4X 扑克牌如图（1）所示放在桌子上，小敏把其中一X 旋转180º后得到如图（2）所示，那么她所旋转的牌从左数起是( )A ．第一XB ．第二XC ．第三XD ．第四X2．）小明背对小亮，让小亮按下列四个步骤操作：第一步 分发左、中、右三堆牌，每堆牌不少于两X ，且各堆牌的X 数相同； 第二步 从左边一堆拿出两X ，放入中间一堆； 第三步 从右边一堆拿出一X ，放入中间一堆；第四步 左边一堆有几X 牌，就从中间一堆拿几X 牌放入左边一堆. 这时，小明准确说出了中间一堆牌现有的X 数.你认为中间一堆牌的X 数是.4．（2004年XXXX ）图(4)是跳棋盘，其中格点上的黑色点为棋子， 剩余的格点上没有棋子.我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行，跳行一次称为一步.已知点A 为已方一枚棋子，欲将棋子A 跳进对方区域（阴影部分的格点），则跳行的最少步数为（ ） A ．2步 B ．3步 C ．4步 D ．5步 二、空间想象问题1．（2004年XX ）把正方体摆放成如图（5）的形状，若从上至下依次为第1层，第2层，第3层，……，则第n 层有＿＿＿个正方体.2．（2004年XX 日照）如图（6），都是由边长为1的正方体叠成的图形。
图3相帅炮例如第①个图形的表面积为6个平方单位，第②个图形的表面积为18个平方单位，第③个图形的表面积是36个平方单位。
依此规律，则第⑤个图形的表面积个平方单位。
3．水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图（7）,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的.4．.观察下列由棱长为1的小立方体摆成的图形，寻找规律：如图（8）①中：共有1个小立方体，其中1个看得见，0个看不见；如图（8）②中：共有8个小立方体，其中7个看得见，1个看不见；如图（8）③中：共有27个小立方体，其中19个看得见，8个看不见；……，则第⑥个图中，看不见．．．的小立方体有个.５．图（1）是一个黑色的正三角形，顺次连结它的三边的中点，得到如图（2）所示的第2个图形（它的中间为一个白色的正三角形）；在图（2）的每个黑色的正三角形中分别重复上述的作法，得到如图（3）所示的第3个图形。
中考数学复习专题——找规律(含答案)
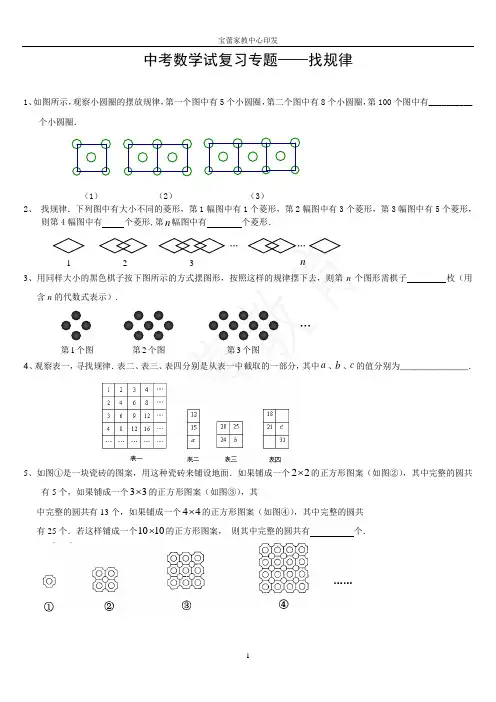
中考数学试复习专题——找规律1、如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有__________个小圆圈．（1） （2） （3）2、 找规律．下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有 个菱形,第n 幅图中有 个菱形．3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.4、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a 、b 、c 的值分别为______________．5、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个22⨯的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个33⨯的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个44⨯的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个1010⨯的正方形图案， 则其中完整的圆共有 个．1 2 3n … … 第1个图 2个图 3个图 …6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n 个图案需要用白色棋子 枚（用含有n 的代数式表示，并写成最简形式）.○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形需 根火柴棒。
8、将正整数按如图5所示的规律排列下去，若有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，2）表示实数9，则表示实数17的有序实数对是 ．9、如图 ２ ，用n 表示等边三角形边上的小圆圈，f(n)表示这个三角形中小圆圈的总数，那么f(n)和n 的关系是10、观察图4的三角形数阵，则第50行的最后一个数是 （ ）1-2 3-4 5 -67 -8 9 -10。
(完整word版)七年级数学找规律练习题和答案
找规律练习题1 •用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案：第X 1=1，第二个数为X 2=3,第三个数开始依次记为 X 3, X 4,…，X n ；从第二个数开始，每个数是它相中有白色地砖 块。
2.我国著名数学家华罗庚曾说过:“数形结合百般好，隔裂分家万事非。
在一个边长为1的正方形纸版上, 形彩色纸片（n 1 规律，计算丄 2为大于1 1 1 48的整数） 1 班1 1 依次贴上面积为 1 , 1 ,2 4 。
请你用“数形结合”的思想, 8 ”如图， 1 丄的矩 2n 依数形变化的 邻两个数和的一半。
（如: X 2=^l X3 ）2 （1）求第三、第四、第五个数，并写出计算过程； （2）根据（1）的结果，推测X 8= （3）探索这一列数的规律，猜想第 k 个数X k = . （ k 是大于2的整数） 4•将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线） .继续对折，对折时每次折痕与上次的折痕保持平行，连 续对折三次后，可以得到 7条折痕，那么对折四次可以得到 ________________ 条折痕.如果对折n 次，可以得到 ______________ 条折 痕• 1 1 1 1 1 1 1 ■ ■ 1 4 1 | 1 1 1 1 1 111 1 1 V 1 1 1 1 1 1 1 hL1 V 1 1 a ii k i 1119 1 l> V i i I I I I l> 1 1 I l> I 1 I I I i 1 >1 1 ■ KPI ■ ・ W P a L h h F 1I 4 1 il >1 I ii ■l >l 4 I A I 第一次对折第二次对折第三友对折5.观察下面一列有规律的数 1 2 _5 _6_ 3,8,15,24,35,48 根据这个规律可知第 n 个数是（n 是正整数） 6.古希腊数学家把数 1, 3, 6, 10, 15, 21 ,……，叫做三角形数，它有一定的规律性，则第 形数的差为 _____________________ 。
七年级数学找规律经典题型
七年级数学找规律经典题型一、数字规律1. 数列规律例1：观察数列1，3，5，7，9，…，求第n个数。
解析：首先观察这个数列，发现相邻两个数的差值都是2。
第1个数是1 = 2×1 1；第2个数是3 = 2×2 1；第3个数是5 = 2×3 1；第4个数是7 = 2×4 1；第5个数是9 = 2×5 1。
所以可以得出第n个数为2n 1。
例2：观察数列2，4，8，16，32，…，求第n个数。
解析：这个数列中，后一个数都是前一个数的2倍。
第1个数是2 = 2^1；第2个数是4 = 2^2；第3个数是8 = 2^3；第4个数是16 = 2^4；第5个数是32 = 2^5。
所以第n个数为2^n。
2. 数字循环规律例：有一组数按照1， 1，1， 1，…的规律排列，求第n个数。
解析：观察这组数字，发现数字是1和 1交替出现。
当n为奇数时，第n个数为1；当n为偶数时，第n个数为 1。
可以用(-1)^(n + 1)来表示，当n = 1时，(-1)^(1+1)=1；当n = 2时，(-1)^(2 + 1)= 1。
二、图形规律1. 图形数量规律例1：用火柴棒搭三角形，搭1个三角形需要3根火柴棒，搭2个三角形需要5根火柴棒，搭3个三角形需要7根火柴棒，…，求搭n个三角形需要多少根火柴棒。
解析：搭1个三角形需要3根火柴棒，即2×1+1；搭2个三角形时，第二个三角形和第一个三角形共用一条边，所以需要3 + 2 = 5根火柴棒，即2×2+1；搭3个三角形时，第三个三角形和前面的三角形共用两条边，所以需要3+2×2 = 7根火柴棒，即2×3 + 1。
所以搭n个三角形需要2n+1根火柴棒。
例2：观察下列图形的点数规律：第1个图形有1个点；第2个图形有1 + 3 = 4个点；第3个图形有1+3 + 5 = 9个点；第4个图形有1+3+5 + 7 = 16个点；求第n个图形的点数。
初中数学找规律专题练习
找规律专题练习1、你喜欢吃拉面吗？拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,2、如以下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按 同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去； (1)填表：(2)如果剪n 次,共剪出多少个小正方形？(3)如果剪了 100次,共剪出多少个小正方形？ (4)观察图形,你还能得出什么规律？3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住局部的整数的和是4、填表并答复以下问题x0.010.11101001000( 100 1 2x(1)根据上表结果,描述所求得的一列数的变化规律 (2)当x 非常大时,学的值接近于什么数? x5、现有黑色三角形“▲和△〞共200个,根据一定规律排列如下:那么黑色三角形有 个,白色三角形有 个7、用火柴棒按如下方式搭三角形:(1)填写下表：反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第 64根细面条.次后可拉出第一次捏合第三次捏合剪的次数 1 2 3 4 5正方形个数第二次捏合 6、仔细观察以下图形.当梯形的个数是n 时,图形的周长是12的规律填空： 502, 第n 个式子呢？①张桌子拼在一起可坐 ________ 入.3张桌子拼在一起可坐 _________ 人,n 张桌子拼在一起可坐 __________ 人. ②一家餐厅有40张这样的长方形桌子,根据上图方式每 5张桌子拼成1张大桌子,那么40张桌子可 拼成8张大桌子,共可坐 ____________ 人.③假设在②中,改成每8张桌子拼成1张大桌子,那么共可坐 __________________ 人. 12、用计算器计算以下各式,并将结果填写在横线上.① 1X7X15873= ______________ ② 2X7 X15873= _____________ ③ 3X7 X15873= _____________ ④ 4X7 X15873= _____________你发现了什么规律？把你发现的规律用简练的语言写出来；13、观察以下顺序排列的等式：9 >0+1=19 >1+2=11 9>2+3=21 9>3+4=31 9X4+5=41猜测：第n 个等式(n 为正整数)应为.14、 一个两位数的个位数是a,十位数字是b,请用代数式表示这个两位数是15、观察以下各式：31=3, 32 =9, 33=27, 34=81, 35=243, 36=729…你能从中发现底数为 3的事的9、一列数：1,- -2 , 3,- -4, 5, —6, 7,…将这列数排成第1行 1第2行 一23第3行 —45 一 6第4行 7 一 8 9 -10第5行 11 -1213 —141510、观察以下算式:1 5 4 32 , 2 6 4 42 ,3 74 52 , 4 8 4 62 ,请你在察规律之后并用你得到(2)照这样的规律搭下去,搭n 个这样的三角形需要 _______________ 根火柴棒8、把编号为1, 2, 3, 4,…的假设干盆花按右图所示摆放,花盆中 蓝、紫的颜色依次循环排列,那么第 8行从左边数第6盆花的颜色为 色.根据上述规律排下去,那么第10行从左边数第5个数等于的花按红、黄、卜列形式:个位数有什么规律吗？根据你发现的规律答复：3 2004的个位数字是16、观察以下各式,你会发现什么规律？3X5=15,而 15=42 1 0 5X7=35,而 35= 62 111X13=143,而 143= 122 1将你猜测到的规律用只含一个字母的式子表示出来：.17、问题：你能比拟20052006和20062005的大小吗？为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比拟n n+1和(n+1)n 的大小(n为正整数),我们从n=1,n=2,n=3 ••…这些简单的情况入手,从中发现规律,经过归纳,猜出结论.(1)通过计算,比拟以下各组数字大小① 12 22 ② 23 32 ③ 34 43④ 45 54⑤ 54 65⑥ 67 7(2)把第(1)题的结果经过归纳,你能得出什么结论？你能用只含有一个字母的式子表示吗? (3)根据上面的归纳猜测得到的结论,试比拟两个数的大小(1分) 20052006200召005 (填〞 >〞," <"),“二〞18、为了美化城市,某商场在门前的空地上用花盆按如下图的方式搭正方形,(1)填写下表正方形的层 数12345花盆的个数4(2)按这个规律搭下去,搭第n 层正方形,需要 _______________________________ 盆花?19、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为 10. (1) 1 5 5 9 =10 ; (2) 3 3 3 3=10 ; (3) 1 1 9 9 =10请你修忙算一算得多少？21、黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图 1),于是它们决定比 一比.黑蚂蚁沿着大半圆从甲处跑到乙处；红蚂蚁沿着两个小半圆也从甲处跑到乙处.两只蚂蚁同时起 跑,说也奇怪,两只蚂蚁同时到达了乙处.(1)两只蚂蚁请你帮助判断：谁跑得快？20、小红和小花在玩一种计算的游戏,计算的规那么是a b ........................... 1 2=ad- bCo 现在轮到小红计算的值,c d3 4(2)两只蚂蚁对你的判断结果很不满意,决定再到(图 2)的几个半圆处再比赛一次,请你猜一猜,哪 一只蚂蚁先从甲处跑到乙处？,总的比赛场数是多少？ 4个球队呢？ m23.按一定规律排列的一串数:1 23 1 2 34 51 2Q , Q , G ,匚, 匚,匚,匚,匚,7,73 3 3 5 5 5 5 57714.下面的算式里,符号.、△、和口分别代表三个不同的自然数,这三个数的和是1111 118. △口24. 一群整数朋友根据一定的规律排成一排,可排在口位置的数跑掉了,请帮它们把跑掉的朋友找回来.(1) 5, 8, 11, 14, □ , 20; (2) 1, 3, 7, 15, 31, 63, □;(3) 1, 1, 2, 3, 5,8, □, 21 25.以下两列数：2, 4, 6, 8, 10, 12,……1994;6, 13, 20, 27, 34, (1994)这两列数中,相同的数的个数是( )A 、 142B 、 143C 、 284D 、 28526. 一串数字的排列规律是：第一个数是 20,从第二个数起,每一个数比前一个数小 8(1)第10个数是多少？ ( 2)第n 个数是多少？ ( 3)第几个数是一6027.某仓库堆放一批圆木,一共 20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根? 28.在如下图的2003年1月份的日历中,用一个方框圈出任意 3X3个数 星期日星期一星期二 星期三 星期四 星期五 星期六1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920212223242526 27 28 29 30 31(1)从左下角到右上角的三个数字之和为 45,那么这9个数的和是多少？这9个日期中最后一天是 1月几日？(2)用这样的方框能否圈出总和为162的9个数？ 37,…中,第98个数是 ______________22. (1) 3个球队进行单循环赛 (参赛的每一个队都与其它所有各队比赛一场) 个球队呢？(代数式表示出来)(2)当m=12时,总共比赛几场？29 .观察以下数据,按某种规律在横线上填上适当的数：♦ 3 5 7 9 1, 一, 一, 一,——, ,…49162530 .如图,△ ABC 中,D 是边BC 上的中点, F 是线段CD 的中点,E 是边AC 的中点,那么图中有 条线段,有 个角,假设4 DEF 的面积是2,那么△ ABC 的面积是31 .平面内两两相交的 6条直线,其交点个数最少为 m 个,最多为n 个,那么m+n 等于〔〕A 、12B 、16C 、20D 、以上都不对32 .如图,可以看成是边长为4的小正方形的巧克力糖,请你用尽可能多的不同方法把它分成形状、大小完全相同的四块,要求不把正方形糖块划破〔至少五种方法〕40、观察公式：公式 1 ： (x a)3 x 3 3x 2a 3xa 2 a 333 .在某月日历上一个竖列相邻的五个数之和为 80,这五个数是34 .某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是 36,那么第三个日期是35 .今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是 36 .如果这个月的5号是星期三,那么20号是星期 37 .三个连续偶数中,n 是最小的一个,这三个数的和为 , 38 .以下图形中三角形的个数是〔〕A.4 个B.6 个C. 9 个D.10 个 91,那么李老师是 号回家的39、至少找出以下几何体的 4个共同点4 4 3_22 3 4公式2：(x a) x 4x a 6x a 4xa a(1) 这两个公式有什么特点？(2) 利用公式计算：_ 4 _ 3 1 __2 1 2 _ 1 3 1242()62()42()() 2 2 2 241、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为10.(1) 1 5 5 9 =10 ; (2) 3 3 3 3 =10 ; (3) 1 1 9 9 =1042 .造一个含有字母p和q的代数式,使得不管p、q取何值,代数式的值永远不是正的.43 .图是2002年6月份的日历,现用一矩形在日历中任意框出4个数| a b] ,请用一个等式表示,a、b、c、d之间的关系. c d日一一三四五六12345678910111213141516171819202122232425262728293044 .右图,是用火柴棒摆成的一个大三角形,它是由九个小三角形组成的,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形哪(每个小三角形内只填一个数) ,要求靠近大三角形每条边的每五个数相加的和相等,请想一想,怎样填这些数才能使五个数的和尽可能大一些,这五个数的和最大是多少？45.王容许了大臣的一个要求：即在国际象棋棋盘上2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到64格〞.但是不久国王九发现国库里没有这么多米,然而国王的话不能不算数,国王又不好意思向别人借,怎么办呢？请你帮国王想一个好方法来解决这个问题. (方法必须符合情理,有创意者可适当多加分.方法多者亦可多加分)46.如果连结多边形的一边上一点与其余各顶点可将某多边形分割成2004个三角形,求该多边形的边数47 .如图1-26,在ABC中,点D,E,F分别是AB,BC,AC三边中点,图中与BOD面积相等的三角形有几个？48 .观察图1-27中有几个三角形？由此你发现三角形的个数有什么规律呢49.求个数图 1-29(1)将下表填写完整. 图形符号52、以下图形经过折叠能否围成一个正方体?一个三角形3个三角形个三角形个三角形(n 个点)(3)(4)53、某种细胞每过54、有一张厚度是 30分便由1个分裂成2个,经过5小时,这种细胞由1个能分裂成0 .1毫米的纸,将它对折 1次后,厚度为2X0.1毫米.(1)图1-28(1)中有多少个三角形？(2)图1-28(2)中有多少个四边形？50.如图1-29所示,图①是一个三角形别连结图②中间的小三角形三边的中点,分别连结这个三角形三边的中点(将这条边分为相等的两局部的点 ,得到图③,按此方法继续下去,请你根据图中三角形个数的规律)得到图②；再分 ,完成以下问(2)〔1〕、对折2次后,厚度为毫米. 〔2〕对折20次后,厚度为毫米.〔3〕对折n次后,厚度为毫米.55、以下图〔1〕表示1张餐桌和6张椅子〔每个小半圆代表1张椅子〕,假设按这种方式摆放20张餐桌需要的椅子张数是.你认为220的末位数字是〔〕.57、某种细菌在培养过程中,每半小时分裂1次,每次一分为二.假设这种细菌由1个分裂到16个,那么这个过程要经过〔〕A. 1.5小时B , 2小时C , 3小时D , 4小时58、计算：1—2+3—4+……+2001 —2002+2003= . .会在与数字2所在的平面相对的平面上.,4 5 6 _1 2pv2 , 22 4, 23 8, 24 1 6, 25 32, 26 64, 27 1 28, 28 2 56, 根据上述算式中的规律,63、(A)观察以下数据,(B)按某种规律在横线上填上适当的数:4 9一列数7二72,7一,1673…72003 ,其中末位数是3的有个.56、观察以下算式: 2159、当下面这个图案被折起来组成一个正方体,数字61、根据规律填上适宜的数：〔1〕—9, —6, —3, /64、在下面的图形中〔62、〕是正方体的展开图.66、指出以下平面图形是什么几何体的展开图〔 6分〕：67、在下面的图形中,〔 〕是正方体的外表展开图68、探索规律：用棋子按下面的方式摆出正方形①按图本规律填写下表: 图形编号 (1) ⑵ (3) (4) ⑸ (6)棋子个数②根据这种方式才g 下去,摆第 n 个正方形需要多少个棋子? ③根据这种方式才g 下去,第第 20个正方形需要多少个棋子?69、,13 1 - 12 22,4,3 c3 c 1 -2 八21 2 9 — 2 3, 4□ □ □ □ □ □,3 八3 八3 "1 2 3 36 32 42⑴猜测填空：1323 334()(2)假设1323 33 240 2,试求n的值.70、用火柴棒按下面方式搭图形,那么20个图形需要的火柴棒是根. 第1 2。
十道初中数学找规律的题型及解题思路
十道初中数学找规律的题型及解题思路这里有10道初中数学找规律的题目，涵盖了常见的数列、图形等多种类型，希望能帮助学生更好地掌握找规律的技巧：数列找规律1.等差数列：1.1, 4, 7, 10, ... 下一个数是多少？2.100, 97, 94, ... 第10个数是多少？2.等比数列：1.2, 4, 8, 16, ... 第8个数是多少？2.81, 27, 9, ... 第6个数是多少？3.混合数列：1.1, 4, 9, 16, 25, ... 下一个数是多少？（提示：考虑每个数的平方）2.2, 5, 10, 17, ... 下一个数是多少？（提示：观察相邻两数的差）4.周期数列：1.1, 2, 3, 1, 2, 3, ... 第20个数是多少？2.A, B, C, A, B, C, ... 第100个数是多少？图形找规律图形的变化：1.一组图形，每个图形由小方块组成，观察图形的变化规律，画出下一个图形。
图形的旋转：1.一个图形不断旋转，观察旋转的规律，画出旋转后的图形。
图形的翻转：1.一个图形不断翻转，观察翻转的规律，画出翻转后的图形。
数字与图形结合数字与图形对应：1.一组图形，每个图形对应一个数字，找出数字与图形之间的对应关系。
图形中的数字规律：1.一个图形中包含多个数字，找出数字之间的规律。
综合题型1.数字和图形的综合：1.一组图形和数字交替出现，找出数字和图形之间的关系。
解题技巧：•观察：仔细观察数列或图形的变化规律，找出其中的共同点和差异点。
•比较：比较相邻的数或图形，找出它们的递增、递减或其他变化关系。
•联想：将题目与以前学过的知识联系起来，寻找解题思路。
•归纳：根据观察和比较的结果，归纳出一般性的规律。
•验证：将得到的规律代入后面的数或图形中进行验证，确保规律的正确性。
注意事项：•找规律题的答案可能不唯一，只要找到一种合理的规律即可。
•遇到困难时，可以尝试从不同的角度去观察和分析。
初一数学上册：找规律题型11种常考类型+真题演练(含答案)
初一数学上册：找规律题型11种常考类型+真题演练（含答案）【找规律题目的类型】★设计类（1）用图形反映规律★数字类（1）与数阵有关的问题（2）等差型数列规律（3）等比型数列规律（4）含平方型数列规律（5）其它数列规律列举（6）循环型数列★计算类（1）根据已知等式探究规律（2）探究算式的计算规律★图形类（1）与视图、展开图有关的问题（2）几何图形变化规律题真题演练一、观察下列各算式：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42按此规律（1）试猜想：1+3+5+7+…+2005+2007的值？（2）推广：1+3+5+7+9+…+（2n-1)+（2n+1)的和是多少？答案：（1）1004的平方（2）n+1的平方二、下面数列后两位应该填上什么数字呢？23581217____答案：23 30。
数列中每两个相邻数字间的差分别是1，2，3，4，5，6，7。
三、请填出下面横线上的数字。
112358____21答案：13。
数列后面一个数是前面相邻两个数的和。
四、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么？答案：34 。
考虑时，可以从第一个数开始，每3个数加一个括号（1，2，3），（2，3，4），（3，4，5），……一共加了33个括号，剩下的一个必是第100个。
每个括号的第一个数分别是1，2，3，……因此第100个数必然是34。
五、有一串数字36101521___第6个是什么数？答案：28。
3+3=6 6+4=10 10+5=15 15+6=21 21+7=28, 所以第6个是28。
其实一般这类的规律题无非就是在数的基础上加减乘除，有些麻烦点的就是一个数乘上倍数后在加1或减1。
六、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（A）A．1B．2C．3D．4七、100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1，0，那么这100个数中“0”的个数为___个．答案：33八、观察排列规律(其中●是实心球，○是空心球)：●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止，共有实心球个答案：602、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、2、观察下列图形排列规律（其中△是三角形，□是正方形，○是圆），□○△□□○△□○△□□○△□┅┅，若第一个图形是正方形，则第2008个图形是（填图形名称）答案：圆九、观察下面的几个算式：1+2+1=4，1+2+3+2+1=9，1+2+3+4+3+2+1=16，1+2+3+4+5+4+3+2+1=25，…根据你所发现的规律，请你直接写出下面式子的结果：1+2+3+…+99+100+99+…+3+2+1=____.答案：10000。
七年级数学有理数找规律题型
七年级数学有理数找规律题型一、数字规律。
题1。
观察下列数：1， -2， 3， -4， 5， -6，…，按照这样的规律，第100个数是多少？解析。
可以发现这些数的绝对值是连续的自然数，且奇数项为正，偶数项为负。
第100个数是偶数项，所以为 - 100。
题2。
给出一组数： - 1，2， - 4，8， - 16，32，…，则第7个数是多少？解析。
先看绝对值，后一个数是前一个数绝对值的2倍，再看符号，奇数项为负，偶数项为正。
第7个数是奇数项，绝对值为2^6=64，所以第7个数是 - 64。
题3。
有一列数：(1)/(2)，(2)/(3)，(3)/(4)，(4)/(5)，…，那么第n个数是多少？解析。
分子依次是1，2，3，4，…，n；分母依次是2，3，4，5，…，n + 1。
所以第n 个数是(n)/(n + 1)。
题4。
观察数：1，4，9，16，25，…，第10个数是多少？解析。
这组数是1^2，2^2，3^2，4^2，5^2，…，第n个数是n^2，所以第10个数是10^2=100。
题5。
数列：0，3，8，15，24，…，第n个数是多少？解析。
这组数可以写成1^2-1，2^2-1，3^2-1，4^2-1，5^2-1，…，第n个数是n^2-1。
二、算式规律。
题6。
观察下列算式：1 = 1^2；1+3 = 2^2；1 + 3+5=3^2；1+3 + 5+7 = 4^2；…，求1+3+5+·s+99的值。
解析。
从算式可以看出，从1开始连续奇数的和等于数的个数的平方。
1到99的奇数有50个，所以1+3+5+·s+99 = 50^2=2500。
题7。
观察算式：2^1=2，2^2=4，2^3=8，2^4=16，2^5=32，2^6=64，…，求2^20的个位数字是多少？解析。
通过观察2^n的个位数字依次是2、4、8、6循环。
20÷4 = 5，刚好整除，所以2^20的个位数字是6。
题8。
有这样一组算式：(1-(1)/(2))(1+(1)/(2))=(1)/(2)×(3)/(2)=(3)/(4)；(1 -(1)/(3))(1+(1)/(3))=(2)/(3)×(4)/(3)=(8)/(9)；(1-(1)/(4))(1+(1)/(4))=(3)/(4)×(5)/(4)=(15)/(16)；…，求(1-(1)/(10))(1+(1)/(10))的值。
找规律
专题找规律例1：盒子里放了一只球,一位魔术师第一次从盒子里将这只球取出,变成4只球后放回盒子里；第二次从盒子里取出2只球,将每只球各变成4只球后,放进盒子里；……；第十次从盒子里取出10只球,将每只球各变成4只球的放回盒子里.问：这时盒子里共有多少只球?分析：在此题中,变化的量有以下几个：①操作的次数,即取球的次数；②取出的球数；③每次取出球以后,盒中剩余的球数；④每次放回的球数⑤盒中每次增加的球数；⑥每次操作结束后盒子中的球数.这每一个量都随着操作次数的变化而变化,正因如此,把每次操作的情况列成表格,在表格中的数据上寻找出数据的规律：操作次数1 2 3 (10)取出球数1 2 3 (10)盒中剩球数0 2 7 … A放回的球数4 8 12 …B盒中增加球数3 6 9 …C总球数4 10 19 …D在上表中,若能把A、B、C、D这四处的数据找到,那么此题也就完成了解题.从表中容易得到结果的是B为4N、C为3N.因此对所要求的D的结果就显而易见了：每次变化后的球的数目分别为：1、1+3=4、10=1+3+6、1+3+6+9=19、1+3+6+9+12=31……1+3+6+9+12+15+18+21+24+27+30=166.即D为166.说明：解决此类问题时,应将每一过程产生的结果用表格把数据一一列出,再观察数据的变化,从变化的数据中寻找规律,从而得出结论.例2：有10个朋友聚会,见面时如果每人和其余的每个人只握一次手,那么10个人共握手多少次?若N个朋友呢?分析：学生必须明白：1）每两个人握一次手；2）甲和乙握手的结果与乙和甲握手的结果只能看成是一种结果.3）若设这10个人为A1、A2、A3、A4、A5、A6、A7、A8、A9、A10.则A1与其它9个人握9次手；A2则与剩下的8个人握8次手；A3则与剩下的7个人握7次手；……A9与A10握1次手.因此,所有握手的次数就是9+8+7+6+5+4+3+2+1=45（次）.说明：解决此类问题时,应将出现的各种结果按一定规律一一给出,从而整理出所有结果来. 第二类：数字型题例3：观察下面依次排列的一列数,它的排列规律是什么?请接着写出后面的3个数.你能说出第100个数、第2004个数、第10000个数吗?①2,-2,2,-2,2,-2,……②-1,3,-5,7,-9,11,……③- ,- ,- ……分析：①容易发现这一窜数字是正负相间、绝对值都等于2的数构成的,即第奇数个数字是2,第偶数个数是-2.因此接下来的三个数就是2,-2,2.第100个数是-2,第2004个数是-2,第10000个数是-2.②容易发现这一窜数字除了符号有变化外,数字都是奇数；符号是一负一正相间；（第奇数个数是负的,第偶数个数是正的.因此,符号的确定可以用（-1）N来作为每一个数的系数.而奇数常常用（2N-1）来表示,固此数列的第N个数可以用（-1）N（2N-1）来表示,原数列中的接下来的三个数为：-13,15,-17.第100个数为199,第2004个数为4007,第10000个数为19999.③容易发现此数列的符号特征与第2小题的符号特征一样,可以用（-1）N来表示.而每一个分数可以看成是偶数的倒数,即,因此,此数列中的第N个数可表示为（-1）N ,故,接下来的三个数为,- ,.第100个数为,第2004个数为,第10000个数为.说明：此例中的数字规律学生寻找起来不是很困难的,只须了解一系特殊数列的表示方法就可以了,如奇数数列、偶数数列的表示方法；当然,符号的表示也是要求掌握的.例4：研究下列算式,你会发现什么规律?1×3+1=4=222×4+1=9=323×5+1=16=424×6+1=25=52请你将找出的规律用公式表示出来：▁▁▁▁▁这个公式是否对全体整数适用?分析：在第一个式子中去寻找“1”；在第二个式子中去寻找“2”；……；在第N个式子中去寻找“N”.同时,在相应的式子中寻找与“1”、“2”、……、“N”有关的数字.若发现式子“2”、……、中的“1”、“N”的位置是个固定的位置,则第N个式子中的“N”就在“1”、“2”、……、的位置上,相应的“N+1”、“N-1”等其它的与N有关的数字就因规律式子中的具体情况而定了.此题中各式的第一个数据即可看出是N的位置,第二个数据比第一个数据大2,则第二个数据可认为是N+2,第三个数据为常量1,第四个数据即为（N+1）2的结果,而最后的结论则是明确了（N+1）2.因此,找出的规律用公式表达为：N（N+2）+1=N2+2N+1=（N+1）2.例5：观察下列各式：13+23=9=（1+2）213+23+33=36=（1+2+3）213+23+33+43=（1+2+3+4）2……13+23+33+43+……+993+1003=?分析：从给出的三个条件式子中不难发现各式的特点：从1开始的几个连续自然数的立方和,等于这几个数的和的平方.学生不难找到第N个式子为：13+23+33+……+N3=（1+2+3+……+N）2.因此,13+23+33+43+……+993+1003=（1+2+3+4+……+99+100）2=50502.（用不完全归纳法来证明第N式的结论并不困难,限于篇幅,这里不给予证明了.）第三类：几何图形型例6：用火柴棒按图中的方式搭图：(1) 填写下表：图形编号①②③④⑤⑥火柴棒根数(2) 第N个图形需要多少根火柴?分析：在解此类问题时,方法很明确；就是把图形型问题转化为数字型问题,再从数字的特点来寻找出规律来解答.显然,第一个图形中有3根火柴棒；第二个图形中有9根火柴棒；第三个图形中有18根火柴棒；第四个图形中有30根火柴棒；……而3=1×3；9=3×3=（1+2）×3；18=6×3=（1+2+3）×3；30=10×3=（1+2+3+4）×3……因此,第N个图形中的火柴棒的根数为：（1+2+3+……+N）×3根.从而表中的每一个数据就不难填写出来了.类似此题的题目有下面一些题,供大家参考：1、当一条线段上标上一个点时,此时图中共有3条线段,若再标上一个点时,此时图中共有6条线段,……依次类推,则第N个图中共有多少条线段?2、从一个三角形的一个顶点向它的对边引一条线段,此时图中共有3个三角形（如图2）；若再向它的对边引一条线段,此时图中共有6个三角形（如图3）；……依次类推,则第N个图中共有多少个三角形?说明：（1）在数图形的数量时,如能掌握：先单一、后2个复合、再3个复合……依次类推数出相应所有的结论,这样做不易重复和遗漏.（2）道一些特殊数列的规律和一般表达式,才能较为轻松地完成此类问题的解答.如下表：自然数列1 2 3 ……N偶数数列2 4 6 ……2N奇数数列1 3 5 ……2N-1自然数的平方1 4 9 ……N2前N个自然数的和1（1）1+2（3）1+2+3（6）……1+2+3+……+N（）前N个奇数的和1（1）1+3（4）1+3+5（9）……1+3+5+……+（2N-1）（N2）前N个偶数的和2（2）2+4（6）2+4+6（12）......2+4+6+ (2)N（N+1）为了大家进一步巩固这方面的知识点,以下练习题,供大家参考：1）观察下列各式,你会发现什么规律?3×5=15=42-15×7=35=62-1……11×13=143=122-1将你猜想到的规律用只含一个字母的式子表示出来.2）观察下列各式：A1=5×1-3=2A2=5×2-3=7A3=5×3-3=12A4=5×4-3=17……（1）根据以上规律,猜测计算AN=（2）当N=100时,A100=你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如图所示,这样捏合拉伸到多少次,就可拉出128根细面条?4）如图,正方形的棱长都是1,按图中规律堆放,若依次由上向下称之为第一层、第二层、第三层、……、第N层,请填表：小正方体排列层数N 1 2 3 4 5 …N最低层小正方体的个数1 3 6 …数学题,可以分为两大类,一类是应用数学规律题,一类是发现数学规律题.应用数学规律题,指的是需要学生应用以前学习过的数学规律解答的题目.发现数学规律题,指的是与学生以前学习的数学规律没有什么关系,需要学生先从已知的事物中找出规律,才能够解答的题目.学生所做数学题,绝大多数属于第一类.由于发现数学规律题,能够增强学生的创造意识,提高学生的创新能力.因此,近几年来,人们开始逐渐重视这一类数学题.尤其是最近两年,全国多数地市的中招考试,都有这类题目.研究发现数学规律题的解题思想,不但能够提高学生的考试成绩,而且更有助于创新型人才的培养.一、要善于抓主要矛盾有些题目看上去很大、很复杂,实际上,关键性的内容并不多.对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低,问题也就容易解决了.还有,邵阳市2006年初中毕业学业考试试题卷（课改区）的数学试题“图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第n个等腰直角三角形的斜边长为_____________.”也可以按照这个思想求解.二、要抓题目里的变量找数学规律的题目,都会涉及到一个或者几个变化的量.所谓找规律,多数情况下,是指变量的变化规律.所以,抓住了变量,就等于抓住了解决问题的关键.例如,用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第（3）个图形中有黑色瓷砖块,第个图形中需要黑色瓷砖块（用含的代数式表示）.（海南省2006年初中毕业升考试数学科试题（课改区））这一题的关键是求第个图形中需要几块黑色瓷砖?在这三个图形中,前边4块黑瓷砖不变,变化的是后面的黑瓷砖.它们的数量分别是,第一个图形中多出0×3块黑瓷砖,第二个图形中多出1×3块黑瓷砖,第三个图形中多出2×3块黑瓷砖,依次类推,第n个图形中多出（n-1）×3块黑瓷砖.所以,第n个图形中一共有4+（n-1）×3块黑瓷砖.云南省2006年课改实验区高中（中专）招生统一考试也出有类似的题目：“观察图（l）至（4）中小圆圈的摆放规律,并按这样的规律继续摆放,记第n个图中小圆圈的个数为m,则,m= （用含n 的代数式表示）.”三、要善于比较“有比较才有鉴别”.通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律. 找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律.揭示的规律,常常包含着事物的序列号.所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘.例如,观察下列各式数：0,3,8,15,24,…….试按此规律写出的第100个数是.”解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数.我们把有关的量放在一起加以比较：给出的数：0,3,8,15,24,…….序列号：1,2,3, 4, 5,…….容易发现,已知数的每一项,都等于它的序列号的平方减1.因此,第n项是n2-1,第100项是1002-1.如果题目比较复杂,或者包含的变量比较多.解题的时候,不但考虑已知数的序列号,还要考虑其他因素.譬如,日照市2005年中等学校招生考试数学试题“已知下列等式：①13＝12；②13＋23＝32；③13＋23＋33＝62；④13＋23＋33＋43＝102 ；…………由此规律知,第⑤个等式是．”这个题目,在给出的等式中,左边的加数个数在变化,加数的底数在变化,右边的和也在变化.所以,需要进行比较的因素也比较多.就左边而言,从上到下进行比较,发现加数个数依次增加一个.所以,第⑤个等式应该有5个加数；从左向右比较加数的底数,发现它们呈自然数排列.所以,第⑤个等式的左边是13＋23＋33＋43＋53.再来看等式的右边,指数没有变化,变化的是底数.等式的左边也是指数没有变化,变化的是底数.比较等式两边的底数,发现和的底数与加数的底数和相等.所以,第⑤个等式右边的底数是（1+2+3+4+5）,和为152.四、要善于寻找事物的循环节有些题目包含着事物的循环规律,找到了事物的循环规律,其他问题就可以迎刃而解.“观察下列球的排列规律(其中●是实心球,○是空心球)：譬如,玉林市2005年中考数学试题：●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个.”这些球,从左到右,按照固定的顺序排列,每隔10个球循环一次,循环节是●○○●●○○○○○.每个循环节里有3个实心球.我们只要知道2004包含有多少个循环节,就容易计算出实心球的个数.因为2004÷10=200（余4）.所以,2004个球里有200个循环节,还余4个球.200个循环节里有200×3=600个实心球,剩下的4个球里有2个实心球.所以,一共有602个实心球.五、要抓住题目中隐藏的不变量有些题目,虽然形式发生了变化,但是本质并没有改变.我们只要在观察形式变化的过程中,始终注意寻找它的不变量,就可以揭示出事物的本质规律.例如,2006年芜湖市（课改实验区）初中毕业学业考试题“请你仔细观察图中等边三角形图形的变换规律,写出你发现关于等边三角形内一点到三边距离的数学事实：.”在这三个图形中,白色的三角形是等边三角形,里边镶嵌着三个黑色三角形.从左向右观察,其中上边两个黑色三角形按照顺时针的方向发生了旋转,但是形状没有发生变化,当然黑色三角形的高也没有发生变化.左起第一个图形里黑色三角形高的和是等边三角形里一点到三边的距离和,最后一个图形里,三个黑色三角形高的和是等边三角形的高.所以,等边三角形里任意一点到三边的距离和等于它的高.六、要进行计算尝试找规律,当然是找数学规律.而数学规律,多数是函数的解析式.函数的解析式里常常包含着数学运算.因此,找规律,在很大程度上是在找能够反映已知量的数学运算式子.所以,从运算入手,尝试着做一些计算,也是解答找规律题的好途径.例如,汉川市2006年中考试卷数学“观察下列各式：0,x,x2,2x3,3x4,5x5,8x6,…….试按此规律写出的第10个式子是.”这一题,包含有两个变量,一个是各项的指数,一个是各项的系数.容易看出各项的指数等于它的序列号减1,而系数的变化规律就不那么容易发现啦.然而,如果我们把系数抽出来,尝试做一些简单的计算,就不难发现系数的变化规律.系数排列情况：0,1,1,2,3,5,8,…….从左至右观察系数的排列,依次求相邻两项的和,你会发现,这个和正好是后一项.也就是说原数列相邻两项的系数和等于后面一项的系数.使用这个规律,不难推出原数列第8项的系数是5+8=13,第9项的系数是8+13=21,第10项的系数是13+21=34.所以,原数列第10项是34x9.“条条道路通罗马”.解答找规律这一类题的思路有许多条,这里只是把“常用”的解题思路做一个简单的总结.有兴趣的老师还可以从解方程组的角度、拉格郎日插值定理的角度、求函数解析式的角度进一步研究解决这一类问题的新途径.（1）1,（2)1+5=6,(3)1+5+9=16.请问第n个为多少?请写出过程.第一个数为1第二个数为1＋5＝6第三个数为1＋5＋9＝15第四个数为1＋5＋9＋13＝28由以上的规律中可以发现,每增加一层,所增加的数比前一个数多4,第n个数最后增加数的求法为4×(n－1)＋1 ∴由第1个数连续加到最后一个数的总和为(1＋最后一个数)÷2n再把前2个算式综合起来就可得到第n个数为[2＋4⨉(n－1)]÷2n 即n（2n-1）设有一列数：1,1/2,2/1,1/3,2/2,3/1,1/4,2/3,3/2,4/1,1/5,……（1）数1/5后的第一个数是什么?（2）如果我们从左边第一个数开始一直往右数,那么1/9是这列数的第几个数?由数列：1,1/2,2/1,1/3,2/2,3/1,1/4,2/3,3/2,4/1,1/5,……可知往后分子上的数字逐渐增大直到5为止, 分母上的数字逐渐减小直到1为止,所以数后的第一个数是= . 由题意知从左边第一个数开始一直往右数,1到1是1个数,1到为2个数, 到为3个数, 到为4个数字, ⋯到为8个数字, 所以1+2+3+4+5+6+7+8=36. 所以是这列数的37个数.3,10,29,66下一个数是多少?3=13+2 10=23+2 29=33+2 66=43+2 下一个数是：53+2=127（1）－1,2,－4,8,－16,32,……,第10个数是__________各数分别可写为次数依次为0、1、2、3……当次数为偶数时,前面有负号,所以第10个数表示为.（2）1,－3,5,－7,…,第15个数是__________．各数的绝对值分别表示为, , ……,（n表示个数）且个数是偶数时,前面有负号,所以第15个数的绝对值为.初中数学考试中,经常出现数列的找规律题,本文就此类题的解题方法进行探索：一、基本方法——看增幅（一）如增幅相等（此实为等差数列）：对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为：a+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅.然后再简化代数式a+(n-1)b.例：4、10、16、22、28……,求第n位数.分析：第二位数起,每位数都比前一位数增加6,增幅相都是6,所以,第n位数是：4+(n-1)×6＝6n－2（二）如增幅不相等,但是,增幅以同等幅度增加（即增幅的增幅相等,也即增幅为等差数列）.如增幅分别为3、5、7、9,说明增幅以同等幅度增加.此种数列第n位的数也有一种通用求法. 基本思路是：1、求出数列的第n-1位到第n位的增幅；2、求出第1位到第第n位的总增幅；3、数列的第1位数加上总增幅即是第n位数.举例说明：2、5、10、17……,求第n位数.分析：数列的增幅分别为：3、5、7,增幅以同等幅度增加.那么,数列的第n-1位到第n位的增幅是：3+2×(n-2)=2n-1,总增幅为：［3+（2n-1）］×(n-1)÷2＝（n+1）×(n-1)＝n2-1所以,第n位数是：2+ n2-1= n2+1此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察凑的方法求出,方法就简单的多了.（三）增幅不相等,但是,增幅同比增加,即增幅为等比数列,如：2、3、5、9,17增幅为1、2、4、8.（三）增幅不相等,且增幅也不以同等幅度增加（即增幅的增幅也不相等）.此类题大概没有通用解法,只用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧.二、基本技巧（一）标出序列号：找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律.找出的规律,通常包序列号.所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘.例如,观察下列各式数：0,3,8,15,24,…….试按此规律写出的第100个数是.解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数.我们把有关的量放在一起加以比较：给出的数：0,3,8,15,24,…….序列号：1,2,3, 4, 5,…….容易发现,已知数的每一项,都等于它的序列号的平方减1.因此,第n项是n2-1,第100项是1002-1.（二）公因式法：每位数分成最小公因式相乘,然后再找规律,看是不是与n2、n3,或2n、3n,或2n、3n有关.例如：1,9,25,49,（）,（）,的第n为（2n-1）2 （三）看例题：A：2、9、28、65.增幅是7、19、37.,增幅的增幅是12、18 答案与3有关且.即：n3+1B：2、4、8、16.增幅是2、4、8.. .答案与2的乘方有关即：2n（四）有的可对每位数同时减去第一位数,成为第二位开始的新数列,然后用（一）、（二）、（三）技巧找出每位数与位置的关系.再在找出的规律上加上第一位数,恢复到原来.例：2、5、10、17、26……,同时减去2后得到新数列：0、3、8、15、24……,序列号：1、2、3、4、5分析观察可得,新数列的第n项为：n2-1,所以题中数列的第n项为：（n2-1）+2＝n2+1 （五）有的可对每位数同时加上,或乘以,或除以第一位数,成为新数列,然后,在再找出规律,并恢复到原来.例：4,16,36,64,?,144,196,…?（第一百个数）同除以4后可得新数列：1、4、9、16…,很显然是位置数的平方.（六）同技巧（四）、（五）一样,有的可对每位数同加、或减、或乘、或除同一数（一般为1、2、3）.当然,同时加、或减的可能性大一些,同时乘、或除的不太常见.（七）观察一下,能否把一个数列的奇数位置与偶数位置分开成为两个数列,再分别找规律.三、基本步骤1、先看增幅是否相等,如相等,用基本方法（一）解题.2、如不相等,综合运用技巧（一）、（二）、（三）找规律3、如不行,就运用技巧（四）、（五）、（六）,变换成新数列,然后运用技巧（一）、（二）、（三）找出新数列的规律4、最后,如增幅以同等幅度增加,则用用基本方法（二）解题四、练习题例1：一道初中数学找规律题0,3,8,15,24,······2,5,10,17,26,·····0,6,16,30,48······（1）第一组有什么规律?（2）第二、三组分别跟第一组有什么关系?（3）取每组的第7个数,求这三个数的和?2、观察下面两行数2,4,8,16,32,64,．．．（1）5,7,11,19,35,67．．．（2）根据你发现的规律,取每行第十个数,求得他们的和.（要求写出最后的计算结果和详细解题过程.）3、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?4、3^2-1^2=8×1 5^2-3^2=8×2 7^2-5^2=8×3 ……用含有N的代数式表示规律写出两个连续技术的平方差为888的等式五、对于数表1、先看行的规律,然后,以列为单位用数列找规律方法找规律2、看看有没有一个数是上面两数或下面两数的和或差。
初中数学找规律问题
规律探索【1、数字问题】例1 观察一列数：1，－,3611,259,167,95,43--……根据规律，请你写出第10个数是 。
解： 正负控制：1(1)n +- 形式一致：1357,,, (14916)， 分子规律：21n - 分母规律：2n则该数列的规律为：12(21)(1)n n n +-- ，令n=10，第10个数为：19100-例2 古希腊数学家把1，3，6，10，15，21，… 叫做三角形数，根据它的规律，则第100个与第98个的差为 ________解：第1个数：1第2个数：1+2=3 第3个数：1+2+3=6 第4个数：1+2+3+4=10 依次类推。
第98个数：1+2+3+….+98 第100个数：1+2+3+…+100则第100个与第98个的差为：100+99=199 练习：（1）观察一列数：21，52-，103，174-，265，376-……根据规律，请你写出第10个数是？解：正负控制：1(1)n +- 分子规律：n分母规律 2211=+，2521=+，21031=+，以此类推………则该数列的规律为：12(1)1n n n +⨯-+，令n=10，第10个数为：10101- （2）按一定规律排列的一列数依次为11113102635---11，，，，，，，215按此规律排列下去，这列数中第七个数是解：正负控制：(1)n - 分子规律：1 分母：2,3,10,15…….分母规律：2222211,321,1031,1541=+=-=+=-，以此类推：2(1)n n --则该数列的规律为：2(1)(1)n nn ---，令n=7，第7个数为：150- （3）某种细胞开始有2个，1小时后分裂成4并死去1个，2小时后分裂成6个并死去1个，3小时后分裂成10个并死去1个，按此规律，5小时后细胞存活数是____，n 小时后细胞存活数是____ 解：读题该数列为： 3，5，9，17……..（一般一个数列知道前3个可推出规律，再知道第4个进行验证） 不难发现：123321,521,92 1......=+=+=+，故该数列规律：21n + 令n=5，第5个数为：52132133+=+=【2、图形规律】例3 观察图给出的四个点阵，s 表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n 个点阵中的点的个数s 为（ ）A 、32n -B 、31n -C 、41n +D 、43n -解：第1个图：1=1+4×0 第2个图：1+4=1+4×1 第3个图：1+4+4=1+4×2以此类推 第n 个图：1+4×（n －1）=4n －3例4 若按下图方式摆放餐桌和椅子，请探索规律并填表：餐桌张数 1 234 ….. 10 n可坐人数 6+4×06+4×1=10 6+4×2=1418…..4242n +练习：（1）观察下列图形，则第n 个图形中三角形的个数是（ ）A 、22n +B 、44n +C 、44n -D 、4n解：第1个图：4个 第2个图：8个 第3个图：12个 规律：4n（2） 如图是一组有规律的图案， 第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……第8个图案由_____个基础图形组成，第n (n 是正整数)个图案中由 ___ 个基础图形组成。
初中数学找规律习题大全
1找规律专项训练一：数式问题223344aa2222，?4??48??8??3?2，，3???2?为正整数）……，若b（1.（湛江）已知a、1515bb3388a?b?则．2.（贵阳）有一列数a，a，a，a，a，…，a，其中a＝5×2＋1，a＝5×3＋2，a＝5×4＋3，a45122n3314＝5×5＋4，a＝5×6＋5，…，当a＝2009时，n的值等于（）n5A．2010 B．2009 C．401 D．334345aaa23.（沈阳）有一组单项式：a，－，，－，…．观察它们构成规律，用你发现的规律写出第10个单234项式为．1234，??，，，…，那么第7个数是．4.（牡丹江）有一列数105172 233547a?ba?ba?b b?a，……，其中第10，，，个式子是5.（南充）一组按规律排列的多项式：()1910191017102110b?ba?bbaa?a?B． D ．C．A．112233?1?2??2?3??3?1?（安徽）观察下列等式：6.，，……，422343 2）证明你写出的等式的正确性．n个等式；（（1）猜想并写出第7.（绵阳）将正整数依次按下表规律排成四列，则根据表中的排列规律，数2009应排的位置是第行第列．第1列第2列3第列4列第?n；▲22，3，…从小到大按下面规律排列．若第4行第列的数为32，则①18.（台州）将正整数，jj ii．表示）▲（用②第，行第列的数为n321第…列列第第列第列n1312…第行22n3??2nn?1n2…第行33n3?2n?22nn2?1…第行………………二：定义运算问题22b?a?a?b???24x? 3，其法则为：），求方程（4（定西）在实数范围内定义运算“1.的解．”aaaa?a21，与它前面那个数的倒数的差，每一个数都等于，，若，2.有一列数从第二个数开始，，，1321n a 为（则）200712007?21Ｄ．Ｂ．Ａ．Ｃ．2三：剪纸问题1．（2004年河南）如图（9），把一个正方形三次对折后沿虚线剪下则得到的图形是（）2．（2004年浙江湖州）小强拿了一张正方形的纸如图（10）①，沿虚线对折一次得图②，再对折一次得图③，然后用剪刀沿图③中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是（）3．（2004年浙江衢州）如图（11），将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，……，根据以上操作方法，请你填写下表：3N 4 5 1 2 3 操作次数N ……7 10 4 正方形的个数……x A、A、AA、A、A?A?OAAA?AA?AA过点，轴的正半轴上依次截取3.（莆田）如图，在??x P、、PP、P、P0?xy?，得直角三角形轴的垂线与反比例函数的图象相交于点分别作53214532314142253124x，PAPA、AAAP、APA、AAOP、并设其面积分别为514224131243352?y x yS，、S、S、S、SS的值为则．551432P1P 2 P3PP4 5O x AAAAA5 3 4 1 2 10题图）（第（长春）用正三角形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案都比上一个4.的代数式n （用含n图案多一个正六边形和两个正三角形，则第个图案中正三角形的个数为. 表示）题）（第4100，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第6（丹东）如图5.4枚．个图案需棋子……32图案图案1图案6图n个图中最小的三角形的个数有 6.（抚顺）观察下列图形（每幅图中最小的三角形都是全等的），请写出第．．．．个．个图第4 第3个图第1个图第2个图题图）（第167.（哈尔滨）观察下列图形：它们是按一定规律排列的，依照此规律，第16个图形共有个★．五：对称问题、1.（伊春）在平面直角坐标系中，已知3个点的坐标分别为、. 一只电子蛙位于，A1)(11) 1，A(0，2)A(132坐标原点处，第1次电子蛙由原点跳到以为对称中心的对称点，第2次电子蛙由点跳到以为对APAP2111称中心的对称点，第3次电子蛙由点跳到以为对称中心的对称点，…，按此规律，电子蛙分别PPAP3223以、、为对称中心继续跳下去．问当电子蛙跳了2009次后，电子蛙落点的坐标是（_______ ，AAAP3122009_______）.2.（2004年宁波）仔细观察下列图案，如图（12），并按规律在横线上画出合适的图形。
初中数学找规律习题大全
初中数学找规律习题大全TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】找规律专项训练一：数式问题 1.（湛江）已知22223322333388+=⨯+=⨯，，244441515+=⨯，……，若288a ab b +=⨯（a 、b 为正整数）则a b += ．2.（贵阳）有一列数a 1，a 2，a 3，a 4，a 5，…，a n ，其中a 1＝5×2＋1，a 2＝5×3＋2，a 3＝5×4＋3，a 4＝5×5＋4，a 5＝5×6＋5，…，当a n ＝2009时，n 的值等于（ ）A ．2010B ．2009C ．401D ．3343.（沈阳）有一组单项式：a 2，－a 32，a 43，－a 54，…．观察它们构成规律，用你发现的规律写出第10个单项式为 ．4.（牡丹江）有一列数1234251017--，，，，…，那么第7个数是 ． 5.（南充）一组按规律排列的多项式：a b +，23a b -，35a b +，47a b -，……，其中第10个式子是( )A ．1019a b +B ．1019a b -C ．1017a b -D ．1021a b -6.（安徽）观察下列等式：111122⨯=-，222233⨯=-，333344⨯=-，…… （1）猜想并写出第n 个等式；（2）证明你写出的等式的正确性．7.（绵阳）将正整数依次按下表规律排成四列，则根据表中的排列规律，数2009应排的位置是第 行第 列．（台8.州）将正整数1，2，3，…从小到大按下面规律排列．若第4行第2列的数为32，则①n = ▲ ；②第i 行第j 列的数为 ▲ （用i ，j 表示）．第1列 第2列 第3列 … 第n 列 第1行 … 第2行 … 第3行 … ………………二：定义运算问题1.（定西）在实数范围内定义运算“⊕”，其法则为：22a b a b ⊕=-，求方程（4⊕3）⊕24x =的解． 2.有一列数1a ，2a ，3a ，，n a ，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若12a =，则2007a 为（ ） Ａ．2007Ｂ．2Ｃ．12Ｄ．1-三：剪纸问题1． （2004年河南）如图（9），把一个正方形三次对折后沿虚线剪下则得到的图形是（ ）2． （2004年浙江湖州）小强拿了一张正方形的纸如图（10）①，沿虚线对折一次得图②，再对折一次得图③，然后用剪刀沿图③中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是（ ）3． （2004年浙江衢州）如图（11），将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，……，根据以上操作方法，请你填写下表：第4行 12 11 10 ……操作次数N1 2 34 5 … N …3.（莆田）如图，在x 轴的正半轴上依次112233445OA A A A A A A A A ====，截取过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、，得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为 ．4.（长春）用正三角形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案都比上一个图案多一个正六边形和两个正三角形，则第n 个图案中正三角形的个数为 （用含n 的代数式表示）.5.（丹东）如图6，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第100个图案需棋子 枚．6.（抚顺）观察下列图形（每幅图中最小．．的三角形都是全等的），请写出第n 个图中最小．．的三角形的个数有 个．7.（哈尔滨）观察下列图形：它们是按一定规律排列的，依照此规律，第16个图形共有 个★． 五：对称问题1.（伊春）在平面直角坐标系中，已知3个点的坐标分别为1(11)A ，、2(02)A ，、3(11)A -，. 一只电子蛙位于坐标原点处，第1次电子蛙由原点跳到以1A 为对称中心的对称点1P ，第2次电子蛙由1P 点跳到以2A 为对称中心的对称点2P ，第3次电子蛙由2P 点跳到以3A 为对称中心的对称点3P ，…，按此规律，电子蛙分别以1A 、2A 、3A 为对称中心继续跳下去．问当电子蛙跳了2009次后，电子蛙落点的坐标是2009P （_______ ，_______）.2.（2004年宁波）仔细观察下列图案，如图（12），并按规律在横线上画出合适的图形。
(完整word)初中数学找规律
例题：（10西城二模）一组按规律排列的整数 5, 7, 11, 19,…，第6个整数为，根据上述规律，第n 个整数为 _____________ （ n 为正整数）•••第6个整数是26 3 67，第n 个整数是2n 3 （n 为正整数）.练习:1 4 9 16 1' （10怀柔二莫）按一定规律排列的一列数依次为：3,产，亍……，按此规 律排列下去，这列数中的第5个数是 ____________ ，第n 个数是 ______________________________________2、（09东城一模）按一定规律排列的一列数依次为： -…，按此规律排列下去，这列数中的第 9个数是 35 答案：12 n1n ( 1)例题：（10通州一模）某些植物发芽有这样一种规律：当年所发新芽第二年不发 芽，老芽在以后每年都发芽.发芽规律见下表（设第一年前的新芽数为 a ）照这样下去，第8年老芽数与总芽数的比值为.解：第8年的老芽数是21a ，新芽数是13a ，总芽数是34a ,贝吐匕值为 •34 练习：1、（ 08石景山一模）小说《达•芬奇密码》中的一个故事里出现了一串神秘排列 的数，将这串令人费解的数从小到大的顺序排列为：1,1, 2, 3, 5, 8 ，则答案: 25 n 211 ， 2n 11 ] 丄 丄 丄2，3，10，15， 26这列数的第8个数是______________ .2答案:212、（09房山二模）填在下面三个田字格内的数有相同的规律，根据此规律，请填 出图4中的数字.答案：7,9,11,176（（1）n 与（1）n1）例题：（09通州二模）12.观察并分析下列数据，寻找规律：0,..、36 ,3,- 2、.3，,15，— 3・.2，……那么第10个数据是 _____________ ;第n 个数据 是 ______ .•••第10个数据是3-3，第n 个数据是（1）n1.. 3n 3 . 练习：1、（10房山一模）一组按规律排列的式子： 4，%~|，■16，...（a 0），其中第a a a a 8个式子是 _____ ，第n 个式子是 ________ （n 为正整数）. 答案： 64( 1)n 1 n 223 3n 1aa58112、（10门头沟二模）一组按一定规律排列的式子：一a 2，-，—-，—，…,23 4（a ^ 0）,则第n 个式子是 ________ （n 为正整数）3n 1答案：（1）0-—n3、（09崇文一模）一组按规律排列的数：2, 0, 4, 0, 6, 0,…，其中第7个数 是 ________ ，第n 个数是 _________ （ n 为正整数）. 答案：8,』^（n 1）57 9108例题：（08通州二模）世界上著名的莱布尼茨三角形如图所示：贝U排在第10行从左边数第3个位置上的数是_______ .•••第10行倒数第三个数是———.72 90 360练习：1、（08大兴一模）自然数按一定规律排成下表，那么第200行的第5个数是_____ .12 34 5 67 89 101113 14 1512答案：199052、如图的数字方阵中，方框所缺的数，按照适宜的规律填上（A、100B、128C、129D、130答案：C例题：（11平谷二模）如图，将连续的正整数1,2,3,4……依次标在下列三角形中，那么2011这个数在第 ____ 个三角形的 ________ 顶点处（第二空填：上，左下，右下）.• 2011 这个数在第671个三角形的上顶点处.故答案为：671, 上.练习:1、(08 崇文一模)观察下列等式：31 1 2 , 32 1 8 , 33 1 26 , 34 1 80 , 35 1 242 ,…….通过观察，用你所发现的规律确 定32008 1的个位数字是 ______ . ___ 答案：32、右图为手的示意图，在各个手指间标记字母A ，B ，C, D 请你按图中箭头所指 方向（即A — B ^C T C T B ^B^d …的方式）从 A 开始 数连续的正整数1, 2, 3, 4,…，当数到12时，对应的字母是 当字母C 第201次出现时，恰好数到的数是 当字母C 第2n 1次出现时（n 为正整数），恰 好数到的数是 ____ （用含n 的代数式表示）. 答案：B, 603, 6n+3例题：（09平谷一模）已知：£2£2232 34 44 4……若b x1 1 '2 2 ‘3 3'10=a +10 （a 、b 都是正整数），则a+b 的最小值是 _________ . 二a+b 的最小值是19 练习：1. （ 10密云一模）下面是按一定规律排列的一列数：第1个数： 1 1 122第2个数： 1 1 11 (1)211 1323 第3个数： 1 1 11 (1)2 1423232n 11 1L 1(“第n 个数:2n(1)3；4 ；4 5 6那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（）A.第10个数B .第11个数 C.第12个数 D.第13个数答案：A例题1: （10昌平一模）观察下列图案：照这样它们是按照一定规律排列的，依照此规律，第5个图案中共有________ 个三角形，第n （n 1，且n为整数）个图案中三角形的个数为_________ （用含有n的式子表示）.解答：解：第5个图案中，有6+4X4=22 （个）三角形；第n个图案中，有6+4（n-1 ）=4n+2 （个）三角形.例题2. （10西城一模）在平面直角坐标系中，我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形.如图，在菱形ABCD中，四个顶点坐标分别是（一8,0 ），（0,4 ），（8,0 ），（0，点正方形的个数是个；若菱形ABGD n的四个顶点坐标分别为（—2n,0 ），（0, n）, （2n，0）, （0，—n）（n 为正整数），则菱形ABnG D n能覆盖的单位格点正方形的个数为_______________________ （用含有n的式子表示）.答案为：4n2-4n .—4），贝U菱形ABCD能覆盖的单位格练习：.1、（10大兴一模）如图4所示，把同样大小的黑色棋子摆放在正多边形的边上，按的规律摆下去，则第n个图形需要黑色棋子的个数是_______________第1个图形第2个图形第3个图形第4个图形（图4）答案：n（n 2）2、（08顺义二模）如图，图①，图②，图③，图④……是用围棋棋子摆成的一列图①图②图③图④具有一定规律的“山”字•则第n个“山”字中的棋子个数是______________答案：5n+23、（08丰台二模）用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：请问第n个图案中有白色纸片的张数为A. 4n 3B. 3n 1C. nD. 2n 2答案：B第1个第2个第3个4、（10丰台一模）在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点•请你观察图中正方形ABCD, ABC2D2，AB3C3D3…每个正方形四条边上的整点答案：80个.的个数•按此规律推算出正方形Ao BwC o D。
完整)初中数学找规律专项练习题(有答案)
完整)初中数学找规律专项练习题(有答案)1、观察规律：1=1；1+3=4；1+3+5=9；1+3+5+7=16；…，则2+6+10+14+…+2014的值是多少？2、用四舍五入法对取近似数，并精确到千位，用科学计数法表示为多少？3、观察下面的一列数：-1，2，-3，4，-5，6…请找出其中排列的规律，并按此规律填空。
（1）第10个数是多少？第21个数是多少？（2）-40是第几个数？26是第几个数？4、一组按规律排列的数：1，3，6，10，15…请推断第9个数是多少？5、计算：（-100）+（-101）=多少？（-2）+（-2）=多少？6、若。
则等于多少？7、大肠杆菌每过20分钟便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成多少个？8、猜数字游戏中，XXX写出如下一组数：1，3，5，7，9…n个数是…，XXX猜想出第六个数字是多少？根据此规律，第9、10个数字分别是多少？9、若。
与｜b+5|的值互为相反数，则等于多少？10、在计数制中，通常我们使用的是“十进位制”，即“逢十进一”.而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表：十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx（二）写成十进位制数为多少？11、为求。
值，可令S=。
则2S=。
因此所以。
仿照以上推理计算出的值是多少？二、选择题13、的值是多少？【】A．-2 B．-1 C．0 D．114、已知8.62=73.96，若x=0.7396，则x的值等于（）A.86.2B.862C.±0.862D.±86215、计算：(-2)+(-2)的值是多少？A.2B.-1C.-2D.-416、计算等于多少？A． B． C． D．17、已知a、b互为相反数，c、d互为倒数，m的绝对值为1，p是数轴到原点距离为1的数，那么的值是多少？A．3 B．2 C．1 D．018、若。
初中数学找规律题及其答案
整式的加减——专题训练与提升1、根据下列5个图形及相应点的个数的变化规律，试猜测第n个图中有个点．2、找规律．下列图中有大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第n幅图中共有个．3、如图，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第100个图案需棋子枚．4、观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有个．5、观察下列图形，它们是按一定规律排列的，依照此规律，第16个图形共有个★．6、如图①，图②，图③，图④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是，第n个“广”字中的棋子个数是．7、如图1是二环三角形，可得S=∠A1+∠A2+…+∠A6=360°，下图2是二环四边形，可得S=∠A1+∠A2+…+∠A7=720°，图3是二环五边形，可得S=1080°，…聪明的同学，请你根据以上规律直接写出二环n边形（n≥3的整数）中，S=度．（用含n的代数式表示最后结果）8、观察下列图形（每幅图中最小的三角形都是全等的），请写出第n个图中最小的三角形的个数有个．9、将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表．则an= ．（用含n的代数式表示）所剪次数正三角形个数10、用正三角形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案都比上一个图案多一个正六边形和两个正三角形，则第n个图案中正三角形的个数为（用含n的代数式表示）．11、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个10×10的正方形图案，则其中完整的圆共有个．12、根据下列图形的排列规律，第2008个图形是福娃（填写福娃名称即可）．13、用火柴棒按照如图所示的方式摆图形，则第n个图形中，所需火柴棒的根数是．14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成：拼搭第1个图案需4根小木棒，拼搭第2个图案需10根小木棒，…，依次规律，拼搭第8个图案需小木棒根．15、一张长方形桌子需配6把椅子，按如图方式将桌子拼在一起，那么8张桌子需配椅子把．16、下列每个图是由若干个圆点组成的形如四边形的图案，当每条边（包括顶点）上有n（n≥2个圆点时，图案的圆点数为Sn ．按此规律推断Sn关于n的关系式为：Sn= ．17、如图是由火柴棒搭成的几何图案，则第n个图案中有根火柴棒．（用含n的代数式表示）18、观察下列图形的构成规律，根据此规律，第8个图形中有个圆．19、观察表一，寻找规律．表二，表三分别是从表一中选取的一部分，则a+b 的值为 ． 表一：表二：表三：20、如图所示的图案是由正六边形密铺而成，黑色正六边形周围第一层有六个白色正六边形，则第n 层有 个白色正六边形．21、把边长为3的正三角形各边三等分，分割得到图①，图中含有1个边长是1的正六边形；把边长为4的正三角形各边四等分，分割得到图②，图中含有3个边长是1的正六边形；把边长为5的正三角形各边五等分，分割得到图③，图中含有6个边长是1的正六边形；…依此规律，把边长为7的正三角形各边七等分，并按同样的方法分割，得到的图形中含有 个边长是1的正六边形．0 1 2 3 .... 1 3 5 7 .... 2 5 8 11 .... 3 7 11 15 .... .... .... .... .... .... 11 14 a 11 1317 b22、观察下列图形的排列规律（其中☆，□，●分别表示五角星、正方形、圆）●□☆●●□☆●□☆●●□☆●…若第一个图形是圆，则第2008个图形是（填名称）．23、下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，按照图示的规律摆下去，则第n幅图中有个菱形．24、如图，观察下列图案，它们都是由边长为1cm的小正方形按一定规律拼接而成的，依此规律，则第16个图案中的小正方形有个．25、用同样大小的黑色棋子按图所示的方式摆图形，按照这样的规律摆下去，则第n个图形需棋子枚．（用含n的代数式表示）27、如图所示是一副“三角形图”，第一行有一个三角形，第二行有2个三角形，第三行有4个三角形，第四行有8个三角形，…，你是否发现三角形的排列规律，请写出第七行有个三角形．28、如图，用3根小木棒可以摆出第（1）个正三角形，加上2根木棒可以摆出第（2）个正三角形，再加上2根木棒可以摆出第（3）个正三角形…这样继续摆下去，当摆出第（n）个正三角形时，共用了木棒根．29、观察下列图形，根据变化规律推测第100个与第个图形位置相同．30、如图，用火柴棒按以下方式搭小鱼，搭1条小鱼用8根火柴棒，搭2条小鱼用14根，…，则搭n条小鱼需要根火柴棒．（用含n的代数式表示）整式的加减——专题训练与提升参考答案1．n2-n+1 2．（2n-1）3．302 4．121 5．49 6．152n+5 7．360（n-2）8．4n-19．3n+1 10．2n+2 11．181 12．欢欢13．3n+1 14．88 15．20 16．4n-4 17．2n（n+1）18．65 19．37 20．6n 21．15 22．正方形23．（2n-1）24．136 26．3n+1 27．64 28．2n+1 29．1或4 30．6n+2。
初中数学找规律题及其标准答案
初中数学找规律题及其答案————————————————————————————————作者：————————————————————————————————日期：整式的加减——专题训练与提升1、根据下列5个图形及相应点的个数的变化规律，试猜测第n个图中有个点．2、找规律．下列图中有大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第n幅图中共有个．3、如图，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第100个图案需棋子枚．4、观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有个．5、观察下列图形，它们是按一定规律排列的，依照此规律，第16个图形共有个★．6、如图①，图②，图③，图④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是，第n个“广”字中的棋子个数是．7、如图1是二环三角形，可得S=∠A1+∠A2+…+∠A6=360°，下图2是二环四边形，可得S=∠A1+∠A2+…+∠A7=720°，图3是二环五边形，可得S=1080°，…聪明的同学，请你根据以上规律直接写出二环n边形（n≥3的整数）中，S= 度．（用含n的代数式表示最后结果）8、观察下列图形（每幅图中最小的三角形都是全等的），请写出第n个图中最小的三角形的个数有个．9、将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表．则an= ．（用含n的代数式表示）所剪次数三角形个数10、用正三角形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案都比上一个图案多一个正六边形和两个正三角形，则第n个图案中正三角形的个数为（用含n的代数式表示）．11、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个10×10的正方形图案，则其中完整的圆共有个．12、根据下列图形的排列规律，第2008个图形是福娃（填写福娃名称即可）．13、用火柴棒按照如图所示的方式摆图形，则第n个图形中，所需火柴棒的根数是．14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成：拼搭第1个图案需4根小木棒，拼搭第2个图案需10根小木棒，…，依次规律，拼搭第8个图案需小木棒根．15、一张长方形桌子需配6把椅子，按如图方式将桌子拼在一起，那么8张桌子需配椅子把．16、下列每个图是由若干个圆点组成的形如四边形的图案，当每条边（包括顶点）上有n （n≥2个圆点时，图案的圆点数为S n ．按此规律推断S n 关于n 的关系式为：S n = ．17、如图是由火柴棒搭成的几何图案，则第n 个图案中有 根火柴棒．（用含n的代数式表示）18、观察下列图形的构成规律，根据此规律，第8个图形中有 个圆．19、观察表一，寻找规律．表二，表三分别是从表一中选取的一部分，则a+b的值为．表一：表二：表三：20、如图所示的图案是由正六边形密铺而成，黑色正六边形周围第一层有六个白色正六边形，则第n层有个白色正六边形．21、把边长为3的正三角形各边三等分，分割得到图①，图中含有1个边长是1的正六边形；把边长为4的正三角形各边四等分，分割得到图②，图中含有3个边长是1的正六边形；把边长为5的正三角形各边五等分，分割得到图③，图中含有6个边长是1的正六边形；…依此规律，把边长为7的正三角形各边七等分，并按同样的方法分割，得到的图形中含有个边长是1的正六边形．0 1 2 3 ....1 3 5 7 ....2 5 8 11 ....3 7 11 15 ....... ... ... ... ....1114a1 3722、观察下列图形的排列规律（其中☆，□，●分别表示五角星、正方形、圆）●□☆●●□☆●□☆●●□☆●…若第一个图形是圆，则第2008个图形是（填名称）．23、下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，按照图示的规律摆下去，则第n幅图中有个菱形．24、如图，观察下列图案，它们都是由边长为1cm的小正方形按一定规律拼接而成的，依此规律，则第16个图案中的小正方形有个．25、用同样大小的黑色棋子按图所示的方式摆图形，按照这样的规律摆下去，则第n个图形需棋子枚．（用含n的代数式表示）27、如图所示是一副“三角形图”，第一行有一个三角形，第二行有2个三角形，第三行有4个三角形，第四行有8个三角形，…，你是否发现三角形的排列规律，请写出第七行有个三角形．28、如图，用3根小木棒可以摆出第（1）个正三角形，加上2根木棒可以摆出第（2）个正三角形，再加上2根木棒可以摆出第（3）个正三角形…这样继续摆下去，当摆出第（n）个正三角形时，共用了木棒根．29、观察下列图形，根据变化规律推测第100个与第个图形位置相同．30、如图，用火柴棒按以下方式搭小鱼，搭1条小鱼用8根火柴棒，搭2条小鱼用14根，…，则搭n条小鱼需要根火柴棒．（用含n的代数式表示）整式的加减——专题训练与提升参考答案1．n2-n+1 2．（2n-1）3．302 4．121 5．49 6．152n+5 7．360（n-2）8．4n-19．3n+1 10．2n+2 11．181 12．欢欢13．3n+1 14．88 15．20 16．4n-4 17．2n（n+1）18．65 19．37 20．6n 21．15 22．正方形23．（2n-1）24．136 26．3n+1 27．64 28．2n+1 29．1或4 30．6n+2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中考数学探索题训练—找规律
1、我们平常用的数是十进制数，如2639=2×103+6×102+3×101+9×100，表示十进制的数要用10个数码（又叫数字）：0，1，2，3，4，5，6，7，8，9。
在电子数字计算机中用的是二进制，只要两个数码：0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5，10111=1×24+0×23＋1×22＋1×21＋1×20等于十进制中的数23，那么二进制中的1101等于十进制的数 。
2、从1开始，将连续的奇数相加，和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从1开始，将前10个奇数（即当最后一个奇数是19时），它们的和是 。
3、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：
那么，当输入数据是8时，输出的数据是（ ） A 、
618 B 、638 C 、65
8
D 、678
4、如下左图所示，摆第一个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第三个要17枚棋子，则摆第30个“小屋子”要 枚棋子.
5、如下右图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第n 个小房子用了 块石子。
6、如下图是用棋子摆成的“上”字：
第一个“上”字第二个“上”字第三个“上”字
如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上”字分别需用和枚棋子；（2）第n个“上”字需用枚棋子。
7、如图一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，
则这串珠子被盒子遮住的部分有_______颗.
8、根据下列5个图形及相应点的个数的变化规律：猜想第6个图形有
个点，第n个图形中有个点。
9、下面是按照一定规律画出的一列“树型”图：
经观察可以发现：图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，图（7）比图（6）多出个
(1)(2)(3)
第4题
第7题图
(1)
(2)
(3)
(4)
“树枝”。
10、观察下面的点阵图和相应的等式，探究其中的规律：
（1）在④和⑤后面的横线上分别写出相应的等式；
（2）通过猜想写出与第n 个点阵相对应的等式_____________________。
11、用边长为1cm 的小正方形搭成如下的塔状图形，则第n 次所搭图形的周长是_______________cm （用含n 的代数式表示）。
12、如图，都是由边长为
1的正方体叠成的图形。
例如第（1）个图形的表面积为6个平方单位，第（2）个图形的表面积为18个平方单位，第（3
）个图形的表面积是36个平方单位。
依此规律。
则第（5）个图形的表面积 个平方单位。
……
……
①1=12
； ②1+3=22； ③1+3+5=32
④ ；
⑤ ；
第1次 第2次 第3次 第4次 ···
···
⑴
⑵⑶
13、图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（）
A 25
B 66
C 91
D 120
14、如图是由大小相同的小立方体木块叠入而成的几何体，图⑴中有1个立方体，图⑵中有4个立方体，图⑶中有9个立方体，……
按这样的规律叠放下去，
第8个图中小立方体个数是 .
15、图1是棱长为a的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…、第n层，第n层的小正方体的个数为s．解答下列问题：
（1
(1)
(2)(3)
14题
（2）写出当n =10时，s= ．
16、如图用火柴摆去系列图案，按这种方式摆下去，当每边摆10根时（即10 n ）时，需要的火柴棒总数为 根；
17、用火柴棒按如图的方式搭一行三角形，搭一个三角形需3支火柴棒，搭2个三角形需5支火柴棒，搭3个三角形需7支火柴棒，照这样的规律下去，搭n 个三角形需要S 支火柴棒，那么用n 的式子表示S 的式子是 _______ （n 为正整数）．
18、如图所示，用同样规格的黑、白两色正方形瓷砖铺设矩形地面，请观察下图：则第n 个图形中需用黑色瓷砖 ____ 块．(用含n 的代数式表示)
19、如图，用同样规格的黑白两种正方形瓷砖铺设正方形地面，观察图形并猜想填空：
当黑色瓷砖为20块时，白色瓷砖为块；当白色瓷砖为n2(n为正整数)块时，黑色瓷砖为块．
17题图
20、观察下列由棱长为
1的小立方体摆成的图形，寻找规律：如图1中：共有1 个小立
方体，其中1个看得见，0个看不见；如图2中：共有8个小立方体，其中7个看得见，1个看不见；如图3中：共有27个小立方体，其中有19个看得见，8个看不见；……，则第6个图中，看不见的小立方体有个。
21、下面的图形是由边长为l的正方形按照某种规律排列而组成的．。