高等数学试题五(附答案)
高等数学练习题(附答案)

《高等数学》专业年级学号姓名一、判断题.将√或×填入相应的括号内.(每题2分,共20分)()1.收敛的数列必有界.()2.无穷大量与有界量之积是无穷大量.()3.闭区间上的间断函数必无界.()4.单调函数的导函数也是单调函数.()5.若f (x )在x 0点可导,则f (x )也在x 0点可导.()6.若连续函数y =f (x )在x 0点不可导,则曲线y =f (x )在(x 0,f (x 0))点没有切线.()7.若f (x )在[a ,b ]上可积,则f (x )在[a ,b ]上连续.()8.若z =f (x ,y )在(x 0,y 0)处的两个一阶偏导数存在,则函数z =f (x ,y )在(x 0,y 0)处可微.()9.微分方程的含有任意常数的解是该微分方程的通解.()10.设偶函数f (x )在区间(-1,1)内具有二阶导数,且f ''(0)=f '(0)+1,则f (0)为f (x )的一个极小值.二、填空题.(每题2分,共20分)1.设f (x -1)=x ,则f (x +1)=.22.若f (x )=2-12+11x1x,则lim +=.x →03.设单调可微函数f (x )的反函数为g (x ),f (1)=3,f '(1)=2,f ''(3)=6则---------------------------------------------------------------------------------------------------------------------------------g '(3)=.4.设u =xy +2x,则du =.y35.曲线x =6y -y 在(-2,2)点切线的斜率为.6.设f (x )为可导函数,f '(1)=1,F (x )=f ()+f (x ),则F '(1)=.7.若1x2⎰f (x )0t 2dt =x 2(1+x ),则f (2)=.8.f (x )=x +2x 在[0,4]上的最大值为.9.广义积分⎰+∞0e -2x dx =.2210.设D 为圆形区域x +y ≤1,⎰⎰y D1+x 5dxdy =.三、计算题(每题5分,共40分)111+Λ+).1.计算lim(2+22n →∞n (n +1)(2n )2.求y =(x +1)(x +2)(x +3)ΛΛ(x +10)在(0,+∞)内的导数.23103.求不定积分⎰1x (1-x )dx .4.计算定积分⎰πsin 3x -sin 5xdx .3225.求函数f (x ,y )=x -4x +2xy -y 的极值.6.设平面区域D 是由y =x ,y =x 围成,计算⎰⎰Dsin ydxdy .y7.计算由曲线xy =1,xy =2,y =x ,y =3x 围成的平面图形在第一象限的面积.---------------------------------------------------------------------------------------------------------------------------------8.求微分方程y '=y -2x的通解.y四、证明题(每题10分,共20分)1.证明:arc tan x=arcsinx 1+x 2(-∞<x <+∞).2.设f (x )在闭区间[a ,b ]上连续,且f (x )>0,F (x )=⎰f (t )dt +⎰x xb1dt f (t )证明:方程F (x )=0在区间(a ,b )内有且仅有一个实根.《高等数学》参考答案一、判断题.将√或×填入相应的括号内(每题2分,共20分)1.√;2.×;3.×;4.×;5.×;6.×;7.×;8.×;9.√;10.√.二、填空题.(每题2分,共20分)21.x +4x +4; 2.1; 3.1/2;4.(y +1/y )dx +(x -x /y )dy ;25.2/3;6. 1;7.336;8.8;9.1/2;10.0.三、计算题(每题5分,共40分)n +1111n +1<++L +<1.解:因为(2n )2n 2(n +1)2(2n )2n 2且lim 由迫敛性定理知:lim(n →∞n +1n +1=0lim ,=0n →∞(2n )2n →∞n 2111++Λ+)=0222n (n +1)(2n )2.解:先求对数ln y =ln(x +1)+2ln(x +2)Λ+10ln(x +10)---------------------------------------------------------------------------------------------------------------------------------∴11210y '=++Λ+y x +1x +2x +10∴y '=(x +1)Λ(x +10)(3.解:原式=21210++Λ+)x +1x +2x +10⎰11-xd x =2⎰11-(x )2d x=2arcsin4.解:原式=x +c⎰πsin 3x cos 2xdxπ32=⎰π2020cos x sin xdx -⎰cos x sin xdx232ππ32=⎰sin xd sin x -⎰ππ2sin xd sin x32222-[sin 2x ]π=[sin 2x ]0π552=4/525.解:f x'=3x -8x -2y =0f y'=2x -2y =05π5故⎨⎧x =0⎧x =2或⎨⎩y =0⎩y =2当⎨⎧x =0''(0,0)=-2,f xy ''(0,0)=2''(0,0)=-8,f yy 时f xx⎩y =0---------------------------------------------------------------------------------------------------------------------------------Θ∆=(-8)⨯(-2)-22>0且A=-8<0∴(0,0)为极大值点且f (0,0)=0当⎨⎧x =2''(2,2)=-2,f xy ''(2,2)=2''(2,2)=4,f yy 时f xxy =2⎩Θ∆=4⨯(-2)-22<0∴无法判断6.解:D=(x ,y )0≤y ≤1,y 2≤x ≤y{}∴⎰⎰D1y sin y 1sin y sin y dxdy =⎰dy ⎰2dx =⎰[x ]y dyy 20y 0y y y =⎰(sin y -y sin y )dy1=[-cos y ]+10⎰1yd cos y 1=1-cos1+[y cos y ]0-⎰cos ydy 01=1-sin17.解:令u =xy ,v =y;则1≤u ≤2,1≤v ≤3x1x uJ =yuxv =2uv y vv-u 2v v =12v u2u v231dv =ln 3∴A =⎰⎰d σ=⎰du ⎰112v D8.解:令y =u ,知(u )'=2u -4x由微分公式知:u =y =e ⎰22dx 2(⎰-4xe ⎰-2dx dx +c )---------------------------------------------------------------------------------------------------------------------------------=e 2x (⎰-4xe -2x dx +c )=e 2x (2xe -2x +e -2x +c )四.证明题(每题10分,共20分)1.解:设f (x )=arctan x -arcsinx 1+x 221Θf '(x )=-21+x 1x 1-1+x 221+x -⋅1+x 2x 21+x 2=0∴f (x )=c-∞<x <+∞令x =0Θf (0)=0-0=0∴c =0即:原式成立。
高等数学复旦大学出版社习题答案五
在总利润最大的基础上再多生产100台时,利润的增量为
ΔL(x)= .
即此时总利润减少1万元.
21.某企业投资800万元,年利率5%,按连续复利计算,求投资后20年中企业均匀收入率为200万元/年的收入总现值及该投资的投资回收期.
解:投资20年中总收入的现值为
在(3,0)处的切线是y=2x+6
两切线交点是( ,3).故所求面积为
(7)
(8)摆线x=a(tsint),y=a(1cost)的一拱(0t2)与x轴;
解:当t=0时,x=0,当t=2时,x=2a.
所以
(8)
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.求下列各曲线所围成图形的公共部分的面积:
1.求下列各曲线所围图形的面积:
(1) 与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组 得交点A(2,2)
(1)
∴ ,
.
(2) 与直线y=x及x=2;
解: .
(2)
(3)y=ex,y=ex与直线x=1;
解: .
(3)
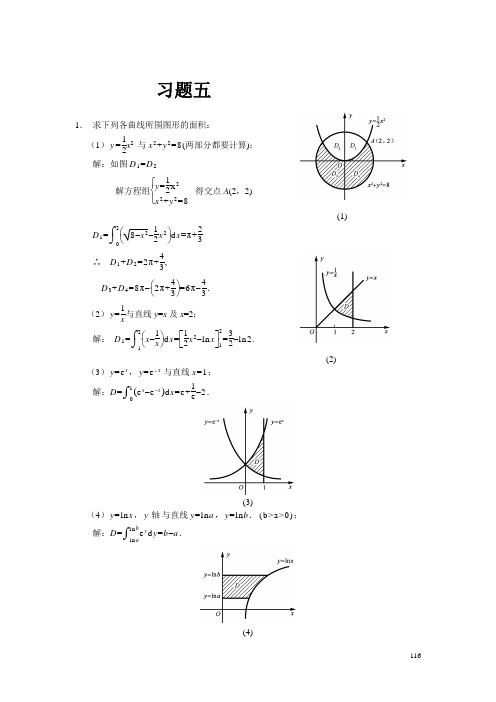
(4)y=lnx,y轴与直线y=lna,y=lnb.(b>a>0);
≈0.385386万元=3853.86元.
yt′=3asin2tcost
xt′2+yt′2=9a2sin2tcos2t,利用曲线的对称性,
.
9.求对数螺线 相应θ=0到θ=φ的一段弧长.
解:
.
10.求半径为R,高为h的球冠的表面积.
高数习题5 3答案

高数习题5 3答案高数习题5-3答案高等数学是大学数学的一门重要课程,对于理工科学生来说尤为重要。
学习高等数学不仅需要掌握理论知识,还需要通过大量的习题来巩固和提高自己的能力。
本文将为大家提供高数习题5-3的答案,希望能够帮助到大家。
习题5-3是一道关于极限的题目。
在这道题目中,我们需要求出函数f(x) =(x^2 - 1) / (x - 1) 在x趋近于1时的极限。
首先,我们可以将函数进行化简,得到 f(x) = x + 1。
因此,当x趋近于1时,f(x)也会趋近于2。
所以,答案是2。
在解答这道题目的过程中,我们需要运用到一些数学的基本概念和技巧。
首先,我们需要了解极限的概念,即当自变量趋近于某个特定的值时,函数的取值会趋近于一个确定的值。
在这道题目中,我们需要求出当x趋近于1时,函数f(x)的极限。
其次,我们需要运用到函数的化简技巧,将给定的函数进行简化,以便更好地求解极限。
最后,我们需要运用到极限的性质,即当两个函数的极限存在且相等时,它们的极限值也相等。
通过解答这道题目,我们不仅能够巩固自己对于极限概念的理解,还能够提高自己的运算能力和思维能力。
在学习高等数学的过程中,通过大量的习题练习,我们能够更好地掌握和应用数学知识,提高自己的解决问题的能力。
除了解答这道具体的习题,我们还可以通过类似的题目来拓展自己的思维。
比如,我们可以考虑当x趋近于其他值时,函数的极限会有什么变化。
我们还可以思考,如果给定的函数无法通过化简来求解极限,我们应该如何处理。
通过这样的思考和探索,我们能够更好地理解和应用极限的概念。
总之,高等数学是一门重要的课程,通过大量的习题练习,我们能够更好地掌握和应用数学知识。
本文提供了高数习题5-3的答案,并对解答过程进行了简要的分析。
希望这篇文章能够帮助到大家,提高大家的数学能力。
同时,也希望大家在学习数学的过程中保持积极的态度,勇于挑战和探索,不断提升自己的数学水平。
高等数学试题(含答案)

高等数学试题(含答案)高等数学试题(含答案)一、选择题1.已知函数f(x)=x^2+3x+2,下列哪个选项是f(x)的导数?A. 2x+3B. 2x+2C. x^2+3D. 3x+22.若函数f(x)=e^x,那么f'(x)等于:A. e^-xB. e^xC. ln(x)D. e^x+13.设函数y=f(x)在点x=2处可导,且f'(2)=3,则曲线y=f(x)在点(2,f(2))处的切线斜率为:A. 2B. 3C. 1D. 6二、计算题1.计算极限lim(x→1) [(x-1)/(x^2-1)]答案:1/22.计算积分∫(0 to 1) (2x+1) dx答案:3/23.设曲线C的方程为y=x^3,计算曲线C的弧长。
答案:∫(0 to 1) √(1+9x^4) dx三、证明题证明:若函数f(x)在区间[a,b]上连续,且在(a,b)可导,那么必然存在c∈(a,b),使得 f'(c) = [f(b)-f(a)] / (b-a)。
证明过程:由于f(x)在区间[a,b]上连续,根据连续函数的介值定理,f(x)在[a,b]上会取到最大值M和最小值m。
设在点x=c处取得最大值M(即f(c)=M)。
根据费马定理,如果f(x)在点x=c处可导,并且f'(c)存在,那么f'(c)=0。
由于f(x)在(a,b)可导,故f'(c)存在。
那么,根据导数的定义,f'(c)=[f(c)-f(a)]/(c-a)。
又因为f(c)=M,将其代入上式得到f'(c)=(M-f(a))/(c-a)。
同理,根据费马定理,如果f(x)在点x=d处取得最小值m(即f(d)=m),那么f'(d)也等于0。
将f(d)=m代入上式得到f'(d)=(m-f(a))/(d-a)。
由于f(x)是连续函数,故在区间[a,b]上必然存在一个点c∈(a,b),使得它处于最大值M和最小值m之间,即m<f(c)<M。
高等数学考试题目及答案

高等数学考试题目及答案一、单项选择题(每题3分,共30分)1. 函数f(x)=x^2+2x+1的导数是:A. 2x+2B. x^2+2C. 2xD. 2x+1答案:A2. 曲线y=x^3在点(1,1)处的切线斜率是:A. 0B. 1C. 3D. -3答案:C3. 极限lim(x→0) (sin(x)/x)的值是:A. 0B. 1C. πD. -1答案:B4. 不定积分∫x^2 dx等于:A. (x^3)/3 + CB. x^3 + CC. (x^2)/2 + CD. 2x^3 + C答案:A5. 函数y=e^x的原函数是:A. e^x + CB. e^x - CC. e^(-x) + CD. -e^x + C答案:A6. 函数y=ln(x)的二阶导数是:A. 1/x^2B. 1/xC. -1/x^2D. -1/x答案:A7. 曲线y=x^2+2x+1与x轴的交点个数是:A. 0B. 1C. 2D. 3答案:A8. 函数y=x^3-3x的拐点是:A. (0,0)B. (1,-2)C. (-1,2)D. (2,2)答案:C9. 函数y=x^2-4x+4的极值点是:A. (2,0)B. (0,4)C. (4,0)D. (-2,0)答案:A10. 函数y=sin(x)的周期是:A. 2πB. πC. 1D. 0答案:A二、填空题(每题4分,共20分)11. 函数f(x)=x^3的导数是_________。
答案:3x^212. 曲线y=cos(x)在点(π/2,0)处的切线斜率是_________。
答案:013. 极限lim(x→∞) (1/x)的值是_________。
答案:014. 不定积分∫1/x dx等于_________。
答案:ln|x| + C15. 函数y=e^(-x)的原函数是_________。
答案:-e^(-x) + C三、解答题(每题10分,共50分)16. 求函数f(x)=x^2-4x+4在区间[1,3]上的最大值和最小值。
高等数学考试题及答案

高等数学考试题及答案一、选择题(每题2分,共20分)1. 函数f(x) = x^2 - 3x + 2在区间[1, 4]上的最大值是:A. 0B. 3C. 5D. 62. 级数∑(1/n^2)从n=1到∞的和是:A. π^2/6B. eC. 1D. 23. 微分方程dy/dx + y = x^2的通解是:A. y = x^2 - x + CB. y = x^2 + CC. y = x^2 + x + CD. y = x^2 - 2x + C4. 曲线y = x^3 - 2x^2 + 3x在点(1, 2)处的切线斜率是:A. -1B. 0C. 1D. 25. 函数f(x) = sin(x) + cos(x)的周期是:A. πB. 2πC. π/2D. 16. 曲线y = x^2与直线y = 4x在第一象限的交点坐标是:A. (2, 8)B. (0, 0)C. (1, 4)D. (4, 16)7. 极限lim(x→∞) (1 + 1/x)^x的值是:A. eB. 1C. 0D. ∞8. 函数f(x) = x^3 - 6x^2 + 11x - 6的零点个数是:A. 0B. 1C. 2D. 39. 已知函数f(x) = x^2 + 2x + 1,求f'(x):A. 2x + 2B. 2x + 1C. 2x - 1D. x^2 + 210. 函数y = ln(x)的导数是:A. 1/xB. xC. ln(x)D. 1二、填空题(每题2分,共20分)11. 函数f(x) = x^3 - 3x^2 + 2的极值点是________。
12. 函数f(x) = sin(x)的反函数是________。
13. 曲线y = x^2 - 4x + 4在x轴上的截距是________。
14. 曲线y = 1/x在点(1, 1)处的切线斜率是________。
15. 函数f(x) = x^2 - 4的根是________。
高等数学试题及及答案

高等数学试题及及答案高等数学试题及答案一、选择题(每题4分,共20分)1. 函数f(x)=x^2-2x+1的最小值是()。
A. 0B. 1C. -1D. 22. 极限lim(x→0) (sin(x)/x)的值是()。
A. 0B. 1C. -1D. 23. 函数y=e^x的导数是()。
A. e^xB. -e^xC. 1/e^xD. 04. 曲线y=x^3-3x+2在x=1处的切线斜率是()。
A. 0B. 1C. -1D. 25. 积分∫(0 to 1) (x^2 dx)的值是()。
A. 1/3B. 1/2C. 1D. 2二、填空题(每题4分,共20分)6. 函数f(x)=3x^2-6x+5的顶点坐标是()。
7. 函数y=ln(x)的定义域是()。
8. 函数y=x^3的二阶导数是()。
9. 曲线y=e^x与直线y=x相切的切点坐标是()。
10. 积分∫(0 to 1) (x dx)的值是()。
三、解答题(每题15分,共60分)11. 求函数f(x)=x^3-3x+2在区间[-1, 2]上的定积分,并画出积分图。
12. 求极限lim(x→∞) ((x^2+1)/(x^3+x))。
13. 求函数y=x^2-4x+3的极值点,并说明极值点的性质。
14. 求曲线y=x^2+2x-3在点(1, -2)处的切线方程。
四、附加题(10分)15. 证明:对于任意正整数n,有1/n^2 < 1/(n^2-1) + 1/(n^2+1)。
答案:一、选择题1. B2. B3. A4. C5. A二、填空题6. (1, 2)7. (0, +∞)8. 6x9. (1, e)10. 1/2三、解答题11. ∫(-1 to 2) (x^3-3x+2 dx) = (1/4x^4 - 3/2x^2 + 2x) | (-1 to 2) = 17/4积分图略。
12. 原式=lim(x→∞) (x^2+1)/(x^3+x) = lim(x→∞) (1/x + 1/x^3) = 013. y'=2x-4,令y'=0,得x=2,此时y=3,为极小值点。
高数试题及答案 五套

高学试题及答案一、单项选择题(本大题共5小题,每小题2分,共10分)1.设f(x)=lnx ,且函数ϕ(x)的反函数1ϕ-2(x+1)(x)=x-1,则[]ϕ=f (x)( ) ....A B C D x-2x+22-x x+2 ln ln ln ln x+2x-2x+22-x2.()02lim1cos t t xx e e dtx-→+-=-⎰( )A .0B .1C .-1D .∞3.设00()()y f x x f x ∆=+∆-且函数()f x 在0x x =处可导,则必有( ).lim 0.0.0.x A y B y C dy D y dy ∆→∆=∆==∆= 4.设函数,131,1x x x ⎧≤⎨->⎩22x f(x)=,则f(x)在点x=1处( )A.不连续B.连续但左、右导数不存在C.连续但不可导D. 可导5.设C +⎰2-x xf(x)dx=e,则f(x)=( )2222-x -x -x -x A.xe B.-xe C.2e D.-2e二、填空题(本大题共10小题,每空3分,共30分) 请在每小题的空格中填上正确答案。
错填、不填均无分。
6.设函数f(x)在区间[0,1]上有定义,则函数f(x+14)+f(x-14)的定义域是__________. 7.()()2lim 1_________n n a aq aq aq q →∞++++<=8.arctan lim _________x x x→∞=9.已知某产品产量为g 时,总成本是2g C(g)=9+800,则生产100件产品时的边际成本100__g ==MC10.函数3()2f x x x =+在区间[0,1]上满足拉格朗日中值定理的点ξ是_________.11.函数3229129y x x x =-+-的单调减少区间是___________.12.微分方程3'1xy y x -=+的通解是___________. 13.设2ln 2,6aa π==⎰则___________.14.设2cos xz y=则dz= _______.15.设{}2(,)01,01y DD x y x y xe dxdy -=≤≤≤≤=⎰⎰,则_____________. 三、计算题(一)(本大题共5小题,每小题5分,共25分)16.设1xy x ⎛⎫= ⎪⎝⎭,求dy.17.求极限0ln cot lim ln x x x +→18.求不定积分.19.计算定积分I=.⎰20.设方程2z x 2e 1y xz -+=确定隐函数z=z(x,y),求','x y z z 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学》
专业 学号 姓名
一、判断(每小题 2 分,共 20 分)
1. f(x)在点x 0处有定义是f(x)在点x 0处连续的必要条件. ( )
2. 无穷小量与有界变量之积为无穷小量. ( )
3. y=f(x)在x 0处可导,则y=|f(x)|在x 0处也可导. ( )
4. 初等函数在其定义域内必连续. ( )
5. 可导函数f(x)的极值点一定是f(x) 的驻点. ( )
6. 对任意常数k,有⎰dx x kf )(=k ⎰dx x f )(. ( )
7. 若f(x)在[a,b]上可积,则f(x)在[a,b]上有界. ( )
8. 若f(x,y)在区域D 上连续且区域D 关于y 轴对称,则当f(x,y) 为关于x 的奇函数时,⎰⎰D
dxdy y x f ),(=0. ( )
9. )(y '2=-2x -e x 的通解中含有两个独立任意常数. ( )
10. 若z=f(x,y)在P o 的两个偏导数都存在,则z=f(x,y)在P 0连续. ( )
二、填空(每空 2 分,共20 分)
1.∞
→x lim [xsin
x
1+
x
1sinx+(
x
x +2)x ]= .
2. 函数f(x)=x x -3在[0,3]上满足罗尔定理的条件,定理中的数值ξ= .
3. 设f(x)=⎩⎨
⎧≥+<0
0x x
a x e x
当a= 时,f(x)在x=0处连续.
4. 设z=e
y
x 22
+ ,则dz | (0,0)= .
5. 函数f(x)=e x
-x -1在 内单调增加;在 内单调减少.
6. 函数32y ax bx cx d =+++满足条件 时, 这函数没有极值.
7.
dx
d ⎰
b a
x 2
sin dx = 其中a,b 为常数.
8. f '(x)=1且(0)0f =,则⎰dx x f )(= . 9.若I=⎰⎰
1
02
),(x x
y x f dx dxdy 交换积分次序后得 .
三、计算(每小题 5 分,共 40 分)
1. 求0
lim →x (
2
1x
-
xtgx
1) ; 2.
dt t
t x
e ⎰
1
ln +dt t y
)3(cos 1
⎰+=2,求dy ;
3. 求dx x x ⎰
+)
1(1; 4. 求dx x ⎰--1
4
3
1
11 ; 5. 求dx xe
x
⎰
∞+-0
2;
6. 设z=ln(x 2
+y 2
) 求
x
z ∂∂,
y
x z ∂∂∂2
;
7. 计算 I=⎰⎰D
xdxdy .其中D 是由圆x 2+y 2=4围成的区域;
8. 求微分方程-ydx+(x+y 3)dy=0的通解.
四、应用题(每题7分,共14分)
1. 某车间靠墙壁要盖一间长方形小屋,现有存砖只够砌20米长的墙壁,问应围成的长方形的长,宽各为多少才能使这间小屋面积最大.
2. 求由y=
x
1,x=1,x=2与x 轴所围成的图形的面积及该图绕x 轴旋转一周的旋转体的体积.
五、证明(本题6分)
证明:当x >0时,不等式1+
x x +>
121成立.
高等数学参考答案
一、判断正误(每题2分,共20分)
1 √ ;
2 √ ;
3 ╳ ;
4 ╳ ;
5 √ ; 6╳ ; 7 √ ; 8 √ ; 9 ╳ ; 10 ╳.
二、填空题(每题4分,共20分)
1. 21e +;
2. 2 ;
3. 1 ;
4. 2dx ;
5.[0)∞,+,,0]∞(- ;
6. 2
30b ac -<;
7.0; 8.
2
12
x c + ;
9. 10
(,)y
dy f x y dx ⎰⎰
.
三、计算题与证明题(共计60分)
1. 2011lim tan x x x x →⎛⎫- ⎪⎝⎭=20tan lim tan x x x x x →-⎛⎫ ⎪⎝⎭=3
0tan lim x x x x →-⎛⎫
⎪⎝⎭
=20sec 1lim 3x x x →-⎛⎫
= ⎪⎝⎭202sec tan 1lim 63
x x x x →⎛⎫= ⎪⎝⎭ 2. 方程两边同时对x 求导得:
则
ln (cos 3)0x
x
x e e y y e
'++=
(cos 3)0x y ++=
cos 3
x y y '=-
+
cos 3
x dy dx y =-
+
3. ⎰
=
2
1d
x +⎰
=1
2⎰
=2arctan c
4、 令
2
12t x t
dx tdt ==-=-
当 34
x =
时12
t =;当1x =时0t =
原式=
112
21
t dt t --⎰
=11
220
12211
1
t dt dt t t =+
--⎰
⎰
=1
20
2[ln 112ln 2t t +-=-
5.⎰
⎰
∞
+-∞
+-'-
=
20
2)2
1(dx e
x dx xe
x
x
⎰
∞
+-+∞
--
-
-
=0
20
2)2
1()
2
1(dx e
e
x x
x
4
14
10
2=
-
=+∞
-x
e
6.
2
22
2
2
2
2)(1y
x x
y x y
x x z +=
'++=
∂∂
2
2
2
2
2
2
2
)
(42)
(2y x xy y y x x y
x z +-
=+-
=∂∂∂
7.令 ⎩
⎨⎧==θθ
sin cos r y r x ,
⎰
⎰⋅=
π
θθ20
2
cos rdr r d I
0]3
1[][sin cos 2032020
2
2=⋅==
⎰
⎰
r dr r d π
π
θθ
θ
8.解:
2
1y x y
dy
dx =-
)(1
2
1
c dy e
y e
x dy
y dy y +⎰⎰⎰=-
)21(2
c y y +=
∴ 原方程的通解为:)2
1(2
c y y x +=
四、(每题7分,共14分)
1.解:设长方形的长和宽分别为x 和y ,面积为s ,则202=+y x 即 y x 220-= 2
220y y xy s -== )0(>y
0420=-='y s ,得5=y
04<-=''s
∴当长10=x M ;宽5=y M 时,面积最大。
五、(本题6分)
令x x x f +-
+
=12
11)( 01212
1)(>+-
=
'x
x f
∴
0)0()(=>f x f 即x x +>
+1211。
