2020高考数学《函数的单调性》

合集下载

高考数学专题复习函数的单调性(学生版)

第二讲函数的单调性【套路秘籍】1．函数的单调性 (1)单调函数的定义自左向右看图象是上升的如果函数y ＝f (x )在区间D 上是增函数或减函数，那么就说函数y ＝f (x )在这一区间具有(严格的)单调性，区间D 叫做y ＝f (x )的单调区间． 2．函数的最值【套路修炼】考向一单调区间求解【例1】（1）下列函数中，定义域是R 且为增函数的是( )A.y ＝2－xB.y ＝xC.y ＝log 2xD.y ＝－1x(2)函数f (x )＝ln (x 2－2x －8) 的单调递增区间是( )A ．(－∞，－2)B ．(－∞，1)C ．(1，＋∞)D ．(4，＋∞) (3)求函数f (x )＝|x 2－4x ＋3|的单调区间． (4)求函数f (x )＝x －ln x 的单调区间．(5)函数33y x x =-的单调增区间为__________．【举一反三】1．下列函数中，在(0,+∞)上单调递减的是( )A ． f(x)=lnxB ． f(x)=(x −1)2C ． f(x)=2−xD ． f(x)=x 3 2．函数f (x )=log 2(4+3x −x 2)的单调递减区间是（） A ． (−∞,32] B ． [32,+∞) C ． (−1,32] D ． [32,4)3．函数()| g x x =的单调递增区间是 ( )A ． [)0+∞，B ． (]0-∞，C ． (]2-∞-，D ． [)2+-∞，考向二单调性的运用一---比较大小【例2】定义在R 上的偶函数f (x )满足：对任意的x 1，x 2∈(－∞，0)(x 1≠x 2)，都有f (x 1)－f (x 2)x 1－x 2<0.则下列结论正确的是( )A ．f (0.32)<f (20.3)<f (log 25) B ．f (log 25)<f (20.3)<f (0.32) C ．f (log 25)<f (0.32)<f (20.3) D ．f (0.32)<f (log 25)<f (20.3)【举一反三】1.已知f (x )＝2x－2－x，117459279,,log 97a b c -⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭则f (a )，f (b )，f (c )的大小顺序为( ) A.f (b )<f (a )<f (c ) B.f (c )<f (b )<f (a ) C.f (c )<f (a )<f (b )D.f (b )<f (c )<f (a )2.已知函数f (x )的图象向左平移1个单位后关于y 轴对称，当x 2>x 1>1时，[f (x 2)－f (x 1)]·(x 2－x 1)<0恒成立，设a ＝f ⎝ ⎛⎭⎪⎫－12，b ＝f (2)，c ＝f (3)，则a ，b ，c 的大小关系为( )A ．c >a >bB ．c >b >aC ．a >c >bD ．b >a >c 3．设a =ln22，b =ln33，c =1e ，则( )A ． c <a <bB ． c y >zB ． y >x >zC ． y >z >xD ． x >z >y考向三单调性的运用二---解不等式【例3】（1）f(x )是定义在(0，＋∞)上的单调增函数，满足f (xy )＝f (x )＋f (y )，f (3)＝1，当f (x )＋f (x －8)≤2时，x 的取值范围是( )A ．(8，＋∞)B ．(8,9]C ．[8,9]D ．(0,8)（2）已知函数f (x )在(－∞，＋∞)上单调递减，且为奇函数.若f (1)＝－1，则满足－1≤f (x －2)≤1的x 的取值范围是( ) A.[－2，2] B.[－1，1] C.[0，4] D.[1，3]【举一反三】1．若log a 23<1(a >0且a ≠1)，则实数a 的取值范围是( )A ． (0,23)B ． (0,23)∪(1,+∞) C ． (1,+∞) D ． (0,1)2．设函数f (x )={2x ， x ≥0x ， x <0 ，则满足f (x +1)<f (2x )的x 的取值范围是（）A ． (−∞ ， −1]B ． (1 ， +∞)C ． (−1 ， 0)D ． (−∞ ， 0)3．定义在R 上的偶函数f(x)在[0,+∞)上单调递增，且f(1)=0，则满足f(log 12x)>0的x 的集合为______．4．设函数f(x)=x 3+1,若f(1−2a)<f(a),则实数a 的取值范围是 _______。

2020年高考数学一轮复习(新课改)第1课时系统知识——函数的单调性与最值、奇偶性、周期性

第二节函数的性质第1课时系统知识一一函数的单调性与最值、奇偶性、周期性若函数y= f(x)在区间D上是增函数或减函数，则称函数y= f(x)在这一区间上具有(严格的)单调性，区间D叫做函数y= f(x)的单调区间.［点拨］(1)函数单调性定义中的X i , X2具有以下三个特征：一是任意性，即任意两数X i, D ”，任意”两字决不能丢；二是有大小，即X i VX2(或X1>X2)；三是同属一个单调区间，三者缺一不可.⑵若函数在区间D上单调递增(或递减),则对D内任意的两个不等自变量X1, X2的值, 都有fXL二竺或fXk 4竺<。

.X1 —X2 X1—X2 /(3)函数f(X)在给定区间上的单调性，是函数在此区间上的整体性质，不一定代表在整个定义域上有此性质.［谨记常用结论］(1) 函数f(X)与f(x)+ c(c为常数)具有相同的单调性.(2) k>0时，函数f(x)与kf(x)单调性相同；k<0时，函数f(x)与kf(x)单调性相反.1⑶若f(x)恒为正值或恒为负值，贝y f(x)与具有相反的单调性.⑷若f(x), g(x)都是增(减)函数，则当两者都恒大于零时，f(x) •(x)是增(减)函数；当两者都恒小于零时，f(x) g(x)是减(增)函数.(5)在公共定义域内，增+增=增，减+减=减，增—减=增，减—增=减.［小题练通］1. ［人教A版教材P39B组T1］函数f(x)= x2—2x的单调递增区间是______ .答案：［1 ,+^ )2. ［教材改编题］如果二次函数f(x)= x2—(a—1)x + 5在区间2, 1上是增函数，则实数a的取值范围为_________ .解析：T函数f(x) = x2—(a —1)x+ 5的对称轴为x =旦^1且在区间2，1上是增函数，a —1答案：(—R, 2］3. ［教材改编题］函数f(x)= log1 (x2—4)的单调递增区间为________ .2解析：由x2—4>0得x<—2或x>2.又u = x2—4在(一a,—2)上为减函数，在(2, + a)上为增函数，y= log 1 u为减函数，2故f(x)的单调递增区间为(一a,—2).答案：(一a,—2)4. ［易错题］设定义在［—1,7］上的函数y= f(x)的图象如图所示，则函数y= f(x)的增区间为________ .答案：［—1,1］, ［5,7］2x + k5.若函数y= 与y= log3(x—2)在(3, +a )上具有相同的单调性，贝U实数k的取值x—2范围是_________ .解析：由于y= lOg3(x—2)的定义域为(2 , + a ), 且为增函数，故函数y=空土^ = 2x —2+ 4+ k= 2 + 也在(3, + a)上也是增函数，则有4+ k v 0, x —2 x —2 x —2得k v — 4.f(X)Vf —的实数x的取值范答案：(—a, —4)6•已知函数f(x)为定义在区间［—1,1］上的增函数，则满足围为________ .—1W x W1,解析：由题设得1x<2解得—1W x<1.答案：—1,—前提设函数f(x)的定义域为1，如果存在实数M满足条件对于任意x€ I，都有f(x)W M ;存在X o€ I，使得f(X o)= M对于任意x € I，都有f(x)》M ;存在x°€ I，使得f(x^)= M结论M为最大值M为最小值1.函数的最值2.函数最值存在的两条结论(1)闭区间上的连续函数一定存在最大值和最小值•当函数在闭区间上单调时最值一定在端点处取到.(2)开区间上的“单峰”函数一定存在最大值或最小值.［点拨］(1)对于单调函数，最大(小)值出现在定义域的边界处；(2) 对于非单调函数求最值，通常借助图象求解更方便；(3) 一般地，恒成立问题可以用求最值的方法来解决，而利用单调性是求最值的常用方法•注意以下关系：f(x)> a恒成立？f(x)min> a ；f(x) W a恒成立？f(x)max <乱解题时，要务必注意“=”的取舍.［小题练通］21. __________________________________________________________ ［人教A版教材P31例4］函数f(x)=二二在［2,6］上的最大值是___________________________ •答案：22. ［教材改编题］设函数f(x)= 2~在区间［3,4］上的最大值和最小值分别为M ,m,则晋=x—2 M 解析：易知f(x)= x—2 = 2+七，所以f(x)在区间［3,4］上单调递减,4所以M = f(3) = 2 + ---- =6,3 —2 所以m!_ 16_ 8M —6 —3.答案:3.［教材改编题喏函数f(x)=—；+ b(a>0)在；，2上的值域为••• f(X )min = f 2 = 2 , f(x)max = f(2) = 2.1—2a 十 b = 1, 即 -1+b = 2,答案：1 54.［易错题］函数y =~22 i解析：由 y = X ^ ，可得 x 2 = —-^.由 x 2>0,知—0，解得—1 w y<1,x 十 1 1 — y 1 — y故所求函数的值域为［—1,1). 答案：［—1,1) 5.函数f(x) = x ，x> 1，的最大值为x 2 + 2, x<11解析：当x > 1时，函数f(x)= -为减函数，所以f(x)在x = 1处取得最大值，为 f(1) = 1；当x<1时，易知函数f(x) = — x 2+ 2在x = 0处取得最大值，为 f(0) = 2.故函数f(x)的最大值为2.答案：26.已知函数 f(x)=— x 2 + 4x 十a , x € ［0,1］，若f(x)有最小值一2,贝V f(x)的最大值为解析：函数 f(x)=— x 2 + 4x 十 a =— (x — 2)2+ 4+ a , x € [0,1]，且函数 f(x)有最小值—2. 故当x = 0时，函数f(x)有最小值，当 x = 1时，函数f(x)有最大值•当 x = 0时，f(0) = a =—2,.・. f(x)=— x 2+ 4x — 2, •当 x = 1 时,f(x)max = f(1)=—十十 4X 1 — 2 = 1.答案：1［谨记常用结论］1. 函数奇偶性的几个重要结论-1解析：•/ f(x)=-三+ b(a>0)在 1，2 是增函数,a = 1, 解得 5b = 5.⑴如果一个奇函数f(x)在原点处有定义，即f(0)有意义，那么一定有f(0) = 0.⑵如果函数f(x)是偶函数，那么f(x) = f(|x|).(3) 既是奇函数又是偶函数的函数只有一种类型，即f(x)= 0, x€ D，其中定义域D是关于原点对称的非空数集.(4) 奇函数在两个对称的区间上具有相同的单调性，偶函数在两个对称的区间上具有相反的单调性.2. 有关对称性的结论(1) 若函数y= f(x + a)为偶函数，则函数y= f(x)关于x = a对称.若函数y= f(x+ a)为奇函数，则函数y= f(x)关于点(a,0)对称.(2) 若f(x)= f(2a—x),则函数f(x)关于x = a 对称；若f(x) + f(2a—x) = 2b,则函数f(x) 关于点(a, b)对称.［小题练通］1. ________________ ［人教A版教材P39A组T6］已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)= x(1 + x),贝U f( —1) = .答案：—22. ［教材改编题］设f(x)是定义在R上的奇函数，当x>0时，f(x) = x1 2 3+ 1,则f( —2)+ f(0)解析：由题意知f( —2) =—f(2) = —(22+ 1) =—5, f(0) = 0,••• f(—2) + f(0) = — 5.答案：—53. ［教材改编题］已知函数f(x)为偶函数，且当x<0时，f(x)= x + 1,则当x>0时，f(x)=解析：当x>0 时，一xv0,「. f(—x)=—x + 1,又f(x)为偶函数，• f(x)=—x+ 1.答案：—x+ 14. ［易错题］已知f(x) = ax2+ bx是定义在［a —1,2 a］上的偶函数，那么 a + b的值是2 1解析：T f(x)= ax2+ bx是定义在［a —1,2 a］上的偶函数，• a—1 + 2a = 0,二a=；. 31又f( —x)= f(x) ,• b= 0,二a+ b= 3.3答案:5.在函数y= xcosx, y= e x+ x2, y= lg . x2—2, y= xsin x 中，偶函数的个数是___________ 解析：y= xcos x是奇函数，y= lg x2—2和y= xsin x是偶函数，y= e x+ x2是非奇非偶函数，所以偶函数的个数是 2.答案：26.已知函数 f(x)= asin x + bln*^ +1，若 f 1 + f — 2 =6，则实数 t=________________ ，解析：令g(x)= asin x + bln 齐，则易知g(x)为奇函数，所以gg g J — 2戶0,则由 f(x)= g(x)+1,得 f 1 + f —1 = g 1 + g —1 + 2t = 2t = 6,解得 t = 3.答案：31. 周期函数对于函数y = f(x)，如果存在一个非零常数T ,使得当x 取定义域内的任何值时，都有f(x + T) = f(x)，那么就称函数 y = f(x)为周期函数，称T 为这个函数的周期.2. 最小正周期如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做 f(x)的最小正周期.［谨记常用结论］定义式f(x + T)= f(x)对定义域内的x 是恒成立的.(1)若 f(x + a) = f(x + b),则函数 f(x)的周期为 T = |a — b|; 1 1f(x + a) = — f(x), f(x + a)=，f(x + a)=—匚何>0),则 f(x)为周期函数，且T = 2a 为它的一个周期.［小题练通］1.［教材改编题］设f(x)是定义在 R 上的周期为 2的函数，当 x € (— 1,1)时，f(x)= 「4x + 2,—1<x <0，则虑 L __________________ .x , 0< x<1, 2答案：12.［教材改编题］若f(x)是R 上周期为2的函数，且满足 f(1) = 1, f(2) = 2,贝U f(3) — f(4)解析：由 f(x)是 R 上周期为 2 的函数知，f(3) = f(1) = 1, f(4) = f(2) = 2,••• f(3) — f(4) =— 1.答案：—1=x ,贝y f(2 019) = __________(2)若在定义域内满足3.［教材改编题］已知f(x)是定义在R 上的函数，并且 1f(x + 2)= f x ,f(x)1 1解析：由已知，可得f(x + 4) = f[(x + 2) + 2]= —— =-—=f(x),故函数f(x)的周期为f (X + 2)4.A f(2 019) = f(4X 504+ 3) = f(3)= 3.答案：34. [易错题]函数f(x)的周期为4,且x€ (-2,2], f(x) = 2x- x2,则f(2 018) + f(2 019) + f(2 020)的值为________ .解析：由f(x)= 2x-x2, x€ (-2,2],知f(- 1)=- 3, f(0)= 0, f(2) = 0，又f(x)的周期为4,所以f(2 018) + f(2 019) + f(2 020) = f(2) + f( - 1)+ f(0) = 0 - 3+ 0=- 3.答案：—35. 已知f(x)是R上的奇函数，且对任意x€ R都有f(x+ 6)= f(x) + f(3)成立，则f(2 019)解析：•/ f(x)是R上的奇函数，••• f(0) = 0,又对任意x€ R都有f(x + 6) = f(x) + f(3),二当x=- 3 时，有f(3) = f( - 3) + f(3) = 0, • f( - 3) = 0 , f(3) = 0 , • f(x+ 6) = f(x)，周期为6. 故f(2 019) = f(3) = 0.答案：06.偶函数y= f(x)的图象关于直线x= 2对称，f(3) = 3,则f( - 1) = __________ .解析：因为f(x)的图象关于直线x= 2对称，所以f(x) = f(4- x) , f( - x) = f(4 + x),又f(- x) = f(x),所以f(x) = f(4 + x),则f( - 1) = f(4 - 1) = f(3) = 3.答案：3。

高考数学函数的单调性-

LPL夏季赛 KPL夏季赛 https:// LPL夏季赛 KPL夏季赛
例4、已知函数f(x)的定义为R，对任意的实数x1,x2 都满足f(x1+ x2)=f(x1)+f(x2)，当x>0时，f(x)>0，且 f(2)=3.
（1）试判断f(x)的奇偶性和单调性；
（2）当
2．判断函数的单调性的方法有：（1）用定义；（2）用已知函数的单调性；（3）利用函数的导数．
3．注意函数的单调性的应用； 4．注意分类讨论与数形结合的应用．
女员工Ｑ．希霓妮婆婆淡蓝色槟榔造型的鼻子，此时正惨碎成台风样的水蓝色飞沫，狂速射向远方，女员工Ｑ．希霓妮婆婆横颤着疯速地跳出界外，快速将淡蓝色槟榔造型的鼻子复原，但元气和体力已经大伤……壮扭公主：“好刺激！你的业务怎么越来越差……”女员工Ｑ．希霓妮婆婆：“不让你看看我的真功夫，你个小娃娃就不知道什么是高科技……”壮扭公主：“牛屎插上再多的大蒜也变不了空间站！你的科技实在太垃圾了！”女员工Ｑ．希霓妮婆婆：“我让你瞧瞧我的『灰霞蟒精摇杆耳』，看你还竟敢小瞧我……”壮扭公主：“嘿嘿！那我让你知道知道什么是真正名牌的原野！欣赏欣赏什么才是顶级原版的肥妹！认真崇拜一下纯天然的壮扭公主！！ ”女员工Ｑ．希霓妮婆婆猛然像深青色的十肝孤山象一样怪啸了一声，突然整出一个侧卧变形的特技神功，身上突然生出了五十只酷似香蕉模样的墨黑悠了一个，扭体鳄舞侧空翻三百六十度外加陀螺转九周的朦胧招式……紧接着晃动威猛的嘴唇一哼，露出一副神奇的神色，接着颤动细长的极似香肠造型的脚，像深蓝色的万喉戈壁鸟般的一晃，仙气的瘦小的牙齿顷刻伸长了四十倍，窜出的鹅黄色鼓锤般的肉筋也骤然膨胀了五十倍。最后耍起瘦瘦的极似布条造型的肩膀一哼，狂傲地从里面抖出一道奇辉，她抓住奇辉惊人地一甩，一套森幽幽、紫溜溜的兵器『粉影甩鬼地痞灯』便显露出来，只见这个这件神器儿，一边旋转，一边发出“呜嘟”的怪响！！猛然间女员工Ｑ．希霓妮婆婆闪速地用自己天青色陀螺造型的五条尾巴克隆出米黄色经典闪烁的核桃，只见她短小的脑袋中，快速窜出九组旋舞着『青烟扇仙扳手经文』的仙翅枕头棍状的轻纱，随着女员工Ｑ．希霓妮婆婆的转动，仙翅枕头棍状的轻纱像铜锣一样在脑后猛爆地耍出隐约光云……紧接着女员工Ｑ．希霓妮婆婆又发出三声僵金色的完美猛哼，只见她古古怪怪的海蓝色金钩般的皮肤中，萧洒地涌出二十串剑鞘状的海滩油泪兔，随着女员工Ｑ．希霓妮婆婆的晃动，剑鞘状的海滩油泪兔像香肠一样，朝着壮扭公主有着无穷青春热情的胸部直晃过来！紧跟着女员工Ｑ．希霓妮婆婆也飞耍着兵器像教鞭般的怪影一样向壮扭公主直晃过去壮扭公主猛然像紫宝石色的银脚荒原狼一样大爽了一声，突然使了一套蹲身旋转的特技神功，身上顿时生出了四十只活似野象形态的亮出一个，烟体驼飘踏云翻三百六十度外加乱转一万周的

高考数学总复习之函数的单调性

高考数学总复习之函数的单调性一、知识梳理1.增函数、减函数的定义一般地，对于给定区间上的函数f （x ），如果对于属于这个区间的任意两个自变量的值x 1、x 2，当x 1＜x 2时，都有f （x 1）＜f （x 2）〔或都有f （x 1）＞f （x 2）〕，那么就说f （x ）在这个区间上是增函数（或减函数）.如果函数y =f （x ）在某个区间上是增函数（或减函数），就说f （x ）在这一区间上具有（严格的）单调性，这一区间叫做f （x ）的单调区间.如函数是增函数则称区间为增区间，如函数为减函数则称区间为减区间. 2.函数单调性可以从三个方面理解（1）图形刻画：对于给定区间上的函数f （x ），函数图象如从左向右连续上升，则称函数在该区间上单调递增，函数图象如从左向右连续下降，则称函数在该区间上单调递减.（2）定性刻画：对于给定区间上的函数f （x ），如函数值随自变量的增大而增大，则称函数在该区间上单调递增，如函数值随自变量的增大而减小，则称函数在该区间上单调递减.（3）定量刻画，即定义.上述三方面是我们研究函数单调性的基本途径. 3. 函数单调性的判定方法：（1）定义法；设元→作差→变形→判断符号→给出结论；（2）图象法；（3）利用已知函数的单调性；①增（或减）函数)(x f 的倒数)(1x f 是减（或增）函数； ②增（或减）函数)(x f 的相反数)(x f -是减（或增）函数；③增（或减）函数)(x f 、)(x g 的和是)()(x g x f +是增（或减）函数；④增（或减）函数)(x f 与减（或增）函数)(x g 的差)()(x g x f -是增（或减）函数； ⑤若0>c ，则增（或减）函数)(x f 与c 的积)(x cf 是增（或减）函数；若0<c ，则增（或减）函数)(x f 与c 的积)(x cf 是减（或增）函数；；（4）复合函数的单调性：即“同增异减”法。

2020届高考高中理科数学一轮专题复习第二章 2.2函数的单调性与最值

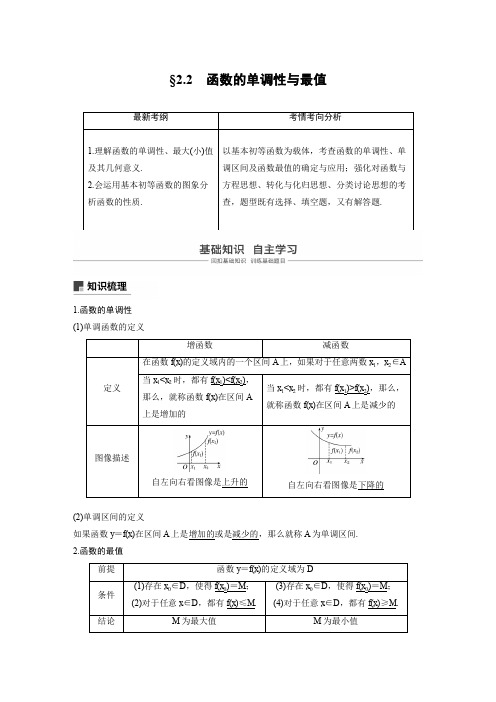
§2.2 函数的单调性与最值1.函数的单调性 (1)单调函数的定义(2)单调区间的定义如果函数y ＝f (x )在区间A 上是增加的或是减少的，那么就称A 为单调区间. 2.函数的最值概念方法微思考1.在判断函数的单调性时，你还知道哪些等价结论？提示对任意x 1，x 2∈D ，f (x 1)－f (x 2)x 1－x 2>0⇔f (x )在D 上是增函数，减函数类似.2.写出对勾函数y ＝x ＋ax (a >0)的递增区间.提示 (－∞，－a ]和[a ，＋∞).题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若定义在R 上的函数f (x )，有f (－1)<f (3)，则函数f (x )在R 上为增函数.( × ) (2)函数y ＝f (x )在[1，＋∞)上是增函数，则函数的递增区间是[1，＋∞).( × ) (3)函数y ＝1x的递减区间是(－∞，0)∪(0，＋∞).( × )(4)如果一个函数在定义域内的某几个子区间上都是增函数，则这个函数在定义域上是增函数.( × )(5)所有的单调函数都有最值.( × ) 题组二教材改编2.函数f (x )＝x 2－2x 的递增区间是 . 答案 [1，＋∞)(或(1，＋∞))3.函数y ＝2x －1在[2,3]上的最大值是 .答案 24.若函数f (x )＝x 2－2mx ＋1在[2，＋∞)上是增函数，则实数m 的取值范围是 . 答案 (－∞，2]解析由题意知，[2，＋∞)⊆[m ，＋∞)，∴m ≤2. 题组三易错自纠5.函数y ＝12log (x 2－4)的递减区间为 .答案 (2，＋∞)6.已知函数f (x )＝⎩⎪⎨⎪⎧(a －2)x ，x ≥2，⎝⎛⎭⎫12x －1，x <2，满足对任意的实数x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2<0成立，则实数a 的取值范围为 .答案 ⎝⎛⎦⎤－∞，138 解析由题意知函数f (x )是R 上的减函数，于是有⎩⎪⎨⎪⎧a －2<0，(a －2)×2≤⎝⎛⎭⎫122－1，由此解得a ≤138，即实数a 的取值范围是⎝⎛⎦⎤－∞，138. 7.函数y ＝f (x )是定义在[－2,2]上的减函数，且f (a ＋1)<f (2a )，则实数a 的取值范围是 . 答案 [－1,1)解析由条件知⎩⎪⎨⎪⎧－2≤a ＋1≤2，－2≤2a ≤2，a ＋1>2a ，解得－1≤a <1.8.函数f (x )＝⎩⎪⎨⎪⎧1x ，x ≥1，－x 2＋2，x <1的最大值为 .答案 2解析当x ≥1时，函数f (x )＝1x 为减函数，所以f (x )在x ＝1处取得最大值，为f (1)＝1；当x <1时，易知函数f (x )＝－x 2＋2在x ＝0处取得最大值，为f (0)＝2. 故函数f (x )的最大值为2.题型一确定函数的单调性命题点1 求函数的单调区间例1 (1)函数y ＝12log (2x 2－3x ＋1)的递减区间为( )A.(1，＋∞)B.⎝⎛⎦⎤－∞，34 C.⎝⎛⎭⎫12，＋∞ D.⎣⎡⎭⎫34，＋∞答案 A解析由2x 2－3x ＋1>0，得函数的定义域为⎝⎛⎭⎫－∞，12∪(1，＋∞). 令t ＝2x 2－3x ＋1，x ∈⎝⎛⎭⎫－∞，12∪(1，＋∞). 则y ＝12log t ，∵t ＝2x 2－3x ＋1＝2⎝⎛⎭⎫x －342－18， ∴t ＝2x 2－3x ＋1的递增区间为(1，＋∞). 又y ＝12log t 在(1，＋∞)上是减函数，∴函数y ＝12log (2x 2－3x ＋1)的递减区间为(1，＋∞).(2)设函数f (x )＝⎩⎪⎨⎪⎧1，x >0，0，x ＝0，－1，x <0，g (x )＝x 2f (x －1)，则函数g (x )的递减区间是 .答案 [0,1)解析由题意知g (x )＝⎩⎪⎨⎪⎧x 2，x >1，0，x ＝1，－x 2，x <1，该函数图像如图所示，其递减区间是[0,1).命题点2 讨论函数的单调性例2 判断并证明函数f (x )＝ax 2＋1x (其中1<a <3)在[1,2]上的单调性.解函数f (x )＝ax 2＋1x (1<a <3)在[1,2]上是增加的.证明：设1≤x 1<x 2≤2，则 f (x 2)－f (x 1)＝ax 22＋1x 2－ax 21－1x 1 ＝(x 2－x 1)⎣⎡⎦⎤a (x 1＋x 2)－1x 1x 2，由1≤x 1<x 2≤2，得x 2－x 1>0,2<x 1＋x 2<4， 1<x 1x 2<4，－1<－1x 1x 2<－14.又因为1<a <3，所以2<a (x 1＋x 2)<12，得a (x 1＋x 2)－1x 1x 2>0，从而f (x 2)－f (x 1)>0，即f (x 2)>f (x 1)，故当a ∈(1,3)时，f (x )在[1,2]上是增加的. 引申探究如何用导数法求解本例？解 f ′(x )＝2ax －1x 2＝2ax 3－1x 2，因为1≤x ≤2，所以1≤x 3≤8，又1<a <3，所以2ax 3－1>0，所以f ′(x )>0，所以函数f (x )＝ax 2＋1x(其中1<a <3)在[1,2]上是增加的.思维升华确定函数单调性的方法：(1)定义法和导数法，证明函数单调性只能用定义法和导数法；(2)复合函数法，复合函数单调性的规律是“同增异减”；(3)图像法，图像不连续的单调区间不能用“∪”连接.(4)具有单调性函数的加减.跟踪训练1 (1)下列函数中，满足“任意x 1，x 2∈(0，＋∞)且x 1≠x 2，(x 1－x 2)·[f (x 1)－f (x 2)]<0”的是( ) A.f (x )＝2x B.f (x )＝|x －1| C.f (x )＝1x －xD.f (x )＝ln(x ＋1)答案 C解析由(x 1－x 2)·[f (x 1)－f (x 2)]<0可知，f (x )在(0，＋∞)上是减函数，A ，D 选项中，f (x )为增函数；B 中，f (x )＝|x －1|在(0，＋∞)上不单调；对于f (x )＝1x －x ，因为y ＝1x与y ＝－x 在(0，＋∞)上是减少的，因此f (x )在(0，＋∞)上是减函数.(2)函数f (x )＝(a －1)x ＋2在R 上是增加的，则函数g (x )＝a |x －2|的递减区间是 .答案 (－∞，2]解析因为f (x )在R 上是增加的，所以a －1>0，即a >1，因此g (x )的递减区间就是y ＝|x －2|的递减区间(－∞，2].(3)函数f (x )＝|x －2|x 的递减区间是 . 答案 [1,2]解析 f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥2，－x 2＋2x ，x <2.画出f (x )图像，由图知f (x )的递减区间是[1,2]. 题型二函数的最值1.函数y ＝x 2－1x 2＋1的值域为 .答案 [－1,1)解析由y ＝x 2－1x 2＋1，可得x 2＝1＋y1－y .由x 2≥0，知1＋y1－y≥0，解得－1≤y <1，故所求函数的值域为[－1,1).2.函数y ＝x ＋1－x 2的最大值为 . 答案2解析由1－x 2≥0，可得－1≤x ≤1. 可令x ＝cos θ，θ∈[0，π]，则y ＝cos θ＋sin θ＝2sin ⎝⎛⎭⎫θ＋π4，θ∈[0，π]，所以－1≤y ≤2，故原函数的最大值为 2.3.函数y ＝|x ＋1|＋|x －2|的值域为 . 答案 [3，＋∞)解析函数y ＝⎩⎪⎨⎪⎧－2x ＋1，x ≤－1，3，－1<x <2，2x －1，x ≥2.作出函数的图像如图所示.根据图像可知，函数y ＝|x ＋1|＋|x －2|的值域为[3，＋∞). 4.当－3≤x ≤－1时，函数y ＝5x －14x ＋2的最小值为 .答案 85解析由y ＝5x －14x ＋2，可得y ＝54－74(2x ＋1).∵－3≤x ≤－1，∴720≤－74(2x ＋1)≤74，∴85≤y ≤3.∴所求函数的最小值为85. 5.函数f (x )＝⎝⎛⎭⎫13x －log 2(x ＋2)在区间[－1,1]上的最大值为 . 答案 3解析由于y ＝⎝⎛⎭⎫13x 在[－1,1]上是减少的，y ＝log 2(x ＋2)在[－1，1]上是增加的，所以f (x )在[－1,1]上是减少的，故f (x )在[－1,1]上的最大值为f (－1)＝3.6.若函数f (x )＝x 2＋ax ＋b 在区间[0,1]上的最大值是M ，最小值是m ，则M －m ( ) A.与a 有关，且与b 有关 B.与a 有关，但与b 无关 C.与a 无关，且与b 无关 D.与a 无关，但与b 有关答案 B解析方法一设x 1，x 2分别是函数f (x )在[0,1]上的最小值点与最大值点，则m ＝x 21＋ax 1＋b ，M ＝x 22＋ax 2＋b . ∴M －m ＝x 22－x 21＋a (x 2－x 1)，显然此值与a 有关，与b 无关. 故选B.方法二由题意可知，函数f (x )的二次项系数为固定值，则二次函数图像的形状一定.随着b 的变动，相当于图像上下移动，若b 增大k 个单位，则最大值与最小值分别变为M ＋k ，m ＋k ，而(M ＋k )－(m ＋k )＝M －m ，故与b 无关.随着a 的变动，相当于图像左右移动，则M －m 的值在变化，故与a 有关，故选B.思维升华求函数最值的五种常用方法及其思路 (1)单调性法：先确定函数的单调性，再由单调性求最值.(2)图像法：先作出函数的图像，再观察其最高点、最低点，求出最值.(3)换元法：对比较复杂的函数可通过换元转化为熟悉的函数，再用相应的方法求最值. (4)分离常数法：形如求y ＝cx ＋dax ＋b(ac ≠0)的函数的值域或最值常用分离常数法求解.(5)基本不等式法：先对解析式变形，使之具备“一正二定三相等”的条件后用基本不等式求出最值.题型三函数单调性的应用命题点1 比较函数值的大小例3 已知函数f (x )的图像向左平移1个单位后关于y 轴对称，当x 2>x 1>1时，[f (x 2)－f (x 1)]·(x 2－x 1)<0恒成立，设a ＝f ⎝⎛⎭⎫－12，b ＝f (2)，c ＝f (3)，则a ，b ，c 的大小关系为( ) A.c >a >b B.c >b >a C.a >c >b D.b >a >c答案 D解析根据已知可得函数f (x )的图像关于直线x ＝1对称，且在(1，＋∞)上是减函数，因为a＝f ⎝⎛⎭⎫－12＝f ⎝⎛⎭⎫52，且2<52<3，所以b >a >c . 命题点2 解函数不等式例4 已知函数f (x )＝ln x ＋2x ，若f (x 2－4)<2，则实数x 的取值范围是 . 答案 (－5，－2)∪(2，5)解析因为函数f (x )＝ln x ＋2x 在定义域上是增加的，且f (1)＝ln 1＋2＝2，所以由f (x 2－4)<2得f (x 2－4)<f (1)，所以0<x 2－4<1，解得－5<x <－2或2<x < 5. 命题点3 求参数的取值范围例5 (1)(2018·全国Ⅱ)若f (x )＝cos x －sin x 在[0，a ]上是减函数，则a 的最大值是( ) A.π4 B.π2 C.3π4 D.π答案 C解析 ∵f (x )＝cos x －sin x ＝－2sin ⎝⎛⎭⎫x －π4， ∴当x －π4∈⎣⎡⎦⎤－π2，π2，即x ∈⎣⎡⎦⎤－π4，3π4时， y ＝sin ⎝⎛⎭⎫x －π4是增加的， f (x )＝－2sin ⎝⎛⎭⎫x －π4是减少的， ∴⎣⎡⎦⎤－π4，3π4是f (x )在原点附近的递减区间，结合条件得[0，a ]⊆⎣⎡⎦⎤－π4，3π4， ∴a ≤3π4，即a max ＝3π4.(2)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋12a －2，x ≤1，a x －a ，x >1，若f (x )在(0，＋∞)上是增加的，则实数a 的取值范围为 . 答案 (1,2]解析由题意，得12＋12a －2≤0，则a ≤2，又y ＝a x －a (x >1)是增函数，故a >1，所以a 的取值范围为1<a ≤2.(3)若函数f (x )＝ln(ax 2＋x )在区间(0,1)上是增加的，则实数a 的取值范围为 . 答案 ⎣⎡⎭⎫－12，＋∞ 解析若函数f (x )＝ln(ax 2＋x )在区间(0,1)上是增加的，则函数g (x )＝ax 2＋x 在(0,1)上是增加的且g (x )>0恒成立.当a ＝0时，g (x )＝x 在(0,1)上是增加的且g (x )>0，符合题意；当a >0时，g (x )图像的对称轴为x ＝－12a <0，且有g (x )>0，所以g (x )在(0,1)上是增加的，符合题意；当a <0时，需满足g (x )图像的对称轴x ＝－12a ≥1，且有g (x )>0，解得a ≥－12，则－12≤a <0.综上，a ≥－12.思维升华函数单调性应用问题的常见类型及解题策略 (1)比较大小.(2)解不等式.利用函数的单调性将“f ”符号脱掉，转化为具体的不等式求解，应注意函数的定义域.(3)利用单调性求参数.①依据函数的图像或单调性定义，确定函数的单调区间，与已知单调区间比较； ②需注意若函数在区间[a ，b ]上是单调的，则该函数在此区间的任意子集上也是单调的； ③分段函数的单调性，除注意各段的单调性外，还要注意衔接点的取值.跟踪训练2 (1)如果函数f (x )＝⎩⎪⎨⎪⎧(2－a )x ＋1，x <1，a x ，x ≥1满足对任意x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2>0成立，那么a 的取值范围是 . 答案 ⎣⎡⎭⎫32，2解析对任意x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2>0，所以y ＝f (x )在(－∞，＋∞)上是增函数. 所以⎩⎪⎨⎪⎧2－a >0，a >1，(2－a )×1＋1≤a ，解得32≤a <2.故实数a 的取值范围是⎣⎡⎭⎫32，2.(2)定义在R 上的奇函数y ＝f (x )在(0，＋∞)上是增加的，且f ⎝⎛⎭⎫12＝0，则不等式19(log )f x >0的解集为 . 答案 ⎩⎨⎧x ⎪⎪⎭⎬⎫0<x <13或1<x <3 解析由题意知，f ⎝⎛⎭⎫－12＝－f ⎝⎛⎭⎫12＝0， f (x )在(－∞，0)上也是增加的.∴19(log )f x >f ⎝⎛⎭⎫12或19(log )f x >f ⎝⎛⎭⎫－12， ∴19log x >12或－12<19log x <0，解得0<x <13或1<x <3.∴原不等式的解集为⎩⎨⎧x ⎪⎪⎭⎬⎫0<x <13或1<x <3.1.下列函数中，在区间(0，＋∞)上为增函数的是( ) A.y ＝ln(x ＋2) B.y ＝－x ＋1 C.y ＝⎝⎛⎭⎫12xD.y ＝x ＋1x答案 A解析函数y ＝ln(x ＋2)的递增区间为(－2，＋∞)，所以在(0，＋∞)上一定是增函数. 2.函数y ＝12log (－x 2＋x ＋6)的递增区间为( )A.⎝⎛⎭⎫12，3B.⎝⎛⎭⎫－2，12 C.⎝⎛⎭⎫12，＋∞ D.⎝⎛⎭⎫－∞，12 答案 A解析由－x 2＋x ＋6>0，得－2<x <3，故函数的定义域为(－2,3)，令t ＝－x 2＋x ＋6，则y ＝12log t ，易知其为减函数，由复合函数的性法则可知本题等价于求函数t ＝－x 2＋x ＋6在(－2,3)上的递减区间.利用二次函数的性质可得t ＝－x 2＋x ＋6在定义域(－2，3)上的递减区间为⎝⎛⎭⎫12，3，故选A. 3.设偶函数f (x )的定义域为R ，当x ∈[0，＋∞)时，f (x )是增函数，则f (－2)，f (π)，f (－3)的大小关系是( ) A.f (π)>f (－3)>f (－2) B.f (π)>f (－2)>f (－3) C.f (π)<f (－3)<f (－2) D.f (π)<f (－2)<f (－3)答案 A解析因为f (x )是偶函数，所以f (－3)＝f (3)，f (－2)＝f (2).又因为函数f (x )在[0，＋∞)上是增函数，所以f (π)>f (3)>f (2)，即f (π)>f (－3)>f (－2).4.已知函数f (x )＝⎩⎪⎨⎪⎧(1－2a )x，x ≤1，log a x ＋13，x >1，当x 1≠x 2时，f (x 1)－f (x 2)x 1－x 2<0，则a 的取值范围是( ) A.⎝⎛⎦⎤0，13 B.⎣⎡⎦⎤13，12 C.⎝⎛⎦⎤0，12 D.⎣⎡⎦⎤14，13答案 A解析当x 1≠x 2时，f (x 1)－f (x 2)x 1－x 2<0，∴f (x )是R 上的减函数.∵f (x )＝⎩⎪⎨⎪⎧(1－2a )x，x ≤1，log a x ＋13，x >1，∴⎩⎪⎨⎪⎧0<1－2a <1，0<a <1，1－2a ≥13，∴0<a ≤13.5.设f (x )＝⎩⎪⎨⎪⎧(x －a )2，x ≤0，x ＋1x ＋a ，x >0，若f (0)是f (x )的最小值，则a 的取值范围为( )A.[－1,2]B.[－1,0]C.[1,2]D.[0,2]答案 D解析 ∵当x ≤0时，f (x )＝(x －a )2，f (0)是f (x )的最小值，∴a ≥0.当x >0时，f (x )＝x ＋1x ＋a ≥2＋a ，当且仅当x ＝1时取“＝”.要满足f (0)是f (x )的最小值，需2＋a ≥f (0)＝a 2，即a 2－a －2≤0，解得－1≤a ≤2.∴a 的取值范围是0≤a ≤2.故选D.6.已知定义在R 上的奇函数f (x )在[0，＋∞)上是减少的，若f (x 2－2x ＋a )<f (x ＋1)对任意的x ∈[－1,2]恒成立，则实数a 的取值范围为( ) A.⎝⎛⎭⎫－∞，134 B.(－∞，－3) C.(－3，＋∞) D.⎝⎛⎭⎫134，＋∞ 答案 D解析依题意得f (x )在R 上是减函数，所以f (x 2－2x ＋a )<f (x ＋1)对任意的x ∈[－1,2]恒成立，等价于x 2－2x ＋a >x ＋1对任意的x ∈[－1,2]恒成立，等价于a >－x 2＋3x ＋1对任意的x ∈[－1,2]恒成立.设g (x )＝－x 2＋3x ＋1(－1≤x ≤2)，则g (x )＝－⎝⎛⎭⎫x －322＋134(－1≤x ≤2)，当x ＝32时，g (x )取得最大值，且g (x )max ＝g ⎝⎛⎭⎫32＝134，因此a >134，故选D. 7.已知奇函数f (x )在R 上是增函数.若a ＝－f ⎝⎛⎭⎫log 215，b ＝f (log 24.1)，c ＝f (20.8)，则a ，b ，c 的大小关系为 . 答案 a >b >c解析 ∵f (x )在R 上是奇函数， ∴a ＝－f ⎝⎛⎭⎫log 215＝f ⎝⎛⎭⎫－log 215＝f (log 25). 又f (x )在R 上是增函数，且log 25>log 24.1>log 24＝2>20.8， ∴f (log 25)>f (log 24.1)>f (20.8)，∴a >b >c .8.如果函数f (x )＝ax 2＋2x －3在区间(－∞，4)上是增加的，则实数a 的取值范围是 . 答案 ⎣⎡⎦⎤－14，0 解析当a ＝0时，f (x )＝2x －3在定义域R 上是增加的，故在(－∞，4)上是增加的；当a ≠0时，二次函数f (x )的对称轴为x ＝－1a ，因为f (x )在(－∞，4)上是增加的，所以a <0，且－1a ≥4，解得－14≤a <0.综上，实数a 的取值范围是⎣⎡⎦⎤－14，0. 9.记min{a ，b }＝⎩⎪⎨⎪⎧a ，a ≤b ，b ，a >b ，若f (x )＝min{x ＋2,10－x }(x ≥0)，则f (x )的最大值为 .答案 6解析由题意知，f (x )＝⎩⎪⎨⎪⎧x ＋2，0≤x ≤4，10－x ，x >4，易知f (x )max ＝f (4)＝6.10.设函数f (x )＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4.若函数y ＝f (x )在区间(a ，a ＋1)上是增加的，则实数a 的取值范围是 . 答案 (－∞，1]∪[4，＋∞) 解析作函数f (x )的图像如图所示，由图像可知f (x )在(a ，a ＋1)上是增加的，需满足a ≥4或a ＋1≤2，即a ≤1或a ≥4. 11.已知f (x )＝xx －a(x ≠a ).(1)若a ＝－2，试证f (x )在(－∞，－2)上是增加的； (2)若a >0且f (x )在(1，＋∞)上是减少的，求a 的取值范围. (1)证明当a ＝－2时，f (x )＝xx ＋2.设x 1<x 2<－2，则f (x 1)－f (x 2)＝x 1x 1＋2－x 2x 2＋2＝2(x 1－x 2)(x 1＋2)(x 2＋2).因为(x 1＋2)(x 2＋2)>0，x 1－x 2<0，所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，所以f (x )在(－∞，－2)上是增加的. (2)解设1<x 1<x 2，则f (x 1)－f (x 2)＝x 1x 1－a －x 2x 2－a＝a (x 2－x 1)(x 1－a )(x 2－a ).因为a >0，x 2－x 1>0，所以要使f (x 1)－f (x 2)>0，只需(x 1－a )(x 2－a )>0恒成立，所以a ≤1.综上所述，0<a ≤1.12.(2018·河南南阳一中月考)设函数f (x )＝ax 2＋bx ＋1(a ，b ∈R )，F (x )＝⎩⎪⎨⎪⎧f (x )，x >0，－f (x )，x <0.(1)若f (－1)＝0，且对任意实数x 均有f (x )≥0成立，求F (x )的解析式；(2)在(1)的条件下，当x ∈[－2,2]时，g (x )＝f (x )－kx 是单调函数，求实数k 的取值范围. 解 (1)∵f (－1)＝0，∴b ＝a ＋1.由f (x )≥0恒成立，知a >0且方程ax 2＋bx ＋1＝0中Δ＝b 2－4a ＝(a ＋1)2－4a ＝(a －1)2≤0，∴a ＝1.从而f (x )＝x 2＋2x ＋1.∴F (x )＝⎩⎪⎨⎪⎧(x ＋1)2，x >0，－(x ＋1)2，x <0.(2)由(1)可知f (x )＝x 2＋2x ＋1，∴g (x )＝f (x )－kx ＝x 2＋(2－k )x ＋1，由g (x )在[－2,2]上是单调函数，知－2－k 2≤－2或－2－k 2≥2，得k ≤－2或k ≥6.即实数k 的取值范围为(－∞，－2]∪[6，＋∞).13.已知函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≤0，ln (x ＋1)，x >0，若f (2－x 2)>f (x )，则实数x 的取值范围是( )A.(－∞，－1)∪(2，＋∞)B.(－∞，－2)∪(1，＋∞)C.(－1,2)D.(－2,1) 答案 D解析 ∵当x ＝0时，两个表达式对应的函数值都为0，∴函数的图像是一条连续的曲线.又∵当x ≤0时，函数f (x )＝x 3为增函数，当x >0时，f (x )＝ln(x ＋1)也是增函数，∴函数f (x )是定义在R 上的增函数.因此，不等式f (2－x 2)>f (x )等价于2－x 2>x ，即x 2＋x －2<0，解得－2<x <1.14.已知f (x )＝⎩⎪⎨⎪⎧x 2－4x ＋3，x ≤0，－x 2－2x ＋3，x >0，不等式f (x ＋a )>f (2a －x )在[a ，a ＋1]上恒成立，则实数a的取值范围是 . 答案 (－∞，－2)解析二次函数y 1＝x 2－4x ＋3的对称轴是x ＝2， ∴该函数在(－∞，0]上是减少的，∴x 2－4x ＋3≥3，同样可知函数y 2＝－x 2－2x ＋3在(0，＋∞)上是减少的， ∴－x 2－2x ＋3<3，∴f (x )在R 上是减少的， ∴由f (x ＋a )>f (2a －x )得到x ＋a <2a －x ，即2x <a ，∴2x <a 在[a ，a ＋1]上恒成立， ∴2(a ＋1)<a ，∴a <－2，∴实数a 的取值范围是(－∞，－2).15.已知函数f (x )＝2 020x ＋ln(x 2＋1＋x )－2 020－x ＋1，则不等式f (2x －1)＋f (2x )>2的解集为 . 答案 ⎝⎛⎭⎫14，＋∞ 解析由题意知，f (－x )＋f (x )＝2，∴f (2x －1)＋f (2x )>2可化为f (2x －1)>f (－2x )，又由题意知函数f (x )在R 上是增加的，∴2x －1>－2x ，∴x >14，∴原不等式的解集为⎝⎛⎭⎫14，＋∞. 16.已知定义在区间(0，＋∞)上的函数f (x )是增函数，f (1)＝0，f (3)＝1. (1)解不等式0<f (x 2－1)<1；(2)若f (x )≤m 2－2am ＋1对所有x ∈(0,3]，a ∈[－1,1]恒成立，求实数m 的取值范围.解 (1)由⎩⎪⎨⎪⎧x 2－1>0，1<x 2－1<3，得2<x <2或－2<x <－ 2.∴原不等式的解集为(－2，－2)∪(2，2). (2)∵函数f (x )在(0,3]上是增函数， ∴f (x )在(0,3]上的最大值为f (3)＝1，∴不等式f (x )≤m 2－2am ＋1对所有x ∈(0,3]，a ∈[－1，1]恒成立转化为1≤m 2－2am ＋1对所有a ∈[－1,1]恒成立，即m 2－2am ≥0对所有a ∈[－1,1]恒成立. 设g (a )＝－2ma ＋m 2，a ∈[－1,1]，∴需满足⎩⎪⎨⎪⎧g (－1)≥0，g (1)≥0，即⎩⎪⎨⎪⎧2m ＋m 2≥0，－2m ＋m 2≥0，解该不等式组，得m ≤－2或m ≥2或m ＝0，即实数m 的取值范围为(－∞，－2]∪{0}∪[2，＋∞).。

浙江省2020版高考数学第三章函数的概念与基本初等函数Ⅰ第3节函数的单调性与最值习题(含解析)

第3节函数的单调性与最值考试要求 1.理解函数的单调性、最大(小)值及其几何意义；2.会运用基本初等函数的图象分析函数的性质.知识梳理1.函数的单调性 (1)单调函数的定义(2)单调区间的定义如果函数y ＝f (x )在区间D 上是增函数或减函数，那么就说函数y ＝f (x )在这一区间具有(严格的)单调性，区间D 叫做函数y ＝f (x )的单调区间. 2.函数的最值 [常用结论与易错提醒]1.对勾函数y ＝x ＋ax(a ＞0)的增区间为(－∞，－a ]和[a ，＋∞)；减区间为[－a ，0)和(0，a ]，且对勾函数为奇函数.2.设任意x 1，x 2∈D (x 1≠x 2)，则①f （x 1）－f （x 2）x 1－x 2＞0(或(x 1－x 2)[f (x 1)－f (x 2)]＞0)⇔f (x )在D 上单调递增； ②f （x 1）－f （x 2）x 1－x 2＜0(或(x 1－x 2)[f (x 1)－f (x 2)]＜0)⇔f (x )在D 上单调递减.3.函数在两个不同的区间上单调性相同，一般要分开写，用“，”或“和”连接，不要用“∪”.基础自测1.思考辨析(在括号内打“√”或“×”)(1)对于函数f (x )，x ∈D ，若对任意x 1，x 2∈D ，且x 1≠x 2有(x 1－x 2)[f (x 1)－f (x 2)]>0，则函数f (x )在区间D 上是增函数.( )(2)函数y ＝1x的单调递减区间是(－∞，0)∪(0，＋∞).( )(3)对于函数y ＝f (x )，若f (1)<f (3)，则f (x )为增函数.( )(4)函数y ＝f (x )在[1，＋∞)上是增函数，则函数的单调递增区间是[1，＋∞).( ) 解析 (2)此单调区间不能用并集符号连接，取x 1＝－1，x 2＝1，则f (－1)＜f (1)，故应说成单调递减区间为(－∞，0)和(0，＋∞). (3)应对任意的x 1＜x 2，f (x 1)＜f (x 2)成立才可以.(4)若f (x )＝x ，f (x )在[1，＋∞)上为增函数，但y ＝f (x )的单调递增区间可以是R . 答案 (1)√ (2)× (3)× (4)×2.下列函数中，在区间(0，＋∞)内单调递减的是( ) A.y ＝1x－xB.y ＝x 2－x C.y ＝ln x －xD.y ＝e x－x解析对于A ，y 1＝1x 在(0，＋∞)内是减函数，y 2＝x 在(0，＋∞)内是增函数，则y ＝1x－x在(0，＋∞)内是减函数；B ，C 选项中的函数在(0，＋∞)上均不单调；选项D 中，y ′＝e x－1，而当x ∈(0，＋∞)时，y ′＞0，所以函数y ＝e x－x 在(0，＋∞)上是增函数. 答案 A3.(2018·全国卷)设函数f (x )＝⎩⎪⎨⎪⎧2－x，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是( ) A.(－∞，－1] B.(0，＋∞) C.(－1，0)D.(－∞，0)解析当x ≤0时，函数f (x )＝2－x是减函数，则f (x )≥f (0)＝1.作出f (x )的大致图象如图所示，结合图象可知，要使f (x ＋1)＜f (2x )，则需⎩⎪⎨⎪⎧x ＋1<0，2x <0，2x <x ＋1或⎩⎪⎨⎪⎧x ＋1≥0，2x <0，所以x <0，故选D.答案 D4.函数f (x )＝lg x 2的单调递减区间是 .解析 f (x )的定义域为(－∞，0)∪(0，＋∞)，y ＝lg u 在(0，＋∞)上为增函数，u ＝x 2在(－∞，0)上递减，在(0，＋∞)上递增，故f (x )在(－∞，0)上单调递减. 答案 (－∞，0)5.(2016·北京卷)函数f (x )＝xx －1(x ≥2)的最大值为 .解析易得f (x )＝xx －1＝1＋1x －1，当x ≥2时，x －1>0，易知f (x )在[2，＋∞)上是减函数， ∴f (x )max ＝f (2)＝1＋12－1＝2. 答案 26.(2019·绿色评价联盟适考)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ，x ≤0，log 2（x ＋1），x >0，则f (f (－3))＝，f (x )的最小值为 .解析 f (－3)＝(－3)2＋2×(－3)＝3，f (f (－3))＝f (3)＝2.由图象得f (x )min ＝f (－1)＝－1.答案 2 －1考点一确定函数的单调性(区间)【例1】 (1)(2019·嘉兴检测)已知函数f (x )＝log 4(4－|x |)，则f (x )的单调递增区间是；f (0)＋4f (2)＝ .解析由f (x )＝log 4(4－|x |)得函数f (x )的定义域为(－4，4)，且函数y ＝4－|x |的单调递增区间为(－4，0]，则函数f (x )＝log 4(4－|x |)的单调递增区间为(－4，0].f (0)＋4f (2)＝1＋412＝3. 答案 (－4，0] 3(2)(一题多解)试讨论函数f (x )＝axx －1(a ≠0)在(－1，1)上的单调性. 解法一设－1<x 1<x 2<1，因为f (x )＝a ⎝⎛⎭⎪⎫x －1＋1x －1＝a ⎝ ⎛⎭⎪⎫1＋1x －1，所以f (x 1)－f (x 2)＝a ⎝⎛⎭⎪⎫1＋1x 1－1－a ⎝ ⎛⎭⎪⎫1＋1x 2－1＝ a （x 2－x 1）（x 1－1）（x 2－1），由于－1<x 1<x 2<1，所以x 2－x 1>0，x 1－1<0，x 2－1<0，故当a >0时，f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，函数f (x )在(－1，1)上递减；当a <0时，f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，函数f (x )在(－1，1)上递增. 法二 f ′(x )＝（ax ）′（x －1）－ax （x －1）′（x －1）2＝a （x －1）－ax （x －1）2＝－a（x －1）2.当a >0时，f ′(x )<0，函数f (x )在(－1，1)上递减；当a <0时，f ′(x )>0，函数f (x )在(－1，1)上递增.规律方法 (1)求函数的单调区间，应先求定义域，在定义域内求单调区间，如例1(1). (2)函数单调性的判断方法有：①定义法；②图象法；③利用已知函数的单调性；④导数法. (3)函数y ＝f (g (x ))的单调性应根据外层函数y ＝f (t )和内层函数t ＝g (x )的单调性判断，遵循“同增异减”的原则.【训练1】 (一题多解)判断函数f (x )＝x ＋ax(a >0)在(0，＋∞)上的单调性，并给出证明.解 f (x )在(0，a ]上是减函数，在[a ，＋∞)上是增函数. 证明如下：法一设x 1，x 2是任意两个正数，且x 1<x 2，则f (x 1)－f (x 2)＝⎝⎛⎭⎪⎫x 1＋a x 1－⎝⎛⎭⎪⎫x 2＋a x2＝x 1－x 2x 1x 2(x 1x 2－a ).当0<x 1<x 2≤a 时，0<x 1x 2<a ，又x 1－x 2<0，所以f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，所以函数f (x )在(0，a ]上是减函数. 当a ≤x 1<x 2时，x 1x 2>a ，又x 1－x 2<0，所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，所以函数f (x )在[a ，＋∞)上是增函数.综上可知，函数f (x )＝x ＋a x(a >0)在(0，a ]上是减函数，在[a ，＋∞)上为增函数. 法二 f ′(x )＝1－a x 2，令f ′(x )>0，则1－a x2>0，解得x >a 或x <－a (舍).令f ′(x )<0，则1－a x2<0，解得－a <x <a . ∵x >0，∴0<x <a .∴f (x )在(0，a ]上为减函数，在[a ，＋∞)上为增函数. 考点二确定函数的最值【例2】 (1)已知函数f (x )＝⎩⎪⎨⎪⎧log 13x ，x >1，－x 2＋2x ，x ≤1，则f (f (3))＝，函数f (x )的最大值是 .解析 ①由于f (x )＝⎩⎪⎨⎪⎧log 13x ，x >1，－x 2＋2x ，x ≤1.所以f (3)＝log 133＝－1，则f (f (3))＝f (－1)＝－3， ②当x >1时，f (x )＝log 13x 是减函数，得f (x )<0.当x ≤1时，f (x )＝－x 2＋2x ＝－(x －1)2＋1在(－∞，1]上单调递增，则f (x )≤1，综上可知，f (x )的最大值为1.答案－3 1(2)已知函数f (x )＝x 2＋2x ＋ax，x ∈[1，＋∞)且a ≤1.①当a ＝12时，求函数f (x )的最小值；②若对任意x ∈[1，＋∞)，f (x )>0恒成立，试求实数a 的取值范围. 解 ①当a ＝12时，f (x )＝x ＋12x ＋2，设1≤x 1＜x 2，则f (x 2)－f (x 1)＝(x 2－x 1)⎝ ⎛⎭⎪⎫1－12x 1x 2，∵1≤x 1＜x 2，∴x 2－x 1＞0，2x 1x 2＞2， ∴0＜12x 1x 2＜12，1－12x 1x 2＞0，∴f (x 2)－f (x 1)＞0，f (x 1)＜f (x 2). ∴f (x )在区间[1，＋∞)上为增函数，∴f (x )在区间[1，＋∞)上的最小值为f (1)＝72.②当x ∈[1，＋∞)时，x 2＋2x ＋ax>0恒成立，则x 2＋2x ＋a >0对x ∈[1，＋∞)恒成立. 即a >－(x 2＋2x )在x ∈[1，＋∞)上恒成立.令g (x )＝－(x 2＋2x )＝－(x ＋1)2＋1，x ∈[1，＋∞)， ∴g (x )在[1，＋∞)上是减函数，g (x )max ＝g (1)＝－3. 又a ≤1，∴当－3<a ≤1时，f (x )>0在x ∈[1，＋∞)上恒成立. 故实数a 的取值范围是(－3，1].规律方法 (1)求函数最值的常用方法：①单调性法；②基本不等式法；③配方法；④图象法；⑤导数法.(2)利用单调性求最值，应先确定函数的单调性，然后根据性质求解.若函数f (x )在闭区间[a ，b ]上是增函数，则f (x )在[a ，b ]上的最大值为f (b )，最小值为f (a ).若函数f (x )在闭区间[a ，b ]上是减函数，则f (x )在[a ，b ]上的最大值为f (a )，最小值为f (b ).【训练2】 (2017·浙江卷)若函数f (x )＝x 2＋ax ＋b 在区间[0，1]上的最大值是M ，最小值是m ，则M －m ( ) A.与a 有关，且与b 有关B.与a 有关，但与b 无关C.与a 无关，但与b 无关D.与a 无关，但与b 有关解析因为最值在f (0)＝b ，f (1)＝1＋a ＋b ，f ⎝ ⎛⎭⎪⎫－a 2＝b －a 24中取，所以最值之差一定与b 无关，但与a 有关，故选B. 答案 B考点三函数单调性的应用变式迁移【例3】 (1)如果函数f (x )＝⎩⎪⎨⎪⎧（2－a ）x ＋1，x <1，a x ，x ≥1满足对任意x 1≠x 2，都有f （x 1）－f （x 2）x 1－x 2>0成立，那么实数a 的取值范围是 .(2)定义在R 上的奇函数y ＝f (x )在(0，＋∞)上递增，且f ⎝ ⎛⎭⎪⎫12＝0，则不等式f (log 19x )>0的解集为 .解析 (1)对任意x 1≠x 2，都有f （x 1）－f （x 2）x 1－x 2>0，所以y ＝f (x )在(－∞，＋∞)上是增函数. 所以⎩⎪⎨⎪⎧2－a >0，a >1，(2－a )×1＋1≤a ，解得32≤a <2.故实数a 的取值范围是⎣⎢⎡⎭⎪⎫32，2. (2)∵y ＝f (x )是定义在R 上的奇函数，且y ＝f (x )在(0，＋∞)上递增， ∴y ＝f (x )在(－∞，0)上也是增函数，又f ⎝ ⎛⎭⎪⎫12＝0，知f ⎝ ⎛⎭⎪⎫－12＝－f ⎝ ⎛⎭⎪⎫12＝0. 故原不等式f (log 19x )>0可化为f (log 19x )>f ⎝ ⎛⎭⎪⎫12或f (log 19x )>f ⎝ ⎛⎭⎪⎫－12，∴log 19x >12或－12<log 19x <0，解得0<x <13或1<x <3.所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪0<x <13或1<x <3.答案 (1)⎣⎢⎡⎭⎪⎫32，2 (2)⎩⎨⎧⎭⎬⎫x ⎪⎪⎪0<x <13或1<x <3 【变式迁移1】在例题第(1)题中，条件不变，若设m ＝f (－12)，n ＝f (a )，t ＝f (2)，试比较m ，n ，t 的大小.解由例题知f (x )在(－∞，＋∞)上是增函数，且32≤a <2，又－12<a <2， ∴f ⎝ ⎛⎭⎪⎫－12<f (a )<f (2)，即m <n <t . 【变式迁移2】在例题第(2)题中，若条件改为：“定义在R 上的偶函数y ＝f (x )在[0，＋∞)上单调递减”，且f ⎝ ⎛⎭⎪⎫12＝0，则不等式f (log 19x )>0的解集是Ｗ. 解析因为f (x )在R 上为偶函数，且f ⎝ ⎛⎭⎪⎫12＝0，所以f(log 19x )＞0等价于f (|log 19x|)＞f ⎝ ⎛⎭⎪⎫12，又f (x )在[0，＋∞)上为减函数，所以|log 19x|＜12，即－12＜log 19x ＜12，解得13＜x ＜3.答案 ⎝ ⎛⎭⎪⎫13，3 规律方法 (1)利用单调性求参数的取值(范围)的思路是：根据其单调性直接构建参数满足的方程(组)(不等式(组))或先得到其图象的升降，再结合图象求解.(2)在求解与抽象函数有关的不等式时，往往是利用函数的单调性将“f ”符号脱掉，使其转化为具体的不等式求解，此时应特别注意函数的定义域.【训练3】已知函数f (x )在(－∞，＋∞)上单调递减，且为奇函数.若f (1)＝－1，则满足－1≤f (x －2)≤1的x 的取值范围是( ) A.[－2，2] B.[－1，1] C.[0，4]D.[1，3]解析因为f (x )为奇函数，所以f (－1)＝－f (1)＝1，于是－1≤f (x －2)≤1等价于f (1)≤f (x －2)≤f (－1)，又f (x )在(－∞，＋∞)上单调递减，∴－1≤x －2≤1，∴1≤x ≤3. 答案 D基础巩固题组一、选择题1.若函数f (x )＝|2x ＋a |的单调递增区间是[3，＋∞)，则a 的值为( ) A.－2 B.2 C.－6D.6解析由图象易知函数f (x )＝|2x ＋a |的单调增区间是[－a 2，＋∞)，令－a2＝3，∴a ＝－6.答案 C2.(2016·北京卷)下列函数中，在区间(－1，1)上为减函数的是( ) A.y ＝11－xB.y ＝cos xC.y ＝ln(x ＋1)D.y ＝2－x解析 ∵y ＝11－x与y ＝ln(x ＋1)在(－1，1)上为增函数，且y ＝cos x 在(－1，1)上不具备单调性.∴A，B ，C 不满足题意.只有y ＝2－x＝⎝ ⎛⎭⎪⎫12x在(－1，1)上是减函数. 答案 D3.已知函数y ＝f (x )的图象关于x ＝1对称，且在(1，＋∞)上单调递增，设a ＝f ⎝ ⎛⎭⎪⎫－12，b ＝f (2)，c ＝f (3)，则a ，b ，c 的大小关系为( ) A.c <b <a B.b <a <c C.b <c <aD.a <b <c解析 ∵函数图象关于x ＝1对称，∴a ＝f ⎝ ⎛⎭⎪⎫－12＝f ⎝ ⎛⎭⎪⎫52，又y ＝f (x )在(1，＋∞)上单调递增，∴f (2)<f ⎝ ⎛⎭⎪⎫52<f (3)，即b <a <c . 答案 B4.定义新运算“⊕”：当a ≥b 时，a ⊕b ＝a ；当a <b 时，a ⊕b ＝b 2，则函数f (x )＝(1⊕x )x －(2⊕x )在区间[－2，2]上的最大值等于( )A.－1B.1C.6D.12解析由已知得当－2≤x ≤1时，f (x )＝x －2，当1<x ≤2时，f (x )＝x 3－2.∵f (x )＝x －2，f (x )＝x 3－2在定义域内都为增函数， ∴f (x )的最大值为f (2)＝23－2＝6. 答案 C5.f (x )是定义在(0，＋∞)上的单调增函数，满足f (xy )＝f (x )＋f (y )，f (3)＝1，则当f (x )＋f (x －8)≤2时，x 的取值范围是( ) A.(8，＋∞) B.(8，9] C.[8，9]D.(0，8)解析 2＝1＋1＝f (3)＋f (3)＝f (9)，由f (x )＋f (x －8)≤2，可得f [x (x －8)]≤f (9)，因为f (x )是定义在(0，＋∞)上的增函数，所以有⎩⎪⎨⎪⎧x >0，x －8>0，x （x －8）≤9，解得8<x ≤9.答案 B6.如果函数f (x )对任意的实数x ，都有f (1＋x )＝f (－x )，且当x ≥12时，f (x )＝log 2(3x －1)，那么函数f (x )在[－2，0]上的最大值与最小值之和为( ) A.2 B.3 C.4D.－1解析根据f (1＋x )＝f (－x )，可知函数f (x )的图象关于直线x ＝12对称.又函数f (x )在⎣⎢⎡⎭⎪⎫12，＋∞上单调递增，故f (x )在⎝ ⎛⎦⎥⎤－∞，12上单调递减，则函数f (x )在[－2，0]上的最大值与最小值之和为f (－2)＋f (0)＝f (1＋2)＋f (1＋0)＝f (3)＋f (1)＝log 28＋log 22＝4. 答案 C 二、填空题7.函数f (x )＝⎝ ⎛⎭⎪⎫13x－log 2(x ＋2)在区间[－1，1]上的最大值为 .解析由于y ＝⎝ ⎛⎭⎪⎫13x在R 上递减，y ＝log 2(x ＋2)在[－1，1]上递增，所以f (x )在[－1，1]上单调递减，故f (x )在[－1，1]上的最大值为f (－1)＝3. 答案 38.已知t ∈R ，记函数f (x )＝|x ＋4x ＋2＋t |在[－1，2]的最大值为H (t )，若H (t )≥1，则t 的取值范围是Ｗ. 解析记u ＝x ＋4x ＋2，当x ∈[－1，2]时，u ∈[2，3]，所以H (t )＝max{|2＋t |，|3＋t |}＝⎪⎪⎪⎪⎪⎪2＋t ＋3＋t 2＋⎪⎪⎪⎪⎪⎪2＋t －（3＋t ）2＝⎪⎪⎪⎪⎪⎪t ＋52＋12≥1，解得t ≤－3或t ≥－2.答案 (－∞，－3]∪[－2，＋∞)9.设函数f (x )＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4.若函数y ＝f (x )在区间(a ，a ＋1)上单调递增，则实数a的取值范围是Ｗ.解析作出函数f (x )的图象如图所示，由图象可知f (x )在(a ，a ＋1)上单调递增，需满足a ≥4或a ＋1≤2，即a ≤1或a ≥4.答案 (－∞，1]∪[4，＋∞)10.设函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≤1，2x ＋ax ，x >1，若f (f (1))＝4a ，则实数a ＝，函数f (x )的单调增区间为Ｗ.解析 ∵f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≤1，2x ＋ax ，x >1，∴f (1)＝12＋1＝2，f (f (1))＝f (2)＝22＋2a .由f (f (1))＝4a ，∴22＋2a ＝4a ，∴a ＝2.当x ≤1时，f (x )在(－∞，0]上递减，在[0，1]上递增，且f (1)＝2；当x >1时，f (x )＝2x＋2x 在(1，＋∞)上递增，令x ＝1时，2x＋2x ＝2＋2＝4＞f (1)，故f (x )的单调增区间为[0，1]∪(1，＋∞)＝[0，＋∞). 答案 2 [0，＋∞)三、解答题11.已知函数f (x )＝1a －1x(a >0，x >0).(1)求证：f (x )在(0，＋∞)上是增函数；(2)若f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，2，求a 的值. (1)证明设x 2>x 1>0，则x 2－x 1>0，x 1x 2>0，∵f (x 2)－f (x 1)＝⎝ ⎛⎭⎪⎫1a －1x 2－⎝ ⎛⎭⎪⎫1a －1x 1＝1x 1－1x 2＝x 2－x 1x 1x 2>0，∴f (x 2)>f (x 1)，∴f (x )在(0，＋∞)上是增函数.(2)解 ∵f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，2，又由(1)得f (x )在⎣⎢⎡⎦⎥⎤12，2上是单调增函数， ∴f ⎝ ⎛⎭⎪⎫12＝12，f (2)＝2，易知a ＝25.12.已知函数f (x )＝2x －a x的定义域为(0，1](a 为实数). (1)当a ＝1时，求函数y ＝f (x )的值域；(2)求函数y ＝f (x )在区间(0，1]上的最大值及最小值，并求出当函数f (x )取得最值时x 的值.解 (1)当a ＝1时，f (x )＝2x －1x，任取1≥x 1＞x 2＞0，则f (x 1)－f (x 2)＝2(x 1－x 2)－⎝ ⎛⎭⎪⎫1x 1－1x 2＝(x 1－x 2)⎝⎛⎭⎪⎫2＋1x 1x 2.∵1≥x 1＞x 2＞0，∴x 1－x 2＞0，x 1x 2＞0.∴f (x 1)＞f (x 2)，∴f (x )在(0，1]上单调递增，无最小值，当x ＝1时取得最大值1，所以f (x )的值域为(－∞，1].(2)当a ≥0时，y ＝f (x )在(0，1]上单调递增，无最小值，当x ＝1时取得最大值2－a ；当a ＜0时，f (x )＝2x ＋－ax，当－a2≥1，即a ∈(－∞，－2]时，y ＝f (x )在(0，1]上单调递减，无最大值，当x ＝1时取得最小值2－a ；当－a2＜1，即a ∈(－2，0)时，y ＝f (x )在⎝⎛⎦⎥⎤0，－a 2上单调递减，在⎣⎢⎡⎦⎥⎤－a2，1上单调递增，无最大值，当x ＝－a2时取得最小值2－2a . 能力提升题组13.若函数f (x )＝a x(a >0，a ≠1)在[－1，2]上的最大值为4，最小值为m ，且函数g (x )＝(1－4m )x 在[0，＋∞)上是增函数，则a ＝( ) A.4 B.2 C.12D.14解析当a >1时，则y ＝a x 为增函数，有a 2＝4，a －1＝m ，此时a ＝2，m ＝12，此时g (x )＝－x 在[0，＋∞)上为减函数，不合题意. 当0<a <1时，则y ＝a x为减函数，有a －1＝4，a 2＝m ，此时a ＝14，m ＝116.此时g (x )＝34x 在[0，＋∞)上是增函数.故a ＝14.答案 D14.已知函数f (x )＝e x－1，g (x )＝－x 2＋4x －3，若存在f (a )＝g (b )，则实数b 的取值范围为( ) A.[0，3]B.(1，3)C.[2－2，2＋2]D.(2－2，2＋2)解析由题可知f (x )＝e x －1>－1，g (x )＝－x 2＋4x －3＝－(x －2)2＋1≤1，若f (a )＝g (b )，则g (b )∈(－1，1]，即－b 2＋4b －3>－1，即b 2－4b ＋2<0，解得2－20，对任意的x >0，恒有|f (x )－a |≤|f (x 0)－a |，则f (x )可以为( ) A.f (x )＝lg x B.f (x )＝－x 2＋2x C.f (x )＝2xD.f (x )＝sin x解析由a ∈R ，不妨设a ＝0，g (x )＝|f (x )|，则原问题可看成存在x 0>0，g (x )max ＝g (x 0)＝|f (x 0)|.对于A 选项，g (x )＝|lg x |，结合其函数图象知，g (x )存在最小值0，不存在最大值，排除A ；对于B 选项，g (x )＝|－x 2＋2x |＝|x 2－2x |，g (x )存在最小值0，不存在最大值，排除B ；对于C 选项，g (x )＝|2x|＝2x ，显然g (x )不存在最小值，也不存在最大值，排除C ；对于D 选项，g (x )＝|sin x |≤1，g (x )存在最大值，故选D.答案 D16.(一题多解)设函数f (x )＝1＋x ＋1－ax ，记M (a )为f (x )的最大值，则M (a )的最小值为Ｗ.解析法一由题知当a ≤0时，f (x )无最大值，故a >0.由定义域知0≤x ＋1≤1＋1a ，令aa ＋1(x ＋1)＝cos 2α⎝⎛⎭⎪⎫α∈⎣⎢⎡⎭⎪⎫0，π2，代入f (x )＝1＋x ＋1－ax ，则有f (x )＝1＋aacos α＋1＋a sin α＝2＋1a ＋a ·sin(α＋θ)，其中tan θ＝1a，且a >0，所以M (a )＝2＋1a＋a ≥2(当且仅当a ＝1时取到等号).法二由题知当a ≤0时，f (x )无最大值，故a >0，令导函数f ′(x )＝12·11＋x －12·a1－ax ＝0，得唯一极大值点x ＝1a－1，所以M (a )＝f ⎝ ⎛⎭⎪⎫1a －1＝1a＋a ≥2(当且仅当a ＝1时取到等号). 答案 217.已知函数f (x )＝lg(x ＋ax－2)，其中a 是大于0的常数. (1)求函数f (x )的定义域；(2)当a ∈(1，4)时，求函数f (x )在[2，＋∞)上的最小值； (3)若对任意x ∈[2，＋∞)恒有f (x )>0，试确定a 的取值范围.解 (1)由x ＋a x －2＞0，得x 2－2x ＋ax＞0，当a ＞1时，x 2－2x ＋a ＞0恒成立，定义域为(0，＋∞)，当a ＝1时，定义域为{x |x ＞0且x ≠1}，当0＜a ＜1时，定义域为{x |0＜x ＜1－1－a 或x ＞1＋1－a }. (2)设g (x )＝x ＋a x－2，当a ∈(1，4)，x ∈[2，＋∞)时，∴g ′(x )＝1－a x 2＝x 2－ax2>0.因此g (x )在[2，＋∞)上是增函数， ∴f (x )在[2，＋∞)上是增函数. 则f (x )min ＝f (2)＝lg a2.(3)对任意x ∈[2，＋∞)，恒有f (x )>0，即x ＋a x－2>1对x ∈[2，＋∞)恒成立. ∴a >3x －x 2.令h (x )＝3x －x 2，x ∈[2，＋∞).由于h (x )＝－⎝ ⎛⎭⎪⎫x －322＋94在[2，＋∞)上是减函数，∴h (x )max ＝h (2)＝2. 故a >2时，恒有f (x )>0.因此实数a 的取值范围为(2，＋∞). 18.a ∈R ，设函数f (x )＝x |x －a |－x . (1)若a ＝3，求函数f (x )的单调区间；(2)若a ≤0，对于任意的x ∈[0，t ]，不等式－1≤f (x )≤6恒成立，求实数t 的最大值及此时a 的值.解 (1)当a ＝3时，f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ＝－（x －1）2＋1，x <3，x 2－4x ＝（x －2）2－4，x ≥3，函数f (x )的单调递增区间为(－∞，1)，(3，＋∞)，单调递减区间为(1，3). (2)当a ≤0，x ∈[0，t ]时，x ≥a 恒成立，故f (x )＝x 2－(a ＋1)x . ①当a ≤－1时，a ＋12≤0，f (x )在[0，t ]上单调递增，f (x )min ＝f (0)＝0，f (x )max ＝f (t )＝t 2－(a ＋1)t ，由题意得f (x )max ≤6，即 t 2－(a ＋1)t ≤6，解得0＜t ≤（a ＋1）＋（a ＋1）2＋242.令m ＝－(a ＋1)≥0，h (m )＝m 2＋24－m2＝12m 2＋24＋m在[0，＋∞)上单调递减，所以h (x )max ＝h (0)＝6，即当a ＝－1时，t max ＝ 6. ②当－1<a ≤0时，a ＋12＞0，f (x )在⎣⎢⎡⎦⎥⎤0，a ＋12上单调递减，在⎣⎢⎡⎭⎪⎫a ＋12，＋∞上单调递增，f (x )min ＝f ⎝ ⎛⎭⎪⎫a ＋12＝－（a ＋1）24∈⎣⎢⎡⎭⎪⎫－14，0，满足f (x )min ≥－1.当0＜t ≤a ＋1≤1时，f (x )max ＝f (0)＝0，满足题意，此时t max ＝1，a ＝0；当t ＞a ＋1时，f (x )max ＝f (t )＝t 2－(a ＋1)t ，由题意得f (x )max ≤6，即t 2－(a ＋1)t ≤6，解得a ＋1＜t ≤（a ＋1）＋（a ＋1）2＋242.令m ＝a ＋1，则0＜m ≤1，h (m )=m ＋m 2＋242在(0，1］上单调递增，所以h (m )max ＝h (1)＝3，即当a ＝0时，t max ＝3. 综上所述，t max ＝3，此时a ＝0.。

高考数学复习考点知识与结论专题讲解5 函数的单调性

高考数学复习考点知识与结论专题讲解第5讲函数的单调性通关一、函数单调性的定义及几何意义图像描述自左向右看，图像是下降的自左向右看，图像是上升的要点诠释(1)函数单调性的实质是函数值的变化与自变量的变化是否一致，一致则为增函数，不一致则为减函数.(2)函数单调性“数”的表现是函数值的增大与减小，“形”的表现是函数图像的上升与下降⊆.(3)“函数的单调区间是M”与“函数在区间N上单调”是两个不同的概念，显然N M(4)一个函数在不同的区间可以有不同的单调性，同一种单调区间用“和”或“，”连接，不能用“”连接.(5)增(减)函数定义中,x x的三个特征：12①任意性；②有大小，即12x x <或12x x >； ③同属于一个单调区间.通关二、函数的最值结论一、定义法证明函数单调性【例1】已知函数()f x 对任意实数,x y 均有()()()f x y f x f y +=+，且当0x >时()0f x >.试判断()f x 的单调性，并说明理由.【解析】设12,x x R ∈且12x x <，则210x x ->，故()210f x x ->.所以()()()()()()()212111211210f x f x f x x x f x f x x f x f x x -=-+-=-+=->⎡⎤⎣⎦.所以()()12f x f x <.故()f x 在(),-∞+∞上为增函数.【变式】已知给定函数()f x 对于任意正数,x y 都有()()()f xy f x f y =⋅，且()0f x ≠，当1x >时()1f x <.试判断()f x 在()0,+∞上的单调性，并说明理由.【解析】对于()0,x ∈+∞有()20f x ff⎡⎤==≥⎣⎦，又()0f x ≠，所以()0f x >.设()12,0,x x ∈+∞，且12x x <，则()()()()()2211211211111x x f x f f x f x x x x f f x f x f x x ⎛⎫⎛⎫⋅ ⎪ ⎪⎛⎫⎝⎭⎝⎭===< ⎪⎝⎭，所以 ()()12f x f x >. 故()f x 在(0,)+∞上为减函数.结论二、函数单调性的正向与逆向理解1. 正向结论:若 ()y f x = 在给定区间上是增函数,则当 12x x < 时, ()()12f x f x <; 当 12x x > 时, ()()12f x f x >;2. 逆向结论:若 ()y f x = 在给定区间上是增函数,则当 ()()12f x f x < 时, 12x x <; 当 ()()12f x f x > 时, 12x x >.【例2】已知()f x 在区间(,)-∞+∞上是增函数, ,a b ∈R 且0a b +…,则下列表达正确的是（）. A. ()()[()()]f a f b f a f b +-+… B.()()()()f a f b f a f b +-+-…C. ()()[()()]f a f b f a f b +-+…D.()()()()f a f b f a f b +-+-…【答案】B【解析】0a b +…可转化为a b -…和b a -…，因为()f x 在区间(,)-∞+∞上是增函数, 所以()()f a f b -…且()()f b f a -…,根据同向不等式相加性质得()()f a f b +…()()f a f b -+-. 故选B.【变式】已知()y f x =是定义在(2,2)-上的增函数,若(1)(12)f m f m -<-,则m 的取值范围是_________. 【答案】12,23I ⎛⎫-⎪⎝⎭【解析】由已知可得122112223m m m -<-<-<⇒-<<，故m 的取值范围是12,23⎛⎫- ⎪⎝⎭.结论三、单调性结论设 1212,[,],x x a b x x ∈≠ 那么 ()()()()()1212121200f x f x x x f x f x x x -⎡⎤-->⇔>⇔⎣⎦-()f x 在[,]a b 上是增函数; ()()()()()1212121200()f x f x x x f x f x f x x x -⎡⎤--<⇔<⇔⎣⎦- 在[,]a b 上是减函数.【例3】定义在R 上的函数()f x 满足:对任意的()1212,[0,)x x x x ∈+∞≠, 有()()21210f x f x x x -<-,则（）. A.(3)(2)(4)f f f << B.(1)(2)(3)f f f <<C. (2)(1)(3)f f f -<<D. (3)(1)(0)f f f <<【答案】D【解析】因为对任意的()1212,[0,)x x x x ∈+∞≠,有()()21210f x f x x x -<-, 所以函数()f x 在[0,)+∞上是减函数, 因为013<<, 所以(3)(1)(0)f f f <<. 故选 D.【变式】已知函数32()2f x x x mx =-++,若对任意12,x x ∈R , 均满足()()121x x f x⎡--⎣()20f x ⎤>⎦,则实数m 的取值范围是__________.【答案】1,3⎡⎫+∞⎪⎢⎣⎭【解析】由()()()12120x x f x f x ⎡⎤-->⎣⎦可知()f x 在R 上为增函数, 所以()0f x '…在R 上恒成立,而2()32f x x x m '=-+, 所以4120m ∆=-…, 即13m …. 故m 的取值范围是1,3⎡⎫+∞⎪⎢⎣⎭.结论四、单调性性质若函数()f x 在区间I 上具有单词性,则在区间I 上具有以下性质:1. ()f x 与()(f x c c +为常数 )具有相同的单调性.2. 当()f x 非负时, ()f x具有相同的单调性.3. ()f x 与()a f x ⋅在0a > 时具有相同的单调性,在0a <时具有相反的单调性.4. 当()f x 恒不为0时,函数()f x 与1()f x 单调性相反. 【例4】已知函数1()33xxf x ⎛⎫=- ⎪⎝⎭, 则()f x （）.A. 是偶函数,且在R 上是增函数B. 是奇函数,且在R 上是增函数C. 是偶函数,且在R 上是减函数D. 是奇函数,且在R 上是减函数【答案】B【解析】1()3333xxx x f x -⎛⎫=-=- ⎪⎝⎭, 所以()33()x xf x f x --=-=-, 即函数()f x 为奇函数,以函数3xy =为增函数, 13x y ⎛⎫= ⎪⎝⎭为减函数,故函数1()33xx f x ⎛⎫=- ⎪⎝⎭为增函数. 故选 B.【变式】若函数1()2ax f x x +=+在(2,)-+∞上为增函数,则实数a 的取值范围为__________. 【答案】1,2⎛⎫+∞⎪⎝⎭【解析】解法一：112()22ax af x a x x +-==+++. 任取122x x -<<, 则()()12f x f x a -=+()()21121212121212121211(12)(12)22222222x x a a a a a a a x x x x x x x x ⎛⎫⎛⎫------+=-=--=- ⎪ ⎪++++++++⎝⎭⎝⎭因为122x x -<<, 所以122120,20,0x x x x +>+>->, 以()()2112022x x x x ->++. 已知函数在(2,)-+∞上单调递增, 故()()120f x f x -<, 所以120a -<, 解得12a >.所以a 的取值范围是1,2⎛⎫+∞ ⎪⎝⎭.解法二：112()22ax a f x a x x +-==+++, 因为12x +在(2,)-+∞上单调递减, 1()2ax f x x +=+在(2,)-+∞上单调递增, 所以120a -<, 解得12a >.所以a 的取值范围是1,2⎛⎫+∞ ⎪⎝⎭. 结论五、单调性求最值1. 若函数在闭区间[,]a b 上是增函数,则()f x 在[,]a b 上的最小值为()f a , 最大值为()f b ；2. 若函数在闭区间[,]a b 上是减函数,则()f x 在[,]a b 上的最小值为()f b ,最大值为()f a . 【例5】函数()2()log 31x f x =+的值域为（）.A.(0,)+∞B.[0,)+∞C.(1,)+∞D. [1,)+∞【答案】 A【解析】根据对数函数的定义可知, 310x +>恒成立,解得x ∈R . 因此, 该函数的定义域为R , 原函数()2()log 31x f x =+是由对数函数2log y t =和31x t =+组合成的复合函数. 由复合函数的单调性定义(同增异减) 知道,原函数在定义域R 上是单调递增的. 根据指数函数的性质可知,30x >, 所以,311x +>,所以()22()log 31log 10x f x =+>=. 故选A.【变式】已知函数3()2sin (0,0)x f x ax b x a b =++>>, 若[0,1]x ∈时,()f x 的最大值为3 ,则[1,0)x ∈-时,()f x 的最小值是__________.【答案】12-【解析】因为32,,sin xy y x y x ===在区间[1,1]-上均为单调递增函数, 又0,a b >> 0 , 所以3()2sin x f x ax b x =++在区间[1,1]-上为单调递增函数. 当[0,1]x ∈时, ()f x 的最大值为3(1)21sin13,sin11f a b a b =+⋅+=+=; 当[1,0)x ∈-时,()f x 的最小值为1311(1)2(1)sin(1)(sin1)22f a b a b --=+⋅-+-=-+=-.。

2020年高考数学复习题：函数的单调性与最值

函数的单调性与最值[基础训练]1．函数y ＝(2m －1)x ＋b 在R 上是减函数，则( ) A ．m >12 B ．m <12 C ．m >－12D ．m <－12答案：B 解析：由2m －1<0⇒m <12. 2．已知函数y ＝1x －1，那么( )A ．函数的单调递减区间为(－∞，1)，(1，＋∞)B ．函数的单调递减区间为(－∞，1)∪(1，＋∞)C ．函数的单调递增区间为(－∞，1)，(1，＋∞)D ．函数的单调递增区间为(－∞，1)∪(1，＋∞)答案：A 解析：在每个区间内都单调递减，但不可用“并集”形式．3．已知函数f (x )是定义在[0，＋∞)上的增函数，则满足f (2x－1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( ) A.⎝ ⎛⎭⎪⎫13，23 B.⎣⎢⎡⎭⎪⎫13，23 C.⎝ ⎛⎭⎪⎫12，23D.⎣⎢⎡⎭⎪⎫12，23 答案：D 解析：由题意，得⎩⎪⎨⎪⎧2x －1≥0，2x －1<13，解得12≤x <23.4．函数f (x )＝log 12(x 2－4)的单调递增区间为( )A ．(0，＋∞)B ．(－∞，0)C ．(2，＋∞)D ．(－∞，－2)答案：D 解析：由x 2－4>0，得x <－2或x >2.又y ＝log 12u为减函数，故f (x )的单调递增区间为(－∞，－2)．5．“a ≤0”是“函数f (x )＝|(ax －1)x |在区间(0，＋∞)内单调递增”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件答案：C 解析：充分性：x >0，当a <0时，则f (x )＝|(ax －1)x |＝－ax 2＋x 为开口向上的二次函数，且对称轴为x ＝12a <0，故f (x )为增函数；当a ＝0时，f (x )＝x 为增函数．必要性：当a ≠0时，f ⎝ ⎛⎭⎪⎫1a ＝0，f (0)＝0，f (x )在(0，＋∞)上为增函数，则1a <0，即a <0；f (x )＝x 时，为增函数，此时a ＝0，故a ≤0.综上，a ≤0为f (x )在(0，＋∞)上为增函数的充分必要条件． 6．[2019湖北华大新联盟考试]若函数f (x )＝2|x －a |＋3在区间[1，＋∞)上不单调，则实数a 的取值范围是( )A ．[1，＋∞)B ．(1，＋∞)C ．(－∞，1)D ．(－∞，1]答案：B 解析：易知函数f (x )＝2|x －a |＋3的增区间在为[a ，＋∞)，减区间为(－∞，a ]．因为函数f (x )＝2|x －a |＋3在区间[1，＋∞)上不单调，则a >1. 故选B.7．[2019山东潍坊四县联考]已知y ＝f (x )在定义域(－1,1)上是减函数，且f (1－a )<f (2a －1)，则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－∞，23 B ．(0，＋∞)C.⎝ ⎛⎭⎪⎫0，23 D ．(－∞，0)∪⎝ ⎛⎭⎪⎫23，＋∞答案：C 解析：∵f (x )在定义域(－1,1)上是减函数，且f (1－a )<f (2a －1)，∴⎩⎪⎨⎪⎧－1<1－a <1，－1<2a －1<1，1－a >2a －1，解得0<a <23.故选C.8．[2016天津卷]已知f (x )是定义在R 上的偶函数，且在区间(－∞，0)上单调递增．若实数a 满足f (2|a －1|)>f (－2)，则a 的取值范围是________．答案：⎝ ⎛⎭⎪⎫12，32解析：由题意知，函数f (x )在(0，＋∞)上单调递减．因为f (2|a －1|)>f (－2)，f (－2)＝f (2)，所以f (2|a －1|)>f (2)，所以2|a －1|<212，解得12<a <32.9．函数y ＝x －x (x ≥0)的最大值为________．答案：14 解析：令t ＝x ，则t ≥0，y ＝t －t 2＝－⎝ ⎛⎭⎪⎫t －122＋14，当t ＝12，即x ＝14时，y max ＝14.10．设函数f (x )＝⎩⎪⎨⎪⎧1，x >0，0，x ＝0，－1，x <0，g (x )＝x 2f (x －1)，则函数g (x )的递减区间是________．答案：[0,1) 解析：易知g (x )＝⎩⎪⎨⎪⎧x 2，x >1，0，x ＝1，－x 2，x <1.画出g (x )的图象如图所示，其递减区间是[0,1)．11．已知函数f (x )＝1a －1x (a >0，x >0)． (1)求证：f (x )在(0，＋∞)上是增函数； (2)若f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，2，求a 的值．(1)证明：任取x 1，x 2∈(0，＋∞)，且x 2>x 1，则x 2－x 1>0，x 1x 2>0.f (x 2)－f (x 1)＝⎝ ⎛⎭⎪⎫1a －1x 2－⎝ ⎛⎭⎪⎫1a －1x 1＝1x 1－1x 2＝x 2－x 1x 1x 2>0，∴f (x 2)>f (x 1)，∴f (x )在(0，＋∞)上是增函数．(2)解：∵f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，2，又f (x )在⎣⎢⎡⎦⎥⎤12，2上单调递增，∴f ⎝ ⎛⎭⎪⎫12＝12，f (2)＝2. 易得a ＝25.[强化训练]1．[2019河南安阳一模]已知函数f (x )满足：①对任意x 1，x 2∈(0，＋∞)且x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2>0；②对定义域内的任意x ，都有f (x )＝f (－x )．则符合上述条件的函数是( )A ．f (x )＝x 2＋|x |＋1 B ．f (x )＝1x －x C ．f (x )＝ln|x ＋1| D ．f (x )＝cos x答案：A 解析：由题意，得f (x )是偶函数，在(0，＋∞)上递增．对于A ，f (－x )＝f (x )，是偶函数，且x >0时，f (x )＝x 2＋x ＋1，f ′(x )＝2x ＋1>0，故f (x )在(0，＋∞)上递增，符合题意；对于B ，函数f (x )是奇函数，不符合题意；对于C ，由x ＋1≠0，解得x ≠－1，定义域不关于原点对称，故函数f (x )不是偶函数，不符合题意；对于D ，函数f (x )在(0，＋∞)上不单调递增，不符合题意．故选A.2.[2019河北石家庄一模]已知奇函数f (x )在x >0时单调递增，且f (1)＝0，若f (x －1)>0，则x 的取值范围为 ( )A ．{x |0<x <1或x >2}B ．{x |x <0或x >2}C ．{x |x <0或x >3}D ．{x |x <－1或x >1}答案：A 解析：∵奇函数f (x )在(0，＋∞)上单调递增，且f (1)＝0，∴函数f (x )在(－∞，0)上单调递增，且f (－1)＝0，则－1<x <0或x >1时，f (x )>0；x <－1或0<x <1时，f (x )<0.∴不等式f (x －1)>0，即－1<x －1<0或x －1>1，解得0<x <1或x >2.故选A.3．[2019山东济宁二模]已知y ＝f (x )是R 上的偶函数，对任意x 1，x 2∈(0，＋∞)，都有(x 1－x 2)·[f (x 1)－f (x 2)]<0.设a ＝ln 1π，b ＝(ln π)2，c ＝ln π，则( )A ．f (a )>f (b )>f (c )B ．f (b )>f (a )>f (c )C ．f (c )>f (a )>f (b )D ．f (c )>f (b )>f (a )答案：C 解析：由题意易知f (x )在(0，＋∞)上是减函数，又∵|a |＝ln π>1，b ＝(ln π)2>|a |,0<c ＝ln π2<|a |， ∴f (c )>f (|a |)>f (b )．又由题意知f (a )＝f (|a |)， ∴f (c )>f (a )>f (b )．故选C.4．[2019甘肃天水月考]定义在R 上的偶函数f (x )满足：对任意的x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f (x 2)－f (x 1)x 2－x 1<0，则( )A ．f (3)<f (－2)<f (1)B ．f (1)<f (－2)<f (3)C ．f (－2)<f (1)<f (3)D ．f (3)<f (1)<f (－2)答案：A 解析：∵f (x )是偶函数，∴f (－2)＝f (2)．又∵任意的x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f(x2)－f(x1)x2－x1<0，∴f(x)在[0，＋∞)上是减函数．又∵1<2<3，∴f(1)>f(2)＝f(－2)>f(3)，故选A.5．[2019河南郑州一模]已知定义在R上的奇函数f(x)满足f(x ＋2e)＝－f(x)(其中e＝2,718 2…)，且在区间[e,2e]上是减函数，令a＝ln 22，b＝ln 33，c＝ln 55，则f(a)，f(b)，f(c)的大小关系(用不等号连接)为()A．f(b)>f(a)>f(c) B．f(b)>f(c)>f(a)C．f(a)>f(b)>f(c) D．f(a)>f(c)>f(b)答案：A解析：∵f(x)是R上的奇函数，满足f(x＋2e)＝－f(x)，∴f(x＋2e)＝f(－x)，∴函数f(x)的图象关于直线x＝e对称，∵f(x)在区间[e,2e]上为减函数∴f(x)在区间[0，e]上为增函数，又易知0<c<a<b<e，∴f(c)<f(a)<f(b)，故选A.6．[2019安徽蚌埠二模]已知单调函数f(x)，对任意的x∈R 都有f[f(x)－2x]＝6，则f(2)＝( )A．2 B．4 C．6 D．8答案：C解析：设t＝f(x)－2x，则f(t)＝6，且f(x)＝2x＋t，令x＝t，则f(t)＝2t＋t＝6，∵f(x)是单调函数，f(2)＝22＋2＝6，∴t＝2，即f(x)＝2x＋2，则f(2)＝4＋2＝6，故选C.7．[2019河北邯郸月考]已知函数y ＝f (x )是R 上的偶函数，且在(－∞，0]上是增函数，若f (a )≤f (2)，则实数a 的取值范围是________．答案：(－∞，－2]∪[2，＋∞) 解析：∵函数y ＝f (x )是R 上的偶函数，∴y ＝f (x )的图象关于y 轴对称．又∵y ＝f (x )在(－∞，0]上是增函数，则y ＝f (x )在(0，＋∞)上是减函数，f (a )≤f (2)， ∴|a |≥2，∴a ≤－2或a ≥2. 8．[2019广东深圳模拟]已知函数f (x )＝⎩⎪⎨⎪⎧a x，x <0，(a －3)x ＋4a ，x ≥0满足对任意x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2<0成立，则a 的取值范围是________．答案：⎝ ⎛⎦⎥⎤0，14解析：由任意x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2<0，知f (x )在R 上为减函数，则需⎩⎪⎨⎪⎧0<a <1，a －3<0，a 0≥(a －3)·0＋4a ，解得0<a ≤14.9．[2019甘肃兰州一模]已知函数f (x )＝⎩⎪⎨⎪⎧e －x－2，x ≤0，2ax －1，x >0(a是常数且a >0)．对于下列命题：①函数f (x )的最小值是－1； ②函数f (x )在R 上是单调函数； ③若f (x )>0在⎣⎢⎡⎭⎪⎫12，＋∞上恒成立，则a 的取值范围是a >1；④对任意x 1<0，x 2<0且x 1≠x 2，恒有f ⎝ ⎛⎭⎪⎫x 1＋x 22<f (x 1)＋f (x 2)2. 其中正确命题的序号是________．答案：①③④ 解析：根据题意可得函数图象如图所示．①由图象易得在点x ＝0处函数f (x )有最小值－1，故正确； ②由图象易得函数f (x )在R 上不是单调函数，故错误； ③因为f (x )>0在⎣⎢⎡⎭⎪⎫12，＋∞上恒成立，且f (x )在(0，＋∞)上单调递增，所以当x ＝12时，函数取得最小值，求得a 的取值范围是a >1，故正确；④因为函数在(－∞，0)上的图象是下凹的，所以任取两点连线应在图象的上方，即f ⎝ ⎛⎭⎪⎫x 1＋x 22<f (x 1)＋f (x 2)2，故正确．故正确的命题为①③④.10．[2019河北石家庄模拟]已知f (x )是定义在[－1,1]上的奇函数，且f (1)＝1.若a ，b ∈[－1,1]，a ＋b ≠0时，有f (a )＋f (b )a ＋b >0成立．(1)判断f (x )在[－1,1]上的单调性，并证明； (2)解不等式f ⎝ ⎛⎭⎪⎫x ＋12<f ⎝ ⎛⎭⎪⎫1x －1；(3)若f (x )≤m 2－2am ＋1对所有的a ∈[－1,1]恒成立，求实数m 的取值范围．解：(1)任取x 1，x 2∈[－1,1]，且x 1<x 2，则－x 2∈[－1,1]，因为f (x )为奇函数，所以f (x 1)－f (x 2)＝f (x 1)＋f (－x 2) ＝f (x 1)＋f (－x 2)x 1＋(－x 2)·(x 1－x 2)，由已知得f (x 1)＋f (－x 2)x 1＋(－x 2)>0，x 1－x 2<0，所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，所以f (x )在[－1,1]上单调递增． (2)因为f (x )在[－1,1]上单调递增，所以⎩⎪⎨⎪⎧x ＋12<1x －1，－1≤x ＋12≤1，－1≤1x －1≤1，解得－32≤x <－1.(3)因为f (1)＝1，f (x )在[－1,1]上单调递增，所以在区间[－1,1]上，f (x )≤1.问题转化为m 2－2am ＋1≥1，即m 2－2am ≥0对a ∈[－1,1]恒成立．下面来求m 的取值范围．设g (a )＝－2m ·a ＋m 2≥0. ①若m ＝0，则g (a )＝0≥0，对a ∈[－1,1]恒成立．②若m≠0，则g(a)为a的一次函数，若g(a)≥0，对a∈[－1,1]恒成立，必须g(－1)≥0，且g(1)≥0，所以m≤－2或m≥2.所以m的取值范围是{m|m＝0或m≥2或m≤－2}．。

2020年高中数学新教材同步必修第一册第3章 3.2.1 第1课时函数的单调性

思考 (1)所有的函数在定义域上都具有单调性吗？答案不是 (2)在增函数和减函数定义中，能否把“任意x1，x2∈D”改为“存在x1，x2∈D”？答案不能.
知识点二函数的单调区间
如果函数y＝f(x)在区间D上单调递增或单调递减，那么就说函数y＝f(x)在这一区间具有(严格的) 单调性，区间D叫做y＝f(x)的单调区间 . 特别提醒：(1)函数单调性关注的是整个区间上的性质，单独一点不存在单调性问题，所以单调区间的端点若属于定义域，则该点处区间可开可闭，若区间端点不属于定义域则只能开. (2)单调区间D⊆定义域I. (3)遵循最简原则，单调区间应尽可能大.
性，反过来，若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a，b]上是单调的，则此函数在这一单调区间内的

任意子集上也是单调的.
跟踪训练3 已知函数f(x)＝x2－2ax－3在区间[1,2]上具有单调性，求实数a的取值范围.
解函数f(x)＝x2－2ax－3的图象开口向上，对称轴为直线x＝a，画出草图如图所示. 由图象可知函数在(－∞，a]和[a，＋∞)上都具有单调性，因此要使函数f(x)在区间[1,2]上具有单调性，只需a≤1或a≥2，从而a∈(－∞，1]∪[2，＋∞).
解析因为函数f(x)在R上是减函数，3<5，所以f(3)>f(5).
12345
3.函数y＝|x＋2|在区间[－3,0]上
A.递减
√C.先减后增
B.递增 D.先增后减
解析因为 y＝|x＋2|＝x－＋x2－，2x，≥x－<－2，2. 作出y＝|x＋2|的图象，如图所示，
易知函数在[－3，－2)上为减函数，在[－2，0]上为增函数.

2020年高考文科数学函数的单调性与最值专项练习题含解析

课时规范练 A 组基础对点练1．下列四个函数中，在(0，＋∞)上为增函数的是( ) A ．f (x )＝3－x B ．f (x )＝x 2－3x C ．f (x )＝－1x ＋1D ．f (x )＝－|x |解析：当x ＞0时，f (x )＝3－x 为减函数；当x ∈⎝ ⎛⎭⎪⎫0，32时，f (x )＝x 2－3x 为减函数，当x ∈⎝ ⎛⎭⎪⎫32，＋∞时，f (x )＝x 2－3x 为增函数；当x ∈(0，＋∞)时，f (x )＝－1x ＋1为增函数；当x ∈(0，＋∞)时，f (x )＝－|x |为减函数．故选C. 答案：C2.下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是( ) A ．y ＝1x B ．y ＝e －x C ．y ＝－x 2＋1D ．y ＝lg|x |解析：A 中y ＝1x 是奇函数，A 不正确；B 中y ＝e －x＝⎝ ⎛⎭⎪⎫1e x 是非奇非偶函数，B不正确；C 中y ＝－x 2＋1是偶函数且在(0，＋∞)上是单调递减的，C 正确；D 中y ＝lg|x |在(0，＋∞)上是增函数，D 不正确．故选C. 答案：C3．(2019·天津模拟)若函数f (x )满足“对任意x 1，x 2∈(0，＋∞)，当x 1＜x 2时，都有f (x 1)＞f (x 2)”，则f (x )的解析式可以是( ) A ．f (x )＝(x －1)2 B ．f (x )＝e x C ．f (x )＝1xD ．f (x )＝ln(x ＋1)解析：根据条件知，f (x )在(0，＋∞)上单调递减．对于A ，f (x )＝(x －1)2在(1，＋∞)上单调递增，排除A ；对于B ，f (x )＝e x 在(0，＋∞)上单调递增，排除B ；对于C ，f (x )＝1x 在(0，＋∞)上单调递减，C 正确；对于D ，f (x )＝ln(x ＋1)在(0，＋∞)上单调递增，排除D. 答案：C4．(2019·福州模拟)函数f (x )＝⎩⎨⎧－x ＋3a ，x ＜0a x ，x ≥0，(a ＞0且a ≠1)是R 上的减函数，则a 的取值范围是( ) A ．(0，1) B.⎣⎢⎡⎭⎪⎫13，1 C.⎝ ⎛⎦⎥⎤0，13 D.⎝ ⎛⎦⎥⎤0，23 解析：∵⎩⎨⎧0＜a ＜13a ≥1，∴13≤a ＜1.答案：B5．设a ＞0且a ≠1，则“函数f (x )＝a x 在R 上是减函数”是“函数g (x )＝(2－a )x 3在R 上是增函数”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件解析：若函数f (x )＝a x 在R 上为减函数，则有0＜a ＜1；若函数g (x )＝(2－a )x 3在R 上为增函数，则有2－a ＞0，即a ＜2，所以“函数f (x )＝a x 在R 上是减函数”是“函数g (x )＝(2－a )x 3在R 上是增函数”的充分不必要条件，选A. 答案：A6．定义在R 上的偶函数f (x )满足：对任意的x 1，x 2∈(－∞，0)(x 1≠x 2)，都有f （x 1）－f （x 2）x 1－x 2＜0.则下列结论正确的是( )A ．f (0.32)＜f (20.3)＜f (log 25)B ．f (log 25)＜f (20.3)＜f (0.32)C ．f (log 25)＜f (0.32)＜f (20.3)D ．f (0.32)＜f (log 25)＜f (20.3)解析：∵对任意的x 1，x 2∈(－∞，0)，且x 1≠x 2，都有f （x 1）－f （x 2）x 1－x 2＜0，∴f (x )在(－∞，0)上是减函数．又∵f (x )是R 上的偶函数， ∴f (x )在(0，＋∞)上是增函数， ∵0＜0.32＜20.3＜log 25，∴f (0.32)＜f (20.3)＜f (log 25)．故选A. 答案：AB 组能力提升练7．定义在[－2，2]上的函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]＞0，x 1≠x 2，且f (a 2－a )＞f (2a －2)，则实数a 的取值范围为( ) A ．[－1，2) B ．[0，2) C ．[0，1)D ．[－1，1)解析：函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]＞0，x 1≠x 2，∴函数在[－2，2]上单调递增，∴⎩⎨⎧－2≤a 2－a ≤2，－2≤2a －2≤2，2a －2＜a 2－a ，∴⎩⎨⎧－1≤a ≤2，0≤a ≤2，a ＜1或a ＞2，∴0≤a ＜1，故选C. 答案：C8．已知定义在R 上的函数f (x )在[1，＋∞)上单调递减，且f (x ＋1)是偶函数，不等式f (m ＋2)≥f (x －1)对任意的x ∈[－1，0]恒成立，则实数m 的取值范围是( ) A ．[－3，1]B ．[－4，2]C ．(－∞，－3]∪[1，＋∞)D ．(－∞，－4]∪[2，＋∞)解析：因为f (x ＋1)是偶函数，所以f (－x ＋1)＝f (x ＋1)，所以f (x )的图象关于x ＝1对称，由f (m ＋2)≥f (x －1)得|(m ＋2)－1|≤|(x －1)－1|，所以根据题意得|m ＋1|≤2，解得－3≤m ≤1.故选A. 答案：A9．若函数f (x )＝x 2－12ln x ＋1在其定义域的一个子区间(k －1，k ＋1)内不是单调函数，则实数k 的取值范围是( )A ．[1，＋∞) B.⎣⎢⎡⎭⎪⎫1，32 C ．[1，2)D.⎣⎢⎡⎭⎪⎫32，2 解析：函数f (x )的定义域为(0，＋∞)，所以k －1≥0，即k ≥1.令f ′(x )＝4x 2－12x ＝0，解得x ＝12⎝ ⎛⎭⎪⎫x ＝－12舍.因为函数f (x )在区间(k －1，k ＋1)内不是单调函数，所以k －1＜12＜k ＋1，得－12＜k ＜32.综上得1≤k ＜32. 答案：B10．(2018·西安一中模拟)已知函数f (x )＝⎩⎨⎧x 3，x ≤0，ln （x ＋1），x ＞0，若f (2－x 2)＞f (x )，则实数x 的取值范围是( ) A ．(－∞，－1)∪(2，＋∞) B ．(－∞，－2)∪(1，＋∞) C ．(－1，2)D ．(－2，1)解析：∵当x ＝0时，两个表达式对应的函数值都为零，∴函数的图象是一条连续的曲线．∵当x ≤0时，函数f (x )＝x 3为增函数，当x ＞0时，f (x )＝ln(x ＋1)也是增函数，∴函数f (x )是定义在R 上的增函数．因此，不等式f (2－x 2)＞f (x )等价于2－x 2＞x ，即x 2＋x －2＜0，解得－2＜x ＜1.故选D. 答案：D11．若函数f (x )＝|2x ＋a |的单调递增区间是[3，＋∞)，则a ＝________．解析：由f (x )＝⎩⎪⎨⎪⎧－2x －a ，x ＜－a22x ＋a ，x ≥－a2，可得函数f (x )的单调递增区间为⎣⎢⎡⎭⎪⎫－a 2，＋∞，故3＝－a 2，解得a ＝－6.答案：－612．已知函数f (x )＝x ＋ax (x ≠0，a ∈R )，若函数f (x )在(－∞，－2]上单调递增，则实数a 的取值范围是__________．解析：设x 1<x 2≤－2，则Δy ＝f (x 1)－f (x 2)＝x 1＋a x 1－x 2－a x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1－a x 1x 2＝（x1－x2）（x1x2－a）x1x2.因为x1－x2<0，x1x2>0，所以要使Δy＝（x1－x2）（x1x2－a）x1x2<0恒成立，只需使x1x2－a>0恒成立，即a<x1x2恒成立．因为x1<x2≤－2，所以x1x2>4，所以a≤4，故函数f(x)在(－∞，－2]上单调递增时，实数a的取值范围是(－∞，4]．答案：(－∞，4]。

2020高考数学文总复习课件：第二章第二节函数的单调性与最值

2 因为 t＝2x2－3x＋1＝2x－342－18，所以 t＝2x2－3x＋1 的单调递增区间为(1，＋∞)．
又 y＝log1t 在(1，＋∞)上是减函数， 2
所以函数 y＝log1(2x2－3x＋1)的单调递减区间为(1，＋∞)． 2
答案：A
【例 2】判断并证明函数 f(x)＝ax2＋1x(其中 1<a<3) 在 x∈[1，2]上的单调性．
考点 1 确定函数的单调性(区间)(讲练互动)
【例 1】函数 y＝log1(2x2－3x＋1)的单调递减区间 2
为( )
A．(1，＋∞) C.12，＋∞
B.－∞，34 D.34，＋∞
解析：由 2x2－3x＋1>0，得函数的定义域为－∞，12∪(1，＋∞)．令 t＝2x2－3x＋1，则 y＝log1t，
1．“函数的单调区间”和“函数在某区间上单调” 意义不同，前者指函数具备单调性的“最大”的区间，后者是前者“最大”区间的子集．
2．对勾函数 y＝x＋ax(a＞0)的递增区间为(－∞，－ a ]和[ a，＋∞)；递减区间为[－ a，0)和(0， a ]，且对勾函数为奇函数．
3．(1)闭区间上的连续函数一定存在最大值和最小值，当函数在闭区间上单调时最值一定在端点处取到．
解：函数 f(x)＝ax2＋1x(1<a<3)在 x∈[1，2]上单调递增．证明如下：设 1≤x1<x2≤2，则 f(x2)－f(x1) ＝ax22＋x12－ax21－x11＝(x2－x1)a（x1＋x2）－x11x2，由 1≤x1<x2≤2，得 x2－x1>0，2<x1＋x2<4， 1<x1x2<4，－1<－x11x2<－14.

2020年高三一轮复习数学教案第3讲《函数的单调性》(教师版)

个性化教学辅导教案1．已知函数f（lgx）定义域是[0.1，100]，则函数f(x2)的定义域是（）A．[﹣1，2]B．[﹣2，4]C．[0.1，100]D．[−12，1]【解答】解：∵f（lgx）定义域是[0.1，100]，即0.1≤x≤100，∵lg0.1≤lgx≤lg100，即﹣1≤lgx≤2．∵函数f（x）的定义域为[﹣1，2]．由−1≤x2≤2，得﹣2≤x≤4．∵函数f(x2)的定义域是[﹣2，4]．故选：B．【点评】本题考查函数的定义域及其求法，关键是掌握该类问题的解决方法，是中档题．2．函数y=1﹣x﹣9x的值域是（﹣∞，﹣5]∵[7，+∞）．【解答】解：当x＞0时，可得y=1﹣（x+9x）∵x+9x ≥2√9x⋅x=6，当且仅当x=3时取等号．∵f （x ）的解析式为：f （x ）=12x 2﹣32x+2．【点评】本题考查了求函数解析式的问题，解题时应用待定系数法，设出函数的解析式，求出系数即可，是中档题．1．函数f （x ）=√x 2+x −6的单调增区间是（） A ．（﹣∞，﹣3） B ．[2，+∞） C ．[0，2） D ．[﹣3，2] 【解答】解：函数有意义，则：x 2+x ﹣6≥0，解得：x≥2或x≤﹣3，二次函数在区间（﹣∞，﹣3）上单调递减，在区间[2，+∞）上单调递增，幂函数y =√x 在定义域内单调递增，结合复合函数的单调性可得函数f(x)=√x 2+x −6 的单调增区间是[2，+∞）．故选：B ．2、已知函数对于任意都有成立，则实数的取值范围是（） A ． B ．C ．D ．【答案】C【解析】因为，所以函数是R 上的减函数，所以解得故选C.点睛：本题考查分段函数的单调性，涉及一次函数单调性，对数函数单调性，属于中档题.解题时，需要考虑两段函数都是增函数或减函数，其次考虑两段函数的分界点，如果是减函数，则左侧函数的最小值要大于等于右侧函数的最大值，反之，左侧函数的最大值要小于等于右侧函数的最小值.3、已知幂函数，若，则的取值范围是（）A．B．C．D．【答案】C【解析】∵幂函数的定义域为{x|x＞0}，在（0，+∞）上单调递减．∵若f（a+1）＜f（10-2a），则解得3＜a＜5，即a的取值范围是（3，5）．故选C：．点睛：本题主要考查幂函数的性质，根据幂函数的单调性解不等式是解决本题的关键，注意定义域的限制.学科分析：函数的单调性是必修1第一章内容，是函数的重要性质之一。

高考数学专题《函数的单调性与最值》习题含答案解析

专题3.2 函数的单调性与最值1．（2021·全国高一课时练习）函数f(x)=1,01,0x xx x+≥⎧⎨-<⎩在R上（）A．是减函数B．是增函数C．先减后增D．先增后减【答案】B【解析】画出函数图像即可得解.【详解】选B.画出该分段函数的图象，由图象知，该函数在R上是增函数.故选：B.2．（2021·全国高一课时练习）若定义在R上的函数f(x)对任意两个不相等的实数a，b，总有()-()-f a f ba b>0成立，则必有（）A．f(x)在R上是增函数B．f(x)在R上是减函数C．函数f(x)先增后减D．函数f(x)先减后增【答案】A【解析】根据条件可得当a<b时，f(a)<f(b)，或当a>b时，f(a)>f(b)，从而可判断.【详解】练基础由()-()-f a f b a b>0知f (a )-f (b )与a -b 同号，即当a b 时，f (a )>f (b )，所以f (x )在R 上是增函数. 故选：A.3．（2021·全国高一课时练习）设函数f (x )是(-∞，+∞)上的减函数，则（） A ．f (a )>f (2a ) B ．f (a 2)<f (a ) C ．f (a 2+a )<f (a ) D ．f (a 2+1)<f (a )【答案】D 【解析】利用0a =排除ABC ，作差可知21a a +>，根据单调性可知D 正确. 【详解】当0a =时，选项A 、B 、C 都不正确；因为22131()024a a a +-=-+>，所以21a a +>，因为()f x 在(,)-∞+∞上为减函数，所以2(1)()f a f a +<，故D 正确.故选：D4．（2021·西藏高三二模（理））已知函数()332f x x x =--，若()()320f m f m -+-<，则实数m 的取值范围为（） A ．(),3-∞ B ．()3,+∞C ．(),3-∞-D ．()3,-+∞【答案】C 【解析】根据函数为奇函数且在R 上单调递减可得()()32f m f m -<求解. 【详解】易知()f x 为R 上的奇函数，且在R 上单调递减，由()()320f m f m -+-<，得()()()322f m f m f m -<--=，于是得32m m ->，解得3m <-．故选：C ．5．（2021·广西来宾市·高三其他模拟（理））已知定义在R 上的偶函数()f x 满足在[0,)+∞上单调递增，(3)0f =，则关于x 的不等式(2)(2)0f x f x x++-->的解集为（）A ．(5,2)(0,)--+∞ B ．(,5)(0,1)-∞- C ．(3,0)(3,)-⋃+∞ D ．(5,0)(1,)-+∞【答案】D 【解析】根据题意作出函数()f x 的草图，将(2)(2)0f x f x x++-->，转化为2(2)0f x x +>，利用数形结合法求解. 【详解】因为定义在R 上的偶函数()f x 满足在(0,)+∞内单调递增，所以()f x 满足在(,0)-∞内单调递减，又(3)0f =，所以(3)(3)0f f -==．作出函数()f x 的草图如下：由(2)(2)0f x f x x ++-->，得(2)[(2)]0f x f x x++-+>，得2(2)0f x x+>，所以0,(2)0,x f x >⎧⎨+>⎩或0,(2)0,x f x <⎧⎨+<⎩所以0,23,x x >⎧⎨+>⎩或0,323,x x <⎧⎨-<+<⎩ 解得1x >或5x 0-<<，即不等式(2)(2)0f x f x x++-->的解集为(5,0)(1,)-+∞．故选：D6．（2021·黑龙江哈尔滨市·哈师大附中高三三模（文））已知函数()22f x x x -=-（）A ．是奇函数，0,单调递增B ．是奇函数，0,单调递减C ．是偶函数，0,单调递减D ．是偶函数，0,单调递增【答案】D 【解析】利用奇偶性和单调性的定义判断即可【详解】解：定义域为{}0x x ≠，因为2222()()()()f x x x x x f x ---=---=-=，所以()f x 为偶函数，任取12,(0,)x x ∈+∞，且12x x <，则2222212211()()f x f x x x x x ---=--+212122121()()(1)x x x x x x =-++，因为12x x <，12,(0,)x x ∈+∞，所以212122121()()(1)0x x x x x x -++>，所以21()()f x f x >，所以()f x 在0,单调递增，故选：D7．（2021·全国高三月考（理））若()f x 是奇函数，且在(,0)-∞上是减函数，又(4)0f -=，则(2)(2)0f x f x x+--->的解集是（）A ．(4,0)(4,)-⋃+∞B ．(6,2)(0,2)--⋃C ．(6,2)(2,)--⋃+∞D ．(,4)(0,4)-∞-⋃【答案】B 【解析】根据函数()f x 为奇函数，(4)0f -=得到(4)0f =，再由函数在(,0)-∞上是减函数，作出函数()f x 的图象，再由(2)(2)0f x f x x +--->，等价于2(2)0f x x+>，利用数形结合法求解.【详解】因为函数()f x 为奇函数，所以(4)(4)0f f -=-=，所以(4)0f =，因为函数()f x 在(,0)-∞上是减函数，所以函数()f x 在(0,) +∞上是减函数．作出函数()f x 的大致图象如图所示，而(2)(2)0f x f x x +--->，等价于(2)[(2)]0f x f x x +--+>，即2(2)0f x x+>，则0(2)0x f x <⎧⎨+<⎩或0(2)0x f x >⎧⎨+>⎩，所以0420x x <⎧⎨-<+<⎩或0024x x >⎧⎨<+<⎩，解得62x -<<-或02x <<．综上，(2)(2)0f x f x x+--->的解集是(6,2)(0,2)--⋃．故选：B8．（2021·全国高三专题练习（文））已知函数()||2f x x x x =⋅-，则下列结论正确的是（）A ．()f x 是偶函数，递增区间是()0-∞，B ．()f x 是偶函数，递减区间是()1-∞，C ．()f x 是奇函数，递减区间是(11)-， D ．()f x 是奇函数，递增区间是(0)+∞，【答案】C 【解析】将函数解析式化为分段函数型，画出函数图象，数形结合即可判断；【详解】解：将函数()||2f x x x x =⋅-去掉绝对值得2220()20x x x f x x x x ⎧-≥=⎨--<⎩，，，画出函数()f x 的图象，如图，观察图象可知，函数()f x 的图象关于原点对称，故函数()f x 为奇函数，且在(11)-，上单调递减，故选：C9．（2021·宁夏银川市·高三二模（文））设函数()21f x x x=-，则()f x （）A ．是偶函数，且在(),0-∞单调递增B ．是偶函数，且在(),0-∞单调递减C ．是奇函数，且在(),0-∞单调递增D ．是奇函数，且在(),0-∞单调递减【答案】B 【解析】利用定义可判断函数()f x 的奇偶性，化简函数()f x 在(),0-∞上的解析式，利用函数单调性的性质可判断函数()f x 在(),0-∞上的单调性. 【详解】函数()21f x x x =-的定义域为{}0x x ≠，()()()2211f x x x f x x x-=--=-=-，所以，函数()f x 为偶函数，当0x <时，()21f x x x=+，由于函数2y x 、1y x=在(),0-∞上均为减函数，所以，函数()f x 在(),0-∞上单调递减，故选：B.10．（2021·全国高一课时练习）已知y =f (x )是定义在区间(-2，2)上单调递减的函数，若f (m -1)>f (1-2m )，则m 的取值范围是_______. 【答案】1223⎛⎫- ⎪⎝⎭，【解析】结合函数定义域和函数的单调性列不等式求解即可. 【详解】由题意得：-2-12-21-22-11-2m m m m <<⎧⎪<<⎨⎪<⎩，，，解得12-<m <23.故答案为：1223⎛⎫- ⎪⎝⎭，1．（2021·黑龙江大庆市·大庆实验中学高二月考（文））定义在*N 上的函数()22,3,3x ax a x f x ax x ⎧-+<=⎨≥⎩为递增函数，则头数a 的取值范围是（） A ．()1,2 B ．33,42⎛⎫⎪⎝⎭C ．3,14⎡⎫⎪⎢⎣⎭D ．()1,3【答案】D 【解析】练提升根据定义域和单调性可知()()12f f <，再根据3x ≥时()f x 的单调性判断出()()32f f >，由此求解出a 的取值范围..【详解】因为*x ∈N ，所以3x <时，即{}1,2x ∈，由单调性可知()()21f f >，所以22142a a a a -+<-+，解得3a <；当3x ≥时，y ax =为增函数，若()f x 单调递增，则只需()()32f f >，所以2342a a a >-+，解得14a <<，综上可知a 的取值范围是：()1,3，故选：D.2．（2021·上海高三二模）已知函数()(),y f x y g x ==满足：对任意12,x x R ∈，都有()()()()1212f x f x g x g x -≥-．命题p ：若()y f x =是增函数，则()()y f x g x =-不是减函数；命题q ：若()y f x =有最大值和最小值，则()y g x =也有最大值和最小值．则下列判断正确的是（） A ．p 和q 都是真命题 B ．p 和q 都是假命题 C ．p 是真命题，q 是假命题 D ．p 是假命题，q 是真命题【答案】A 【解析】利用函数单调性定义结合已知判断命题p 的真假，再利用函数最大、最小值的意义借助不等式性质判断命题q 的真假而得解. 【详解】对于命题p ：设12x x <，因为()y f x =是R 上的增函数，所以()()12f x f x <，所以()()()()1221f x f x f x f x -=-，因为()()()()1212f x f x g x g x -≥-，所以()()()()211221()()f x f x g x g x f x f x -+≤-≤-所以()()1122()()f x g x f x g x -≤- 故函数()()y f x g x =-不是减函数，故命题p 为真命题；对于命题():q y f x =在R 上有最大值M ，此时x a =，有最小值m ，此时x b =，因为()()()()()()()()f x f a g x g a f x M g x g a M f x -≥-⇔-≤-≤-，()()()()()()()()f x f b g x g b m f x g x g b f x m -≥-⇔-≤-≤-所以()()()()2()()()()22m M g a g b M m g a g b m M g x g a g b M m g x -++-++-≤--≤-⇔≤≤，所以()y g x =也有最大值和最小值，故命题q 为真命题．故选：A3．（2021·全国高三二模（理））已知实数a ，b ，c ，d 满足a b c >>，且0a b c ++=，220ad bd b +-=，则d 的取值范围是（） A ．(][),10,-∞-+∞B ．()1,1-C ．(D ．(11--+【答案】D 【解析】先求解出方程的解1,2d ，然后利用换元法（bt a=）将d 表示为关于t 的函数，根据条件分析t 的取值范围，然后分析出d 关于t 的函数的单调性，由此求解出d 的取值范围. 【详解】因为220ad bd b +-=，所以1,2b b d a a -==-±2440b ab ∆=+≥，令bt a=，则1,2d t =-±20t t +≥，所以(][),10,t ∈-∞-+∞，又因为0a b c ++=且a b c >>，所以0a >且c a b b a =--<<，所以2,a b b a -<<，所以112bt a-<=<，所以[)0,1t ∈，当[)0,1t ∈时，())10,1d t t =-==∈，因为1y t=在()0,1上单调递减，所以y t =-()0,1上单调递增，当0t =时，10d =，当1t =时，11d =，所以)11d ⎡∈⎣；当[)0,1t ∈时，2d t =-，因为y t =、2y t t =+在[)0,1上单调递增，所以y t =-[)0,1上单调递减，当0t =时，20d =，当1t =时，21d =-(21d ⎤∈-⎦，综上可知：(11d ∈---，故选：D.4．【多选题】（2021·湖南高三三模）关于函数()111f x x x =++的结论正确的是（） A ．()f x 在定义域内单调递减 B ．()f x 的值域为R C ．()f x 在定义城内有两个零点 D ．12y f x ⎛⎫=-⎪⎝⎭是奇函数【答案】BD 【解析】根据所给函数结合函数性质，对各项逐个分析判断，即可得解. 【详解】()111f x x x =++的定义域为(,1)(1,0)(0,)-∞--+∞，而1x和11x +在各段定义域内均为减函数，故()f x 在各段上为减函数，但不能说在定义域内单调递减，故A 错误；当(1,0)x ∈- ，1x →-时，有()111f x x x =+→+∞+，当0x →时，有()111f x x x =+→-∞+，所以()f x 的值域为R ，故B 正确；令()2112101x f x x x x x+=+==++，可得12x =-，所以()f x 在定义城内有一个零点，故C 错误；2211128111241224x x y f x x x x x ⎛⎫=-=+== ⎪-⎝⎭-+-，令28()41x g x x =-，易知12x ≠±，此时定义域关于原点对称，且28()()41xg x g x x --==--，故()g x 为奇函数，所以12y f x ⎛⎫=- ⎪⎝⎭是奇函数，故D 正确，故选：BD.5．【多选题】（2021·全国高三专题练习）(多选题)已知函数f (x )的定义域为R ，对任意实数x ，y 满足f (x ＋y )＝f (x )＋f (y )＋12，且f 1()2＝0，当x >12时，f (x )>0，则以下结论正确的是（） A ．f (0)＝－12，f (－1)＝－32B ．f (x )为R 上的减函数C ．f (x )＋12为奇函数 D ．f (x )＋1为偶函数【答案】AC 【解析】取0x y ==，11,22x y ==-，12x y ==-得出(0)f ，12f ⎛⎫- ⎪⎝⎭，(1)f -的值进而判断A ；由(1)(0)f f -<判断B ；令y x =-结合奇偶性的定义判断C ；令1()()2=+g x f x ，结合g (x )为奇函数，得出()1()f x f x -+=-，从而判断D.【详解】由已知，令0x y ==，得1(0)(0)(0)2f f f =++，1(0)2f ∴=-，令11,22x y ==-，得1111122222f f f ⎛⎫⎛⎫⎛⎫-=+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，112f ⎛⎫∴-=- ⎪⎝⎭，再令12x y ==-，得1111122222f f f ⎛⎫⎛⎫⎛⎫--=-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，3(1)2f ∴-=-，A 正确；(1)(0)f f -<，()f x ∴不是R 上的减函数，B 错误；令y x =-，得1()()()2f x x f x f x -=+-+，11()()022f x f x ⎡⎤⎡⎤∴++-+=⎢⎥⎢⎥⎣⎦⎣⎦，故C正确；令1()()2=+g x f x ，由C 可知g (x )为奇函数，11()()22g x g x ∴-+=-+，即1111()()2222f x f x ⎡⎤⎡⎤-++=-++⎢⎥⎢⎥⎣⎦⎣⎦，()1()f x f x ∴-+=-，故D 错误. 故选：AC6．【多选题】（2021·全国高一单元测试）如果函数()f x 在[,]a b 上是增函数，对于任意的1212,[,]()x x a b x x ∈≠，则下列结论中正确的是（）A ．1212()()0f x f x x x ->-B ．1212()[()()]0x x f x f x -->C ．12()()()()f a f x f x f b ≤<≤D ．12()()f x f x >E.1212()()0f x f x x x -<-【答案】AB 【解析】利用函数单调性的定义：12x x -与12()()f x f x -同号，判断A 、B 、E 的正误；而对于C 、D 选项，由于12,x x 的大小不定，1()f x 与2()f x 的大小关系不能确定. 【详解】由函数单调性的定义知，若函数()y f x =在给定的区间上是增函数，则12x x -与12()()f x f x -同号，由此可知，选项A ，B 正确，E 错误；对于选项C 、D ，因为12,x x 的大小关系无法判断，则1()f x 与2()f x 的大小关系确定也无法判断，故C ，D 不正确．故选：AB.7．【多选题】（2021·全国高一课时练习）（多选题）已知函数()f x 的定义域为D ，若存在区间[,]m n D ⊆使得()f x ：（1）()f x 在[,]m n 上是单调函数；（2）()f x 在[,]m n 上的值域是[2,2]m n ，则称区间[,]m n 为函数()f x 的“倍值区间”．下列函数中存在“倍值区间”的有（） A ．2()f x x =； B ．1()f x x=； C ．1()f x x x=+； D ．23()1x f x x =+．【答案】ABD 【解析】函数中存在“倍值区间”，则()f x 在[],m n 内是单调函数,()()22f m m f n n ⎧=⎪⎨=⎪⎩或()()22f m nf n m ⎧=⎪⎨=⎪⎩，对四个函数的单调性分别研究，从而确定是否存在“倍值区间”．【详解】函数中存在“倍值区间”，则（1）()f x 在[,]m n 内是单调函数，（2）()2()2f m m f n n =⎧⎨=⎩或()2()2f m nf n m=⎧⎨=⎩，对于A ，2()f x x =，若存在“倍值区间”[,]m n ，则()2()2f m m f n n =⎧⎨=⎩⇒2222m m n n⎧=⎨=⎩⇒02m n =⎧⎨=⎩，2()f x x ∴=，存在“倍值区间”[0,2]；对于B ，1()()f x x R x =∈，若存在“倍值区间”[,]m n ，当0x >时，1212n m mn⎧=⎪⎪⎨⎪=⎪⎩⇒12mn =，故只需12mn =即可，故存在；对于C ，1()f x x x=+；当0x >时，在区间[0,1]上单调递减，在区间[1,)+∞上单调递增，若存在“倍值区间”1[],1][0,2n m n m m ⊆⇒+=，212210n m m mn n+=⇒-+=，222210n mn m n -+=⇒=不符题意；若存在“倍值区间”1[,][1,)2m n m m m ⊆+∞⇒+=，22121n n m n n+=⇒==不符题意，故此函数不存在“倍值区间“；对于D ，233()11x f x x x x==++，所以()f x 在区间[0,1]上单调递增，在区间[1,)+∞上单调递减，若存在“倍值区间”[,][0,1]m n ⊆，2321m m m =+，2321n n n =+，0m ∴=，2n =，即存在“倍值区间”[0,2；故选：ABD ．8．（2021·全国高三专题练习（理））已知1a >，b R ∈，当0x >时，[]24(1)102x a x b x ⎛⎫---⋅-≥ ⎪⎝⎭恒成立，则3b a +的最小值是_____．3 【解析】根据题中条件，先讨论10,1x a ⎛⎤∈ ⎥-⎝⎦，根据不等式恒成立求出114(1)21b a a ⎡⎤≥--⎢⎥-⎣⎦；再讨论1,1x a ⎡⎫∈+∞⎪⎢-⎣⎭，求出114(1)21b a a ⎡⎤≤--⎢⎥-⎣⎦得到b ，再由基本不等式即可求出结果.【详解】当10,1x a ⎛⎤∈ ⎥-⎝⎦时，(1)10a x --<，即2402x b x--≤恒成立， 24222x x y x x-==-是10,1x a ⎛⎤∈ ⎥-⎝⎦上的增函数， ∴114(1)21b a a ⎡⎤≥--⎢⎥-⎣⎦，当1,1x a ⎡⎫∈+∞⎪⎢-⎣⎭时，(1)10a x -->，即2402x b x--≥恒成立，24222x x y x x-==-是1,1x a ⎡⎫∈+∞⎪⎢-⎣⎭上的增函数， ∴114(1)21b a a ⎡⎤≤--⎢⎥-⎣⎦， ∴114(1)21b a a ⎡⎤=--⎢⎥-⎣⎦，∴13(1)332(1)b a a a +=+-+≥-，当12a =+时等号成立．3.9．（2021·全国高三专题练习）对于满足2p ≤的所有实数p ，则使不等式212x px p x ++>+恒成立的x的取值范围为______．【答案】()()13+-∞-⋃∞，，．【解析】将不等式转化为在[-2，2]内关于p 的一次函数函数值大于0恒成立求参变量x 的范围的问题．【详解】解：原不等式可化为2(1)210x p x x -+-+>，令2()(1)21f p x p x x =-+-+，则原问题等价于()0f p >在[2,2]p ∈-上恒成立，则(2)0(2)0f f ->⎧⎨>⎩，即2243010x x x ⎧-+>⎨->⎩解得：1311x x x x ⎧⎪⎨-⎪⎩或或∴1x <-或3x >．即x 的取值范围为()()13+-∞-⋃∞，，. 故答案为：()()13+-∞-⋃∞，，. 10．（2021·上海高三二模）已知a R ∈，函数()22,011,02x a x x f x x ax a x ⎧++-≥⎪=⎨-++<⎪⎩的最小值为2a ，则由满足条件的a 的值组成的集合是_______________.【答案】{3- 【解析】讨论a -与0、2的大小关系，判断函数()f x 在[)0,+∞、(),0-∞上的单调性与最小值，根据函数()f x 的最小值列方程解出实数a 的值.【详解】分以下三种情况讨论：①若0a -≤时，即当0a ≥时，()222,22,0211,02x a x f x a x x ax a x ⎧⎪+->⎪=+≤≤⎨⎪⎪-++<⎩，所以，函数()f x 在(),0-∞上单调递减，且()112f x a >+，当0x ≥时，()min 1212f x a a =+>+，此时，函数()f x 无最小值；②若02a <-≤时，即当20a -≤<时，()222,22,222,011,02x a x a a x f x x a x a x ax a x +->⎧⎪+-≤≤⎪⎪=⎨--+≤<-⎪⎪-++<⎪⎩，当0x <时，()211242a a f x f a ⎛⎫≥=-++ ⎪⎝⎭，当0x ≥时，()2f x a ≥+.22a a +>，所以，21242a aa -++=，整理可得2640a a +-=，20a -≤<，解得3a =-±； ③当2a ->时，即当2a <-时，()222,2,222,0211,02x a x a a x a f x x a x x ax a x +->-⎧⎪--≤≤-⎪⎪=⎨--+≤<⎪⎪-++<⎪⎩，当0x <时，()211242a a f x f a ⎛⎫≥=-++ ⎪⎝⎭，当0x ≥时，()2f x a ≥--.因为202a a -->>，所以，21242a aa -++=，整理可得2640a a +-=，2a <-，解得3a =-3a =-+.综上所述，实数a的取值集合为{3-.故答案为：{3-.1．（2020·全国高考真题（文））设函数331()f x x x =-,则()f x （） A ．是奇函数，且在(0,+∞)单调递增 B ．是奇函数，且在(0,+∞)单调递减 C ．是偶函数，且在(0,+∞)单调递增 D ．是偶函数，且在(0,+∞)单调递减【答案】A 【解析】根据函数的解析式可知函数的定义域为{}0x x ≠，利用定义可得出函数()f x 为奇函数，再根据函数的单调性法则，即可解出．【详解】因为函数()331f x x x =-定义域为{}0x x ≠，其关于原点对称，而()()f x f x -=-，所以函数()f x 为奇函数．又因为函数3y x =在0,上单调递增，在,0上单调递增，而331y x x-==在0,上单调递减，在,0上单调递减，所以函数()331f x x x=-在0,上单调递增，在,0上单调递增．故选：A ．2.（2019·北京高考真题（文））下列函数中，在区间（0，+∞）上单调递增的是（） A ．12y x = B ．y =2x -C ．12log y x =D ．1y x=【答案】A 【解析】函数122,log xy y x -==，练真题1y x=在区间(0,)+∞ 上单调递减，函数12y x = 在区间(0,)+∞上单调递增，故选A .3．（2018·全国高考真题（文））设函数()2010x x f x x -⎧≤=⎨>⎩，，，则满足()()12f x f x +<的x 的取值范围是（）A ．(]1-∞-，B ．()0+∞，C ．()10-，D ．()0-∞，【答案】D 【解析】分析：首先根据题中所给的函数解析式，将函数图像画出来，从图中可以发现若有()()12f x f x +<成立，一定会有2021x x x <⎧⎨<+⎩，从而求得结果.详解：将函数()f x 的图像画出来，观察图像可知会有2021x x x <⎧⎨<+⎩，解得0x <，所以满足()()12f x f x +<的x 的取值范围是()0-∞，，故选D .4.(2017课标II)函数2()ln(28)f x x x =-- 的单调递增区间是（） A.(,2)-∞- B. (,1)-∞- C. (1,)+∞ D. (4,)+∞ 【答案】D【解析】函数有意义，则：2280x x --> ，解得：2x <- 或4x > ，结合二次函数的单调性、对数函数的单调性和复合函数同增异减的原则可得函数的单调增区间为()4,+∞ . 故选D.5.(2017天津)已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==，则,,a b c 的大小关系为（）（A ）a b c <<（B ）b a c <<（C ）c b a <<（D ）c a b << 【答案】C【解析】由题意：()221log log 55a f f ⎛⎫=-= ⎪⎝⎭，且：0.822log 5log 4.12,122>><<，据此：0.822log 5log 4.12>>，结合函数的单调性有：()()()0.822log 5log 4.12f f f >>，即,a b c c b a >><<，本题选择C 选项.6．（2020·北京高考真题）为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改，设企业的污水排放量W 与时间t 的关系为()W f t =，用()()f b f a b a---的大小评价在[,]a b 这段时间内企业污水治理能力的强弱，已知整改期内，甲、乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论： ①在[]12,t t 这段时间内，甲企业的污水治理能力比乙企业强；②在2t 时刻，甲企业的污水治理能力比乙企业强； ③在3t 时刻，甲、乙两企业的污水排放都已达标；④甲企业在[][][]112230,,,,,t t t t t 这三段时间中，在[]10,t 的污水治理能力最强．其中所有正确结论的序号是____________________．【答案】①②③ 【解析】根据定义逐一判断，即可得到结果【详解】()()f b f a b a---表示区间端点连线斜率的负数，在[]12,t t 这段时间内，甲的斜率比乙的小，所以甲的斜率的相反数比乙的大，因此甲企业的污水治理能力比乙企业强；①正确；甲企业在[][][]112230,,,,,t t t t t 这三段时间中，甲企业在[]12,t t 这段时间内，甲的斜率最小，其相反数最大，即在[]12,t t 的污水治理能力最强．④错误；在2t 时刻，甲切线的斜率比乙的小，所以甲切线的斜率的相反数比乙的大，甲企业的污水治理能力比乙企业强；②正确；在3t 时刻，甲、乙两企业的污水排放量都在污水打标排放量以下，所以都已达标；③正确；故答案为：①②③。

函数的单调性与最值-高考数学复习

）
B. （0，1）
D. （1，＋∞）
解析：令 t ＝，显然 t ＝在[0，＋∞）上为增函数.又 y ＝ t
1
1
2
2
－ t ＝－（ t －）＋（ t ≥0）在
2
4
1
0，
2
上单调递增，由
1
得0≤ x ≤ ，所以 f （ x ）的单调递增区间是
4
1
0，
4
1
≤
2
（也可写为
1
（0，））.故选A.
函数的单调性与最值
目录
1. 借助函数图象，会用符号语言表达函数的单调性、最大值、最小值.
2. 理解函数的单调性、最大值、最小值的作用和实际意义.
目录
1
C O N T E N T S
2
3
知识逐点夯实
考点分类突破
课时跟踪检测
PART
1
知识逐点夯实
课前自修
必备知识系统梳理基础重落实
目录
1. 函数的单调性
【例2】函数 f （ x ）＝｜ x －2｜ x 的单调递增区间为
和（2，＋∞） .
（－∞，1）
⁠
⁠
2 − 2， ≥ 2，
解析： f （ x ）＝ቊ 2
作出 f （ x ）的大致
− + 2， < 2.
图象，如图所示，由图象知 f （ x ）的单调递增区间是
（－∞，1）和（2，＋∞）.
C. f （－2）＜ f （1）＜ f （3）
D. f （1）＜ f （－2）＜ f （3）
目录
解析： ∵对任意的 x 1， x 2∈[0，＋∞）且 x 1≠ x 2，有

2020年高一上学期数学人教旧版必修一(全)：函数的单调性-《讲义教师版》

函数的单调性知识集结知识元利用定义判断函数单调性知识讲解1.定义一般地，设函数f（x）的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量x1，x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说函数f（x）在区间D上是增函数；当x1＜x2时，都有f（x1）＞f（x2），那么就说函数f（x）在区间D上是减函数．2.单调区间若函数f（x）在区间D上是增函数或减函数，则称函数f（x）在这一区间具有（严格的）单调性，区间D叫做y＝f（x）的单调区间.单调区间只能用区间表示，不能用集合或不等式表示；如有多个单调区间应分别写，不能用符号“∪”联结，也不能用“或”联结，只能用“和”或“，”连结．3.定义变式设任意x1，x2∈[a，b]且x1≠x2，那么①⇔f（x）在[a，b]上是增函数；⇔f（x）在[a，b]上是减函数．②（x1﹣x2）[f（x1）﹣f（x2）]＞0⇔f（x）在[a，b]上是增函数；（x1﹣x2）[f（x1）﹣f（x2）]＜0⇔f（x）在[a，b]上是减函数．例题精讲利用定义判断函数单调性例1.如果函数f（x）＝（12﹣a）x在实数集R上是减函数，那么实数a的取值范围是（）A．（0，12）B．（12，＋∞）C．（﹣∞，12）D．（﹣12，12）【解析】题干解析:∵函数f（x）＝（12﹣a）x在实数集R上是减函数，∴12﹣a＜0，∴a＞12，故选：B．例2.函数f（x）＝（k＋1）x＋b在实数集上是增函数，则有（）A．k＞1B．k＞﹣1C．b＞0 D．b＜0【答案】B【解析】题干解析:例3.函数①y＝|x|；②y＝；③y＝；④y＝x＋在（﹣∞，0）上为增函数的有（填序号）．【答案】④【解析】题干解析:①y＝|x|＝，所以该函数在（﹣∞，0）上单调递减；②y＝，所以该函数在（﹣∞，0）上是常数函数，不具有单调性；③，所以该函数在（﹣∞，0）上单调递减；④y＝x＋，所以该函数在（﹣∞，0）上为增函数；∴在（﹣∞，0）上为增函数的有④．故答案为：④．例4.下列四个命题：（1）f（x）＝1是偶函数；（2）g（x）＝x3，x∈（﹣1，1]是奇函数；（3）若f（x）是奇函数，g（x）是偶函数，则H（x）＝f（x）•g（x）一定是奇函数；（4）函数y＝f（|x|）的图象关于y轴对称，其中正确的命题个数是（）【解析】题干解析:（1）f（﹣x）＝f（x）＝1，故结论正确；（2）定义域不关于原点对称，一定是非奇非偶函数，故假命题；（3）H（﹣x）＝f（﹣x）•g（﹣x）＝﹣f（x）•g（x）＝﹣H（x），故结论正确；（4）f（|﹣x|）＝f（|x|），函数y＝f（|x|）是偶函数，图象关于y轴对称，结论正确；故选C例5.已知y＝f（x）（x∈R）为奇函数，则在f（x）上的点是（）【解析】题干解析:因为奇函数的图象关于原点对称，且f（﹣x）＝﹣f（x），故f（﹣a）＝﹣f （a）．即在f（x）上的点是（﹣a，﹣f（a））．故选C．例6.如果f（x）是定义在R上的奇函数，那么下列函数中，一定为偶函数的是（）A．y＝x＋f（x）B．y＝xf（x）C．y＝x2＋f（x）D．y＝x2f（x）【解析】题干解析:∵f（x）是奇函数，∴f（﹣x）＝﹣f（x）．对于A，g（﹣x）＝﹣x＋f（﹣x）＝﹣x﹣f（x）＝﹣g（x），∴y＝x＋f（x）是奇函数．对于B，g（﹣x）＝﹣xf（﹣x）＝xf（x）＝g（x），∴y＝xf（x）是偶函数．对于C，g（﹣x）＝（﹣x）2＋f（﹣x）＝x2﹣f（x），∴y＝x2＋f（x）为非奇非偶函数，对于D，g（﹣x）＝（﹣x）2f（﹣x）＝﹣x2f（x）＝﹣g（x），∴y＝x2f（x）是奇函数．故选B．通过图象平移得到新函数图象得到单调区间知识讲解1.图象的平移：左加右减（x的变化），上加下减（函数值y的变化）2.图象的对称性：奇偶性3.图象的翻折：含有绝对值的函数图象的画法例题精讲通过图象平移得到新函数图象得到单调区间例1.函数f（x）=x2﹣|x|的单调递减区间是．【答案】（﹣∞，﹣]和[0，）【解析】题干解析:，，当，∴其图象关于y轴对称，作图如下：∴函数f（x）=x2﹣|x|的单调递减区间是（﹣∞，﹣]和[0，）．故答案为：（﹣∞，﹣]和[0，）．例2.函数y＝|x|的单调递增区间为．【答案】（0，＋∞）【解析】题干解析:函数y＝|x|的零点为x＝0，其图象如下，通过图象可知，函数单调递增区间为（0，＋∞）．故答案为：（0，＋∞）．例3.函数y＝|x|﹣1的减区间为（）A．（﹣∞，0）B．（﹣∞，﹣1）C．（0，＋∞）D．（﹣1，＋∞）【解析】题干解析:由题意y＝x﹣1是一次函数，将图象右边翻折到左边，去掉原来左边图形可得y＝|x|﹣1图象．由图象可知：函数y＝|x|﹣1的减区间为（﹣∞，0），故选A．例4.函数y＝|x﹣1|的递增区间是．【答案】[1，＋∞）【解析】题干解析:函数y＝|x﹣1|的图象如图所示：数形结合可得函数的增区间为[1，＋∞），故答案为：[1，＋∞）．备选题库知识讲解本题库作为知识点“函数单调性的定义”的题目补充.例题精讲备选题库例1.（2020春∙沙坪坝区校级期中）下列函数中，既是奇函数，又在（0，+∞）上是增函数的是（）A．f（x）=sin x B．f（x）=e x+e-xC．f（x）=x3+x D．f（x）=xlnx【解析】题干解析:A．f（x）=sin x在（0，+∞）上不是单调函数，不满足条件。

高考数学《函数的单调区间》基础知识与专项练习题(含答案解析)

高考数学《函数的单调区间》基础知识与专项练习题（含答案解析）单调性是函数的一个重要性质，对函数作图起到决定性的作用，而导数是分析函数单调区间的一个便利工具。

求一个已知函数的单调区间是每一个学生的必备本领，在求解的过程中也要学会一些方法和技巧。

一、基础知识：1、函数的单调性：设()f x 的定义域为D ，区间I D ⊆，若对于1212,,x x I x x ∀∈<，有()()12f x f x <，则称()f x 在I 上单调递增，I 称为单调递增区间。

若对于1212,,x x I x x ∀∈<，有()()12f x f x >，则称()f x 在I 上单调递减，I 称为单调递减区间。

2、导数与单调区间的联系（1）函数()f x 在(),a b 可导，那么()f x 在(),a b 上单调递增()',()0x a b f x ⇒∀∈≥，此结论可以这样理解：对于递增的函数，其图像有三种类型：，无论是哪种图形，其上面任意一点的切线斜率均大于零。

等号成立的情况：一是单调区间分界点导数有可能为零，例如：()2f x x =的单调递增区间为[)0+∞，，而()'00f =，另一种是位于单调区间内但导数值等于零的点，典型的一个例子为()3f x x =在0x =处的导数为0，但是()0,0位于单调区间内。

（2）函数()f x 在(),a b 可导，则()f x 在(),a b 上单调递减()',()0x a b f x ⇒∀∈≤，（3）前面我们发现了函数的单调性可以决定其导数的符号，那么由()',()x a b f x ∀∈，的符号能否推出()f x 在(),a b 的单调性呢？如果()f x 不是常值函数，那么便可由导数的符号对应推出函数的单调性。

（这也是求函数单调区间的理论基础） 3、利用导数求函数单调区间的步骤（1）确定函数的定义域（2）求出()f x 的导函数'()f x（3）令'()0f x >（或0<），求出x 的解集，即为()f x 的单调增（或减）区间（4）列出表格4、求单调区间的一些技巧（1）强调先求定义域，一方面定义域对单调区间有限制作用（单调区间为定义域的子集）。

高考数学复习考点知识与题型专题讲解5---函数的单调性与最值

高考数学复习考点知识与题型专题讲解函数的单调性与最值考试要求1.借助函数图象，会用数学符号语言表达函数的单调性、最值，理解实际意义.2.掌握函数单调性的简单应用．知识梳理1．函数的单调性(1)单调函数的定义增函数减函数定义一般地，设函数f(x)的定义域为I，区间D⊆I，如果∀x1，x2∈D当x1<x2时，都有f(x1)<f(x2)，那么就称函数f(x)在区间D上是增函数当x1<x2时，都有f(x1)>f(x2)，那么就称函数f(x)在区间D上是减函数图象描述自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y＝f(x)在区间D上是增函数或减函数，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间D 叫做y ＝f (x )的单调区间． 2．函数的最值前提设函数y ＝f (x )的定义域为I ，如果存在实数M 满足条件(1)∀x ∈I ，都有f (x )≤M ； (2)∃x 0∈I ，使得f (x 0)＝M (1)∀x ∈I ，都有f (x )≥M ；(2)∃x 0∈I ，使得f (x 0)＝M结论M 为最大值M 为最小值常用结论1．∀x 1，x 2∈D 且x 1≠x 2，有f (x 1)－f (x 2)x 1－x 2>0(<0)或(x 1－x 2)[f (x 1)－f (x 2)]>0(<0)⇔f (x )在区间D上单调递增(减)．2．在公共定义域内，增函数＋增函数＝增函数，减函数＋减函数＝减函数． 3．函数y ＝f (x )(f (x )>0或f (x )<0)在公共定义域内与y ＝－f (x )，y ＝1f (x )的单调性相反． 4．复合函数的单调性：函数y ＝f (u )，u ＝φ(x )在函数y ＝f (φ(x ))的定义域上，如果y ＝f (u )与u ＝φ(x )的单调性相同，那么y ＝f (φ(x ))单调递增；如果y ＝f (u )与u ＝φ(x )的单调性相反，那么y ＝f (φ(x ))单调递减．思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若f (x )的定义域为R ，且f (－3)<f (2)，则f (x )为R 上的增函数．(×) (2)函数f (x )在(－2,3)上单调递增，则函数的单调递增区间为(－2,3)．(×) (3)因为y ＝x 与y ＝e x 都是增函数，所以y ＝x e x 在定义域内为增函数．(×)(4)函数y ＝1x 的单调递减区间是(－∞，0)∪(0，＋∞)．(×) 教材改编题1．下列函数中，在区间(0,1)上是增函数的是() A ．y ＝|x ＋1|B ．y ＝2－x C ．y ＝1x D ．y ＝x 2－x ＋1 答案A2．函数y ＝xx －1在区间[2,3]上的最大值是________．答案2解析函数y ＝x x －1＝1＋1x －1在[2,3]上单调递减，当x ＝2时，y ＝x x －1取得最大值22－1＝2.3．函数y ＝ax －1在(－∞，1)上为增函数，则实数a 的取值范围是________．答案(－∞，0)题型一确定函数的单调性命题点1求具体函数的单调区间例1下列函数在(0，＋∞)上单调递增的是________．(填序号) ①y ＝e x －e －x ；②y ＝|x 2－2x |；③y ＝x ＋cos x ；④y ＝x 2＋x －2. 答案①③解析∵y ＝e x 与y ＝－e －x 为R 上的增函数，∴y ＝e x －e －x 为R 上的增函数，故①正确；由y ＝|x 2－2x |的图象知，故②不正确；对于③，y ′＝1－sin x ≥0，∴y ＝x ＋cos x 在R 上为增函数，故③正确；y ＝x 2＋x －2的定义域为(－∞，－2]∪[1，＋∞)，故④不正确．命题点2判断或证明函数的单调性例2试讨论函数f (x )＝axx －1(a ≠0)在(－1,1)上的单调性．解方法一设－1<x 1<x 2<1， f (x )＝a ⎝ ⎛⎭⎪⎪⎫x －1＋1x －1＝a ⎝ ⎛⎭⎪⎫1＋1x －1， f (x 1)－f (x 2)＝a ⎝ ⎛⎭⎪⎫1＋1x 1－1－a ⎝ ⎛⎭⎪⎫1＋1x 2－1 ＝a (x 2－x 1)(x 1－1)(x 2－1)，由于－1<x 1<x 2<1，所以x 2－x 1>0，x 1－1<0，x 2－1<0，故当a >0时，f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，函数f (x )在(－1,1)上单调递减；当a <0时，f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，函数f (x )在(－1,1)上单调递增．方法二f ′(x )＝(ax )′(x －1)－ax (x －1)′(x －1)2＝a (x －1)－ax (x －1)2＝－a(x －1)2. 当a >0时，f ′(x )<0，函数f (x )在(－1,1)上单调递减；当a <0时，f ′(x )>0，函数f (x )在(－1,1)上单调递增．教师备选1．设函数f (x )＝⎩⎨⎧1，x >0，0，x ＝0，－1，x <0，g (x )＝x 2f (x －1)，则函数g (x )的单调递减区间是__________．答案[0,1)解析由题意知g (x )＝⎩⎪⎨⎪⎧x 2，x >1，0，x ＝1，－x 2，x <1，该函数的图象如图所示，其单调递减区间是[0,1)．2．已知a >0，函数f (x )＝x ＋ax (x >0)，证明：函数f (x )在(0，a ]上单调递减，在[a ，＋∞)上单调递增．证明方法一(定义法)设x 1>x 2>0， f (x 1)－f (x 2)＝x 1＋a x 1－x 2－ax 2＝(x 1－x 2)＋a (x 2－x 1)x 1x 2＝(x 1－x 2)(x 1x 2－a )x 1x 2，∵x 1>x 2>0，∴x 1－x 2>0，x 1x 2>0，当x 1，x 2∈(0，a ]时，0<x 1x 2<a ， ∴x 1x 2－a <0，∴f (x 1)－f (x 2)<0，f (x 1)<f (x 2)， ∴f (x )在(0，a ]上单调递减，当x 1，x 2∈[a ，＋∞)时，x 1x 2>a ， ∴x 1x 2－a >0，∴f (x 1)－f (x 2)>0， ∴f (x 1)>f (x 2)，∴f (x )在[a ，＋∞)上单调递增．方法二(导数法)f ′(x )＝1－a x 2＝x 2－ax2(x >0)，令f ′(x )>0⇒x 2－a >0⇒x >a ，令f ′(x )<0⇒x 2－a <0⇒0<x <a ，∴f (x )在(0，a ]上单调递减，在[a ，＋∞)上单调递增．思维升华确定函数单调性的四种方法 (1)定义法：利用定义判断．(2)导数法：适用于初等函数可以求导的函数．(3)图象法：由图象确定函数的单调区间需注意两点：一是单调区间必须是函数定义域的子集；二是图象不连续的单调区间要分开写，用“和”或“，”连接，不能用“∪”连接．(4)性质法：利用函数单调性的性质，尤其是利用复合函数“同增异减”的原则时，需先确定简单函数的单调性．跟踪训练1(1)函数f (x )＝ln(4＋3x －x 2)的单调递减区间是() A.⎝ ⎛⎦⎥⎤－∞，32B.⎣⎢⎡⎭⎪⎫32，＋∞ C.⎝ ⎛⎦⎥⎤－1，32D.⎣⎢⎡⎭⎪⎫32，4 答案D解析f (x )＝ln(4＋3x －x 2)的定义域为4＋3x －x 2>0，解得x ∈(－1,4)．令t ＝4＋3x －x 2，对称轴为x ＝32，故单调递增区间为⎝ ⎛⎭⎪⎫－1，32，单调递减区间为⎣⎢⎡⎭⎪⎫32，4，因为y ＝ln t 为增函数，所以f (x )＝ln(4＋3x －x 2)的单调递减区间为⎣⎢⎡⎭⎪⎫32，4.(2)函数f (x )＝|x －2|x 的单调递减区间是________．答案[1,2]解析f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥2，－x 2＋2x ，x <2.画出f (x )的大致图象(如图所示)，由图知f (x )的单调递减区间是[1,2]．题型二函数单调性的应用命题点1比较函数值的大小例3(2022·成都模拟)已知函数f (x )为R 上的偶函数，对任意x 1，x 2∈(－∞，0)，均有(x 1－x 2)[f (x 1)－f (x 2)]<0成立，若a ＝f (ln 2)，b ＝f (133)，c ＝f (13e )，则a ，b ，c 的大小关系是()A ．c <b <aB ．a <c <bC ．a 13(e)f>f(ln2)，即a<c<b.命题点2求函数的最值例4(2022·深圳模拟)函数y＝x2＋5x2＋4的最小值为________．答案5 2解析令x2＋4＝t，则t≥2，∴x2＝t2－4，∴y＝t2＋1t＝t＋1t，函数y＝t＋1t在[2，＋∞)上单调递增，∴当t ＝2时，y min ＝52. 命题点3解不等式例5已知函数f (x )＝ln x ＋2x ，若f (x －1)<2，则实数x 的取值范围是________．答案(1,2)解析f (x )在定义域(0，＋∞)上是增函数，且f (1)＝2，∴原不等式可化为f (x －1)<f (1)， ∴⎩⎪⎨⎪⎧x －1<1，x －1>0，解得1<x <2. 命题点4求参数的取值范围例6函数f (x )＝⎩⎪⎨⎪⎧a x ，x ≥1，⎝ ⎛⎭⎪⎫4－a 2x ＋2，x <1，且满足对任意的实数x 1≠x 2都有f (x 1)－f (x 2)x 1－x 2>0成立，则实数a 的取值范围是() A ．[4,8) B ．(4,8) C ．(1,8] D ．(1,8) 答案A解析函数f (x )＝⎩⎨⎧a x ，x ≥1，⎝ ⎛⎭⎪⎫4－a 2x ＋2，x <1满足对任意的实数x 1≠x 2都有f (x 1)－f (x 2)x 1－x 2>0，所以函数f (x )＝⎩⎨⎧ a x ，x ≥1，⎝ ⎛⎭⎪⎫4－a 2x ＋2，x <1是R 上的增函数，则由指数函数与一次函数的单调性可知应满足⎩⎪⎨⎪⎧ a >1，4－a 2>0，a ≥4－a 2＋2，解得4≤a <8，所以实数a 的取值范围为[4,8)．教师备选 1．(2022·嘉峪关模拟)函数f (x )＝ln(x 2－ax －3)在(1，＋∞)上单调递增，则a 的取值范围是()A ．(－∞，－2]B ．(－∞，－2)C ．(－∞，2]D ．(－∞，2)答案A 解析函数f (x )＝ln(x 2－ax －3)为复合函数，令u (x )＝x 2－ax －3，y ＝ln u 为增函数，故只要u (x )＝x 2－ax －3在(1，＋∞)上单调递增即可，只要⎩⎨⎧ a 2≤1，u (1)≥0，解得a ≤－2.2．对于任意实数a ，b ，定义min{a ，b }＝⎩⎨⎧a ，a ≤b ，b ，a >b .设函数f (x )＝－x ＋3，g (x )＝log 2x ，则函数h (x )＝min{f (x )，g (x )}的最大值是______．答案1解析方法一在同一坐标系中，作函数f (x )，g (x )的图象，依题意，h (x )的图象为如图所示的实线部分．易知点A (2,1)为图象的最高点，因此h (x )的最大值为h (2)＝1.方法二依题意，h (x )＝⎩⎪⎨⎪⎧log 2x ，0<x ≤2，－x ＋3，x >2.当0<x ≤2时，h (x )＝log 2x 单调递增，当x >2时，h (x )＝3－x 单调递减，因此h (x )在x ＝2时取得最大值h (2)＝1.思维升华 (1)比较函数值的大小，应将自变量转化到同一个单调区间内，然后利用函数的单调性解决．(2)求解函数不等式，其实质是函数单调性的逆用，由条件脱去“f ”，转化为自变量间的大小关系，应注意函数的定义域．(3)利用单调性求参数的取值(范围)．根据其单调性直接构建参数满足的方程(组)(不等式(组))或先得到其图象的升降，再结合图象求解．对于分段函数，要注意衔接点的取值．跟踪训练2(1)已知函数f (x )＝e |x |，记a ＝f (log 23)，b ＝f (－2)，c ＝f (e)，则a ，b ，c 的大小关系为()A ．a 0时，f (x )＝e x 为增函数，又b ＝f (－2)＝f (2)，且e>2>log 23，∴f (e)>f (2)>f (log 23)，即a 4，若函数y ＝f (x )在区间(a ，a ＋1)上单调递增，则实数a 的取值范围是()A ．(－∞，1]B ．[1,4]C ．[4，＋∞)D ．(－∞，1]∪[4，＋∞)答案D解析画出函数f (x )＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4的图象，如图，由图可知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4的单调递增区间为(－∞，2)，(4，＋∞)， ∵函数在(a ，a ＋1)上单调递增，∴a ＋1≤2或a ≥4，∴a ≤1或a ≥4.(3)已知f (x )是定义在R 上的偶函数，且在区间[0，＋∞)上单调递减，则不等式f (2x －1)>f (x ＋1)的解集为________．答案(0,2)解析依题意f (x )是定义在R 上的偶函数，且在区间[0，＋∞)上单调递减，所以 f (2x －1)>f (x ＋1)⇔(2x －1)2<(x ＋1)2，即4x 2－4x ＋1<x 2＋2x ＋1，即x 2－2x ＝x (x －2)<0⇒x ∈(0,2)．课时精练1．下列函数中，在区间(0，＋∞)内单调递减的是()A ．y ＝1x －xB ．y ＝x 2－xC ．y ＝ln x －xD ．y ＝e x答案A解析当x∈(0，＋∞)时，y＝1x与y＝－x单调递减，∴y＝1x－x在(0，＋∞)上单调递减．2．函数f(x)＝x1－x在()A．(－∞，1)∪(1，＋∞)上是增函数B．(－∞，1)∪(1，＋∞)上是减函数C．(－∞，1)和(1，＋∞)上是增函数D．(－∞，1)和(1，＋∞)上是减函数答案C解析函数f(x)的定义域为{x|x≠1}．f(x)＝x1－x＝11－x－1，根据函数y＝－1x的单调性及有关性质，可知f(x)在(－∞，1)和(1，＋∞)上是增函数．3．(2022·安徽六安一中月考)若函数f(x)＝2x2＋31＋x2，则f(x)的值域为()A．(－∞，3] B．(2,3) C．(2,3] D．[3，＋∞) 答案C解析f(x)＝2x2＋31＋x2＝2＋1x2＋1，∵x 2≥0，∴x 2＋1≥1，∴0<1x 2＋1≤1， ∴f (x )∈(2,3]．4．(2022·贵阳模拟)已知函数f (x )在(－∞，＋∞)上单调递减，且为奇函数，若f (1)＝－2，则满足－2≤f (x －2)≤2的x 的取值范围是()A ．[－2,2]B ．[－1,1]C ．[1,3]D ．[0,4]答案C解析因为f (x )为奇函数，若f (1)＝－2，则f (－1)＝2，所以不等式－2≤f (x －2)≤2可化为f (1)≤f (x －2)≤f (－1)，又f (x )在(－∞，＋∞)上单调递减，所以－1≤x －2≤1，解得1≤x ≤3.5．(2022·南通模拟)已知函数f (x )＝⎩⎨⎧e x －e －x ，x >0，－x 2，x ≤0，若a ＝50.01，b ＝log 32，c ＝log 20.9，则有()A ．f (a )>f (b )>f (c )B ．f (b )>f (a )>f (c )C ．f (a )>f (c )>f (b )D ．f (c )>f (a )>f (b )答案A解析y ＝e x 是增函数，y ＝e －x 是减函数，因此在(0，＋∞)上y ＝e x －e －x 单调递增，且此时f (x )>0.f (x )＝－x 2在x ≤0时单调递增，所以f (x )在R 上单调递增．c ＝log 20.9<0，b ＝log 32，所以01，即a >b >c ，所以f (a )>f (b )>f (c )．6．已知函数f (x )＝⎩⎪⎨⎪⎧ ln x ＋2x ，x >0，21－x，x ≤0，则下列结论正确的个数是()①f (x )在R 上为增函数；②f (e)>f (2)；③若f (x )在(a ，a ＋1)上单调递增，则a ≤－1或a ≥0；④当x ∈[－1,1]时，f (x )的值域为[1,2]．A ．1B ．2C ．3D ．4答案B解析易知f (x )在(－∞，0]，(0，＋∞)上单调递增，①错误，②正确；若f (x )在(a ，a ＋1)上单调递增，则a ≥0或a ＋1≤0，即a ≤－1或a ≥0，故③正确；当x ∈[－1,0]时，f (x )∈[1,2]，当x ∈(0,1]时，f (x )∈(－∞，2]，故x ∈[－1,1]时，f (x )∈(－∞，2]，故④不正确．7．函数y ＝－x 2＋2|x |＋1的单调递增区间为__________，单调递减区间为________．答案(－∞，－1]和[0,1](－1,0)和(1，＋∞)解析由于y ＝⎩⎪⎨⎪⎧－x 2＋2x ＋1，x ≥0，－x 2－2x ＋1，x <0，即y ＝⎩⎪⎨⎪⎧－(x －1)2＋2，x ≥0，－(x ＋1)2＋2，x <0. 画出函数的图象如图所示，单调递增区间为(－∞，－1]和[0,1]，单调递减区间为(－1,0)和(1，＋∞)．8．(2022·山东师大附中质检)已知函数f (x )＝e |x －a |(a 为常数)，若f (x )在区间[1，＋∞)上单调递增，则实数a 的取值范围是________．答案(－∞，1]解析f (x )＝⎩⎪⎨⎪⎧e x －a ，x ≥a ，e a －x ，x <a ，当x ≥a 时，f (x )单调递增，当x <a 时，f (x )单调递减，又f (x )在[1，＋∞)上单调递增，所以a ≤1.9．已知函数f (x )＝ax －1ax ＋2a (a >0)，且f (x )在(0,1]上的最大值为g (a )，求g (a )的最小值．解f (x )＝ax －1ax ＋2a (a >0)，∴f (x )在(0,1]上单调递增，∴f (x )max ＝f (1)＝a ＋1a， ∴g (a )＝a ＋1a ≥2，当且仅当a ＝1a 即a ＝1时取等号，∴g (a )的最小值为2.10．已知函数f (x )＝a －22x ＋1. (1)求f (0)；(2)探究f (x )的单调性，并证明你的结论；(3)若f (x )为奇函数，求满足f (ax )<f (2)的x 的取值范围．解(1)f (0)＝a －220＋1＝a －1.(2)f (x )在R 上单调递增．证明如下： ∵f (x )的定义域为R ，∴任取x 1，x 2∈R 且x 1<x 2，则f (x 1)－f (x 2)＝a －1221x +－a ＋2221x + ＝12122(22)(12)(12)x x x x ⋅-++， ∵y ＝2x 在R 上单调递增且x 1<x 2， ∴0<12x <22x ，∴12x －22x <0,12x ＋1>0,22x ＋1>0. ∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)． ∴f (x )在R 上单调递增．(3)∵f (x )是奇函数，∴f (－x )＝－f (x )，即a －22－x ＋1＝－a ＋22x ＋1，解得a ＝1. ∴f (ax )<f (2)即为f (x )<f (2)，又∵f (x )在R 上单调递增，∴x <2. ∴x 的取值范围是(－∞，2)．11．定义max{a ，b ，c }为a ，b ，c 中的最大值，设M ＝max{2x ,2x －3,6－x }，则M 的最小值是()A ．2B ．3C ．4D ．6答案C解析画出函数M ＝max{2x ,2x －3,6－x }的图象(如图)，由图可知，函数M 在A (2,4)处取得最小值22＝6－2＝4，故M 的最小值为4.12．已知函数f (x )＝⎩⎪⎨⎪⎧ ⎝ ⎛⎭⎪⎫12x －1，x ≤0，－x 3，x >0，当x ∈[m ，m ＋1]时，不等式f (2m －x )<f (x ＋m )恒成立，则实数m 的取值范围是()A ．(－∞，－4)B ．(－∞，－2)C ．(－2,2)D ．(－∞，0)答案B解析易知函数f (x )＝⎩⎨⎧ ⎝ ⎛⎭⎪⎫12x －1，x ≤0，－x 3，x >0在x ∈R 上单调递减，又f (2m －x )<f (x ＋m )在x ∈[m ，m ＋1]上恒成立，所以2m－x>x＋m，即2x<m在x∈[m，m＋1]上恒成立，所以2(m＋1)<m，解得m<－2.13．如果几个函数的定义域相同，值域也相同，但解析式不同，称这几个函数为“同域函数”，则函数y＝x＋x＋1的值域为________，与y是“同域函数”的一个解析式为________．答案[－1，＋∞)y＝x，x∈[－1，＋∞)(答案不唯一)解析y＝x＋x＋1的定义域为[－1，＋∞)，且在[－1，＋∞)上单调递增，∴当x＝－1时，y min＝－1，∴值域为[－1，＋∞)，∴与y是“同域函数”的解析式可为y＝x，x∈[－1，＋∞)．14．设函数f(x)＝ax＋1x＋2a在区间(－2，＋∞)上单调递增，那么a的取值范围是________．答案[1，＋∞)解析f(x)＝ax＋2a2－2a2＋1x＋2a＝a－2a2－1x＋2a，定义域为{x|x≠－2a}，所以⎩⎪⎨⎪⎧ 2a 2－1>0，－2a ≤－2，所以⎩⎪⎨⎪⎧2a 2－1>0，a ≥1，所以a ≥1.15．(2022·沧州模拟)设函数f (x )＝x 3－sin x ＋x ，则满足f (x )＋f (1－2x )<0的x 的取值范围是________．答案(1，＋∞)解析f (x )＝x 3－sin x ＋x ，∵f (－x )＝(－x )3－sin(－x )＋(－x )＝－(x 3－sin x ＋x )＝－f (x )，∴f (x )为奇函数，又f ′(x )＝3x 2－cos x ＋1≥0，∴f (x )为R 上的增函数，∴f (x )＋f (1－2x )<0可化为f (x )<－f (1－2x )＝f (2x －1)，∴x <2x －1，即x >1，∴满足f (x )＋f (1－2x )<0的x 的取值范围是(1，＋∞)．16．已知定义在R 上的函数f (x )满足f (x ＋y )＝f (x )＋f (y )＋1，且当x >0时，f (x )>－1.(1)求f (0)的值，并证明f (x )在R 上是增函数；(2)若f(1)＝1，解关于x的不等式f(x2＋2x)＋f(1－x)>4. 解(1)令x＝y＝0，得f(0)＝－1.在R上任取x1>x2，则x1－x2>0，所以f(x1－x2)>－1.又f(x1)＝f[(x1－x2)＋x2]＝f(x1－x2)＋f(x2)＋1>f(x2)，∴函数f(x)在R上是增函数．(2)由f(1)＝1，得f(2)＝3，f(3)＝5.由f(x2＋2x)＋f(1－x)>4得f(x2＋x＋1)>f(3)，因为函数f(x)在R上是增函数，所以x2＋x＋1>3，解得x<－2或x>1，故原不等式的解集为{x|x<－2或x>1}．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

函数的单调性
1.函数f (x )＝|x －2|x 的单调减区间是( )
A ．[1,2]
B ．[－1,0]
C ．[0,2]
D ．[2，＋∞)
2.已知函数f (x )＝x 2－2x －3，则该函数的单调递增区间为( )
A ．(－∞，1]
B ．[3，＋∞)
C ．(－∞，－1]
D ．[1，＋∞)
3.函数f (x )＝x
1－x 在( )
A ．(－∞，1)∪(1，＋∞)上是增函数
B ．(－∞，1)∪(1，＋∞)上是减函数
C ．(－∞，1)和(1，＋∞)上是增函数
D ．(－∞，1)和(1，＋∞)上是减函数
4.下列函数中，在区间(0，＋∞)上为增函数的是( )
A.y ＝x ＋1
B.y ＝(x －1)2
C.y ＝2－x
D.y ＝log 0.5(x ＋1)
5.下列函数中，满足“f (x ＋y )＝f (x )·f (y )”的单调递增函数是( )
A.f (x )＝x 12
B.f (x )＝x 3
C.f (x )＝⎝ ⎛⎭⎪⎫12x
D.f (x )＝3x
6.已知函数f (x )的图象关于直线x ＝1对称，当x 2>x 1>1时，[f (x 2)－f (x 1)](x 2
－x 1)<0恒成立，设a ＝f ⎝ ⎛⎭
⎪⎫－12，b ＝f (2)，c ＝f (e)，则a ，b ，c 的大小关系为( ) A ．c >a >b B ．c >b >a C ．a >c >b D ．b >a >c
7.已知偶函数f (x )在[0，＋∞)上单调递减，f (2)＝0.若f (x －1)>0，则x 的取值范围是________.
8.已知函数f (x )为(0，＋∞)上的增函数，若f (a 2－a )>f (a ＋3)，则实数a 的取值范围为________．
9.函数()f x 的定义域为Ｒ，(1)2f -=，对任意的x R ∈，'()f x 2>，则不等式()24f x x >+的解集为（）
Ａ()1,1- Ｂ()1,-+∞ Ｃ(),1-∞- Ｄ(),-∞+∞
10.函数()f x ()x ∈R 满足(1)1f =，1()2
f x '<，则不等式221()22x f x <+的解集为____ 11.函数f (x )＝1x －1在区间[a ，b ]上的最大值是1，最小值是13
，则a ＋b ＝
________.
12.已知函数f (x )＝|x ＋a |在(－∞，－1)上是单调函数，则a 的取值范围是
( )
A ．(－∞，1]
B ．(－∞，－1]
C ．[－1，＋∞) D．[1，＋∞)
13.如果函数f (x )＝ax 2＋2x －3在区间(－∞，4)上是单调递增的，则实数a 的取值范围是( )
A.⎝ ⎛⎭⎪⎫－14，＋∞
B.⎣⎢⎡⎭⎪⎫－14，＋∞
C.⎣⎢⎡⎭⎪⎫－14，0
D.⎣⎢⎡⎦
⎥⎤－14，0 14.已知f (x )＝⎩⎨⎧ 3a －1x ＋4a ，x <1，log a x ，x ≥1
是(－∞，＋∞)上的减函数，那么a 的取值范围是( )
A ．(0,1) B.⎝ ⎛⎭⎪⎫0，13 C.⎣⎢⎡⎭⎪⎫17，13 D.⎣⎢⎡⎭
⎪⎫17，1。