11-乘法器
4位乘法器
一、概述利用四位二进制寄存器、全加器以及D触发器等元器件,实现四位二进制乘法器的控制部分和乘法的实现部分。
成法是加法的简便运算乘法运算只能通过加法运算以及移位运算来实现。
在控制端用四个触发器产生四个控制信号来控制实现的加法移位功能,实现端在控制端信号作用下依次执行置零、加法、移位和循环操作。
二、方案说明设计一个4位二进制乘法器,可以存储其乘积。
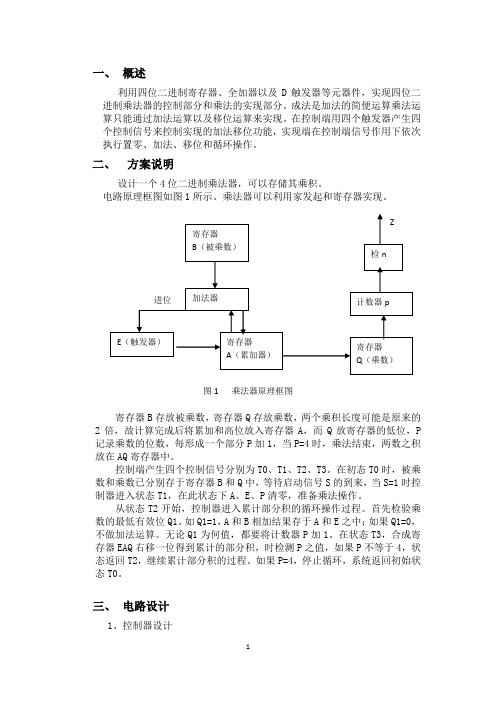
电路原理框图如图1所示。
乘法器可以利用家发起和寄存器实现。
图1 乘法器原理框图寄存器B存放被乘数,寄存器Q存放乘数,两个乘积长度可能是原来的2倍,故计算完成后将累加和高位放入寄存器A,而Q放寄存器的低位,P 记录乘数的位数,每形成一个部分P加1,当P=4时,乘法结束,两数之积放在AQ寄存器中。
控制端产生四个控制信号分别为T0、T1、T2、T3。
在初态T0时,被乘数和乘数已分别存于寄存器B和Q中,等待启动信号S的到来,当S=1时控制器进入状态T1,在此状态下A、E、P清零,准备乘法操作。
从状态T2开始,控制器进入累计部分积的循环操作过程。
首先检验乘数的最低有效位Q1。
如Q1=1,A和B相加结果存于A和E之中;如果Q1=0,不做加法运算。
无论Q1为何值,都要将计数器P加1。
在状态T3,合成寄存器EAQ右移一位得到累计的部分积,时检测P之值,如果P不等于4,状态返回T2,继续累计部分积的过程。
如果P=4,停止循环,系统返回初始状态T0。
三、电路设计1、控制器设计根据图2所示的ASM图表,可以设计二进制乘法器的控制器。
图2 二进制乘法器ASM图表四个D触发器的驱动方程为:D0=T0S’+T3Z=((T0S’)’·(T3Z)’)’D1=T0S=((T0S)’)’D2=T1+T3Z’=(T1’·(T3Z’)’)’D3=T2控制器仿真电路如图2所示。
控制器中S为启动信号,高电平有效,系统开始工作时应使T0=1,T1=T2=T3=0,故图中设置了Reset信号(负脉冲)图2 二进制乘法器的控制逻辑图2. 二进制乘法器数据处理器(1) A寄存器A寄存器具有并入、移位、同步清0和保持功能。
乘法器的verilog实现(并行、移位相加、查找表)

乘法器的verilog实现(并⾏、移位相加、查找表)并⾏乘法器,也就是⽤乘法运算符实现,下⾯的代码实现8bit⽆符号数的乘法。
代码:1module mult_parrell(rst_n,2 clk,3 a,4 b,5 p6 );7parameter DATA_SIZE = 8;89input rst_n;10input clk;11input [DATA_SIZE - 1 : 0] a;12input [DATA_SIZE - 1 : 0] b;1314output [2*DATA_SIZE - 1 : 0] p;1516reg [DATA_SIZE - 1 : 0] a_r;17reg [DATA_SIZE - 1 : 0] b_r;1819wire [2*DATA_SIZE - 1 : 0] p_tmp;20reg [2*DATA_SIZE - 1 : 0] p;2122//输⼊数据打⼀拍23always@(posedge clk)24if(!rst_n)25begin26 a_r <= 8'd0;27 b_r <= 8'd0;28end29else30begin31 a_r <= a;32 b_r <= b;33end3435assign p_tmp = a*b; //只能做⽆符号数的相乘,若要做有符号数乘法,需将数据声明为signed类型3637//输出数据打⼀拍38always@(posedge clk)39if(!rst_n)40begin41 p <= 16'd0;42end43else44begin45 p <= p_tmp;46end4748endmodule移位相加乘法器,下⾯的代码可实现8bit有符号数的相乘,注意符号扩展以及MSB位的处理://输⼊数据取反assign a_r_inv = ~a_r + 1;assign a_shift0 = b_r[0] ? {{8{a_r[7]}},a_r} : 0;assign a_shift1 = b_r[1] ? {{7{a_r[7]}},a_r,1'b0} : 0;assign a_shift2 = b_r[2] ? {{6{a_r[7]}},a_r,2'b0} : 0;assign a_shift3 = b_r[3] ? {{5{a_r[7]}},a_r,3'b0} : 0;assign a_shift4 = b_r[4] ? {{4{a_r[7]}},a_r,4'b0} : 0;assign a_shift5 = b_r[5] ? {{3{a_r[7]}},a_r,5'b0} : 0;assign a_shift6 = b_r[6] ? {{2{a_r[7]}},a_r,6'b0} : 0;assign a_shift7 = b_r[7] ? {{1{a_r_inv[7]}},a_r_inv,7'b0} : 0; //被乘数为⽆符号数时,特别处理代码:1module mult_shift_add(rst_n,2 clk,3 a,4 b,5 p6 );7parameter DATA_SIZE = 8;89input rst_n;10input clk;11input [DATA_SIZE - 1 : 0] a;12input [DATA_SIZE - 1 : 0] b;1314output [2*DATA_SIZE - 2 : 0] p;1516//输⼊数据打⼀个时钟节拍17reg [DATA_SIZE - 1 : 0] a_r;18reg [DATA_SIZE - 1 : 0] b_r;1920//输⼊数据取反21wire [DATA_SIZE - 1 : 0] a_r_inv;2223//输⼊数据移位24wire [2*DATA_SIZE - 1 : 0] a_shift0;25wire [2*DATA_SIZE - 1 : 0] a_shift1;26wire [2*DATA_SIZE - 1 : 0] a_shift2;27wire [2*DATA_SIZE - 1 : 0] a_shift3;28wire [2*DATA_SIZE - 1 : 0] a_shift4;29wire [2*DATA_SIZE - 1 : 0] a_shift5;30wire [2*DATA_SIZE - 1 : 0] a_shift6;31wire [2*DATA_SIZE - 1 : 0] a_shift7;3233//输出数据打⼀个时钟节拍34wire [2*DATA_SIZE - 1 : 0] p_tmp;35reg [2*DATA_SIZE - 1 : 0] p;3637//输⼊数据打⼀个时钟节拍38always@(posedge clk)39if(!rst_n)40begin41 a_r <= 8'd0;42 b_r <= 8'd0;43end44else45begin46 a_r <= a;47 b_r <= b;48end49//输⼊数据取反50assign a_r_inv = ~a_r + 1;5152//输⼊数据移位,注意符号扩展,不仅仅是最⾼位扩展53//对每⼀个bit都需扩展54assign a_shift0 = b_r[0] ? {{8{a_r[7]}},a_r} : 0;55assign a_shift1 = b_r[1] ? {{7{a_r[7]}},a_r,1'b0} : 0;56assign a_shift2 = b_r[2] ? {{6{a_r[7]}},a_r,2'b0} : 0;57assign a_shift3 = b_r[3] ? {{5{a_r[7]}},a_r,3'b0} : 0;58assign a_shift4 = b_r[4] ? {{4{a_r[7]}},a_r,4'b0} : 0;59assign a_shift5 = b_r[5] ? {{3{a_r[7]}},a_r,5'b0} : 0;60assign a_shift6 = b_r[6] ? {{2{a_r[7]}},a_r,6'b0} : 0;61assign a_shift7 = b_r[7] ? {{1{a_r_inv[7]}},a_r_inv,7'b0} : 0; //被乘数为⽆符号数时,特别处理6263assign p_tmp = a_shift0 + a_shift1 + a_shift2 + a_shift3 + a_shift464 + a_shift5 + a_shift6 + a_shift7;6566always@(posedge clk)67if(!rst_n)68begin69//p <= 16'd0;70 p <= 15'd0;71end72else73begin74//p <= p_tmp[15:0];75 p <= p_tmp[14:0];76end7778endmoduletestbench:1module mult_shift_add_tb;23// Inputs4reg rst_n;5reg clk;6reg [7:0] a;7reg [7:0] b;89// Outputs10wire [14:0] p;1112// Instantiate the Unit Under Test (UUT)13 mult_shift_add uut (14 .rst_n(rst_n),15 .clk(clk),16 .a(a),17 .b(b),18 .p(p)19 );2021parameter CLK_PERIOD = 10;2223initial begin24 rst_n = 0;25 clk = 0;2627 #100;28 rst_n = 1;29end3031always #(CLK_PERIOD/2) clk = ~clk;3233always@(posedge clk)34if(!rst_n)35begin36 a = 8'd0;37 b = 8'd0;38end39else40begin41 a = a + 1;42 b = b - 1;43end4445endmoduleISIM仿真结果:移位相加乘法器树:将assign p_tmp = a_shift0 + a_shift1 + a_shift2 + a_shift3 + a_shift4 + a_shift5 + a_shift6 + a_shift7;换为:assign sum_01 = a_shift0 + a_shift1;assign sum_23 = a_shift2 + a_shift3;assign sum_45 = a_shift4 + a_shift5;assign sum_67 = a_shift6 + a_shift7;assign sum_0123 = sum_01 + sum_23;assign sum_4567 = sum_45 + sum_67;assign p_tmp = sum_0123 + sum_4567;就成为乘法器树。
模拟乘法器应用实验

二、综合设计实验说明
本次综合设计实验,由大家独自依据所学的有关高频电子 线路中频率变换技术的相关理论知识,以模拟乘法器为核心器 件,设计出实现普通调幅、平衡调制、混频、倍频和同步检波 等功能的实际电路。并完成对所设计的各种功能电路的仿真调 试。
三、实验任务与要求
一、实验任务:
用模拟乘法器实现振幅调制(含AM与DSB)、同步检波、混频、倍频等频 率变换电路的设计。 已知:模拟乘法器为1496,采用双电源供电,Vcc=12V Vee=-8V.
② 同步检波器电路设计与仿真
实现对DSB信号的解调。 基本条件;载波信号UX:f=1MHZ /50-100mV 调制信号Uy: f=2KHz/200mV,并按信号流程记录各级信号波形。
三、实验任务与要求
二、实验要求:
③ 混频器电路设计与仿真 实现对信号的混频。 基本条件:AM信号条件:(载波信号UX:f=1MHZ /50mV ,调制信号Uy: f=2KHz/200mV,M=30%)中频信号:465KHZ,本地载波:按接收机制式自定。 记录各级信号波形。 ④ 倍频器电路设计与仿真 实现对信号的倍频。 基本条件:Ux=Uy(载波信号UX:f=1MHZ /50mV )完成电路设计与仿真, 并记录各级信号波形。推证输入、输出信号的关系。
U 0 (t )
1 KU sU 0 cos( 0 s )t 2
0 s i
为所需要的中频频率,可见
用模拟乘法器实现混频,就是在 U x 端和 U y 端分别加上两个不同频率的信号,两信号 相差一中频,再经过带通滤波器取出中频信号。
四、实验原理说明及设计思路提示
5.模拟乘法器实现混频
U 0 t 1 m Ucm cos c t cos c t 2 m Ucm cos c t cost
定点小数的乘法运算及实现

补码两位乘
将比较Yi-1Yi的状态与比较YiYi+1的状态所执行的运算合成一 步 对照:补码一位乘法 2(Yi- Yi-1 ) + (Yi+1-Yi) = Yi+ 1+ Yi - 2Yi-1 Yi+ Yi+1- 2Yi-1 0 1 1 2 -2 -1 -1 0 操作 +0,2→ +[X]补, 2→ +[X]补, 2→ +2[X]补, 2→ +2[-X]补, 2→ +[-X]补, 2→ +[-X]补, 2→ +0, 2→ 17
+
+
+ +
1 1 1 1
1 1 1 1
积低部
∴[Z]原=1,10001111
原码两位乘
原码一位乘依据Yi 决定操作,原码两位乘每次根据 连续两位乘数Yi+1Yi (=2Yi+1+Yi)决定本次操作 n位数的乘法一般只需n/2次操作
Yi+1 Yi 00
01 10 2 11
1 1 2 i 1 1 2 2
0
0→Cj,2→ -|X|
1→Cj,2→ +|X| 0→Cj,1→
00011100
1
00001110
0
积高位
积低位
最后一步只移一位 10
[Z]原=1,00111000000111
4.3.2 补码乘法运算
Booth法。目标:求[X· Y]补 设被乘数X、乘数Y均为n+1位的定点小数,
X补=x0.x1x2…xn, Y补=y0.y1y2…yn。 则[Y]补=y0· 20+y1· 2-1+· · · · · · +yn· 2-n
数字电路课程设计之乘法器

X
Y
C
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
最简积之和式为 S=X`Y+XY`=X○+ Y;C=XY.
电路图为:
X`
1
3
Y
2
X
1
3
Y`
2
X
1
3
S
Y
2
1
3
S
2
X
1
Y
2
3
C
1
3
C
2
2.2 全加器
全加器是为三输入两输出,输入存在进位,真值表如下图所示,输入 X,Y,Z,输出 C,S
X
Y
Z
C
S
0
0
0
0
0
0
0
1
0
carry_look_add cla1 (.A(v),.B(w),.Cin(0),.Cout(d[4]),.S(d[3:0])); assign S[1]= d[0]; and (z[0],A[2],B[0]); and (z[1],A[2],B[1]); and (z[2],A[2],B[2]); and (z[3],A[2],B[3]); carry_look_add cla2 (.A(d[4:1]),.B(z),.Cin(0),.Cout(d1[4]),.S(d1[3:0])); assign S[2]=d1[0];
and (x[0],A[3],B[0]); and (x[1],A[3],B[1]); and (x[2],A[3],B[2]); and (x[3],A[3],B[3]); carry_look_add cla3 (.A(d1[4:1]),.B(x),.Cin(0),.Cout(d2[4]),.S(d2[3:0])); assign S[7:3]=d2[4:0]; endmodule 3.6 Verilog 测试平台语言编写 `timescale 1ns/1ps module mul_tb(); reg[3:0] A,B; wire [7:0] S; mul mu (.A(A),.B(B),.S(S)); initial begin
清华大学 微机原理课件 CPU设计ALU

ALU电路设计
(2)移位器
采用2:1多路选择器构造的8位右移位器
A7 A6 A5 A4 A3 A2 A1 A0 S2 S1 S0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0 R7
1
0 R6
1 R5
0
1 R4
0
1 R3
0
1 R2
0
1 R1
0
1 R0
0
MSB的输入如何? 32位移位器需要多少级?
CPU逻辑设计
—— ALU电路设计
1
MIPS对ALU的需求
Add, AddU, Sub, SubU, AddI, AddIU =>带溢出检测和反向器的补码加法器 SltI, SltIU(Set Less than) =>带反向器的补码加法器,检测结果的符号 And, Or, AndI, OrI =>逻辑或、逻辑与
B12 B11 B10 B9
B11 B10 B9 B8
B6 B5 B4 B3
B5 B4 B3 B2
B4
B3 B2
B1
B3
B2 B1
B0 S1 S0
3
2
1 0
3
2
1 0
3
2
1 0
3
2
1 0
3
2
1 0
3
2
1 0
3
2
锁定放大器的设计(C题)

1
������ ������ ������5
������ ������������5
+ ������28
=
1 1 + ������������������5 ������28
������29 ������29 1 ������������ + (1 + ) ������27 ������27 1 + ������������������5 ������28 ������������ = 1 − ������������������5 ������28 1 + ������������������5 ������28
图 11 开关乘法器电路图 调整移相器得到与待测信号同相的方波,CD4053 得到如图 12 所示的输出波形
图 12 整流输出波形 3.1.9 低通滤波及直流放大电路 开关乘法器输出的电压值并不是直流, 经过一个截止频率很低的低通滤波器 可以得到直流,经过直流放大输出到单片机进行显示。
OPA4227PA VCC
12V
图 5 交流放大电路图 3.1.4 带通滤波器的设计 本系统要求带通滤波器的通频带为 900Hz~1100Hz,通带窄,而且要求通频带之 外的频率衰减的越快越好,因此我们要选择二阶带通滤波器。我们使用 TI 公司 提供滤波器设计软件 Filter Pro 进行初步设计,并在 Multisim 中进行参数的微 调,在实际电路中将 R17 和 R21 变为滑动变阻器,使得带通滤波器的截止频率和 Q 值可以微调。最终形成图 6 所示的带通滤波器。其幅频特性如图 7 所示:
图 1 整体系统框图
2 理论分析与计算
2.1 锁相放大器原理 锁相放大器由信号通道、参考通道、相敏检波器以及输出电路组成,是一种 对交变信号进行相敏检波的放大器。 它利用和被测信号有相同频率和相位关系的 参考信号作为比较基准,只对被测信号本身和那些与参考信号同频、同相的信号 有响应。所以它能大幅度抑制噪声信号,提取出有用信号。一般锁相放大器具有
乘法器真值表

乘法器真值表
乘法器是一种电子数字逻辑电路,它可以将两个二进制数相乘。
乘法器的真值表描述了它的输入和输出之间的关系。
一个简单的4位乘法器的真值表如下所示:
输入A 输入B 输出
0 0 0
0 1 0
1 0 0
1 1 1
在这个真值表中,输入A和B分别表示乘法器的两个输入位。
输出表示乘法器的输出位。
根据真值表,我们可以看出,当A和B都为1时,输出位为1,表示两个数相乘的结果为1。
其它情况下,输出位都为0,表
示两个数相乘的结果为0。
真值表可以进一步扩展为更多位数的乘法器,以实现更复杂的计算。
真值表是设计和分析电子数字逻辑电路的重要工具之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 7 y 6 y 5 y 4 y 3 y 2 y 1 y 0 y -1
booth编码
Y8
Y8 Y8 y 7 y 6 y 5 y 4 y 3 y 2 y 1 y 0 y -1 booth2编码
2016-11-27
Fudan University, Jinmei Lai
乘法实现
归纳为: 1. 部分积产生? 2. 部分积压缩? 3. 将Sum和Carry相加产生最终结果
CMOS Subsystem Design(2)
来金梅
2016-11-27
jmlai
Booth 乘法器
Why booth Multiplier ? 编码方法 拓扑结构
2016-11-27
Fudan University, Jinmei Lai
Basic Mathematics
2016-11-27
Fudan University, Jinmei Lai
提高运算速度
为了进一步提高运算速度,通常采用: 根据0/1结构的特征,对于成串的1,利用 减少部分积的数目。
变长位数移位方式: 充分考虑了乘数中不同长度的“1”串 算法的速度强烈依赖于0/1的结构 难以进行统一时序控制和阵列化设计 固定位数移位方式:booth算法
1.反码运算时,其符号位与数值一起参加运算。 2.反码的符号位相加后,如果有进位出现,则要把它送回到最低 位去相加(循环进位)。 3.用反码运算,其运算结果亦为反码。
2016-11-27
Fudan University, Jinmei Lai
补码
补码可表示为(X为符号数) :
1.补码运算时,其符号位与数值部分一起参加运算。 2.补码的符号位相加后,如果有进位出现,要把这个进位舍去 (自然丢失)。 3.用补码运算,其运算结果亦为补码。
n1
i0even n2
i i y 2 y 2 i i y1 i1odd n3
n2
n3
i0even
y 2 y 2
i i i1odd i i0even i y 2 i i n2 n2
i1
2 yi 2 y1
i1 i1odd n4
n3
2 y(n2)1 2n2
i2even
i i y 2 2 y 2 i1 y1 i1 i0even
i0even
(y
n2
i1
yi 2yi1) 2
2016-11-27
i取偶数 Fudan University, Jinmei Lai
2016-11-27
Fudan University, Jinmei Lai
Booth乘法实现步骤
第一步:根据输入的被乘数与乘数,产生部分积 Booth编码:部分积无减少,但解决了符号位问题 Booth2编码:部分积减少一半,同时解决了符号位问题 Booth4,Booth8,Booth32,Booth64。。。:通过增 加预计算和Booth编码器的复杂度,部分积更少(自学) 第二步:将生成的部分积压缩得到和(Sum)和进位(Carry) 多个部分积进行压缩,需选择合理的并行方案,即选择 合理拓扑结构。 第三步:将Sum和Carry相加产生最终结果
2016-11-27
Fudan University, Jinmei Lai
经典booth算法
X被乘数,Y乘数 PPi= (-Yi+1+ Yi)X
yi+1 yi 0 1 0 1 PPi +0 +X -X +0
y7 y6 y5 y4 y3 y2 y1 y0 y-1
0 0 1 1
Booth算法取数操作
2016-11-27
Fudan University, Jinmei Lai
编码中的符号位处理
第一步正数乘法器情况:假定乘数和被乘数的 符号位是0(正数) 首先讨论:部分积全部为负 其次讨论:部分积可正可负 第二步推广到有符号乘法器:乘数和被乘数的 符号位或是0或是1的情况 部分积可正、可负
Fudan University, Jinmei Lai
2016-11-27
有符号数乘法 又如何呢?
2016-11-27
Fudan University, Jinmei Lai
符号位的处理
机器数
符号数:在数的绝对值前加上正负号,就成了符号 数,例:+1101,-1101 机器数:正号用0表示、负号用1表示,称为机器数。 如“01101”“11101”。 机器数分为:
i
i
i取偶数
部分积的个数为 [(n+1)/2]
Fudan University, Jinmei Lai
PP i (yi1 yi 2yi1)X
Booth2算法
每次交叠检验三位,每个部分积 对应2比特数, 使部分积减少一 半,从而提高了运算速度并降 低了硬件复杂度 2X:左移X一位 -X:取反加 1 -2X:左移X一位,再取反加 1 电路实现时,先对补码形式的n 位乘数Y = yn-1 yn-2 ··· y1 y0扩 充附加位y-1=0 若n是奇数,还需扩充一位附加 符号位yn = yn-1 继续扩充有必要么? Fudan University, Jinmei Lai 2016-11-27
2016-11-27
Fudan University, Jinmei Lai
反码和补码
为了减少设备,解决机器内负数的符号位参加 运算的问题,将减法运算变成加法运算,就引 进了反码和补码这两种机器数。
2016-11-27
Fudan University, Jinmei Lai
反码
反码可表示为(X为符号数) :
Fudan University, Jinmei Lai
Booth 算法:免去特殊操作(减)
X被乘数,Y乘数
XY (Yi Y(i1) )2 X PP i2
i i0 i0
N 1Βιβλιοθήκη N 1i(3-5)
部分积
PP i (Y i Y (i1) ) X
式(3-5)、式(3-12)表达形式是相同的, 无符号数与符号数的乘法就统一起来了 Fudan University, Jinmei Lai 2016-11-27
2016-11-27
Fudan University, Jinmei Lai
Booth 乘法器
Why booth Multiplier ? 编码方法 拓扑结构
2016-11-27
Fudan University, Jinmei Lai
编码方法:如何有效地获得部分积呢?
采用booth编码方法:
2016-11-27
Fudan University, Jinmei Lai
A为符号数
若
A 补 A N 1 2 N 1 A 0 2 0
A (符号数)可表示为:
2016-11-27
Fudan University, Jinmei Lai
Booth 算法:免去特殊操作(减)
2016-11-27
经典booth算法
经典的Booth算法(1951,A.D. Booth )主要是 为了解决有符号运算中复杂的符号修正问题而研 究的 对于补码表示的两数相乘无需进行符号位特殊 操作 经典Booth算法通过每次在乘数中交叠地取两 位(Yi+1, Yi)来产生部分积PPi= (-Yi+1+ Yi)X,X是 被乘数
部分积均为负时成立!
s 1,s ss 011
2016-11-27
Fudan University, Jinmei Lai
编码中的符号位处理
第一步假定:乘数和被乘数的符号位是0(正 数) 首先讨论:部分积为负 其次讨论:部分积可正可负 第二步推广到乘数和被乘数符号位或是0或是1 的情况
G.Bewick,“Fast Multiplication:Algorithms and Implementation”, Ph.D. Dissertation, E.E. Dept. of Stanford Univ., 1994. Fudan University, Jinmei Lai 2016-11-27
表1.1:Booth算法规则
其中:Y-1=0是附加考察位,帮助分析Y0 X是被乘数 Fudan University, Jinmei Lai 2016-11-27
Booth2算法
Y yn1 2 yi 2 y1
n1 i i0 n2
yn1 2n1 yn1 2
2016-11-27
Fudan University, Jinmei Lai
Complete 16 bit Booth 2 multiplication
2016-11-27
Fudan University, Jinmei Lai
编码中的符号位处理
第一步假定:乘数和被乘数的符号位是0(正 数) 首先讨论:部分积为负 其次讨论:部分积可正可负 第二步推广到乘数和被乘数符号位或是0或是1 的情况
2016-11-27
Fudan University, Jinmei Lai
编码中的符号位处理
第一步假定:乘数和被乘数的符号位是0(正 数) 首先讨论:部分积全部为负 其次讨论:部分积可正可负 第二步推广到乘数和被乘数符号位或是0或是1 的情况
2016-11-27
Fudan University, Jinmei Lai
Booth2算法 乘上被乘数得到 X Y
