反三角函数(正课)复习课程
高考复习指导讲义————三角及反三角函数

高考复习指导讲义 第二章 三角、反三角函数一、考纲要求1.理解任意角的概念、弧度的意义,能正确进行弧度和角度的互换。
2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义。
3.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式。
4.能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式的证明。
5.了解正弦函数、余弦函数,正切函数的图像和性质,会用“五点法”画正弦函数,余弦函数和函数y=Asin(wx+ϕ)的简图,理解A 、w 、ϕ的物理意义。
6.会由已知三角函数值求角,并会用符号a r csi n x 、arcco s x 、arcot x 表示。
7.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决三角形的计算问题。
8.理解反三角函数的概念,能由反三角函数的图像得出反三角函数的性质,能运用反三角函数的定义、性质解决一些简单问题。
9.能够熟练地写出最简单的三角方程的解集。
二、知识结构1.角的概念的推广: (1)定义:一条射线O A 由原来的位置OA ,绕着它的端点O 按一定方向旋转到另一位置O B ,就形成了角α。
其中射线O A 叫角α的始边,射线OB 叫角α的终边,O 叫角α的顶点。
(2)正角、零角、负角:由始边的旋转方向而定。
(3)象限角:由角的终边所在位置确定。
第一象限角:2k π<α<2k π+2π,k ∈Z 第二象限角:2k π+2π<α<2k π+π,k ∈Z 第三象限角:2k π+π<α<2k π+23π,k ∈Z第四象限角:2k π+23π<α<2k π+2π,k ∈Z(4)终边相同的角:一般地,所有与α角终边相同的角,连同α角在内(而且只有这样的角),可以表示为k ²360°+α,k ∈Z 。
7.15反三角函数教案
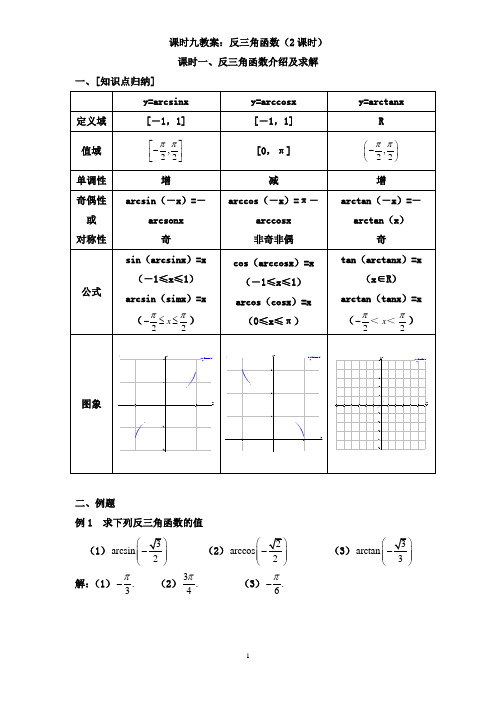
课时九教案:反三角函数(2课时) 课时一、反三角函数介绍及求解一、[知识点归纳]y=arcsinx y=arccosx y=arctanx定义域 [-1,1][-1,1] R值域 ,22ππ⎡⎤-⎢⎥⎣⎦[0,π] ,22ππ⎛⎫- ⎪⎝⎭单调性 增减增奇偶性或 对称性arcsin (-x )=-arcsonx 奇arccos (-x )=π-arccosx 非奇非偶 arctan (-x )=-arctan (x )奇公式sin (arcsinx )=x (-1≤x ≤1)arcsin (simx )=x(22x ππ-≤≤)cos (arccosx )=x (-1≤x ≤1) arcos (cosx )=x (0≤x ≤π)tan (arctanx )=x(x ∈R ) arctan (tanx )=x(<<22x ππ-)图象1-112-1-2xy y = ar csi n(x)1-1123xyy = ar ccos(x)123456-1-2-3-4-5-612345-1-2-3-4-5xyy = ar ct an(x)二、例题例1 求下列反三角函数的值(1)3arcsin 2⎛⎫- ⎪ ⎪⎝⎭ (2)2arccos 2⎛⎫- ⎪ ⎪⎝⎭ (3)3arctan 3⎛⎫- ⎪ ⎪⎝⎭解:(1).3π- (2)3.4π (3).6π-例2 用反三角函数表示下列各式中得x(1)3cos ,[0,]4x x π=-∈(2)2sin ,[,]522x x ππ=-∈- (3)3tan ,,222x x ππ⎛⎫=-∈- ⎪⎝⎭(4)13sin [,]322x x ππ=∈(5)1cos ,[,2]3x x ππ=-∈解:(1)33arccos arccos .44x π⎛⎫=-=- ⎪⎝⎭(2)2arcsin.5x = (3)33arctan arctan .22x ⎛⎫=-=- ⎪ ⎪⎝⎭ (4)1arcsin .3x π=-(5)1arccos .3x π=+例3 化简下列各式(1)arcsin(sin10) (2)arctan(tan10) 解:(1)sin10sin(310)π=- ,且有310[,].22πππ-∈-arcsin(sin10)arcsin[sin(310)]310.ππ∴=-=-(2)tan10tan(103)π=- ,且有103,.22πππ⎛⎫-∈- ⎪⎝⎭arctan(tan10)arctan[tan(103)]103.ππ∴=-=-例4 求函数2()lg arccos 84x x f x ⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦的定义域与值域解:2arccos 0.84x x ⎛⎫+> ⎪⎝⎭ 21 1.84x x∴-≤+<解上述不等式,得4 2.x -<<2()lg arccos 84x x f x ⎡⎤⎛⎫∴=+⎢⎥ ⎪⎝⎭⎣⎦的定义域为(4,2).-22211111(21)(1)8488888x x x x x +=++-=+-≥-210arccos arccos .848x x ⎛⎫⎛⎫∴<+≤- ⎪ ⎪⎝⎭⎝⎭所以函数2()lg arccos 84x x f x ⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦的值域为1(,lg arccos ].8⎛⎫-∞- ⎪⎝⎭例5 判断下列函数的奇偶性 (1)sin(arctan ),y x x R =∈ (2)arccos ,[1,1]2y x x π=-∈-(3)arccos(cos ),y x x R =∈解:(1)sin[arctan()]sin(arctan )sin(arctan ).x x x -=-=- 所以sin(arctan )y x =是奇函数。
上海市高三数学反余弦函数和反正切函数复习课件沪教

称为反正弦函数 3 .反正弦函数
y arcsin x(1 x 1) 有哪些性质?
, 2 2
答:①定义域是[-1,1] ②值域是
③它是奇函数
④它在[-1,1]上是增函数 4.反正弦有哪两个重要公式?
答:
sin(arcsinx) x
x [1,1]
x [1,1]
0 arccos(2 x 5) 1 0 arccos(2 x 5) 4 4
1 arccos(2 x 5) 0 4 4 4
1 arccos( ) (2)根据单调性比较大小 2
>
1 arccos( ) 3
解: y arccosx, x [1,1] 是减函数
cos 3
(3) arccos 0
(4) arccos 1
4 cos 4 0 1
2
0
arccos 0 arccos 1 02
课堂练习一
求下列反三角函数值 (1) arccos( (2) (3)
arccos
答案
3 ) 2
2 2
3 3 (1) arccos( ) arccos 2 2 5 6 6
x [1,1]
x [1,1]
cos(arccosx) x
x [1,1]
arccos( x) arccosx, x [1,1]
例1
1 (1)函数 y arccos( 2 x 5) 4 4
[2,3]
的定义域是 值域是
[
4
,0]
解: 1 2 x 5 1 2 x 3
第五章 反三角函数与简单的三角方程第一节 反三角函数

由例7可知,等式
cos
6
3 2
6
arccos
3 2
所以
cos arccos
3 2
23.
一般地,如果x-1,1,那么 cosarccos x x
(53)
例8 求下列各式的值.
(1) cosarccos1;
(2)
cos
arccos
-
1 2
.
解 (1)因为1-1,1,根据公式(53),所以cosarccos1 1;
arctanx arctan x
arccotx arccot x
(57) (58)
例13 求下列各式的值. (1) arctan 33; (2) arccot0; (3) arctan(-1); (4) arccot(- 3).
解
(1)
因为tan6
3 3
,且6
2
,2
,所以arctan
3 3
6
;
(2) 因为cot 0,且 (0, ),所以arccot0 ;
22
2
(3) 根据公式(5-7),可知:arctan-1 arctan14;
(4)
根据公式(5-8),可知:arccot
-
3
=
-arccot
3 6 56.
例14 求下列各式的值.
(1)
arctan
tan
4
;
(2)
arctan
正切函数y=
tan
x在
-
2
,2
上的反函数称为反正切
函数,记作x=arctan y(或x=tan-1 y),如图5-6所示.
y
2
y arctan x
高三数学一轮复习:反三角函数(教案)

第一课时反三角函数(教案)【复习目标】【知识与技能】1.理解反三角函数的定义,掌握反三角函数的图像及性质.2.能正确使用反三角函数的符号表示一个角的大小,会根据有关反三角函数的恒等式进行一些简单的变形.3.能够运用反三角函数的图像及性质解决一些简单的数学问题.【过程与方法】通过原函数与反函数的关系,以及三角函数的图像与性质,记忆反三角函数的图像与性质,体会概念之间的联系与区别,强化数形结合的思想方法.【情感态度与价值观】通过原有知识与新知识的联系,体验数学知识体系的形成过程,提升逻辑思维能力.【教学重点.难点】对反三角函数的定义的理解,用反三角函数的记号表示一个角,反三角函数的图像及性质【教学过程】【基础练习】1. 若x x ∈-∈[,]arcsin 10则,02π⎡⎤-⎢⎥若x x ∈-[,)arccos 112则 若x ∈-[,)13,则2.arcsin arccos ,x x x >时3.设a a ≤+1,arccos 则4.函数y x =1arcsin 5 A .4)1arctan(π-=- C. 53)]53(sin[arcsin -=-D.2)2cot cot(=arc 6. 若23,41sin ππ<<-=x x ,则x 的值( C ) A.)41arcsin(- B.)41arcsin(-+πC.)41arcsin(--πD.)41arcsin(2-+π7.)45arcsin(cos π的值( A ) A.4π- B.43π C.4π D.43π8.计算:11sin(arccos )28=49.函数arccos(2)y x =-的图像为C ,函数()f x 的图像与C 关于原点对称,则()f x 的解析式arccos(2)y x π=+-10.等式arccos(cos )x x =成立的充要条件是x ∈[0,]π 【典型例题】【例1】若1cos 3α=-,求满足下列条件的α的值 (1)3(,0);(2)(,)2παπαπ∈-∈ 解:函数cos y x =与直线13y =-位于cos y x =主值区间[]0,π内的交点A 的横坐标为1arccos(),3-则位于区间(,0)π-的交点B 和位于区间3(,)2ππ的交点C 分别与点A 关于y 轴和直线x π=对称,(,0)απ∴∈-,则11arccos()arccos 33απ=--=-;当311(,),2arccos()arccos 233παπαππ∈=--=+ 减【例3】求满足下列条件的x 的范围21(1)arcsin (2)arccos arccos 3x x x >->解:(1)根据反三角函数图象,11sin()sin 33-=-,且反正弦函数在[1,1]-单调递增,11arcsin (sin ,1]33x x >-⇒∈- (2)原不等式等价于22111110x x x x x -≤≤⎧⎪-≤≤⇒-≤<⎨⎪<⎩注意反函数的定义域及函数在定义域上单调性【例4】求函数arcsin arctan y x x =+的定义域及值域.解:定义域[1,1]x ∈-;函数arcsin arctan y x y x ==在[1,1]-单调递增值域为33,44ππ⎡⎤-⎢⎥⎣⎦ 【变式】求函数2arcsin()y x x =-定义域、值域、单调区间.解:函数定义域1122⎡+⎢⎣⎦,值域1[arcsin ,]42π-,1122⎡⎤⎢⎥⎣⎦递减,11,22⎡+⎢⎣⎦递增. 【例5】 求函数 tan 2xy arc π=+的反函数.解:arctan ,tan()tan ,22x xy y y ππ=-∴=-=故2tan 2tan x y y x =⇒=所以,反函数为:32tan ,(,)22y x x ππ=∈ 求反函数的步骤:①用y 表示②,x y 互换③求出反函数的定义域,即原函数的值域.【例6】求1sin(2arctan )4的值.解:设11arctan,tan ,(0,)sin 4428sin 22sin cos 17παααααααα==∈⇒====【例7】已知7c o s 2,0,252παα⎛⎫=∈ ⎪⎝⎭, 5sin 13β=-,3,2πβπ⎛⎫∈ ⎪⎝⎭,求αβ+(用反三角函数表示).解:由题设得sin α==53,从而cos α=54,且cos β=1213-又αβ+∈ (,2)ππ, αβπ+-(0,)π∈33cos()cos cos sin sin 65αβαβαβ+=-=-. ∴33cos()cos(())65αβππαβ+-=-+=. ∴παβ-++=33arccos 65,即αβ+=33arccos 65π+ 【备用例题】1.解不等式2(arctan )3arctan 20x x -+>.解:(arctan 2)(arctan 1)0x x -->∴arctan 1x <或arctan 2x >.又-2π<arctan x <2π. ∴2π-<arctan x <1,即有x <tan12.满足arccos(1)arccos x x -≥的x 的取值范围是( D )A. 11,2⎡⎤--⎢⎥⎣⎦ B. 1,02⎡⎤-⎢⎥⎣⎦C. 10,2⎡⎤⎢⎥⎣⎦D. 1,12⎡⎤⎢⎥⎣⎦解:反余弦函数的定义域为[]1,1-,且为减函数.-1≤1x -≤1 ∴ -1≤x ≤1 ⇒21≤x ≤1 1x -≤x【巩固练习】1.函数sin y x =,35,22x ππ⎡⎤∈⎢⎥⎣⎦的反函数是(D ) A. ()11arcsin ≤≤-=x x y B. ()11arcsin ≤≤-+=x x y π C. ()11arcsin 2≤≤--=x x y π D. ()11arcsin 2≤≤-+=x x y π 2.下例各式中错误的是(A )A.2>B.arccos arccos 22⎛⎫-> ⎪ ⎪⎝⎭C.(arctan arctan 2⎛-> ⎝⎭D.arctan 2<3.直线)0,0(<<=+b a ab ay bx 的倾斜角为(C )A.arctan()b -B.tan()aarc -C.tan barc a π-D.tan aarc bπ-4.函数()2arcsin -=x y 的值域是,22ππ⎡⎤-⎢⎥⎣⎦,定义域是[1,3];5.函数1arctan y x =的定义域是(,0)(0,)-∞+∞ ,值域是,0(0,)22ππ⎛⎫- ⎪⎝⎭6.函数11arcsin +-=x x y 的反函数是1sin ,,1sin 22x y x x ππ+⎡⎫=∈-⎪⎢-⎣⎭; 7.若()5arctan 2f x ax b x =+⋅+,若()102=f 则()=-2f 6- 8.求下列函数的定义域和值域:⑴()423arcsin 2π+-=x y 参考解答:定义域1,13⎡⎤⎢⎥⎣⎦,值域为35,44A ππ⎡⎤=-⎢⎥⎣⎦ ⑵()arctan sin 3y x π=-参考解答:定义域为R ,值域为7,1212ππ⎡⎤⎢⎥⎣⎦ 9.已知函数)41arcsin()(2-=x x f , (1)求)(x f 的定义域; (2)求)(x f 的值域;(3)设)(x f 的最大值为α,最小值为β,求)sin(βα-的值. 解:(1)定义域⎡⎢⎣⎦;(2)值域:1arcsin ,42π⎡⎤-⎢⎥⎣⎦; (3)11sin(arcsin )cos(arcsin )2444π-== 10.函数()()x x x f -=2arccos ,求函数定义域,值域和单调区间,解关于a 不等式()⎪⎭⎫ ⎝⎛+<212a f a f .解:函数定义域1122⎡+⎢⎣⎦,值域10,arccos 4π⎡⎤-⎢⎥⎣⎦,在1122⎡⎤⎢⎥⎣⎦递增.11,22⎡⎢⎣⎦递减()11122221112(,)226122a a f a f a a a ⎧⎧->+-⎨⎪⎩⎛⎫<+⇒<<⇒- ⎪⎝⎭<+<⎪⎩11.若12,x x 是方程2670x x ++=的两根,求12arctan arctan x x +的值. 解:34π-。
《反三角函数》 讲义

《反三角函数》讲义在数学的广阔天地中,三角函数无疑是一颗璀璨的明星。
而反三角函数,则是这颗明星的另一面,为我们解决众多数学问题提供了独特的视角和强大的工具。
一、什么是反三角函数我们先从熟悉的三角函数说起。
正弦函数、余弦函数、正切函数等,它们将角度作为输入,给出对应的函数值。
而反三角函数,则是反过来,已知三角函数的值,求对应的角度。
例如,正弦函数 sin x,当我们知道 sin x = 05 时,想知道 x 是多少度,这就需要用到反正弦函数 arcsin 05 来求解。
反三角函数包括反正弦函数(arcsin)、反余弦函数(arccos)、反正切函数(arctan)等。
二、反三角函数的定义域和值域要深入理解反三角函数,必须清楚它们的定义域和值域。
反正弦函数 arcsin x 的定义域是-1, 1,值域是π/2, π/2。
这意味着输入的 x 值必须在-1 到 1 之间,得到的角度值在π/2 到π/2 之间。
反余弦函数 arccos x 的定义域也是-1, 1,值域是0, π。
反正切函数arctan x 的定义域是R(全体实数),值域是(π/2, π/2)。
三、反三角函数的图像图像是直观理解函数性质的重要工具。
反正弦函数 arcsin x 的图像是一段在π/2, π/2之间的曲线,它关于原点对称,且在定义域内单调递增。
反余弦函数 arccos x 的图像则是在0, π之间的曲线,同样关于原点对称,在定义域内单调递减。
反正切函数arctan x 的图像是一条在(π/2, π/2)之间无限延伸的曲线,它的斜率逐渐趋近于 0,并且在定义域内单调递增。
四、反三角函数的基本性质1、对称性反正弦函数和反余弦函数互为相反数,即 arcsin(x) = arcsin x ,arccos(x) =π arccos x 。
2、恒等式例如,sin(arcsin x) = x (x∈-1, 1),cos(arccos x) = x (x∈-1, 1)。
反三角函数大全

反三角函数Inverse trigonometric functions第1节反三角函数·概述原创/O客把反正弦函数y=arc sinx,反余弦函数y=arc cosx,反正切函数y=arc tanx,反余切函数y=arc cotx统称为反三角函数。
它们都是三角函数的反函数。
严格地说,准确地说,它们是三角函数在某个单调区间上的反函数。
以反正弦函数为例,其他反三角函数同理可推。
●反正弦的值域先从反正弦函数的原函数正弦函数说起。
正弦函数y=sinx在定义域R上没有反函数。
因为它在定义域R上不单调,是分段单调。
从逆向映射来看,正弦函数y=sinx的每一个函数值y,对应着无数个自变量x的值。
当我们从y=sinx中解出x后,x与y不能构成函数关系,所以不存在反函数。
但是,当我们取正弦函数y=sinx的一个单调区间,如[-π/2,π/2]。
这时,每一个函数值y,对应着唯一的一个自变量x的值。
当我们从y=sinx中解出 x后,x与y构成函数关系,所以存在反函数。
记为y=arc sinx。
把原函数y=sinx,x∈[-π/2,π/2]的值域[-1,1],叫做反函数y=arc sinx的定义域。
并把原函数y=sinx,x∈[-π/2,π/2]的定义域[-π/2,π/2],叫做反函数y=arc sinx的值域。
●请参考我的三角函数salon第2节反三角函数·理解与转化原创/O客以反正弦函数为例,其他反三角函数同理可推。
●符号理解初学反三角函数者往往被它那长长的字符串所迷惑,很不习惯。
一方面,arc sinx这七个字母是一个整体,缺一不可。
另一方面,符号arc sinx 可以用下面的三句话来理解:①它是一个角。
即一个实数。
arc sinx ∈R .②这个角在-π/2到π/2之间(含端点)。
-π/2≤arc sinx ≤π/2。
③这个角的正弦值等于x 。
sin(arc sinx)=x.●互化反三角函数问题往往要转化为三角函数问题,因为后者拥有数十个公式资源,使你解决问题时如虎添翼。
精品课件-反三角函数

需要考 虑正弦
函数
y=sinx 的反函
数?
复习反函数的概念:
一般地,对于函数y=f(x).设它的定义域为D, 值域为A.如果对A中的任意一个值y,在D中总
有唯一确定的x值与它对应,满足y=f(x),这样得 到的x关于y的函数叫做y=f(x)的反函数. 提问:怎样的函数存在反函数?
答:自变量与因变量是一一对应的函数存在反函数.
2
yarcx, sxi n [ 1 , 1] 1
定义域
-1, 1
o1
x
值域
2
,
2
- 2
单调性 在[1, 1]上单调递增 x 0时,
奇偶性
奇函数
arcsinx是一个锐角;
分段
x0, 1时, y0,
2
x 0时,
x1, 0时, y, 0 arcsinx是一个负角. 2
重要 2 : ar 等 c x ) s a i式 n rx , c (x s [ 1 i, 1 ] n
例1:判断下列各式是否正确?并简 述理由。
(1)arcsin 3
23
(2)arcsin 3
32
对
错
1 3
(3)arcsin12k(kZ) 错
2
(4)arcsin()arcsin
反三角函数
引入课题:(一)1、追溯历史 提出问题
引入课题:
测量实际计算中的两类相反问题:
一类是已知角值求比值
例如:在正弦函数 y =sinx中
x,
6
yx s i6n612;
x2,ysin2
一类是已知比值求角值
例如sin x 1 , 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x3
-arccosa -2 arccosa
2π-arccosa 2π+arccosa
下页 上页 主页
例1:判断下列各式是否正确?并简 述理由。
(1)arccos 1
对
23
(2)arccos 1
32
错 1
3
(3)arccos02k(kZ) 错
2
(4)arccos()arccos
3
3
错
1 3
下页 上页 主页
3、熟记特殊值的反正弦函数值
(1) arccos1 __0 ____(2) arccos(1) ______
(3)
arccos
0
___2 ___(4)
arccos
1 2
__3____
2
(5) arccos( 1 ) __3 ____(6) arccos 2
2 2
__4 ______
反三角函数
下页 上页 主页
(1)什么样的函数有反函数?
一一对应函数有反函数
(2)互为反函数图象之间有什么关系
关于直线y=x对称
(3)正弦函数y=sinx ,余弦函数y=cosx, 正切函数y=tanx在定义域上有反函数吗?
(4)正弦函数y=s没inx有在,因[ 为他, 不 ]是一上一有对反应函函数数吗? 22
(13) a、rc熟sin记1 特_殊_2 __值__的(2反) a正rcs弦in(函1数) 值__ _2___
(3)
arcsin
0
__0 ____(4) arcsin
1 2
___6 ___
(5)
arcsin(
1
)
___6 ___(6)
arcsin
2
2 2
__4 ______
(7) arcsin(
的图象与性质:
(1)定义域:[-1,1]。
(2)值域:
[ , ] 22
y
-3
(3)单调性: 是增函数。
yarcsinx,x [ 1 ,1 ],y [, ]
2
22
1.5
2 -1
-2
-1
21
0.5
o
-0.5
ysinx,x [,],y [1,1]
22
1
2
12
x3
-1
-1.5
y x -2
2
下页
上页
主页
(7) arccos(
2 2
)
3
__4 ______(8)
arccos
3 2
_6_____
(9) arccos(
3 2
)
5
__6 ______
下页 上页 主页
4、已知三角函数值求角
只有余弦函数主值区 间[0,π]上的角才能 用反余弦表示
2
ycox,x s [0,]
a
F
πLeabharlann -2x x OE1
1
2
x2
2 2
)
_ __4 _____(8)
arcsin
3 2
__3 ____
(9) arcsin(
3 2
)
___3 _____
下页 上页 主页
只有正弦4、函数已主知值三区角间函数[ 值求, 角 ] 上的角才能用
反正弦表示
22
2
a
F
x4
x3
-2 2
O
E1
x=?
2x1
2
x2
ysinx,x[,]
22
-2
22
叫反正切函数,记作 xarctany (本义反函数)
习惯记作 yarctanx(矫正反函数)
xR, y( ,)
22 若 x a R ,有 y a rc ta n a ,
这里的“ arctana ”是一个角的符号.
下页 上页 主页
理解和掌握 arctana(aR) 符号
(1)、arctana 表示一个角
22
2、反余弦函数y=arccosx,x∈[-1,1]的图 象与性质
(1)定义域: [-1,1]。
(2)值域: [0,π]。
y
5 y=arccosx,x∈[-1,1]
4.5
4 y∈[0,π]
3.5 3
2.5
2
1.5
1
(3)单调性:
0.5
π
-4
-3
-2
-1
-1
o-0.5
11
2
3
x4
是减函数。
-1
yx
y=cosx,x∈[0,π] y∈[-1,1]
若 x a [ 1 ,1 ],有 y a rc s in a ,
这里的“arcsina ”是一个角的符号.
下页 上页 主页
理解和掌握 arcsina(a 1) 符号
(1)、arcsin a 表示一个角
(2)、这个角的范围是
2
,
2
即arcsina2,2.
下页 上页 主页
2、反正弦函数y=arcsinx,x∈[-1,1]
正弦函数 ytanx(xk,kz) 有反函数吗?
2
没有,因为他不是一一对应函数,同一个三角函数值会对应
许多角。
2
2
正弦函数 ytanx,x(,) 有反函数吗?
22
有,因为它是一一对应函数,
同一个三角函数值只对应一个角。
下页 上页 主页
三、反正切函数
1、定义:正切函数 ytanx(x(,)的反函数
arcsina
下页 上页 主页
例1:判断下列各式是否正确?并简 述理由。
(1)arcsin 3
对
23
(2)arcsin
3
32
错 1
3
(3)arcsin12k(kZ) 错
2
(4)arcsin( )arcsin
3
3
错
1 3
余弦函数 ycosx(xR)有反函数吗?
没有,因为他不是一一对应函数,同一个三角函数值会对应
(2)、这个角的范围是 ( , ) 22
即arctana(,).
22
下页 上页 主页
2、反正切函数 y=arctanx,x∈R的图象与性质
(1)定义域R
(2)值域: ( , )
22
(3)单调性:
是增函数
-4
-3
-2
-1
2
yarcx,txa R n,y (,)
22
yx
y tanx,x( ,)
许多角。
y
1
· · -2
-
o
· · · ·x
2 3
4
-1
余弦函数 ycosx(x[0,])有反函数吗?
有,因为它是一一对应函数,
同一个三角函数值只对应一个角。
下页 上页 主页
二、反余弦函数
1、定义:余弦函数 ycosx(x[0,]) 的反函数
叫反余弦函数,记作 xarccosy (本义反函数)
习惯记作yarccosx(矫正反函数)
余弦函数y=cosx在[0,π] 上有反函数吗? 正切函数y=tanx在 ( , ) 上有反函数吗?
22
下页 上页 主页
下页 上页 主页
一、反正弦函数
1、定义:正弦函数ysinx(x[,]) 的反函数
22
叫反正弦函数,记作 xarcsiny
习惯记作 yarcsinx
x[1,1],y[ , ] 22
x[1,1],y[0,]
若 x a [ 1 ,1 ] ,有 y a r c c o s a ,
这里的“ arccos a ”是一个角的符号.
下页 上页 主页
理解和掌握 arccos(a 1) 符号
(1)、arccosa表示一个角
(2)、这个角的范围是 0 ,
即arccos0,.
下页 上页 主页
