人教版八年级上册数学《多边形的内角和》三角形精品PPT教学课件
合集下载
人教版八年级数学上册《多边形及其内角和》PPT

多边形的外角和
如果广场的形状是六边形、八 边形,那么还有类似的结论吗?
多边形 内角的一边与另一边的反 向延长线所组成的角叫做这个多边 形的外角。
多边形的外角和等于360°
在每个顶点处取这个多边形的一个 外角,它们的和叫做这个多边形的 外角和。
An A1
A8 A7
A2
A6
A3
A5
A4
n 180 (n 2) 180
A
180°×4 - 360°= 360°
A 如图2,在四边形的一边上任取一点P,连
接PB、PC,将四边形变成有一个公共顶 P 点的三个三角形,四边形内角和等于
D 180° ×3- 180° = 360°
A
P
如图3,在四边形外任取一点P,连接PA、 PB、PC、PD将四边形变成有一个公共顶
D 点的四个三角形,四边形内角和等于180° ×3- 180° = 360°
课后思考
1、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角, 求得的内角和1680° ,你能否求得正确结果呢?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截 去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变
B、增加 180°
C、减少 180° D、无法确定
三角形 A
B 1800
四边形
五边形
A A
D E
B
CB
CC
D
2× 180°
3× 180°
= 3600
=5400
那么六边形、七边形的内角和呢?
六边形
七边形
4× 180° =7200
5× 180° =9000
学一学
四边形的内角和 (4-2)× 180° = 360° 五边形的内角和 (5-2)× 180°=540° 六边形的内角和(6-2)× 180°=720°
初中数学人教版八年级上册11.3.2多边形的内角和 教学课件(共23张PPT)

=360°-180°=180°.
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做 六边形的外角和.六边形的外角和等于多少? 问题1:任意一个外角和它相邻的内角有什么关系?
互补 问题2:六边形的6个外角加上与它们 相邻的内角,所得总和是多少?
解得:n=10,∴ 这个多边形的边数是10. 故答案为:10.
练习6(1)根据图中的相关数据,求出x 的值:
(2)一个多边形内角和的度数比外角和的度数的4倍多180度, 求多边形的边数.
解:(1)(x+9)°+115°+90°+x°=(4-2)×180°, 解得:x=73.
(2)设多边形的边数为n, ∵多边形的外角和是360°,内角和的度数比外角和的度数的4倍多180度, ∴可得方程(n-2)180°=4×360°+180° 解得n=11,
练习4一个多边形的内角和是外角和的2倍,则这个多边形是(C )
A.四边形
B.五边形
C.六边形
D.八边形
解析:设所求正n 边形边数为n ,由题意得 (n-2) ·180°=360°×2 解得n=6. 则这个多边形是六边形.故选C.
练习5一个多边形的内角和是其外角和的4倍,则这个 多边形的边数是10 . 解析:设这个多边形的边数为n, 则该多边形的内角和 为(n-2)×180°,依题意得:(n-2)×180°=360°×4,
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫 做
六边形的外角和.六边形的外角和等于多少? 问 题 3 :上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和 因此六边形的外角和
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做 六边形的外角和.六边形的外角和等于多少? 问题1:任意一个外角和它相邻的内角有什么关系?
互补 问题2:六边形的6个外角加上与它们 相邻的内角,所得总和是多少?
解得:n=10,∴ 这个多边形的边数是10. 故答案为:10.
练习6(1)根据图中的相关数据,求出x 的值:
(2)一个多边形内角和的度数比外角和的度数的4倍多180度, 求多边形的边数.
解:(1)(x+9)°+115°+90°+x°=(4-2)×180°, 解得:x=73.
(2)设多边形的边数为n, ∵多边形的外角和是360°,内角和的度数比外角和的度数的4倍多180度, ∴可得方程(n-2)180°=4×360°+180° 解得n=11,
练习4一个多边形的内角和是外角和的2倍,则这个多边形是(C )
A.四边形
B.五边形
C.六边形
D.八边形
解析:设所求正n 边形边数为n ,由题意得 (n-2) ·180°=360°×2 解得n=6. 则这个多边形是六边形.故选C.
练习5一个多边形的内角和是其外角和的4倍,则这个 多边形的边数是10 . 解析:设这个多边形的边数为n, 则该多边形的内角和 为(n-2)×180°,依题意得:(n-2)×180°=360°×4,
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫 做
六边形的外角和.六边形的外角和等于多少? 问 题 3 :上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和 因此六边形的外角和
人教版八年级上册第十一章三角形113多边形的内角和课件共18张

? ? B ? ? D ? 3600 ? (? A ? ? C)
即:
? 1800
四边形的一组对角互补,另一组对角也互补
;
(3)从中任取三种来组合,能铺满地面的正多边形组合是:
.
自我总结
收获?
作业:P27 4、5
应用新知
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
D A
B
解:如图,在四边形ABCD 中,
? A ? ? C ? 180 0
?? A? ? B ? ? C ? ? D
C
? ( 4 ? 2 ) ? 180 0 ? 360 0
第十一章 三角形 11.3 多边形的内角和
C目 录 ONTENTS
多边形的内角和
学习目标和重难点 回顾旧知 探索新知 应用新知 拓广探索 自我小结 课后作业
多边形内角和
学习目标
01 掌握多边形的 内角和公式 . 02 通过把多边形转化为三角形
体会转化思想在几何中的运用 体会从特殊到一般的认识问题的方法.
(n≥3 且n为整数)
应用新知
1 八边形内角和是 1080 度
十边形内角和是 1440 度
01
2
一个多边形内角和等 于 1800 °,则它的边
数为 12 。
06
3 一个六边形每个内角
都相等,则每个内角 05
度数为 120° 。
04
4
一个多边形的边数增 加1时,它的内角和增
加 180° 据①与②的求解过程,请你猜想∠1+∠2与∠A的关系 是__∠_1_+∠_2= 180°+ ∠A _;
剪去两个角?
剪去三个角?
应用新知 现有一批边长相等的正多边形瓷砖 (如图所示),设计能铺满地面的瓷砖图案.
人教版八年级数学上册课件 11.3.2 多边形的内角和(共20张PPT)

2、通过探索多边形的内角和公式,我们尝试了从不 同的角度寻求解决问题的方法,并且能有效地解 决问题。
3、我们还学会了运用多边形内角和公式进行相关计 算。
作业 这节课我们学习到这里,再见!
2、我们也可以利用下列不同的方法分割多
边形,得到n边形的内角和公式
An
A1
A5
A4
An
p
A1
A5
A4
A2 An
A3
A5
A2
An
A3
A5
A4
A1
A2
p
A3
A1
A2 p
A4 A3
例题讲解
例1:如果一个四边形的一组对角互补,那么另一组 对角有什么关系?
例题讲解
例2:如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和.六边形的外角
和等于多少?
E
4D
5
F
3
6
C
2
A1 B
结论:多边形外角和等于3600 .
巩固练习1
(抢答) 8边形的内角和等于多少度? 十边形呢?
(8-2) × 180°= 1080° (10-2) × 180°= 1440°
巩固练习2
求下列图形中x的值:
1400
x0
计算得到,而是按照如图所
示,利用辅助线将四边形分
割成两个三角形的方法,利
用三角形内角和等于180°,
得到四边形内角和等于360°。
你能说明它的合理性吗?并
且启发你能否借助辅助线找
到不同的分割方法呢?
B
C 图1
P
A
D
如图1,在四边形内任 取一点P,连接PA、PB、 PC、PD将四边形变成 有一个公共顶点的四 个三角形,四边形内 角和等于180°×4 - 360°= 360°
3、我们还学会了运用多边形内角和公式进行相关计 算。
作业 这节课我们学习到这里,再见!
2、我们也可以利用下列不同的方法分割多
边形,得到n边形的内角和公式
An
A1
A5
A4
An
p
A1
A5
A4
A2 An
A3
A5
A2
An
A3
A5
A4
A1
A2
p
A3
A1
A2 p
A4 A3
例题讲解
例1:如果一个四边形的一组对角互补,那么另一组 对角有什么关系?
例题讲解
例2:如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和.六边形的外角
和等于多少?
E
4D
5
F
3
6
C
2
A1 B
结论:多边形外角和等于3600 .
巩固练习1
(抢答) 8边形的内角和等于多少度? 十边形呢?
(8-2) × 180°= 1080° (10-2) × 180°= 1440°
巩固练习2
求下列图形中x的值:
1400
x0
计算得到,而是按照如图所
示,利用辅助线将四边形分
割成两个三角形的方法,利
用三角形内角和等于180°,
得到四边形内角和等于360°。
你能说明它的合理性吗?并
且启发你能否借助辅助线找
到不同的分割方法呢?
B
C 图1
P
A
D
如图1,在四边形内任 取一点P,连接PA、PB、 PC、PD将四边形变成 有一个公共顶点的四 个三角形,四边形内 角和等于180°×4 - 360°= 360°
(人教版)八年级数学上册:11.3.2《多边形内角和》ppt课件

11.3.2多边形的内角和
第1页,共18页。
回顾
1.三角形的内角和是多少?
三角形的内角和是180°
2.n边形从一个顶点出发的对角线有 (__n-__3)_条?它们将n边形分成 (n-2个) 三 角形?
3.你知道长方形和正方形的内角和是多 少?其它四边形的内角和是多少?
第2页,共18页。
任意一个四边形的内角和也是360 °吗?
(n≥3且为正整数)
第9页,共18页。
例1:一个多边形的内角和为1080°, 它是几边形? 解:设这个多边形的边数为n 则(n-2)•180°= 1080° 解得 n = 8
所以这个多边形是八边形。
第10页,共18页。
应用知识解决问题(1)
1、七边形的内角和等于 900 度;
一个n边形的内角和为1800º,则n= 12。 2、从多边形一个顶点出发可引7条对角线, 则这个n边形的内角和为( D ) A、1620º B、1800º C、900º D、1440º 3、一个多边形边数每增加1条时,其内角和 增加( A ) A、180º B、360º C、不变 D、不能确定
4
5
6… n
图形
以多边形任一边 上的一点为起点与各 顶点的连线的条数
上面的连线将多 边形分成的三角形个 数
多边形的内角和
…
2
3
4 … n-2
3
4
5 … n-1
360° 540° 720°…(n-1)·180°-180°
n 边形的内角和为:(n-1)·180°-180 °
第7页,共18页。
探索多边形的内角和
第11页,共18页。
例2: 如图,在五边形的每个顶点处各取 一个外角,这些外角的和叫做五边形的 外角和,五边形的外角和等于多少?
第1页,共18页。
回顾
1.三角形的内角和是多少?
三角形的内角和是180°
2.n边形从一个顶点出发的对角线有 (__n-__3)_条?它们将n边形分成 (n-2个) 三 角形?
3.你知道长方形和正方形的内角和是多 少?其它四边形的内角和是多少?
第2页,共18页。
任意一个四边形的内角和也是360 °吗?
(n≥3且为正整数)
第9页,共18页。
例1:一个多边形的内角和为1080°, 它是几边形? 解:设这个多边形的边数为n 则(n-2)•180°= 1080° 解得 n = 8
所以这个多边形是八边形。
第10页,共18页。
应用知识解决问题(1)
1、七边形的内角和等于 900 度;
一个n边形的内角和为1800º,则n= 12。 2、从多边形一个顶点出发可引7条对角线, 则这个n边形的内角和为( D ) A、1620º B、1800º C、900º D、1440º 3、一个多边形边数每增加1条时,其内角和 增加( A ) A、180º B、360º C、不变 D、不能确定
4
5
6… n
图形
以多边形任一边 上的一点为起点与各 顶点的连线的条数
上面的连线将多 边形分成的三角形个 数
多边形的内角和
…
2
3
4 … n-2
3
4
5 … n-1
360° 540° 720°…(n-1)·180°-180°
n 边形的内角和为:(n-1)·180°-180 °
第7页,共18页。
探索多边形的内角和
第11页,共18页。
例2: 如图,在五边形的每个顶点处各取 一个外角,这些外角的和叫做五边形的 外角和,五边形的外角和等于多少?
人教版八年级数学上册 11.3.2 多边形的内角和 课件(共29张PPT)
5
知识点一:多边形的内角和
新知探究
四边形内角和
D
4
C
如图,在四边形ABCD中,连接 对角线AC,则四边形ABCD被分为
△ABC和△ACD两个三角形.
2
A
1
3 B
你能推出五
由此可得:∠DAB+∠B+∠BCD+∠D
边形和六边形
=∠1+∠2+∠B+∠3+∠4+∠D 的内角和吗?
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
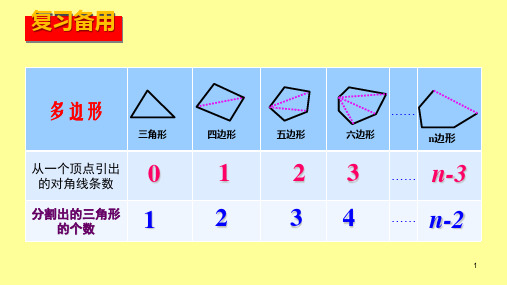
复习备用
多边形
三角形
四边形
五边形
……
六边形
n边形
从一个顶点引出 的对角线条数
0
1
2 3 …… n-3
1 分割出的三角形 的个数
2
3 4 …… n-2
1
激情引入
1.看完这些图案你能抽象出哪些几何图形? 2.生活中有如此多的几何图形,你对它们了 解多少?
我们知道三角形的内角和是180度,正方 形、长方形的内角和是360度,那么四边形、 五边形、六边形的呢?
2
人教版八年级数学上册 第十一章 三角形
11.3 多边形及内角和
11.3.2 多边形的内角和
3
学习目标 1.会通过不同方法探索多边形的内角和与外角和
公式,并会用它们进行有关计算. 2.通过将多边形问题转化为三角形问题解决,体 会化归思想的应用方法,提高分析问题和解决问 题的能力.
重点难点
重点:多边形的内角和与外角和. 难点:多边形的内角和公式的推导.
A.360° B.540° C.720° D.900°
14
人教版八年级数学上册11.3 多边形及其内角和 (共62张PPT)

创设情境,导入新知
多边形的定义: 在平面内,由一些线段首尾顺次相接组成的封闭图 形叫做多边形.
(在同一个平面内)
说出下面图形的名称:
四边形
六边形 五边形
八边形
(1)多边形的表示方法:
A
用它的各个顶点的字母
按顺序表示,顺时针或 B
者逆时针,如图,可表
示为五边形ABCDE或者
AEDCB。
C
E D
(2)多边形相邻两组边组成的角叫做它的内角。 如图,∠A,∠B,∠C,∠D,∠E分别是五边形 ABCDE的五个内角。
了解一下
可表示为:五边形ABCDE或
五边形DCBAE
A
内角
顶点
E
B
边 C
对角线:连接多边形不相邻的两个顶 点的线段。
D 对角线
创设情境,导入新知
如图,从五边形ABCDE 的顶点A 出发共有几条对 角线?
A
B E
C
D
1.四边形中经过每一个顶点的对角线有__1_条 其中每一条都重复了__1_次,所以,四边形 共有__2_条对角线。 41
温故而知新
1、由不在同一直线上的三条线段首尾顺次相连所 组成的图形叫做三角形
2、三角形的内角和:三角形三个内角之和为 180°
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻 的两个内角的和。 ②三角形的一个外角大于任何一个与它 不相邻的内角。 2、三角形的外角和是360°
观察下列图案
E
小明清晨沿一个五边形广场周围的小跑, 按逆时针方向跑步的效果图. 请你观察并
2
4
思考如下几个问题:
CD
3
(1)小明每从一条街道转到下一条街道时,身
《多边形》三角形PPT精品课件

①从所截角的两边截,边数增加1. ②从所截角的相邻两角的顶点截,边数减少1. ③从所截角的一边及相邻角的顶点截,边数不变.
巩固练习
下列图形包含了哪些多边形?
六边形
四边形
五边形和六边形
探究新知
知识点 2 多边形的对角线
定义:
A
连接多边形不相邻的两个顶点的线 B
E
段,叫做多边形的对角线.
D C
线段AC是五边形ABCDE的一条对角线, 多边形的对角线通常用虚线表示.Байду номын сангаас
素养考点 1 多边形的截角问题
例 凸六边形纸片剪去一个角后,得到的多边形的边 数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况, ∴新多边形的边数为7、5、6三种情况, 如图所示.
探究新知
归纳总结
一个多边形截去一个角后,多边形的边数可能 增加了一条,也可能不变或减少了一条.
∴n-3+n-2=21, 解得n=13. 答:该多边形的边数有13条.
巩固练习
画一画:画出下列多边形的全部对角线.
巩固练习 观察下列图形,并阅读图形下面的相关文字,解答下 列问题:
十边形有多少条对角线?n边形呢?
巩固练习
解:∵四边形的对角线条数为4×(4-3)×12 =2.
五边形的对角线条数为5×(5-3)×
n(n≥3)边形共有对角线 n(n 3) 条.
2
探究新知
素养考点 2 利用多边形的对角线相关公式求边数
例 过多边形的一个顶点的所有对角线的条数与这些对角 线分割多边形所得三角形的个数的和为21,求这个多边 形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所 分得的三角形个数为n-2,
巩固练习
下列图形包含了哪些多边形?
六边形
四边形
五边形和六边形
探究新知
知识点 2 多边形的对角线
定义:
A
连接多边形不相邻的两个顶点的线 B
E
段,叫做多边形的对角线.
D C
线段AC是五边形ABCDE的一条对角线, 多边形的对角线通常用虚线表示.Байду номын сангаас
素养考点 1 多边形的截角问题
例 凸六边形纸片剪去一个角后,得到的多边形的边 数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况, ∴新多边形的边数为7、5、6三种情况, 如图所示.
探究新知
归纳总结
一个多边形截去一个角后,多边形的边数可能 增加了一条,也可能不变或减少了一条.
∴n-3+n-2=21, 解得n=13. 答:该多边形的边数有13条.
巩固练习
画一画:画出下列多边形的全部对角线.
巩固练习 观察下列图形,并阅读图形下面的相关文字,解答下 列问题:
十边形有多少条对角线?n边形呢?
巩固练习
解:∵四边形的对角线条数为4×(4-3)×12 =2.
五边形的对角线条数为5×(5-3)×
n(n≥3)边形共有对角线 n(n 3) 条.
2
探究新知
素养考点 2 利用多边形的对角线相关公式求边数
例 过多边形的一个顶点的所有对角线的条数与这些对角 线分割多边形所得三角形的个数的和为21,求这个多边 形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所 分得的三角形个数为n-2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18
我们也可以在问题4 的基础上这样理 解多边形外角和等于360°.
如图,从多边形的 一个顶点A 出发,沿多 边形的各边走过各顶点, 再回到点A,然后转向 A 出发的方向.
2020/11/23
19
在行程中转过的各
个角的和,就是多边形
的外角和.由于走了一
周,所转过的各个角的
和等于一个周角,所以
多边形外角和等于 360°.
∠ADC +∠4 =180°,
D4
得∠BAD + ∠1 + ∠ABC
3C
+∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,得
∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°.
2020/11/23
14
形的外角和是360°.得出三角形的外角和是360°有
多种方法.
如图,你能说说怎样由外角与相邻内E 角互补的关系
得出这个结论吗?
A
1
B2 F
3
C
D
2020/11/23
12
由 ∠1 +∠BAE =180°,∠2 +∠CBF =180°,
∠3 +∠ACD =180°,
得 ∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD =540°.
问题3 五边形的外角和等于多少度? 六边形呢? 仿照上面的方法试一试.
5× 180°-(5-2)×180°= 2× 180°=360°
பைடு நூலகம்
2020/11/23
15
6× 180°-(6-2)×180°= 2× 180°=360°
2020/11/23
16
类比求三角形、四边形的外角和 的方法求出五边形的外角和是360°, 六边形的外角和是360°.
=(∠BAC +∠BCA +∠B)
D
+ (∠DAC +∠DCA +∠D),B
C
= 180° 2020/11/23 + 180° = 360° .
3
探究2 你能利用三角形内角和定理证明你的结
论吗?
从四边形的一个顶点出发,
A
可以作___1__条对角线,它们将
四边形分为 2 个三角形,
D
四边形的2内角和3等60于
n 边形的内角和等于(n -2)×180°.
2020/11/23
9
练习巩固
例1 填空. (1)十边形的内角和为 1440 °. (2)已知一8 个多边形的内角和为1 080°,则它的边数
为______.
2020/11/23
10
例2 如果一个四边形的一组对角互补,那么另一
组对角有什么关系?
解:如图,四边形ABCD 中, ∠A +∠C =180°.
x = 60
x = 95
22
2.下列各个度数中,不可能是多边形的内角和的是( A)
A.600° B.720° C.900° D.1 080°
3.若多边形的边数由3增加到5,则其外角和的度数( C )
A.增加 B.减少 C.不变 D.不能确定
2020/11/23
23
2020/11/23
1
问题情境
回忆 长方形、正方形的内角和等于__3_6_0_°_. 思考 任意一个四边形的内角和是否也等于360°呢?
2020/11/23
2
合作探究
探究1 你能利用三角形内角和定理证明你的
已知:如图结,论在吗四?边形ABCD中.
证明:连接对角线AC,
A
∠BAD +∠B +∠BCD +∠D
E
B
D
2020/11/23
C
6
思考
你能从四边形、五边形、六边形……的内角和的研究过 程获得启发,发现多边形的内角和与边数的关系吗?能 证明你发现的结论吗?
2020/11/23
7
归纳
边数
图形
三角形
四边形
五边形
六边形
······
n 边形 2020/11/23
······
从多边形的一个顶点 分割出三角 引出的对角线条数 形的个数
2020/11/23
17
问题4 你能仿照上面的方法求n 边形(n 是不小于3 的任意整数)的外角和吗?
因为n 边形的每个内角与它相邻的外角是邻补角,它们 的和是180°,所以n 边形内角和加外角和等于n ·180°,
所以,n 边形的外角和为:
n ·180°-(n -2)·180°= 360°.
2020/11/23
多边形内角和
3 -3 = 0
3 -2 = 1
180º
4 -3 = 1
4 -2 = 2
360º
5 -3 = 2
5 -2 = 3
540º
6 -3 = 3
6 -2 = 4
720º
······
n -3
······
n -2
······
( n -2 )·1880º
从n 边形的一个顶点出发,可以作(n -3)条对角 线,它们将n 边形分为(n -2)个三角形,这(n -2) 个三角形的内角和就是n 边形的内角和,所以,
由 ∠1 + ∠2 + ∠3 = 180°,得 ∠BAE +∠CBF +∠ACD
= 540° - 180°
E
A
1
= 360°.
B2 F
3
C
D
2020/11/23
13
问题2 如图,你能仿照上面的方法求四边形的外
角和吗?
由 ∠BAD +∠1 =180°, ∠ABC +∠2 =180°,
A1 B
2
∠BCD +∠3 =180°,
B
C
180°×____=
°.
2020/11/23
4
探究3 类比前面的过程,你能探索五边形的内角和
吗?六边形呢?
如图,从五边形的一个顶点 A 出发,可以作 2 条对角线,它 们将五边形分为__3__个三角形,
五边形的内角和3 等于 540
B
180°× =
2020/11/23
°.
E D
C
5
如图,从六边形的一个顶点出发,可以作___3__条 对角线,它们将六边形分为___4__个三角形,六边形的 内角和等于180°×A__4__=___7_2F_0__°.
A
2020/11/23
20
精讲例题
例3 一个多边形的内角和等于它的外角和的3 倍,它
是几边形?
解:设这个多边形为 n 边形,
根据题意,可列方程 ( n -2)×180°=3×360°.
解得 n =8. 答:它是八边形.
2020/11/23
21
随堂练习
1. 求出下列图形中 x 的值.
x = 65
2020/11/23
∵ ∠A +∠B +∠C +∠D =(4 - 2)×180° =360°,
∴ ∠B +∠D =360°-(∠A + ∠C) =360°- 180° =180°.
C D
A
B
如果2020四/11/23边形的一组对角互补,那么另一组对角也互补11 .
探究新知
问题1 我们知道,三角形的内角和是180°,三角
