复合轮系的传动比计算
复合轮系传动比的计算

H
对差动轮系:
齿数比前面的负号,是由 该轮系的结构决定的。
z z 48 90 H H 3 1 2 i 6 (1) 13 z 24 30 H z 3 1 2 '
对定轴轮系
3 z4 z5 i 3' 5 5 z3' z4 z5 80 4 z3' 20
§8.4复合轮系传动比的计算
计算方确地划分出各个基本轮系;
⒉分别计算各基本轮系的传动比; ⒊找出各个基本轮系之间的联系;
⒋联立求解。
正确地划分出各个基本轮系
⑴ 先找出各个单一的周转轮系 先找出行星轮: 几何轴线绕其它齿轮的固定轴线转动的齿轮, 即由活动构件支承的齿轮 。 再找系杆:支承行星轮的构件。
(2)
, 因为 3 3 H 5
将式(1)、(2)联立可得:
i 6 i 3 H31 1 H7
注意:
在计算过程中,代入各轮齿数的 数值后可以化为整数或进行约分;不 宜化为带有小数的近似值,以免使最 后结果产生误差。 最后的结果,既可以保留分数形 式,也可以化为近似小数。
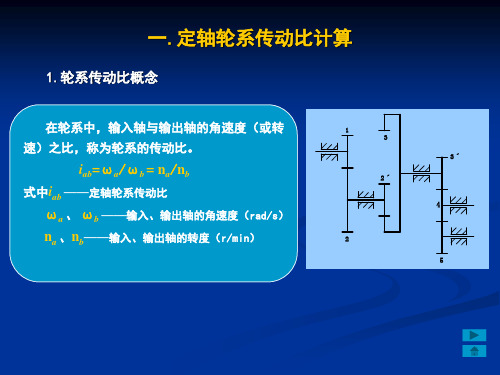
例2: 在轮系中,已知各轮齿数:Z1=20, Z2=40, Z2 ' =20,
Z3=30, Z4=80,求传动比i1H 。
解: 首先正确地划分出各个基本轮系。
有一个中心轮是固定的
行星轮系: 3、 H 、 2 、 4 定轴轮系:1、2
然后找出中心轮: 直接与行星轮啮合且几何轴线的位置固定的齿轮。 这一由系杆、行星轮、中心轮组成的轮系就是一个基本周转 轮系(一般情况下为2K-H 型) 重复上述过程,将各个周转轮系逐一找出。一般情况下, 一个复合轮系中有几个系杆,就包含几个单一的周转轮系。
定轴轮系传动比的计算分解
3
2
H
1
4
四、复合轮系传动比计算
1.复合轮系的概念 若轮系由定轴轮系与行星轮系或由几个行星轮系组合而成,则该轮系称为
复合轮系。
1 4 H
2
3
5
1
2
4
H1
H2
3 3' 5
2.复合轮系的传动比计算
五、轮系的功用
1.传递相距较远的两轴间的运动和动力 2.可获得大的传动比 3.可实现分路、变速传动 4.用于运动的合成或分解
♥ 2.一对齿轮啮合时主、从动轮之间的转向关系
外啮合圆柱齿轮传动时,主从动轮转向相反。 i12=-Z2/Z1 内啮合圆柱齿轮传动时,主从动轮转向相反。i12 =+Z2/Z1
蜗杆传动时,蜗杆转向用左右手定则判断。 i12 =Z2/Z1 箭头应同时指向啮合点或同时背离啮合点。 i12 =Z2/Z1
♥ 3.轮系传动比计算式
2 5
例14-1 如图所示车床溜板箱进给刻度盘轮系中,运动由齿轮1传入,由 齿轮5传出。各齿轮的齿数Z1=18,Z2=87,Z3=28,Z4=20, Z5=84,试计算轮系传 动比i15,
1
2
3
4
5
1
2
3
4
5
定轴轮系的啮合线图为: 1——2 ====3——4 ——5
例14-2 如图所示的轮系中,已知Z1=15,Z2=25,Z2ˊ=Z4=14, Z3=24 Z4ˊ=20, Z5=24,Z6=40, Z7=2,Z8=60,若n1=800r/min,求传动比i18,蜗轮8 的转速和转向
连乘积比之前冠以正负号。
4)iGKH ≠iGK iGKH —为转化轮系中G、K两轮的转速之比,其大小及正负号按定轴轮系传动比
复合轮系的传动比计算举例

复合轮系的传动比计算举例例1图示轮系中,各轮模数和压力角均相同,都是标准齿轮,各轮齿数为Z , 23,Z 2 51,z 392,Z 3' 40, Z 4 40,乙,17,Z s 33,n 11500 r/min ,转向如图示。
试求齿轮2'的齿数Zr 及n A 的大小和方向。
解:(1)齿轮1,2啮合的中心距等于齿轮 2,3啮合的中心距,所以得,Z 9 24。
轴A 按图示方向以1250r/min 的转速回转, 回转,求轴C 的转速n C 的大小和方向。
57 n HnH33口3nH66n H(3) 63n H3门1门人nH £15007143r/min2121(4)负号表明 n H 转向与m 相反。
n1nH图示轮系,已知各轮齿数:Z 232,Z 3 34 , Z 4 36 ,Z 5 64 , Z 7 32 , z 17Z 2 Z 3 Z 2' Z 3Z 2'N 92 23 51 18(2 2) 3 (A)组成差动轮系,3 (44) 5 (A)组成行星轮系.H11n i 匹 n 3 n H51 92 23 1834 3 i3'H门3, n3n Hn H1 is? Z 4Z 540 33 4050 1734轴B 按图示方向以600r/min 的转速 2r解:(1)分析轮系结构:Z9 (3)i25n2由式①得:由式②得: (4) n sn sn7n s3门9n6B2- 3- 4-5-6为差动轮系,7-8- 9为定轴轮系。
32 424 3Z3Z5Z2Z434 6432 363 600450r/min49(门2门6)17(1250 450)450 264717r/min方向与轴A相同。
例3在图示的轮系中,已知各轮齿数为Z2 Z4 25,Z2 20,各轮的模数相同, n41000r/min。
试求行星架的转速 H H的大小和方向。
W求 i 4H :n 3代入上两式得n H 的方向与n 4相反。
传动比计算举例

可见: 可见:1 轮与 5 轮方向相同
6. P.360 图 9-18 汽车后桥差动轮系 ---- 转向用
已知: 各轮齿数; 已知: 各轮齿数; 分析汽车两后轮1, 求: 分析汽车两后轮 ,3 的转速 n1及 n3 解: 一. 正确划分轮系 差动轮系: , , , 二. 差动轮系:1,4,3,2 i13H = i134 = n1H / n3H = ( n1 – n4 ) / (n3– n4) = - z3 / z1 = - 1 三. 定轴轮系 i45 = n4 / n5 = z5 / z4 n1 + n3 = 2 n4 n4 = (z5 / z4)n5 n1 + n3 = 2×z5 / z4 × n5 × 四. 讨论 n1 = n3 :n1 = n3 = n4 → 2 轮不自转,相当于离合器 轮不自转, n1≠n3 : n4 与 n1,n3 不同 → 2 为星轮,差动轮系 为星轮,
1
5. P.384习题 习题9-15 复合轮系 习题
已知: 各轮齿数; 已知: 各轮齿数; n1= 3549 r/min 求 : nH 划分轮系, 解: ①.划分轮系,如图 划分轮系 ②周转轮系:H,8,9,7 周转轮系: , , , n7 H = n7 - nH ; n9 H = n9 - nH ; i79H = n7H / n9H = ( n7 – nH ) / (n9– nH ) = ( n7 – nH ) / ( – nH ) = - z9 / z7 周转轮系: , , , ③ 周转轮系:7,5,6,4' n4'H = n4' – n7; n6H = n6 – n7 ; i4'6H = n4'H / n6H = ( n4 – n7 ) / ( – n7) = - z6 / z4' ④ 定轴轮系 i14 = n1 / n4 = z1 z3 / z2 z4
行星齿轮传动比分析与计算

行星齿轮传动比分析与计算一、行星轮系传动比的计算 (一)行星轮系的分类若轮系中,至少有一个齿轮的几何轴线不固定,而绕其它齿轮的固定几何轴线回转,则称为行星轮系。
行星轮系的组成:行星轮、行星架(系杆)、太阳轮 (二)行星轮系传动比的计算以差动轮系为例(反转法) 转化机构(定轴轮系) T 的机构1234差动轮系:2个运动行星轮系:,对于行量轮系:H H W W W -=111W H H W W W -=222W H H W W W -=333W 0=-=H H H H W W W H W 13313113)1(Z Z W W W W W W i H HH H H⋅'-=--==03=W 1310Z Z W W W H H-=--11311+==Z Z W W i H H )(z f W W W W W W iH B H A H BH A HAB=--==0=B W∴∴例12.2:图示为一大传动比的减速器,Z 1=100,Z 2=101,Z 2'=100,Z 3=99。
求:输入件H 对输出件1的传动比i H1解:1,3中心轮;2,2'行星轮;H 行星架 给整个机构(-W H )绕OO 轴转动∵W 3=0∴∴若Z 1=99行星轮系传动比是计算出来的,而不是判断出来的。
AHHA H H A H AB i W WW W W i -=-=--=110HAB AH i i -=1213223113)1('⋅⋅⋅-=--=Z Z Z Z W W W W i H HHH H Hi Z Z Z Z W W W 13213210'=--H H i Z Z Z Z W W 13213211'=+-HH i i 131100100991011⨯⨯-=100001001009910111111=⨯⨯-==HH i i 1001-=H i(三)复合轮系传动比的计算复合轮系:轮系中既含有定轴轮系又含有行星轮系,或是包含由几个基本行星轮系的复合轮系。
复合轮系的传动比计算举例

复合轮系的传动比计算举例标准化管理部编码-[99968T-6889628-J68568-1689N]复合轮系的传动比计算举例例1 图示轮系中,各轮模数和压力角均相同,都是标准齿轮,各轮齿数为z 123=,z z z z z z n 23344515192404017331500=======,,,,,,'' r /min ,转向如图示。
试求齿轮2'的齿数z 2'及n A 的大小和方向。
解:(1)齿轮1,2啮合的中心距等于齿轮2',3啮合的中心距,所以得(2))(3)22(1A --'--组成差动轮系,)(5)44(3A --'--'组成行星轮系(3)6331n n H =-n n n A H ==-=-=-1211500217143.r/min (4)负号表明n H 转向与n 1相反。
例2 图示轮系,已知各轮齿数:322=z ,343=z ,364=z ,645=z ,327=z ,178=z ,z 924=。
轴A 按图示方向以1250r/min 的转速回转,轴B 按图示方向以600r/min 的转速回转,求轴C 的转速n C 的大小和方向。
解:(1)分析轮系结构:2-3-4-5-6为差动轮系,7-8-9为定轴轮系。
(2)i n n z z 979779322443==== ① (3)917363264344253656225-=⨯⨯-=-=--=z z z z n n n n i H ② 由式①得:n n 793436004450==⨯= r/min 由式②得:n n n n 5626917-=--() (4)n 591250450174502647=-⨯-+=(). r/min 方向与轴A 相同。
例3 在图示的轮系中,已知各轮齿数为2425z z ==,220z '=,各轮的模数相同,4n =1000r/min 。
试求行星架的转速H n 的大小和方向。
轮系传动比计算
126§5-6 定轴轮系传动比的计算一、轮系的基本概念● 轮系:由一系列相互啮合的齿轮组成的传动系统; ● 轮系的分类: 定轴轮系: 所有齿轮轴线的位置固定不动; 周转轮系:至少有一个齿轮的轴线不固定; ● 定轴轮系的分类:平面定轴轮系:轴线平行; 空间定轴轮系:不一定平行;● 轮系的传动比:轮系中首、末两轮的角速度(或转速)之比,包括两轮的角速比的大小和转向关系。
传动比的大小:当首轮用“1”、末轮用“k ”表示时,其传动比的大小为: i 1k = ω1/ωk =n 1/n k 传动比的方向:首末两轮的转向关系。
相互啮合的两个齿轮的转向关系:二、平面定轴轮系传动比的计算特点:●轮系由圆柱齿轮组成,轴线互相平行;●传动比有正负之分: 首末两轮转向相同为“+”,相反为“-”。
1、传动比大小设Ⅰ为输入轴,Ⅴ为输出轴; 各轮的齿数用Z 来表示;127角速度用ω表示;首先计算各对齿轮的传动比:所以:结论: 定轴轮系的传动比等于各对齿轮传动比的连乘积,其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比; 2、传动比方向在计算传动比时,应计入传动比的符号: 首末两轮转向相同为“+”,相反为“-”。
(1)公式法式中:m 为外啮合圆柱齿轮的对数 举例:(2)箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向,转向相同为“+”,相反为“-”。
举例:122112z z i ==ωω32223332z i z ωωωω'''===33434443z i z ωωωω'''===455445z z i ==ωω11211)1(--==k k m k k z z z z i ωω128三、空间定轴轮系的传动比特点:●轮系中包含有空间齿轮(如锥齿轮、蜗轮蜗杆、螺旋齿轮等); ●首末两轮的轴线不一定平行。
1 传动比的大小2 传动比的方向注意:只能采用箭头标注法,不能采用(-1)m 法判断。
周转轮系与复合轮系的传动比

既然周转轮系的转化轮系为一定轴轮系, 就可应用定轴轮系传动比的公式进行计算。
z z n1H n1 nH (1)1 2 3 H n3 n3 nH z1 z 2
H i13 为转化轮系的传动比,并不是原周转轮系的传动比。但 n1、n3、n H 三个运动参
数中,若已知任意两个,就可确定第三个,从而求出周转轮系的传动比。 一般公式: n H nm n H 在转化轮系中由 m到n各从动齿轮齿数乘积 H imn m (1) K ; H nn n H 主动 nn
教 学内 容
备注
机构 太阳轮 1 太阳轮 3 行星轮 2 行星架 H 机架 即
H i13
原有转速
转化机构中的转速
n1
n3
n1H n1 nH
H n3 n3 nH
n2
nH
n机架 0
H n2 n2 n H H nH nH nH 0
H n机架 0 nH nH
i12
n1 z 1 n2 z2
得n a n 2
z1 20 n1 300 200rpm z2 30
教 学内 容
H iab
备注
na n H z b nb nH za
200 nH 80 0 nH 20 nH 40rpm.
(2) i13
H
若 n1 1450r / min , n H
n1 1450 46.77r / min i1H 31
=18, =30, Z g 例 3、在图示双螺旋桨飞机减速器中,已知 Za=26,Zg=20,Zb=66, Z a
=66,若 na=15000rpm,求 nP 及 nQ 的大小及转向。 Zb
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复合轮系的传动比计算
对图卜6J的原点倾响两数.,频率低于第t阶I^1有额率时.两阶模态(主振创)相同.似一阶模态的贞献城远人十代阶模态:’场领J扭高于第几阶l司有倾率时.两阶模态《卜振型》也相
卜J.们几阶模态的贡献狱远大于阶模态,也就是说.靠近某阶161有频率.该阶模态的贡献址就
比其他阶大,模态参效U毛别的单自山度法就是以此为依据的.’.1倾率处于两阶l^]有翻率之间
时.原点预响曲线图,!,出现反向尖峰.这·点你为反共振点.该点领率称为反」七振倾率.
对图8一6!,的跨点顿响两数。
It低l;第·阶l^1有橄率和高于第引价I^1有粕率时的特征与原
点翻响呐数相同,而处十两阶lA1有钾率之间时.跨点领响曲线!铆卜不一定会出现反共振点。
排!”到多r石I月度无阳尼系统.它有n个共振板率.1〔原点板响函数曲线l几,两共振点之间一定会出现反共振点:跨点脚晌雨数曲浅则无此规律.而且.栩距越远的两点.其顿响函数出现反共振点的一:I蓄指性越小地磅
有汉l尼多自由度系统的抓响函数辐知图.J无份11己多「!山度系统的祛本们ll.刁,只是山全
附厄的存在。
共振点及反共振点处的曲线变得圆钝.如}钊8一7所不
计算结果为正.表明行星架H的转向与齿轮l的转向相同,与齿轮3相反.
注意:对于由谁齿轮所组成的周转轮系,由于其行星轮与中心轮或行星架的回转
轴线不平行,因此不能用式(7·3)来计算行星轮的转速(或角速度).
7.4复合轮系的传动比计算
在实际机械中,除了广泛应用单一的定轴轮系和单一的周转轮系外,还大最使用由
定轴轮系与周转轮系组成的复合轮系,或由几个单一的周转轮系组合而成的复合轮系。
在计算复合轮系传动比时,这种轮系既不能转化成单一的定轴轮系,也不能转化
成单一的周转轮系,所以不能用一个公式来求解。
计算复合轮系传动比的正确步骤如下。
(”首先将各个基本轮系正确区分开来;
(2〕找出把各基本轮系联系起来的构件;
(3)分别列出计算各基本抡系传动比的方程式,
(4)将各基本轮系传动比方程式联立求解.即可求得复合轮系的传动比。
本文来源于衡器,转载请注明来源于。
