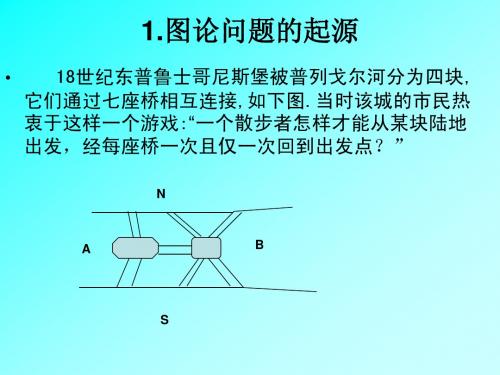
图论第1讲
合集下载
图论1—图论基础PPT课件

的度减去最小点的度,将最小点
的度设为0。
如果最后得到全0序列,则输出
yes,否则输出no
42 2
31
22 0
20
00 0
例题:给出一个非负整数组 成的有限序列s,s是否是某 个简单图的度序列?
332211 Yes
3331 No
首先利用图论第一定理。
然后把所有顶点排序,将最大点
的值设为0,然后将其后部最大点
在图G中,与顶点v相关联的边的总数 称为是v的度,记为deg v
图论第一定理
deg v 2m
vV (G)
证明:在计算G中所有顶点度的和时,每一条 边e被计数了两次。
例题:给出一个非负整数组 成的有限序列s,s是否是某 个图(无自环)的度序列?
242 Yes
31 No
首先利用图论第一定理。
然后把所有顶点排序,用最大点
图, 记 为G = (V, E ), 其中
① V称为G的顶点集, V≠, 其元素称为顶点或
结点, 简称点; ② E称为G的边集, 其元素称为边, 它联结V 中
的两个点, 如果这两个点是无序的, 则称该边为无 向边, 否则, 称为有向边.
如果V = {v1, v2, … , vn}是有限非空点集, 则称G 为有限图或n阶图.
如果某个有限图不满足(2)(3)(4),可在某条 边上增设顶点使之满足.
定义2 若将图G的每一条边e都对应一个实数F (e), 则称F (e)为该边的权, 并称图G为赋权图(网络), 记为G = (V, E , F ).
定义3 设G = (V, E)是一个图, v0, v1, …, vk∈V, 且1≤i≤k, vi-1vi∈E, 则称v0 v1 … vk是G的一条通路. 如果通路中没有相同的边, 则称此通路为道路. 始 点和终点相同的道路称为圈或回路. 如果通路中 既没有相同的边, 又没有相同的顶点, 则称此通路 为路径, 简称路.
第一章(图论的基本概念)
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理,图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
离散数学图论基础知识文稿演示

图的定义
定义8.1 一个图是一个序偶<V,E>,记为 G=<V,E>,其中: 1) V={v1,v2,v3,…,vn}是一个有限的非空集合,
vi(i=1,2,3,…,n)称为结点,简称点,V为结 点集; 2) E={e1,e2,e3,…,em}是一个有限的集合, ei(i=1,2,,…,m)称为边,E为边集,E中的 每个元素都有V中的结点对与之对应。即对任 意e∈E,都有e与<u,v>∈VV或者(u,v)∈ V&V相对应。
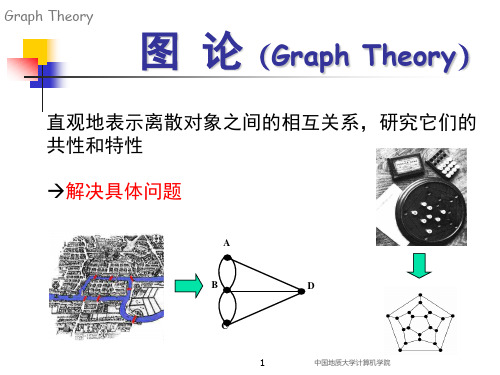
图论
▪ 一个图就是一个离散的拓扑结构,经常用于描 述和研究许多领域中的各种问题。
▪ 随着计算机科学的飞速发展,图论组合和算法 的研究在近代也成为计算机科学和数学中发 展最快的基础学科之一,也受到国际上的学术 界和高新技术企业方面特别重视。
图论
▪ 理论计算机科学中的算法理论经典问题(图中点对之 间最短路,货郎担问题,图重抅问题,HAMILTON 问 题,P-NP问题等),通信网络通讯(网络设计, 通讯速度 和容量, 网络可靠性和容错性等) ;
图论本身是应用数学的一部份,因此,历史上图论曾经 被好多位数学家各自独立地建立过。关于图论的文字 记载最早出现在欧拉1736年的论着中,他所考虑的原 始问题有很强的实际背景
图论
图论起源于著名的哥尼斯堡七桥 问题。
欧拉证明了这个问题没有解,并 且推广了这个问题,给出了对于 一个给定的图可以某种方式走遍 的判定法则。 这项工作使欧拉成为图论〔及拓 扑学〕的创始人。
1976年,美国数学家阿佩尔与哈肯在美国伊利诺斯大学 的两台不同的电子计算机上,用了1200个小时,作了 100亿判断,终于完成了四色定理的证明。
不过不少数学家并不满足于计算机取得的成就,他们认 为应该有一种简捷明快的书面证明方法。
图论1

定义 1) 若H是赋权图G的一个子图,则称H的各 边的权和 w( H ) w(e) 为H的权. 类似地,若
eE ( H )
若P(u,v)是赋权图G中从u到v的路,称 w( P) 称为路P的权.
eE ( P )
w(e)
2) 在赋权图G中,从顶点u到顶点v的具有最小权 的路P*(u,v),称为u到v的最短路. 3) 把赋权图G中一条路的权称为它的长,把(u,v) 路的最小权称为u和v之间的距离,并记作 d(u,v).
uavdxcw 路或路径:
圈或回路:uavbwcxfygu
3.最短路问题及算法
最短路问题是图论应用的基本问题,很多实际 问题,如线路的布设、运输安排、运输网络最小费 用流等问题,都可通过建立最短路问题模型来求解. •最短路的定义 •最短路问题的两种方法:Dijkstra和Floyd算法 . 1) 求赋权图中从给定点到其余顶点的最短路. 2) 求赋权图中任意两点间的最短路.
例 设 H (V ( H ), E ( H )) ,其中:
V ( H ) {u1, u2 , u3 , u4 , u5},
E ( H ) {a1, a2 , a3 , a4 , a5 , a6 , a7 }, a1 (u1, u2 ) , a2 (u2 , u2 ) , a3 (u4 , u2 ) ,
(见图 2)
定义 若一个图的顶点集和边集都是有限集,则称 其为有限图. 只有一个顶点的图称为平凡图,其他的
所有图都称为非平凡图.
定义若图G中的边均为有序偶对 (vi , v j ),称G为有向 图. 称边 e (vi , v j ) 为有向边或弧,称 e (vi , v j )是从vi 连接 v j ,称 vi为e的尾,称 v j为e的头. 若图G中的边均为无序偶对 vi v j ,称G为无向图.称 边 e vi v j 为无向边,称e连接 vi 和 v j,顶点 vi 和 v j 称 为e的端点. 既有无向边又有有向边的图称为混合图.
代数结构-图论
记作Nn,特别地,称N1为平凡图(Trivial graph)。 在图的定义中规定结点集V为非空集,但在图的运算
中可能产生结点集为空集的运算结果,为此规定结
点集为空集的图为空图(Empty Graph),并将空图
记为。阶为有限的图称为有限图(Finite Graph),
否则称为无限图(Infinite Graph)。结点没有标号
的图称为非标号图(Unlabeled Graph),否则为标
号图(Labeled heory
10.2 图与图模型
如果图中存在某两条边的端点都相同,则称该
图为多重图(Multigraph),该两条边称为平行边。
如果一条边关联的两个结点是相同的结点,则称该边 为圈或自环(Loop)。
请你思考?
如何找到物流运输的最优路径? 如何找到最优的网络通信线路? 如果你想周游全国所有城市,如何设计旅游线路? 化学化合物分析:结构是否相同? 程序结构度量:程序是否结构相似? 如何为考试分配教室,使得资源利用率最优? 如何安排工作流程而达到最高效率? 如何设计为众多的电视台频道分配最优方案? 如何设计通信编码以提高信息传输效率? 操作系统中,如何调度进程而使得系统效率最优?
图的类型:
(1)有向图/无向图;简单图/多重图/伪图;零图,平凡图,空图; 有限图/无限图;带权图、标记图;
(2)特殊图:环图(Cn)、轮图(Wn)、立方图(Qn)、网格、正则图 (r-图);偶图(G(V1,V2), 二分图/二部图, Bipartite graph) 、 完全偶图(Km,n);
(3)特殊图:子图、完全图、补图 (4)特殊图:Euler图、Hamilton图、树图、平面图
主要内容
8
中国地质大学计算机学院
图论第一章课后习题解答

bi 个 (i = 1,2,…,s),则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分,称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ,E H E G , 重数,则称 H 是 G 的子图,记为 H G 。有时又称 G 是 H 的母图。 当 H G ,但 H G 时,则记为 H G ,且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集,以两端点均在 V 中的边的全体为边集 所组成的子图,称为 G 的由 V 导出的子图,记为 G[ V ];简称为 G 的导出子图,导出子图 G[V\ V ]记为 G V ; 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集,以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图,记为 G E ;简称为 G 的边导出子图,边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ,则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图(包括 G 和空图)的个数是 2m 个。 定义 2 设 G1,G2 是 G 的子图。若 G1 和 G2 无公共顶点,则称它们是不相交的;若 G1 和 G2 无公共边,则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图,其顶点 集为 V(G1)∪V(G2),其边集为 E(G1)∪E(G2);如果 G1 和 G2 是不相交的,有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2,但此时 G1 和 G2 至少要有一个公共顶点。
图论讲义1图路树

这便证明了 G 是一个二部图。 证毕。
7. 连通性 图中两点的连通:如果在图 G 中 u,v 两点有路相通,则称顶点 u,v 在图 G 中连通。 连通图(connected graph):图 G 中任二顶点都连通。 图的连通分支(connected branch, component):若图 G 的顶点集 V(G)可划分为若干非空子集
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
3
(8) 完全图(complete graph)
(9) 图的顶点数(图的阶)ν 、边数 ε
(10) 顶点 v 的度(degree):d(v) = 顶点 v 所关联的边的数目(环边计两次)。
(11) 图 G 的最大度: ∆(G) = max{dG (v) | v ∈V (G)}
图 G 的最小度:δ (G) = min{dG (v) | v ∈V (G)}
证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
7. 连通性 图中两点的连通:如果在图 G 中 u,v 两点有路相通,则称顶点 u,v 在图 G 中连通。 连通图(connected graph):图 G 中任二顶点都连通。 图的连通分支(connected branch, component):若图 G 的顶点集 V(G)可划分为若干非空子集
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
3
(8) 完全图(complete graph)
(9) 图的顶点数(图的阶)ν 、边数 ε
(10) 顶点 v 的度(degree):d(v) = 顶点 v 所关联的边的数目(环边计两次)。
(11) 图 G 的最大度: ∆(G) = max{dG (v) | v ∈V (G)}
图 G 的最小度:δ (G) = min{dG (v) | v ∈V (G)}
证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
图论1

d<u,v> + d<v,w> ≥ d<u,w> 《定义》:在简单有向图中,若图中任何一 定义》 对结点间,至少有一点到另一结点是可达 的,则称此图是单侧连通的;如果两结 点均是互相可达的,则称是强连通的。 如果在图中略去边的方向,将它看成无向 图后,图是连通的,则称此图为弱连通 的. 强连通⇒单侧连通⇒弱连通
(10)闭路(自回路): 闭路(自回路):图中起始且终止于同一结 闭路 ): 点的边 (闭路的箭头方向是没有意义的 )例:
(11)多重边(平行边): 多重边(平行边):二个结点之间 多重边 ): 方向相同的二条(多条)边 例:
多重图,非多重 《定义》:含有多重边的图称为多重图 定义》 多重图 图称为线图 线图。 线图 简单图: 简单图。 简单图:无自回路的线图称为简单图。由定义可 简单图 见,简单图是没有自回路和多重边的图。 例:
图论不断发展,它在解决运筹学,网络理 论,信息论,控制论,博奕论以及计算 机科学等各个领域的问题时,显示出越 来越大的效果。 对于这样一门应用广泛的学科,其包含的 内容是丰富的,本篇我们只准备介绍基 本的概念和定理,为今后有关学科及课 程的学习和研究提供方便。 第七章 图论
§1图的基本概念
1.基本名词和定义 1.基本名词和定义 定义》 《定义》一个图G是一个三元组<V(G),E(G), ΦG>, 其中V(G)为有限非空结点(或叫顶点)集合, E(G)是边的集合, ΦG是从边集E到结点偶对集 合上的函数。 (1). V(G) ={V1,V2,…,Vn}为有限非空集合, Vi称为结点,简称V是点集。 (2). E(G)={e1,…,em}为有限的边集合,ei称为边。 。 每个边ei都有V中的结点对与之相对应,称E为边集。 。 即每条边是连结V中的某两个点的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在日常生活中我们常常可以遇到组合数学的问题。 比如一个著名的世界难题“四色猜想” :一张地图, 用一种颜色对一个地区着色,那么一共只需要四种 颜色就能保证每两个相邻的地区颜色不同。
四色问题
1852年,刚从伦敦大学毕业的Francis Guthrie提 出了四色猜想。 1878年著名的英国数学家Cayley向数学界征求解答。 此后数学家 Heawood 花费了毕生的精力致力于四 色研究,于1890年证明了五色定理(每个平面图都 是5顶点可着色的)。 直到1976年6月,美国数学家 K. Appel与 W. Haken, 在3台不同的电子计算机上,用了1200小时,才终 于完成了“四色猜想”的证明,从而使"四色猜想" 成为了四色定理。
3、计算机系统的认知、分析、设计和应用能力 村庄被抽象成一个结点
二、本课程特点
课程名称: 《图论及其应用》
特点:
1.蕴含了丰富的思想、漂亮的图形和巧妙的证明;
2. 涉及的问题多且广泛,问题外表简单朴素,本 质上却十分复杂; 3.解决问题的方法千变万化,非常灵活,常常是一 种问题一种解法。
三、教学内容
A村:男性居民人数、女性居 民人数、党员人数、邮编、 逻辑思维:人们对客观规律的认识。认识客观世 11公里 3.5公里 区号、……
E村 10 C村
界的规律需要逻辑思维。逻辑思维包括概念、判 D村 5公里 断和推理。
13公里 3公里
村庄情况登记
村庄被抽象出来更丰富的信息 A村 10公里 B村 2、算法设计与分析能力、程序设计能力 邮递员投递:求A村到C村的最优投递路线
Welcome to you!
Graph Theory
图 论
●这门课讲什么? ●有什么地位? ●课程重点是什么? ●如何学好这门课? ……
提纲
大学学习几个注意点 本课程特点 本课程教学内容 本课程教学目的 教学方式 考核方式 学习要求 参考书
一、几个注意点
★课程学习要成体系
图论的基本概念 哥尼斯堡七桥问题 欧拉图、哈密顿图问题 最短路径问题 中国邮递员问题 人员分派问题
稳定匹配问题
竞赛图问题
最小费用最大流问题(网络选址问题)
四、教学目的
了解图论的基本原理 掌握图论方法的应用 掌握应用图论方法解决实际问题 初步建立抽象问题图论化方法 掌握与交叉学科之间的联系(运筹、组合数 学、数值分析、网络分析、数学建模等)
Thank you very much!
每学习一门新课程,要设法弄清楚本课程在整个课程 体系中的位置,本课程是做什么用的。每学完一门课 程,能将其与之前学习的课程进行联系,做到知识点 的融会贯通。
★ 注重专业能力的培养
1、计算思维能力-抽象思维能力、逻辑思维能力
抽象思维:抽取事物本质的、关注的方面进行研究, 抛弃其他不关心或者细节的部分。
货郎担问题
用图论的术语说,就是在一个赋权完全图 中,找出一个具有最小权的Hamilton 圈 (包含图G的每个顶点的圈)。 这个问题目前还没有有效的算法。 Hamilton问题是图论的一个重要问题,图 论中的许多问题,包括四色问题、图的因 子问题,最终都与Hamilton问题有关。
四色定理
中国邮递员问题
1962年中国组合数学家管梅谷教授提出 了著名的“中国邮递员问题”。 一个邮递员从邮局出发,要走完他所管 辖的每一条街道,然后返回邮局。那么 如何选择一条尽可能短的路线。
最短网络问题
如何用最短的线路将三部电话连起来? 此问题可抽象为设△ABC为等边三角 形,,连接三顶点的路线(称为网络)。 这种网络有许多个,其中最短路线者显 然是二边之和(如AB∪AC)。
图论的历史
近代图论的历史可追溯到18世纪的七桥问题—穿过 Kö nigsberg城的七座桥,要求每座桥通过一次且仅 通过一次。
C
A D
B
哥尼斯堡七桥示意图
Euler1736年证明了不可能存在这样的路线。
Kö nigsberg Bridge Problem C
陆地为点
C
A D
B
桥为边
A
B D
Q: 是否存在一种走法,可以走过每条边一次,并回 到起点? Ans: 因为每次经过一个点,都需要从一条边进入该点,再用另 一条边离开,所以经过每个点一次要使用掉一对边。 每个点上连接的边数必须是偶数才行 此种走法不存在
人员分配问题
设某企业有n个员工和n个工作,已知每个员工 各胜任一些工作。能否使每个员工都分派到一 件他胜任的工作?
稳定匹配问题
假设有一百个男人和一百个女人,每个男人都凭自己 的好恶给每个女人打分,最爱a,其次爱b,再次爱c (假定没有相同的)…给个女人也同样给每个男人打 分….然后就是求婚过程…如此周而复始直到最后大 家都订了婚,便一起结婚。问是否每个人都可以找到 自己的意中人?
拉姆赛理论
1958年,美国的《数学月刊》上登载着这 样一个有趣的问题:“任何6个人的聚会, 其中总会有3个人相互认识,或3个人相互 不认识”。 用6个顶点表示6个人,用红色连线表示两 者相识,用蓝色连线表示两者不相识。于 是问题化为下述命题:
拉姆赛理论
对6个顶点的完全图K6任意进行红、蓝两 边着色,则图中一定存在一个同色三角 形。
Ramsey数
推广为一般问题: 给定任意正整数a和b,总存在一个最小 整数 r (a ,b),使得r (a ,b) 个人中或者有 a 个人互相认识,或者有 b 个人互相不 认识。称 r(a,b) 为Ramsey数。
最短路径问题
假设要在计算机上建立一个交通资讯系统,这 个系统可以回答旅客提出的各种问题。如,给定连 接若干城市的铁路网,找一条给路径或者 最省钱的路径等。那么可以用图的结构来表示实际 交通网络,可对边赋以权值,权值表示两地之间的 距离,或途中所需时间或交通费用等等。
网络流问题
1956年Ford 和Fulkerson 提出了关于网络 流问题的一个重要定理。 最大流最小割定理:在任何网络中,最大 流的值等于最小割的容量。 由这个定理可以引出求网络最大流的一个 算法——标号法。 1970年,Edmonds和Karp 对标号程序加 以改进,使之成为一个好的算法。
平面图与非平面图
国王遗嘱大意:把国土分成5块给儿子,规定各块 之间都要有边界。儿子又提出在自己分到的领土 上都要修一个王宫,并且各王宫之间都要有路直 接相通而不能交叉。
能否解决? 用点表示王宫,用线表 示王宫间的道路,便抽 象成图。问题变成该图 是否为平面图?
图论的主要应用
1 电网络、通讯网络的分析与综合。 2印刷电路与集成电路的布线和测试。
八、参考书
参考教材:
1.《图论》
北京理工大学出版社
2. 《应用图论》 国防科技大学
第一讲
序
图论概述 图论发展历史 图论中典型的问题(欧拉图与哈密顿图、四色定理、
拉姆赛问题、 最短网络问题、匹配定理、平面图)
图论的应用
图论概述
现代数学可以分为两大类:一类是研究 连续对象的,如分析、方程等;另一类 就是研究离散对象的组合数学。 计算机出现以后,由于离散对象的处理 是计算机科学的核心,研究离散对象的 组合数学得到迅猛发展。
图论概述
图论模型属于离散类数学模型,是数学模 型中比较容易接受的一类模型,具有直观 性、趣味性和简洁性。 图论模型属于较为近代的前沿性数学知识, 具有强烈的为学生接受的数学建模味道, 对于培养学生通过建模解决实际问题的能 力与学习兴趣不可多得的知识内容,越来 越受数学家和建模工作者的喜爱。
环球旅行与哈密顿圈
在一个画在平面上有20个顶点的图中,把所有20个 顶点都标上城市名,旅游者从某个城市出发,找一 条经过所有城市但只能经过一次的闭合回路。该回 路称为哈密顿圈。环球旅行就是寻找哈密顿圈。
环球旅行问题的答案:
货郎担问题
一个货郎要去若干城镇卖货,然后
回到出发地,给定各城镇之间所需 的旅行时间后,应怎样计划他的路 线,使他能去每个城镇恰好一次而 且总时间最短?
匹配问题的例子
例 乔太守乱点鸳鸯谱问题 大宋景佑年间,杭州府有孙、刘、裴、徐四家, 孙家有一女一儿分别为孙珠姨和孙润;刘家有一儿 一女分别为刘璞和刘慧娘;裴家有一儿裴政;徐家 有一女徐文姑。就他们几家儿女的婚姻问题告到衙 门府,乔太守最终乱点鸳鸯谱,成为千年佳话。 二部完美匹配 • 存在性?
• 算法?
A
B
C
最短网络问题
但若增加一个周转站(新点P),连接4点的 新网络的最短路线为PA+PB+PC。最短新 路径之长N比原来只连三点的最短路径O要短。 这样得到的网络不仅比原来节省材料,而且稳 定性也更好。
A
P
B
C
网络流问题
随着中国经济快速的增长,城市化是未来中国 的发展方向。人大通过的“十五”规划,把物 流业作为战略重点列入要大力发展的新兴服务 产业。如何制定一个运输计划使生产地到销售 地的产品输送量最大。这就是一个网络最大流 问题。
3 运筹学、数值分析、数学建模、拓扑学等。
4 在理论物理和统计力学的应用。(杨振宁、李政道)
5 在化学领域的应用。(同分异构体)
6在心理学领域的应用。(1936年,K.Lewin:拓扑心 理学) 7在经济学领域的应用。(税率涨落、商品流通、供 求关系)
8在计算机科学领域的应用。(计算机网络)
注意
开头讲到图论是从七桥问题和哈密顿周游世界等 游戏性问题起家的。我们不可不加分析的瞧不起 游戏性问题,它们有时可以成为一门很有生命力 的学科的种子。 这是许多及其有用的数学理论起源的典型例子: 对一些微不足道的最初解答,开始只是出于对数 学无心插柳的好奇心,结果却培植出一颗根深叶 茂的参天大树,并最终成为人类知识海洋中的一 座宝藏!
四色问题
1852年,刚从伦敦大学毕业的Francis Guthrie提 出了四色猜想。 1878年著名的英国数学家Cayley向数学界征求解答。 此后数学家 Heawood 花费了毕生的精力致力于四 色研究,于1890年证明了五色定理(每个平面图都 是5顶点可着色的)。 直到1976年6月,美国数学家 K. Appel与 W. Haken, 在3台不同的电子计算机上,用了1200小时,才终 于完成了“四色猜想”的证明,从而使"四色猜想" 成为了四色定理。
3、计算机系统的认知、分析、设计和应用能力 村庄被抽象成一个结点
二、本课程特点
课程名称: 《图论及其应用》
特点:
1.蕴含了丰富的思想、漂亮的图形和巧妙的证明;
2. 涉及的问题多且广泛,问题外表简单朴素,本 质上却十分复杂; 3.解决问题的方法千变万化,非常灵活,常常是一 种问题一种解法。
三、教学内容
A村:男性居民人数、女性居 民人数、党员人数、邮编、 逻辑思维:人们对客观规律的认识。认识客观世 11公里 3.5公里 区号、……
E村 10 C村
界的规律需要逻辑思维。逻辑思维包括概念、判 D村 5公里 断和推理。
13公里 3公里
村庄情况登记
村庄被抽象出来更丰富的信息 A村 10公里 B村 2、算法设计与分析能力、程序设计能力 邮递员投递:求A村到C村的最优投递路线
Welcome to you!
Graph Theory
图 论
●这门课讲什么? ●有什么地位? ●课程重点是什么? ●如何学好这门课? ……
提纲
大学学习几个注意点 本课程特点 本课程教学内容 本课程教学目的 教学方式 考核方式 学习要求 参考书
一、几个注意点
★课程学习要成体系
图论的基本概念 哥尼斯堡七桥问题 欧拉图、哈密顿图问题 最短路径问题 中国邮递员问题 人员分派问题
稳定匹配问题
竞赛图问题
最小费用最大流问题(网络选址问题)
四、教学目的
了解图论的基本原理 掌握图论方法的应用 掌握应用图论方法解决实际问题 初步建立抽象问题图论化方法 掌握与交叉学科之间的联系(运筹、组合数 学、数值分析、网络分析、数学建模等)
Thank you very much!
每学习一门新课程,要设法弄清楚本课程在整个课程 体系中的位置,本课程是做什么用的。每学完一门课 程,能将其与之前学习的课程进行联系,做到知识点 的融会贯通。
★ 注重专业能力的培养
1、计算思维能力-抽象思维能力、逻辑思维能力
抽象思维:抽取事物本质的、关注的方面进行研究, 抛弃其他不关心或者细节的部分。
货郎担问题
用图论的术语说,就是在一个赋权完全图 中,找出一个具有最小权的Hamilton 圈 (包含图G的每个顶点的圈)。 这个问题目前还没有有效的算法。 Hamilton问题是图论的一个重要问题,图 论中的许多问题,包括四色问题、图的因 子问题,最终都与Hamilton问题有关。
四色定理
中国邮递员问题
1962年中国组合数学家管梅谷教授提出 了著名的“中国邮递员问题”。 一个邮递员从邮局出发,要走完他所管 辖的每一条街道,然后返回邮局。那么 如何选择一条尽可能短的路线。
最短网络问题
如何用最短的线路将三部电话连起来? 此问题可抽象为设△ABC为等边三角 形,,连接三顶点的路线(称为网络)。 这种网络有许多个,其中最短路线者显 然是二边之和(如AB∪AC)。
图论的历史
近代图论的历史可追溯到18世纪的七桥问题—穿过 Kö nigsberg城的七座桥,要求每座桥通过一次且仅 通过一次。
C
A D
B
哥尼斯堡七桥示意图
Euler1736年证明了不可能存在这样的路线。
Kö nigsberg Bridge Problem C
陆地为点
C
A D
B
桥为边
A
B D
Q: 是否存在一种走法,可以走过每条边一次,并回 到起点? Ans: 因为每次经过一个点,都需要从一条边进入该点,再用另 一条边离开,所以经过每个点一次要使用掉一对边。 每个点上连接的边数必须是偶数才行 此种走法不存在
人员分配问题
设某企业有n个员工和n个工作,已知每个员工 各胜任一些工作。能否使每个员工都分派到一 件他胜任的工作?
稳定匹配问题
假设有一百个男人和一百个女人,每个男人都凭自己 的好恶给每个女人打分,最爱a,其次爱b,再次爱c (假定没有相同的)…给个女人也同样给每个男人打 分….然后就是求婚过程…如此周而复始直到最后大 家都订了婚,便一起结婚。问是否每个人都可以找到 自己的意中人?
拉姆赛理论
1958年,美国的《数学月刊》上登载着这 样一个有趣的问题:“任何6个人的聚会, 其中总会有3个人相互认识,或3个人相互 不认识”。 用6个顶点表示6个人,用红色连线表示两 者相识,用蓝色连线表示两者不相识。于 是问题化为下述命题:
拉姆赛理论
对6个顶点的完全图K6任意进行红、蓝两 边着色,则图中一定存在一个同色三角 形。
Ramsey数
推广为一般问题: 给定任意正整数a和b,总存在一个最小 整数 r (a ,b),使得r (a ,b) 个人中或者有 a 个人互相认识,或者有 b 个人互相不 认识。称 r(a,b) 为Ramsey数。
最短路径问题
假设要在计算机上建立一个交通资讯系统,这 个系统可以回答旅客提出的各种问题。如,给定连 接若干城市的铁路网,找一条给路径或者 最省钱的路径等。那么可以用图的结构来表示实际 交通网络,可对边赋以权值,权值表示两地之间的 距离,或途中所需时间或交通费用等等。
网络流问题
1956年Ford 和Fulkerson 提出了关于网络 流问题的一个重要定理。 最大流最小割定理:在任何网络中,最大 流的值等于最小割的容量。 由这个定理可以引出求网络最大流的一个 算法——标号法。 1970年,Edmonds和Karp 对标号程序加 以改进,使之成为一个好的算法。
平面图与非平面图
国王遗嘱大意:把国土分成5块给儿子,规定各块 之间都要有边界。儿子又提出在自己分到的领土 上都要修一个王宫,并且各王宫之间都要有路直 接相通而不能交叉。
能否解决? 用点表示王宫,用线表 示王宫间的道路,便抽 象成图。问题变成该图 是否为平面图?
图论的主要应用
1 电网络、通讯网络的分析与综合。 2印刷电路与集成电路的布线和测试。
八、参考书
参考教材:
1.《图论》
北京理工大学出版社
2. 《应用图论》 国防科技大学
第一讲
序
图论概述 图论发展历史 图论中典型的问题(欧拉图与哈密顿图、四色定理、
拉姆赛问题、 最短网络问题、匹配定理、平面图)
图论的应用
图论概述
现代数学可以分为两大类:一类是研究 连续对象的,如分析、方程等;另一类 就是研究离散对象的组合数学。 计算机出现以后,由于离散对象的处理 是计算机科学的核心,研究离散对象的 组合数学得到迅猛发展。
图论概述
图论模型属于离散类数学模型,是数学模 型中比较容易接受的一类模型,具有直观 性、趣味性和简洁性。 图论模型属于较为近代的前沿性数学知识, 具有强烈的为学生接受的数学建模味道, 对于培养学生通过建模解决实际问题的能 力与学习兴趣不可多得的知识内容,越来 越受数学家和建模工作者的喜爱。
环球旅行与哈密顿圈
在一个画在平面上有20个顶点的图中,把所有20个 顶点都标上城市名,旅游者从某个城市出发,找一 条经过所有城市但只能经过一次的闭合回路。该回 路称为哈密顿圈。环球旅行就是寻找哈密顿圈。
环球旅行问题的答案:
货郎担问题
一个货郎要去若干城镇卖货,然后
回到出发地,给定各城镇之间所需 的旅行时间后,应怎样计划他的路 线,使他能去每个城镇恰好一次而 且总时间最短?
匹配问题的例子
例 乔太守乱点鸳鸯谱问题 大宋景佑年间,杭州府有孙、刘、裴、徐四家, 孙家有一女一儿分别为孙珠姨和孙润;刘家有一儿 一女分别为刘璞和刘慧娘;裴家有一儿裴政;徐家 有一女徐文姑。就他们几家儿女的婚姻问题告到衙 门府,乔太守最终乱点鸳鸯谱,成为千年佳话。 二部完美匹配 • 存在性?
• 算法?
A
B
C
最短网络问题
但若增加一个周转站(新点P),连接4点的 新网络的最短路线为PA+PB+PC。最短新 路径之长N比原来只连三点的最短路径O要短。 这样得到的网络不仅比原来节省材料,而且稳 定性也更好。
A
P
B
C
网络流问题
随着中国经济快速的增长,城市化是未来中国 的发展方向。人大通过的“十五”规划,把物 流业作为战略重点列入要大力发展的新兴服务 产业。如何制定一个运输计划使生产地到销售 地的产品输送量最大。这就是一个网络最大流 问题。
3 运筹学、数值分析、数学建模、拓扑学等。
4 在理论物理和统计力学的应用。(杨振宁、李政道)
5 在化学领域的应用。(同分异构体)
6在心理学领域的应用。(1936年,K.Lewin:拓扑心 理学) 7在经济学领域的应用。(税率涨落、商品流通、供 求关系)
8在计算机科学领域的应用。(计算机网络)
注意
开头讲到图论是从七桥问题和哈密顿周游世界等 游戏性问题起家的。我们不可不加分析的瞧不起 游戏性问题,它们有时可以成为一门很有生命力 的学科的种子。 这是许多及其有用的数学理论起源的典型例子: 对一些微不足道的最初解答,开始只是出于对数 学无心插柳的好奇心,结果却培植出一颗根深叶 茂的参天大树,并最终成为人类知识海洋中的一 座宝藏!
