05第5讲 图论模型
图论模型

图论模型此模型解决的是垃圾清运路线的最佳方案。
1、收集路线方案:用中国邮递员问题解决达到最佳经济效益和环保效果的垃圾清运路线问题是在车辆限载约束条件下的最优路径选择的问题,同时本项目涉及到深圳市南山区38个垃圾中转站,而每个中转站所覆盖的收集区域的选取需要满足最大覆盖域(即总体能够消耗最少资源来覆盖整片区域),收集区域的划分又要同时考虑实地情况(地形、路线、用地性质、人流量、垃圾量等)。
1.1模型建立:为简化问题讨论,在转运站覆盖区域的划分的问题上,需要运用“最大覆盖”及“模糊划分”的思想,具体划分出每个转运站所对应 的片区的近似最优划分。
将问题简化后,所要求解的问题就是每个垃圾中转站所对应的每个小分区的街道所构成的收集网络的垃圾收运车辆优化路线的问题,也就是要求每一条街道至少有一辆垃圾收运车经过并且车辆重复走过的街道的总长度最小化的问题。
对于这个问题,我们采用图论模型,将每个小分区的街道及收集点简化成网络图(也叫赋权图)。
对于网络图中的圈用圈点来表示,计算各个圈点的垃圾量(也即围成圈的街道上的垃圾量的和),将相邻(有公共顶点)的圈点用线连接起来,这就构成了圈点图。
遵循以垃圾中转站为圆心沿径向发散求最小生成树的原则将圈点图中相邻的圈点组块,使得每块的垃圾量近似于垃圾收运车载限,对应于圈点分块,网络图分开成了各个子网络图,对于每一个子网络图即可利用欧拉回路求得其最小路径线路。
现在给出最短欧拉回路求解举例:图代表的是其中一个收集子网络图,其中直线表示车辆需要经过的街道,线上的数字表示该街道的长度,该子网络图各条街道的垃圾量之和近似于收集车辆的载限。
现要求的是车辆经过每一条街道至少一次的最短回路,现在对这个问题分步求解:第一步:找出图中的奇点,如图中橙色小圆点所在处为奇点。
第二步:将各对奇点沿街道连接起来,使得连接奇点的所有街道总长度最小。
如下图绿色线条:第三步:得出经过每条街道至少一次的最短路径长度为所有街道的总长加上连接奇点的街道的长度。
图论模型实例优秀课件

存在,考虑增环,增环后权值应减小 ▪ 换枝原则 环路上某顶点长出一条枝,该枝末梢和环路另
一顶点接近,可考虑换枝
问题1的分析与求解--最小生成树法
问题1的分析与求解 --TSP方法
公路边的数字为该路段的公里数.
问题分析:
本题给出了某县的公路网络图,要求的是在不 同的条件下,灾情巡视的最佳分组方案和路线.
将每个乡(镇)或村看作一个图的顶点,各乡 镇、村之间的公路看作此图对应顶点间的边,各条 公路的长度(或行驶时间)看作对应边上的权,所 给公路网就转化为加权网络图,问题就转化图论中 一类称之为旅行售货员问题,即在给定的加权网络 图中寻找从给定点O出发,行遍所有顶点至少一次 再回到点O,使得总权(路程或时间)最小.
图论模型实例
专题
❖ 图的表示与锁具问题 ❖ 最小生成树、TSP和灾区巡视问题 ❖ 最短路、网络流和运输问题 ❖ 作业
图的表示与锁具问题
不积硅步,无以至千里 --荀子·劝学
图的矩阵表示
邻接矩阵: (以下均假设图为简单图).
1) 对无向图 G,其邻接矩阵 A(aij),其中:
1, aij 0,
若vi与vj相邻 , 若vi与vj不相.邻
i1
定义 称
为最大容许均衡度.
为该分组的实际均衡度.
显然0 0 1,0越小,说明分组的均衡性越 好. 取定一个 后,0与 满足条件 3)的分组是
一个均衡分组. 条件 4)表示总巡视路线最短.
此问题包含两方面:a)对顶点分组, b)在每组中求 (单个售货员)最佳旅行售货员回路.
因单个售货员的最佳旅行售货员回路问题不存在多 项式时间内的精确算法.因此多个售货员的最佳旅行售 货员回路问题也不存在多项式时间内的精确算法.
图论模型(最优连线问题最短路问题)PPT课件

(3)当(2)不能继续执行时停止。
(其思想是:在剩余边集中找边权最小的边添加到生成树中,同时又 不能产生回路即以局部的最优谋求全局的最优。)
上述的描述实际上是最小生成树的逐 步生长过程,上例的最小生成树如下:
A 5
1 3
D
8 E
水厂
9
B 7
6 10
著名数学家欧拉
七桥问题
图的基本概念
无 向 图
1 定义:由顶点和边组成的图形称为图。 有 向 图
赋
权
图
2 边e与顶点u、v相关联。顶点u与v相邻。
e
u
边e1与e2相邻。
e1
v
e2
u=v时,边e称为环。
3度
定义:与顶点v关联的边的数目称为顶点的度数, 记为d(v)。(注:环算2度。)
对于有向图的顶点的度数,还可分为出度 d ( v ) 和 入度 d ( v ) 。
u3
u6
0 8
1
6
u8
5
10
5
2
6
1
1
u4
10
u7
第五步:min{8,11,11,9,8,12,7,11,11},u3。
u2
1
2
u5
3
2
7
5
3
9
u1
u3
u6
0
8
7
1
6
u8
5
10
5
2
6
1
1
u4
10
u7
第六步:min{11,12,11,11,9},u7。
u2
1
2
数学建模图论模型

任意两点均有通路的图称为连通图。
连通而无圈的图称为树,常用T=<V,E>表示树。
若图G’是图 G 的生成子图,且G’又是一棵树, 则称G’是图G 的生成树。
例 Ramsey问题
图1
图2
并且常记: V = v1, v2, … , vn, |V | = n ; E = {e1, e2, … , em}ek=vivj , |E | = m
称点vi , vj为边vivj的端点 在有向图中, 称点vi , vj分别为边vivj的 始点和终点. 该图称为n,m图
8
对于一个图G = V, E , 人们常用图形来表示它, 称其 为图解 凡是有向边, 在图解上都用箭头标明其方向.
4、P'代替P,T'代替T,重复步骤2,3
定理2 设 T为V的子集,P=V-T,设 (1)对P中的任一点p,存在一条从a到p的最短路径,这条路径仅有P中的
点构成, (2)对于每一点t,它关于P的指标为l(t),令x为最小指标所在的点, 即:
l(x)mli(tn )} t{ ,T
(3)令P’=P Ux,T’=T-{x},l’(t)表示T'中结点t关于P'的指标,则
解:用四维01向量表示人,狼,羊,菜例在过河西河岸问的题状态(在
岸则分量取1;否则取0),共有24 =16 种状态; 在河东岸 态类似记作。
由题设,状态(0,1,1,0),(0,0,1,1),(0,1,1,1)是不允许的
其对应状态:(1,0,0,1), (1,1,0,0),(1,0,0,0)也是不允许
图论模型及其解答

各种图论模型及其解答摘要:本文用另一种思路重新组织《图论及其应用》相关知识。
首先,用通俗化语言阐述了如何对事物间联系的问题进行图论建模;接着从现实例子出发,给出各种典型图论模型,每种图论模型对应于图论一个重要内容;再者,介绍相关知识对上述提到的图论模型涉及的问题进行解答;最后,补充一些图论其他知识,包括图论分支、易混概念。
符号约定:Q(Question)表示对问题描述,M(Modeling)表示数学建模过程,A(Answer)表示原问题转化为何种图论问题。
一、引言图论是研究点、线间关系的一门学科,属于应用数学的一部分。
现实生活中,凡是涉及到事物间的关系,都可以抽象为图论模型。
点表示事物,连线表示事物间的联系。
整个求解过程如下:原问题——>图论建模——>运用图论相关理论求解——>转化为原问题的解整个过程关键在于图论建模,所谓图论建模,就是明确点表示什么,连线表示什么,原问题转化为图论中的什么问题。
存在以下两种情况:①若事物间联系是可逆的(比如双行道,朋友),则抽象成无向图②若事物间联系是不可逆的(比如单行道,状态转化不可逆),则抽象成有向图如果需要进一步刻画事物间的联系(比如城市间的距离),就给连线赋一个权值,从而抽象成赋值图。
综上,根据实际问题,可建模成下列图论模型的一种:无向赋权图、有向赋权图、无向非赋权图、有向非赋权图。
例1.宴会定理:任何一宴会中,一定存在两个人有相同的数量朋友M:点表示人,连线表示当且仅当该两个人是朋友A:问题转化为任何一个图一定存在两个顶点的度相等二、图论模型接下来介绍若干典型的图论模型,每种模型几乎对应于图论的一个重要内容,这些内容将在第三章进行讨论,也就给出了这些模型的解答思路。
2.1 偶图模型凡涉及两类事物间的联系(即只考虑两类事物间的联系,而不考虑同类事物间的联系),均可抽象成偶图模型。
作图时,将两类事物分成两行或者两列。
这类模型通常被包含在后续的模型中,但因许多现实问题可抽象成该模型,所以单列出来讨论。
图论模型

图论模型图是为了解决一些具体问题而产生的模型,这可以从它的发源“哥尼斯堡的七桥问题”看到。
一个图表示了某些对象集合元素之间的关系,所以它被广泛用来作为许多与对象的离散安排有关问题的模型。
它已在物理、化学、经济、管理、信息、控制等所有离散系统中应用。
本章仅介绍几类图论模型。
9.1 连线问题一、问题的背景与提出现实社会中,我们可以看到,公路、铁路、通信、输电线路等的建设中,都涉及到“如何设计建造一个既能畅通无阻又造价小的网络”问题,即连线问题。
二、模型假设与符号说明假设要建造一个连接若干城镇的通信网络,第i个城镇与第j个城镇之间直通线路的造价为cij。
三、模型的建立与求解把每个城镇看作是一个点v;两个城镇直通线路看作边e;城镇vi与城镇vj之间直通线路的造价看作边vivj的权w(vivj)=cij,这样我们得到了一个赋权图G。
设计一个总造价最小的通信网络,就转化为:在赋权图G,找出具有最小权的连通生成子图,即寻找赋权图的最小权的生成树(最优数)。
1956年Kruskal给出了一种求最优树的算法,称为避圈法,算法如下: 10 选择边e1,使得w(e1)尽可能小;20 若已选定边e1, e2, …, ei, 则从边集E\{e1, e2, …, ei}中选取ei+1,使(ⅰ)G[{e1, e2, …, ei+1}]为无圈图;(ⅱ)w(ei+1)是满足(ⅰ)的尽可能小的权, 30 当20不能继续执行时停止。
对于p个点ε条的赋权图G,该算法就是先将赋权图的边按权的递增顺序排列:a1, a2, …, aε设e1=a1, e2=a2, 检查a3,如果a3与e1, e2不构成圈,则令e3=a3,否则放弃a3,检查a4,1。
图论模型简介
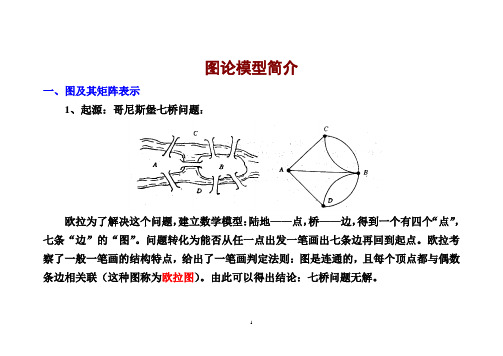
图论模型简介一、图及其矩阵表示1、起源:哥尼斯堡七桥问题:欧拉为了解决这个问题,建立数学模型:陆地——点,桥——边,得到一个有四个“点”,七条“边”的“图”。
问题转化为能否从任一点出发一笔画出七条边再回到起点。
欧拉考察了一般一笔画的结构特点,给出了一笔画判定法则:图是连通的,且每个顶点都与偶数条边相关联(这种图称为欧拉图)。
由此可以得出结论:七桥问题无解。
2、基本概念:图(graph):由顶点和边(又称线,边的两端必须是顶点)组成的一个结构。
邻接:一条边的两个端点称是邻接的;关联:边与其两端的顶点称是关联的。
无向图(graph):边无方向的图;有向图(digraph):边有方向的图。
路(path):由相邻边组成的序列,其中中间顶点互不相同。
圈(cycle):首、尾顶点相同的路,即闭路。
连通图(connected graph):图中任意两顶点间都存在路的图。
树(tree):无圈连通图完全图(complete graph):任意两个顶点之间都有边相连的无向图,记为K n。
竞赛图(tournament):由完全图给每条边定向而得到的有向图。
二部图(bipartite graph):图的顶点分成两部分,只有不同部分顶点之间才有边相连。
图G的子图H(subgraph):H是一个图,H的顶点(边)是图G的顶点(边)。
网络(Network):边上赋了权的有向图。
3、图的矩阵表示无向图 有向图01000101100101101100010⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡011101000001001000001104、著名的图论问题例1 最短路问题(shortest path problem)出租车司机要从城市甲地到乙地,在纵横交错的路中如何选择一条最短的路线?例2 最小生成树问题(minimum-weight spanning tree problem)为了给小山村的居民送电,每户立了一根电杆,怎样连接可使连线最短?例3 中国邮递员问题(chinese postman problem)一名邮递员负责投递某个街区的邮件。
图论模型

65
2 3 4 2 2 3 4 5 70 2 3 4 2 4 2 3 4 5 1 3 4 5
1 80
50 2 30
5
100
20
3
第三次迭代后得到:
130 0 50 0 80 ( 3) 30 0 20 110, D 0 70 65 115 100 120 0
2 3 4 5 2 3 4 5 2 3 4 5 2 3 4 5 2 3 4 5
2 3 4 5 2 3 4 5 2 3 4 5 2 3 4 5 1 3 4 5
3
第二次迭代后得到:
1 0 50 130 1 0 80 ( 2) ( 2) 30 0 20 110, P 1 D 0 70 1 0 65 115 100 1
1 1 ( 3) 1 P 1 1
2 3 4 2 2 3 4 5 2 3 4 2 2 3 4 5 1 3 3 5
第四次迭代后得到:
130 0 50 0 80 ( 4) 30 0 20 90 , D 0 70 65 115 100 120 0
65
1 1 ( 4) 1 P 1 1 2 3 4 2 2 3 4 5 2 3 4 4 2 3 4 5 1 3 3 5
1 80
50 2 30
5 70 4
100
20
3
第五次迭代后得到:
50 230 250 130 0 145 0 180 200 80 (5) 155 30 0 20 90 , D 135 185 170 0 70 65 115 100 120 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
目标函数是使得 z wij xij 最小化。
i 1 j 1
n
n
约束条件分成如下 4 类: (1)根 v1 至少有一条边连接到其他的顶点,
v1
4 2 4 5 3
v2
1 3 4 4 2
v3
v1
1
v8
1
v0
1
v4
1
v8
v7
2
v2 1
v0
1
v3 1 v4 v5
5
v7
2 v6 (a)
5
v5
2 3
v6
2
图 5.4 生成的最小生成树
v0 , v1 ,
求最小生成树的 Kruskal 算法的 MATLAB 程序如下(用 MATLAB 计算时,顶点 : , v8 分别编号为 1, 2, ,9 ) clc, clear a=zeros(9); a(1,[2:9])=[2 1 3 4 4 2 5 4]; a(2,[3 9])=[4 1]; a(3,4)=1; a(4,5)=1; a(5,6)=5; a(6,7)=2; a(7,8)=3; a(8,9)=5; a=a'; %转成 MATLAB 需要的下三角元素 a=sparse(a); %转换为稀疏矩阵 b=graphminspantree(a,'Method','Kruskal') %注意要写 Kruskal 算法,否则使用 Prim 算法 L=sum(sum(b)) %求最小生成树的权重 view(biograph(b,[],'ShowArrows','off','ShowWeights','on')) %画最小生成树,
顶点vi 与v j 之间边的权重, (vi , v j ) E wij 0 ) , vi 与v j 之间无边时. (或
注 5.1
(1)
当两个顶点之间不存在边或弧时,根据实际问题的含义或算法需要,对应的权 重可以取为 0 或 。 当顶点与顶点之间的关系是对称关系时,对应的图是无向图,除非特殊说明,我们所说 的图都是指无向图。当顶点与顶点之间的关系是非对称关系时,对应的图为有向图。 定义 5.3 有向图 有向图 D 是一个二元组,记为 D (V , A) ,其中 V 为顶点集合, A 为弧(带箭头的边) 的集合。 定义 5.4 赋权有向图 赋权有向图 D 是一个三元组,记为 D (V , A,W ) ,其中 V {v1 , , vn } 为顶点集合, A 为 弧(带箭头的边)的集合, W (wij )nn 为邻接矩阵,其中
v6
v3
v5
图 5.2 非赋权有向图
clc, clear a=zeros(6); a(1,[2 3])=1; a(2,3)=1; a(3,[2 5])=1; a(4,[2 6])=1; a(5,[2 4 6])=1; a(6,5)=1; b=sparse(a); h=biograph(b,[],'ShowArrows','on') %生成图形对象 set(h,'LayoutType','equilibrium'); %设置属性:图形的布局是平衡的 view(h) %显示图形
顶点vi v j的弧的权重, 当vi v j 有弧时 wij 0 ) , 当vi v j 无弧时. (或
(2)
当 G (或 D )为非赋权图时,也可以看成赋权图,邻接矩阵
1, 当vi 与v j间有边(弧)时, wij 0, 当vi 与v j间无边(弧)时.
例 5.2 0 0 0 A 0 0 0
图 5.2 所表示的有向图的邻接矩阵
1 0 1 1 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 , 1 1 0
用 MATLAB 重新画出图 5.2。
v2
v4
ቤተ መጻሕፍቲ ባይዱv1
用 MATLAB 重新画出图 5.1。 clc, clear a=zeros(5); %邻接矩阵初始化 a(1,[2:5])=[9 2 4 7]; a(2,[3 4])=[3 4]; %输入邻接矩阵的上三角元素 a(3,[4 5])=[8 4]; a(4,5)=6; a=a'; b=sparse(a) %变成下三角矩阵,并转化为稀疏矩阵 h=biograph(b,[],'ShowWeights','on','ShowArrows','off') %生成图形对象 set(h,'LayoutType','equilibrium'); %设置属性:图形的布局是平衡的 view(h) %显示图形
3
v1
4 2 4 5 3
v2
1 3 4 4 2
v3
v1
1
v8
1
v0
1
v4
1
v8
v7
2
v2 1
v0
1
v3 1 v4 v5
5
v7
2 v6
5
v5
2 3
v6 (b)
2
图 5.3 连通图及对应的最小生成树
解 列:
这就是一个最小生成树问题,用 Kruskal 算法求解。先将边按大小顺序由小至大排
(v0 , v2 ) 1 , (v2 , v3 ) 1 , (v3 , v4 ) 1 , (v1 , v8 ) 1 , (v0 , v1 ) 2 , (v0 , v6 ) 2 , (v5 , v6 ) 2 , (v0 , v3 ) 3 , (v6 , v7 ) 3 , (v0 , v4 ) 4 , (v0 , v5 ) 4 , (v0 , v8 ) 4 , (v1 , v2 ) 4 , (v0 , v7 ) 5 , (v7 , v8 ) 5 , (v4 , v5 ) 5
1
邻接矩阵的对应元素为 0。 5.1.3 例题 例 5.1 图 5.1 所示的图,其邻接矩阵为
v5
0 9 A 2 4 7
9 2 4 7 0 3 4 0 3 0 8 4 4 8 0 6 0 5 6 0
6 7
v1
4 4 2 8 3
v3
v4
9
v2
4
图 5.1 赋权无向图
5.3
最小生成树
5.3.1 prim 算法构造最小生成树 构造连通赋权图 G (V , E,W ) 的最小生成树, 设置两个集合 P 和 Q ,其中 P 用于存放 G 的 最小生成树中的顶点,集合 Q 存放 G 的最小生成树中的边。令集合 P 的初值为 P {v1} (假 设构造最小生成树时, 从顶点 v1 出发) , 集合 Q 的初值为 Q (空集) 。 prim 算法的思想是, 从所有 p P , v V P 的边中,选取具有最小权值的边 pv ,将顶点 v 加入集合 P 中,将边 pv 加入集合 Q 中,如此不断重复,直到 P V 时,最小生成树构造完毕,这时集合 Q 中包 含了最小生成树的所有边。 prim 算法如下: (1) P {v1} , Q ; (2)while P ~ V 找最小边 pv ,其中 p P, v V P ; P P {v} ; Q Q { pv} ; end 5.3.2 Kruskal 算法构造最小生成树 科茹斯克尔(Kruskal)算法是一个好算法。Kruskal 算法如下: (1)选 e1 E ,使得 e1 是权值最小的边。 (2)若 e1 , e2 , , ei 已选好,则从 E {e1 , e2 , , ei } 中选取 ei 1 ,使得 i) {e1 , e2 , , ei , ei 1} 中无圈,且 ii) ei 1 是 E {e1 , e2 , , ei } 中权值最小的边。 (3)直到选得 e|V |1 为止。 5.3.2 最小生成树举例 例 5.3 一个乡有 9 个自然村,其间道路及各道路长度如图 5.3 所示,各边上的数字表 示距离,问架设通讯线时,如何拉线才能使用线最短。
(3)
5.1.2 MATLAB 中邻接矩阵的表示 在 MATLAB 中邻接矩阵以稀疏矩阵的格式存储。 在数学上,稀疏矩阵是指矩阵中零元素很多,非零元素很少的矩阵。对于计算机的数 据结构,稀疏矩阵只是一种存储格式,只存放非零元素的行地址、列地址和非零元素本身的 值,即按如下方式存储 (非零元素的行地址,非零元素的列地址) ,非零元素的值。 在 MATLAB 中无向图和有向图邻接矩阵的使用上有很大差异。 对于有向图,只要写出邻接矩阵,直接使用 MATLAB 的 sparse 命令,把邻接矩阵转化 为稀疏矩阵的表示方式,供 MATLAB 工具箱使用。 对于无向图,由于邻接矩阵是对称阵,MATLAB 中只使用邻接矩阵的下三角元素,即 需要 MATLAB 先截取邻接矩阵的下三角部分,再用 sparse 命令转化为稀疏矩阵。 在 MATLAB 中,普通矩阵使用 sparse 命令变成稀疏矩阵,稀疏矩阵使用 full 命令变成 普通矩阵。 另外要注意,在数学上按照邻接矩阵的定义式(1),如果两个顶点间无边连接,对应的 元素为 0 或 。 在 MATLAB 工具箱中, 由于使用稀疏矩阵, 隐含着两个顶点间无边连接时,
5.2
MATLAB 图论工具箱的命令
2
MATLAB 图论工具箱的命令见表 5.1。
表 5.1 命令名 graphallshortestpaths graphconncomp graphisdag graphisomorphism graphisspantree graphmaxflow graphminspantree graphpred2path graphshortestpath graphtopoorder graphtraverse MATLAB 图论工具箱的相关命令 功能 求图中所有顶点对之间的最短距离 找无向图的连通分支,或有向图的强(弱)连通分支 测试有向图是否含有圈,不含圈返回 1,否则返回 0 确定两个图是否同构,同构返回 1,否则返回 0 确定一个图是否是生成树,是返回 1,否则返回 0 计算有向图的最大流 求图的最小生成树 把前驱顶点序列变成路径的顶点序列 求图中指定的一对顶点间的最短距离和最短路径 执行有向无圈图的拓扑排序 求从一顶点出发,所能遍历图中的顶点
