数学建模中常见的十大模型
数学建模常用模型方法总结
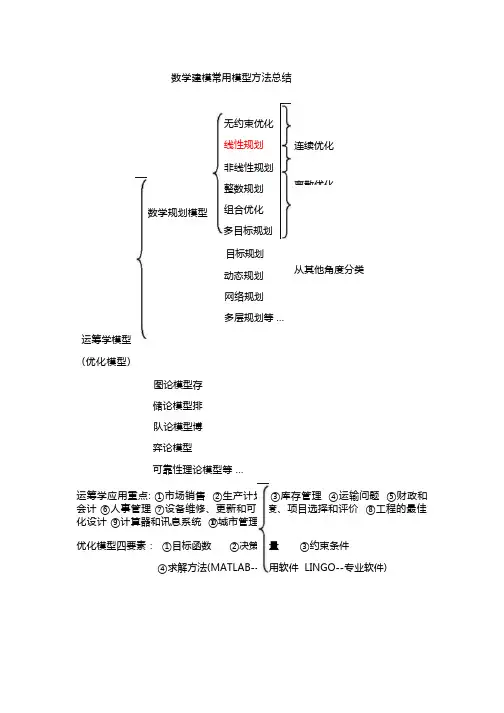
数学建模常用模型方法总结无约束优化 线性规划 非线性规划 整数规划组合优化 多目标规划 目标规划 动态规划 网络规划 多层规划等 …运筹学模型 (优化模型)图论模型存 储论模型排 队论模型博 弈论模型可靠性理论模型等 …运筹学应用重点: ①市场销售 ②生产计划 ③库存管理 ④运输问题 ⑤财政和 会计 ⑥人事管理 ⑦设备维修、更新和可靠度、项目选择和评价 ⑧工程的最佳 化设计 ⑨计算器和讯息系统 ⑩城市管理优化模型四要素： ①目标函数 ②决策变量 ③约束条件④求解方法(MATLAB--通用软件 LINGO--专业软件)连续优化离散优化从其他角度分类数学规划模型概率论与数理统计模型多元分析模型假设检验模型相关分析回归分析聚类分析、主成分分析因子分析判别分析典型相关性分析对应分析多维标度法方差分析贝叶斯统计模型时间序列分析模型决策树逻辑回归马尔萨斯人口预测模型Logistic 人口预测模型灰色预测模型回归分析预测模型预测分析模型差分方程模型马尔可夫预测模型时间序列模型插值拟合模型神经网络模型系统动力学模型(SD)模糊综合评判法模型数据包络分析综合评价与决策方法灰色关联度主成分分析秩和比综合评价法理想解读法等旅行商(TSP)问题模型背包问题模型车辆路径问题模型物流中心选址问题模型经典 NP 问题模型路径规划问题模型着色图问题模型多目标优化问题模型车间生产调度问题模型最传染病模型微分方程模型人口预测控制模型经济增长模型优树问题模型二次分配问题模型模拟退火算法(SA)遗传算法(GA)智能算法(启发式)神经网络算法常用算法模型蒙特卡罗算法元胞自动机算法穷蚁群算法(ACA)举搜索算法小波分析算法确定性数学模型三类数学模型随机性数学模型。
比较好用的数学模型
比较好用的数学模型
在实际生活中，数学模型被广泛应用于各种问题的解决。
以下是一些比较好用的数学模型：
1. 线性回归模型：用于预测一个因变量与一个或多个自变量之间的线性关系。
2. 逻辑回归模型：用于预测一个二元因变量与一个或多个自变量之间的关系。
3. 时间序列模型：用于预测时间上的变化，包括季节性和趋势性变化。
4. 聚类模型：用于将一组数据分成不同的群组，每个群组内数据的相似性最大，而不同群组之间的差异最大。
5. 决策树模型：用于帮助做出决策，通过将数据分成不同的子集并逐步做出决策。
这些模型都有着广泛的应用，可以帮助人们更好地理解和解决各种实际问题。
但是，在使用这些模型时，我们需要注意模型的局限性，以及模型预测的不确定性。
- 1 -。
数学建模中常见的十大模型讲课稿
数学建模中常见的十大模型数学建模常用的十大算法==转(2011-07-24 16:13:14)转载▼1. 蒙特卡罗算法。
该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用MA TLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法，竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法：模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的，数据可以是连续的，而计算机只能处理离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话，那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关，即使问题与图形无关，论文中也会需要图片来说明问题，这些图形如何展示以及如何处理就是需要解决的问题，通常使用MATLAB 进行处理。
十大经典数学模型
1、蒙特卡罗算法（该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，是比赛时必用的方法）2、数据拟合、参数估计、插值等数据处理算法（比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具）3、线性规划、整数规划、多元规划、二次规划等规划类问题（建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现）4、图论算法（这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备）5、动态规划、回溯搜索、分支定界等计算机算法（这些算法是算法设计中比较常用的方法，很多场合可以用到竞赛中）6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法（这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用）元胞自动机7、网格算法和穷举法（网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具）8、一些连续离散化方法（很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的）9、数值分析算法（如果在比赛中采用高级语言进行编程的话，那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用）10、图象处理算法（赛题中有一类问题与图形有关，即使与图形无关，论文中也应该要不乏图片的，这些图形如何展示以及如何处理就是需要解决的问题，通常使用Matlab进行处理）以上为各类算法的大致介绍，下面的内容是详细讲解，原文措辞详略得当，虽然不是面面俱到，但是已经阐述了主要内容，简略之处还望大家多多讨论。
数学建模常用算法和模型全集
数学建模常用算法和模型全集数学建模是一种将现实世界的问题转化为数学问题，并通过建立数学模型来求解的方法。
在数学建模中，常常会用到各种算法和模型，下面是一些常用的算法和模型的全集。
一、算法1.线性规划算法：用于求解线性规划问题，例如单纯形法、内点法等。
2.非线性规划算法：用于求解非线性规划问题，例如牛顿法、梯度下降法等。
3.整数规划算法：用于求解整数规划问题，例如分支定界法、割平面法等。
4.动态规划算法：用于求解具有最优子结构性质的问题，例如背包问题、最短路径问题等。
5.遗传算法：模拟生物进化过程，用于求解优化问题，例如遗传算法、粒子群算法等。
6.蚁群算法：模拟蚂蚁寻找食物的行为，用于求解优化问题，例如蚁群算法、人工鱼群算法等。
7.模拟退火算法：模拟固体退火过程，用于求解优化问题，例如模拟退火算法、蒙特卡罗模拟等。
8.蒙特卡罗算法：通过随机抽样的方法求解问题，例如蒙特卡罗模拟、马尔科夫链蒙特卡罗等。
9.人工神经网络：模拟人脑神经元的工作原理，用于模式识别和函数逼近等问题，例如感知机、多层感知机等。
10.支持向量机：用于分类和回归问题，通过构造最大间隔超平面实现分类或回归的算法，例如支持向量机、核函数方法等。
二、模型1.线性模型：假设模型的输出与输入之间是线性关系，例如线性回归模型、线性分类模型等。
2.非线性模型：假设模型的输出与输入之间是非线性关系，例如多项式回归模型、神经网络模型等。
3.高斯模型：假设模型的输出服从高斯分布，例如线性回归模型、高斯朴素贝叶斯模型等。
4.时间序列模型：用于对时间序列数据进行建模和预测，例如AR模型、MA模型、ARMA模型等。
5.最优化模型：用于求解优化问题，例如线性规划模型、整数规划模型等。
6.图论模型：用于处理图结构数据的问题，例如最短路径模型、旅行商问题模型等。
7.神经网络模型：用于模式识别和函数逼近等问题，例如感知机模型、多层感知机模型等。
8.隐马尔可夫模型：用于对具有隐藏状态的序列进行建模，例如语音识别、自然语言处理等。
数学建模中的常见模型
数学建模中的常见模型数学建模综合评价模型是一种通过对各个评价指标进行量化，并将它们按照权重进行加权，最终得到一个综合评价值的方法。
这个模型可以应用于多指标决策问题，用于对被评价对象进行排名或分类。
常见的数学建模综合评价模型包括模糊综合评价模型、灰色关联分析模型、Topsis（理想解法）、线性加权综合评价模型、熵值法和秩和比法等。
模糊综合评价模型是一种基于模糊数学理论的方法，它将评价指标的模糊程度考虑在内，得到一个模糊评价结果。
该模型的步骤包括确定评价指标及其权重、构建模糊评价矩阵、进行模糊运算、得到模糊评价结果。
灰色关联分析模型是一种用于分析指标间关联性的方法，它可以帮助我们确定各个指标对被评价对象的影响程度。
该模型的步骤包括确定关联度计算方法、计算各个指标的关联度、得到综合关联度。
Topsis（理想解法）是一种基于距离的方法，它通过计算每个评价对象与理想解的距离，得到一个综合评价值。
该模型的步骤包括确定正负理想解、计算距离、得到综合评价值。
线性加权综合评价模型是一种常用的多指标决策方法，它将各个评价指标的权重与指标值线性组合起来，得到一个综合评价值。
该模型的优点是简单易操作，计算方便，可以对各个指标的重要性进行量化，并将其考虑在评价中。
但是，该模型的权重确定较为主观，且假设指标之间相互独立，不考虑相关性。
熵值法是一种基于信息熵理论的方法，它通过计算每个指标的熵值，得到一个综合评价值。
该模型的步骤包括计算指标的熵值、计算权重、得到综合评价值。
秩和比法是一种用于处理多指标决策问题的方法，它通过计算指标的秩和比，得到一个综合评价值。
该模型的步骤包括编秩、计算秩和比、得到综合评价值。
根据具体的评价需求和问题特点，我们可以选择合适的数学建模综合评价模型来进行评价。
每个模型都有其优点和缺点，需要根据具体情况进行选择和应用。
<span class="em">1</span><spanclass="em">2</span><span class="em">3</span> #### 引用[.reference_title] - *1* *2* *3* [数学建模——评价模型]()[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_sourc e":"vip_chatgpt_mon_search_pc_result","utm_medium":"di stribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_itemstyle="max-width: 100%"] [ .reference_list ]。
数学建模中的多分类模型
数学建模中的多分类模型是一种用于解决多类别分类问题的算法。
在多分类问题中，输入变量x 对应着多个输出变量y，其中每个输出变量表示一个类别。
多分类模型的目标是根据输入变量x 的取值，预测其对应的输出变量y 的类别。
以下是一些常见的多分类模型：1. 感知机（Perceptron）：感知机是一种二分类模型，它可以扩展到多分类问题。
在多分类问题中，感知机需要训练多个模型，每个模型对应一个类别。
训练过程中，感知机通过调整权重和阈值来实现分类。
2. 决策树（Decision Tree）：决策树是一种基于树结构的分类模型，它可以根据输入变量的取值将数据划分为不同的类别。
在多分类问题中，决策树通常采用树状结构，每个叶子节点对应一个类别。
3. 支持向量机（Support Vector Machine，SVM）：支持向量机是一种基于最大间隔原则的二分类模型，它可以扩展到多分类问题。
在多分类问题中，SVM 通常采用“一对一”（one-vs-one）或“一对多”（one-vs-all）策略。
4. 贝叶斯分类器（Bayesian Classifier）：贝叶斯分类器基于贝叶斯定理，通过计算输入变量x 属于每个类别的概率来确定其类别。
在多分类问题中，贝叶斯分类器可以采用多项式分布或高斯分布等概率模型。
5. 神经网络（Neural Network）：神经网络是一种模拟人脑神经元结构的计算模型，它可以用于多分类问题。
神经网络通过多层神经元组成，每层神经元根据前一层的输入进行计算，最终输出类别。
常见的神经网络有多层感知机（MLP）和深度神经网络（DNN）等。
6. 集成学习（Ensemble Learning）：集成学习是一种组合多个弱分类器的方法，以提高分类性能。
常见的集成学习方法有Bagging（Bootstrap Aggregating，引导随机森林）、Boosting（如Adaboost）等。
7. 聚类算法（Clustering Algorithm）：聚类算法可以将无标签的数据划分为多个类别。
大学生数学建模--常用模型与算法
数学建模常用模型与算法一、常用模型☐（一）、评价模型：☐AHP(层次分析法)（确定权重)、模糊评价、聚类分析、因子分析、主成份分析、回归分析、神经网络、多指标综合评价、熵值法(确定权重)等☐（二）、预测模型：☐指数平滑法、灰色预测法、回归模型、神经网络预测、时间序列模型、马尔科夫预测、差分微分方程☐（三）、统计模型：☐方差分析、均值比较的假设检验☐（四）、方程模型：☐常微分方程、差分方程、偏微分方程、以及各种方程的求解（数值解和解析解）☐（五）运筹优化类：☐线性规划、非线性规划、目标规划、整数规划、图论模型（最短路、最大流、遍历问题等）、排队论、对策论、以及各种模型的算法☐(六)其他模型：☐随机模拟模型、等二、十大算法1、蒙特卡罗算法（该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟可以来检验自己模型的正确性，是比赛时必用的方法）2、数据拟合、参数估计、插值等数据处理算法（比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具）3、线性规划、整数规划、多元规划、二次规划等规划类问题（建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现）4、图论算法（这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备）5、动态规划、回溯搜索、分治算法、分支定界等计算机算法（这些算法是算法设计中比较常用的方法，很多场合可以用到竞赛中）6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法（这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用）7、网格算法和穷举法（网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具）8、一些连续离散化方法（很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的）9、数值分析算法（如果在比赛中采用高级语言进行编程的话，那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用）10、图象处理算法（赛题中有一类问题与图形有关，即使与图形无关，论文中也应该要不乏图片的，这些图形如何展示以及如何处理就是需要解决的问题，通常使用Matlab进行处理）。
数学建模中常见的十大模型
数学建模中常见的十大模型集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#数学建模常用的十大算法==转(2011-07-24 16:13:14)1. 蒙特卡罗算法。
该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用MATLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法，竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法：模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的，数据可以是连续的，而计算机只能处理离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话，那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关，即使问题与图形无关，论文中也会需要图片来说明问题，这些图形如何展示以及如何处理就是需要解决的问题，通常使用MATLAB 进行处理。
美赛数学建模常用模型及解析
美赛数学建模常用模型及解析
数学建模是数学与实际问题的结合，解决实际问题的具体数学模型是数学建模的核心。
以下是一些美赛中常用的数学模型及其解析。
1. 线性规划模型
线性规划模型是一种最常见的优化模型，它的目标是在给定的约束条件下，寻找一个线性函数的最大值或最小值。
线性规划模型可以用于解决资源分配、生产计划、运输优化等问题。
2. 整数规划模型
整数规划是线性规划的一个扩展，它要求决策变量只能取整数值。
整数规划模型可以应用于旅行商问题、装配线平衡问题等需要整数解决方案的实际问题。
3. 动态规划模型
动态规划是一种将多阶段决策问题转化为单阶段决策问题求解的方法。
动态规划模型可以用于解决背包问题、序列对齐问题等需要在不同阶段做出决策的问题。
4. 排队论模型
排队论模型用于分析系统中的排队现象，包括到达率、服务率、系统稳定性等指标。
排队论模型可以用于研究交通流量、电话系统、服务器排队等实际问题。
5. 随机过程模型
随机过程模型用于描述随机事件的演变过程，其中最常见的是马尔可夫链和布朗运动。
随机过程模型可以用于模拟金融市场、天气预测、股票价格等随机变化的问题。
这些模型只是数学建模中常用的几种类型，实际问题通常需要综合运用多种模型进行分析和求解。
对于每个具体的问题，需根据问题的特点和要求选择合适的数学模型，进行合理的建模和求解。
常见的数学模型
常见的数学模型
数学模型是用数学语言描述现实世界的方法。
它在现代科学和工程领域中已经应用广泛，被应用于各种各样的问题，如流体力学，风险评估，经济学和社会科学等领域。
在本文中，我们将介绍一些常见的数学模型。
1. 线性回归模型
线性回归模型是一种用于建立自变量和因变量之间线性关系的模型。
它被广泛应用于各种领域，如经济学、统计学和工程学等。
该模型的主要目标是确定自变量与因变量之间的关系，并使用回归分析来计算出自变量的相关系数和误差项。
2. 微分方程模型
微分方程模型是计算机模拟自然过程最有用的数学工具之一。
它描述了一个系统的受力和受时间影响产生的运动和变化。
这种模型被广泛应用于风险评估、天气预测和医学等领域。
3. 费马数理模型
费马数理模型是半实数规划问题的一种数学模型。
在这种模型中，我们寻找最小的正数整数，满足行列式等于给定的值。
这种模型可以用于信息安全和密码学等领域。
4. 离散事件模型
离散事件模型是一种用于描述因果关系的数学模型。
该模型与连续时间模型不同，它只考虑在特定时间发生的事件。
这种模型可以用于确定一个大型系统的运作方式，并预测其未来的行为。
5. 优化问题模型
优化问题模型是以精确的方式确定最佳方案的一种数学模型。
该模型主要涉及将所需资源最小化或最大化，并找到实现这些目标的最佳方法。
这种模型可以用于政策决策，供应链管理和金融分析等领域。
总之，各种数学模型都是用于解决实际问题和分析复杂数据的有用工具。
每个模型都具有自己的特点和应用场景，需要根据实际问题的性质来选择合适的模型。
十大经典数学模型
1、蒙特卡罗算法〔该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，是比赛时必用的方法〕2、数据拟合、参数估计、插值等数据处理算法〔比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具〕3、线性规划、整数规划、多元规划、二次规划等规划类问题〔建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现〕4、图论算法〔这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备〕5、动态规划、回溯搜索、分支定界等计算机算法〔这些算法是算法设计中比拟常用的方法，很多场合可以用到竞赛中〕6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法〔这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比拟困难，需慎重使用〕元胞自动机7、网格算法和穷举法〔网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具〕8、一些连续离散化方法〔很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进展差分代替微分、求和代替积分等思想是非常重要的〕9、数值分析算法〔如果在比赛中采用高级语言进展编程的话，那一些数值分析中常用的算法比方方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进展调用〕10、图象处理算法〔赛题中有一类问题与图形有关，即使与图形无关，论文中也应该要不乏图片的，这些图形如何展示以及如何处理就是需要解决的问题，通常使用Matlab进展处理〕以上为各类算法的大致介绍，下面的内容是详细讲解，原文措辞详略得当，虽然不是面面俱到，但是已经阐述了主要内容，简单之处还望大家多多讨论。
十大经典数学模型
十大经典数学模型十大经典数学模型是指在数学领域中具有重要意义和广泛应用的数学模型。
这些模型涵盖了不同的数学分支和应用领域，包括统计学、微积分、线性代数等。
下面将介绍十大经典数学模型。
1. 线性回归模型线性回归模型用于描述两个变量之间的线性关系。
它通过最小化观测值与模型预测值之间的差异来拟合一条直线，并用该直线来预测未知的观测值。
线性回归模型在统计学和经济学等领域有广泛应用。
2. 概率模型概率模型用于描述随机事件发生的可能性。
它通过定义事件的概率分布来描述事件之间的关系，包括离散型和连续型概率分布。
概率模型在统计学、金融学、生物学等领域中被广泛应用。
3. 微分方程模型微分方程模型用于描述物理系统、生物系统和工程系统中的变化过程。
它通过描述系统中各个变量之间的关系来解释系统的动态行为。
微分方程模型在物理学、生物学、经济学等领域中具有重要应用。
4. 矩阵模型矩阵模型用于表示线性关系和变换。
它通过矩阵和向量的乘法来描述线性变换，并用于解决线性方程组和特征值问题。
矩阵模型在线性代数、网络分析、图像处理等领域中广泛应用。
5. 图论模型图论模型用于描述物体之间的关系和连接方式。
它通过节点和边的组合来表示图形，并用于解决最短路径、网络流和图着色等问题。
图论模型在计算机科学、电信网络等领域中有广泛应用。
6. 最优化模型最优化模型用于寻找最佳解决方案。
它通过定义目标函数和约束条件来描述问题，并通过优化算法来找到使目标函数最优的变量取值。
最优化模型在运筹学、经济学、工程优化等领域中被广泛应用。
7. 离散事件模型离散事件模型用于描述在离散时间点上发生的事件和状态变化。
它通过定义事件的发生规则和状态转移规则来模拟系统的动态行为。
离散事件模型在排队论、供应链管理等领域中有重要应用。
8. 数理统计模型数理统计模型用于从样本数据中推断总体特征和进行决策。
它通过概率分布和统计推断方法来描述数据的分布和抽样误差，包括参数估计和假设检验等方法。
数学建模模型大全
97
海湾收成模型
多项式拟合
磁带播放模型
高阶多项式敏感度很强
光滑化
115
停止距离模型（2）
三阶样条法。有自然和强制样条两种
134
预测
时间序列
GM(1,1)，指数平滑，线性平滑
因果分析法
聚类分析
灰色关联度分析
聚类分析
因子分析
模拟方法
蒙特卡罗算法
硬币投掷模型
149
汽油储存模型
逆线性样条（可改变随机数范围）
8，打假问题的机理数学分析
9，足球比赛排名问题
10，大象群落的稳定性分析
11，火车便餐最有价格方案
12，施肥效果分析
13，迷宫问题
14，锁具装箱问题
15，密码问题
16，席位分配模型
初等模型
17，双重玻璃窗功效模型
18，储存模型
优化模型
19，森林救火模型
20，消费者均衡模型
21，加工奶制品模型
数学规划模型
196
冲突目标
Minmax与maxmin
机会约束
约束满足概率性>P
矛盾约束
约束相互矛盾
单纯形法
木匠生产模型
注意步骤性。
215
组合模型
参数模型
动态规划
决策法
背包问题
排序问题
多步骤形的规划
数值搜索法
工业流程优化
黄金分割搜索法
还有二分搜索法
233
网络流
最大树
最大流
最短路
关键路线法
网络计划
布点问题
中心问题
重心问题
捕食者-食饵模型
Scheafer微分方程模型
数学建模主要运用的模型
数学建模主要运用的模型
数学建模是一门跨学科的学科，涉及到多个领域和学科的知识。
在数学建模中，模型是非常重要的一部分，它是问题的抽象表现，是对问题的形式化描述。
本文将介绍数学建模主要运用的模型，包括线性规划模型、非线性规划模型、动态规划模型、贝叶斯网络模型、支持向量机模型等。
线性规划模型是数学建模中应用最广泛的一种模型，它适用于各种资源的优化配置问题。
线性规划模型的目标是在一组线性约束条件下，最大化或最小化某一目标函数的值。
其优点在于求解方法简单，计算效率高，适用范围广泛。
非线性规划模型是指目标函数或约束条件中至少有一个是非线
性的规划模型。
非线性规划模型中的问题通常较为复杂，求解难度较大。
但是，非线性规划模型适用范围广泛，可以解决许多线性规划模型无法解决的问题。
动态规划模型是解决最优化问题的一种方法，特别适用于具有重叠子问题和最优子结构的问题。
动态规划模型的优点在于可以减少计算量，提高计算效率，适用于一些复杂的问题。
贝叶斯网络模型是一种概率图模型，用于描述变量之间的条件依赖关系。
贝叶斯网络模型适用于各种领域的问题，包括数据挖掘、机器学习、生物信息学等。
其优点在于可以处理不确定性问题，提高预测的准确性。
支持向量机模型是一种监督学习方法，用于分类和回归分析。
支
持向量机模型的优点在于可以解决高维数据的分类问题，具有较好的泛化能力和鲁棒性。
总之，数学建模主要运用的模型包括线性规划模型、非线性规划模型、动态规划模型、贝叶斯网络模型、支持向量机模型等。
这些模型在不同的问题中都有着广泛的应用，并且不断地得到发展和完善。
数学建模常用的模型
10
图论模型
解决最短路径、最小生成树、最小费用最大流等问题的模型
城市规划、电路设计、通信网络优化等领域
11
现代智能算法
包括神经网络、遗传算法、蚁群算法等，用于解决复杂优化问题
机器学习、数据挖掘、自动化设计等
金融、保险、风险管理等领域
4
优化模型
求解在满足一定约束条件下的最优解，包括线性规划、非线性规划等
经济计划、工程设计、生产管理等领域
5
统计模型
对数据进行统计分析，包括分布检验、均值T检验、方差分析等
数据分析、市场研究、来自动调整模型参数，以实现对新数据的预测和分类
数学建模常用的模型
序号
模型类型
描述
应用场景
1
代数模型
使用代数方程来描述系统的行为，通常用于连续变化过程的研究
物理学、工程学、生物学等领域，如流体动力学、电磁场理论等
2
微分方程模型
描述连续变化过程的模型，常用于物理、化学等领域
物理学中的运动规律、化学中的反应速率等
3
概率模型
使用概率论和统计方法来描述系统中的随机现象和不确定性
图像处理、语音识别、自然语言处理等人工智能领域
7
网络和图论模型
使用节点和边来描述系统的结构，常用于研究系统的连接关系和流动问题
社交网络分析、物流优化、交通网络设计等
8
离散事件仿真模型
通过模拟离散事件来模拟系统的行为，常用于研究系统的动态性能和效率
供应链管理、排队系统、生产调度等领域
9
动态模型
描述系统随时间变化的行为，包括微分方程模型、差分方程模型等
数学建模中常见的十大模型
数学建模经常使用的十年夜算法==转之迟辟智美创作(2011-07-24 16:13:14)转载▼1. 蒙特卡罗算法.该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，几乎是角逐时必用的方法.2. 数据拟合、参数估计、插值等数据处置算法.角逐中通常会遇到年夜量的数据需要处置，而处置数据的关键就在于这些算法，通常使用MATLAB 作为工具.3. 线性规划、整数规划、多元规划、二次规划等规划类算法.建模竞赛年夜大都问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo 软件求解.4. 图论算法.这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备.5. 静态规划、回溯搜索、分治算法、分支定界等计算机算法.这些算法是算法设计中比力经常使用的方法，竞赛中很多场所会用到.6. 最优化理论的三年夜非经典算法：模拟退火算法、神经网络算法、遗传算法.这些问题是用来解决一些较困难的最优化问题的，对有些问题非常有帮手，可是算法的实现比力困难，需慎重使用.7. 网格算法和穷举法.两者都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型自己而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具.8. 一些连续数据离散化方法.很多问题都是实际来的，数据可以是连续的，而计算机只能处置离散的数据，因此将其离散化后进行差分取代微分、求和取代积分等思想是非常重要的.9. 数值分析算法.如果在角逐中采纳高级语言进行编程的话，那些数值分析中经常使用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用.10. 图象处置算法.赛题中有一类问题与图形有关，即使问题与图形无关，论文中也会需要图片来说明问题，这些图形如何展示以及如何处置就是需要解决的问题，通常使用MATLAB 进行处置.以下将结合历年的竞赛题，对这十类算法进行详细地说明.以下将结合历年的竞赛题，对这十类算法进行详细地说明.2 十类算法的详细说明2.1 蒙特卡罗算法年夜大都建模赛题中都离不开计算机仿真，随机性模拟是非经罕见的算法之一.举个例子就是97 年的A 题，每个零件都有自己的标定值，也都有自己的容差品级，而求解最优的组合方案将要面对着的是一个极其复杂的公式和108 种容差选取方案，根本不成能去求解析解，那如何去找到最优的方案呢？随机性模拟搜索最优方案就是其中的一种方法，在每个零件可行的区间中依照正态分布随机的选取一个标定值和选取一个容差值作为一种方案，然后通过蒙特卡罗算法仿真出年夜量的方案，从中选取一个最佳的.另一个例子就是去年的彩票第二问，要求设计一种更好的方案，首先方案的优劣取决于很多复杂的因素，同样不成能刻画出一个模型进行求解，只能靠随机仿真模拟.2.2 数据拟合、参数估计、插值等算法数据拟合在很多赛题中有应用，与图形处置有关的问题很多与拟合有关系，一个例子就是98 年美国赛A 题，生物组织切片的三维插值处置，94 年A 题逢山开路，山体海拔高度的插值计算，还有吵的沸沸扬扬可能会考的“非典”问题也要用到数据拟合算法，观察数据的走向进行处置.此类问题在MATLAB中有很多现成的函数可以调用，熟悉MATLAB，这些方法都能游刃有余的用好.2.3 规划类问题算法竞赛中很多问题都和数学规划有关，可以说很多的模型都可以归结为一组不等式作为约束条件、几个函数表达式作为目标函数的问题，遇到这类问题，求解就是关键了，比如98年B 题，用很多不等式完全可以把问题刻画清楚，因此列举出规划后用Lindo、Lingo 等软件来进行解决比力方便，所以还需要熟悉这两个软件.2.4 图论问题98 年B 题、00 年B 题、95 年锁具装箱等问题体现了图论问题的重要性，这类问题算法有很多，包括：Dijkstra、Floyd、Prim、Bellman-Ford，最年夜流，二分匹配等问题.每一个算法都应该实现一遍，否则到角逐时再写就晚了.2.5 计算机算法设计中的问题计算机算法设计包括很多内容：静态规划、回溯搜索、分治算法、分支定界.比如92 年B 题用分枝定界法，97 年B 题是典范的静态规划问题，另外98 年 B 题体现了分治算法.这方面问题和ACM 法式设计竞赛中的问题类似，推荐看一下《计算机算法设计与分析》（电子工业出书社）等与计算机算法有关的书.2.6 最优化理论的三年夜非经典算法这十几年来最优化理论有了飞速发展，模拟退火法、神经网络、遗传算法这三类算法发展很快.近几年的赛题越来越复杂，很多问题没有什么很好的模型可以借鉴，于是这三类算法很多时候可以派上用场，比如：97 年A 题的模拟退火算法，00 年B 题的神经网络分类算法，象01 年B 题这种难题也可以使用神经网络，还有美国竞赛89 年A 题也和BP 算法有关系，那时是86 年刚提出BP 算法，89 年就考了，说明赛题可能是现今前沿科技的笼统体现.03 年B 题伽马刀问题也是目前研究的课题，目前算法最佳的是遗传算法.2.7 网格算法和穷举算法网格算法和穷举法一样，只是网格法是连续问题的穷举.比如要求在N 个变量情况下的最优化问题，那么对这些变量可取的空间进行采点，比如在[a; b] 区间内取M +1 个点，就是a; a+(b-a)/M; a+2 (b-a)/M; …… ; b 那么这样循环就需要进行(M + 1)N 次运算，所以计算量很年夜.比如97 年A 题、99 年B 题都可以用网格法搜索，这种方法最好在运算速度较快的计算机中进行，还有要用高级语言来做，最好不要用MATLAB 做网格，否则会算很久的.穷举法年夜家都熟悉，就不说了.2.8 一些连续数据离散化的方法年夜部份物理问题的编程解决，都和这种方法有一定的联系.物理问题是反映我们生活在一个连续的世界中，计算机只能处置离散的量，所以需要对连续量进行离散处置.这种方法应用很广，而且和上面的很多算法有关.事实上，网格算法、蒙特卡罗算法、模拟退火都用了这个思想.2.9 数值分析算法这类算法是针对高级语言而专门设的，如果你用的是MATLAB、Mathematica，年夜可不用准备，因为象数值分析中有很多函数一般的数学软件是具备的.2.10 图象处置算法01 年A 题中需要你会读BMP 图象、美国赛98 年A 题需要你知道三维插值计算，03 年B 题要求更高，不单需要编程计算还要进行处置，而数模论文中也有很多图片需要展示，因此图象处置就是关键.做好这类问题，重要的是把MATLAB 学好，特别是图象处置的部份.。
数学建模30种经典模型matlab
一、概述数学建模是数学与实际问题相结合的产物，通过建立数学模型来解决现实生活中的复杂问题。
Matlab作为一个强大的数学计算工具，在数学建模中具有重要的应用价值。
本文将介绍30种经典的数学建模模型，以及如何利用Matlab对这些模型进行建模和求解。
二、线性规划模型1. 线性规划是数学建模中常用的一种模型，用于寻找最优化的解决方案。
在Matlab中，可以使用linprog函数对线性规划模型进行建模和求解。
2. 举例：假设有一家工厂生产两种产品，分别为A和B，要求最大化利润。
产品A的利润为$5，产品B的利润为$8，而生产每单位产品A 和B分别需要8个单位的原料X和10个单位的原料Y。
此时，可以建立线性规划模型，使用Matlab求解最大化利润。
三、非线性规划模型3. 非线性规划是一类更加复杂的规划问题，其中目标函数或约束条件存在非线性关系。
在Matlab中，可以使用fmincon函数对非线性规划模型进行建模和求解。
4. 举例：考虑一个有约束条件的目标函数，可以使用fmincon函数在Matlab中进行建模和求解。
四、整数规划模型5. 整数规划是一种特殊的线性规划问题，其中决策变量被限制为整数。
在Matlab中，可以使用intlinprog函数对整数规划模型进行建模和求解。
6. 举例：假设有一家工厂需要决定购物哪种机器设备，以最大化利润。
设备的成本、维护费用和每台设备能生产的产品数量均为已知条件。
可以使用Matlab的intlinprog函数对该整数规划模型进行建模和求解。
五、动态规划模型7. 动态规划是一种数学优化方法，常用于多阶段决策问题。
在Matlab 中，可以使用dynamic programming toolbox对动态规划模型进行建模和求解。
8. 举例：考虑一个多阶段生产问题，在每个阶段都需要做出决策以最大化总利润。
可以使用Matlab的dynamic programming toolbox对该动态规划模型进行建模和求解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数学建模常用的十大算法==转
(2011-07-24 16:13:14)
转载▼
1. 蒙特卡罗算法。
该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用MA TLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法，竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法：模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的，数据可以是连续的，而计算机只能处理离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话，那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关，即使问题与图形无关，论文中也会需要图片来说明问题，这些图形如何展示以及如何处理就是需要解决的问题，通常使用MA TLAB 进行处理。
以下将结合历年的竞赛题，对这十类算法进行详细地说明。
以下将结合历年的竞赛题，对这十类算法进行详细地说明。
2 十类算法的详细说明
2.1 蒙特卡罗算法
大多数建模赛题中都离不开计算机仿真，随机性模拟是非常常见的算法之一。
举个例子就是97 年的A 题，每个零件都有自己的标定值，也都有自己的容差等级，而求解最优的组合方案将要面对着的是一个极其复杂的公式和108 种容差选取方案，根本不可能去求解析解，那如何去找到最优的方案呢？随机性模拟搜索最优方案就是其中的一种方法，在每个零件可行的区间中按照正态分布随机的选取一个标定值和选取一个容差值作为一种方案，然后通过蒙特卡罗算法仿真出大量的方案，从中选取一个最佳的。
另一个例子就是去年的彩票第二问，要求设计一种更好的方案，首先方案的优劣取决于很多复杂的因素，同样不可能刻画出一个模型进行求解，只能靠随机仿真模拟。
2.2 数据拟合、参数估计、插值等算法
数据拟合在很多赛题中有应用，与图形处理有关的问题很多与拟合有关系，一个例子就是98 年美国赛A 题，生物组织切片的三维插值处理，94 年A 题逢山开路，山体海拔高度的插值计算，还有吵的沸沸扬扬可能会考的“非典”问题也要用到数据拟合算法，观察数据的
走向进行处理。
此类问题在MA TLAB中有很多现成的函数可以调用，熟悉MA TLAB，这些方法都能游刃有余的用好。
2.3 规划类问题算法
竞赛中很多问题都和数学规划有关，可以说不少的模型都可以归结为一组不等式作为约束条件、几个函数表达式作为目标函数的问题，遇到这类问题，求解就是关键了，比如98年B 题，用很多不等式完全可以把问题刻画清楚，因此列举出规划后用Lindo、Lingo 等软件来进行解决比较方便，所以还需要熟悉这两个软件。
2.4 图论问题
98 年B 题、00 年B 题、95 年锁具装箱等问题体现了图论问题的重要性，这类问题算法有很多，包括：Dijkstra、Floyd、Prim、Bellman-Ford，最大流，二分匹配等问题。
每一个算法都应该实现一遍，否则到比赛时再写就晚了。
2.5 计算机算法设计中的问题
计算机算法设计包括很多内容：动态规划、回溯搜索、分治算法、分支定界。
比如92 年B 题用分枝定界法，97 年B 题是典型的动态规划问题，此外98 年B 题体现了分治算法。
这方面问题和ACM 程序设计竞赛中的问题类似，推荐看一下《计算机算法设计与分析》（电子工业出版社）等与计算机算法有关的书。
2.6 最优化理论的三大非经典算法
这十几年来最优化理论有了飞速发展，模拟退火法、神经网络、遗传算法这三类算法发展很快。
近几年的赛题越来越复杂，很多问题没有什么很好的模型可以借鉴，于是这三类算法很多时候可以派上用场，比如：97 年A 题的模拟退火算法，00 年B 题的神经网络分类算法，象01 年B 题这种难题也可以使用神经网络，还有美国竞赛89 年A 题也和BP 算法有关系，当时是86 年刚提出BP 算法，89 年就考了，说明赛题可能是当今前沿科技的抽象体现。
03 年B 题伽马刀问题也是目前研究的课题，目前算法最佳的是遗传算法。
2.7 网格算法和穷举算法
网格算法和穷举法一样，只是网格法是连续问题的穷举。
比如要求在N 个变量情况下的最优化问题，那么对这些变量可取的空间进行采点，比如在[a; b] 区间内取M +1 个点，就是a; a+(b-a)/M; a+2 (b-a)/M; ……; b 那么这样循环就需要进行(M + 1)N 次运算，所以计算量很大。
比如97 年A 题、99 年B 题都可以用网格法搜索，这种方法最好在运算速度较快的计算机中进行，还有要用高级语言来做，最好不要用MATLAB 做网格，否则会算很久的。
穷举法大家都熟悉，就不说了。
2.8 一些连续数据离散化的方法
大部分物理问题的编程解决，都和这种方法有一定的联系。
物理问题是反映我们生活在一个连续的世界中，计算机只能处理离散的量，所以需要对连续量进行离散处理。
这种方法应用很广，而且和上面的很多算法有关。
事实上，网格算法、蒙特卡罗算法、模拟退火都用了这个思想。
2.9 数值分析算法
这类算法是针对高级语言而专门设的，如果你用的是MA TLAB、Mathematica，大可不必准备，因为象数值分析中有很多函数一般的数学软件是具备的。
2.10 图象处理算法
01 年A 题中需要你会读BMP 图象、美国赛98 年A 题需要你知道三维插值计算，03 年
B 题要求更高，不但需要编程计算还要进行处理，而数模论文中也有很多图片需要展示，因此图象处理就是关键。
做好这类问题，重要的是把MA TLAB 学好，特别是图象处理的部分。