阜阳市2017高中数学竞赛复试人员名单
2017年全国高中数学联赛获奖名单公示(四川赛区)
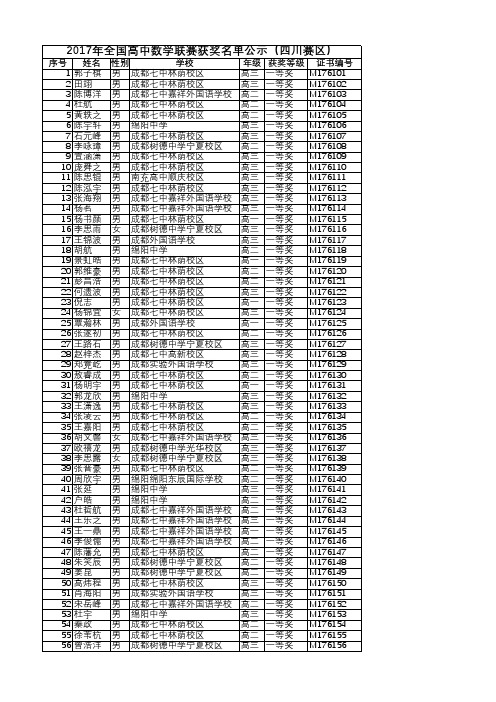
2017年全国高中数学联赛获奖名单公示（四川赛区）序号姓名性别学校年级获奖等级证书编号1郭子棋男成都七中林荫校区高三一等奖M176101 2田翊男成都七中林荫校区高三一等奖M176102 3陈博洋男成都七中嘉祥外国语学校高二一等奖M176103 4杜航男成都七中林荫校区高二一等奖M176104 5黄轶之男成都七中林荫校区高二一等奖M176105 6陈宇轩男绵阳中学高三一等奖M176106 7石元峰男成都七中林荫校区高三一等奖M176107 8李咏璋男成都树德中学宁夏校区高二一等奖M176108 9宣涵潇男成都七中林荫校区高三一等奖M176109 10庞舜之男成都七中林荫校区高三一等奖M176110 11陈思锟男南充高中顺庆校区高三一等奖M176111 12陈泓宇男成都七中林荫校区高三一等奖M176112 13张海翔男成都七中嘉祥外国语学校高三一等奖M176113 14杨茗男成都七中嘉祥外国语学校高三一等奖M176114 15杨书颜男成都七中林荫校区高一一等奖M176115 16李思雨女成都树德中学宁夏校区高三一等奖M176116 17王锦波男成都外国语学校高三一等奖M176117 18胡航男绵阳中学高二一等奖M176118 19景虹皓男成都七中林荫校区高一一等奖M176119 20郭维豪男成都七中林荫校区高二一等奖M176120 21彭昌浩男成都七中林荫校区高二一等奖M176121 22何遗波男成都七中林荫校区高三一等奖M176122 23倪志男成都七中林荫校区高一一等奖M176123 24杨锦宜女成都七中林荫校区高三一等奖M176124 25覃瀚林男成都外国语学校高一一等奖M176125 26张遂初男成都七中林荫校区高二一等奖M176126 27王路石男成都树德中学宁夏校区高三一等奖M176127 28赵梓杰男成都七中高新校区高三一等奖M176128 29郑竟屹男成都实验外国语学校高三一等奖M176129 30敖睿成男成都七中林荫校区高二一等奖M176130 31杨明宇男成都七中林荫校区高一一等奖M176131 32郭龙欣男绵阳中学高三一等奖M176132 33王潇逸男成都七中林荫校区高三一等奖M176133 34张凌云男成都七中林荫校区高二一等奖M176134 35王嘉阳男成都七中林荫校区高二一等奖M176135 36胡文馨女成都七中嘉祥外国语学校高三一等奖M176136 37欧禧龙男成都树德中学光华校区高三一等奖M176137 38李思露女成都树德中学宁夏校区高三一等奖M176138 39张晋豪男成都七中林荫校区高二一等奖M176139 40周欣宇男绵阳绵阳东辰国际学校高二一等奖M176140 41张延男绵阳中学高三一等奖M176141 42户皓男绵阳中学高二一等奖M176142 43杜哲航男成都七中嘉祥外国语学校高二一等奖M176143 44王乐之男成都七中嘉祥外国语学校高三一等奖M176144 45王一鼎男成都七中嘉祥外国语学校高一一等奖M176145 46李俊儒男成都七中嘉祥外国语学校高二一等奖M176146 47陈藩允男成都七中林荫校区高二一等奖M176147 48朱笑辰男成都树德中学宁夏校区高二一等奖M176148 49姜昆男成都树德中学宁夏校区高二一等奖M176149 50高炜程男成都七中林荫校区高三一等奖M176150 51肖海阳男成都实验外国语学校高三一等奖M176151 52宋岳峰男成都七中嘉祥外国语学校高二一等奖M176152 53杜宇男绵阳中学高三一等奖M176153 54秦政男成都七中林荫校区高二一等奖M176154 55徐苇杭男成都七中林荫校区高二一等奖M176155 56曾浩洋男成都树德中学宁夏校区高三一等奖M17615657卢禹杰男成都市石室中学文庙校区高三一等奖M17615758杨文韬男成都七中林荫校区高三一等奖M17615859马文俊男绵阳中学高二一等奖M17615960杭子涵男成都七中嘉祥外国语学校高三一等奖M17616061唐果男成都七中林荫校区高一一等奖M17616162黄思成女成都树德中学宁夏校区高三一等奖M17616263干正浩男绵阳中学高二一等奖M17616364陈泳西女绵阳中学实验学校高三一等奖M17616465钟梁骏男成都七中林荫校区高一一等奖M17616566邓书豪男成都七中林荫校区高三一等奖M17616667漆林男遂宁遂宁卓同国际学校高二一等奖M17616768江柏杉男成都七中林荫校区高二一等奖M17616869牛晗汀男成都市石室中学文庙校区高二一等奖M17616970唐艺铭男成都七中嘉祥外国语学校高二一等奖M17617071余其蓉女绵阳中学高二一等奖M17617172胡梦箫男成都市树德中学宁夏校区高二一等奖M17617273周浩男成都市石室中学文庙校区高二一等奖M17617374李夏鲲男成都七中林荫校区高二二等奖M217610001 75卓汐聪男成都实验外国语学校高三二等奖M217610002 76甘祚男成都树德中学光华校区高三二等奖M217610003 77陈克发男绵阳中学高二二等奖M217610004 78江孝奕男成都七中高新校区高三二等奖M217610005 79王琦淏男成都市石室中学文庙校区高三二等奖M217610006 80周昱昊男成都七中高新校区高二二等奖M217610007 81付乐天男成都七中林荫校区高三二等奖M217610008 82徐展鹏男成都七中嘉祥外国语学校高二二等奖M217610009 83张馨璇女绵阳中学高三二等奖M217610010 84赵宇智男成都七中林荫校区高二二等奖M217610011 85高信男成都实验外国语学校高三二等奖M217610012 86关景瑞男成都七中嘉祥外国语学校高二二等奖M217610013 87田恒瑞男成都市石室中学文庙校区高二二等奖M217610014 88张庭瑞男成都树德中学宁夏校区高三二等奖M217610015 89刘雨芝女成都树德中学宁夏校区高二二等奖M217610016 90蒲钰男成都七中林荫校区高二二等奖M217610017 91唐堂男成都七中嘉祥外国语学校高二二等奖M217610018 92杨宸玮男南充高中顺庆校区高二二等奖M217610019 93贾志杰男成都棠湖外国语学校高三二等奖M217610020 94唐龙天男成都七中嘉祥外国语学校高一二等奖M217610021 95文子龙男成都七中林荫校区高二二等奖M217610022 96钟孟言男成都七中林荫校区高二二等奖M217610023 97陈浩志男广元天立国际学校高三二等奖M217610024 98张鳌男成都七中林荫校区高三二等奖M217610025 99刘昱丁男成都外国语学校高二二等奖M217610026 100曾浩洋男成都市石室中学文庙校区高三二等奖M217610027 101杨力源男成都树德实验中学初三二等奖M217610028 102刘勉之男成都七中林荫校区高三二等奖M217610029 103何俊杰男绵阳绵阳东辰国际学校高二二等奖M217610030 104王涵章男成都树德中学宁夏校区高三二等奖M217610031 105赵红阳男绵阳中学高二二等奖M217610032 106褚文笛男成都七中林荫校区高三二等奖M217610033 107王优男遂宁遂宁卓同国际学校高三二等奖M217610034 108罗春雨男绵阳中学高三二等奖M217610035 109潘亮男成都实验外国语学校高二二等奖M217610036 110李卓潼女成都七中林荫校区高三二等奖M217610037 111王敬飞男成都实验外国语学校高一二等奖M217610038 112杨天成男成都七中林荫校区高一二等奖M217610039 113田梓茂男成都七中育才学校水井坊校初三二等奖M217610040 114邓皓元男成都七中林荫校区高二二等奖M217610041115刘皓瑞男成都七中嘉祥外国语学校高二二等奖M217610042 116何奥东男绵阳东辰国际学校高三二等奖M217610043 117黄清扬男南充高中老校区高三二等奖M217610044 118唐得山男成都树德中学宁夏校区高三二等奖M217610045 119蒋宇骁男成都七中嘉祥外国语学校高三二等奖M217610046 120邓浩毅男成都树德中学宁夏校区高三二等奖M217610047 121苏洋男成都七中嘉祥外国语学校高三二等奖M217610048 122唐一夫男成都七中林荫校区高一二等奖M217610049 123张昭阳男成都市石室中学文庙校区高二二等奖M217610050 124杜奕宏男成都七中林荫校区高三二等奖M217610051 125杨涵男成都七中嘉祥外国语学校高三二等奖M217610052 126黄儒惟男成都树德中学宁夏校区高三二等奖M217610053 127王彦桥男绵阳东辰国际学校高一二等奖M217610054 128古丹妮女成都市石室中学文庙校区高三二等奖M217610055 129刘键一男成都树德中学宁夏校区高三二等奖M217610056 130陈昌睿男成都七中高新校区高三二等奖M217610057 131刘泓麟男绵阳中学高二二等奖M217610058 132余锦潼男成都树德中学宁夏校区高三二等奖M217610059 133曾添男绵阳中学实验学校高三二等奖M217610060 134袁鑫凤女成都七中嘉祥外国语学校高二二等奖M217610061 135罗一浦男绵阳东辰国际学校高三二等奖M217610062 136雷轩昂男成都七中嘉祥外国语学校高三二等奖M217610063 137陈泳岐男成都七中林荫校区高二二等奖M217610064 138焦梦翰男成都市石室中学文庙校区高三二等奖M217610065 139谭泽男成都七中嘉祥外国语学校高三二等奖M217610066 140黎翔宇男成都树德中学光华校区高三二等奖M217610067 141刘昱男成都七中嘉祥外国语学校高三二等奖M217610068 142舒牧葳男成都七中嘉祥外国语学校高三二等奖M217610069 143赵谦男广元天立国际学校高二二等奖M217610070 144张乐男成都七中林荫校区高三二等奖M217610071 145江玮佳男绵阳东辰国际学校高三二等奖M217610072 146唐天楠男成都市石室中学文庙校区高二二等奖M217610073 147龙城轩男自贡自贡富顺二中高三二等奖M217610074 148鲁俊杰男绵阳东辰国际学校高二二等奖M217610075 149李炤男广元天立国际学校高三二等奖M217610076 150王今迈男成都七中高新校区高三二等奖M217610077 151郭鹏男成都外国语学校高二二等奖M217610078 152胥畅男遂宁遂宁射洪中学高三二等奖M217610079 153张书恺男成都实验外国语学校高三二等奖M217610080 154张洋海男成都七中万达学校高三二等奖M217610081 155龚雨豪男绵阳中学高二二等奖M217610082 156叶夏汐女成都七中林荫校区高二二等奖M217610083 157雷雨寒男成都棠湖外国语学校高三二等奖M217610084 158曲星宇男成都七中嘉祥外国语学校高三二等奖M217610085 159何轩霆男成都外国语学校高三二等奖M217610086 160彭祖泽男成都七中林荫校区高三二等奖M217610087 161左欣悦女成都七中嘉祥外国语学校高二二等奖M217610088 162余明哲男成都七中嘉祥外国语学校高三二等奖M217610089 163张涵男成都七中嘉祥外国语学校高三二等奖M217610090 164范珂男成都七中林荫校区高三二等奖M217610091 165陈翰凝男成都市石室中学文庙校区高二二等奖M217610092 166程玺玮男成都市石室中学文庙校区高二二等奖M217610093 167陈泽坤男成都七中嘉祥外国语学校高一二等奖M217610094 168傅于恒男成都七中嘉祥外国语学校高一二等奖M217610095 169胡芳铭男成都树德中学外国语校区高三二等奖M217610096 170杨乾宇男绵阳东辰国际学校高二二等奖M217610097 171欧阳乐铮女绵阳东辰国际学校高三二等奖M217610098 172代家葳男成都七中林荫校区高三二等奖M217610099173夏熙林男成都七中林荫校区高三二等奖M217610100 174肖逸航男成都七中嘉祥外国语学校高二二等奖M217610101 175贺南棋男绵阳中学高二二等奖M217610102 176康宁女成都七中林荫校区高三二等奖M217610103 177黄玉茂男成都七中嘉祥外国语学校高一二等奖M217610104 178冯书瀚男成都树德中学光华校区高三二等奖M217610105 179刘朗辰男成都实验外国语学校高三二等奖M217610106 180陈子奕男成都七中林荫校区高二二等奖M217610107 181郑博文男遂宁遂宁卓同国际学校高二二等奖M217610108 182杨弘毅男成都七中嘉祥外国语学校高二二等奖M217610109 183文鑫源男遂宁卓同国际学校高三二等奖M217610110 184刘卿莆男成都实验外国语学校高三二等奖M217610111 185刘育诚男成都七中高新校区高三二等奖M217610112 186付云帆男成都七中林荫校区高三二等奖M217610113 187符心亮男绵阳中学高三二等奖M217610114 188李郝添男成都树德中学宁夏校区高二二等奖M217610115 189赵睿达男成都市石室中学文庙校区高二二等奖M217610116 190何文杰男成都师大一中高中部高二二等奖M217610117 191陈柘芃男成都实验外国语学校高二二等奖M217610118 192黎杰扬男成都七中嘉祥外国语学校高三二等奖M217610119 193杨奕旻男绵阳中学高二二等奖M217610120 194王逸帆男绵阳东辰国际学校高三二等奖M217610121 195钟汉峰男成都七中林荫校区高三二等奖M217610122 196何光烜男成都七中林荫校区高三二等奖M217610123 197张舒翔男成都外国语学校高三二等奖M217610124 198刘与乐男绵阳中学实验学校高三二等奖M217610125 199李浩宇男成都外国语学校高一二等奖M217610126 200谭钰晖男绵阳中学高二二等奖M217610127 201吴王茂男成都棠湖外国语学校高三二等奖M217610128 202张天择男成都树德实验中学初三二等奖M217610129 203廖珩男成都七中嘉祥外国语学校高一二等奖M217610130 204罗之尧男成都七中嘉祥外国语学校高一二等奖M217610131 205谢天男绵阳绵阳南山中学实验学校高三二等奖M217610132 206廖予扬男成都外国语学校高三二等奖M217610133 207罗靖东男成都树德中学光华校区高三二等奖M217610134 208何睿杰男成都七中林荫校区高二二等奖M217610135 209侯廷强男南充高中老校区高三二等奖M217610136 210李泓辛男成都七中林荫校区高三二等奖M217610137 211王淇男成都七中高新校区高三二等奖M217610138 212郭嘉美女成都七中林荫校区高二二等奖M217610139 213陈钦阳男泸州高中高三二等奖M217610140 214唐思渝男绵阳中学高二二等奖M217610141 215廖娅娴女成都树德中学光华校区高三二等奖M217610142 216李玉龙男成都树德中学宁夏校区高三二等奖M217610143 217黄文志男绵阳外国语学校高一二等奖M217610144 218李雨浓男成都树德中学光华校区高三二等奖M217610145 219宋帆男成都树德中学宁夏校区高三二等奖M217610146 220龙俊潇男成都七中林荫校区高三二等奖M217610147 221杨英杰男成都七中林荫校区高三二等奖M217610148 222赵修民男绵阳东辰国际学校高二二等奖M217610149 223胡凌风男成都新都一中高三二等奖M217610150 224唐越男成都树德中学宁夏校区高三二等奖M217610151 225胥仁涛男成都七中林荫校区高三二等奖M217610152 226杨雨奇男成都实验外国语学校高三二等奖M217610153 227蒋芮女遂宁卓同国际学校高二二等奖M217610154 228李睿丁男成都实验外国语学校高二二等奖M217610155 229袁子涵男成都七中林荫校区高二二等奖M217610156 230冯宇晨男成都七中嘉祥外国语学校高三二等奖M217610157231曾义鹏男绵阳江油中学高三二等奖M217610158 232张家乐男绵阳中学高三二等奖M217610159 233孙中天男成都七中嘉祥外国语学校初二二等奖M217610160 234李远政男成都树德中学光华校区高二二等奖M217610161 235刘恒瑞男成都实验外国语学校高二二等奖M217610162 236张钟天男南充高中新校区高三二等奖M217610163 237周明玺男广元天立国际学校高三二等奖M217610164 238黄可一男成都七中林荫校区高一二等奖M217610165 239龙沭尧男成都七中林荫校区高三二等奖M217610166 240戴维男成都树德中学宁夏校区高三二等奖M217610167 241杜俊江男绵阳江油市第一中学高三二等奖M217610168 242龚新至男成都实验外国语学校高三二等奖M217610169 243谭畅男成都七中高新校区高三二等奖M217610170 244张凌霄男绵阳东辰国际学校高三二等奖M217610171 245王研男绵阳中学高三二等奖M217610172 246蒋京轩女成都七中林荫校区高三二等奖M217610173 247梁天翼男成都树德中学光华校区高二二等奖M217610174 248曾治霖男自贡荣县中学高三二等奖M217610175 249邓智远男成都七中嘉祥外国语学校高一二等奖M217610176 250田昀禾女成都实验外国语学校高二二等奖M217610177 251唐宣女成都七中林荫校区高二二等奖M217610178 252杨宇昂男成都交大附中高二二等奖M217610179 253胡伟男成都七中林荫校区高三二等奖M217610180 254冉植尹男成都七中高新校区高三二等奖M217610181 255王彦睿男绵阳中学实验学校高三二等奖M217610182 256杨豪佶男成都嘉祥外国语学校郫县分高三二等奖M217610183 257张殊培男南充白塔中学高三二等奖M217610184 258刘杰男成都实验外国语学校高三二等奖M217610185 259王霖轩男绵阳中学高三二等奖M217610186 260唐瑞晨女成都七中林荫校区高三二等奖M217610187 261肖翰林男绵阳东辰国际学校高三二等奖M217610188 262易云飞男成都七中嘉祥外国语学校高一二等奖M217610189 263刘云杰男宜宾翠外高三二等奖M217610190 264邓力男绵阳东辰国际学校高二二等奖M217610191 265蒋良航男成都树德中学光华校区高三二等奖M217610192 266王錾沣男泸州高中高三二等奖M217610193 267肖云洋男成都七中嘉祥外国语学校高二二等奖M217610194 268王奕达男成都树德中学宁夏校区高三二等奖M217610195 269尹浩儒男成都七中林荫校区高三二等奖M217610196 270谭玺扬男成都七中林荫校区高三二等奖M217610197 271王逸男成都第十二中学高三二等奖M217610198 272姜琪瑶女成都树德中学宁夏校区高二二等奖M217610199 273李可峰男绵阳中学高二二等奖M217610200 274周瀚宇男绵阳东辰国际学校高三二等奖M217610201 275曹家伟男成都七中万达学校高三二等奖M217610202 276宋康健男成都七中林荫校区高三二等奖M217610203 277周高川男遂宁射洪外国语学校高三二等奖M217610204 278刘祥龙男绵阳中学高二二等奖M217610205 279裴泓宇男绵阳中学高二二等奖M217610206 280肖力文男成都市石室中学文庙校区高二二等奖M217610207 281吕云帆男德阳什邡中学高三二等奖M217610208 282穆星宇男成都市石室中学文庙校区高三二等奖M217610209 283庞祥鹤男成都七中林荫校区高三二等奖M217610210 284杨展鹏男成都市石室中学文庙校区高三二等奖M217610211 285秦天男成都新都一中高一二等奖M217610212 286王俊杰男成都七中嘉祥外国语学校高二二等奖M217610213 287蔡乐衡男泸州高中高三二等奖M217610214 288秦溯女成都树德中学宁夏校区高三二等奖M217610215289周溪又男成都七中林荫校区高二二等奖M217610216 290陈俊鹏男成都新都一中高三二等奖M217610217 291董浩宇男泸州高中高三二等奖M217610218 292梅新宇男成都七中嘉祥外国语学校高三二等奖M217610219 293余春霖男成都七中高新校区高三二等奖M217610220 294杨柯宇男成都市石室中学北湖校区高二二等奖M217610221 295杨文骁男绵阳中学高二二等奖M217610222 296郑宇航男绵阳南山中学高二二等奖M217610223 297董林瀚男成都树德中学宁夏校区高三二等奖M217610224 298彭思叡男成都七中嘉祥外国语学校高三二等奖M217610225 299张紫洋男遂宁射洪中学高三二等奖M217610226 300周寓瑾女成都七中嘉祥外国语学校高二二等奖M217610227 301侯宇恒男南充高中老校区高三二等奖M217610228 302闫锐男成都树德中学宁夏校区高三二等奖M217610229 303何一航男成都棠湖外国语学校高三二等奖M217610230 304阚浚晖男成都树德中学宁夏校区高三二等奖M217610231 305刘曦雨男成都树德中学宁夏校区高三二等奖M217610232 306马昊文男成都树德中学外国语校区高三二等奖M217610233 307王可容男成都外国语学校高三二等奖M217610234 308骆彦萌男成都七中林荫校区高一二等奖M217610235 309靳雁女成都七中嘉祥外国语学校高三二等奖M217610236 310倪立女遂宁卓同国际学校高三二等奖M217610237 311任芋霖男成都七中林荫校区高二二等奖M217610238 312王睿知男成都七中林荫校区高二二等奖M217610239 313杨江林男南充高中顺庆校区高二二等奖M217610240 314杨然男绵阳中学高二二等奖M217610241 315何雪吟女德阳外国语学校高三二等奖M217610242 316宾心瑜男德阳市第五中学高三二等奖M217610243 317陈铭双男宜宾市一中高三二等奖M217610244 318李鸿坤男德阳市第五中学高三二等奖M217610245 319欧阳显峥男成都双流中学高三二等奖M217610246 320邵新哲男成都七中林荫校区高三二等奖M217610247 321文瑞阳男成都七中林荫校区高三二等奖M217610248 322曹翔男成都七中嘉祥外国语学校高三二等奖M217610249 323黎凯男攀枝花市第三高级中学校高三二等奖M217610250 324李鑫智男成都外国语学校高三二等奖M217610251 325欧阳维一男德阳什邡中学高三二等奖M217610252 326马潇健男成都树德中学宁夏校区高三二等奖M217610253 327徐浩瀚男广安武胜中学高三二等奖M217610254 328韩子睿男成都七中林荫校区高二二等奖M217610255 329罗大禹男成都市石室中学文庙校区高二二等奖M217610256 330陈嘉睿女成都外国语学校高二二等奖M217610257 331潘逸鸣男成都七中嘉祥外国语学校高三二等奖M217610258 332齐立洲男成都七中林荫校区高三二等奖M217610259 333王嘉怡女绵阳东辰国际学校高二二等奖M217610260 334丁春瑞男德阳外国语学校高三二等奖M217610261 335张志豪男成都市龙泉中学高三二等奖M217610262 336郭朋男成都新都一中高三二等奖M217610263 337陈世轩男成都市石室中学文庙校区高二二等奖M217610264 338胡杰昊男成都七中林荫校区高二二等奖M217610265 339李泓民男成都七中林荫校区高三二等奖M217610266 340肖宇辰男成都树德中学宁夏校区高三二等奖M217610267 341尹罗毅男绵阳中学实验学校高三二等奖M217610268 342詹一丁男成都树德中学宁夏校区高三二等奖M217610269 343赵子毅男成都实验外国语学校高二二等奖M217610270 344余昊亮男成都石室天府中学高二二等奖M217610271 345竹子林男成都七中万达学校高三二等奖M217610272 346伍靖波男成都七中林荫校区高二二等奖M217610273347向灿男成都七中嘉祥外国语学校高二二等奖M217610274 348何志霄男南充南部中学高三二等奖M217610275 349何金津男绵阳中学高二二等奖M217610276 350段迪文男成都树德中学宁夏校区高三二等奖M217610277 351孙思危女南充高中老校区高三二等奖M217610278 352张佳驰男成都树德中学光华校区高三二等奖M217610279 353唐骁男宜宾市三中高三二等奖M217610280 354马润峰男成都实验外国语学校高二二等奖M217610281 355文彦博男绵阳中学高三二等奖M217610282 356杨宗茂男成都棠湖外国语学校高三二等奖M217610283 357张思勰男成都树德中学宁夏校区高三二等奖M217610284 358何佳政男广元天立国际学校高二二等奖M217610285 359陈斯佳女自贡富顺二中高三二等奖M217610286 360吴俊江男内江六中高三二等奖M217610287 361任恬叶女成都树德中学宁夏校区高二二等奖M217610288 362霍漪漪女成都七中林荫校区高三二等奖M217610289 363陈德铭男成都七中嘉祥外国语学校高二二等奖M217610290 364刘镇谋男南充高中老校区高三二等奖M217610291 365周琦欣男资阳市资阳中学高三二等奖M217610292 366李骞男成都七中嘉祥外国语学校高一二等奖M217610293 367罗王贤男成都七中林荫校区高一二等奖M217610294 368龙之源男成都七中林荫校区高三二等奖M217610295 369杨桐女成都七中高新校区高三三等奖M317610001 370谢安昊男成都树德中学光华校区高三三等奖M317610002 371彭林男成都玉林中学高三三等奖M317610003 372刘雪女宜宾市一中高三三等奖M317610004 373魏煜江男自贡蜀光中学高三三等奖M317610005 374张虒源男自贡蜀光中学高三三等奖M317610006 375张翔洲男成都市四川师大附中高三三等奖M317610007 376唐子琳女广元中学高三三等奖M317610008 377陈星佐男成都树德中学宁夏校区高三三等奖M317610009 378李沛洋男成都七中林荫校区高三三等奖M317610010 379骆言男成都外国语学校高三三等奖M317610011 380鲜唯佳男成都实验外国语学校高三三等奖M317610012 381张抒扬男成都七中嘉祥外国语学校高三三等奖M317610013 382王湜轶女成都市石室中学文庙校区高二三等奖M317610014 383刘鑫男绵阳绵阳南山中学实验学校高三三等奖M317610015 384孟群康男成都市四川师大附中高三三等奖M317610016 385邵瀚雍男德阳市第五中学高三三等奖M317610017 386辛雨男成都七中万达学校高一三等奖M317610018 387阳晨曦男成都七中嘉祥外国语学校高一三等奖M317610019 388宋秋池女成都市石室中学文庙校区高三三等奖M317610020 389邹铭睿女成都实验外国语学校高三三等奖M317610021 390甘泽昊男成都市石室中学文庙校区高二三等奖M317610022 391林博阳男成都市西南交大附中高三三等奖M317610023 392黄越男南充高中老校区高三三等奖M317610024 393白弈文女成都市石室中学文庙校区高二三等奖M317610025 394王鹏宇男成都七中万达学校高二三等奖M317610026 395李玮哲男成都树德中学光华校区高三三等奖M317610027 396邹佳良男成都树德中学宁夏校区高三三等奖M317610028 397黄奕为男成都七中嘉祥外国语学校高一三等奖M317610029 398张译元女成都市石室中学高三三等奖M317610030 399邱子莹女成都七中嘉祥外国语学校高二三等奖M317610031 400蒋誉豪男绵阳南山中学实验学校高三三等奖M317610032 401唐嘉慧女成都七中林荫校区高三三等奖M317610033 402张海粟男成都七中万达学校高二三等奖M317610034 403白胜泷男成都树德中学宁夏校区高三三等奖M317610035 404孙文轩男成都七中林荫校区高一三等奖M317610036。
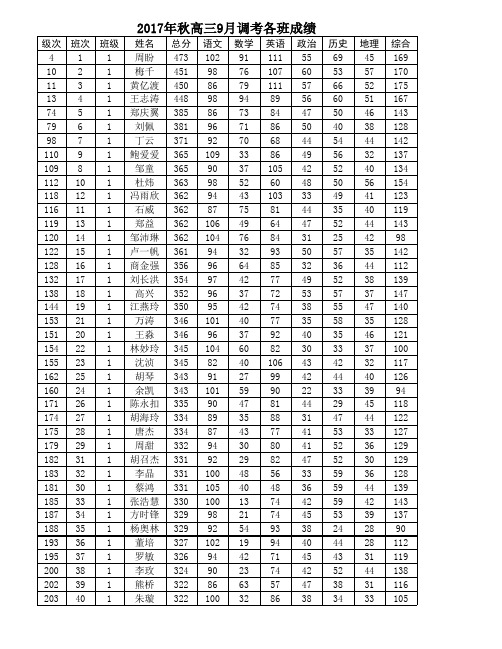
麻城三中2017年秋高三9月调考各班成绩
2017阜阳一级教师通过名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单
通过人员名单。
2017年全国高中数学联赛河北赛区获奖名单
孙一涵 陈明煜 刘子祺 齐霄雨 朱波 王梓怡 白移梦 王子杰 吕紫宸 焦宝澄 赵一冰 刘亦忱 刘岳昂 翟擎宇 王浩宇 董志鹏 袁紫怡 王文豪 封宇昊 田雨松 孙婧 侯艳楠 王猛 许嘉璐 周华伦 王浩天 尹子宇 赵家璇 戎梓正 刘汉卿 刘晓涵 刘泽辉 马宇佳 吴鹏飞 刘晨宇 李佳龙 刁洪滨 宫佳国 李响 王 彬
男 男 男 男 男 女 男 男 男 男 男 女 男 男 男 男 女 男 男 男 女 女 男 女 男 男 男 男 男 男 男 男 女 男 男 男 男 男 男 男
河北安国中学 河北安国中学 河北安国中学 高阳中学 高碑店一中 定兴三中 定兴三中 保定一中 保定一中 保定一中 保定一中 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第一中学 保定市第三中学 保定市第三中学 保定市第三中学 保定市第二中学 保定市第二中学 保定市第二中学 保定市第二中学 安新中学 安国中学 安国中学 安国中学 承德第一中学 承德县一中 平泉一中 兴隆县第一中学
焦正阔 张润泽 李春昊 李昊泽 高晶晶 李一辰 董健安 陈凯歌 张文远 司航旭 陈伯旭 宋林硕 祝学雯 赵雨菲 谢士博 杨叶青 潘宇迪 刘宇涵 刘子辰 董浩 张子棋 甄博源 安名扬 张博帅 杨辰 黄天豪 边佳伟 张泽楠 王洪辰 吴沫璇 赵天烁 陈鑫 李鹏飞 王士宁 辛择康 燕灏宇 王渊博 唐泽伟 王思博 刘子涵
男 女 男 男 女 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 男 女 女 男 男 男 男 女 男 男 男 男
衡水中学 衡水中学 衡水中学 衡水中学 衡水中学 沙河市第一中学 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄二中 石家庄一中 唐山一中 唐山一中 唐山一中 唐山一中 唐山一中 正定中学 正定中学 正定中学 易县中学 易县中学 易县中学 易县中学 易县中学 徐水综合高中 徐水综合高中 徐水综合高中 徐水综合高中 徐水区第一中学 徐水区第一中学 徐水区第一中学 徐水区第一中学 雄县中学
2017年全国高中数学联赛一试(B卷)答案
成立，求实 成立．由于
解：设 t 2 x ，则 t [2, 4] ，于是
对所有
t a 5 t (t a ) 2 (5 t ) 2 (2t a 5)(5 a ) 0 ． ………………8 分 对给定实数 a ，设 f (t ) (2t a 5)(5 a ) ，则 f (t ) 是关于 t 的一次函数或常 值函数．注意 t [2, 4] ，因此 f (t ) < 0 等价于 f (2) (1 a )(5 a ) 0, ………………12 分 f (4) (3 a )(5 a ) 0, 解得 3 a 5 ． 所以实数 a 的取值范围是 3 a 5 ． ………………16 分 10. （ 本 题 满 分 20 分 ） 设 数 列 {an } 是 等 差 数 列 ， 数 列 {bn } 满 足 2 , n 1, 2, ． bn an1an2 an （1）证明：数列 {bn } 也是等差数列； （2） 设数列 {an } 、 并且存在正整数 s, t ， 使得 as bt {bn } 的公差均是 d 0 ， 是整数，求 a1 的最小值． 解： （1）设等差数列 {an } 的公差是 d ，则 2 2 bn1 bn ( an2an3 an 1 ) ( an1an2 an ) an2 ( an3 an1 ) ( an1 an )( an1 an ) an2 2d ( an1 an ) d
2017 年全国高中数学联合竞赛一试（B 卷） 参考答案及评分标准
说明： 1. 评阅试卷时，请依据本评分标准. 填空题只设 8 分和 0 分两档；其他各题的 评阅，请严格按照本评分标准的评分档次给分，不得增加其他中间档次. 2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可 参考本评分标准适当划分档次评分， 解答题中第 9 小题 4 分为一个档次， 第 10、 11 小题 5 分为一个档次，不得增加其他中间档次． 一、填空题：本大题共 8 小题，每小题 8 分，共 64 分． 1. 在等比数列 {an } 中， a2 2, a3 3 ，则
2017数学竞赛命题研讨会材料汇总
2017年全国数学竞赛命题研讨会试题汇编2017年6月目录代数代数1 不等式…………………………………………………人大附中张端阳1 代数2 不等式…………………………………………………人大附中张端阳1 代数3 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利3 代数4 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利4 代数5 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利7 代数6 不等式…………………………………………华东师大二附中唐立华8 代数7 不等式……………………………………………湖南师大附中张湘君9 代数8 不等式……………………………………………湖南师大附中张湘君10 代数9 不等式……………………………………………湖南师大附中汤礼达11 代数10 不等式……………………………………………湖南师大附中汤礼达12 代数11 不等式………………………………………吉大附中石泽晖、王庶赫13 代数12 不等式…………………………………绵阳东辰学校袁万伦、姚先伟14 代数13 不等式……………………………………………绵阳东辰学校袁万伦15 代数14 三角不等式……………………………………………广州二中程汉波16 代数15 不等式……………………………………………大连二十四中邰海峰17 代数16 数列…………………………………………………东北育才学校张雷18 代数17 不等式………………………………………………东北育才学校张雷19 代数18 不等式………………………………………………大连二十四中李响23 代数19 多项式……………………………………学而思培优苏州分校李家夫24 代数20 不等式…………………………………………………华东师大张丽玉24 代数21 不等式……………………………………………………杭州二中赵斌25几何几何1……………………………………复旦附中李朝晖、施柯杰、肖恩利28几何2………………………………………………………湖南师大附中苏林29 几何3………………………………………………………湖南师大附中苏林30 几何4……………………………………………………………郑州一中张甲31 几何5………………………………………………………西安铁－中杨运新32 几何6………………………………………………………西安交大附中金磊33 几何7………………………………………………………西安交大附中金磊34 几何8………………………………………………………西安交大附中金磊35 几何9………………………………………………………西安交大附中金磊36 几何10………………………………………………………西安交大附中金磊36 几何11………………………………………………………西安交大附中金磊37 几何12……………………………………………………东北育才学校缠祥瑞38 几何13………………………………………………学而思培优北京分校陈楷39 几何14………………………………………………学而思培优北京分校陈楷40 几何15 ……………………………………………学而思培优北京分校杨溢非41 几何16 ……………………………………………………………北京四中侯彬42 几何17 ………………………………………………………西安交大附中金磊43数论数论1…………………………………………………………东北育才学校张雷45 数论2………………………………………………………………杭州二中赵斌45 数论3………………………………………复旦附中李朝晖、施柯杰、肖恩利47 数论4………………………………………………………东北育才学校缠祥瑞48 数论5……………………………………………………………杭州二中胡克元50 数论6………………………………………………学而思培优杭州分校李卓伦52 数论7………………………………………………学而思培优杭州分校李卓伦54 数论8………………………………………………学而思培优武汉分校巩鸿文55 数论9………………………………………………学而思培优武汉分校巩鸿文55 数论10……………………………………………学而思培优深圳分校涂小林58 数论11……………………………………………学而思培优深圳分校涂小林60组合1……………………………………………………………人大附中张端阳62 组合2…………………………………………………………西安交大附中金磊63 组合3…………………………………………………………西安交大附中金磊64 组合4…………………………………………………………西安交大附中金磊65 组合5………………………………………………学而思培优广州分校余泽伟66 组合6………………………………………………学而思培优广州分校余泽伟67 组合7………………………………………………学而思培优苏州分校李家夫68 组合8………………………………………………学而思培优北京分校杨溢非69 组合9……………………………………………………………北京四中范兴亚71命题小品一苇渡江……………………………………………江西科技师范大学陶平生73代数1(人大附中张端阳)代数2(人大附中张端阳)代数3（复旦附中李朝晖、施柯杰、肖恩利）求最佳常数c ，使得对任意1234,,,0a a a a >，有{}2123414max4i j a a a a c ≤<≤+++.解：注意到对于任意的1234,,,0x x x x >，有如下恒等式：222222212341234()2()x x x x x x x x +++-=-++-. (1)不妨设1234x x x x ≥≥≥，则{}221414()max ()i j i j x x x x ≤<≤-=-14x x ≥. 从而2214()x x ≤-. (2)若14x x =，则 (2) 式显然成立. 当14x x ≠时，令14L x x =-，则341201,01x x x x L L--≤≤≤≤. 从而 223434231212()1x x x x L x x x x x x L L L L L ------⎛⎫⎛⎫+≤+=≤ ⎪ ⎪⎝⎭⎝⎭. 因此2222123414()()()x x x x L x x -+-≤=-. 结合 (1), (2)两式，得222221234143()x x x x x x +++--.(3)令2,1,2,3,4i i a x i ==. 由 (3) 即得{}21234143max44i j a a a a ≤<≤+++.下面证明若结论成立，则34c ≥. 假设对12340a a a a ≥≥≥>，存在34c <使得结论成立. 则取1234211,(1)a a a a n n ====≥，则结论可重写为2213114n c n +⎛⎫≤- ⎪⎝⎭. (4)其中3,14c n <≥.注意到当n →∞时，左边34→，右边c →，矛盾！故最佳常数为34c =.代数4（复旦附中李朝晖、施柯杰、肖恩利）将不小于2的正整数n 表示为若干个正整数12,,,t b b b 之和，即12t n b b b =+++，当t 与12,,,t b b b 变化时，求2112tti i i i S ib b ===+∑∑的最小值.解：定义12(;,,,)t f t b b b S =.设12(;,,,)t t b b b 使得S 最小，则对任何,{1,2,,}i j t ∈，i j ≠，令'1,i i b b =+'1,j j b b =-'(,)k k b b k i j =≠.考虑下面三种情况： 情形1若'0j b =，且i j <，则'''''121111112221111211(1;,,,,,,)2(1)2(1)22(1),j j t j j i i k k i i kk k k k i k i ttkk k j k j f t b b b b b b kb b i b bkb bk b -+----===+=+=+=+-=+++++++++-∑∑∑∑∑∑而12111122221111211(;,,,)22222,t j j i i k k ii kk j j k k k i k i ttkk k j k j f t b b b b kb b ib bkb b jb bkb ----===+=+=+=+=+++++++++∑∑∑∑∑∑由'''''121112(1;,,,,,,)(;,,,)j j t t f t b b b b b f t b b b -+-≥得，222(1)2(1)22i i i i j jb i b b ib b jb +++≥+++； 情形2若'0j b =，且i j >，则''''''121111112221111211(1;,,,,,,,,)22(1)(1)2(1)(1)2(1),j j i t j j i i kk kk i i k k k j k j ttkk k i k i f t b b b b b b b kb bk b b i b bk b -+----===+=+=+=+-=+++-+++-+++-∑∑∑∑∑∑而12111122221111211(;,,,)22222,t j j i i kk jj kk i i k k k j k j ttkk k i k i f t b b b b kb b jb bkb b ib bkb ----===+=+=+=+=+++++++++∑∑∑∑∑∑由'''''121112(1;,,,,,,)(;,,,)j j t t f t b b b b b f t b b b -+-≥得，222(1)2(1)(1)22i i i i j jb i b b ib b jb ++-+≥+++； 情形3若'0j b >，则由'''1212(;,,,)(;,,,)t t f t b b b f t b b b ≥得2222(1)2(1)(1)2(1)22i i j j i i j j b i b b j b b ib b jb ++++-+-≥+++. 上面的三种情形都表明，2222(1)2(1)(1)2(1)22i i j j i i j jb i b b j b b ib b jb ++++-+-≥+++, 即1i j b i b j ++≥+.由,i j 的任意性得，1j i b j b i ++≥+. 所以，当S 取得最小值时，所有的(1,2,,)i b i i t +=至多可以取到两个不同值（若恰取两个不同的值，则这两个不同值是两个相邻的正整数）. 由排序不等式，此时12t b b b ≥≥≥.若11b =，则121t b b b ====且2t ≥，212(;,,,)2(1;)t f t b b b t t f t =+=.即可将12(;,,,)t t b b b 换成(1;)t ，而S 不变. 因此，不妨假设12b ≥，则 1212(;,,,)(1;1,,,,1)t t f t b b b f t b b b ≤+-，整理得，112b t +≤+，又1t b t t +≥+，故由(1,2,,)i b i i t +=的不同值组成的集合为{1},{2},{1,2},{,1}t t t t t t +++++.（1）当集合为{1}t +时，1i b t i =+-，(1)2t t n +=，t =，22211(1)(21)()(1)6ttk k k t t t S b k k t t ==++=+-=+-∑∑，令1t m +=，则(1)2m m n -=，12m +=，上式可化为(1)(1)(21)3m m m S m n -+=+-；（2）当集合为{2}t +时，2i b t i =+-，(3)2t t n +=，32t -+=，22211(1)(21)()(2)6t tk k k t t t S b k k t t ==++=+-=+-∑∑，令1t m +=，则(1)(2)2m m n -+=，1122m ⎡⎢⎣-+==⎦，上式可化为(1)(1)(21)3m m m S m n -+=+-；（3）当集合为{1,2}t t ++时，设(1,2,,)i b i i t +=中，值为2t +的个数为{1,2,,1}x t ∈-，值为1t +的个数为t x -，则2t ≥，且22(1)(1)232(2)()(1),2222t t t t t t t t n x t t x t x ⎡⎤+++++-=++-+-=+∈⎢⎥⎣⎦， 令1t m +=，则(1)2(1)4,22m m m m n -++-⎡⎤∈⎢⎥⎣⎦，12m ⎡=⎢⎣⎦，(1)2m mx n -=-，且22221122(1)(21)()(2)()(1)6(1)(21)(1)(23)6(1)(1)(21)(1)(21)26(1)(1)(21)3ttk k k t t t S b k k x t t x t t t t t t t x m m m m m m m m n m m m m n ==++=+-=++-+-++=+++----⎛⎫=-++--⎪⎝⎭-+=+-∑∑；（4）当集合为{,1}t t +时，设(1,2,,)i b i i t +=中，值为1t +的个数为{1,2,,1}x t ∈-，值为t 的个数为t x -，则2t ≥，且22(1)(1)22(1)(),2222t t t t t t t t n x t t x t x ⎡⎤+--++-=++--=+∈⎢⎥⎣⎦， 令t m =，则(1)2(1)2,22m m m m n -++-⎡⎤∈⎢⎥⎣⎦，m =⎣⎦，(1)2m mx n -=-，且22221133(1)(21)()(1)()6(1)(21)(21)6(1)(1)(21)(21)26(1)(1)(21).3ttk k k t t t S b k k x t t x t t t t t t x m m m m m m m n m m m m n ==++=+-=++--++=++--++⎛⎫=++--⎪⎝⎭-+=+-∑∑ 综上，2112t ti i i i S ib b ===+∑∑的最小值是(1)(1)(21)3m m m m n -++-，其中12m ⎡+=⎢⎣⎦.代数5（复旦附中李朝晖、施柯杰、肖恩利）求最大的实数M ，使得不等式22333()()()x y M x y xy x y +≥+--对一切满足0x y +≥的实数,x y 均成立.解：所求M 的最大值为32.首先，取4x y ==，可得32M ≤.下证：22333()32()()x y x y xy x y +≥+-- 对一切满足0x y +≥的实数,x y 均成立.记22s x y =+，t x y =+. 已知22s t ≥，0t ≥.要证的不等式转化为：3228(3)(2)s t s t t t s ≥---设s rt =，上述不等式等价于：38(3)(2)r r t t r ≥---，其中20r t ≥≥，由32328(3)(2)8(21)8168r r t t r t r r r r ----=--+-+- 322816(4)0r r r r r ≥-+=-≥，所以38(3)(2)r r t t r ≥---，其中20r t ≥≥成立.代数6（华东师大二附中唐立华）A ：设正数c b a ,,满足：3222=++c b a ，求证：2444222≤-+-+-c cb ba a. 证明: 先证如下引理引理设正数c b a ,,满足：3222=++c b a ，则18)414141(9)(2222≤-+-+-+++cb ac b a . (*) 引理证明: ,)()()()(92222a c c b b a c b a -+-+-=++-9)414141(9222--+-+-cb a 9)414141)](4()4()4[(222222--+-+--+-+-=c b a c b a 222224444∑⎪⎪⎭⎫⎝⎛-----=b aa b ， 故(*)⇔222224444∑⎪⎪⎭⎫⎝⎛-----b aa b 222)()()(a c c b b a -+-+-≤.记2221444c ab c a bI -+-+-=,2222444c bb aa cI -+-+-=. 要证原不等式,只要证明:222222)(4444b a b a a b -≤⎪⎪⎭⎫⎝⎛----- 222222222)()4)(4()()4)(4()(b a b a b a b a b a +≥--⇔-≤---⇔而22222222)()()1)(1()4)(4(b a c b a c a c b b a +>++≥++++=--， 上式成立，故引理得证.下证原题：记∑-=++=2241,9)(a y c b a x ，则由引理有：2≤+y x . 由柯西不等式,有222224222414141)(444⎪⎭⎫ ⎝⎛-+-+-⋅++≤⎪⎪⎭⎫ ⎝⎛-+-+-c b a c b a c cb b a a 3323229)2(29932=⎪⎭⎫ ⎝⎛++⋅≤⋅⋅==y y x y y x xy ， 所以 23324444222<≤-+-+-c c b ba a，故原不等式得证.注记：利用已证问题(见2015命题研讨会题目)：设正数c b a ,,满足：3222=++c b a ，有32444222≤-++-++-+cb a ba c ac b .我们有如下：B ：设正数c b a ,,满足：3222=++c b a ，求证：)31(2)414141)((222+≤-+-+-++cbac b a .代数7（湖南师大附中张湘君）设,1,2,,i x R i n +∈=，试确定最小实数c ，使得111()()n nnab n a b ii i i i i c xx x +===≥⋅∑∑∏.分析：由齐次，且,1,2,,i x R i n +∈=，不妨设11nii x==∏.原不等式11111()()()n nna b a b i iii i i nnab n ab n iii i x x x c c xx===++==⋅⇔≥⇔≥∑∏∑∑∑，则只需求11()na bi i nab n ii x S x=+==∑∑的最大值.由幂平均不等式，1111()()nnab a iii i abaxxnn ==≥∑∑111()nnb ab a b ii i i nxx -==⇒≥∑∑，则111nb ab ii nab n ii n xS x-=+=≤∑∑.由Chebyshev 不等式，12111111()()nn nn nnab n n ab ab ab n ab iiin i ii i i i i i i n xx x nx x x x xx ++======≥≥⇒≥∑∑∑∑∑∑.于是1b S n-≤，当121n x x x ====时取等号，所以11max min b b S n c n --=⇒=.代数8（湖南师大附中张湘君）给定3m ≥且m N ∈，设12,,,0m a a a >，n m ≥且n N ∈，求证：11()2mn i n i i i a ma a =+≥+∑，其中11m a a +=.分析：令1,1,2,,i i iab i m a +==，则11m i i b ==∏，原不等式11()12mn n i imb =⇔≥+∑.由幂平均不等式知≥，于是只需证明：11()12mm m i i m b =≥+∑. 考虑到0,1,2,,i b i m >=，可设,1,2,,ic i b e i m ==，则10mii c==∑.记1()()1mt f t e =+，则11111()()()12122i m m mm m i c m m m i i i im m m f c b e ===≥⇔≥⇔≥++∑∑∑. 求1()()1m tf t e=+的二阶导数得2''()(1)(1)t t m tf t me e me --=+-，下面分两种情况讨论：(i) 当(1,2,,)i b i m =中至少有一个小于1m 时，111()()111mm m i ib m=>++∑， 于是只需证明111()(1)2121m mm m m m m≥⇔+⋅≤+. 设1(),3xg x x x =≥，则121'()(1ln )0xg x x x x=⋅⋅-<，所以()g x 在3x ≥时单调递减，所以11311(1)(1)323m m m +⋅≤+⋅<.(ii) 当(1,2,,)i b i m =都大于等于1m时，''()0f t ≥，则()f t 是下凸函数， 由琴生不等式得11()()(0)2mimi i mi cm f c m f m f m==≥⋅=⋅=∑∑. 综上所述，11()12mm m i i mb =≥+∑，证毕.代数9（湖南师大附中汤礼达）设+∈R a a a n ,...,,21，求证：1)1(1211≥-+∑∏=≠--ni ji jn i n i a n a a .证明：首先我们证明局部不等式：n n nn n n n nn n n n n n n n nn n n n GM AM n n nn n n n aan aa an aaan aaaa 11222121221111221212211221212211)1()1(2))1(()...(222222++++--++-----⋅⋅⋅-+⋅⋅⋅-+=⋅⋅⋅-++++≥n n n n n n n nn n nn n n a a a n aa aan a⋅⋅⋅-+=⋅⋅⋅-+≥--------2112111112)1(211211)1()1(2222222所以有])1([)1()...(2121111211212122121221111222222n n n n n n n n n n n n nn n n n n a a a n a aa a an aaaa a ⋅⋅⋅-+=⋅⋅⋅-+≥+++---------故n n nn n n n n n nn n aaaaa a a n a a 2121221121132211112222......)1(------+++≥-+同理有),...,3,2()1(1212121122n i aaa n a a ni n n i n n ij i jn i n i =≥-+∑∏=--≠--将上式相加，即得.1)1(1211≥-+∑∏=≠--ni ji jn i n i a n a a代数10（湖南师大附中汤礼达）给定*,k n N ∈,1k n ≤-，2n k ≠，设12,,,n a a a ⋯是{}1,2,,n ⋯的一个排列，令11i i i i k S a a a ++-=++⋯+（其中1i n ≤≤，下标mod n 考虑），记{}12min ,,,n S S S S =⋯.求证：(1)S 1.2k n +⎡⎤≤-⎢⎥⎣⎦证明：反设(1)2k n S +⎡⎤≥⎢⎥⎣⎦，因1k n ≤-，故1112k a a S S +≠⇒≠，故必有1S S >或2S S >， 故11(1)2nni i i i kn n nS S k a ==+<==∑∑. 当k 为偶数或n 为奇数，得(1)2k n Z +∈(1)2k n S +⇒<，与假设矛盾. 故只须再考虑k 为奇数，n 为偶数的情况, 对1i n ≤≤，(1)12i k n S +-≥.记(1)1{|}2i k n P i S +-==，(1)1{|}2j k n Q j S ++=≥，则{}1,2,,P Q n =⋯，P Q φ=. 因为11,(1).i i k i i k n a a S S i n ++≤-≠≠≤≤所以得到故P 中任意的两元素之差都大于1，又2nP Q n P +=⇒≤1(1)2n i i i i i P i Qkn n S =S S =∈∈+⇒=+∑∑∑(1)1(1)122k n k n P Q +-++≥+(1)1(1)1(1)()2222(1),2k n k n kn n nP n P P kn n +-+++=+-=+-+≥ 等号必须成立，即2n P =,且(1)12i k n S +-=或(1)1(1)2kn n i n ++≤≤. 不妨1(1)12k n S +-=则(1)12(1)12i k n i S k n i +-⎧⎪⎪=⎨++⎪⎪⎩，为奇数，为偶数（*）1(1)12k n S +-=，211(1)112k+k n S a a =++=⇒-. 又因为k 为奇数1(1)12k+k n S =++⇒，211(1)112k+k+2k+k n S =a a =+-⇒⇒-. 故112k+a =a ,所以2n k ｜，但22k n n <⇒2k =,与题设相矛盾.代数11（吉大附中石泽晖、王庶赫）已知正数序列{}{}n n a b ，满足11nni i i i a b ===∑∑，且12n a a a ≤≤≤，111n n n a b b b a -≥≥≥≥≥，对任意的1i j n ≤<≤，均有j i j i a a b b -≥-，证明：11n ni i i i a b ==≤∏∏.证明：由于j i j i a a b b -≥-，则j j i i a b a b -≥-（1i j n ≤<≤）. 这说明数列1{}n i i i a b =-是单调不减序列. 又0n n a b -≥，110a b -≤.（1）当110a b -<时，必存在1m n <≤，使得：当1i m ≤<时，i i a b <，此时记i i i b a β=-；当m i n ≤≤时，i i a b ≥，此时记i i i a b α=-.由11n n i i i i a b ===∑∑可知：11n m i i i mi αβ-===∑∑. 而要证明的11n n i i i i a b ==≤∏∏可变形为11ni i ia b =≤∏.由均值不等式可知：11()nini n ii i i a a bb n ==≤∑∏，故只需证1n i i ia nb =≤∑（*）即可，往证（*）式成立. 事实上，111nnm i i i i ii i m i i i i a b b b b b αβ-===+-=+∑∑∑111111n n mm n n mm n b b b b b αααββ----=++++---111nn mm mmmm mn n b b b b b αααββ--≤++++---=，这是由于n i m ≥≥时，0i m b b ≥>，0i α≥，故有i i imb b αα≤；1i m ≤<时，0i m b b <≤，0i β≥，故有iiimb b ββ--.（2）当110a b -=时，则对1i n ≤≤，均有i i a b ≥，又11nni i i i a b ===∑∑，故对1i n ≤≤，均有i i a b =，此时结论也成立.代数12（绵阳东辰学校袁万伦、姚先伟）设0,0,0>>>c b a ，求证：)212)(212)(212()43)(43)(43(222+++≥++++++c b a a c c b b a .（问题来源：2005年白俄罗斯数学奥林匹克试题的推广，原题：设0,0>>b a ，求证：)212)(212()43)(43(22++≥++++b a a b b a ，）证明：因为2121414322++≥+++=++b a b a b a ，同理2143,214322++≥++++≥++a c a c c b c b ，所以≥++++++)43)(43)(43(222a c c b b a )21)(21)(21(++++++a c c b b a ，即证)21)(21)(21(++++++a c c b b a )212)(212)(212(+++≥c b a ，将此式左，右两端分别展开，即证)(21222222222c b a bc c b ac c a ab b a ++++++++)(216ca bc ab abc +++≥)(*因为ca a c bc c b ab b a 2,2,2222222≥+≥+≥+，三式相加得ca bc ab c b a ++≥++222，所以)(21222222222c b a bc c b ac c a ab b a ++++++++)(21)()()(222222222c b a b a c c a b c b a ++++++++=cabbac abc 222++≥)(216)(21ca bc ab abc ca bc ab +++=+++， 即)(*成立，故)212)(212)(212()43)(43)(43(222+++≥++++++c b a a c c b b a成立，当且仅当21===c b a 时取等号.代数13（绵阳东辰学校袁万伦）正数b a ,c 满足1=++c b a ，证明：32232323≥++++++++b a a c a c c b c b b a . 问题来源：韩京俊《初等不等式的证明方法》地6页例1.2：正数c b a ,,满足1=++c b a ，证明：ba ac a c c b c b b a ++++++++2222≥. 证法1:因为b a ac a c c b c b b a ++++++++222++=c b a 3b a a a c c c b b b a c a c b +++++++++22233，由cauchy 不等式的推论得21)(2)(2222=++++≥+++++c b a c b a b a a a c c c b b ， )(2)(2222444333ca bc ab c b a cb ca c ba bc b ac ab a b a c a c b c b a ++++≥+++++=+++++， 又因为)(3)(2ca bc ab c b a ++≥++，即,31≤++ca bc ab由cauchy 不等式1)()(32222=++≥++c b a c b a ，即31222≥++c b a ， 所以61)(2)(2222≥++++ca bc ab c b a ，即61333≥+++++b a c a c b c b a ，故 b a a c a c c b c b b a ++++++++222322161=+≥.证法2：因为b a ac a c c b c b b a ++++++++222++=c b a 3b a a a c c c b b b a c a c b +++++++++22233，由cauchy 不等式的推论得21)(2)(2222=++++≥+++++c b a c b a b a a a c c c b b ， 因为2323234)(,4)(,4)(c b a c b a c b a c b a c b a c b a c b a ≥+++≥+++≥+++，所以)(21222333ca bc ab c b a b a c a c b c b a ++-++≥+++++ )(25)(2ca bc ab c b a ++-++=)(251ca bc ab ++-=，又因为)(3)(2ca bc ab c b a ++≥++，即,31≤++ca bc ab所以6131251)(251=⨯-≥++-ca bc ab ，即61333≥+++++b a c a c b c b a . 故b a a c a c c b c b b a ++++++++222322161=+≥.代数14（广州市第二中学程汉波）已知,,C A B 为ABC ∆的三个内角，求n *∈N的最小值．解（1）当1n =时，因为()21sin sin sin 3A B A ≤≤∑∑2193sin 334A B C ++⎛⎫≤ ⎪⎝⎭， 所以()31sin sin 3sin sin 4A B A B -=-≥∑∑． （2）当2n =时，由万能公式及柯西不等式得2224tantan 4tan tan 2222sin sin 1tan 1tan 1tan tan 2222A B A B A B A B A B =≤⎛⎫⎛⎫⎛⎫+++ ⎪⎪⎪⎝⎭⎝⎭⎝⎭ 当且仅当2tan 2tan BA =，即AB =时取等号． 所以有≥=．设tantan 22A B x =，tan tan 22B C y =，tan tan 22C Az =，则x ，y ，z 均为正数，因为tantan tan tan tan tan 1222222A B B C C A++=，故有1=++z y x ．于是2y z x y z +≥=++∑， 在Nesbitt 不等式：()3,,02a abc b c ≥>+∑中，令a x y =+，b y z =+，c z x =+即得322y z x y z +≥++∑，当且仅当3π===C B A 时，等号成立． （2）当3n =时，同第（2）种情况可得，≥==()()()332242y z x y z x y z y z+≥==++++++当且仅当z y x ==，即3π===C B A 时，等号成立． （3）当4n ≥时，同第（2）种情况可得，()12x ≥=>-=∑， 当2,0π→=→C B A 时，等号成立．综上所述，当1n =时，原式的最小值为34；当2n =时，原式的最小值为32；当3n =时，原式的最小值为2；当4n ≥时，原式没有最小值，但下确界为2．代数15（大连市第二十四中学 邰海峰）无穷个非钝角三角形,将其最短边、次长边、最长边分别相加,得到一个新的大三角形,求证：这个大三角形的最大角小于23π.解:设这无穷多个三角形的最短边依次为12,,a a ,次长边依次为12,,b b ,最长边依次为12,,c c ,其中222i i i a b c +,且i i i a b c .设111,,i i i i i i a a b b c c ∞∞∞======∑∑∑,最大角余弦为2222a b c ab +-.对于两个不同的正整数,i j ,因为i j i j i j i j a a bb a a bb +=+ 又因为i j i j i j i j a a bb a b b a +>-，所以22()()i j i j i j i j a a bb a b b a ++-222()1)()1)()i j i j i j i j i j i j i j i j a a bb a a bb a b b a a b b a <+++-+-2(1))i j i j i j i j a a bb a b b a =++-，所以222222()()(i i a b c a b +-+-∑∑222i j i j i ji ji ja ab b <<<=+-∑∑(222)2)()i ji j i i i ja b b a a b <--->-∑∑∑，所以2221122a b c ab +->>-,从而最大角小于23π.代数16（东北育才学校张雷）数列11121{}:1,n n nu u u u u u +==+++,问:是否存在常熟,αβ使得12lim1nx u u u nβα→∞+++=,若存在请求出,αβ,若不存在请说明理由. 解: 12αβ==,下面证明:第一步:证明:引理:111*)321n N n +++<∈-,用数学归纳法,(1)当1n=时,不等式成立;(2)假设n 时不等式成立,则1n +时我们只要证明121n ≤=+,只要证明121n ≤+,该不等式成立,故1n +时,不等式成立.综上所述,引理成立. 第二步:由1211n n u u u u ++++=,1211(2)n nu u u n u -+++=≥可得111(2)n n n u n u u +=+≥,21u =,设12111(2)n n nu u u a n u --+++==≥,则111,1n n n a a a a +=+=,则12lim lim n n x x u u u a nn ββαα→∞→∞+++=.第三步:由111,1n n n a a a a +=+=,得22212122n n n na a a a +=++>+,故 221n a n >-， (*)则22212112221n n n n a a a a n +=++<++-,累加可得 21121(1)(2)323n an n n <-++++≥-,由引理可知:21121(1)21323n a nn n <-++++<-+- (**)故由(*),(**)，22122n a n n n -<<,而21lim12n n n n →∞→∞-==,故2lim 1,lim 1,2n n n a n →∞→∞==,则12αβ==满足条件.试题背景:常见题目:1112,n n na a a a +==+,证明n a <<.由于无法求出具体的通项公式,又希望能改进成为具体的值,而不只限于不等式,进而发现极限可以实现这一目标.代数17（东北育才学校张雷）12...1(2),01(1,2,...,)n i a a a n a i n +++=≥≤≤=,求222122...n na a a a ++++的最小值.解:最小值为12,3,4115n n n n ⎧=⎪-⎪⎨⎪+≥⎪⎩下面证明:我们解决4n =情形,不妨设12,a a 固定,则222343434()2a a a a a a ++=+-+,故可知34,a a =或者40a =,当40a =时,可有均值得最小值为13; 当34,a a =固定34,,a a 调整12,a a ,同样的情况,最后调整13,a a 及24,a a 可知,都取等为61163>. 2,3n =也容易证明.下证5n ≥情形,我们证明更强的结论:222122...(02)n n a a a a s ++++≤≤的最小值当1i a n=取等.一.当5n =时,都取等,值为1n +,而其中一个等于0,最小值111n n >+-,故而有利于我们调整. 同样的调整法,我们可以调整4个相等,即1541a a +=,证明:22515145a a ++≥+,不妨设1515111,,4(0)5520a a a x a x x ≥=+=-≤≤,则带入后,只要证明2510x +≥,显然我们只要证明2s =时成立.2 510x +≥若2 510x ≥,则不等式成立, 若2 510x <,则只要证:2 5 2210)x ≥-,由于443111()()4()555x x +≥+,故只要证43 522111[()4()](4)10)555x x x +-≥-即5 32115()1005x -≥,由于2 510x <我们只要证5 3 5115()5-≥,可知成立. 当6n =时,我们可以通过调整化归为15122a a +=,证明:2221515311221226s s a a a a ++≥+,不妨设1515111,,20)6612a a a x a x x ≥=+=-≤≤（,则不等式等价于2231116()(226626s s x x x ++-≥）,我们正要证明2s =的时候,即2231116()(2666x x x ++-≥） (*) 而2111()+6363x x +≥,代入(*),我们即可证明.下面考虑7n ≥情形,我们用数学归纳法,若2n -时成立,则n 时,我们通过调整使得1,12n n n a a a t -=-=,则122...(01)n a a a t t -+++=≤≤,令(1,2,...,2)i i ab i n t==-,则122 (1)n b b b -+++=,我们求2222212222(...)2n n n t b b b b a --+++++的最小值,由归纳可知1221...,n n na a a a a --====,故问题化归为1(2)21n n a a -+=,求221(2)2n n a a -++的最小值,我们不妨设11122,(0)2(2)n na x a x x n n n n -=+=-≤≤-,我们只要证明2211(2)2n n a an-++≥+(**)则代入(**),我们只要证明:22(2)2n n x -+≥而22221221121()()2n n n n x xn n n-----⎛⎫+≥+ ⎪⎝⎭(对于指数是分数的时候,只要两边平方证明即可 ),代入上式可知结论成立.注: (1)数学归纳法解决了调整法中无限调整的问题; (2)6n =时的解决方法给整个题以提示. (3)5n =时的证明是本题证明的难点. (4)加强归纳的技巧也是值得借鉴的.(5)本题涉及猜想,分类,跳跃归纳,加强归纳,调整法,放缩以及联想探索等能力,是训练学生的较好题目.(6)受5n =的启发,我们也可以直接归纳,问题化归为1(1)1n n a a -+=,求221(1)n n a a -++的最小值,设111,(1)n a x a n x n n=+=--,同样我们得到,只要证明2(1)n n x -+≥我们依旧分类讨论,当2(1)n n x -<时,移项平方,我们只要证明122114()((1)(1))n x n x n n x n n -+--≥-,将112111()()(1)()n n n x n x n n n ---+≥+-代入,且注意到2(1)n n x -<我们只要证明2212(1)4(1)n n n n -⎛⎫-- ⎪⎝⎭,成立(7) 取等条件为全相等或者一个等于0,由此比较两个最小值,觉得系数2比较适合.(8)题目思想来源:(全国高中数学联赛)实数,,a b c 满足1,0a b c abc ++=>,求证:14ab bc ca ++<+. 发现:一正二负的情况,不妨设0,,0a b c ><,则()(1)0ab bc ca b a c ac b b ++=++<-<,我们只要考查,,0a b c >情形,经化归222211222()()22ab bc ca a b c a b c ⇔++<⇔++-++<,即证明2221(*)2a b c +++>.下面证之:不妨设a 不变,则222221(1)(*)2a b c a a ++=+-->抛物线,10,2a-=取得最小值,0c =时,可知不等式成立;12a-=时,232)0a a a ⇔-->,不妨设a 最大,令t =∈,323210t t t ⇔--+>(**)本来是求导数证明的,后来发现:332112,2722t t ++≥我们只要证明3222249275()(2)3274927t t t >⇔>⇔->. 由此启发,继续研究,发现上述的题目形式:代数18（大连市第二十四中学李响）定义有序正数组(a 1,a 2,…,a n )的特征值为a 12a 2+a 22a 3+⋯+a n2a 1(n ≥2)，设有序正数组(x 1,x 2,…,x 2017)的特征值为k ，(1).求证：可以将(x 1,x 2,…,x 2017)划分为m (m ≤1008)个有序数组，并设每组的特征值为k 1,k 2,…,k m ，使得k 1+k 2+⋯+k m ≥k ；(2).将2017改为2018，结论是否成立，并证明.解：(1)我们证明可以将(x 1,x 2,…,x 2017)划分为m-1个二元数组和一个非二元数组满足题中条件，下面用数学归纳法证明：m=1时，显然成立；假设m=p 时结论成立，即可划分为p-1个二元数组和一个非二元数组， 使得k 1+k 2+⋯+k p ≥k 成立；则m=p+1时，保持m=p 时划分出去的p-1个二元数组不变，下面对非二元数组进行划分，设非二元数组为(b 1,b 2,…,b q )(q ≥4)，其特征值为k p ，取其中一个二元数组(b i ,b i+1)(i =1,2,…,q)，其特征值为k pi ，其中b i =b q+i ，设除去(b i ,b i+1)的有序q-2元数组的特征值为k pi ′，则对于m=p+1，只要证明存在i(i =1,2,…,q)使得k pi +k pi ′≥k p 成立， 即(b i 2b i+1+b i+12b i)+(b i+22bi+3+b i+32bi+4+⋯+b i−12bi+2)≥b i 2bi+1+b i+12bi+2+⋯+b i−12b i成立， 即b i+12b i+b i−12bi+2−b i+12bi+2−b i−12b i≥0成立，即(b i+2−b i )(b i+1−b i−1)(b i+1+b i−1)b i b i+2≥0成立，即(b i+2−b i )(b i+1−b i−1)≥0成立，设c i =b i+2−b i ，由于(c 1c 2)(c 2c 3)…(c q c 1)=c 12c 22…c q 2≥0，q 为奇数，所以至少存在一个i 使得c i c i+1≥0，对于m=p+1原结论成立，所以原题结论成立.(2)成立，同(1)只要证存在i 使得(b i+2−b i )(b i+1−b i−1)≥0成立，设c i =b i+2−b i ，若存在c i =0，则显然成立，若c i 均不为零，用反证法，假设c i c i+1均小于零，则c i ,c i+2为同号，由于q 为偶数，有c 1,c 3,…,c q−1为同号，由于c 1+c 3+⋯+c q−1=(b 3−b 1)+(b 5−b 3)+⋯+(b 1−b q−1)=0， 与同号产生矛盾，所以存在i 使得(b i+2−b i )(b i+1−b i−1)≥0成立， 所以对于2018依然成立.代数19（学而思培优·苏州分校李家夫）已知：432()f x x ax bx cx d =++++有四个复数根1234,,,αααα，3222()(4)4g x x bx ac d x bd a d c =-+-+--有三个复数根123,,βββ.求证：221413()()i j i j i j i j ααββ≤<≤≤<≤-=-∏∏解析为记号简单起见，不妨设1234{,,,}{,,,}e f g h αααα= 由韦达定理有()+fh+gh c ()a e f g h b ef eg eh fg efg efh fgh egh d efgh=-+++⎧⎪=+++⎪⎨=-+++⎪⎪=⎩ 我们来证明：（1）123123413241423()+fh+gh ()()()b ef eg eh fg βββαααααααααααα++=--=+++=+++++（2）. . 直接展开验证即可. 于是证毕！代数20（华东师大张丽玉）设x 、y 、z 为正实数，求证：.一、命题背景:原题：P 为三角形ABC 内一点，求证：BP CP BC AP CP AC AP BP AB AB BC AC ++≥.特别地，当∠APB =∠BPC =∠CP A =120°时，这个几何不等式仍然成立，设P A =x ，PB =y ，PC =z ，则得到题2.二、解答过程当然我们可以先解答原几何题，再等价转化为我们所需要的代数不等式. 下面我们给出一个纯代数的解法，解答过程如下：1≥首先证明222y zx yz xy z++++.22222()()()22y z y z y zx yz x x yz x x yz xy z+++⇔++≤++-+++222222222()()()2()2()2y zx y xy x z xz x yz x y z y zxy z y zx yz x+++++-++++⇔≤-++++22223()()42()()2x y z x y zy z y zx yz x--⇔≤++++23()()22y zx yz x x y z+++≥+而2()223()22y z y zx yz x xy zxz xy x x y z++++>+≥++=+222y zx yz xy z++++成立.222()()yz yz y zy z yz y zx yz xy z+≥=+++++∑.()()zx z xyz y z+≥+∑，()()xy x yyz y z+≥+∑，上面三个式子相加，即是我们需要证明的不等式.代数21（杭州二中赵斌）几何几何1（复旦附中李朝晖、施柯杰、肖恩利）已知锐角ABC ∆，AC BC >，点,K N 在边AC 上，点,M L 在边BC 上，且1122BC AN CK CL BM AC <===<. KL 与MN 交于点P . 点R 为边BC 的中点，点Q 为ABC ∆外接圆上弧ACB 的中点. 求证：RPN QPK ∠=∠.证明：延长MN 、KL 分别交BC 于点X 、Y . 由梅涅劳斯定理，直线MN 、KL 截ABC ∆得：1BX AN CM AY BL CKXA NC MB YB LC KA⋅⋅==⋅⋅（1） 由条件：AN CK =，NC KA =，CM BL =，MB LC =.代入（1）得：BX BYXA YA=， 进而：AX BY =（2）因为R 为边BC 的中点，Q 为ABC ∆外接圆上弧ACB 的中点，所以QR 为线段AB 的中垂线，结合（2）可知QR 为线段XY 的中垂线.因为QA QB =，AN BM =，QAN QBM ∠=∠，所以QAN QBM ∆≅∆， 所以QM QN =，MQA BQA ACB ∠=∠=∠，进而,,,M C Q N 四点共圆. 所以QCM QNX ∠=∠. 又QCM QAX ∠=∠， 可得QAX QNX ∠=∠，可得,,,Q N A X 四点共圆，所以22ACBABC CABQXN QAC QAB CAB CAB π-∠∠-∠∠=∠=∠-∠=-∠=.又22ACB ABC CABKYX CBA BLY CBA π-∠∠-∠∠=∠-∠=∠-=所以QXN KYX ∠=∠，由QX QY =，所以：PXY PYQ ∠=∠所以,QX QY 为PXY ∆的外接圆的切线，所以QP 为PXY ∆的陪位中线， 所以：QPK XPR RPN ∠=∠=∠.几何2（湖南师大附中苏林）已知I 是ABC ∆内心，过I 作BC 的垂线，交ABC ∆的外接圆于E D 、(A D 、在BC 同侧)，延长DA 交直线BC 于F ，过I 作AE 的垂线交直线BC 于G .求证：EGI DFI ∠=∠.证明：引理：F 是O ⊙的弦BC 延长线上一点，D 是弧BC 中点，弦交弦BC 于G ，DF 交圆于H D 、，则DE DG DF DH DC⋅=⋅=2.引理的证明：连结CH CE 、.因为D 是弧BC 中点，所以BCD E ∠=∠，因此DCE DGC ∆∆∽，所以DE DG DC⋅=2.因为弧=DH 弧-DC 弧HC =弧BD －弧HC ， 所以F CDH BCD DCH ∠=∠-∠=∠， 因此DCF DHC ∆∆∽， 所以DE DG DF DH DC ⋅=⋅=2.回到原题：延长AI 交O ⊙于P ，设BC 于DE 的交点为M ，连结DF 交BC 于L ，延长DO 交O ⊙于K .下证G E P 、、三点共线：延长PE 交BC 延长线于G '，连结G I '交AE 于N .由鸡爪定理及引理知G P PE PC PI '⋅==22，故G PI PEI '∆∆∽，故I G P PIE '∠=∠，于是B G I E G B IEA IAE '∠+'∠=∠+∠， 而E G B PCE IAE '∠=∠=∠， 所以N G M MEN '∠=∠，因此N G E M 、、、'四点共圆.而G EM '∠= ︒90，所以AE G I ⊥'， 因此G '即G ，所以G E P 、、三点共线.再证DF LI ⊥：由鸡爪定理及引理知：PD PL PC PI ⋅==22，所以PID PLI ∆∆∽，从而IDP LIP ∠=∠， 因此EDP DPA LIP DPA DLI ∠+∠=∠+∠=∠. 所以EDP ADE DPA LDF DLI ∠+∠+∠=∠+∠2. 在DBC ∆中熟知DE DO 、是等角线，从而EDK ADE DFA LDF DLI ∠+∠+∠=∠+∠= ︒90. 所以DF LI ⊥.最后证明EGI DFI ∠=∠：由DF LI ⊥、LF DI ⊥知I 是DLF ∆垂心， 所以LDF DFI DLI ∠-︒=∠=∠90. 因为DPA DEA IGL ∠=∠=∠， 所以I G P L 、、、四点共圆. 从而EGI DLI ∠=∠. 所以EGI DFI ∠=∠.几何3（湖南师大附中苏林）如图，21O O ⊙、⊙相切，且均与O ⊙切，O ⊙的弦径AB 是21O O ⊙、⊙的外公切线，21O O ⊙、⊙的两条外公切线EF CD 、分别交AB 于E C 、，F D 、在O ⊙上，且F D 、、21O O 、均不在直线AB 同侧，EF 交AD 于P ，CD 交BF 于Q . 求证：AB PQ ∥.证明：分别延长DC FE 、交O ⊙于S T 、，连结TB TA SB SA 、、、.设21O O ⊙、⊙分别切AB 于L K 、，切SD 于V U 、，切FT 于X Y 、. 对1O ⊙及点圆B S A ⊙、⊙、⊙用开世定理有：SU AB AK SB BK SA ⋅=⋅+⋅.对2O ⊙及点圆B S A ⊙、⊙、⊙用开世定理有：SV AB AL SB BL SA ⋅=⋅+⋅.两式相减得：UV AB KL SB KL SA ⋅-=⋅-⋅， 从而KLUVAB SA SB ⋅=-.同理：KLXYAB TA TB ⋅-=-.。
2017阜阳市技能大赛获奖名单
动画片制作
计算机辅助设计 （ 冯勇 黄毅威 潘梦祝 王国征 张雷 赵建军 宫傲 张万杰 管佳豪 郭敏 高敬雨 时慧如 刘家成 张志强 张传敬 蔡雷 陈允泽 朱世荣 张虎 孙庆帆 马猛 韩兆祥 卞功成 徐伟杰 于庆才 季小虎 贺凤飞 张姣姣 华家良 李伟杰 曹腾 苏玉虎 孙威 韩晓燕 徐帅 刘攀 朱晓倩 倪肖男 吕文博 刘 征 段粤雷 朱慧慧 梁晴晴 焦大猛 陈晴文 韩志恒 孟宇 徐文静 陈甜甜 陈梦雨 袁梦如 郭允凤
二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 一等奖 一等奖 二等奖 二等奖 二等奖 二等奖 二等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 一等奖 一等奖 一等奖 一等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖
殷毅 丁娟 王云龙 陈瑞龙 赵树山 胡婷婷 於祖光 李可 赵志勇 於祖光 陈瑞龙 汝阳 许浩 刘启金 王艳梅 刘启金 李明 李兴权 李琦 赵树山 徐志伟 马聪 曾海 岳峰 孙培培 樊玲玲 孙培培 魏影 岳峰 魏影 贾兴州 李玉玲 宋明 石丽 孙艳 李玉玲 李玉玲 陈涛 梁叶伟 陈涛 梁叶伟 方燕 汝春晓 魏海 魏海 汝春晓 梁叶伟 汝春晓 武登聚 周建宗 周建宗 臧永涛 韦朋祥 周建宗 周建宗 王丽
张永成 徐少瑛 明鸣 唐盼 王倩 马晓旭 李占杰 周伟 李占杰 陈亮 徐少瑛 张雷 吴玉琼 季阳光 马晓旭 叶涛 王倩 徐少瑛 王薇 李占杰 叶涛 孙志宏 杨文锐 吴磊 吴磊 王琳琳 李可 饶胜 王秀平 乔顶峰 王明 王秀平 王艳梅 朱卫华 饶胜 王秀平 胡勇伟 高辉 王云龙 刘飞艳 殷毅 陈慧慧 宋有声 侯雪峰 高辉 郭曼丽 郭曼丽 刘清泉 刘飞艳 宋有声 张殿刚 陈慧慧 刘梅 刘飞艳 刘梅 郭曼丽
阜阳2017中小学高级教师专业技术资格评审
男
初中语文
94
阜南县张寨镇中心学校
周军
男
初中语文
95
阜南县新村镇中心学校
李龙
男
初中语文
96
阜南县田集镇中心学校
吴玉兰
女
初中语文
97
阜南县田集镇孙寨中学
尹显标男Biblioteka 初中语文98阜南县田集镇孙寨中学
张保秀
女
初中语文
99
阜南县黄岗镇中心学校
季晓东
男
初中语文
100
阜南县黄岗镇中心学校
高学颖
女
初中语文
101
于彦娉
女
高中语文
15
安徽省太和中学
孙影
女
高中语文
16
安徽省太和中学
孙奕
女
高中语文
17
安徽省太和中学
张彩慧
女
高中语文
18
安徽省太和中学
刘艳丽
女
高中语文
19
颍上县垂岗乡中心学校
杨勇
男
初中语文
20
颍上甘罗乡村教育社
曾立红
女
初中语文
21
颍上建颍乡管仲职中
王学友
男
初中语文
22
颍上县第五中学
刘凤桂
女
初中语文
23
阜南县郜台乡段台九年制学校
余洪贵
男
初中语文
102
阜南县柴集高级职业中学
王康
男
初中语文
103
临泉滑集镇中心学校
汪辉
男
中学语文
104
临泉白庙镇中心学校
刘志强
男
初中语文
阜阳市2017年度中小学高级教师专业技术资格评审041019130318
21 颍上建颍乡管仲职中王学友男初中语文22 颍上县第五中学刘凤桂女初中语文23 颍上县第五中学王守全男初中语文24 颍上县八里河中心学校崔家航男初中语文25 颍上县半岗镇中心学校卞景发男初中语文26 颍上县半岗镇中心学校李磊男初中语文27 颍上县半岗镇中心学校王顶义男初中语文28 颍上县半岗镇中心学校王心云女初中语文29 颍上县陈桥镇中心学校程丽女初中语文30 颍上县垂岗乡中心学校崔芹女初中语文31 颍上县红星镇中心学校高洁女初中语文32 颍上县建颍乡中心学校郭恬女初中语文33 颍上县江店孜镇中心学校王宇新男初中语文34 颍上县江店孜镇中心学校沈久彬男初中语文35 颍上县江店孜镇中心学校任学云女初中语文36 颍上县刘集乡中心学校龙涛男初中语文37 颍上县刘集乡中心学校李燕善男初中语文38 颍上县刘集乡中心学校朱华昌男初中语文39 颍上县鲁口镇中心学校李克男初中语文40 颍上县南照镇中心学校崔云周男初中语文41 颍上县南照镇中心学校周萍女初中语文42 颍上县南照镇中心学校金德林男初中语文43 颍上县润河镇中心学校刘健男初中语文44 颍上县润河镇中心学校李金亮男初中语文45 颍上县赛涧回族乡中心学校穆良丰男初中语文46 颍上县慎城镇陈屯初级中学张贺珍女初中语文47 颍上县慎城镇陈屯初级中学蒋琼男初中语文48 颍上县盛堂乡中心学校郑永男初中语文49 颍上县盛堂乡中心学校张广奎男初中语文50 颍上县十八里铺镇中心学校曹利男初中语文51 颍上县五十铺乡中心学校王文献男初中语文52 颍上县夏桥镇中心学校郑蕊女初中语文53 颍上县夏桥镇中心学校夏开波男初中语文54 颍上县谢桥镇广源中学姜玲女初中语文55 颍上县谢桥镇张庄中学陈德虎男初中语文56 颍上县谢桥镇张庄中学姜桂男初中语文57 颍上县谢桥中心学校栾峰男初中语文58 颍上县新集镇中心学校樊家虎男初中语文59 颍上县新庙高级职业中学姜允发男初中语文60 颍上县杨湖镇中心学校李鸣男初中语文61 颍上县职业技术教育中心张梅女初中语文62 安徽省颍上第二中学郭亚男高中语文63 安徽省颍上第一中学姜栋栋男高中语文64 安徽省颍上第一中学武晓丽女高中语文65 阜南县一职高李仲胜男高中语文66 阜南第二初级中学谢家刚男初中语文67 阜南县第一初级中学郭勇男初中语文68 阜南县第一初级中学李芳女初中语文69 阜南县第一初级中学马勇男初中语文70 阜南第一初级中学张新成男初中语文71 阜南县一职高张亚军男初中语文72 阜南县第五初级中学张海波男初中语文73 阜南县第五初级中学张弘男初中语文74 阜南县方集镇中心学校张云亮男初中语文75 阜南县洪河桥镇曾沃中学周涛男初中语文76 阜南县焦陂高级职业中学郝淑华女初中语文77 阜南县焦陂高级职业中学李英女初中语文78 阜南县焦陂高级职业中学王俊杰男初中语文79 阜南县许堂乡中心学校邵振儒男初中语文80 阜南县许堂乡大桥中学刘正友男初中语文81 阜南县于集乡中心学校于锐男初中语文82 阜南县赵集镇中心学校刘瑞男初中语文83 阜南县朱寨镇小肖九年制学校顾志才男初中语文84 阜南县朱寨镇中心学校马大友男初中语文85 阜南县朱寨镇小肖九年制学校赵亮男初中语文86 阜南县朱寨镇中心学校韩忠标男初中语文87 阜南县朱寨镇中心学校徐淼男初中语文88 阜南县地城镇中心学校杨丽梅女初中语文89 阜南县地城镇中心学校锁丽丽女初中语文90 阜南县地城镇中心学校董自魁男初中语文91 阜南县地城镇中心学校王振平男初中语文92 阜南县经开区中心学校陈绪侠女初中语文93 阜南县苗集镇中心学校张恩华男初中语文94 阜南县张寨镇中心学校周军男初中语文95 阜南县新村镇中心学校李龙男初中语文96 阜南县田集镇中心学校吴玉兰女初中语文97 阜南县田集镇孙寨中学尹显标男初中语文98 阜南县田集镇孙寨中学张保秀女初中语文99 阜南县黄岗镇中心学校季晓东男初中语文100 阜南县黄岗镇中心学校高学颖女初中语文101 阜南县郜台乡段台九年制学校余洪贵男初中语文102 阜南县柴集高级职业中学王康男初中语文103 临泉滑集镇中心学校汪辉男中学语文104 临泉白庙镇中心学校刘志强男初中语文105 临泉县张集中学陶相锋男初中语文106 临泉黄岭镇中心校张合成男中学语文107 临泉滑集镇谢集中心校陈鑫男初中语文108 临泉城东街道中心学校牛保良男初中语文109 临泉一中徐如岭男高中语文110 临泉一中谢敬敬女高中语文111 临泉一中李倩女高中语文112 临泉一中任晓伟女高中语文113 临泉高塘镇中心学校张启涛男初中语文114 临泉高塘镇中心学校张国部男初中语文115 临泉田家炳实验中学姜江男高中语文116 临泉艾亭镇中心学校谢忠实男初中语文117 临泉艾亭镇中心学校谢尚功男初中语文118 临泉艾亭镇中心学校李朋男初中语文119 临泉杨桥高级职业中学李俊红男高中语文120 临泉杨桥高级职业中学刘平女高中语文121 临泉杨桥高级职业中学郭申男初中语文122 临泉杨桥高级职业中学牛琨男初中语文123 临泉杨桥高级职业中学王晓梅女初中语文124 临泉杨桥高级职业中学刘朝山男初中语文125 临泉宋集镇杨小街中心学校刘磊男初中语文126 临泉宋集镇杨小街中心学校吴怀河男初中语文127 临泉宋集镇杨小街中心学校高兰婷女初中语文128 临泉宋集镇杨小街中心学校孙海艳女初中语文129 临泉宋集镇杨小街中心学校周维礼男初中语文130 临泉二中刘晓艳女高中语文131 临泉二中董艳艳女高中语文132 临泉二中柳海男高中语文133 临泉老集镇中心校李为东男初中语文134 临泉四中马伟男初中语文135 临泉高塘镇范集中心学校王玲玲女初中语文136 临泉县关庙镇中心校王坤男初中语文137 临泉县关庙镇中心校姚金志男初中语文138 临泉县关庙镇中心校王志男初中语文139 临泉谭棚镇中心学校张旭男初中语文140 临泉谭棚镇中心学校孙武男初中语文141 临泉谭棚镇中心学校孟春男初中语文142 临泉鲖城镇中心学校马永男初中语文143 临泉鲖城镇中心学校张勇敢男初中语文144 临泉鲖城镇中心学校辛光辉男初中语文145 临泉庙岔镇中心学校韩寅男初中语文146 临泉庙岔镇中心学校卯俊伟男初中语文147 临泉庙岔镇中心学校王玉玲女初中语文148 临泉陈集镇中心学校赵影女初中语文149 临泉宋集镇中心学校王伟男初中语文150 临泉宋集镇中心学校王治军男初中语文151 临泉宋集镇中心学校李继武男初中语文152 临泉宋集镇中心学校李绍山男初中语文153 临泉土陂乡中心学校张士锋男初中语文154 临泉迎仙镇中心学校张文青男初中语文155 临泉迎仙镇中心学校郑振男初中语文156 颍州区三十里铺中心学校亓明建男初中语文157 颍州区十五中马丙印男初中语文158 颍州区程集镇中心学校张玉香女初中语文159 颍州区三合镇中心学校刘莉华女初中语文160 阜阳市第十九中学唐邵勇男初中语文161 阜阳市第十九中学谭胜杰男初中语文162 阜阳市五职高王影女初中语文163 颍泉区抱龙初级中学董慷男初中语文164 颍泉区周棚中学魏华利男初中语文165 颍泉区行流中学陈东亚男初中语文166 颍东区阜阳市第十中学陶守成男语文167 颍东区插花镇二学区中心学校李效龙男语文168 颍东区插花镇二学区中心学校杜付连男语文169 颍东区口孜镇汪庙初级中学邬继成男语文170 颍东区口孜镇汪庙初级中学訾化文男语文171 颍东区口孜镇汪庙初级中学白春萌男语文172 颍东区冉庙乡中心学校张李志男语文173 颍东区袁寨镇临颍中学王冠男语文174 颍东区枣庄镇中心学校张超男语文175 颍东区正午镇中心学校周凤娟女语文176 界首第一中学陈龙男高中数学177 界首市界首中学贾林男高中数学178 太和县北城中学教育集团北城中学校区李素梅女初中数学179 太和县郭庙镇中心学校刘加飞男初中数学180 太和县洪山镇中心学校祝西贤男初中数学181 太和县税镇镇中心学校曹杰峰男初中数学182 太和县苗集镇中心学校刘利萍女初中数学183 太和县第八中学随祥恩男高中数学184 颍上县半岗镇庙台中学孙振男初中数学185 颍上县红星镇中心学校吴刚明男初中数学186 颍上县黄坝乡中心学校朱占坤男初中数学187 颍上县建颍乡管仲职中范平刚男初中数学188 颍上县建颍乡中心学校李军男初中数学189 颍上县江店孜镇姜岳中学胡秀章男初中数学190 颍上县江店孜镇中心学校常文军男初中数学191 颍上县江口镇中心学校宋近男初中数学192 颍上县刘集乡中心学校江乃玉男初中数学193 颍上县六十铺镇中心学校唐瑞盟男初中数学194 颍上县鲁口镇中心学校陈祥龙男初中数学195 颍上县南照镇中心学校张军男初中数学196 颍上县润河镇中心学校刘池军男初中数学197 颍上县慎城镇陈屯初级中学江向阳男初中数学198 颍上县十八里铺镇中心学校曹华男初中数学199 颍上县谢桥镇张庄中学姜允凯男初中数学200 颍上县职业技术教育中心张士海男初中数学201 安徽省颍上第二中学沈浏男高中数学202 安徽省颍上第二中学吴永剑男高中数学203 安徽省颍上第二中学徐昊男高中数学204 安徽省颍上第一中学魏岐峰女高中数学205 阜南县第一中学张德勤男高中数学206 阜南二中司伟男高中数学207 阜南县第一初级中学丁振云女初中数学208 阜南县第一初级中学焦岩男初中数学209 阜南县第五初级中学赵春风男初中数学210 阜南县第五初级中学李春楠女初中数学211 阜南县第五初级中学鞠徽男初中数学212 阜南县第五初级中学温广起男初中数学213 阜南县第五初级中学郭秀珍女初中数学214 阜南县第四初级中学陈丽华女初中数学215 阜南三中王其刚男初中数学216 阜南县方集镇中心学校王克中男初中数学217 阜南县公桥乡陈庄初级中学方德玉男初中数学218 阜南县洪河桥镇中心学校丁永亮男初中数学219 阜南县洪河桥镇中心学校刘胜男初中数学220 阜南县焦陂高级职业中学苏丽君女初中数学221 阜南县焦陂高级职业中学刘智男初中数学222 阜南县焦陂高级职业中学苏明男初中数学223 阜南县柳沟镇中心学校苗华堂男初中数学224 阜南县许堂乡大桥中学孙萍女初中数学225 阜南县于集乡中心学校卢达男初中数学226 阜南县朱寨镇中心学校孟凡清男初中数学227 阜南县朱寨镇人民九年制学校常广红男初中数学228 阜南县地城镇中心学校张俊杰男初中数学229 阜南县经开区中心学校温树森男初中数学230 阜南县龙王乡中心学校杨俊杰男初中数学231 阜南县苗集镇马塘中学邵国林男初中数学232 阜南县新村镇曙光小学孙辉男初中数学233 阜南县黄岗镇中心学校杨玉金男初中数学234 临泉白庙镇中心学校王国起男初中数学235 临泉县张集中学闫良男初中数学236 临泉滑集镇谢集中心校李群男初中数学237 临泉一中熊文文女高中数学238 临泉一中郑大鹏男高中数学239 临泉一中胡志成男高中数学240 临泉一中闫平继男高中数学241 临泉一中于玲玲女高中数学242 临泉陶老乡中心校庞慧女初中数学243 临泉陶老乡中心校单传义男初中数学244 临泉陶老乡中心校陈家杰男初中数学245 临泉高塘镇杨新中学李继明男初中数学246 临泉田家炳实验中学沈玉山男高中数学247 临泉田家炳实验中学安登峰男高中数学248 临泉艾亭镇中心学校李伟男初中数学249 临泉艾亭镇中心学校郑艳冰女初中数学250 临泉杨桥高级职业中学韦倩女初中数学251 临泉宋集镇杨小街中心学校肖永男初中数学252 临泉二中吴允女高中数学253 临泉二中戴家豪男高中数学254 临泉二中顾宣强男高中数学255 临泉二中蒋利敏女高中数学256 临泉四中闫超武男初中数学257 临泉谭棚镇中心学校代宗文男初中数学258 临泉高塘镇范集中心学校张晖男初中数学259 临泉陈集镇中心学校苏利女初中数学260 临泉陈集镇中心学校马鑫男初中数学261 临泉宋集镇中心学校张明龙男初中数学262 临泉宋集镇中心学校邹金军男初中数学263 临泉土陂乡中心学校张振体男初中数学264 临泉土陂乡中心学校王雷男初中数学265 临泉土陂乡中心学校周兴荣女初中数学266 临泉城关街道张营中心学校刘树春男初中数学267 临泉迎仙镇中心学校李月星男初中数学268 颍州区马寨乡中心学校张克化男初中数学269 颍州区颍西办事处中心学校王国慎男初中数学270 颍州区民族中学徐利锋男初中数学271 阜阳市第十九中学程亮男初中数学272 颍泉区伍明镇三门中学许守昌男初中数学273 颍泉区四九初中张广强男初中数学274 颍泉区苏屯中学程付友男初中数学275 颍东区阜阳市城郊中学杨利娜女数学276 颍东区阜阳市城郊中学武绍利女数学277 颍东区阜阳市城郊中学王丽云女数学278 颍东区阜阳市城郊中学吴桃李男数学279 颍东区阜阳市第十中学孙文英女数学280 颍东区插花镇二学区中心学校宫守华男数学281 颍东区插花镇一学区中心学校武保龙男数学282 颍东区阜阳市第十六中学徐兰敏女数学283 颍东区阜阳市第十六中学尹洪男数学284 颍东区冉庙乡中心学校申成卫男数学285 颍东区袁寨镇临颍中学赵卫东男数学286 颍东区枣庄镇中心学校杜德士男数学287 阜阳市第五中学唐晓雯女高中数学288 （市直）阜阳市特殊教育学校张英女初中数学289 界首第一中学阮静静女高中英语290 界首市界首中学吕楠楠女高中英语291 太和县宫集镇中心学校刘伟男初中英语292 太和县北城中学教育集团北城中学校区乔海云女初中英语293 太和县三塔镇中心学校江平女初中英语294 太和县第八中学高凤玲女高中英语295 太和县第二中学王芙侠女高中英语296 安徽省太和中学张学艳女高中英语297 安徽省太和第一中学牛亚男女高中英语298 安徽省太和第一中学刘萍女高中英语299 安徽省太和第一中学郑丽芳女高中英语300 安徽省太和第一中学王冬梅女高中英语301 颍上古城镇中心学校徐奇玉女初中英语302 颍上县半岗镇中心学校王莉女初中英语303 颍上县谢桥镇广源中学姜克鹏男初中英语304 颍上县建颍乡中心学校化建军男初中英语305 颍上县建颍乡中心学校李静女初中英语306 颍上县江店孜镇中心学校王新男初中英语307 颍上县江店孜镇中心学校甄远旭男初中英语308 颍上县江口镇中心学校汤文星男初中英语309 颍上县刘集乡中心学校李明男初中英语310 颍上县鲁口镇中心学校茹龙强男初中英语311 颍上县南照镇中心学校刘灵才男初中英语312 颍上县盛堂乡中心学校刘为朝男初中英语313 颍上县盛堂乡中心学校孙慧女初中英语314 颍上县五十铺乡中心学校周小林男初中英语315 颍上县夏桥镇中心学校万法亮男初中英语316 颍上县杨湖镇中心学校杨屹峰女初中英语317 安徽省颍上第一中学郑多新女高中英语318 阜南县第一中学王瑞侠女高中英语319 阜南二中朱丽女高中英语320 阜南县第一初级中学王玲女初中英语321 阜南三中杜慧荣女初中英语322 阜南县公桥高级职业中学刘丙亮男初中英语323 阜南县焦陂高级职业中学张贺男初中英语324 赵集镇中心学校李俊男初中英语325 赵集镇大聂九年制学校张贺梅女初中英语326 阜南县地城镇中心学校乔保金男初中英语327 阜南县地城镇中心学校张炳坤男初中英语328 经开区中心学校刘朝艳女初中英语329 阜南县王店孜乡职高随芳女初中英语330 阜南县苗集镇中心学校韩勇女初中英语331 阜南县苗集镇中心学校张影女初中英语332 阜南县段郢乡李城九年制学校张西建男初中英语333 阜南县王化镇中心学校程坤照男初中英语334 曹集镇九年制学校乔娟女初中英语335 阜南县黄岗镇张集中学程广运男初中英语336 阜南县焦陂中心学校李铠男初中英语337 临泉城东街道中心学校石宾俊男初中英语338 临泉一中王明付男高中英语339 临泉一中石一君女高中英语340 临泉高塘镇中心学校吴莉萍女初中英语341 临泉高塘镇中心学校牛朝龙男初中英语342 临泉田家炳实验中学马素娟女高中英语343 临泉杨桥高级职业中学郭英军男高中英语344 临泉宋集镇杨小街中心学校柳絮男初中英语345 临泉宋集镇杨小街中心学校柳塘男初中英语346 临泉宋集镇杨小街中心学校朱丛女初中英语347 临泉二中商凌云女高中英语348 临泉二中高翔男高中英语349 临泉老集镇中心校姜明男初中英语350 临泉四中李存金男初中英语351 临泉四中吴桂影女初中英语352 临泉县关庙镇中心校李远离男初中英语353 临泉谭棚镇中心学校张健男初中英语354 临泉庙岔镇中心学校殷守建男初中英语355 临泉庙岔镇中心学校李月勤女初中英语356 临泉陈集镇中心学校顾海霞女初中英语357 临泉迎仙镇中心学校常振生男初中英语358 颍州区颍州中学汪月萍女初中英语359 颍州区十五中马玉女初中英语360 颍州区红旗中学刘静女高中英语361 颍泉区伍明镇三门中学袁香辉男初中英语362 颍泉区曹寨九年一贯制学校谢旭男初中英语363 颍泉区姜堂中学钱利琴女初中英语364 颍泉区苏屯中学徐晓利女初中英语365 颍东区插花镇二学区中心学校张云飞男英语366 颍东区插花镇二学区中心学校陈怀敏女英语367 颍东区插花镇二学区中心学校刘锋男英语368 颍东区阜阳市第十六中学徐磊女英语369 颍东区老庙镇中心学校刘春莲女英语370 颍东区阜阳市口孜高级职业中学杨永红男英语371 阜阳市开发区京九路办事处颍南中学胡开歌男初中英语372 阜阳市第五中学胡晓娟女高中英语373 阜阳师范学院第二附属中学赵辛佩女高中英语374 阜阳师范学院附属中学段静女初中英语375 界首第一中学邹检查男高中物理376 界首第一中学裴明良男高中物理377 界首市界首中学韩家庆男高中物理378 太和县坟台镇中心学校钟献彬男初中物理379 太和县洪山镇中心学校刘文启男初中物理380 太和县清浅中心校张湘男初中物理381 太和县第二中学王海彬男高中物理382 安徽省太和中学张志鹏男高中物理383 安徽省太和中学董红伟男高中物理384 安徽省太和中学潘正海男高中物理385 颍上县半岗镇中心学校姜传涛男初中物理386 颍上县江口镇马圩中学韩涛男初中物理387 颍上县南照镇中心学校李新红男初中物理388 颍上县润河镇中心学校刘春泽男初中物理389 颍上县慎城镇城关中心学校周敏男初中物理390 阜南县第一中学郜峰兴男高中物理391 阜南县一职高张阿梅女初中物理392 阜南县第四初级中学邵振洋男初中物理393 阜南县会龙中心学校聂广彦男初中物理394 张寨镇华佗九年制王学童男初中物理395 阜南县段郢乡中心学校谢忠实男初中物理396 阜南县黄岗镇中心学校吴云男初中物理397 临泉一中柳旭东男高中物理398 临泉一中刘天军男高中物理399 临泉一中金小青女高中物理400 临泉高塘镇杨新中学王喜男初中物理401 临泉二中马善杰男高中物理402 临泉二中徐宾男高中物理403 颍州区三合镇中心学校王春超男初中物理404 颍州区大田中学李夫康男高中物理405 阜阳市第九中学李盛男初中物理406 颍泉区二十中胡卫民男初中物理407 颍泉区姜堂中学唐超波男初中物理408 颍东区阜阳市第十一中学张永坦男物理409 颍东区阜阳市第二十一中学段影女物理410 颍东区口孜镇中心学校岳效新男物理411 颍东区新乌江镇中心学校刘勇男物理412 阜阳市第三中学刘秀女高中物理413 阜阳市第三中学张士伟男高中物理414 界首第一中学胡卫林男高中化学415 界首市界首中学徐上辰男高中化学416 太和县皮条孙镇中心学校张克影女初中化学417 太和县三堂镇中心学校薛林男初中化学418 太和县清浅中心校李建明男初中化学419 安徽省太和第一中学刁文忠男高中化学420 安徽省太和中学杨亚利女高中化学421 安徽省太和中学李咏女高中化学422 安徽省太和中学李自强男高中化学423 颍上县第五中学李成锋男初中化学424 颍上县第五中学刘家清男初中化学425 颍上县迪沟镇中心学校高超男初中化学426 颍上县南照镇清河学校赵新杰男初中化学427 颍上县南照镇中心学校冯照明男初中化学428 颍上县南照镇中心学校唐彬男初中化学429 安徽省颍上第一中学岳俊女高中化学430 安徽省颍上第一中学王利女高中化学431 安徽省颍上第一中学唐德乐男高中化学432 阜南县第一初级中学谢尚超男初中化学433 阜南县会龙中心学校张玉柱男初中化学434 阜南县许堂乡大桥中学李元奎男初中化学435 临泉一中陶相雷男高中化学436 临泉一中马加伟男高中化学437 临泉一中邵建男高中化学438 临泉一中高汉华男高中化学439 临泉田家炳实验中学彭阳女高中化学440 临泉艾亭镇中心学校赵辉男初中化学441 临泉二中李昆男高中化学442 临泉二中郭腾飞男高中化学443 颍州区程集中心学校张涛男初中化学444 颍州区红旗中学王灵柱男高中化学445 颍州区红旗中学陈东男高中化学446 颍泉区阜阳市第四中学许冰男高中化学447 颍东区阜阳市第十中学王永金男化学448 颍东区阜阳市第十中学于佳男化学449 阜阳市第三中学牛文付男高中化学450 阜阳师范学院第二附属中学王丽女初中化学451 界首第一中学李庆友男高中生物452 界首第一中学李坤山男高中生物453 安徽省太和第一中学曹磊男高中生物454 安徽省太和中学辛涛男高中生物455 颍上县第五中学李想男初中生物456 颍上县南照镇中心学校田树安男初中生物457 安徽省颍上第一中学汪燕珂女高中生物458 阜南县第一初级中学焦志猛男初中生物459 临泉黄岭镇中心校刘贇女初中生物460 临泉一中蒋秀权男高中生物461 临泉艾亭镇中心学校李翠萍女初中生物。
NOIP2017复赛提高组成绩-安徽
姓名编号省份总分math complexity p ark treasure phalanx 白亦璠AH-0001安徽180208001030柏景琪AH-0002安徽1600400400鲍元昆AH-0003安徽906030000鲍志远AH-0004安徽000000毕翼飞AH-0005安徽20003004030边智睿AH-0006安徽000000卞博AH-0007安徽000000蔡正坤AH-0008安徽120500530蔡宗健AH-0009安徽1001000000操铄AH-0010安徽240100004030曹旭AH-0011安徽20000304030曹彦臣AH-0012安徽000000曹逸中AH-0013安徽4801001002010060曹致远AH-0014安徽22010070000曹梓健AH-0015安徽130301002030常天择AH-0016安徽1250600530常昊冉AH-0017安徽35060100107030陈炳宇AH-0018安徽2500050陈博文AH-0019安徽550000陈巩固AH-0020安徽255560204030陈嘉琪AH-0021安徽1101000000陈俊言AH-0022安徽000000陈俊一AH-0023安徽20010000400陈启航AH-0024安徽16010050000陈实AH-0025安徽1206000300陈世豪AH-0026安徽000000陈硕AH-0027安徽1301000000陈天昊AH-0028安徽000000陈桐飞AH-0029安徽3351009004045陈衍德AH-0030安徽5501001001009060陈彦楠AH-0031安徽000000陈一诺AH-0032安徽906000030陈宇AH-0033安徽42010090307030陈宇昂AH-0034安徽42010090010030陈智鹏AH-0035安徽853020050陈中达AH-0036安徽906000030陈子安AH-0037安徽225100500530陈子聪AH-0038安徽2801000104030陈怿阳AH-0039安徽3551008004530陈潇扬AH-0040安徽000000程佳志AH-0041安徽2503010002020程龙廷AH-0042安徽1701003001030程启东AH-0043安徽2701003004030程锐诚AH-0044安徽3601001000600程赛AH-0045安徽3051005004530程少文AH-0046安徽60500530程小定AH-0047安徽000000程宇昊AH-0048安徽000000程泽瑞AH-0049安徽525100*********程至柔AH-0050安徽310100*********程子恒AH-0051安徽25010050000崔婉彤AH-0052安徽10060100030崔皓玮AH-0053安徽38030100307050戴易彤AH-0054安徽60300000戴雨欣AH-0055安徽1451000050戴骥AH-0056安徽220100002030代攀AH-0057安徽45500020单辰宇AH-0058安徽000000单宇强AH-0059安徽2751006002530邓伊凡AH-0060安徽60600000邓玉成AH-0061安徽27060006050翟冉星AH-0062安徽450200250丁海鹏AH-0063安徽450100*********丁捷AH-0064安徽3001004004030丁瑞AH-0065安徽1000000丁一凡AH-0066安徽1001000000董坤AH-0067安徽155********杜宜宸AH-0068安徽35300050樊昊天AH-0069安徽3601009004030范辰一AH-0070安徽504000100范天予AH-0071安徽22010080000范之闽AH-0072安徽405100100207035范昊妍AH-0073安徽37010060107030房原嵩AH-0074安徽803000030冯效贤AH-0075安徽130********冯易AH-0076安徽803020000凤奕鸣AH-0077安徽50010080709555傅广文AH-0078安徽12010020000干志鹏AH-0079安徽445100*********高梦洁AH-0080安徽230303004030高琼AH-0081安徽1003000400高邱杨AH-0082安徽4701001001010060高翔宇AH-0083安徽3701007007030高宇鑫AH-0084安徽325309009530高震AH-0085安徽000000高子健AH-0086安徽400100100304030高子健AH-0087安徽415100100010035高梓又AH-0088安徽1705000200高鑫瑞AH-0089安徽165100200250葛晨笛AH-0090安徽26510080050葛一凡AH-0091安徽305100900530耿心旷AH-0092安徽1450600530巩若屿AH-0093安徽000000谷梦龙AH-0094安徽1000000桂丽如AH-0095安徽60600000郭启帆AH-0096安徽210100400030郭一凡AH-0097安徽2601003002030郭毅安AH-0098安徽30300000郭子笑AH-0099安徽1603030000韩金铂AH-0100安徽2253040203530韩瑾怡AH-0101安徽000000韩昊君AH-0102安徽1706000030郝跃生AH-0103安徽1356040050何朝旭AH-0104安徽23060004030何家乐AH-0105安徽1001000000何天承AH-0106安徽185353003030何天浚AH-0107安徽235100002530何泽华AH-0108安徽21030700300呼延泽AH-0109安徽355100*********胡博涵AH-0110安徽230308004030胡剑铮AH-0111安徽3601008007050胡骏诚AH-0112安徽3000000胡润琦AH-0113安徽35510070302530胡思琪AH-0114安徽000000胡天睿AH-0115安徽2701003001030胡叶烨AH-0116安徽24010000400胡永基AH-0117安徽4000000胡宇澍AH-0118安徽300010004060胡周国AH-0119安徽280100007030胡子健AH-0120安徽9060100100胡婕AH-0121安徽90100000胡昕AH-0122安徽60600000胡睿睿AH-0123安徽1001000000花鹏祥AH-0124安徽3201004007030黄喆AH-0125安徽856000250黄柏扬AH-0126安徽000000黄丽丽AH-0127安徽1201000000黄全鑫AH-0128安徽225100100530黄斯谙AH-0129安徽000000黄天阳AH-0130安徽60600000黄文晓AH-0131安徽753000150黄一展AH-0132安徽1401000000黄韵桐AH-0133安徽23010000400黄振东AH-0134安徽55500050黄峙AH-0135安徽35300050黄馨悦AH-0136安徽250100100400黄轶昕AH-0137安徽11515300100惠浩AH-0138安徽23008002030贾宇航AH-0139安徽1001000000贾志宇AH-0140安徽1003020000贾倩茹AH-0141安徽753020050贾昊瑞AH-0142安徽57010010070100100姜凡希AH-0143安徽200100300030姜露AH-0144安徽000000姜若蓉AH-0145安徽10530100250姜玉喜AH-0146安徽220301000400姜诏升AH-0147安徽000000江芬AH-0148安徽110303001030江景文AH-0149安徽1001000000江睿翔AH-0150安徽16070500100蒋炳衡AH-0151安徽450100*********蒋梦旭AH-0152安徽3556010008015蒋文哲AH-0153安徽1301000000接中亚AH-0154安徽000000解家祥AH-0155安徽803000030金博涵AH-0156安徽000000金典AH-0157安徽3451001000450金远卓AH-0158安徽200303003030金祖峰AH-0159安徽55550000金溥原AH-0160安徽295100800035孔方宇AH-0161安徽1001000000孔冠霖AH-0162安徽20020000孔令宇AH-0163安徽1206040000孔子睿AH-0164安徽12010020000来永强AH-0165安徽000000兰天AH-0166安徽220100004030黎鳌AH-0167安徽550000李骋AH-0168安徽37010010004030李达宇AH-0169安徽250301000030李豪AH-0170安徽1503000400李浩南AH-0171安徽1303000030李浩洋AH-0172安徽1001000000李弘毅AH-0173安徽275100004550李嘉乾AH-0174安徽320100007050李君宝AH-0175安徽000000李可凡AH-0176安徽000000李可新AH-0177安徽305100800450李梦遥AH-0178安徽30300000李孟旭AH-0179安徽555030200李仁轩AH-0180安徽35010010002030李若辰AH-0181安徽145100200250李坦AH-0182安徽1001000000李天赐AH-0183安徽60500520李文博AH-0184安徽125452001030李文浩AH-0185安徽000000李贤海AH-0186安徽1303000030李孝德AH-0187安徽1401030000李玉妍AH-0188安徽25500100李蕴琪AH-0189安徽550000李泽涵AH-0190安徽215100500530李泽林AH-0191安徽706000100李哲宇AH-0192安徽1201000000李振屹AH-0193安徽000000李志伟AH-0194安徽200100002030李智昊AH-0195安徽953000530李卓原AH-0196安徽260100400200李紫浩AH-0197安徽180301000200李馨凝AH-0198安徽10000100李宸AH-0199安徽20045200530李姝彤AH-0200安徽1056000150李铮然AH-0201安徽270100400030廖世立AH-0202安徽703000400廖言彬AH-0203安徽000000廖睿欣AH-0204安徽8010100400林伊俊AH-0205安徽185********林振AH-0206安徽80600000凌典AH-0207安徽30300000凌童AH-0208安徽50500250凌琛AH-0209安徽180100300030刘柄政AH-0210安徽10030300030刘晨阳AH-0211安徽000000刘锋AH-0212安徽2550000刘奉明AH-0213安徽1253000250刘浩文AH-0214安徽803010000刘宏晖AH-0215安徽130********刘天AH-0216安徽2000007030刘皖豫AH-0217安徽255100004530刘晓奕AH-0218安徽255100200530刘欣悦AH-0219安徽20020000刘洋AH-0220安徽240100001030刘易成AH-0221安徽150********刘元彻AH-0222安徽2001001001030刘云蛰AH-0223安徽495100100209580刘展AH-0224安徽410100*********刘振AH-0225安徽000000刘正阳AH-0226安徽130********刘知源AH-0227安徽240100001030刘瀚中AH-0228安徽60600000刘鑫AH-0229安徽130********芦嘉诚AH-0230安徽35000530卢明AH-0231安徽2301002001030路宇翔AH-0232安徽856000250陆天宇AH-0233安徽22010002000陆宇凡AH-0234安徽405100100304530陆泽宇AH-0235安徽2301005004030吕岸桐AH-0236安徽30559006050吕法科AH-0237安徽000000吕天成AH-0238安徽20030300400吕炎昌AH-0239安徽255108003530罗嘉文AH-0240安徽000000罗天傲AH-0241安徽000000罗文博AH-0242安徽706000100罗逸恒AH-0243安徽1101000000罗应松AH-0244安徽28010010204030骆正兴AH-0245安徽3500050马南禺AH-0246安徽12545200030马燕妮AH-0247安徽1651000050马志成AH-0248安徽225100100150梅戈林AH-0249安徽6030100100孟凡石AH-0250安徽20510000025孟昊宸AH-0251安徽1350100450孟鑫AH-0252安徽190305004030穆展鸿AH-0253安徽1604040000潘恩楦AH-0254安徽856000520潘际东AH-0255安徽2151002003530潘舒羽AH-0256安徽3756580010030潘卓成AH-0257安徽14005004030潘昊天AH-0258安徽3606010007030裴丹琳AH-0259安徽12030400030彭弘毅AH-0260安徽600001030彭嘉祺AH-0261安徽60600000彭昕睿AH-0262安徽265100500530皮雳AH-0263安徽36510010004530齐毅恒AH-0264安徽50300000齐晟慰AH-0265安徽110300000钱芃昕AH-0266安徽1355004030钱其轩AH-0267安徽16010004030钱善民AH-0268安徽3101008004030钱晓临AH-0269安徽1455100000秦朗AH-0270安徽180100400400秦逸凡AH-0271安徽165305010530任兵涛AH-0272安徽000000任栗晗AH-0273安徽115000350任鹏程AH-0274安徽260306004030任天宇AH-0275安徽1550000任彦羽AH-0276安徽390100100207030任奕凡AH-0277安徽225100900250荣浩岐AH-0278安徽60600000融凯源AH-0279安徽5501001007010080桑浩翔AH-0280安徽240303007030尚耀坤AH-0281安徽653500030沈盎AH-0282安徽140500530沈康宁AH-0283安徽200105004030沈凌翔AH-0284安徽4001000507080盛存玉AH-0285安徽9052001530盛海洋AH-0286安徽180100100030盛嘉薇AH-0287安徽450200250盛紫阳AH-0288安徽1105000030施耀炜AH-0289安徽270100700200施益凡AH-0290安徽1352000035石浩瀚AH-0291安徽30000030石潇AH-0292安徽500050史嘉豪AH-0293安徽1051000050史卓然AH-0294安徽3751001000750疏智磊AH-0295安徽1506000030宋家辉AH-0296安徽1001000000宋若琪AH-0297安徽30000030宋鑫语AH-0298安徽603000030苏弋炜AH-0299安徽1753000450苏睿AH-0300安徽245603003035孙乐旋AH-0301安徽550000孙伟中AH-0302安徽3000000孙彦哲AH-0303安徽000000孙皓宇AH-0304安徽200100300030谭亦轩AH-0305安徽37560100307530谭宇辰AH-0306安徽14060001030汤子唯AH-0307安徽155302002530汤曜坤AH-0308安徽1201000000唐昌平AH-0309安徽000000唐浩然AH-0310安徽706010000唐正举AH-0311安徽245601004530陶晨蕊AH-0312安徽150100200030陶文琪AH-0313安徽37510010004530陶应智AH-0314安徽1601000000陶子扬AH-0315安徽30510030301530田博宇AH-0316安徽550000田鹏飞AH-0317安徽270100004030童揽岳AH-0318安徽000000屠韬AH-0319安徽60600000汪晨曦AH-0320安徽2856080102530汪洪韬AH-0321安徽75500030汪坤灿AH-0322安徽17030300030汪欣然AH-0323安徽2805050104030汪修平AH-0324安徽2851000203530汪宇峰AH-0325安徽245601004530汪子骏AH-0326安徽115300050汪珉玥AH-0327安徽30300000汪煜凯AH-0328安徽1301000000王才艺AH-0329安徽000000王超樊AH-0330安徽165060050王成文AH-0331安徽80600000王冠玺AH-0332安徽1753000450王洁AH-0333安徽3050050王金龙AH-0334安徽000000王晶晶AH-0335安徽220455004530王晶玉AH-0336安徽000000王康安AH-0337安徽90300000王乐天AH-0338安徽550000王梦雨AH-0339安徽000000王瑞祺AH-0340安徽4651001001003530王润坤AH-0341安徽60600000王若楠AH-0342安徽215100100250王少杰AH-0343安徽4550000王诗琪AH-0344安徽550000王腾AH-0345安徽905000030王兴泽AH-0346安徽120500530王修远AH-0347安徽150********王叶会AH-0348安徽10520300250王叶伟AH-0349安徽3401008020400王一言AH-0350安徽330808004030王又禾AH-0351安徽22060400200王宇轩AH-0352安徽2401004004030王云骥AH-0353安徽40010080307030王致远AH-0354安徽250100004030王子涵AH-0355安徽21065600250王子权AH-0356安徽800003030王子扬AH-0357安徽285100800250王子悦AH-0358安徽220601000400王奕璇AH-0359安徽10060200020王淞雷AH-0360安徽2301001000030王琛AH-0361安徽10000100王昊AH-0362安徽250100300030王昊宇AH-0363安徽270100020500王昱晨AH-0364安徽2801005002030王隽伟AH-0365安徽265607002530韦润晨AH-0366安徽2601001004030韦一AH-0367安徽2751005001530魏冰青AH-0368安徽100000030魏立恒AH-0369安徽500050魏啸冲AH-0370安徽2851004002025魏一鸣AH-0371安徽953000530魏一鸣AH-0372安徽35010010010400位祥AH-0373安徽000000吴翰儒AH-0374安徽6501002530吴航霄AH-0375安徽130********吴华昊AH-0376安徽35500030吴家慧AH-0377安徽30000030吴舒涵AH-0378安徽260100600030吴思航AH-0379安徽230305004030吴天意AH-0380安徽375100*********吴天宇AH-0381安徽205100200250吴心远AH-0382安徽25030900030吴绪禹AH-0383安徽250100004030吴逊AH-0384安徽000000吴耀轩AH-0385安徽58510010010010085吴一非AH-0386安徽2501002004030吴悦AH-0387安徽000000吴昊达AH-0388安徽1001000000武弘勋AH-0389安徽5601001007010090武孝元AH-0390安徽1001000000夏浩然AH-0391安徽2805010003020夏禹扬AH-0392安徽2501004004030向济寒AH-0393安徽10100000谢滨竹AH-0394安徽20010000030谢润菁AH-0395安徽175********谢悦AH-0396安徽400100100304030邢若凡AH-0397安徽2000000邢志伟AH-0398安徽000000熊凯歌AH-0399安徽1101000000徐承熙AH-0400安徽135********徐杭AH-0401安徽12060100030徐加宝AH-0402安徽200100200030徐李昊AH-0403安徽190100002030徐若凝AH-0404安徽30520050徐世豪AH-0405安徽550000徐思琪AH-0406安徽2801003004030徐苏洋AH-0407安徽17080300030徐天雨AH-0408安徽000000徐天泽AH-0409安徽175********徐心成AH-0410安徽000000徐兴业AH-0411安徽000000徐震昊AH-0412安徽200100700030徐志骏AH-0413安徽490100100707050徐志远AH-0414安徽455010030徐奕明AH-0415安徽11551002030徐灏然AH-0416安徽195451003030徐昕怡AH-0417安徽4000000徐晏辰AH-0418安徽9525004030许浩泽AH-0419安徽3101007004050许思远AH-0420安徽1051000050许振宇AH-0421安徽24056004530许仲远AH-0422安徽550000薛敬扬AH-0423安徽17030001030杨汭AH-0424安徽3101004004030杨珖AH-0425安徽3706080604030杨晨霖AH-0426安徽000000杨季敬汝AH-0427安徽2153020304530杨佳木AH-0428安徽95450000杨明AH-0429安徽60600000杨沛然AH-0430安徽65600050杨汝清AH-0431安徽000000杨思锐AH-0432安徽1503000400杨毅AH-0433安徽200100200200杨雨琪AH-0434安徽000000杨卓凡AH-0435安徽1000000杨子AH-0436安徽30300000杨子豪AH-0437安徽60600000杨茜木AH-0438安徽55020050杨茗AH-0439安徽30300000杨逍AH-0440安徽000000杨晟潇AH-0441安徽15150000姚学然AH-0442安徽3104080204030叶染景AH-0443安徽000000叶苏廷AH-0444安徽1704500250叶宇钦AH-0445安徽50300000殷开颜AH-0446安徽400100100304030尹天乐AH-0447安徽100600000尹宇阳AH-0448安徽275100004035英艺博AH-0449安徽550000余辰昕AH-0450安徽2501070204030余师剑AH-0451安徽3659510003040余学锋AH-0452安徽12030200030余卓然AH-0453安徽380100100104030俞子睿AH-0454安徽130500000袁伟豪AH-0455安徽1301000000袁子辰AH-0456安徽1900800400袁栎宬AH-0457安徽906000030袁昱明AH-0458安徽2708010004030岳晓颖AH-0459安徽165503003530曾致远AH-0460安徽465100*********占金涛AH-0461安徽150000500章安凡AH-0462安徽45450000章博文AH-0463安徽3205010004030章文澜AH-0464安徽180********张晨龙AH-0465安徽1555300200张房龙志AH-0466安徽550000张宏鑫AH-0467安徽1055500200张佳华AH-0468安徽210303002030张金涛AH-0469安徽155100200530张骏颉AH-0470安徽60600000张乐天AH-0471安徽33010010004030张铭文AH-0472安徽36010070204030张时钊AH-0473安徽24056004530张舒怡AH-0474安徽2500050张天陵AH-0475安徽23001003000张天舒AH-0476安徽000000张天泽AH-0477安徽380100100104030张笑阳AH-0478安徽11010000100张新科AH-0479安徽2801006020400张心琦AH-0480安徽250100500200张一鸣AH-0481安徽25000250张一鸣AH-0482安徽19510000250张宜宁AH-0483安徽1302000300张宇桐AH-0484安徽806020000张宇翔AH-0485安徽60600000张越AH-0486安徽55000025张哲康AH-0487安徽000000张正诚AH-0488安徽1255100030张智伟AH-0489安徽190100600030张智洋AH-0490安徽1655007030张子牛AH-0491安徽2901004002030张子卿AH-0492安徽40000100张子希AH-0493安徽150********张子洋AH-0494安徽245100900450张丞AH-0495安徽000000张瀚文AH-0496安徽21065300530赵博睿AH-0497安徽600300030赵晨阳AH-0498安徽50300000赵涵AH-0499安徽1001500530赵佳鸣AH-0500安徽000000赵敏达AH-0501安徽225100400250赵瑞琦AH-0502安徽2601005002030赵思航AH-0503安徽230100200030赵雨杰AH-0504安徽000000赵雨扬AH-0505安徽3501008010555赵子健AH-0506安徽205301004025赵昕鹏AH-0507安徽360100900700郑卜俊宏AH-0508安徽000000郑敏AH-0509安徽50500250郑茹敏AH-0510安徽000000郑瑞AH-0511安徽16510000530郑天AH-0512安徽9060200100郑奕AH-0513安徽165100300530郑睿AH-0514安徽1751000050职浩然AH-0515安徽130********钟妍钊AH-0516安徽10000100周陈悦AH-0517安徽000000周何AH-0518安徽290606030400周家亮AH-0519安徽2003010104030周俊杰AH-0520安徽3001005004030周顺AH-0521安徽20020000周涛AH-0522安徽10530002530周文杰AH-0523安徽503010000周秀涵AH-0524安徽1000000周一鸣AH-0525安徽6530200150周宇AH-0526安徽450100*********周子涵AH-0527安徽19051000450周子涵AH-0528安徽135550000周子航AH-0529安徽39010010004050周怡然AH-0530安徽16060010030珠齐明AH-0531安徽390100100204030朱晨曦AH-0532安徽3551009003530朱成儒AH-0533安徽1853040201530朱广恩AH-0534安徽220304004030朱浩宇AH-0535安徽16010000200朱鸿涛AH-0536安徽25520000朱启孟AH-0537安徽24060700030朱屠越AH-0538安徽60600000朱文天AH-0539安徽40565100308030朱晓瑞AH-0540安徽000000朱永琦AH-0541安徽000000朱宇AH-0542安徽903000100朱震霆AH-0543安徽3901009020800朱知非AH-0544安徽1500400030朱璨AH-0545安徽10030100030朱煜AH-0546安徽30300000朱锴宏AH-0547安徽800100030宗晓煜AH-0548安徽135********邹晨雪AH-0549安徽510100807010080祖文智AH-0550安徽000000佘骏一AH-0551安徽550000邬登科AH-0552安徽330609007030奚兆阳AH-0553安徽255100700350奚子淇AH-0554安徽000000闫瑾AH-0555安徽505200250缪其跃AH-0556安徽35010010002030缪志远AH-0557安徽2801004001030窦天阳AH-0558安徽16010000030瞿冠中AH-0559安徽245358004030cheese备注4080100807010010050403080201001060103030601001001003040100100807010080201006010020 0 60 0 100 0 100 90 10 0 80 0 100 0 40 80 100 20 30 30 100 0 90 100 30 100 100 80 0 100 80 100 20 80 80 50 0 10 0 40 80 0 100 700 80 30 10060 30 100 0 100 100 40 100 80 10 80 0 0 80 0 0 20 80 0 0 30 40 90 0 0 100 60 100 0 50 20 100 40 0 40 50 0 10 0 30 100 100 300 200 100 800 50 0 100 90 80 70 0 80 100 0 0 80 0 0 100 0 0 30 20 0 70 100 10 0 30 0 20 0 50 30 100 30 0 100 30 100 0 0 20 50 20 0 20 20 100 20 700 100 50 50 100 100 0 80 100 0 0 0 70 0 100 100 10 100 0 100 100 0 0 0 10 80 30 30 60 100 10 80 80 40 80 0 30 100 20 100 20 20 0 80 90 20 80 60 8080 100 10 70 10 0 100 80 0 100 70 100 20 40 0 30 80 80 0 0 0 100 60 0 0 0 100 90 0 30 0 40 80 40 50 20 0 0 100 0 100 60 1000 1000 80 400 30 0 100 20 100 20 0 50 0 60 0 0 100 0 80 40 0 10 80 100 30 100 100 100 30 90 80 60 20 80 20 0 0 0 90 100 80 80 80 80 70 0 100 30 1000 2060 100 80 0 100 60 0 0 100 0 80 40 0 70 80 100 20 0 10 20 20 50 40 0 0 80 30 0 40 0 0 0 100 0 50 80 40 0 50 0 100 0 100 100 1000 60 5010 0 0 30 0 0 0 100 0 100 20 100 40 100 0 80 100 40 100 80 30 70 0 20 20 80 100 0 100 50 100 0 30 100 0 0 60 100 100 20 100 0 1000 60 800 70 800 60 100 30 50 10 0 80 0 20 50 0 60 60 80 0 100 100 100 0 20 0 30 0 0 70 0 0 0 100 80 80 0 20 10 10 0 100 40 80 100 60 100 100 50 80 400 800 100100 80 30 0 40 0 80 0 0 80 50 0 0 100 100 30 60。
最新2017物理竞赛成绩通报.doc
第三十四届（2017年）全国高中物理竞赛襄阳赛区竞赛成绩通报第三十四届全国高中物理奥林匹克竞赛我市共有十五所学校参加，共有12位同学获湖北赛区全国一等奖。
我市获湖北赛区全国三等奖以上的学生共98名。
竞赛期间，市竞赛委员会派人巡视了各考点，绝大多数考点考风端正，考纪严明，做到了单人单桌，交叉监考，当众按时拆封试卷，按时回收试卷；少数学校考室人数太多，监考老师较少，考前准备工作不周密，影响考生发挥正常水平。
希望各校认真做好考前各项准备工作，端正考风考纪，加强竞赛前的辅导工作，有条件的重点高中要办好奥赛班，争取更好成绩。
现将本次竞赛获奖学生、优秀辅导教师名单公布如下。
襄阳市物理学会竞赛委员会二○一七年十一月附：获奖名单湖北赛区全国一等奖(12人)襄阳四中：张正熙张骋浩张瑀卓石蔚雨辛运泽闫学瀚张一凡米子龙襄阳五中：吕涌波孔金鑫刘诗逸贾晨阳湖北赛区全国二等奖(39人)襄阳四中：朱新宇耿植吴韶光吴杰雄刘浩民肖晓旻李昀泽姚双捷李泽坤左思成贺思远周鑫付伟程高耀安王俊达张俊石徐玉曌襄阳五中：刘宇航王一璠邱淇智朱珈毅张浩天李振宇李秉航唐刘田刘雨辰孔凌飞刘昊阳孙楠王海天谌金垚叶华辰冯兴盛杨卓然王宇帆陈跃渊陈梓馨周子靖肖遥飞羽湖北赛区全国三等奖(47人)襄阳四中：刘纯民李睿哲徐一逍孙傲然刘昱怡龚伟东胡轶彬周天哲张子诚邢宏博李不言杨绎凡王若汀任婷钰襄阳五中：周祺睿滕嘉彦张仲立吴一希肖海川夏春秋襄阳一中：谌相龙李博祥代志博襄阳三中：王天池柳赛庭常钰坤张俊襄州一中：尚若禹周文龙枣阳一中：周子康姚欣怡枣阳二中：郭鹏辉宜城一中：李金雨张国辰张建豪周正夫郑轶通李子尧南漳一中：陈志文许万龙保康一中：王安立王彦铭李志浩河口一中：赵世隆潘春阳张世奇孟昆明湖北省一等奖(12人)以下12名学生为湖北省一等奖获得者：襄阳五中：宫裕凯刘书懿李紫璇刘思雨李子程襄阳四中：杨晓彤李孙润泽襄阳一中：衡周佳欣襄阳三中：余励航东风中学：李泽宇宜城二中：张宇航宜城三中：胡青翔各参赛学校获得湖北省二等奖和三等奖的人数如下表：优秀辅导教师1、辅导学生获湖北赛区全国一等奖的辅导教师：襄阳四中：李红伟吴国庆襄阳五中：喻涛何清余光2、辅导学生获湖北赛区全国二、三等奖的辅导教师襄阳四中：叶红云徐曙光马波李涛彭勤海襄阳五中：匡缘褚伟刘晶晶襄阳一中：易珺襄阳三中：汪黎高锐襄州一中：曾贞卢旭兵枣阳一中：杨俊波崔小军枣阳二中：李顺友宜城一中：陈尔华胡云峰南漳一中：罗玉荣吴云河口一中：簿涛李建龙熊晓辉孙新颜保康一中：李明贺汉东周启艳赠送相关资料考试答题的技巧拿到试卷之后，可以总体上浏览一下，根据以前积累的考试经验，大致估计一下试卷中每部分应该分配的时间。
2017年全国高中数学联赛北京赛区获奖名单
2017年全国高中数学联赛北京赛区获奖名单一等奖（65名）编号姓名性别学校年级M171001陈泉霖男人大附中早9M171002杨舍男人大附中高三M171003邓明扬男人大附中早9M171004焦宇翔男人大附中高三M171005杨诚远男人大附中高一M171006张凯勃男十一学校高三M171007魏宇辰男清华附中高三M171008徐浩轩男北师大实验中学高二M171009孔鼎问男人大附中高三M171010杨泓暕男人大附中高三M171011仇傲男人大附中高二M171012魏澜男人大附中高二M171013冯梓轩男人大附中高二M171014顾博森男北师大实验中学高三M171015王天洋男人大附中高二M171016周鼎昌男人大附中高二M171017王一鸣男人大附中高二M171018宋子萌男清华附中高二M171019盛翊伦男人大附中早12M171020李璟颢男人大附中高二M171021王梓晗男人大附中高三M171022沈家河男人大附中高三M171023胡小龙男人大附中高二M171024房东柯男人大附中高三M171025曾柯淏男十一学校高二M171026李立缘女人大附中高二M171027唐静吾男清华附中高二M171028肖子豪男十一学校高三M171029方政清男清华附中高三M171030丘铱可男清华附中高三M171031陈天杨男人大附中高二M171032周凌波男清华附中高二M171033樊天行男人大附中高一二等奖（180名）编号姓名性别学校年级编号姓名性别学校年级M217100001王进一男清华附中初三M217100038林炎龙男清华附中高二M217100002依嘉男人大附中早9M217100039赵福民男北师大实验中学高二M217100003刘骏男人大附中早9M217100040卜通男民大附中高三M217100004孙睿男人大附中早9M217100041吴昊男人大附中高三M217100005刘景和男人大附中早9M217100042王悦女人大附中早12 M217100006黄奕文男人大附中早9M217100043赵云潇男人大附中早9 M217100007漆沛羽男北师大实验中学高二M217100044刘嘉熙女北师大实验中学高一M217100008艾秋富男北京一零一中高一M217100045孙方圆男北京一零一中高三M217100009向洋女人大附中高二M217100046庞小杨男北京十二中高二M217100010邹鸿刚男十一学校高二M217100047夏瀚洋男北师大二附中高三M217100011吴寒羽男北师大实验中学高二M217100048刘若怡女北师大实验高二M217100012王靖涵男北师大实验中学高三M217100049胡嘉铭女北京四中高二M217100013李子雍男十一学校高二M217100050蒋楷男北京四中高二M217100014赵泠然男人大附中高三M217100051白钰卓女北京四中高三M217100015范一喆男人大附中高三M217100052梁元成男人大附中高一M217100016曹浩轩男首师大附中高三M217100053李经纬男北师大实验中学高三M217100017孙修远男人大附中高二M217100054杨其帆女育英学校高三M217100018王泽韬男人大附中高二M217100055童圣博男清华附中高二M217100019陈通男北师大实验中学高三M217100056贺思凯男人大附中高一M217100020冯家睿男人大附中高二M217100057张锐翀男十一学校高一M217100021惟明男北师大实验中学高二M217100058赵赫扬男人大附中高三M217100022李子恒男北师大实验中学高三M217100059张峻恺男十一学校高三M217100023王卓峣男人大附中高三M217100060姚有恒男民大附中高三M217100024王乐桐女民大附中高三M217100061鲁妍女人大附中高二M217100025周天翔男人大附中高三M217100062秦岭男人大附中高二M217100026刘溯晨男人大附中高二M217100063郭世圆男北京一零一中高三M217100027王彦焜男北京四中高三M217100064成嘉维男十一学校高三M217100028易睿哲女北师大实验中学高二M217100065周显昊男北京四中高二M217100029沈元哲男人大附中高三M217100066董辰语男十一学校高三M217100030刘雨辰男十一学校高三M217100067张睿齐男北京五中高三M217100031农钧翔男人大附中高二M217100068鹿星怡女人大附中高三M217100032韩百洋女北师大实验中学高三M217100069王紫晨女北师大实验中学高三M217100033钱博翀男十一学校高三M217100070陈瑛新男北师大实验中学高三M217100034胡凌女人大附中高二M217100071刘辰飞男清华附中高三M217100035吴润东男北师大实验中学高三M217100072曾若凡男人大附中高三M217100036高天伟男北京四中高二M217100073郑荣坤男人大附中高三M217100037张海墨男人大附中早9M217100074郭思成男北师大实验中学高三三等奖（120名）编号姓名性别学校年级编号姓名性别学校年级M317100001潘言男人大附中高二M317100022张有辰男北师大实验中学高二M317100002薛司旸男北师大实验中学高三M317100023吕沐航男人大附中高三M317100003倪行健男十一学校高一M317100024李宜芳女北师大实验中学高三M317100004张弋丰男北京一零一中高三M317100025姚梓晗女人大附中高三M317100005应润凯男十一学校高三M317100026崔子昂男十一学校高二M317100006刘哲男十一学校高二M317100027李伟楷男清华附中高二M317100007王逸钦男清华附中高二M317100028牛山水男人大附中高二M317100008胡思源男人大附中高一M317100029白雨石男人大附中高三M317100009宋在男十一学校高三M317100030侯悦石男人大附中高三M317100010黄怡然女人大附中高二M317100031白浩辰男北师大实验中学高三M317100011李华女北京八中高三M317100032王雨轩男人大附中早8 M317100012李沛阳男朝阳外国语学校高二M317100033彭丁宇男景山学校高三M317100013李斯羽女清华附中初三M317100034姜岚曦男人大附中高二M317100014谭镇枢男北京八十中高三M317100035郝梓涵男清华附中高一M317100015徐炜男首师大附中高三M317100036杨东林男北师大实验中学高二M317100016郭天瑜男北大附中高三M317100037熊天翼男北京四中高二M317100017邱子龙男人大附中高三M317100038郑绚文女十一学校高二M317100018孙亦非男北京五中高一M317100039张博然男人大附中高二M317100019王非石男北京四中高二M317100040吴垒男人大附中高一M317100020赵圆圆女十一学校高三M317100041童昊原男北京一零一中高一M317100021崔逸童男北京四中高三M317100042彭济民男人大附中高一。
2017年全国高中数学联赛广西赛区桂林市获奖名单
2017年全国高中数学联赛广西赛区桂林市获奖名单桂林市2017年高中联赛广西赛区全国一、二、三等奖获奖名单姓名性别学校获奖等级编号梁展照男师大附外一等M175302刘喆天男师大附中一等M175304兰义森男师大附外一等M175314刘二龙男师大附外一等M175315刘嘉联男师大附外一等M175316周勤男桂电中学一等M175329龙一匀男师大附外一等M175331唐煜程男师大附外一等M175332陈思宇男师大附中一等M175334义勇杰男师大附中一等M175338闭龙云男桂林中学一等M175340胡雪松男师大附外一等M175342吴平凡男师大附外二等M217530006刘康宁男桂电中学二等M217530017罗桢男师大附外二等M217530019叶倚伶女师大附外二等M217530035秦鹏男师大附外二等M217530047秦智翔男桂林中学二等M217530048申子博男师大附中二等M217530053 梁玮峰男师大附外二等M217530060 廖文庆男全州高中二等M217530067 石纪辉男灵川中学二等M217530072 李子郁女师大附外二等M217530080 钟忠男桂林中学二等M217530082易颖笛女十八中学二等M217530085 查君威男师大附外二等M217530086 谷静雨女师大附中二等M217530093 韦赵晗男桂林中学二等M217530097 梁浩源男师大附外二等M217530102 王铮男兴安中学二等M217530104张德龙男师大附外二等M217530118 唐吉祥男全州高中二等M217530123 侯乐涵男师大附外二等M217530124 王易女兴安中学二等M217530129秦浩然男桂林中学二等M217530134 范林琰男灌阳高中二等M217530138 粟孙鼎凯男师大附中二等M217530139 李嘉睿男师大附外二等M217530144 张宇男师大附中二等M217530151周思杰男中山中学二等M217530168 闫超美女全州高中二等M217530171 伍岳梅女师大附中二等M217530172 邓洁女恭城中学二等M217530175 吕宗铭男桂林中学二等M217530179 覃秋万男师大附外二等M217530188 文翔男师大附中二等M217530192 蒋心怡女师大附外二等M217530193 张蔚喆男桂林中学二等M217530194 蒋怡雯女师大附外二等M217530197 潘存慧女桂电中学二等M217530201 李慧儿女十八中学二等M217530202 刘又滔男师大附中二等M217530208 胡冉婷女师大附中二等M217530209 刘雨时男桂电中学二等M217530223 李声豪男师大附中二等M217530224 唐湛秋男师大附中二等M217530227 蒋方翼男桂电中学二等M217530239 蒋旻霏男师大附外二等M217530264 蒋镇远男中山中学二等M217530266 梁家文男十八中学二等M217530267刘希女十八中学二等M217530274 蓝海萍女师大附外二等M217530281 沈逸岚男全州高中二等M217530283 周琦男桂林中学二等M217530290 罗菁雯女师大附中二等M217530292 王宁欣男师大附中二等M217530303 蒋鑫男灌阳高中二等M217530312罗易佳男师大附外三等M317530008 曾德华男永福中学三等M317530014 邓艳虹女恭城中学三等M317530021 宾一鸣男师大附外三等M317530023 刘疏影女师大附中三等M317530028 秦文嘉男灵川中学三等M317530040 易子淳男师大附中三等M317530044 黄鑫男恭城中学三等M317530046 宋佳瑶女师大附中三等M317530047 胡子威男桂电中学三等M317530049 唐可意男师大附中三等M317530053 黄一珉男永福中学三等M317530081 唐文龙男桂林中学三等M317530086陈水男恭城中学三等M317530095李坤翼男师大附外三等M317530106王明双女兴安中学三等M317530113陈桐安男师大附中三等M317530115张家亮男中山中学三等M317530119时福海男首师桂林附中三等M317530142 邓凯中男师大附中三等M317530145黄鑫伟男荔浦中学三等M317530147肖杨光男师大附中三等M317530148韦佳昕女桂林中学三等M317530159邱兆奇男师大附外三等M317530161蒋宏轩男灵川中学三等M317530162谢荣博男桂林中学三等M317530170黄雅女桂电中学三等M317530179贾云嵩男桂林中学三等M317530182廖诗雨女十八中学三等M317530203石远涛男临桂中学三等M317530210黄河男恭城中学三等M317530223李文涛男桂林中学三等M317530228赵栋男师大附外三等M317530238梁志杰男师大附中三等M317530240陆禹江男师大附中三等M317530252秦路彦女师大附中三等M317530259 容超男阳朔中学三等M317530264 蒋竹婷女兴安中学三等M317530272 邓程方男中山中学三等M317530273 周明东男灌阳高中三等M317530285 陈奥思男师大附中三等M317530297 秦慧伶女灵川中学三等M317530308 林慧忠女恭城中学三等M317530314 陆云翔男荔浦中学三等M317530318 谢远骁男桂林中学三等M317530327 杨小芳男恭城中学三等M317530329 胡志伟男师大附中三等M317530331 周杨頔女桂电中学三等M317530336 伍旭男恭城中学三等M317530339 余周泉男师大附中三等M317530344 岳湘男桂电中学三等M317530348 王生发男十八中学三等M317530350 冯倜龙男中山中学三等M317530351 刘坤瓒男师大附中三等M317530357 唐睿玲女师大附中三等M317530365 钟源女师大附中三等M317530371 陆海知女桂林中学三等M317530372李英豪男阳朔中学三等M317530388尹伊伊女师大附中三等M317530393彭可可女灵川中学三等M317530396张紫怡女兴安中学三等M317530407郑冰男恭城中学三等M317530412石礼青女灵川中学三等M317530413何翔宇男首师桂林附中三等M317530423孙瑞扬男兴安中学三等M317530449骆鹤云女全州高中三等M317530459杨曜泽男桂林中学三等M317530471林可女桂林中学三等M317530472赵侯臻男中山中学三等M317530476唐若然男首师桂林附中三等M317530512李庆辉男桂林八中三等M3175305132017年全国高中数学联赛广西赛区广西三等奖、桂林市一等奖获奖名单序号学校姓名指导老师获奖等级1 桂林中学周一帆柳建显广西三等奖2 桂林中学蒙云龙陈洁广西三等奖3 桂林中学罗翔云柳建显广西三等奖4 桂林中学钟宇哲柳建显广西三等奖5 桂林中学唐浩然陈洁广西三等奖6 桂林中学张哲萌柳建显广西三等奖7 桂林中学蒋桨也柳建显广西三等奖8 桂林中学唐志成柳建显广西三等奖9 桂林八中李国豪田晓宇广西三等奖10 桂林八中梁倍源田晓宇广西三等奖11 桂林八中王一博田晓宇广西三等奖12 中山中学李泳琪秦柔广西三等奖13 中山中学晁阳金萍广西三等奖14 中山中学文诗远秦柔广西三等奖15 中山中学蒙陈铸秦柔广西三等奖16 中山中学刘家鑫金萍广西三等奖17 师大附中唐湛秋卢晓岚广西三等奖18 师大附中义勇杰卢晓岚广西三等奖19 师大附中唐可意卢晓岚广西三等奖20 师大附中秦路彦卢晓岚广西三等奖21 师大附中余周泉卢晓岚广西三等奖22 师大附中陈思宇蒋荣广西三等奖23 师大附中陆禹江蒋荣广西三等奖24 师大附中陈奥思蒋荣广西三等奖25 师大附中钟源蒋荣广西三等奖26 师大附中刘喆天林佳利广西三等奖27 师大附中王宁欣林佳利广西三等奖29 师大附中罗菁雯林佳利广西三等奖30 师大附中刘疏影林佳利广西三等奖31 师大附中李声豪林佳利广西三等奖32 师大附中伍岳梅谢玫丽广西三等奖33 师大附中申子博张小雄广西三等奖34 师大附中尹伊伊张小雄广西三等奖35 师大附中刘又滔刘敏峰广西三等奖36 师大附中刘坤瓒王华奇广西三等奖37 师大附外贺诗璐黄志武广西三等奖38 师大附外徐传晟蒋诗承广西三等奖39 师大附外谢辛宇王勇广西三等奖40 师大附外黄睿王勇广西三等奖41 师大附外黄德正黄志武广西三等奖42 师大附外李靖黄志武广西三等奖43 师大附外秦景轩黄利魁广西三等奖44 师大附外王凯民蒋诗承广西三等奖45 师大附外吴承龙唐立东广西三等奖46 师大附外秦大林俞海荣广西三等奖47 师大附外杨示奇黄志武广西三等奖48 师大附外阳文博高一老师广西三等奖49 师大附外宾一鸣蒋诗承广西三等奖51 师大附外张洁黄利魁广西三等奖52 师大附外舒玥蒋诗承广西三等奖53 师大附外蒋可铭黄利魁广西三等奖54 师大附外郑显颖蒋诗承广西三等奖55 师大附外贺敬东王勇广西三等奖56 师大附外孙歆杰俞海荣广西三等奖57 师大附外梁瀚丹黄志武广西三等奖58 师大附外黄盈熹黄志武广西三等奖59 师大附外汪泽宇高一广西三等奖60 师大附外张光泽黄利魁广西三等奖61 师大附外戴书钰王勇广西三等奖62 师大附外李至萌黄志武广西三等奖63 师大附外刘文绪高一广西三等奖64 师大附外朱艺轩高一广西三等奖65 师大附外张师旖黄利魁广西三等奖66 师大附外朱国栋黄利魁广西三等奖67 师大附外唐宇辰蒋诗承广西三等奖68 师大附外李一民蒋诗承广西三等奖69 师大附外祝弘华黄志武广西三等奖70 师大附外石耀宗黄志武广西三等奖71 师大附外韦海婷高一广西三等奖72 师大附外易峻菲高一广西三等奖73 师大附外刘韬高一广西三等奖74 师大附外颜文琛黄利魁广西三等奖75 师大附外陈纪元王勇广西三等奖76 师大附外王云飞唐立东广西三等奖77 师大附外刘智鹏高一广西三等奖78 师大附外文东勰高一广西三等奖79 师大附外张晴晴黄利魁广西三等奖80 师大附外张羽王勇广西三等奖81 师大附外梁才黄志武广西三等奖82 师大附外孙浩翔高一广西三等奖83 桂电中学汪静莹蒋荣荣广西三等奖84 桂电中学郭静颖朱建新广西三等奖85 桂电中学胡敏娟朱建新广西三等奖86 桂电中学周紫芸蒋荣荣广西三等奖87 桂电中学曾洁朱建新广西三等奖88 桂电中学黄志宏朱建新广西三等奖89 首师大桂林附中祝小红钟琳广西三等奖90 首师大桂林附中赵思远韦刚广西三等奖91 首师大桂林附中魏纪荧胡琴广西三等奖92 首师大桂林附中唐哲蒋海波广西三等奖93 恭城中学龙镕基陈龙广西三等奖95 恭城中学嵇晓岚吴建平广西三等奖96 恭城中学俸晓雪吴建平广西三等奖97 恭城中学曾炤宇吴建平广西三等奖98 恭城中学李慧吴建平广西三等奖99 恭城中学蓝达楷吴建平广西三等奖100 恭城中学梁欢萍吴建平广西三等奖101 灌阳高中邓雅雯刘拥军广西三等奖102 灌阳高中王雅萍刘拥军广西三等奖103 灌阳高中陈文林刘拥军广西三等奖104 灌阳高中唐伟丽刘拥军广西三等奖105 灌阳高中文龙飞刘拥军广西三等奖106 灌阳高中李振刘拥军广西三等奖107 灌阳高中李玉琴邓美芳广西三等奖108 灌阳高中唐好奇黄邓剑广西三等奖109 灌阳高中文世进刘拥军广西三等奖110 灵川一中袁文姣孙梦遥广西三等奖111 灵川一中肖晓孙梦遥广西三等奖112 灵川一中刘鑫孙梦遥广西三等奖113 潭下中学杨雨晴周冬立广西三等奖114 潭下中学曾婷婷周冬立广西三等奖115 永福中学粟杨钧莫月红广西三等奖117 临桂中学阳丰红吴冬华广西三等奖118 荔浦中学黄慧张平广西三等奖119 荔浦中学邓洁张平广西三等奖120 荔浦中学伍子豪张平广西三等奖121 荔浦中学何婷婷计昌葵广西三等奖122 荔浦中学李霜韦科兴广西三等奖123 荔浦中学韦浩李艳芳广西三等奖124 龙胜中学梁项睿吴达球广西三等奖125 龙胜中学吴浩洋吴达球广西三等奖126 全州高中蒋人为俞勇军广西三等奖127 全州高中陈龙俞勇军广西三等奖128 全州高中王海洋龙新生广西三等奖129 全州高中唐悦文龙新生广西三等奖130 全州高中唐洁龙新生广西三等奖131 全州高中唐祎旸龙新生广西三等奖132 全州高中赵笠君龙新生广西三等奖133 全州高中吴颖菲龙新生广西三等奖134 全州高中王嘉伟龙新生广西三等奖135 兴安中学王腾胡纯军广西三等奖136 兴安中学龙玲芳胡纯军广西三等奖137 兴安中学王强胡纯军广西三等奖139 兴安中学刘倩胡纯军广西三等奖140 兴安中学张紫亮熊素玲广西三等奖141 兴安中学张轩豪熊素玲广西三等奖142 兴安中学唐攀熊素玲广西三等奖143 兴安中学唐文雯熊素玲广西三等奖144 兴安中学蒋佳宇蒋宗彬广西三等奖145 兴安中学王海琪蒋宗彬广西三等奖146 阳朔中学陈习鹏广西三等奖147 阳朔中学莫婷婷广西三等奖148 资源中学段煜蒋明广西三等奖149 资源中学莫振潜蒋明广西三等奖150 桂林中学袁伟豪柳建显桂林市一等奖151 桂林中学谭云龙飞跃桂林市一等奖152 桂林中学巫殷豪袁芳桂林市一等奖153 桂林中学孔令豪袁芳桂林市一等奖154 桂林中学刘文斌龙飞跃桂林市一等奖155 桂林中学曾志辉柳建显桂林市一等奖156 桂林中学刘畅畅柳建显桂林市一等奖157 桂林中学张哲熙柳建显桂林市一等奖158 桂林八中蒋宝霖田晓宇桂林市一等奖159 桂林八中林建凯田晓宇桂林市一等奖160 桂林八中李想田晓宇桂林市一等奖161 桂林八中蒋宇岚田晓宇桂林市一等奖162 桂林八中范政田晓宇桂林市一等奖163 中山中学胡媛媛秦柔桂林市一等奖164 中山中学刘唐云妮秦柔桂林市一等奖165 中山中学邹世龙秦柔桂林市一等奖166 中山中学向盛龙秦柔桂林市一等奖167 中山中学刘毓秦柔桂林市一等奖168 中山中学金煜杨金萍桂林市一等奖169 中山中学覃大恒金萍桂林市一等奖170 中山中学卢世源秦柔桂林市一等奖171 师大附中胡志伟卢晓岚桂林市一等奖172 师大附中唐睿玲卢晓岚桂林市一等奖173 师大附中粟孙鼎凯卢晓岚桂林市一等奖174 师大附中文翔卢晓岚桂林市一等奖175 师大附中宋佳瑶蒋荣桂林市一等奖176 师大附中谷静雨蒋荣桂林市一等奖177 师大附中梁志杰蒋荣桂林市一等奖178 师大附中陈桐安林佳利桂林市一等奖179 师大附中易子淳林佳利桂林市一等奖180 师大附中胡冉婷林佳利桂林市一等奖181 师大附中邓凯中张小雄桂林市一等奖182 师大附中肖杨光张小雄桂林市一等奖183 师大附外文靖凯王勇桂林市一等奖184 师大附外李元园黄利魁桂林市一等奖185 师大附外范佳怡王勇桂林市一等奖186 师大附外江炳锟王勇桂林市一等奖187 师大附外黄禹豪王勇桂林市一等奖188 师大附外韦永燊俞海荣桂林市一等奖189 师大附外陈家瀚黄利魁桂林市一等奖190 师大附外翁嘉伟黄志武桂林市一等奖191 师大附外李逸伦黄志武桂林市一等奖192 师大附外唐琦宇黄志武桂林市一等奖193 师大附外梁宁罡王勇桂林市一等奖194 师大附外韦祎潇阳黄利魁桂林市一等奖195 师大附外覃博文黄利魁桂林市一等奖196 师大附外廖浩鹏黄利魁桂林市一等奖197 师大附外林小彤蒋诗承桂林市一等奖198 师大附外唐菲凡王勇桂林市一等奖199 师大附外蒋或哲黄志武桂林市一等奖200 师大附外邓志成高一桂林市一等奖201 师大附外蒋深远黄利魁桂林市一等奖202 师大附外李千千蒋诗承桂林市一等奖204 师大附外吕恒婕王勇桂林市一等奖205 师大附外林乐萱王勇桂林市一等奖206 师大附外张云深王勇桂林市一等奖207 师大附外甘诗娆唐立东桂林市一等奖208 师大附外覃煜鸣俞海荣桂林市一等奖209 师大附外唐霏伊俞海荣桂林市一等奖210 师大附外谢奇伶俞海荣桂林市一等奖211 师大附外雷周凡星黄志武桂林市一等奖212 师大附外谢可暄黄志武桂林市一等奖213 师大附外蒋浩立黄志武桂林市一等奖214 师大附外蒋舒越黄志武桂林市一等奖215 师大附外舒文俊高一桂林市一等奖216 师大附外黄健聪高一桂林市一等奖217 师大附外赵俊高一桂林市一等奖218 师大附外朱兰心黄志武桂林市一等奖219 师大附外陈清黄志武桂林市一等奖220 师大附外李浩达黄志武桂林市一等奖221 师大附外林熹黄利魁桂林市一等奖222 师大附外李淳支黄利魁桂林市一等奖223 师大附外贝东潮黄利魁桂林市一等奖224 师大附外陆欣怡蒋诗承桂林市一等奖226 师大附外潘子豪王勇桂林市一等奖227 师大附外黄子栩王勇桂林市一等奖228 师大附外罗粟海王勇桂林市一等奖229 师大附外诸葛佳棋唐立东桂林市一等奖230 师大附外周彦希俞海荣桂林市一等奖231 师大附外李依晨俞海荣桂林市一等奖232 师大附外莫国康黄志武桂林市一等奖233 师大附外张业黄志武桂林市一等奖234 师大附外庞杨洋黄志武桂林市一等奖235 师大附外刘卉萱黄志武桂林市一等奖236 师大附外杨佟承颖黄志武桂林市一等奖237 师大附外韦炳均高一桂林市一等奖238 师大附外莫乾坤高一桂林市一等奖239 师大附外文泽艺王勇桂林市一等奖240 师大附外苏勇博高一桂林市一等奖241 师大附外李培榛高一桂林市一等奖242 师大附外张捷焘王勇桂林市一等奖243 师大附外唐千俞海荣桂林市一等奖244 师大附外李文滔黄志武桂林市一等奖245 师大附外韦城志黄志武桂林市一等奖246 桂电中学周方元邓炜桂林市一等奖247 桂电中学石继强蒋荣荣桂林市一等奖248 桂电中学周志威朱建新桂林市一等奖249 桂电中学李思齐朱建新桂林市一等奖250 桂电中学熊子淦邓炜桂林市一等奖251 桂电中学曾麟晴蒋荣荣桂林市一等奖252 桂电中学莫少恒朱建新桂林市一等奖253 桂电中学李文杰朱建新桂林市一等奖254 桂电中学蒋诗怡邓炜桂林市一等奖255 桂电中学黄杨惠朱建新桂林市一等奖256 桂电中学高旻亮蒋荣荣桂林市一等奖257 首师大桂林附中唐源懋韦景依桂林市一等奖258 首师大桂林附中周键涛茹雪梅桂林市一等奖259 首师大桂林附中石嘉超覃玉杰桂林市一等奖260 首师大桂林附中蔡泽斌蒋海波桂林市一等奖261 首师大桂林附中张邦政梁聪桂林市一等奖262 恭城中学吴柳振谭建明桂林市一等奖263 恭城中学欧琛吴建平桂林市一等奖264 恭城中学欧晓琦吴建平桂林市一等奖265 恭城中学兰心伟吴建平桂林市一等奖266 恭城中学彭文军容新林桂林市一等奖267 恭城中学朱源吴建平桂林市一等奖268 恭城中学邓家俊吴建平桂林市一等奖269 恭城中学蒙海平吴建平桂林市一等奖270 恭城中学江春梅吴建平桂林市一等奖271 恭城中学廖世新吴建平桂林市一等奖272 恭城中学陈泽宗吴建平桂林市一等奖273 恭城中学陈婷吴建平桂林市一等奖274 恭城中学蒋倩妮吴建平桂林市一等奖275 恭城中学李蔚吴建平桂林市一等奖276 恭城中学欧柳娟吴建平桂林市一等奖277 恭城中学黄璐吴建平桂林市一等奖278 灌阳高中唐万成刘拥军桂林市一等奖279 灌阳高中盘佳静刘拥军桂林市一等奖280 灌阳高中施云黄邓剑桂林市一等奖281 灌阳高中王旭宇黄邓剑桂林市一等奖282 灌阳高中周赟嵘黄邓剑桂林市一等奖283 灌阳高中蒋鹏刘拥军桂林市一等奖284 灌阳高中周怡王楠刘拥军桂林市一等奖285 灌阳高中蒋宾阳文春义桂林市一等奖286 灵川中学刘让成余永相桂林市一等奖287 灵川一中骆俊仁阳秀琳桂林市一等奖288 灵川一中汪宜林孙梦遥桂林市一等奖289 灵川一中匡毅孙梦遥桂林市一等奖290 潭下中学蒋怀文赵景奇桂林市一等奖292 永福中学陈俞冰莫月红桂林市一等奖293 临桂中学黄恒广吴冬华桂林市一等奖294 荔浦师范何家穗陈益华桂林市一等奖295 荔浦师范廖承业陈益华桂林市一等奖296 荔浦师范赖春月陈益华桂林市一等奖297 荔浦师范黄声涛何丽珍桂林市一等奖298 龙胜中学侯璇吴达球桂林市一等奖299 全州高中蒋顺林俞勇军桂林市一等奖300 全州高中文博蒋书生桂林市一等奖301 全州高中文清泉蒋书生桂林市一等奖302 全州高中唐天云唐高明桂林市一等奖303 全州高中宾欣荣唐亚萍桂林市一等奖304 兴安中学尹倩胡纯军桂林市一等奖305 兴安中学侯俊辉蒋宗彬桂林市一等奖306 兴安中学唐文馨周建红桂林市一等奖307 兴安中学谢珊珊胡纯军桂林市一等奖308 兴安中学唐秋敏熊素玲桂林市一等奖309 兴安中学胡冯翔蒋宗彬桂林市一等奖310 兴安中学赵诣熊素玲桂林市一等奖311 兴安中学韦怡熊素玲桂林市一等奖312 兴安中学蒋旺鑫熊素玲桂林市一等奖314 兴安中学曾钰皓胡纯军桂林市一等奖315 兴安中学王紫逸蒋宗彬桂林市一等奖316 阳朔中学周灵桂林市一等奖317 阳朔中学朱桂华桂林市一等奖318 资源中学阳岷桂蒋明桂林市一等奖319 资源中学陈世杰蒋明桂林市一等奖320 资源中学申浠霖刘建明桂林市一等奖321 资源中学曾莫玲蒋玉祥桂林市一等奖。
2017数模竞赛辽宁赛区获奖名单
姓名2
阚宁 王洋 赵登涛 温佳琪 张书生 胡锐锋 肖海华 黄键 胡冰 杨铭 闻宜江 乔春晓 李博一 任泓霖 张怡 于上海 卢进 李思琦 母博文 王若愚 蔡小华 郑豪 范鑫 薛峰 王伟旭 杜浩萌 王慧 董劲松 郑丹 付春方 杨培源 周宇 徐嘉文 林睿琦 刘桓荣 李坤香 阎文亮 闫博 饶莉 丁子凡 侯以恒 任胜楠 于德源 张嘉凝 丁宇鑫 朱柏霖 王文浩 宋志伟 支元祺 何雄男 盛锡华
教师组 教师组 教师组 靖新 教师组 教师组 教师组 教师组 教师组 宫华 雷鸣 惠淑荣 屈巍 孙欣 孙丽 罗敏娜 姜希伟 韩丽艳 孙德才 刚家泰 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 张明 屈磊磊 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组 教师组
陈森 王泓桢 赵子贤 王泽云 茆雪瑞 胡成芳 王怡茹 徐栋 张啸 王超琦 崔瑞 胡肖楠 陈一鸣 安侠 刘昌 葛东维 曾尧 范朋奎 李佳茜 李芷晴 卢怀宝 李鹏宇 朱海乐 梁玉红 张琳 李倩 雷严 张泽军 张晓博 许亚洁 傅昇 程世健 苗延豪 程宇翔 刘伟 王家兵 乔记山 叶慧珊 曲虹阳 侯逸 张升旺 卢冠丞 王行哲 赵鹤阳 朱世鹏 吕航 毛俊 付昌雨 陈嘉彤 刘美璐 张皓然 王若桐 任嘉欣 孔吴为
大连理工大学 大连理工大学 大连理工大学 大连理工大学 大连理工大学 大连理工大学 大连理工大学城市学院 东北财经大学 东北财经大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 东北大学 海军大连舰艇学院 海军大连舰艇学院 辽宁大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁工业大学 辽宁科技大学 辽宁科技学院 辽宁科技学院 辽宁师范大学 辽宁石油化工大学 辽宁石油化工大学 沈阳城市建设学院 沈阳工程学院 沈阳工业大学 沈阳工业大学 沈阳工业大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学 沈阳航空航天大学
2017年全国中学生物理竞赛(安徽)赛区获奖名单
第6页，共
页
熊绍炎 李承浩 李德龙 李德勇 宋书伟 俞震元 叶其城 韩开元 吴冉 杨天宇 陈乾凯 周易睿 陈金翰 杨宇豪 江鑫宇 刘隽喆 谢一文 陈音含 张子曦 钱成昊 宋文杰 王珮宇 林俊杰 任栗晗 陶竹 柯彦哲 范之闽 黄海东 江庭辉 王陈玉珩 孙志航 杨皓博 魏浩林
芜湖市安徽师范大学附属中学 芜湖市安徽师范大学附属中学 宿州市萧县中学 滁州市定远中学 合肥一六八中学 合肥一中 淮北市第一中学 马鞍山市第二中学 安徽省金寨第一中学 安徽省蒙城第一中学 六安市舒城县舒城中学 合肥六中 铜陵市第一中学 宣城市广德县广德中学 安徽省霍山中学 合肥六中 合肥一中 合肥一中 芜湖市安徽师范大学附属中学 芜湖市第一中学 芜湖市第一中学 宿州市宿城一中 滁州市全椒中学 合肥一六八中学 合肥一六八中学 黄山市屯溪一中 铜陵市第一中学 芜湖市无为县无为中学 马鞍山市第二中学 安庆市第一中学 合肥八中 合肥一中 淮北市安徽省濉溪中学
谢健 谢健 江长军 孙学刚 王茂群/章洲 张道武 姚亮 董书平 马媛媛 许陵钢 余有志 束仁义 丁春花 靳彪 蔡胜国、赵传冉 吴新宽 徐东升 汪昆仑 程希应 姚继东 王自力 董书平 姚亮 张道武 吴晓明 王世权 卢先立 邢小军、刘敏、何家传 朱华勇、邓中良、李军 台运金 李万里 欧其武
二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖
蔡胜国、赵传冉 王世权 吴晓明 王苏 卢先立 汪昆仑 胡桐庆 章洲、王茂群 徐言先 雷慧 王亚伟
第4页，共
页
刘昊男 卢宇航 王文灏 汪文至 梅仕杰 宣源昊 陈林锟 陈天琪 朱海鹏 程杰 杨欣晨 刘蒙蒙 朱重阳 王昌明 郑远航 谷峰 陈旭雯 严冬 万家正 黄鼎元 夏天 李坤 孙骁 董智辰 陈洋 席天琦 孙伟豪 丁冉 汪鸣 付伟辰 李思逸 余雨 史浩楠
阜阳市第四批学科带头人(骨干教师)通过人员名单公示
樊
亮
阜阳一中
阜阳市第三中学 颍上县教育局教研室 颍上县教育局教研室 颍上县八里河镇中心学校 临泉实验中学 界首市王集中心学校 临泉一中 阜南三中 临泉一中 太和县坟台中心校
高中
高中 初中 初中 初中 初中 初中 高中 初中 高中 初中
生物
生物 生物 数学 数学 数学 数学 体育 体育 物理 物理
徐新河 汤丽 汪佃才 程永康 柳军 王素敏 刘山 梁军 马鸿飞 胡卫民
尚晓枫 吴玉宝 刘淇 丁艳 张文娟 王瑞 董艳艳 马绪霞 王国锋 刘 芹
丁仁梅 马心芳 李 婧
郭大伟 马丙印 王震 杨春梅 张玉香 宋娟 李慧敏
第 5 页
阜阳市第四批学科带头人（骨干教师）通过人员名单公示
序号 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 姓名 谭胜杰 邢国锋 唐晓泉 张莉梅 胡利利 王 捷 工作单位 阜阳市第十九中学 颍东区正午镇中心学校 阜阳一中 阜阳开发区京九路颍南中学 临泉一中 太和县第十一中学 太和八中 安徽省太和第一中学 太和县阮桥镇斤沟中学 界首一中 界首一中 界首市邴集中心校 颍州中学 阜阳市十五中学 颍州区袁集镇中心学校 阜阳二中 阜阳一中 阜阳市铁路学校 临泉四中 太和二中 太和县双浮镇中心学校 阜阳九中 阜阳市城郊中学 阜阳市第十中学 阜阳市第三中学 任教学段 初中 初中 高中 中学 高中 初中 初中 高中 初中 高中 高中 初中 初中 初中 初中 高中 高中 八年级 初中 高中 初中 初中 高中 高中 高中 任教学科 语文 语文 语文 语文 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 英语 音乐 物理 物理 物理 物理 物理 物理 学科带头人/骨干 教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师 骨干教师
何天成：从高联到IMO金牌,超详细数学竞赛学习方法(一)
何天成：从高联到IMO金牌，超详细数学竞赛学习方法〔一〕本文作者何天成，第58届国际数学奥林匹克〔IMO〕金牌获得者，华南师大附中2017届毕业生，大学数学科学学院2017级新生。
本文首发于数学新星网。
作者非常详细地阐述了从高联一试/二试，到参加CMO，国家集训队，走向IMO，各级竞赛的心路历程和学习方法，对于参加竞赛的同学具有非常大的指导意义，因为篇幅较长，故分为三篇分享给大家。
请看过的同学温故知新，没看过的同学一定要认真做好笔记，满满的干货~正文如下：2017年7月，我有幸作为中国国家队的一员参加了第 58 届国际中学生数学奥林匹克竞赛〔 IMO ) ，并获得了一枚金牌。
回顾六年竞赛之路，我从开始的一个懵懂无知的新人，一路上经历了不少挫折，走了不少弯路，在跌跌撞撞中算是摸索出了自己的一套学习竞赛的方法，最后的结局也是幸运的。
而正是这份幸运，让我觉得有责任把自己学习数学竞赛的经验与心得分享出来，希望后来者能吸取我的经验和教训，找到自己的不足，并更好地看清未来。
引言对于一场考试，我喜欢用以下 3 个参数来衡量最终的分数：最终分数=实力分 x 运气分 x 状态分。
其中实力，运气，状态均为非负实数。
这里，“实力〞顾名思义，尽管不好量化，但是一般来说实力相差很大还是能看出来的。
“运气〞主要代表“题目是否对路〞，比如一个擅长几何的选手参加一场几何送分的考试，当然运气分较低；而参加一场几何难度他刚刚好能做出来的考试，运气分就比拟高了。
当然，运气分是取决于考试本身的，可以认为主观上不能改变它，但是在集训队这样的屡次考试中，平均下来，运气会比拟稳定；并且，我们可以用比如“补短板〞或者“狂刷一科〞等方法改变运气分的波动大小。
另一方面的运气来自于改卷，即能不能得到预想中的分数，这一点理论上来说也是不能自己操纵的，但是可以通过加强书写等方法提升。
“状态〞源于自身，常见的影响状态的因素有，比如考前一晚睡不着，考试很冻手、冻僵了，旁边的同学一直发出噪音等等。
2017年全国高中数学联赛获奖名单公示（四川赛区）
2017年全国高中数学联赛获奖名单公示（四川赛区）2017年全国高中数学联赛获奖名单公示（四川赛区）序号姓名性别学校年级获奖等级证书编号1郭子棋男成都七中林荫校区高三一等奖M176101 2田翊男成都七中林荫校区高三一等奖M176102 3陈博洋男成都七中嘉祥外国语学校高二一等奖M176103 4杜航男成都七中林荫校区高二一等奖M176104 5黄轶之男成都七中林荫校区高二一等奖M176105 6陈宇轩男绵阳中学高三一等奖M176106 7石元峰男成都七中林荫校区高三一等奖M176107 8李咏璋男成都树德中学宁夏校区高二一等奖M176108 9宣涵潇男成都七中林荫校区高三一等奖M176109 10庞舜之男成都七中林荫校区高三一等奖M176110 11陈思锟男南充高中顺庆校区高三一等奖M176111 12陈泓宇男成都七中林荫校区高三一等奖M176112 13张海翔男成都七中嘉祥外国语学校高三一等奖M176113 14杨茗男成都七中嘉祥外国语学校高三一等奖M176114 15杨书颜男成都七中林荫校区高一一等奖M176115 16李思雨女成都树德中学宁夏校区高三一等奖M176116 17王锦波男成都外国语学校高三一等奖M176117 18胡航男绵阳中学高二一等奖M176118 19景虹皓男成都七中林荫校区高一一等奖M176119 20郭维豪男成都七中林荫校区高二一等奖M176120 21彭昌浩男成都七中林荫校区高二一等奖M176121 22何遗波男成都七中林荫校区高三一等奖M176122 23倪志男成都七中林荫校区高一一等奖M176123 24杨锦宜女成都七中林荫校区高三一等奖M176124 25覃瀚林男成都外国语学校高一一等奖M176125 26张遂初男成都七中林荫校区高二一等奖M176126 27王路石男成都树德中学宁夏校区高三一等奖M176127 28赵梓杰男成都七中高新校区高三一等奖M176128 29郑竟屹男成都实验外国语学校高三一等奖M176129 30敖睿成男成都七中林荫校区高二一等奖M176130 31杨明宇男成都七中林荫校区高一一等奖M176131 32郭龙欣男绵阳中学高三一等奖M176132 33王潇逸男成都七中林荫校区高三一等奖M176133 34张凌云男成都七中林荫校区高二一等奖M176134 35王嘉阳男成都七中林荫校区高二一等奖M176135 36胡文馨女成都七中嘉祥外国语学校高三一等奖M176136 37欧禧龙男成都树德中学光华校区高三一等奖M176137 38李思露女成都树德中学宁夏校区高三一等奖M176138 39张晋豪男成都七中林荫校区高二一等奖M176139 40周欣宇男绵阳绵阳东辰国际学校高二一等奖M176140 41张延男绵阳中学高三一等奖M176141 42户皓男绵阳中学高二一等奖M176142 43杜哲航男成都七中嘉祥外国语学校高二一等奖M176143 44王乐之男成都七中嘉祥外国语学校高三一等奖M176144 45王一鼎男成都七中嘉祥外国语学校高一一等奖M176145 46李俊儒男成都七中嘉祥外国语学校高二一等奖M176146 47陈藩允男成都七中林荫校区高二一等奖M176147 48朱笑辰男成都树德中学宁夏校区高二一等奖M176148 49姜昆男成都树德中学宁夏校区高二一等奖M176149 50高炜程男成都七中林荫校区高三一等奖M176150 51肖海阳男成都实验外国语学校高三一等奖M176151 52宋岳峰男成都七中嘉祥外国语学校高二一等奖M176152 53杜宇男绵阳中学高三一等奖M176153 54秦政男成都七中林荫校区高二一等奖M176154 55徐苇杭男成都七中林荫校区高二一等奖M176155 56曾浩洋男成都树德中学宁夏校区高三一等奖M17615657卢禹杰男成都市石室中学文庙校区高三一等奖M17615758杨文韬男成都七中林荫校区高三一等奖M17615859马文俊男绵阳中学高二一等奖M17615960杭子涵男成都七中嘉祥外国语学校高三一等奖M17616061唐果男成都七中林荫校区高一一等奖M17616162黄思成女成都树德中学宁夏校区高三一等奖M17616263干正浩男绵阳中学高二一等奖M17616364陈泳西女绵阳中学实验学校高三一等奖M17616465钟梁骏男成都七中林荫校区高一一等奖M17616566邓书豪男成都七中林荫校区高三一等奖M17616667漆林男遂宁遂宁卓同国际学校高二一等奖M17616768江柏杉男成都七中林荫校区高二一等奖M17616869牛晗汀男成都市石室中学文庙校区高二一等奖M17616970唐艺铭男成都七中嘉祥外国语学校高二一等奖M17617071余其蓉女绵阳中学高二一等奖M17617172胡梦箫男成都市树德中学宁夏校区高二一等奖M17617273周浩男成都市石室中学文庙校区高二一等奖M17617374李夏鲲男成都七中林荫校区高二二等奖M217610001 75卓汐聪男成都实验外国语学校高三二等奖M217610002 76甘祚男成都树德中学光华校区高三二等奖M217610003 77陈克发男绵阳中学高二二等奖M217610004 78江孝奕男成都七中高新校区高三二等奖M217610005 79王琦淏男成都市石室中学文庙校区高三二等奖M217610006 80周昱昊男成都七中高新校区高二二等奖M217610007 81付乐天男成都七中林荫校区高三二等奖M217610008 82徐展鹏男成都七中嘉祥外国语学校高二二等奖M217610009 83张馨璇女绵阳中学高三二等奖M217610010 84赵宇智男成都七中林荫校区高二二等奖M217610011 85高信男成都实验外国语学校高三二等奖M217610012 86关景瑞男成都七中嘉祥外国语学校高二二等奖M217610013 87田恒瑞男成都市石室中学文庙校区高二二等奖M217610014 88张庭瑞男成都树德中学宁夏校区高三二等奖M217610015 89刘雨芝女成都树德中学宁夏校区高二二等奖M217610016 90蒲钰男成都七中林荫校区高二二等奖M217610017 91唐堂男成都七中嘉祥外国语学校高二二等奖M217610018 92杨宸玮男南充高中顺庆校区高二二等奖M217610019 93贾志杰男成都棠湖外国语学校高三二等奖M217610020 94唐龙天男成都七中嘉祥外国语学校高一二等奖M217610021 95文子龙男成都七中林荫校区高二二等奖M217610022 96钟孟言男成都七中林荫校区高二二等奖M217610023 97陈浩志男广元天立国际学校高三二等奖M217610024 98张鳌男成都七中林荫校区高三二等奖M217610025 99刘昱丁男成都外国语学校高二二等奖M217610026 100曾浩洋男成都市石室中学文庙校区高三二等奖M217610027 101杨力源男成都树德实验中学初三二等奖M217610028 102刘勉之男成都七中林荫校区高三二等奖M217610029 103何俊杰男绵阳绵阳东辰国际学校高二二等奖M217610030 104王涵章男成都树德中学宁夏校区高三二等奖M217610031 105赵红阳男绵阳中学高二二等奖M217610032 106褚文笛男成都七中林荫校区高三二等奖M217610033 107王优男遂宁遂宁卓同国际学校高三二等奖M217610034 108罗春雨男绵阳中学高三二等奖M217610035 109潘亮男成都实验外国语学校高二二等奖M217610036 110李卓潼女成都七中林荫校区高三二等奖M217610037 111王敬飞男成都实验外国语学校高一二等奖M217610038 112杨天成男成都七中林荫校区高一二等奖M217610039 113田梓茂男成都七中育才学校水井坊校初三二等奖M217610040 114邓皓元男成都七中林荫校区高二二等奖M217610041115刘皓瑞男成都七中嘉祥外国语学校高二二等奖M217610042 116何奥东男绵阳东辰国际学校高三二等奖M217610043 117黄清扬男南充高中老校区高三二等奖M217610044 118唐得山男成都树德中学宁夏校区高三二等奖M217610045 119蒋宇骁男成都七中嘉祥外国语学校高三二等奖M217610046 120邓浩毅男成都树德中学宁夏校区高三二等奖M217610047 121苏洋男成都七中嘉祥外国语学校高三二等奖M217610048 122唐一夫男成都七中林荫校区高一二等奖M217610049 123张昭阳男成都市石室中学文庙校区高二二等奖M217610050 124杜奕宏男成都七中林荫校区高三二等奖M217610051 125杨涵男成都七中嘉祥外国语学校高三二等奖M217610052 126黄儒惟男成都树德中学宁夏校区高三二等奖M217610053 127王彦桥男绵阳东辰国际学校高一二等奖M217610054 128古丹妮女成都市石室中学文庙校区高三二等奖M217610055 129刘键一男成都树德中学宁夏校区高三二等奖M217610056 130陈昌睿男成都七中高新校区高三二等奖M217610057 131刘泓麟男绵阳中学高二二等奖M217610058 132余锦潼男成都树德中学宁夏校区高三二等奖M217610059 133曾添男绵阳中学实验学校高三二等奖M217610060 134袁鑫凤女成都七中嘉祥外国语学校高二二等奖M217610061 135罗一浦男绵阳东辰国际学校高三二等奖M217610062 136雷轩昂男成都七中嘉祥外国语学校高三二等奖M217610063 137陈泳岐男成都七中林荫校区高二二等奖M217610064 138焦梦翰男成都市石室中学文庙校区高三二等奖M217610065 139谭泽男成都七中嘉祥外国语学校高三二等奖M217610066 140黎翔宇男成都树德中学光华校区高三二等奖M217610067 141刘昱男成都七中嘉祥外国语学校高三二等奖M217610068 142舒牧葳男成都七中嘉祥外国语学校高三二等奖M217610069 143赵谦男广元天立国际学校高二二等奖M217610070 144张乐男成都七中林荫校区高三二等奖M217610071 145江玮佳男绵阳东辰国际学校高三二等奖M217610072 146唐天楠男成都市石室中学文庙校区高二二等奖M217610073 147龙城轩男自贡自贡富顺二中高三二等奖M217610074 148鲁俊杰男绵阳东辰国际学校高二二等奖M217610075 149李炤男广元天立国际学校高三二等奖M217610076 150王今迈男成都七中高新校区高三二等奖M217610077 151郭鹏男成都外国语学校高二二等奖M217610078 152胥畅男遂宁遂宁射洪中学高三二等奖M217610079 153张书恺男成都实验外国语学校高三二等奖M217610080 154张洋海男成都七中万达学校高三二等奖M217610081 155龚雨豪男绵阳中学高二二等奖M217610082 156叶夏汐女成都七中林荫校区高二二等奖M217610083 157雷雨寒男成都棠湖外国语学校高三二等奖M217610084 158曲星宇男成都七中嘉祥外国语学校高三二等奖M217610085 159何轩霆男成都外国语学校高三二等奖M217610086 160彭祖泽男成都七中林荫校区高三二等奖M217610087 161左欣悦女成都七中嘉祥外国语学校高二二等奖M217610088 162余明哲男成都七中嘉祥外国语学校高三二等奖M217610089 163张涵男成都七中嘉祥外国语学校高三二等奖M217610090 164范珂男成都七中林荫校区高三二等奖M217610091 165陈翰凝男成都市石室中学文庙校区高二二等奖M217610092 166程玺玮男成都市石室中学文庙校区高二二等奖M217610093 167陈泽坤男成都七中嘉祥外国语学校高一二等奖M217610094 168傅于恒男成都七中嘉祥外国语学校高一二等奖M217610095 169胡芳铭男成都树德中学外国语校区高三二等奖M217610096 170杨乾宇男绵阳东辰国际学校高二二等奖M217610097 171欧阳乐铮女绵阳东辰国际学校高三二等奖M217610098 172代家葳男成都七中林荫校区高三二等奖M217610099173夏熙林男成都七中林荫校区高三二等奖M217610100 174肖逸航男成都七中嘉祥外国语学校高二二等奖M217610101 175贺南棋男绵阳中学高二二等奖M217610102 176康宁女成都七中林荫校区高三二等奖M217610103 177黄玉茂男成都七中嘉祥外国语学校高一二等奖M217610104 178冯书瀚男成都树德中学光华校区高三二等奖M217610105 179刘朗辰男成都实验外国语学校高三二等奖M217610106 180陈子奕男成都七中林荫校区高二二等奖M217610107 181郑博文男遂宁遂宁卓同国际学校高二二等奖M217610108 182杨弘毅男成都七中嘉祥外国语学校高二二等奖M217610109 183文鑫源男遂宁卓同国际学校高三二等奖M217610110 184刘卿莆男成都实验外国语学校高三二等奖M217610111 185刘育诚男成都七中高新校区高三二等奖M217610112 186付云帆男成都七中林荫校区高三二等奖M217610113 187符心亮男绵阳中学高三二等奖M217610114 188李郝添男成都树德中学宁夏校区高二二等奖M217610115 189赵睿达男成都市石室中学文庙校区高二二等奖M217610116 190何文杰男成都师大一中高中部高二二等奖M217610117 191陈柘芃男成都实验外国语学校高二二等奖M217610118 192黎杰扬男成都七中嘉祥外国语学校高三二等奖M217610119 193杨奕旻男绵阳中学高二二等奖M217610120 194王逸帆男绵阳东辰国际学校高三二等奖M217610121 195钟汉峰男成都七中林荫校区高三二等奖M217610122 196何光烜男成都七中林荫校区高三二等奖M217610123 197张舒翔男成都外国语学校高三二等奖M217610124198刘与乐男绵阳中学实验学校高三二等奖M217610125 199李浩宇男成都外国语学校高一二等奖M217610126 200谭钰晖男绵阳中学高二二等奖M217610127 201吴王茂男成都棠湖外国语学校高三二等奖M217610128 202张天择男成都树德实验中学初三二等奖M217610129 203廖珩男成都七中嘉祥外国语学校高一二等奖M217610130 204罗之尧男成都七中嘉祥外国语学校高一二等奖M217610131 205谢天男绵阳绵阳南山中学实验学校高三二等奖M217610132 206廖予扬男成都外国语学校高三二等奖M217610133 207罗靖东男成都树德中学光华校区高三二等奖M217610134 208何睿杰男成都七中林荫校区高二二等奖M217610135 209侯廷强男南充高中老校区高三二等奖M217610136 210李泓辛男成都七中林荫校区高三二等奖M217610137 211王淇男成都七中高新校区高三二等奖M217610138 212郭嘉美女成都七中林荫校区高二二等奖M217610139 213陈钦阳男泸州高中高三二等奖M217610140 214唐思渝男绵阳中学高二二等奖M217610141 215廖娅娴女成都树德中学光华校区高三二等奖M217610142 216李玉龙男成都树德中学宁夏校区高三二等奖M217610143 217黄文志男绵阳外国语学校高一二等奖M217610144 218李雨浓男成都树德中学光华校区高三二等奖M217610145 219宋帆男成都树德中学宁夏校区高三二等奖M217610146 220龙俊潇男成都七中林荫校区高三二等奖M217610147 221杨英杰男成都七中林荫校区高三二等奖M217610148 222赵修民男绵阳东辰国际学校高二二等奖M217610149 223胡凌风男成都新都一中高三二等奖M217610150 224唐越男成都树德中学宁夏校区高三二等奖M217610151 225胥仁涛男成都七中林荫校区高三二等奖M217610152 226杨雨奇男成都实验外国语学校高三二等奖M217610153 227蒋芮女遂宁卓同国际学校高二二等奖M217610154 228李睿丁男成都实验外国语学校高二二等奖M217610155 229袁子涵男成都七中林荫校区高二二等奖M217610156 230冯宇晨男成都七中嘉祥外国语学校高三二等奖M217610157231曾义鹏男绵阳江油中学高三二等奖M217610158 232张家乐男绵阳中学高三二等奖M217610159 233孙中天男成都七中嘉祥外国语学校初二二等奖M217610160 234李远政男成都树德中学光华校区高二二等奖M217610161 235刘恒瑞男成都实验外国语学校高二二等奖M217610162 236张钟天男南充高中新校区高三二等奖M217610163 237周明玺男广元天立国际学校高三二等奖M217610164 238黄可一男成都七中林荫校区高一二等奖M217610165 239龙沭尧男成都七中林荫校区高三二等奖M217610166 240戴维男成都树德中学宁夏校区高三二等奖M217610167 241杜俊江男绵阳江油市第一中学高三二等奖M217610168 242龚新至男成都实验外国语学校高三二等奖M217610169 243谭畅男成都七中高新校区高三二等奖M217610170 244张凌霄男绵阳东辰国际学校高三二等奖M217610171 245王研男绵阳中学高三二等奖M217610172 246蒋京轩女成都七中林荫校区高三二等奖M217610173 247梁天翼男成都树德中学光华校区高二二等奖M217610174 248曾治霖男自贡荣县中学高三二等奖M217610175 249邓智远男成都七中嘉祥外国语学校高一二等奖M217610176 250田昀禾女成都实验外国语学校高二二等奖M217610177 251唐宣女成都七中林荫校区高二二等奖M217610178 252杨宇昂男成都交大附中高二二等奖M217610179 253胡伟男成都七中林荫校区高三二等奖M217610180 254冉植尹男成都七中高新校区高三二等奖M217610181 255王彦睿男绵阳中学实验学校高三二等奖M217610182 256杨豪佶男成都嘉祥外国语学校郫县分高三二等奖M217610183 257张殊培男南充白塔中学高三二等奖M217610184 258刘杰男成都实验外国语学校高三二等奖M217610185 259王霖轩男绵阳中学高三二等奖M217610186 260唐瑞晨女成都七中林荫校区高三二等奖M217610187 261肖翰林男绵阳东辰国际学校高三二等奖M217610188 262易云飞男成都七中嘉祥外国语学校高一二等奖M217610189 263刘云杰男宜宾翠外高三二等奖M217610190 264邓力男绵阳东辰国际学校高二二等奖M217610191 265蒋良航男成都树德中学光华校区高三二等奖M217610192 266王錾沣男泸州高中高三二等奖M217610193 267肖云洋男成都七中嘉祥外国语学校高二二等奖M217610194 268王奕达男成都树德中学宁夏校区高三二等奖M217610195 269尹浩儒男成都七中林荫校区高三二等奖M217610196 270谭玺扬男成都七中林荫校区高三二等奖M217610197 271王逸男成都第十二中学高三二等奖M217610198 272姜琪瑶女成都树德中学宁夏校区高二二等奖M217610199 273李可峰男绵阳中学高二二等奖M217610200 274周瀚宇男绵阳东辰国际学校高三二等奖M217610201 275曹家伟男成都七中万达学校高三二等奖M217610202 276宋康健男成都七中林荫校区高三二等奖M217610203 277周高川男遂宁射洪外国语学校高三二等奖M217610204 278刘祥龙男绵阳中学高二二等奖M217610205 279裴泓宇男绵阳中学高二二等奖M217610206 280肖力文男成都市石室中学文庙校区高二二等奖M217610207 281吕云帆男德阳什邡中学高三二等奖M217610208 282穆星宇男成都市石室中学文庙校区高三二等奖M217610209 283庞祥鹤男成都七中林荫校区高三二等奖M217610210 284杨展鹏男成都市石室中学文庙校区高三二等奖M217610211 285秦天男成都新都一中高一二等奖M217610212 286王俊杰男成都七中嘉祥外国语学校高二二等奖M217610213 287蔡乐衡男泸州高中高三二等奖M217610214 288秦溯女成都树德中学宁夏校区高三二等奖M217610215289周溪又男成都七中林荫校区高二二等奖M217610216 290陈俊鹏男成都新都一中高三二等奖M217610217 291董浩宇男泸州高中高三二等奖M217610218 292梅新宇男成都七中嘉祥外国语学校高三二等奖M217610219 293余春霖男成都七中高新校区高三二等奖M217610220 294杨柯宇男成都市石室中学北湖校区高二二等奖M217610221 295杨文骁男绵阳中学高二二等奖M217610222 296郑宇航男绵阳南山中学高二二等奖M217610223 297董林瀚男成都树德中学宁夏校区高三二等奖M217610224 298彭思叡男成都七中嘉祥外国语学校高三二等奖M217610225 299张紫洋男遂宁射洪中学高三二等奖M217610226 300周寓瑾女成都七中嘉祥外国语学校高二二等奖M217610227 301侯宇恒男南充高中老校区高三二等奖M217610228 302闫锐男成都树德中学宁夏校区高三二等奖M217610229 303何一航男成都棠湖外国语学校高三二等奖M217610230 304阚浚晖男成都树德中学宁夏校区高三二等奖M217610231 305刘曦雨男成都树德中学宁夏校区高三二等奖M217610232 306马昊文男成都树德中学外国语校区高三二等奖M217610233 307王可容男成都外国语学校高三二等奖M217610234 308骆彦萌男成都七中林荫校区高一二等奖M217610235 309靳雁女成都七中嘉祥外国语学校高三二等奖M217610236 310倪立女遂宁卓同国际学校高三二等奖M217610237 311任芋霖男成都七中林荫校区高二二等奖M217610238 312王睿知男成都七中林荫校区高二二等奖M217610239 313杨江林男南充高中顺庆校区高二二等奖M217610240 314杨然男绵阳中学高二二等奖M217610241 315何雪吟女德阳外国语学校高三二等奖M217610242 316宾心瑜男德阳市第五中学高三二等奖M217610243 317陈铭双男宜宾市一中高三二等奖M217610244 318李鸿坤男德阳市第五中学高三二等奖M217610245 319欧阳显峥男成都双流中学高三二等奖M217610246 320邵新哲男成都七中林荫校区高三二等奖M217610247 321文瑞阳男成都七中林荫校区高三二等奖M217610248 322曹翔男成都七中嘉祥外国语学校高三二等奖M217610249 323黎凯男攀枝花市第三高级中学校高三二等奖M217610250 324李鑫智男成都外国语学校高三二等奖M217610251 325欧阳维一男德阳什邡中学高三二等奖M217610252 326马潇健男成都树德中学宁夏校区高三二等奖M217610253 327徐浩瀚男广安武胜中学高三二等奖M217610254 328韩子睿男成都七中林荫校区高二二等奖M217610255 329罗大禹男成都市石室中学文庙校区高二二等奖M217610256 330陈嘉睿女成都外国语学校高二二等奖M217610257 331潘逸鸣男成都七中嘉祥外国语学校高三二等奖M217610258 332齐立洲男成都七中林荫校区高三二等奖M217610259 333王嘉怡女绵阳东辰国际学校高二二等奖M217610260 334丁春瑞男德阳外国语学校高三二等奖M217610261 335张志豪男成都市龙泉中学高三二等奖M217610262 336郭朋男成都新都一中高三二等奖M217610263 337陈世轩男成都市石室中学文庙校区高二二等奖M217610264 338胡杰昊男成都七中林荫校区高二二等奖M217610265 339李泓民男成都七中林荫校区高三二等奖M217610266 340肖宇辰男成都树德中学宁夏校区高三二等奖M217610267 341尹罗毅男绵阳中学实验学校高三二等奖M217610268 342詹一丁男成都树德中学宁夏校区高三二等奖M217610269 343赵子毅男成都实验外国语学校高二二等奖M217610270 344余昊亮男成都石室天府中学高二二等奖M217610271 345竹子林男成都七中万达学校高三二等奖M217610272 346伍靖波男成都七中林荫校区高二二等奖M217610273347向灿男成都七中嘉祥外国语学校高二二等奖M217610274 348何志霄男南充南部中学高三二等奖M217610275 349何金津男绵阳中学高二二等奖M217610276 350段迪文男成都树德中学宁夏校区高三二等奖M217610277 351孙思危女南充高中老校区高三二等奖M217610278 352张佳驰男成都树德中学光华校区高三二等奖M217610279 353唐骁男宜宾市三中高三二等奖M217610280 354马润峰男成都实验外国语学校高二二等奖M217610281 355文彦博男绵阳中学高三二等奖M217610282 356杨宗茂男成都棠湖外国语学校高三二等奖M217610283 357张思勰男成都树德中学宁夏校区高三二等奖M217610284 358何佳政男广元天立国际学校高二二等奖M217610285 359陈斯佳女自贡富顺二中高三二等奖M217610286 360吴俊江男内江六中高三二等奖M217610287 361任恬叶女成都树德中学宁夏校区高二二等奖M217610288 362霍漪漪女成都七中林荫校区高三二等奖M217610289 363陈德铭男成都七中嘉祥外国语学校高二二等奖M217610290 364刘镇谋男南充高中老校区高三二等奖M217610291 365周琦欣男资阳市资阳中学高三二等奖M217610292 366李骞男成都七中嘉祥外国语学校高一二等奖M217610293 367罗王贤男成都七中林荫校区高一二等奖M217610294 368龙之源男成都七中林荫校区高三二等奖M217610295 369杨桐女成都七中高新校区高三三等奖M317610001 370谢安昊男成都树德中学光华校区高三三等奖M317610002 371彭林男成都玉林中学高三三等奖M317610003 372刘雪女宜宾市一中高三三等奖M317610004 373魏煜江男自贡蜀光中学高三三等奖M317610005 374张虒源男自贡蜀光中学高三三等奖M317610006 375张翔洲男成都市四川师大附中高三三等奖M317610007 376唐子琳女广元中学高三三等奖M317610008 377陈星佐男成都树德中学宁夏校区高三三等奖M317610009 378李沛洋男成都七中林荫校区高三三等奖M317610010 379骆言男成都外国语学校高三三等奖M317610011 380鲜唯佳男成都实验外国语学校高三三等奖M317610012 381张抒扬男成都七中嘉祥外国语学校高三三等奖M317610013 382王湜轶女成都市石室中学文庙校区高二三等奖M317610014 383刘鑫男绵阳绵阳南山中学实验学校高三三等奖M317610015 384孟群康男成都市四川师大附中高三三等奖M317610016 385邵瀚雍男德阳市第五中学高三三等奖M317610017 386辛雨男成都七中万达学校高一三等奖M317610018 387阳晨曦男成都七中嘉祥外国语学校高一三等奖M317610019 388宋秋池女成都市石室中学文庙校区高三三等奖M317610020 389邹铭睿女成都实验外国语学校高三三等奖M317610021 390甘泽昊男成都市石室中学文庙校区高二三等奖M317610022 391林博阳男成都市西南交大附中高三三等奖M317610023 392黄越男南充高中老校区高三三等奖M317610024 393白弈文女成都市石室中学文庙校区高二三等奖M317610025 394王鹏宇男成都七中万达学校高二三等奖M317610026 395李玮哲男成都树德中学光华校区高三三等奖M317610027 396邹佳良男成都树德中学宁夏校区高三三等奖M317610028 397黄奕为男成都七中嘉祥外国语学校高一三等奖M317610029 398张译元女成都市石室中学高三三等奖M317610030 399邱子莹女成都七中嘉祥外国语学校高二三等奖M317610031 400蒋誉豪男绵阳南山中学实验学校高三三等奖M317610032 401唐嘉慧女成都七中林荫校区高三三等奖M317610033 402张海粟男成都七中万达学校高二三等奖M317610034 403白胜泷男成都树德中学宁夏校区高三三等奖M317610035 404孙文轩男成都七中林荫校区高一三等奖M317610036405周涛男泸州老窖天府中学高三三等奖M317610037 406李佳航女乐山外国语学校高三三等奖M317610038 407侯昊然男广元中学高三三等奖M317610039 408苗阳男南充高中老校区高三三等奖M317610040 409黄思成男成都树德中学宁夏校区高三三等奖M317610041 410张霄男成都七中林荫校区高三三等奖M317610042 411周体又男泸县二中高三三等奖M317610043 412秦棋男成都市石室中学文庙校区高二三等奖M317610044 413余佳岭女四川省自贡蜀光中学高三三等奖M317610045 414向梵烨男成都树德实验中学高三三等奖M317610046 415傅宇千男成都七中林荫校区高三三等奖M317610047 416郑汇川男成都树德中学宁夏校区高三三等奖M317610048 417吴环宇男绵阳东辰国际学校高三三等奖M317610049 418陈一潇男成都实验外国语学校高二三等奖M317610050 419徐屹男成都市树德中学宁夏校区高二三等奖M317610051 420代沁欣女成都新都一中高三三等奖M317610052 421孙伊琳女成都双流中学高三三等奖M317610053 422张智琳女成都树德中学宁夏校区高三三等奖M317610054 423戴瑞诚男成都七中林荫校区高三三等奖M317610055 424李梓禾男资阳市资阳中学高三三等奖M317610056 425刘鼎男成都七中林荫校区高三三等奖M317610057 426张思淼男成都七中林荫校区高一三等奖M317610058 427张泽豪男绵阳东辰国际学校高三三等奖M317610059 428吴熙楠男成都七中林荫校区高二三等奖M317610060 429郑雅洁女成都列五中学高三三等奖M317610061 430付乐豪男成都七中（高新校区）高一三等奖M317610062 431朱灿宇男成都七中林荫校区高三三等奖M317610063 432储德明男成都七中林荫校区高二三等奖M317610064 433杨辰宇男成都树德中学光。
阜阳2017年中小学高级教师专业技术资格评审
姓名 周萍 金德林 刘健 李金亮 穆良丰 张贺珍 蒋琼 郑永 张广奎 曹利 王文献 郑蕊 夏开波 姜玲 陈德虎 姜桂 栾峰 樊家虎 姜允发 李鸣 张梅
性别 女 男 男 男 男 女 男 男 男 男 男 女 男 女 男 男 男 男 男 男 女
申报学科 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文 初中语文
序号 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Байду номын сангаас
单位 颍上甘罗乡村教育社 颍上建颍乡管仲职中 颍上县第五中学 颍上县第五中学 颍上县八里河中心学校 颍上县半岗镇中心学校 颍上县半岗镇中心学校 颍上县半岗镇中心学校 颍上县半岗镇中心学校 颍上县陈桥镇中心学校 颍上县垂岗乡中心学校 颍上县红星镇中心学校 颍上县建颍乡中心学校 颍上县江店孜镇中心学校 颍上县江店孜镇中心学校 颍上县江店孜镇中心学校 颍上县刘集乡中心学校 颍上县刘集乡中心学校 颍上县刘集乡中心学校 颍上县鲁口镇中心学校 颍上县南照镇中心学校
颍东区插花镇二学区中心学校 李效龙 颍东区插花镇二学区中心学校 杜付连 颍东区口孜镇汪庙初级中学 颍东区口孜镇汪庙初级中学 颍东区口孜镇汪庙初级中学 颍东区冉庙乡中心学校 颍东区袁寨镇临颍中学 颍东区枣庄镇中心学校 颍东区正午镇中心学校 界首第一中学 界首市界首中学 邬继成 訾化文 白春萌 张李志 王冠 张超 周凤娟 陈龙 贾林
阜南县郜台乡段台九年制学校 余洪贵 阜南县柴集高级职业中学 临泉滑集镇中心学校 王康 汪辉
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
姓名 毕志军 孙骁 万家正 张旭 徐忠诚 项梓纭 陈施毅 姚永乐 曹丹 张硕 于坤 刘浩 牛国阳 桑环宇 韩修甲 叶宏顺 解奎 陈天旭 邢昌浩 孙浩 张景伟 张海祥 邱怿琛 耿心旷 李龙 靳影 张何 李鹏 赵阳春 周家亮 马骁 江奉天 杜宏洋 代忠龙 吴帅 姚舜禹 庄永琪
性别 女 男 男 男
年级
男 男 男 女 男
男 男 男 女 男 男 女 男
高二
高二
20 男 男 男 女 男 女 男 男 男 男 男 男 女 女 男 女
18 高二 高二
颍上一中 路桂安 阜阳市第三中学 陈新荥 界首一中 刘志勇 太和一中 靳传递 太和一中 靳传递 太和中学 韩长峰 太和一中 李洪清 太和一中 刘丽影 界首一中 王亚飞 界首一中 段嘉华 临泉一中 程佰畏 太和一中 靳传递 太和一中 靳传递 阜阳市第三中学 陈伟 临泉一中 牛明 太和一中 程晓彤 太和中学 韩长峰 太和一中 方友梅 太和中学 韩长峰 阜阳一中 丁京川 颍上一中 路桂安 太和中学 于彩霞 太和中学 王宁 太和一中 邱秉磊 太和一中 韩金亮 太和一中 方友梅 太和中学 刘 阳 阜阳市第三中学 陈伟 太和一中 杨祎帆 太和一中 靳传递 太和中学 王涛 太和中学 阮飞 阜阳市成效中学 贾艳丽 安徽省阜南一中 李林 临泉一中 李晓燕 太和一中 邱秉磊 太和一中 方友梅 太和中学 牛春雷
名次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
0635 738 4 170126 170521 170624 861 126 130 170314 170330 171026 171201 2E+08 1133 2E+06 23 2E+07 106 333 0538 2E+06 2E+07 365 2E+08 20 2E+08 916 2E+07 1230 171523 171628 953 125 970
男 男 男 男 男
男 男 男 男
女 男
所在学校 任课老师 成绩 太和一中 韩金亮 104 高二 安徽省阜南一中 李林 95 25 阜阳一中 姚孝猛 94 太和中学 韩长峰 90 87 阜阳市第三中学 彭猛 太和一中 杨祎帆 86 红旗中学 李庆 85 25 阜阳一中 姚孝猛 84 界首一中 孙晓洁 82 太和一中 岳峰 82 太和中学 阮飞 82 25 阜阳一中 姚孝猛 81 太和中学 刘 阳 80 太和一中 洪末凤 80 太和一中 张奇 80 颍上一中 刘干 80 颍上一中 路桂安 80 太和一中 靳传递 79 太和一中 靳传递 79 太和一中 乔金永 79 高二 临泉一中 程佰畏 78 太和一中 方友梅 78 25 阜阳二中 吕伟 78 颍上一中 刘干 78 颍上一中 周厚强 78 界首一中 孙晓洁 76 太和一中 岳峰 76 太和一中 洪末凤 76 太和一中 方友梅 76 76 阜阳市第三中学 陈伟 太和一中 靳传递 75 颍上一中 周厚强 75 颍上一中 陈久仓 75 太和一中 方友梅 74 太和一中 方友梅 73 25 阜阳一中 姚孝猛 73 26 阜阳二中 吴生才 73
男
男 女 女 男 男
阜阳一中 唐晓雯 阜阳市第三中学 陈伟 界首一中 刘志勇 太和一中 方友梅 太和中学 王宁 太和一中 洪末凤 阜阳市第三中学 董海涛 高二 安徽省阜南一中 唐成宇 高二 安徽省阜南一中 唐成宇 太和一中 岳峰 太和一中 靳传递 太和一中 乔金永 太和中学 王宁 17 阜阳市成效中学 贾艳丽 25 阜阳一中 姚孝猛 颍上一中 路桂安 界首一中 段嘉华 高二 临泉一中 曹丽 高二 安徽省阜南一中 唐成宇 阜阳市第三中学 陈伟 23 阜阳二中 吴生才 颍上二中 杜世宝 高二 临泉二中 张婷 红旗中学 杨蓓蓓 阜阳市城郊中学 王辉 界首中学 陈美丽 阜阳市第五中学 范振振 高二 阜南县实验中学 朱美 高二 临泉田家炳实验中学 徐凤玲 1 阜阳四中 李治国 太和八中 徐桂兰 太和二中 石林山 阜南县第二中学 汪树付 阜阳师范学院附属中学 刘萍 阜南县春晖学校 邵长军
2E+06 13 1 170306 170324 170801 171016 171202 12 18 2E+07 170218 170328 494 2E+07 170224 170705 170724 170805 0817 2E+06 170501 170523 170406 170612 170620 170623 69 170408 170414 171203 171313 2E+08 231 2E+07 170302 170726 171323
基础指标
省级示范 高中 分配到学 校
,共80分钟。全国高 共150分钟。
73 73 72 72 72 72 72 72 71 71 71 71 71 71 70 70 70 70 70 70 70 69 69 68 68 68 68 68 67 67 67 67 67 66 66 66 66 66
38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
黄可 程瑞松 张富强 何赛亚 王逸龙 车以诺 谢冰清 陈梦宇 张润涛 代亚飞 李正浩 韩颂 李国虎 郭心仪 唐心悦 丁培员 刘俊杰 范志国 刘子程 张开拓 胡一鸣 唐朝伟 孙明健 刘潇翔 邵哲 张霄汉 邱鑫冉 沈梦楠 张浩燃 范非凡 谢梦龙 王云杰 李贵贵 贾明浩 马醒醒 昝嘉慧 刘东晓 齐心童
女 男 男 女 男
说明：
1：如有疑问课可以申请复查； 2、请各位老师辛苦通知到学生，督促学校认真辅导。 3:全国高中数学联赛（一试）考试时间： 2017年9月10日（星期日）8：00—9：20,共80分钟。全国高 中数学联赛加试（二试）考试时间： 2017年9月10日（星期日）9：40—12：10，共150分钟。
备注
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
考号 170704 236 1109 170717 544 170222 347 1107 27 170310 171127 1113 170605 170706 171304 2E+06 2E+06 170226 170418 171324 2E+07 170812 0824 2E+06 2E+06 19 170316 170616 170622 429 170420 2E+06 2E+06 170714 170710 1125 1138
13
66 66 65 65 65 65 65 65 65 65 65 64 64 64 64 64 63 63 62 62 60 63 56 56 49 45 41 37 36 35 30 27 24 20 45
76 77 78 79 80 81 82 83 84 85 86 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
刘凯 张宇 陈晓东 张奥宇 史赛飞 齐科杰 来桐彬 王启航 杨涛 郭马路 方潇 谢迪 李豪 张昊 王金涛 朱远远 陈国强 王龙 王海涛 苗江海 范俊宇 吴世纪 任振山 郭祥道 马成才 饶帅强 马晶晶 崔晴晴 徐晨 张家乐 付钦海 李家俊 焦俊杰 鲍婧 周会永男源自男 男 男 男 男 男 男 男 男
男 男