用三点共线的向量结论解决平几中的一类求值问题1
专题：利用三点共线结论解平面向量问题——高三数学二轮专题复习
专题：利用三点共线结论解平面向量知识梳理：三点共线定理 OC →＝ (1－t )OA →＋tOB →的证明： 若OA →＝a ，OB →＝b 是平面内两不共线向量，对于平面内任一向量OC →＝c ，存在一对实数λ，μ使c ＝λa ＋μb .证明A 、B 、C 三点共线的充要条件是λ＋μ＝1.证明：（必要性）若A ，B ，C 三点共线，则存在实数t ，使得AC →＝tAB →， 即OC →－OA →＝t (OB →－OA →)所以OC →＝ (1－t )OA →＋tOB → 令λ＝1－t ，μ＝t ，则有c ＝λa ＋t b ，即λ＋μ＝1.（充分性）若λ＋μ＝1，则c ＝λa ＋(1－λ)b 即c －b ＝λ(a －b ) 即OC →－OB →＝λ(OA →－OB →)即BC →＝λBA →.所以A 、B 、C 三点共线．(思考：当t=21时，会发现A,B,C 是什么情况？)典型例题：例1：（全国高考）设D 为△ABC 所在平面内一点，BC →＝3CD →，则( )A.AD →＝－13AB →＋43AC →B.AD →＝13AB →－43AC →C.AD →＝43AB →＋13AC →D.AD →＝－43AB →－13AC →例2：已知平面内的三点A ，B ，O 不共线，且AP →＝λOA →＋μOB →，则A ，P ，B 三点共线的一个必要不充分条件是( )A ．λ＝μB ．|λ|＝|μ|C ．λ＝－μD ．λ＝1－μ例3：如图所示，在△ABC 中，H 为BC 上异于B ，C 的任一点，M 为AH 的中点，若AM →＝λAB →＋μAC →，则λ＋μ＝________.例4：如图，在△ABC 中，点O 是BC 边的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M,N ，若N nA C A M mA B A==,,则m+n 的值为_______．练习：1、已知等差数列{a n }的前n 项和为S n ，若3OA →＝a 5OB →＋a 9OC →，且A ，B ，C 三点共线，则S 13＝________．2、［2021•江苏卷，10］设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC .若DE →＝λ1AB →＋λ2AC →(λ1，λ2为实数)，则λ1＋λ2的值为________．3、（2021华美）在△ABC 中，N 是AC 边上一点，且AN →＝12NC →，P 是BN 上一点，若AP →＝mAB →＋29AC →，则实数m 的值为4、(2021·郑州质检)如图，在△ABC 中，N 为线段AC 上靠近A 的三等分点，点P 在BN 上且A P →＝⎪⎭⎫ ⎝⎛+112m AB →＋211B C →，则实数m 的值为________.5、（2021华美）A ，B ，C 是圆O 上不同的三点，线段CO 与线段AB 交于点D (点O 与点D 不重合)，若OC →＝λOA →＋μOB →(λ，μ∈R )，则λ＋μ的取值范围是__________.专题：利用三点共线结论解平面向量例1：[解析] 由BC →＝3CD →知，B 、C 、D 三点共线，从四个选项知系数和为1的仅有A ，故选A.例2：解析 A ，P ，B 三点共线，即存在一个实数m ，使得AP →＝mAB →，∵AP →＝λOA →＋μOB →，∴mAB →＝λOA →＋μOB →，即m (OB →－OA →)＝λOA →＋μOB →，∴(m －μ)OB →＝(m ＋λ)OA →，∵A ，B ，O 三点不共线，∴m －μ＝0，m ＋λ＝0，即λ＝－μ＝－m ，∴A ，B ，P 三点共线的充要条件为λ＝－μ，结合各选项知A ，B ，P 三点共线的一个必要不充分条件为|λ|＝|μ|.故选B. 例3：解析 由于B ，H ，C 三点共线，可令AH →＝xAB →＋(1－x )AC →，又M 是AH 的中点， 所以AM →＝12AH →＝12xAB →＋12(1－x )AC →.又AM →＝λAB →＋μAC →，所以λ＋μ＝12x ＋12(1－x )＝12.例4：解析 解法一：AO →＝12(AB →＋AC →)＝m 2AM →＋n 2AN →.∵M ，O ，N 三点共线，∴m 2＋n2＝1.∴m ＋n ＝2.解法二：MN 绕O 旋转，当N 与C 重合时，M 与B 重合，此时m ＝n ＝1，∴m ＋n ＝2.练习：1、[解析] 由3OA →＝a 5OB →＋a 9OC →，得OA →＝a 53OB →＋a 93OC →因为A ，B ，C 三点共线，所以a 53＋a 93＝1，即a 5＋a 9＝3，所以S 13＝13（a 1＋a 13）2＝13（a 5＋a 9）2＝392.所以S 13＝3922、解析 DE →＝DB →＋BE →＝12AB →＋23BC →＝12AB →＋23(AC →－AB →)＝－16AB →＋23AC →，∵DE →＝λ1AB →＋λ2AC →，∴λ1＝－16，λ2＝23，故λ1＋λ2＝12.（提示，过A 作DE 平行线交BC 延长线于点F,利用B,C,F 共线）3、 答案1/34、 解析 设BP →＝λBN →＝λ(AN →－AB →)＝λ⎝⎛⎭⎫13 AC →－AB →＝－λAB →＋λ3 AC →(0≤λ≤1)， ∴A P →＝AB →＋B P →＝(1－λ) AB →＋λ3AC →. 又A P →＝⎝⎛⎭⎫m ＋211AB →＋211 BC →＝⎝⎛⎭⎫m ＋211AB →＋211(AC →－AB →)＝mAB →＋211AC →，∴⎩⎪⎨⎪⎧λ3＝211，m ＝1－λ，解得⎩⎨⎧λ＝611，m ＝511，∴m ＝511.5、【答案】(1，＋∞) [设OC →＝mOD →，则m >1，因为OC →＝λOA →＋μOB →，所以mOD →＝λOA →＋μOB →，即OD →＝λm OA →＋μm OB →， 又知A ，B ，D 三点共线，所以λm ＋μm＝1，即λ＋μ＝m ，所以λ＋μ>1。
向量三点共线定理等于1的几何意义
向量三点共线定理等于1的几何意义向量三点共线定理是高中数学中的一个重要定理，它描述的是三个点在平面上共线的几何条件。
这个定理是在向量的基础上得出的，所以我们首先要了解什么是向量，向量的性质和运算规则，然后再来讨论向量三点共线定理的几何意义。
首先，向量是数学中的一个重要概念，它可以用来表示空间中的一个点到另一个点的位移。
向量通常用箭头表示，箭头的方向表示位移的方向，箭头的长度表示位移的大小。
向量有一些重要的性质，比如零向量的长度为0，且方向无所谓；两个向量相等当且仅当它们的长度相等且方向相同；向量的加法满足交换律和结合律等等。
在向量的基础上，我们可以定义向量的数量积和向量的叉积，这两种积在几何上有着重要的意义。
数量积是一个标量，它可以用来计算向量的夹角和长度，而叉积是一个向量，它可以用来表示一个平行四边形的面积。
通过向量的数量积和叉积，我们可以定义出两个向量的夹角、平行和垂直等几何性质。
接下来，我们来讨论向量三点共线定理的几何意义。
向量三点共线定理的表述是：三个点A、B、C在平面上共线的充分必要条件是存在实数k，使得向量AB=k*向量AC。
这个定理意味着如果三个点在平面上共线，那么它们的位移向量之间存在一定的线性关系。
几何上，这个定理的意义可以通过向量的线性组合来描述。
假设三个点A、B、C在平面上共线，则它们的位移向量可以表示为向量AB和向量AC。
根据向量三点共线定理，存在实数k，使得向量AB=k*向量AC。
这意味着向量AB和向量AC是线性相关的，它们的方向是一致的，只是长度不同。
也就是说，从A到B的位移是从A到C的位移的k倍，这就是三点共线的几何意义。
进一步地，我们可以将向量三点共线定理应用到实际问题中。
比如，如果我们知道一个平面上的三个点共线，可以利用这个定理来求出它们的线性关系，进而解决一些几何问题。
另外，向量三点共线定理还可以用来证明一些三角形的性质和定理，比如中垂线定理、垂径定理等等。
在日常生活中，我们也会经常遇到向量三点共线的情况。
向量三点共线结论
向量三点共线结论
向量三点共线是线性代数中一个重要且基础的概念，其结论是指
在三维空间中，若存在三个点A(x1, y1, z1)、B(x2, y2, z2)、C(x3, y3, z3)，如果向量AB和向量AC共线，则这三个点共线。
这个结论也可以表示为向量AB和向量AC的向量积为零，即(AB)×(AC) = 0。
这个结论是由向量叉积的定义推得的，向量叉积定
义为向量的乘积，垂直于两个向量的平面。
利用向量三点共线结论，我们可以快速求解一些与平面相关的问题。
例如，我们可以利用三点共线结论来判断三角形是否为等腰三角
形或者等边三角形，或者计算平面几何中的面积等问题。
此外，向量三点共线结论还能应用到其他一些数学问题中。
例如，我们可以利用这个结论来解决某些最优化问题，或者优化回归模型、
分类问题等数学问题。
最后，我们需要注意的是，在现实世界中，我们通过测量三个点
的坐标并不总是完全准确的，误差往往是存在的。
因此，在应用向量
三点共线结论时，我们需要注意误差的来源，并进行充分的数据处理
和调整，以保证结论的准确性。
总之，向量三点共线结论是线性代数中一个基础而重要的结论，
具有广泛的应用。
我们可以利用这个结论来解决许多数学和几何问题，是我们学习和应用线性代数的一个重要知识点。
平面向量中的三点共线结论的应用
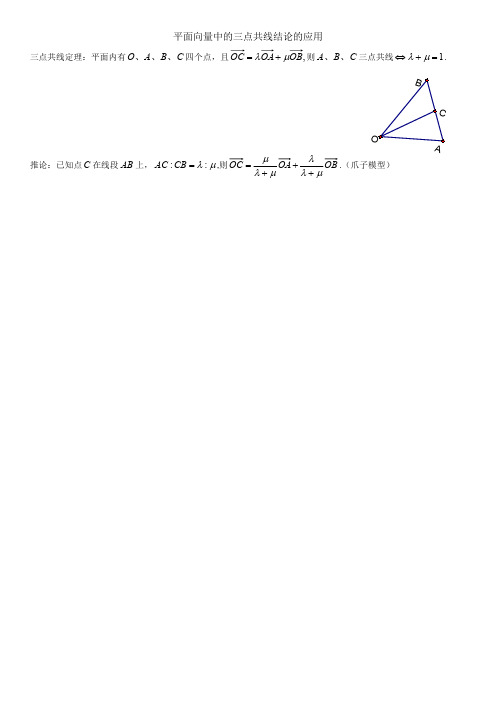
若，3.已知B 为OAC 边AC 上一点，且满足OC y OA x OB +=4，不等式222313x y m m x y +≥-++恒成立时，实数m 的最值范围为___________.巩固练习1.在ABC ∆中，4AB =，O 为三角形的外接圆的圆心，若),(R y x AC y AB x AO ∈+=且21x y +=，则ABC ∆的面积的最大值为_____．2.在P AB ∆中，,60,9,80=∠==APB PB P A 点C 满足PB y P A x PC +=,且,0,0,532≥≥=+y x y x 其中则||PC 的最大值为______，最小值为______.3.已知ABC ∆的外心为O 满足AC y AB x AO +=,若,10,6==AC AB 且,5102=+y x 则=∠BAC cos ______.例5.如图，M 为△ABC 的中线AD 的中点，过点M 的直线分别交线段AB 、AC 于点P 、Q 两点，设AP xAB =，AQ y AC =，记()y f x =，设32()32g x x a x a =++，[0,1]x ∈，若对任意11[,1]3x ∈，总存在2[0,1]x ∈，使得12()()f x g x =成立，则实数a 的取值范围为______.巩固练习2.（2022·辽宁葫芦岛·高三期末）如图，在等腰ABC 中，已知2AB AC ==，120A ∠= ，E ，F 分别是边AB ，AC 上的点，且AE AB λ= ，AF AC μ=，其中λ，R μ∈，且21λμ+=，若线段EF ，BC 的中点分别为M ，N ，则MN的最小值是（）A ．77B ．217C ．2114D ．213．（2023·全国·高三专题练习）直角三角形ABC 中，P 是斜边BC 上一点，且满足2BP PC =，点M 、N 在过点P 的直线上，若AM m AB = ，AN nAC =，()0,0m n >>，则下列结论错误的是（）A ．12m n+为常数B ．m n +的最小值为169C ．2m n +的最小值为3D ．m 、n 的值可以为12m =，2n =巧用杠杆原理处理三角形中的向量问题数值，各线段上得如图所示各点的标数则根据杠杆平衡原理可，已知三角形中的赋值标数法,d,cNC AN b a MB AM ==点数值乘数值等于点数值乘线段上，段数值乘积相等。
用三点共线解决平几中的一类问题
《用三点共线的向量结论解决平几中的一类求值问题》教案说明向量是数与形的高度统一，它集几何图形的直观与代数运算的简捷于一身，在解决平面几何问题时能起到奇特的作用。
在用向量解决平面几何问题时，首先就是要将几何关系转化为向量表示（即选择适当的基底），然后再借助向量运算来解决。
因此，本节课实际就是让学生学会：在三点共线条件下，知道将几何关系转化为向量问题来解决。
本节课的教学目标是按三维目标来确定的。
它包括知识与技能、过程与方法、情感态度与价值观三个方面。
知识与技能目标有4点，它们是相互联系层层递进的关系。
目标1是基础，目标2是内容，目标3是获得技能，目标4才是这节课的根本意图。
我国新一轮课程改革提出：改变课程过于注重知识传授的倾向，强调形成积极的学习态度，使获得知识与形成技能的过程成为学会学习和形成价值观的过程。
这就要求我们的教学过程应更多的考虑学生，要让他们在课堂上参与适应的探索并能在这一过程中感受成功的喜悦。
本内容是学生学习了向量的一些基本概念、向量的加法与减法、向量共线的充要条件、平面向量基本定理和三点共线的向量结论后进行的一节探究式的习题课。
平面向量基本定理这一节的例5学生知道了这样一个结论：A 、B 、C 三点共线的充要条件是：有唯一的实数对λ、μ，使OC OA OB λμ=+，其中λ+μ=1。
并且通过上节课的学习，学生还知道了在三点共线条件下写向量表达式的一种方法：如右图,图1 图2分母m+n 代表线段AB 的份数，即右边两向量终点表示的线段，m 代表线段CB 的份数，即左边向量OC 和右边向量OB 两向量终点表示的线段，n 代表线段CA 的份数，即左边向量OC 和右边向量OA 两向量终点表示的线段。
系数m 、n 与它对应的线段恰好是交叉关系；当分点在线段的外部时，添加一个负号，其位置由系数和为1确定。
在三点共线的条件下学生能较为熟练的写出向量表达式作为基础来进行这节课的教学。
AOm n OC OA OBm nm n=+++m+nnm对λμ的几何意义的探求分四个阶段进行：先由1、2两个特例得猜想：λμ=CBCA；再由检验特例2的系数完善猜想，得猜想2：|λμ|=CBCA；然后指出这一猜想的正确性（不证明）；最后通过课堂的应用1、应用2和课堂练习来巩固知识。
向量三点共线结论证明
向量三点共线结论证明摘要：1.向量共线的定义和性质2.证明向量三点共线的条件3.举例说明向量三点共线的应用4.总结向量三点共线结论的重要性正文：在数学和物理领域，向量是一个重要的基本概念。
向量三点共线是一个基本的向量性质，掌握这个性质对我们理解和解决实际问题有很大帮助。
接下来，我们将详细探讨向量三点共线的结论及其证明，并探讨其在实际问题中的应用。
首先，我们来了解一下向量共线的定义和性质。
向量共线指的是两个或多个向量在平面上或空间中，沿着同一条直线。
换句话说，如果两个向量之间的角度为零或π，那么这两个向量就是共线的。
在向量共线的性质中，最重要的是平行四边形法则，它告诉我们，共线的向量可以相互平移，而平移后的向量仍然共线。
接下来，我们来证明向量三点共线的条件。
设三点A、B、C的坐标分别为(x1, y1)、(x2, y2)、(x3, y3)，对应的向量分别为→AB、→BC、→AC。
根据向量共线的性质，如果→AB与→AC共线，那么→BC与→AC也共线。
我们可以通过计算向量→AB和→AC的叉乘来判断它们是否共线。
如果→AB与→AC的叉乘结果为零向量，那么→AB与→AC共线。
同样地，计算向量→BC和→AC的叉乘，如果结果为零向量，那么→BC与→AC也共线。
通过这种方法，我们可以证明向量三点共线的条件。
在实际问题中，向量三点共线的结论有很多应用。
例如，在几何学中，如果一条直线与两个定点确定，那么这条直线是唯一的。
这是因为通过两个定点可以确定一个平面，而直线在该平面上，因此第三个点必须在该直线上，从而保证了直线的唯一性。
另一个应用是在物理学中的力的合成，当三个力共线时，它们可以合并为一个合力，使得物体受到的合力为零。
总之，向量三点共线结论在数学、物理等领域具有广泛的应用。
通过理解并向量共线的定义和性质，我们可以更好地解决实际问题，并加深对向量这一基本概念的认识。
平面向量三点共线结论
平面向量三点共线结论
平面向量三点共线结论是指在平面上，如果三个不共线的向量都在同一直线上，则这三个向量共线。
该定理可用来证明三个点是否共线，从而得出相应的结论。
首先，我们来回顾一下向量的基本概念，在数学中，向量是一种有方向性的对象。
它表示从一个位置指向另一个位置的直线，它可以用大写字母来表示，例如a、b、c。
向量可以用二维和三维空间来表示，它的方向可以沿着X 轴，Y轴或Z轴方向改变，它的大小也可以改变。
平面向量三点共线结论是指，如果在平面上有三个不共线的向量，即a、b、c，且这三个向量都在同一直线上，则这三个向量共线。
证明：
假设a、b、c是平面上三个不共线的向量，且这三个向量都在同一直线上，则有：
(1) 向量a、b、c在同一平面内。
(2) 向量a、b、c的头部和尾部都在同一直线上。
(3) 向量a、b、c有一定的比例关系，即
a/b=c/d=e/f，其中d、e和f也是向量。
由此可知，如果三个不共线的向量都在同一直线上，则这三个向量共线。
这里给出的证明是在平面空间中的三点共线定理，而同样的定理也适用于空间三点共线定理，即当三个向量分别位于三个不同的点时，如果这三个点都在同一直线上，则这三个向量共线。
该定理的应用非常广泛，可以用来证明三个点是否共线，同时也可用于证明两点之间的向量是否平行，从而得出相应的结论。
三点共线向量式的巧妙运用
三点共线向量式的巧妙运用三点共线向量式是利用向量的几何性质来解决几何问题的一种方法。
它是基于以下事实：如果三点A、B、C在同一直线上，那么向量AB与向量BC是共线的。
这个性质可以用来解决很多几何问题，下面我们将介绍几个巧妙运用三点共线向量式的例子。
例子1：判断四边形的对角线是否相交考虑一个四边形ABCD，我们想判断它的对角线AC和BD是否相交。
我们可以选择一个顶点，比如A点，并用向量表示其他三个顶点相对于A点的位置。
向量AC=C-A向量AD=D-A向量AB=B-A如果AC与AD共线，即向量AC与向量AD的方向相同或相反，那么对角线AC与BD相交；如果AC与AB共线，即向量AC与向量AB的方向相同或相反，那么对角线AC与BD不相交。
例子2：判断线段是否相交考虑两条线段AB和CD，我们想判断它们是否相交。
首先，我们可以选择一个顶点，比如A点，并用向量表示其他三个顶点相对于A点的位置。
向量AB=B-A向量AC=C-A向量AD=D-A如果AB与AC共线且AB与AD共线，即向量AB与向量AC以及向量AB与向量AD的方向相同或相反，那么线段AB和线段CD相交；如果AB与AC共线但AB与AD不共线，即向量AB与向量AC的方向相同或相反但向量AB与向量AD的方向不同，那么线段AB和线段CD不相交。
例子3：判断四边形是否能构成平行四边形考虑四边形ABCD，我们想判断它是否能构成平行四边形。
我们可以选择一个顶点，比如A点，并用向量表示其他三个顶点相对于A点的位置。
向量AB=B-A向量AC=C-A向量AD=D-A如果AB与AD共线且AC与AB共线，即向量AB与向量AD以及向量AC与向量AB的方向相同或相反，那么四边形ABCD能构成平行四边形；如果AB与AD共线但AC与AB不共线，即向量AB与向量AD的方向相同或相反但向量AC与向量AB的方向不同，那么四边形ABCD不能构成平行四边形。
以上是三点共线向量式的几个巧妙运用，它们可以帮助我们在解决几何问题时更加便捷地判断线段是否相交、对角线是否相交以及判断四边形是否能构成平行四边形。
平面向量中“三点共线定理”妙用.doc
平面向量中“三点共线定理”妙用对平面内任意的两个向量a,b（b^O\a//b的充要条件是：存在唯一的实数2,使心疝由该定理可以得到平面内三点共线定理：三点共线定理：在平面中A、B、P三点共线的充要条件是：对于该平面内任意一点的0,存在唯一的一对实数x,y使得：OP = xOA + yOB且x+y = l。
特别地有：当点P在线段AB上时，x>0,y>0当点P在线段AB之外时，巧<0笔者在经过多年高三复习教学中发现，运用平面向量中三点共线定理与它的两个推广形式解决高考题，模拟题往往会使会问题的解决过程变得十分简单！本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用，供同行交流。
例1 （06年江西高考题理科第1题）已知等差数列｛窟的前n项和为Sn,若OB =a x OA+a^OC,且A、B、C三点共线，（设直线不过点0）,则鼻二（）A. 100B. 101C. 200D. 201解：由平面三点共线的向量式定理可知：a’+吐。
二1, ••”缈二沁字血= 100,故选A。
点评：本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起，是一道经典的高考题。
—►—・---- ► 1 4例2已知P是AABC的边BC上的任一点，且:满足AP = xAB+yAQx.y w R，则一+ —xy 的最小值是—解：•.•点P落在“BC的边BC上.•.B, P,C三点共线••• AP = xAB + yAC :.x+y = \且x>0, y>01 4 J 4X 1 1 4x z x t y 4x . c y 4.v・•.一 + — = (- + —)xl = (- + —)x(x+y)=l + — + — + 4 = 5 + — + —x y x y x y x y x yV x>0, y>0 -.2：>0,—>0 由基本不等式可知：2 + 11>2 gx—=4,取等号时X y X y Vx yy 4 V* "»■»] 2 —=—.•・ y2 = 4x2 /. y = ±2x •/ x>0,y>0 :. y = 2x x+y = \ :.x = -,y = —,符合x y・ 3 ” 3所以丄+ 土的最小值为9 兀y点评：本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3 （湖北省2011届高三八校第一次联考理科）如图2,在AABC中，丽=1疋，点P是BC上的一点，^AP = mAB + — AC,则实数m的3 11值为（）A 9 n 5 厂3 n 2图2 A. — B. — C. — D.—11 11 11 11解：••• BP N三点共线,乂••• AP = mAB + — AC = mAB + —x 4AN = mAB + —AN11 11 118 3= 1 Hl = -j-y ,故选C例4 (07年江西高考题理科)如图3,在AABC中，点0是BC的中点，过点0的直线分别交直线AB、AC于不同的两点M、N,若丽=mAM , AC = 的值为解：•••因为0是BC的中点，故连接A0,如图4,由向量加法的平行四边形法则可知：皿弓丽+0 ••• AB=mAM , AC = nANAO = — (mAM + nAN):,AO=^AM+!L AN2 2乂三点共线,由平面内三点共线定理可得:分严—2例5 （广东省2010届高三六校第三次联）如图5所示：点G是△OAB的重心，P、Q分别是边04、OB上的动点，且P、G、Q三点共线.设OP = xOA , OQ = yOB，证明：丄+丄是泄值：x yn证明：•••因为G是△OAB的重心,_ 2 1 - _ 1 _ _OG = -x-(OA + OB) = -(OA + OB)3 2 3OP = xOA•9OA = -OP - OQ = yOB x：.OB = -OQy^OG =L(OA+OB)=L(L OP+丄宛)乂・.・p,G,0三点共线，.•£+存1 .-4+7=3•••士为定值3例6 （汕头市东山中学2013届高三第二次模拟考试）如图6所示, 在平行四边形ABCD中，AE = ^-AB9 AF = -AD,CE与BF相交于G3 4点，i^AB = a, AD = b9则走=人2- 1 72- 3厂「3- 1 rA. —“ + ―彷B. -a + — b C・—a + —Z?7 7 7 7 7 7分析：本题是以平面儿何为背景，为载体, 想到点F、G、B以及E, G,C三点在一条直线上，4 -* 2 厂D. —u + — b7 7求向量的问题，可用平面内三点共线定理求解。
向量中三点共线常用结论
向量中三点共线常用结论在向量的研究中，三点共线是一个重要的概念。
当三个点在一条直线上时，我们称它们为共线点。
在向量中，我们可以利用一些常用结论来判断三个向量是否共线。
本文将介绍向量中三点共线的常用结论，并对其进行详细解析。
1. 三点共线的定义在二维平面上，设有三个点A(x1, y1)，B(x2, y2)和C(x3, y3)，如果这三个点满足以下关系式：(x2 - x1)(y3 - y1) = (x3 - x1)(y2 - y1)则称A、B、C三个点共线。
2. 向量表示法判断在向量表示法中，设有两个向量AB和AC，如果这两个向量满足以下关系式：AB = k * AC其中k为一个实数，则可以判断A、B、C三个点共线。
3. 向量坐标法判断在向量坐标法中，设有两个向量AB和AC，若这两个向量满足以下关系式：AB = r * i + s * j AC = p * i + q * j其中i和j分别为x轴和y轴的单位向量，则可以通过计算行列式来判断A、B、C 三个点共线。
行列式的计算公式为：r s |p q |若行列式值为0，则A、B、C三个点共线。
4. 向量夹角法判断在向量夹角法中，设有两个向量AB和AC，若这两个向量的夹角θ满足以下关系式：cosθ = AB·AC / (|AB| * |AC|)其中·表示向量的数量积，|AB|和|AC|分别表示向量AB和AC的模长，则可以通过计算夹角的余弦值来判断A、B、C三个点共线。
若cosθ等于1或-1，则A、B、C 三个点共线。
5. 向量比例法判断在向量比例法中，设有两个向量AB和AC，若这两个向量满足以下关系式：AB/AC = k其中k为一个实数，则可以通过计算向量的比例来判断A、B、C三个点共线。
6. 解析几何法判断在解析几何法中，设有两条直线L1和L2，若这两条直线满足以下关系式：L1: Ax + By + C1 = 0 L2: Ax + By + C2 = 0其中A、B、C1和C2为常数，则可以通过计算直线方程的系数来判断A、B、C三个点共线。
三点共线问题的一个重要结论及应用
三点共线问题的一个重要结论及应用一．命题及证明命题 已知非零向量OA 、OP 、OB 满足OP mOA nOB =+ ，若1m n +=(m n R ∈，，0)mn ≠且，则点A 、P 、B 共线，且P 分AB 所成的比为mn =λ． 证明：∵OP mOA nOB =+ ， 1=+n m ，0mn ≠，∴ 1n OP OA OB m m =+ ， ∴ m n n OP OA OB m m +=+ ， ∴ ()n OP OA OB OP m -=- ， 即n AP PB m = ． ∴ 点A 、P 、B 共线，且P 分AB 所成的比为mn =λ． 下面思考其逆命题，即逆命题 若点A 、P 、B 共线，且P 分AB 所成的比为λ，则有且只有一对非零实数m n ，，使得OP mOA nOB =+ ，且1=+n m （O 为平面上不同于A 、P 、B 的一点）．证明：∵ 点A 、P 、B 共线，设 01AP PB λλλ=≠≠- （且）， ∴ ()OP OA OB OP λ-=- ， ∴ ()1OP OA OB λλ+=+ ，∴ 111OP OA OB λλλ=+++ ． 令111m n λλλ==++，，则有OP mOA nOB =+ ，且1=+n m ，m n =λ． 于是，综上可得结论 三点A 、P 、B 共线的充要条件是存在实数m n 、满足1=+n m ，且使得OP mOA nOB =+ ．（O 为平面上不同于A 、P 、B 的一点）． 特别地，当12m n ==时， 1()2OP OA OB =+ ，点P 是线段AB 的中点；当0m =或0n =时，点P 与点B 或A 重合．二．结论的应用例１．（1）已知点Ａ、Ｂ、Ｃ三点共线，Ｏ在直线ＡＢ外，设, , OA a OB b OC c === ，且存在实数m 使30ma b c -+= ，则点Ａ分BC 所成的比为（ ）Ａ．3 Ｂ．－3 Ｃ．31 Ｄ．31- 解：∵ 30ma b c -+= ，∴ 133m OB OA OC =+ ．∵ 点Ａ、Ｂ、Ｃ三点共线， ∴1133m +=，2m =． ∴ 3122OA OB OC =- ，∴ 点Ａ分BC 所成的比为131():223λ=-=-．故选Ｄ． （2）已知如图1，, , OA a OB b OC c === ，点Ｃ为线段ＡＢ的距Ａ较近的一个三等分点，点Ｄ为线段ＢＣ的距Ｃ较近的一个三等分点，则OD = （ ） Ａ．1(45)9a b + Ｂ．1(97)16a b + Ｃ．1(2)3a b + Ｄ．1(3)4a b + 解：由题意知：2133OC OA OB =+ ，2133OD OC OB =+ ． ∴ 2211421451()(45)3333993999OD OA OB OB a b b a b a b =++=++=+=+ ．故选Ａ． 点评：根据结论不难得出，只要给出线段AB 的任一分点P ，都可以利用向量a 、b 表示OP ，此方法回避了通过向量的加减运算来转化的繁琐过程，显得十分简捷．例2．平面直角坐标系中，O 为坐标原点，已知(3, 1)A 、(1, 3)B -，若点Ｃ满足OC OA OB αβ=+ ，其中1=+∈βαβα，且、R ，则点Ｃ的轨迹方程为（ ）． Ａ．01123=-+y x Ｂ．5)2()1(22=-+-y xＣ．02=-y x Ｄ．052=-+y x (2002年全国新课程高考卷) 解：因1αβ+=，由结论可得点A 、Ｃ、B 共线，所以点C 在直线AB 上运动，故点C 的轨迹为直线AB ，由(3, 1)A 、(1, 3)B -得轨迹方程为052=-+y x ．故选Ｄ．点评：根据本文结论的特殊情况及轨迹的完备性，可知点C 的轨迹是直线AB ． 例3．如图2，平行四边形ABCD 中，14BE BA =，15BF BD =，求证：E 、F 、C 三点共线．分析：根据题目条件，只需寻找BE 、BF 、BC 的关系即可． 证明：∵ BA BC BD += ，14BE BA =，15BF BD =． ∴ 54BF BC BE =+ ， ∴ 4155BF BE BC =+ ， 所以点E 、F 、C 三点共线． 例4．如图3，过抛物线24x y =的对称轴上任一点()()0,0P m m >作直线与抛物线交于A ，A B C D E F 2图OB DC A 1图B 两点，点Q 是点P 关于原点的对称点，设点P 分有向线段AB所成的比为λ． 求证： ()QP QA QB λ⊥- ． （2004年湖南卷）证明：因为点Ｐ分分有向线段AB所成的比为λ，则必然存在实数αβ、， 使 QP QA QB αβ=+ ，且1αβ+=．∵点Ａ、Ｂ在抛物线24x y =上，点Q 是点P 关于原点的对称点，∴ 设221212(,), (,), (0,)44x x A x B x Q m -， ∴ 221212,, ,44x x QA x m QB x m ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭． 图3 则221212(0, 2)(,)(,)44x x QP m x m x m αβ==+++ 221212(, ())44x x x x m αβαβαβ=++++)44,(222121m x x x x +++=βαβα． 所以 1222120, . 44x x x x m αβαβ+=⎧⎪⎨+=-⎪⎩①② 显然有()()()QP QA QB QA QB QA QB βλαβα⋅-=+⋅- 22221()QA QB αβα=- ． 故只需证明22220QA QB αβ-= 即可．而2222QA QB αβ- =2222222121244x x x m x m αβ⎡⎤⎡⎤⎛⎫⎛⎫++-++⎢⎥⎢⎥ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦()22222222121244x x x x m m αβααβ⎡⎤⎛⎫⎛⎫=-++-+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦ ()()222212121212()()04444x x x x x x x x m m αβαβαβαβαβαβ⎛⎫⎛⎫=+-++++⋅-+-= ⎪ ⎪⎝⎭⎝⎭∴ ()QP QA QB λ⊥- ．点评：本解法运用了结论的坐标形式，充分利用向量的知识解决解析几何问题，打破了利用直线与圆锥曲线位置关系进行转化的传统模式，体现了向量与解析的内在联系．另外，设而不求、整体代换等基本方法使得解题思路更加清晰、条理化．。
三点共线向量表示形式的应用举例
三点共线向量表示形式的应用举例三点共线的充要条件：已知o、a、b是不共线的三点，且存在实数x，v使得op=xoa+yob，则a、b、p三点共线的充要条件是x+y=1。
这是三点共线的一个充要条件，主要以向量形式表述，用其来解决一些与三点共线有关的问题，显得非常简便和巧妙。
举例如下：一、解决与三点共线有关的求值问题如图中△abc，an=13ac，p是bn上的一点，若ap=mab+211ac，则m的值为.解：∵an=13ac，∴ap=mab+211ac=mab+611an又b、p、n三点共线，∵m+611=1∴m=511本题直接利用三点共线的向量式中x+y=1来解决.2.△abc中，o点是bc的中点，过点o的直线分别交直线ab、ac 于不同的两点m、n。
若ab=mam，ac=nan，则m+n=.解：∵ao=12ab+12ac又ab=mam，ac=nan∴ao=m2am+n2an又o、m、n三点共线，∴m2+n2=1即m+n=23.变式：△abc中，点o是bc的中点，k为ao上一点，且ao=2ak.过点k的直线分别交直线ab、ac于不同的两点m、n。
若ab=mam，ac=nan，则m+n=.解：∵ao=12ab+12acab=mam，ac=nan∴ao=m2am+n2an，又ao=2ak∴2ak=m2am+n2an∴ak=m4am+n4an又k、m、n三点共线，∴m4+n4=1即m+n=4以上两题实质都是以ao为桥梁，利用三点共线的充要条件整体求值，体现了三点共线的向量式x+y=1中在求值问题（尤其是整体求值）中的重要作用.二、在向量的表示中的应用4.△abc中，点e在ab边上，f在边ac上，且ae=2eb，af=13fc，bf与ce交于点m，设am=xae+yaf，则x+y=.解法一：∵e、m、c三点共线，∴设am=mae+（1-m）ac又ac=4af∴am=mae+4（1-m）af①∵b、m、f三点共线∴设am=nab+（1-n）af又ab=32ae∴am=32nae=（1-n）af②又ae，af又不共线，∴32n=m1-n=4（1-m）解得m=910n=35，∴am=910ae+410af∴x+y=1310此种解法主要通过两组三点共线的向量式设定系数，用同一组基底来表示向量am，再结合平面向量基本定理求解系数。
三点共线向量表示形式的应用举例
三点共线向量表示形式的应用举例作者：祁荣香来源：《读写算》2012年第79期三点共线的充要条件：已知O、A、B是不共线的三点，且存在实数x，v使得OP=xOA+yOB，则A、B、P三点共线的充要条件是x+y=1。
这是三点共线的一个充要条件，主要以向量形式表述，用其来解决一些与三点共线有关的问题，显得非常简便和巧妙。
举例如下：一、解决与三点共线有关的求值问题如图中△ABC，AN=13AC，P是BN上的一点，若AP=mAB+211AC，则m的值为.解：∵AN=13AC，∴AP=mAB+211AC=mAB+611AN又B、P、N三点共线，∵m+611=1∴m=511本题直接利用三点共线的向量式中x+y=1来解决.2.△ABC中，O点是BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N。
若AB=mAM，AC=nAN，则m+n=.解：∵AO=12AB+12AC又AB=mAM，AC=nAN∴AO=m2AM+n2AN又O、M、N三点共线，∴m2+N2=1即m+n=23.变式：△ABC中，点O是BC的中点，K为AO上一点，且AO=2AK.过点K的直线分别交直线AB、AC于不同的两点M、N。
若AB=mAM，AC=nAN，则m+n=.解：∵AO=12AB+12ACAB=mAM，AC=nAN∴AO=m2AM+n2AN，又AO=2AK∴2AK=m2AM+n2AN∴AK=m4AM+n4AN又K、M、N三点共线，∴m4+n4=1即m+n=4以上两题实质都是以AO为桥梁，利用三点共线的充要条件整体求值，体现了三点共线的向量式x+y=1中在求值问题（尤其是整体求值）中的重要作用.二、在向量的表示中的应用4.△ABC中，点E在AB边上，F在边AC上，且AE=2EB，AF=13FC，BF与CE交于点M，设AM=xAE+yAF，则x+y=.解法一：∵E、M、C三点共线，∴设AM=mAE+（1-m）AC又AC=4AF∴AM=mAE+4（1-m）AF①∵B、M、F三点共线∴设AM=nAB+（1-n）AF又AB=32AE∴AM=32nAE=（1-n）AF②又AE，AF又不共线，∴32n=m1-n=4（1-m）解得m=910n=35，∴AM=910AE+410AF∴x+y=1310此种解法主要通过两组三点共线的向量式设定系数，用同一组基底来表示向量AM，再结合平面向量基本定理求解系数。
高中数学解题技巧：平面向量三点共线定理，关键点λμ=1
高中数学解题技巧：平面向量三点共线定理，关键点λμ=1
综述：先对平面向量之三点共线定理进行证明；此定理简称
λ+μ=1；若三点共线，则分解某向量，引进唯一参数λ，再用分解定理的唯一性求λ，此即待定系数法；亦可用平行向量求参数；
这点不难证明，只需证明由这三点A，B，C所组成的向量中有两个向量共线，而本结论可作定理直接使用。
平面向量题型要充分认识平面向量具有几何形式和代数形式的“双重身份”，重视向量的工具作用和应用意识，强化知识的联系，善于构造向量解决问题。
平面向量中“三点共线定理”妙用
平面向量中“三点共线定理”妙用对平面内任意的两个向量 a,b （b 0）,a//b 的充要条件是：存在唯一的实数 ，使a buuuv uv uuuv的 O ，存在唯一的一对实数 x,y 使得：OP xOA yOB 且 x y特别地有： 当点 P 在线段 AB 上时， x 0,y 0当点 P 在线段 AB 之外时， xy 0笔者在经过多年高三复习教学中发现，运用平面向量中三点 共线定理与它的两个推广形式解决高考题，模拟题往往会使会问题的解决过程变得 十分简单！本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点 共线定理与它的两个推广形式的妙用 , 供同行交流。
例 1（06 年江西高考题理科第 7 题）已知等差数列 {a n } 的前 n项和为 S n ，若 uuur uuur uuurOB a 1OA a 200OC ，且 A 、B 、C 三点共线，（设直线不过点 O ），则 S 200=（ ）A ． 100B ．101C ．200D ．201解：由平面三点共线的向量式定理可知： a 1+a 200=1, ∴ S200 200（a1 a200）100, 故选 A 。
2点评： 本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起，是一道经 典的高考题。
例2 已知P 是 ABC 的边BC 上的任一点，且满足 AP xAB yAC,x.yR，则1 4xy的最小值是解：Q 点 P 落在VABC 的边 BC 上 B ， uuur uuur xAB yAC P,C 三点共线uuur Q AP且点共线定在平面中 A 、B 、P 三点共线的充要条件是：对于该平面内任意由该定理可以得到平面内三点共线定理：1。
4x5yx 4x yy4y4x2y4x x y x y 4 ，取等号时y y)1xy 4x 2 2 1 2y2 4x2 y 2xQ x 0,y 0 y 2xQ x y 1 x ,y ，符合x y 3 314所以 1 4的最小值为9 xy点评：本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起，较综合考查了学生基本功.例 3 （湖北省2011 届高三八校第一次联考理科）如图 2 ，在△ ABCuuur AN1uuurNC，点P是BC上的一点，uuur 若APuuur 2 uuurmAB 2 AC ，则实数m的11值为（）9532 A B. C. D.11111111uuur 解：Q B, P, N三点共线，又QuuurmAB2 uuurAC11uuurmAB2 uuur4AN11uuurmAB8 u A u N ur118m 11 m 3，故选 C11例4（07 年江西高考题理科）如图3，在△ ABC中，点O是BC的中点，过点O的直线分别交直线AB、AC 于不同的两点M、的值为．四边形法则可知：uuurAO1 uuur (AB2uuurAC)uuur uuuur uuur uuurQ AB＝mAM ，AC nANuuur 1 uuuur uuurAO (mAM nAN ) 2uuur m uuuur n uuurAO AM AN22又Q M,O,N 三点共线，由平面内三点共线定理可得：m n22 例5（广东省2010 届高三六校第三次联）别是边OA 、OB上的动点，且P、G、Q 三点共线．11设OP xOA ，OQ yOB ，证明：是定值；xy 图2解：Q因为O是BC的中点，故连接AO，N，若AB ＝m AM ，AC ＝n AN ，则m＋n如图5所示：点G是△ OAB的重心，P、Q 分中，例 6（汕头市东山中学 2013 届高三第二次模拟考试）如图 6 所示 , uuur 1uuur uuur 在平行四边形 ABCD 中， AE 1 AB , AF 3uuur r uuur r uuur 点，记 AB a ，AD b ，则 AG由平面内三点共线定理可得： 存在唯一的一对实数 x 使得uuur AG uuur xAE uuur(1 x)AC uuur, Q AE1uuur AB 3 1r a , 3uuur r AC a uuur 1rr r 2x rrAG xa(1 x)(a b) (1 )a (1 x)b332r 1r 2r 3r3r 1r4r 2r A ． ab B. a b C. a b D.a b 7 7 7 7 7 77 7分析：本题是以平面几何为背景，为载体，求向量的问题，所以我们很容易联 想到点 F 、G 、B 以及 E,G,C 三点在一条直线上，可用平面内三点共线定理求解。
利用三点共线巧解一类向量系数问题
利用三点共线巧解一类向量系数问题
高贺清
【期刊名称】《中学生数理化（学研版）》
【年(卷),期】2012(000)011
【摘要】定理1：若不相同的三点A、B、C共线于直线l，
【总页数】1页(P20-20)
【作者】高贺清
【作者单位】广东省深圳市龙华中学
【正文语种】中文
【中图分类】G633.63
【相关文献】
1.利用三点共线巧解等差数列问题 [J], 徐天光
2.利用三点共线巧解数列问题 [J], 杨文光
3.利用三点共线巧解数列问题 [J], 杨文光
4.怎样利用向量证明三点共线与四点共面问题 [J], 任荣民
5.基于学生思维能力提升的数学化归与转化——以一类向量三点共线问题为例 [J], 张传鹏
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用三点共线的向量结论解决平几中的一类求值问题教案
注：为了简单起见，平面几何简称为平几；师指教师，生指学生。
《用三点共线的向量结论解决平几中的一类求值问题》教案说明
向量是数与形的高度统一，它集几何图形的直观与代数运算的简捷于一身，在解决平面几何问题时能起到奇特的作用。
在用向量解决平面几何问题时，首先就是要将几何关系转化为向量表示（即选择适当的基底），然后再借助向量运算来解决。
因此，本节课实际就是让学生学会：在三点共线条件下，知道将几何关系转化为向量问题来解决。
本节课的教学目标是按三维目标来确定的。
它包括知识与技能、过程与方法、情感态度与价值观三个方面。
知识与技能目标有4点，它们是相互联系层层递进的关系。
目标1是基础，目标2是内容，目标3是获得技能，目标4才是这节课的根本意图。
我国新一轮课程改革提出：改变课程过于注重知识传授的倾向，强调形成积极的学习态度，使获得知识与形成技能的过程成为学会学习和形成价值观的过程。
这就要求我们的教学过程应更多的考虑学生，要让他们在课堂上参与适应的探索并能在这一过程中感受成功的喜悦。
本内容是学生学习了向量的一些基本概念、向量的加法与减法、向量共线的充要条件、平面向量基本定理和三点共线的向量结论后进行的一节探究式的习题课。
平面向量基本定理这一节的例5学生知道了这样一个结论：A 、B 、C 三点共线的充要条件是：有唯一的实数对λ、μ，使OC OA OB λμ=+u u r u u r u u r
，其中λ+μ=1。
并且通过上节课的学习，学生还知道了在三点共线条件下写向量表达式的一种方法：如右图,
图1 图2
分母m+n 代表线段AB 的份数，即右边两向量终点表示的线段，m 代表线段CB 的份数，即左边向量OC u u r 和右边向量OB u u r 两向量终点表示的线段，n 代表线段CA 的份数，即左边向量OC u u r
和右边向量OA u u r
两向量终点表示的线段。
系数m 、n 与它对应的线段恰好是交叉关系；当分点在线段的外部时，添加一个负号，其位置由系数和为1确定。
在三点共线的条件下学生能较为熟练的写出向量表达式作为基础来进行这节课的教学。
A
O
m n OC OA OB
m n
m n
=
+
++u u r
u u r
u u r
m+n
n
m
对λ
μ
的几何意义的探求分四个阶段进行：先由1、2两个特例得猜想：
λ
μ
=CB
CA
；再由检
验特例2的系数完善猜想，得猜想2：|λ
μ
|=CB
CA
；然后指出这一猜想的正确性（不证明）；最
后通过课堂的应用1、应用2和课堂练习来巩固知识。
本节课最关键的是教师引导学生得猜想1和猜想2，这也是本节课最难的。
因为这一过程思维跳跃性很强，要反复结合向量表达式和
图形，稍有不慎，学生的思维链一断，这节课就变得毫无意义了！结论|λ
μ
|=CB
CA
在课堂上没
有证明，从这一意义上说失去了数学的理性思维，少了很多的“数学味”，但对高一的学生来说却是很必要的（要知道，正是因为有时我们过分追求理性思维才让学生产生“数学就是繁和难的演绎与推理”这种想法，让他们畏惧数学！）。
有时这种“重过程轻实质”的方法，能减轻学生的学习负担，不会因技巧性强、冗长的证明过程冲淡本节课的主题。
本节
课的最终目的是要让学生感受到一点向量应用的广泛性，并希望能逐步增强学生应用向量解
决数学问题的能力。
若着眼点仅是这一节课，探索λ
μ
的几何意义的过程对高一学生而言有
些难，甚至可以说没必要。
但若将这节课放到整个高中阶段这根知识大链上来看又是怎样的呢仅从以下两个例子就可见向量在中学数学知识中的地位了：
1、向量与三角知识的融合。
在推导正弦定理、余弦定理均用到了向量知识。
但是在教学过程中这一点还没有引起我们足够的重视，甚至有些教师对教材中用向量方法证明正弦和余弦定理弃之不用，课堂教学中仅仅是为了得到一个结论，证明方法仍是沿用以前的老教材中的方法。
应该说这是一种教学资源的浪费！正弦和余弦定理究竟要解决的是什么问题初中解决角与边有哪些方法高中与角和边有关的又有哪些知识通过这种引导，让学生将所学的向量的数量积与三角形知识联系起来，这样既能让学生掌握这种证明方法，又能让学生树立应用向量的意识；
2、向量在立体几何中的应用。
这几年来高考对立体几何知识大题的考查都是能建立直角坐标系，大题的得分率比以前大大提高。
但这也给部分学生（甚至于我们的教师）留下了这样一些印象：只要会建立直角坐标系就行了；立体几何对逻辑推理和空间想像能力的要求降低了；向量在立体几何中的应用关键是能建立直角坐标系等等。
比如高二数学教材下B第51页例2，题如下：
已知在一个60o
的二面角的棱上有两个点A 、B ，AC 、BD 分别是在这个二面角的两个面内，且垂直于AB 的线段，又知AB=4cm, AC=6cm, BD=8cm,求CD 的长。
对于高三的同学来说也很少想到用向量方法来解决的。
在不建立直角坐标系的条件下用向量来证明线线平行、线面平行，求线面角、二面角的平面角这方面的意识学生就更弱了！ 培养学生应用向量的意识不是一朝一夕就能实现的，而要把这种意识转化为一种能力那就更是需要一个长期的、不断训练的过程了。
我从最不理想的角度考虑过这节课的效果，若有学生在上课时由于注意力不集中导致后面的内容听不懂了，若他看到用向量方法能这样简捷的解决平面几何问题时，他只要能这样想：哦，原来还可以这样呀！我就觉得是我这节课的收获了！从这个方面来看，这节课是及时的也是需要的。
在三点共线的条件下让学生写向量表达式都能准确的写出来，但是在探求
λ
μ
的几何意义时还是应特别的注意.因为这需要在向量表达式和图形中反复观察，这也是学生最容易出问题的地方。
此时应该放手让学生自己先探索，教师再去引导，这样的效果会更好的，若探索这个环节处理得不好，后面的内容就会变成老师的独角戏了！另外，学生容易出错的是在例1
中求出了λ的值，是代入(1)BG BA BM λλ=+-u u r
u u r
u u u r
还是代入12
BG BA BC λλ-=+u u r
u u r u u r
求比值。
解题
到此时可再回顾三点共线的向量结论的形式特点，通过课堂上3个题目的和课外1题（课外作业的第一题是要求每个学生必做的，2作为选做）共4个题的训练是能正确区分这一点的。
根据新课改的教育教学理念，在课堂上探究知识时让学生经历：操作实践→观察→猜想、归纳，这是一种以学生为主，还课堂于学生的教学活动。
根据本节课的内容特点，授课时是按照这样一种模式进行的：创设情景→数学活动→猜想、归纳→巩固、应用和拓展。
在数学活动的过程中让学生知道了这样一种解决问题的方法：特例→观察→猜想→验证、→完善猜想→归纳→证明。
通过合作交流的方式探求知识，增强了他们应用向量解决数学问题的意识。
当然，这节课是第一节向量应用课，其中
λ
μ
的几何意义是我的新发现（或许早就有资料介绍了，只是我孤陋寡闻吧！）有些语句描述学生以前没有听到过，学生课堂回答问题不够准确，我也没敢放手的让学生去探求，这是我最大的遗憾！。