配电网潮流计算 ppt课件
合集下载
第11章 电力系统的潮流计算WJYPPT课件

Step5:利用Step4计算得到的节点电压Vb,Vc ,Vd ,重复Step3、Step4,直到精7 度满足要求为止。
电力系统的潮流计算—开式网络的电压和功率分布计算
复杂开式网络潮流的计算机算法 Step2:支路顺序编号(消去叶节点法,分层
方法,等) Step3:回代计算:按照支路编号顺序,计算 A
度满足要求为止。
6
电力系统的潮流计算—开式网络的电压和功率分布计算
开式网络的电压和功率分布计算步骤 Step1:制定一相等值电路; Step2:计算运算负荷Sb,Sc ,Sd ; Step3:回代计算:设定各节点电压初值(VN),从末端d节点开始,计算各支
路功率损耗和首末端功率,直到A点; Step4:前推计算:从A节点开始,计算各各支路电压降落和节点电压;
CH11 电力系统的潮流计算
开式网络的电压和功率分布计算
配电网潮流算法:前推回代法
简单闭式网络的功率分布计算
环网功率分布:循环电势的概念
环网潮流控制
复杂电力系统潮流计算
潮流计算的数学模型
-拉夫逊法潮流计算
P-Q分解法潮流计算
1
电力系统的潮流计算—开式网络的电压和功率分布计算
Review:网络元件的电压降落与功率损耗计算
回代
S
P22 Q22 V22
R
jX
P1 jQ1 P2 jQ2 S
Step3:已知V1, S1
P1
jQ1
,
计算V1
,
V1
,V2(k
1)
,
(k 2
1)
前推
step4:如果
V (k 1) 2
V2(k )
,或k kmax ,计算结束,否则
配电网潮流计算PPT课件

对于源节点的馈出支路电流,有
I1
SˆLi
Vˆ0
Sˆcos sk
0
源节点
1
6
1
6
2
7
2
7
户
节
8
3 点8
3
9
9 4
4
末端节点
5
5 末端节点
图 辐射表的例
2021/5/7
配电网潮流计算
7
第7页/共15页
2配80电21网/5潮/7 流计算
2.5 功率与电压模的关系
0
源节点
设支路i是i节点的馈入支路,k节点的馈出支路,
2021/5/7
配电网潮流计算
12
第12页/共15页
四、 电压模算法
电压模算法也是一种逐条件支路计算法。由哥伦比亚人Renato Cespedes G提出。
4.1 电压模算法计算过程:
1) 顺流计算(顺着功率流向计算) 目的 — 确定节点电压模
2) 逆流计算(逆着功率流向计算) 目的— 确定支路功率(馈入与馈出)
4
第4页/共15页
支节 路点 10 21 32 43 54 61 76 87 98
节支 点路 1 2,6 23 34 45 5— 67 78 89 9—
0
源节点
1
6
1
6
2
7
2
7
户
节
8
3 点8
3
9
9 4
4
末端节点
5
5 末端节点
图 辐射表的例
2021/5/7
配电网潮流计算
5
第5页/共15页
2.4 功率、电流及电压的计算 0 源节点
配电网络电气计算.pptx

(三)谐波分布计算的特点
配电网是输电网和用户之间的纽带,它实现 直接向用户供电的功能,而用户是谐波的滋生 地,因此配电网是谐波的首要受害者和传播者, 它本身的结构和参数以及并联电容器装置的参 数,决定了它对谐波的传播特性,即是放大了 还是抑制了谐波。谐波源应视为电流源,并按 阻抗分流原理确定它在配电网中的分布。
在配电网有功电源的分布一定的情况下, 配电网的有功网损是各节点无功补偿容量 的函数,因此,配电网的有功网损,即无 功补偿的目标函数可以写成
P P (QC1, QC 2 , , QCj , , QCm )
第22页/共38页
经过无功最优补偿以后,无功功率应该满足下面 的平衡方程,即等式约束条件
P QCj
OP , ( j
1,2,, m)
或
第27页/共38页
(二)遗传算法
遗传算法是一种基于自然群体遗传演化机制的高 效探索算法。它摒弃了传统的搜索方式,模拟自 然界生物进化过程,采用人工进化的方式对目标 空间进行随机化搜索。它将问题域中的可能解看 作是群体的一个个体或染色体,并将每一个体编 码成符号串形式,模拟达尔文的遗传选择和自然 淘汰的生物进化过程,对群体反复进行基于遗传 学的操作(选择、交叉和变异),根据预定的目标适 应度函数对每个个体进行评价,依据“适者生存, 优胜劣汰”的进化规则,不断得到更优的群体, 同时以全局并行搜索方式来搜索优化群体中的最 优个体,求得满足要求的最优解。
一、配电网潮流计算的特点
网设施
配电系统多采用闭式网络结构, 具有开式运行的特点,因此,网络 往往呈现放射状。在6~10kV的配 电网中,往往只有一个电源点,因 此线路上的功率通常具有单向流动 性等等。
不能简单套用高压输电网潮流计 第1页/共38页 算常用的高斯-赛德尔法、牛顿法拉夫逊法或PQ分解法等方法。
第3讲-配电网潮流计算20141011

Nij
i j ij
ij
ij
Kij
VV i
(G j
cos ij
B sin
ij
ij
, 当ij)i j时 ij)
Lij ViVj(Gij sinij Bij cosij)
Hii Vi 2Bii Qi
Nii V 2iG ii
,i 当Pi j时
Kii V 2iG ii i P
Lii Vi 2Bii Qi
3.2 牛顿-拉夫逊潮流计算方法
3.2.2 牛顿-拉夫逊潮流算法
❖对上式作移项处理可以得到:
n
) 0 P( P1,2P, ,V 1) i (G ics os i B issini
j1 n
( sin
cos ) 0 ( 1,2, , 1) i
j1
j ij
is
i
ij
ij
is
i
ij P
j ij
i
包含一个有功功率不平衡量方程式和一个无功功率不平衡量方程式。
U iU jBij cos ij U iU jGij cos ij
❖一阶线性化方程组可写成如下形式:
T
如果对节点和支路进行适当编号,可以将An-1表示为 一个上三角形矩阵,对角线元素为1,所有非零线对角元 素为-1 1。
An-1为节点-支路关联矩阵,由网络拓扑决定。
3.2 牛顿-拉夫逊潮流计算方法
3.2.3 牛顿-拉夫逊潮流算法的改进
对于配电系统,改进的牛顿法具有与将要介绍的前推回推算法相 近的收敛性能。近似处理使辐射状配电系统的雅可比矩阵可写为 UDUT形式,其中U为仅依赖于系统拓扑的恒定上三角矩阵,D为块对 角矩阵,该形式的雅可比矩阵不需要显式形成,从而避免了与雅可比 矩阵和LU分解因子相关的可能的病态条件。
电力系统潮计算PPT课件

⑴在 B '中尽量去掉那些对有功功率及电压相角影响较小的因素,如
略去变压器非标准电压比和输电线路充电电容的影响;在 B 中'' 尽
量去掉那些对无功功率及电压幅值影响较小的因素,如略去输电 线路电阻的影响。
⑵为了减少在迭代过程中无功功率及节点电压幅值对有功迭代的影 响,将(2-44)右端U各元素均置为标幺值1.0.
• 潮流计算公式作如下修改:
P i a 1 b 1 u u ii0 c 1 u u ii0 2 P i0 (s) u ij iu jG ijc o ij B s ijs iijn
Q i a 1 b 1 u u ii0 c 1 u u ii0 2 Q i (0 s) u ij iu jG ijs iijn B ijc o ij s
(4)和节点导纳矩阵具有相同稀疏结构的分块雅可比矩阵 在位置上对称,但由于数值上不等,说以,雅可比矩阵式 一个不对称矩阵。
2024/6/4
11
四、牛顿潮流算法的性能分析
• 优点:
⑴收敛速度快。
如果初值选择较好,算法将具有平方收敛性,一般迭代4~5次便 可以收敛到一个非常精确地解,而且其迭代次数与计算的网络规模 基本无关。
方程组的解。而牛顿法出于线性近似,略去了高阶项,因此用每次迭
代所求得的修正量对上一次的估计值加以改进后,仅是向真值接近了
一步而已。
2024/6/4
24
为了推导算法的方便,下面将上述潮流方程写成更普遍的齐次二次方 程的形式。
首先作以下定义:
一个具有n个变量的齐次代数方程式的普遍形式为:
(2-65)
2024/6/4
2024/6/4
3
第三节 牛顿潮流算法
一、牛顿法的基本原理
配电网潮流计算PPT课件
点有多个馈出支路)
负荷功率 -- 任意节点流出到用户中
的功率
15.05.2020
.
4
2.3 配电网的描述 —— (辐射表)
辐射表反映配电网支路与节点的关系
在配电网中,每一个负荷节点只有
源节点(根节点)
0
对应于变电站母
一个馈入支路,其馈入支路编号与
1
6
7
负荷节点编号相一致。馈入支路与
1
6
负荷节点是一对一的。
或已计算得出,计算各支路的功率
对末端节点的馈入电流有
i
I j I Lj
IL j — 负荷电流
ILj
Sˆ Lj Vˆ j
SOjVk Iˆj
Ik
SˆLk Vˆk
Sˆoj
(j末端节点) k
k j
j
这样的计算一直进行到源节点的馈出支路,
末端节点
从而全部节点的各馈出复功率都求解出来。
15.05.2020
.
11
V kV i cosk (i)(PIiRiQIiXi)V i2
V kV i sink(i)(PIiXiQIiRi)
上面两式作平方和,有
V i4 2 ( P I iR i Q I iX i) V k 2 V i2 ( P I i2 Q I i2 )R i 2 ( X i 2 ) 0
5
5 末端节点
图 辐射表的例
Ik
SO k Vˆi
7
由基尔霍夫电流定律,对于节点i,有
I i I Li I ok
Iok 节点i馈出支路的电流
IL i 负荷电流
IL i
Sˆ L i Vˆi
对于源节点的馈出支路电流,有
I1 SˆLi
《电力系统潮流计算》PPT课件

< •
•
Ma |Uxi(K1)UiK|
其中K为迭代次数.
整理ppt
17
三.说明
(1)平衡节点不参加迭代.
(2)PV节点的处理:在迭代中需增加一个判断
如碰到PV节点,每一次迭代出来的电压始终保持幅值为常
量,相位为变量 •
• n *•
UiU i s i(K1),Q iIm Ui( yiU j j)
整理ppt
ቤተ መጻሕፍቲ ባይዱ
19
(1)节点间相位差很大的重负荷系统 (2)包含有负电抗支路(如某些三绕组变压器或线路串联电容
等)的系统. (3)具有较长的辐射性线路的系统. (4)长线路与短线路接在同一节点上,而且长短线路的比值又
很大的系统. 此外,平衡节点的不同选择也会影响到收敛性能.一般取
•
Ui 10o
整理ppt
f
x1
f 1(Χ )
f Χ
f x2
f
(梯 度 ), F (Χ)
f
2
(
Χ
)
f
fn( Χ )
xn
整理ppt
12
f 1 f 1
f
T 1
x1
x2
F
f
T 2
f 2 x1
f 2 x2
fnT
fn
fn
x1 x2
f 1
xn
f 2 xn
fi xj
j1
高斯-赛德尓迭代的算法的计算性能和特点
优点:原理简单,程序设计容易占用内存少.每次计算量也很 少,一般电力系统每个节点平均和2~4个节点相连,相应导 纳矩阵具有对称性和高度稀疏性.
整理ppt
18
缺点:收敛速度很慢.根据迭代公式,各节点在数学上是 松散耦合的,每次迭代,每个节电电压值只能影响与之 相关的几个节点,所以收敛速度很慢.且,算法所需迭代 次数和节点数目有密切关系,将随其数目的增加而急剧 增加.此算法另外一个重要限制是对于如下的病态条件 的系统,往往会收敛困难.
简单电力网络潮流分析与计算讲义课件(ppt 68页)

Sy1j1 2B1 U 2jQy1
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
3) 电力线路的功率平衡计算
线路首 端功率
阻抗支路 首端功率
末端负 荷功率
设已知线路末端运行电压 和负荷功率,求线路首端 功率。
(1)末端导纳支路功率损耗
Sy2j1 2B2 U 2jQy2
查表得τ=3100h/年
P/kW
WZ0cS1.U 9om 02222P0sam 10x2R20aU 2xN211R20331103010031072005000 0
2000
4000
8760 t/h
459.22k65W h 9
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
K为经验系数,一般取0.1-0.4,年负荷率低时取较小值,反之 取较大值
③由上式求电力线路全年电能损耗为 W Z87 6 P m0G ax
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
2. 变压器中的电能损耗
铜损部分(电阻损耗):与输电线路变动损耗的计算相同 铁损部分(电导损耗):变压器空载损耗P0与变压器运行小时数 的乘积(按全年投入的实际小时数计算) 变压器运行小时数等于一年8760h减去因检修而退出运行的小 时数。则变压器中1年内的电能损耗为
Tma2xPbTmPabbxP PccTmacx
Tma3xTmacx
电力系统分析
最大负荷利用小时数Tmax与最大负荷损耗时间的关系
Tmax(h)
(h) cos0.8 cos0.85 cos0.9 cos0.95 cos1
用最大负荷损耗时间法计算电能损耗,由于τ值的确定是近似 的,一般用于电网的规划设计阶段,对于已经运行的电网的电 能损耗计算,常采用等值功率法。本书不作介绍。 电力系统分析
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
3) 电力线路的功率平衡计算
线路首 端功率
阻抗支路 首端功率
末端负 荷功率
设已知线路末端运行电压 和负荷功率,求线路首端 功率。
(1)末端导纳支路功率损耗
Sy2j1 2B2 U 2jQy2
查表得τ=3100h/年
P/kW
WZ0cS1.U 9om 02222P0sam 10x2R20aU 2xN211R20331103010031072005000 0
2000
4000
8760 t/h
459.22k65W h 9
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
K为经验系数,一般取0.1-0.4,年负荷率低时取较小值,反之 取较大值
③由上式求电力线路全年电能损耗为 W Z87 6 P m0G ax
电力系统分析
3.1 电力线路和变压器的功率损耗和电压降落
2. 变压器中的电能损耗
铜损部分(电阻损耗):与输电线路变动损耗的计算相同 铁损部分(电导损耗):变压器空载损耗P0与变压器运行小时数 的乘积(按全年投入的实际小时数计算) 变压器运行小时数等于一年8760h减去因检修而退出运行的小 时数。则变压器中1年内的电能损耗为
Tma2xPbTmPabbxP PccTmacx
Tma3xTmacx
电力系统分析
最大负荷利用小时数Tmax与最大负荷损耗时间的关系
Tmax(h)
(h) cos0.8 cos0.85 cos0.9 cos0.95 cos1
用最大负荷损耗时间法计算电能损耗,由于τ值的确定是近似 的,一般用于电网的规划设计阶段,对于已经运行的电网的电 能损耗计算,常采用等值功率法。本书不作介绍。 电力系统分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
末端节点
15.09.2020
配电网潮流计算
11
第二步计算 1) 顺流计算 计算各节点电压值
已知
Sok Ik
计算各支路电流 Ii ILi Ik
计算各节点电压 V i V kZiIi
k为 i 的上一个节点编号
2) 逆流计算 确定支路功率
0
源节点
2.1 网络描述
节点类型: 源节点(0) 用户节点 末端节点
支路功率:单向流动。
源节点(根节点)
0
对应于变电站母
1
6
7
1
6
2
2
7
户
节 3点
3
户 节 点
4
4
5 5
末端节点
末端节点
图 辐射型配电网的例
末端节点
15.09.2020
配电网潮流计算
3
2.2 名词解释:
源节点(根节点)
0
对应于变电站母
1
6
7
馈入功率--任意节点的流入功率
9
9 4
4
末端节点
5
5 末端节点
图 辐射表的例
Ik
S O k Vˆi
7
由基尔霍夫电流定律,对于节点i,有
Ii ILi Iok
Iok 节点i馈出支路的电流
I L i 负荷电流
I L i
Sˆ L i Vˆi
对于源节点的馈出支路电流,有
I1
SˆLi
Sˆc Vˆ0
ossk
0
源节点
1
6
1
6
2
7
2
7
户
节
8
3 点8
配电网潮流计算
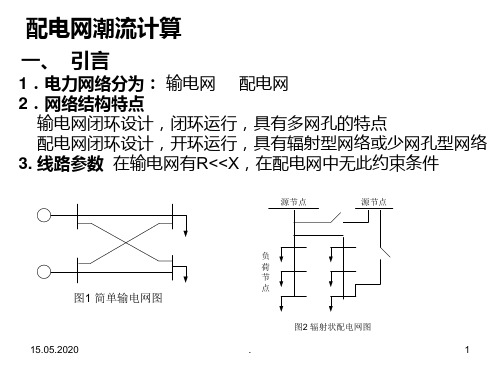
一、 引言
1.电力网络分为: 输电网 配电网 2.网络结构特点
输电网闭环设计,闭环运行,具有多网孔的特点 配电网闭环设计,开环运行,具有辐射型网络或少网孔型网络 3. 线路参数 在输电网有R<<X,在配电网中无此约束条件
源节点
源节点
负 荷 节 点
图1 简单输电网图
15.09.2020
图2 辐射状配电网图6Βιβλιοθήκη 负荷节点是一对一的。2
2
7
辐射表反映了馈出支路与负荷节点的关系。
户 节
3点
支路—负荷节点型辐射表
3 4
户 节 点
具有一对一关系,
4
用户节点—支路型辐射表
5 5
末端节点
末端节
可能具有一对几的关系。
图 辐射型配电网的例
末端节点
常采用支路—用户节点型辐射表。
15.09.2020
配电网潮流计算
5
支节 路点 10 21 32 43 54 61 76 87 98
V kV i cosk (i)(PIiRiQIiXi)V i2
V kV i sink(i)(PIiXiQIiRi)
上面两式作平方和,有
V i4 2 ( P I iR i Q I iX i) V k 2 V i2 ( P I i2 Q I i2 )R i 2 ( X i 2 ) 0
1
6
2
馈入电流 –任意节点流入电流
2
7
馈入支路--馈入功率与馈入电流相
户 节
应的支路(一个节点只能有一个馈
3点
3
户 节 点
入支路);
4
馈出功率--任意节点流出到接续支 路的功率; 馈出电流 -- 流出到接续支路的电流
4
5 5
末端节点
末端节点
图 辐射型配电网的例
末端节点
馈出支路 -- 相应的支路;(一个节
配电网潮流计算
1
潮流计算方法:网络结构和线路参数的不同,使输电网和 配电网的潮流计算方法不同
输电网 --- Newton法,P-Q分解法,区域网络潮流分 裂算法
配电网 --- BBB算法,电压模算法,DisFlow算法,对 少网孔配电网可利用多口网络理论计算
15.09.2020
配电网潮流计算
2
二、辐射型配电网潮流模型
2) 逆流计算 确定支路功率
逆流过程始自各末端节点。假设各节点电压已设定,
或已计算得出,计算各支路的功率
对末端节点的馈入电流有
i
Ij ILj
IL j — 负荷电流
I Lj
Sˆ Lj Vˆ j
SOjVk Iˆj
Ik
SˆLk Sˆoj Vˆk
(j末端节点) k
k j
j
这样的计算一直进行到源节点的馈出支路, 从而全部节点的各馈出复功率都求解出来。
S I i 表示节点i的馈入复功率
S L i 表示节点i的负荷功率
SIi Soi Scosis
S cos s i 表示第i条支路的线损
设支路k是i节点的一条馈出支路,那么
V i
SOkVi Iˆk Ik 分别为节点i的电压和支路k的电流
15.09.2020
配电网潮流计算
1
6
1
6
2
7
2
7
户
节
8
3 点8
3
1) 顺流计算(顺着功率流向计算) 目的 — 确定节点电压
2
7
户
节
8
3 点8
3
9
9 4
4
末端节点
2) 逆流计算(逆着功率流向计算) 目的— 确定支路功率(馈入与馈出)
5
5 末端节点
图 辐射表的例
15.09.2020
配电网潮流计算
10
BBB算法计算过程
第一步计算 1) 顺流计算
给出各节点电压初值 Vi(1) Vi(1)0
15.09.2020
节支 点路 1 2,6 23 34 45 5— 67 78 89 9—
配电网潮流计算
0
源节点
1
6
1
6
2
7
2
7
户
节
8
3 点8
3
9
9 4
4
末端节点
5
5 末端节点
图 辐射表的例
6
2.4 功率、电流及电压的计算 0 源节点
对于任意的节点i,显然有
SokSIi SLi
S ok 表示节点i的馈出复功率
2
7
2
7
户
节
8
3 点8
3
9
9 4
4
末端节点
5
Zi RijXi SIiPIijQ Ii
5
图 辐射表的例
V k V i c k o i ) j s s k i i ) ( n V i 2 ( P I i R ( i Q I i X i ) j ( P I i 末X 端i 节 点 Q I i R i )
点有多个馈出支路)
负荷功率 -- 任意节点流出到用户中 的功率
15.09.2020
配电网潮流计算
4
2.3 配电网的描述 —— (辐射表)
辐射表反映配电网支路与节点的关系
在配电网中,每一个负荷节点只有
源节点(根节点)
0
对应于变电站母
一个馈入支路,其馈入支路编号与
1
6
7
负荷节点编号相一致。馈入支路与
1
15.09.2020
配电网潮流计算
9
三、 BBB算法 辐射型配电网潮流算法
3.1 方法描述
0
源节点
BBB算法意为逐条支路计算法(Branch By Branch Computational Method)由 印度人S.Rajagopalan在1978年提出
1 1
2
6 6
7
3.2 BBB算法计算过程:
3
9
9 4
4
末端节点
5
5 末端节点
图 辐射表的例
15.09.2020
配电网潮流计算
8
2.5 功率与电压模的关系
0
源节点
1
6
设支路i是i节点的馈入支路,k节点的馈出支路, 1 6
I i
Sˆ I i Vˆi
V i V kZiIi Z i — 支路i的阻抗
Vk
Vi
Zi
SˆI i Vˆi
V V (cojssin )
