第五章-低速翼型的气动特性PPT课件
合集下载
低速翼型的气动特性和方程讲解
低速翼型的气动特性和 方程讲解
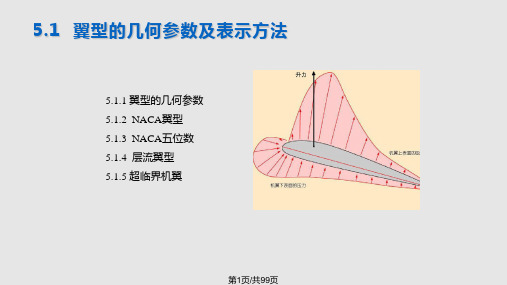
5.1 翼型的几何参数及表示方法
5.1.1 翼型的几何参数 5.1.2 NACA翼型 5.1.3 NACA五位数 5.1.4 层流翼型 5.1.5 超临界机翼
5.1.1 翼型的几何参数
翼的横剖面形状，又称为翼剖面。在空气动力学中，翼型通 常理解为二维机翼，即剖面形状不变的无限翼展机翼。
在上世纪三十年代初期，美国国家航空咨询委员会 （ National Advisory Committee for Aeronautics，NACA， National Aeronautics and Space Administration， NASA ） 对低速翼型进行了系统的实验研究。
将当时的几种优秀翼型的厚度折算成相同厚度时，厚度分布 规律几乎完全一样。在当时认为是最佳的翼型厚度分布作为 NACA翼型族的厚度分布。厚度分布函数为：
莱特兄弟所使用的翼 型与利林塔尔的非常 相似，薄而且弯度很 大。这可能是因为早 期的翼型试验都在极 低的雷诺数下进行， 薄翼型的表现要比厚 翼型好。
随后的十多年里，在反复试验的基础上研制出了大量翼型， 如RAF-6， Gottingen 387，Clark Y。这些翼型成为NACA 翼型家族的鼻祖。
例: NACA 2 3 0 1 2
20 3
C
L设
2
C L设
2
3 20
0.3
2 x f 30 % x f 15 %
中弧线 0：简单型 1：有拐点
t 12%
CL设：来流与前缘中弧线平行时的理论升力系数
1939年，发展了NACA1系列层流翼型族。其后又相继发展 了NACA2系列，3系列直到6系列，7系列的层流翼型族。
(12p)2pxx2
5.1 翼型的几何参数及表示方法
5.1.1 翼型的几何参数 5.1.2 NACA翼型 5.1.3 NACA五位数 5.1.4 层流翼型 5.1.5 超临界机翼
5.1.1 翼型的几何参数
翼的横剖面形状，又称为翼剖面。在空气动力学中，翼型通 常理解为二维机翼，即剖面形状不变的无限翼展机翼。
在上世纪三十年代初期，美国国家航空咨询委员会 （ National Advisory Committee for Aeronautics，NACA， National Aeronautics and Space Administration， NASA ） 对低速翼型进行了系统的实验研究。
将当时的几种优秀翼型的厚度折算成相同厚度时，厚度分布 规律几乎完全一样。在当时认为是最佳的翼型厚度分布作为 NACA翼型族的厚度分布。厚度分布函数为：
莱特兄弟所使用的翼 型与利林塔尔的非常 相似，薄而且弯度很 大。这可能是因为早 期的翼型试验都在极 低的雷诺数下进行， 薄翼型的表现要比厚 翼型好。
随后的十多年里，在反复试验的基础上研制出了大量翼型， 如RAF-6， Gottingen 387，Clark Y。这些翼型成为NACA 翼型家族的鼻祖。
例: NACA 2 3 0 1 2
20 3
C
L设
2
C L设
2
3 20
0.3
2 x f 30 % x f 15 %
中弧线 0：简单型 1：有拐点
t 12%
CL设：来流与前缘中弧线平行时的理论升力系数
1939年，发展了NACA1系列层流翼型族。其后又相继发展 了NACA2系列，3系列直到6系列，7系列的层流翼型族。
(12p)2pxx2
dxja
第五章
低速翼型的气动特性 翼面压力分布
§5.2 低速翼型的流动特点及起动涡
ห้องสมุดไป่ตู้
(a)小迎角无分离 小迎角无分离
(b)厚翼型后缘分离 厚翼型后缘分离
(c )薄翼型前缘分离 薄翼型前缘分离
小迎角无分离时， 小迎角无分离时，粘性作用对翼面压力分布没有本质改变
空气动力学
第五章 低速翼型的气动特性
退出
第五章
低速翼型的气动特性
§5.1 翼型的几何参数
几何弦长、前缘半径、后缘角； 几何弦长、前缘半径、后缘角； 翼面坐标、弯度分布、 翼面坐标、弯度分布、厚度分布
第五章
低速翼型的气动特性
§5.2 低速翼型的流动特点及起动涡
翼型绕流图画
(c) 150迎角绕流
(d) 200迎角绕流
第五章+机翼低速气动特性(4)
第5章 机翼低速气动特性(4) 机翼低速气动特性(4)
7 升力面理论
z
ξ
A
dξ
o
B
x
MdζζC NhomakorabeaD
z
x
升力线理论的应用范围
升力线理论的应用有一定的范围: 升力线理论的应用有一定的范围 (1)迎角不能太大（α<10°)。升力线理论没有考虑空气 迎角不能太大（ 迎角不能太大 °。 的粘性，而在大迎角下的流动出现了明显的分离。 的粘性，而在大迎角下的流动出现了明显的分离。 (2)展弦比不能太小（λ≥5）。 展弦比不能太小（λ≥5）。 展弦比不能太小 (3)后掠角不能太大（χ≤20°）。 后掠角不能太大（ ≤20 后掠角不能太大 ≤20°
∂y ′ V∞ − v =0 ∂x 面
确定γ(ξ，ζ)的积分方程
可取翼面边界条件近似在y=0平面 即XOZ平面 平面(即 平面) 可取翼面边界条件近似在 平面 平面 上满足， 上满足，即根据泰勒级数表示式有
∂v (v)面 = (v) y=0 + ⋅ y +L ∂y y=0
y
V∞
o
x
z
升力面气动模型
求解大后掠角或中小展弦比机翼的迎角—弯度问题虽然 求解大后掠角或中小展弦比机翼的迎角 弯度问题虽然 仍可用П形马蹄涡作为基本解来与直匀流叠加， 仍可用П形马蹄涡作为基本解来与直匀流叠加，但应抛弃 使用一条附着涡线来代替机翼附着涡系的假设， 使用一条附着涡线来代替机翼附着涡系的假设，而是将机 翼改用附着涡面来代替， 翼改用附着涡面来代替，此时涡密度是 γ (ξ,ζ ) 。这就是升 力面模型。 力面模型。 升力面模型： 直匀流+附着涡面 附着涡面+自由涡面 升力面模型： 直匀流 附着涡面 自由涡面
7 升力面理论
z
ξ
A
dξ
o
B
x
MdζζC NhomakorabeaD
z
x
升力线理论的应用范围
升力线理论的应用有一定的范围: 升力线理论的应用有一定的范围 (1)迎角不能太大（α<10°)。升力线理论没有考虑空气 迎角不能太大（ 迎角不能太大 °。 的粘性，而在大迎角下的流动出现了明显的分离。 的粘性，而在大迎角下的流动出现了明显的分离。 (2)展弦比不能太小（λ≥5）。 展弦比不能太小（λ≥5）。 展弦比不能太小 (3)后掠角不能太大（χ≤20°）。 后掠角不能太大（ ≤20 后掠角不能太大 ≤20°
∂y ′ V∞ − v =0 ∂x 面
确定γ(ξ，ζ)的积分方程
可取翼面边界条件近似在y=0平面 即XOZ平面 平面(即 平面) 可取翼面边界条件近似在 平面 平面 上满足， 上满足，即根据泰勒级数表示式有
∂v (v)面 = (v) y=0 + ⋅ y +L ∂y y=0
y
V∞
o
x
z
升力面气动模型
求解大后掠角或中小展弦比机翼的迎角—弯度问题虽然 求解大后掠角或中小展弦比机翼的迎角 弯度问题虽然 仍可用П形马蹄涡作为基本解来与直匀流叠加， 仍可用П形马蹄涡作为基本解来与直匀流叠加，但应抛弃 使用一条附着涡线来代替机翼附着涡系的假设， 使用一条附着涡线来代替机翼附着涡系的假设，而是将机 翼改用附着涡面来代替， 翼改用附着涡面来代替，此时涡密度是 γ (ξ,ζ ) 。这就是升 力面模型。 力面模型。 升力面模型： 直匀流+附着涡面 附着涡面+自由涡面 升力面模型： 直匀流 附着涡面 自由涡面
低速翼型的气动特性PPT课件
第23页/共99页
（2）对于有弯度的翼型升力系数曲线是不通过原点的，
通常把升力系数为零的迎角定义为零升迎角0，而过后缘 点与几何弦线成0的直线称为零升力线。对有弯度翼型0 是一个小负数，一般弯度越大， 0的绝对值越大。
第24页/共99页
（3）阻力 在二维情况下，主要是粘性引起的摩擦与压差阻 力。在小迎角时，翼型的阻力主要是摩擦阻力，阻力系数随 迎角变化不大；在迎角较大时，出现了压差阻力的增量，分 离区扩及整个上翼面，阻力系数大增。 但应指出的是无论摩 擦阻力还是压差阻力都与粘性有关。
后缘分离的发展是
比较缓慢的，流谱
CL
的变化是连续的，
失速区的升力曲线
也变化缓慢，失速
特性好。
第38页/共99页
(2)前缘分离（前缘短泡分离） 中等厚度的翼型（厚度6%-9%），前缘半径较小。 气流绕前缘时负压很大，从而产生很大的逆压梯度，即使在 不大迎角下，前缘附近发生层流边界层分离，此后边界层转 捩成湍流，从外流中获取能量，然后再附到翼面上，由于翼 型具有中等厚度，再附点相对靠前而形成分离短气泡。这种 短气泡的存在对主流没有显著影响，压强分布与无气泡时基 本一样。
第16页/共99页
1967年美国NASA兰利研究中心的Whitcomb主要为了提高亚 声速运输机阻力发散Ma数而提出了超临界翼型的概念。
层流翼型
超临界翼型
第17页/共99页
5.2 翼型的气动参数
1、翼型的迎角与空气动力
在翼型平面上，来流V∞与翼弦线之间的夹角定义为翼型的几何迎角，简称迎 角。对弦线而言，来流上偏为正，下偏为负。
t
yt
(0.29690 0.2
x 0.12600 x 0.35160 x 2 0.28430 x 3 0.10150 x 4 )
89第五章机翼低速气动特性(2)PPT课件
e vi
0
Ve V
V
Δα i
19
下洗角
由于下洗速度远小于来流速度，故可得
i(z)tg1vV i( z)vV i( z)41 V
l 2
d dd
l 2
z
e vi
0
Ve V
V
Δα i
20
升力，诱导阻力
在求作用在机翼微段上的升力之前，我们先引
入“剖面流动”的假设，假设有限翼展的机翼
各剖面所受的气动力与以有效速度Ve流过形状
z
l/ 2
e
vi
Ve
V
V
Δα i
Δα i
z
dv i
d d d x
d
22
升力，诱导阻力
dR的方向垂直于有效速度Ve，它在垂直和平行 V∞方向上的分量分别为升力dL和阻力dDi
d Ldc Ro si(z)d RV (z)dz diD dsRi n i(z)dL i(z)
dX
e
vi
Ve
V
V
dY dR
Δα i
Δα i
23
升力，诱导阻力
沿整个翼展积分，得到整个机翼的升力和阻力为
l
L V
2 l
Γ (z)dz
2
l
Di
V
2 l
Γ (z) i(z)dz
2
dX
e
vi
Ve
V
V
dY dR
Δα i
Δα i
24
升力，诱导阻力
Di这个阻力在理想二维翼上是不存在的，它是由 于有限翼展机翼后面存在自由涡而产生的，或者 说，是因下洗角的出现使剖面有效迎角减小而在 来流方向形成的阻力，故称为诱导阻力。
第五章机翼低速气动特性(3)PPT课件
动图画。在不考虑粘性时，展向分速 V t 是
个常量，而法向分速 V n 不断地改变，所以
流线就会左右偏斜，其形状呈“S”形， 如 右图所示。
后掠翼的绕流图画
后掠翼的绕流图画
这是因为气流从远前方流向机翼前缘时，其 法向分速 V n 受到阻滞而越来越慢，致使气流的合 速越来越向左偏斜。
后掠翼的绕流图画
右图给出了后掠角对剖面升力
系数 CL z 沿展向分布的影响
的例子。
后掠翼的气动特性
后掠翼的升力特性，可用升力面理论来计算。
后掠翼的诱导阻力系数仍可按下式计算：
CDi
CL2 (1)
6 小展弦比机翼的低速气动特性
小展弦比机翼的低速气动特性
通常把<3的机翼称为小展弦比机翼。由 于超声速飞行时小展弦比机翼具有较低的 阻力，所以这种机翼常用于战术导弹和超 声速飞机。
大展弦比直机翼的失速特性
所以，对于椭圆形的机翼，
随着α的增大，整个展向各翼
剖面同时出现分离，同时达
到CLmax∞(翼型的最大升力系
数)， 同时发生失速，失速
i
特性良好，如右图所示。
大展弦比直机翼的失速特性
矩形机翼（＝1）的诱
导下洗速度从翼根向翼尖增
大，翼根翼剖面的有效迎角
将比翼尖大，剖面升力系数
大迎角下的CLmax也小，但 翼根区先分离不会引起副翼
特性的恶化，并可给驾驶员
i
一个快要失速的警告，一般
还是可以接受的。
大展弦比直机翼的失速特性
梯形机翼由于中小迎角下 的升阻特性接近椭圆翼，结构 重量也较轻，使用甚为广泛。 但是，分离首先发生在翼尖附 近，使翼尖先失速，所以就失 i 速特性来说，上述三种机翼中， 梯形直机翼最差。
个常量，而法向分速 V n 不断地改变，所以
流线就会左右偏斜，其形状呈“S”形， 如 右图所示。
后掠翼的绕流图画
后掠翼的绕流图画
这是因为气流从远前方流向机翼前缘时，其 法向分速 V n 受到阻滞而越来越慢，致使气流的合 速越来越向左偏斜。
后掠翼的绕流图画
右图给出了后掠角对剖面升力
系数 CL z 沿展向分布的影响
的例子。
后掠翼的气动特性
后掠翼的升力特性，可用升力面理论来计算。
后掠翼的诱导阻力系数仍可按下式计算：
CDi
CL2 (1)
6 小展弦比机翼的低速气动特性
小展弦比机翼的低速气动特性
通常把<3的机翼称为小展弦比机翼。由 于超声速飞行时小展弦比机翼具有较低的 阻力，所以这种机翼常用于战术导弹和超 声速飞机。
大展弦比直机翼的失速特性
所以，对于椭圆形的机翼，
随着α的增大，整个展向各翼
剖面同时出现分离，同时达
到CLmax∞(翼型的最大升力系
数)， 同时发生失速，失速
i
特性良好，如右图所示。
大展弦比直机翼的失速特性
矩形机翼（＝1）的诱
导下洗速度从翼根向翼尖增
大，翼根翼剖面的有效迎角
将比翼尖大，剖面升力系数
大迎角下的CLmax也小，但 翼根区先分离不会引起副翼
特性的恶化，并可给驾驶员
i
一个快要失速的警告，一般
还是可以接受的。
大展弦比直机翼的失速特性
梯形机翼由于中小迎角下 的升阻特性接近椭圆翼，结构 重量也较轻，使用甚为广泛。 但是，分离首先发生在翼尖附 近，使翼尖先失速，所以就失 i 速特性来说，上述三种机翼中， 梯形直机翼最差。
机翼的几何外形和气动力和气动力矩PPT课件
1. 机翼翼型的几何参数 厚度 中弧线
前缘
后缘
弯度
ቤተ መጻሕፍቲ ባይዱ弦线
后缘角
弦长 连接翼型前缘(翼型最弦长前c面的点)和后缘(翼型最后面 的点)的直线段称为翼弦（也称为弦线），其长度称为弦长， 用c表示。
相对厚度 翼型的厚度是垂直于翼弦的翼型上下表面之间的 直线段长度。翼型最大厚度tmax与弦长c之比，称为翼型的 相对厚度t/c或，并常用百分数表示，即
2. 下翼面出现超音速区，且后移较上翼 面快，下翼面产生较大附加吸力，CL减 小；当激波增强到一定程度，阻力系数急剧
增大,升力系数迅速减小,这种现象称为激波 失速
3. 下翼面扩大到后缘，而上翼面超音速 区还能后缘，上下翼面的附加压力差增 大，CL增加。
临界M数， 机翼上表面 达到音速
②坐标表示法
从右图可以看出，机翼升力的产 生主要是靠机翼上表面吸力的作用， 尤其是上表面的前段，而不是主要 靠下表面正压的作用。
2.4不同迎角对应的压力分布
压力中心 随迎角增大 会向前移动
2.5翼型的跨音速升力特性
I. 升力系数随飞行Ｍ数的变化
1. 考虑空气压缩性，上表面密度下降更 多，产生附加吸力,升力系数CL增加， 且由于出现超音速区，压力更小，附加 吸力更大；
1.3 翼型的几何参数及其发展
通常飞机设计要求，机翼和尾翼的尽可能升力大、阻力 小。
对于不同的飞行速度，机翼的翼型形状是不同的。如 对于低亚声速飞机，为了提高升力系数，翼型形状为圆头 尖尾形；而对于高亚声速飞机，为了提高阻力发散Ma数， 采用超临界翼型，其特点是前缘丰满、上翼面平坦、后缘 向下凹；对于超声速飞机，为了减小激波阻力，采用尖头 、尖尾形翼型。
1.3 翼型的几何参数及其发展
机翼的几何外形和气动力和气动力矩(精品资料)PPT
1.3 翼型的几何参数及其开展
对翼型的研究最早可追溯到19世纪后期 ，那时的人们已经知道带有一定安装角的平 板能够产生升力，有人研究了鸟类的飞行之 后提出，弯曲的更接近于鸟翼的形状能够产 鸟翼具有弯度和大展弦比的特征 生更大的升力和效率。
平板翼型效率较低，失速迎角很小
将头部弄弯以后的平板翼型， 失速迎角有所增加
1.3 翼型的几何参数及其开展
1884年，H.F.菲利普使用早期的风洞测试了一系列翼型， 后来他为这些翼型申请了专利。
早期的风洞
1.3 翼型的几何参数及其开展
与此同时，德国人奥托·利林塔尔设计并测试了许多曲 线翼的滑翔机，他仔细测量了鸟翼的外形，认为试飞成功的 关键是机翼的曲率或者说是弯度，他还试验了不同的翼尖半 径和厚度分布。
t t/ctmax10% 0 c
1.翼型的几何参数及其开展
1、弦长
前后缘点的连线称为翼型的几何弦。但对某些下外表 大局部为直线的翼型，也将此直线定义为几何弦。翼型前、 后缘点之间的距离，称为翼型的弦长，用c表示，或者前、 后缘在弦线上投影之间的距离。
1.1 翼型的几何参数及其开展
2、翼型外表的无量纲坐标
1.5 低速翼型的低速气动特性概述
当迎角大过一定的值之后，就开始弯曲，再大一些，就到达
了它的最大值，此值记为最大升力系数，这是翼型用增大迎
角的方法所能获得的最大升力系数，相对应的迎角称为临界
迎角
。过此再增大迎角，升力系数反而开始下降，这一
cr
现象称为翼型的失速。这个临界迎角也称为失速迎角。
1.5 低速翼型的低速气动特性概述
2.3 翼型的压力分布 ① 矢量表示法
当机翼外表压强低于大气压，称为吸力。
当机翼外表压强高于大气压，称为压力。 用矢量来表示压力或吸力，矢量线段长度为力的大小，方向为
第五章 低速翼型
EXIT
1.3 低速翼型的低速气动特性概述
lj、C y max 以及失速后的 C y 曲线受Re影响较大，当 lj 2 lj1 , C y max 2 C y max 1 Re 2 Re1 时， 。
EXIT
1.3 低速翼型的低速气动特性概述
EXIT
1.1
翼型的几何参数及其发展
在上世纪三十年代初期，美国国家航空咨询委员会（
National Advisory Committee for Aeronautics，缩写为
NACA，后来为NASA，National Aeronautics and Space Administration）对低速翼型进行了系统的实验研究。他们
展了NACA2系列，3系列直到6系列，7系列的层流翼型族。 层流翼型是为了减小湍流摩擦阻力而设计的，尽量使上 翼面的顺压梯度区增大，减小逆压梯度区，减小湍流范围。
EXIT
1.1
翼型的几何参数及其发展
EXIT
1.1
翼型的几何参数及其发展
1967年美国NASA兰利研究中心的Whitcomb主要为了提高
通常飞机设计要求，机翼和尾翼的尽可能升力大、阻力
小。 对于不同的飞行速度，机翼的翼型形状是不同的。如
对于低亚声速飞机，为了提高升力系数，翼型形状为圆头
尖尾形；而对于高亚声速飞机，为了提高阻力发散Ma数， 采用超临界翼型，其特点是前缘丰满、上翼面平坦、后缘
向下凹；对于超声速飞机，为了减小激波阻力，采用尖头
CL f y (Re, Ma, ),CD f x (Re, Ma, ), mz f m (Re, Ma, )
对于低速翼型绕流，空气的压缩性可忽略不计，但必须 考虑空气的粘性。因此，气动系数实际上是来流迎角和Re数 的函数。至于函数的具体形式可通过实验或理论分析给出。 对于高速流动，压缩性的影响必须计入，因此Ma也是其 中的主要影响变量。
第五章 低速翼型的气动特性
在上世纪三十年代初期，美国国家航空咨询委员会 （ National Advisory Committee for Aeronautics，NACA， National Aeronautics and Space Administration， NASA ） 对低速翼型进行了系统的实验研究。 将当时的几种优秀翼型的厚度折算成相同厚度时，厚度分布 规律几乎完全一样。在当时认为是最佳的翼型厚度分布作为 NACA翼型族的厚度分布。厚度分布函数为：
将头部弄弯以后的平板翼型， 失速迎角有所增加
鸟类的飞行研究：
弯曲的平板更接近于鸟翼的形状 能够产生更大的升力和效率。
鸟翼具有弯度和大展弦比的特征
德国人奥托·利林塔尔设计并测试了许多曲线翼的滑翔机，他 仔细测量了鸟翼的外形，认为试飞成功的关键是机翼的曲率 或者说是弯度，他还试验了不同的翼尖半径和厚度分布。
（2）对于有弯度的翼型升力系数曲线是不通过原点的， 通常把升力系数为零的迎角定义为零升迎角0，而过后缘 点与几何弦线成0的直线称为零升力线。对有弯度翼型0
是一个小负数，一般弯度越大， 0的绝对值越大。
（3）阻力 在二维情况下，主要是粘性引起的摩擦与压差
阻力。在小迎角时，翼型的阻力主要是摩擦阻力，阻力系数 随迎角变化不大；在迎角较大时，出现了压差阻力的增量， 分离区扩及整个上翼面，阻力系数大增。 但应指出的是无 论摩擦阻力还是压差阻力都与粘性有关。
低亚声速飞机：圆头尖尾形 提高升力系数 高亚声速飞机：超临界翼型 提高阻力发散Ma数，前缘丰 满、上翼面平坦、下翼面后缘向内凹； 超声速飞机：尖头、尖尾形 减小激波阻力
对翼型的研究最早可追溯到19世纪后期 带有一定安装角的平板能够产生升力
在实践中发现弯板比平板好，能用于 较大的迎角范围
第五章 低速翼型讲解
1.1 翼型的几何参数及其发展
4、厚度
பைடு நூலகம்
厚度分布函数为：
yc (x)
yc b
1 2 ( yu
yl )
相对厚度
c
c b
2 ycmax b
2 ycmax
最大厚度位置
xc
xc b
EXIT
1.1 翼型的几何参数及其发展
r 5、前缘半径 L ，后缘角
翼型的前缘是圆的，要很精确地画出前缘附近的翼型 曲线，通常得给出前缘半径。这个与前缘相切的圆，其圆
0 x xf xf x 1
例: NACA ②
④
①②
f 2% xf 40%
c 12%
EXIT
1.1 翼型的几何参数及其发展
1935年，NACA又确定了五位数翼型族。 五位数翼族的厚度分布与四位数翼型相同。不同的是中 弧线。它的中弧线前段是三次代数式，后段是一次代数式。
EXIT
1.1 翼型的几何参数及其发展
在上世纪三十年代初期，美国国家航空咨询委员会（
National Advisory Committee for Aeronautics，缩写为
NACA，后来为NASA，National Aeronautics and Space
Administration）对低速翼型进行了系统的实验研究。他们
心在 x 0.05处中弧线的切线上。
翼型上下表面在后缘处切线间的夹角称为后缘角。
EXIT
1.1 翼型的几何参数及其发展
三、翼型的发展 通常飞机设计要求，机翼和尾翼的尽可能升力大、阻力
小。
对于不同的飞行速度，机翼的翼型形状是不同的。如 对于低亚声速飞机，为了提高升力系数，翼型形状为圆头 尖尾形；而对于高亚声速飞机，为了提高阻力发散Ma数， 采用超临界翼型，其特点是前缘丰满、上翼面平坦、后缘 向下凹；对于超声速飞机，为了减小激波阻力，采用尖头 、尖尾形翼型。
翼型与机翼的气动特性PPT课件
翼型的几何参数
Leading edge: 前缘 后缘
Chord line:
弦线
弦长
Thickness:
厚度
trailing edge: chord length: camber:
翼型的分类
按几何形状，翼型可分为两类： 圆头尖尾的，用于低速、亚声速和跨声速飞行的飞机机翼
，以及低超声速飞行的超声速飞机机翼； 另一类是尖头尖尾的，用于较高超声速飞行的超声速飞机
迎角不大时，摩擦阻力是主要的， 压差阻力较小；在设计升力系数下 ，此时迎角不大，阻力系数称为最 小阻力系数
随迎角或升力系数的增大，翼面上 边界层增厚，尾迹区加宽，粘性压 差阻力逐渐增大为主要部分；一旦 出现失速，粘性压差阻力剧增
Cy-Cx升阻特性：升阻比
极曲线
粘性流动：翼型阻力
翼型的升力是由于表面上的压力分布造成的。对 作用在翼型上的剪切力沿升力方向上进行积分得到的 值通常是可以忽略的。事实上，升力可以通过 假定无 粘流动并且结合在后缘处的库塔条件精确求得。但是 ，运用相同的方法来预测阻力，得到的阻力值为0，这 个结果与常识相违背，称此为d’Alembert悖论。 d’Alembert是法国数学和物理学家，他第一个运用这 种方法来计算二维翼型无粘扰流产生的阻力
随后的十多年里，在反复试验的基础上研制出了大量翼 型，有的很有名，如RAF-6， Gottingen 387，Clark Y。这 些翼型成为NACA翼型家族的鼻祖。
NACA翼型族
在上世纪三十年代初期，美国国家航空咨询委员会（National Advisory Committee for Aeronautics，缩写为NACA，后来为NASA， National Aeronautics and Space Administration）对低速翼型进行了 系统的实验研究。他们发现当时的几种优秀翼型的折算成相同厚度时， 厚度分布规律几乎完全一样。于是他们把厚度分布就用这个经过实践证 明，在当时认为是最佳的翼型厚度分布作为NACA翼型族的厚度分布。厚 度分布函数为：
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
22
.
23
（1）在升力系数随迎角的变化曲线中，在迎角较小时是一
条直线，这条直线的斜率称为升力线斜率，记为
C
l
dCl
d
这个斜率，薄翼的理论值等于2/弧度
如果迎角较大，流动出现分离。迎角大到一定程度，翼 型上表面出现大面积分离。
由于流动分离，使得升力系数开始下降的迎角称为最大 升力迎角 。对应的升力系数称为最大升力系数Clmax
.
8
对翼型的研究最早可追溯到19世纪后期 带有一定安装角的平板能够产生升力
在实践中发现弯板比平板好，能用于 较大的迎角范围
平板翼型效率较低，失速迎角很小 .
将头部弄弯以后的平板翼型，9 失速迎角有所增加
鸟类的飞行研究：
弯曲的平板更接近于鸟翼的形状
能够产生更大的升力和效率。
鸟翼具有弯度和大展弦比的特征
.
10
德国人奥托·利林塔尔设计并测试了许多曲线翼的滑翔机，他 仔细测量了鸟翼的外形，认为试飞成功的关键是机翼的曲率 或者说是弯度，他还试验了不同的翼尖半径和厚度分布。
.
11
莱特兄弟所使用的翼 型与利林塔尔的非常 相似，薄而且弯度很 大。这可能是因为早 期的翼型试验都在极 低的雷诺数下进行， 薄翼型的表现要比厚 翼型好。
升力下降，意味着飞机可能下掉，失去飞行的正常升力突然
下降的现象称为失速。
.
24
（2）对于有弯度的翼型升力系数曲线是不通过原点的，
通常把升力系数为零的迎角定义为零升迎角0，而过后缘 点与几何弦线成0的直线称为零升力线。对有弯度翼型0 是一个小负数，一般弯度越大， 0的绝对值越大。
.
12
随后的十多年里，在反复试验的基础上研制出了大量翼型， 如RAF-6， Gottingen 387，Clark Y。这些翼型成为NACA 翼型家族的鼻祖。
.
13
在上世纪三十年代初期，美国国家航空咨询委员会 （ National Advisory Committee for Aeronautics，NACA， National Aeronautics and Space Administration， NASA ）对 低速翼型进行了系统的实验研究。
将当时的几种优秀翼型的厚度折算成相同厚度时，厚度分布 规律几乎完全一样。在当时认为是最佳的翼型厚度分布作为 NACA翼型族的厚度分布。厚度分布函数为：
y t 0 t .2 ( 0 .29 x 6 0 .1 9 2 x 0 0 6 .30 5 x 2 0 1 0 .26 8 x 3 0 4 0 .13 0 x 4 ) 0 1
常理解为二维机翼，即剖面形状不变的无限翼展机翼。
.
3
翼型按速度分类有
低速翼型
亚声速翼型
超声速翼型
.
4
翼型按形状分类有
圆头尖尾形
尖头尖尾形
. 圆头钝尾形
5
5.1.1 翼型的几何参数
几何弦长、前缘半径、后缘角； 翼面坐标、弯度分布、厚度分布
前缘
厚度
中弧线
弯度
弦线 弦.长c
后缘
后缘角
6
5.1.1 翼型的几何参数
厚度
y tx y 上 x y 下 x
tmy a 上 － xy下
t t c
弯度
1 yf (x)2(y上y下)
f
f c
[yf
(x)]max
xf
xf c
.
7
5.1.2 NACA翼型
1. 翼型的发展
通常飞机设计要求，机翼和尾翼的升力尽可能大、阻力小。 对于不同的飞行速度，机翼的翼型形状是不同的 低亚声速飞机：圆头尖尾形 提高升力系数 高亚声速飞机：超临界翼型 提高阻力发散Ma数，前缘丰 满、上翼面平坦、下翼面后缘向内凹； 超声速飞机：尖头、尖尾形 减小激波阻力
.
21
•升力和阻力的比值l/d 称为升阻比 •其值随迎角的变化而变化，此值愈大愈好，低速和亚声速飞 机可达17～18，跨声速飞机可达10～12，马赫数为2的超声 速飞机约为4～8。 •把升力和阻力分别除以来流动压头与弦长，就得到升力系数 cl和阻力系数cd
l
cl
1 2
v
2
c
cd
1 2
d
v
2
c
.
层流翼型
超临界翼型
.
18
5.2 翼型的气动参数
1、翼型的迎角与空气动力
在翼型平面上，来流V∞与翼弦线之间的夹角定义 为翼型的几何迎角，简称迎角。对弦线而言，来 流上偏为正，下偏为负。
翼型绕流视为平面流动，翼型上的空气动力简称气 动力可视为无限翼展机翼在展向取单位展长所受的 气动力。
.
19
.
20
当气流绕过翼型时，在翼型表面上每点都作用有压强p（垂直 于翼面）和摩擦切应力（与翼面相切），它们将产生一个合 力R，合力的作用点称为压力中心，合力在来流方向的分量为 阻力D，在垂直于来流方向的分量为升力L。
最大厚度为 x 30%
.
14
中弧线取两段抛物线，在中弧线最高点二者相切。
yf pf2(2pxx2)
yf
f (1p)2
(12p)2pxx2
0xp xp
f为中弧线最高点的纵坐标，p 为最大弯度位置。
1932年，确定了NACA四位数翼型族。
NACA ②
④①②
f 2% x f 40% t 12%
.
15
1935年，NACA又确定了五位数翼型族。
五位数翼族的厚度分布与四位数翼型相同。不同的是中弧线。 它的中弧线前段是三次代数式，后段是一次代数式。
例: NACA 2 3 0 1 2
20 3 C L设 2
C L设
2
3 20
0.3
2 x f 30 % x f 15 %
中弧线 0：简单型 1：有拐点
t 12%
CL设：来流与前缘中弧线平行时的理论升力系数
.
16
1939年，发展了NACA1系列层流翼型族。其后又相继发展 了NACA2系列，3系列直到6系列，7系列的层流翼型族。
层流翼型是为了减小湍流摩擦阻力而设计的，尽量使上翼面
的顺压梯度区增大，减小逆压梯度区，减小湍流范围。
.
17
1967年美国NASA兰利研究中心的Whitcomb主要为了提高亚 声速运输机阻力发散Ma数而提出了超临界翼型的概念。
第5章 低速翼型的气动特性 (Airfoil of low speed)
.
1
5.1 翼型的几何参数及表示方法
5.1.1 翼型的几何参数 5.1.2 NACA翼型 5.1.3 NACA五位数 5.1.4 层流翼型 5.1.5 超临界机翼
.
2
5.1.1 翼型的几何参数
翼的横剖面形状，又称为翼剖面。在空气动力学中，翼型通