高考三角函数经典解答题及答案
(完整版)高考三角函数经典解答题及答案

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值. 解:(1) 由余弦定理:conB=14sin22A B ++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号)故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,,0sin .cos sin 3sin ,cos sin 3)sin(,cos sin 3cos sin cos sin ,cos sin cos sin 3cos sin ,cos sin 2cos sin 6cos sin 2≠==+=+-=-=A B A A B A C B B A B C C B B C B A C B B C R B A R C B R 又可得即可得故则因此.31cos =B(II )解:由2cos ,2==⋅B a 可得,,,0)(,12,cos 2,6,31cos 222222c a c a c a B ac c a b ac B ==-=+-+===即所以可得由故又 所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3,其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
2020高考—三角函数(解答+答案)

2020年高考——三角函数1.(20全国Ⅰ文18)ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a ,b ABC △的面积;(2)若sin A C ,求C .2. (20全国Ⅱ文17)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A π++=. (1)求A ;(2)若b c -=,证明:△ABC 是直角三角形.3.(20全国Ⅱ理 17)ABC △中,sin 2A -sin 2B -sin 2C = sin B sin C .(1)求A ;(2)若BC =3,求ABC △周长的最大值.4.(20新高考Ⅰ17)在①ac =sin 3c A =,③c =这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在ABC △,它的内角,,A B C 的对边分别为,,a b c ,且sin A B ,6C π=,________? 注:如果选择多个条件分别解答,按第一个解答计分.5.(20天津16)(本小题满分14分)在ABC △中,角,,A B C 所对的边分别为,,a b c .已知5,a b c === (Ⅰ)求角C 的大小; (Ⅱ)求sin A 的值; (Ⅲ)求πsin(2)4A +的值.6.(20浙江18)(本题满分14分)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知2sin 0b A =. (Ⅰ)求角B 的大小;(Ⅱ)求cos A +cos B +cos C 的取值范围.7.(20江苏16)(本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,2,45a c B ===︒. (1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值.8.(20全国Ⅱ理21)(12分)已知函数f (x )= sin 2x sin2x .(1)讨论f (x )在区间(0,π)的单调性; (2)证明: 33()f x ≤; (3)设n ∈N *,证明:sin 2x sin 22x sin 24x …sin 22n x ≤34nn .9.(20北京17)(本小题13分)在ABC 中,11a b +=,再从条件①、条件②这两个条件中选择一个作为己知,求: (Ⅰ)a 的值:(Ⅱ)sin C 和ABC 的面积.条件①:17,cos 7c A ==-; 条件②:19cos ,cos 816A B ==.注:如果选择条件①和条件②分别解答,按第一个解答计分.参考答案:1.解:(1)由题设及余弦定理得2222832cos150c c =+-⨯︒,解得2c =-(舍去),2c =,从而a =ABC △的面积为12sin1502⨯⨯︒=(2)在ABC △中,18030A B C C =︒--=︒-,所以sin sin(30)sin(30)A C C C C =︒-=︒+,故sin(30)C ︒+=而030C ︒<<︒,所以3045C ︒+=︒,故15C =︒.2.解:(1)由已知得25sin cos 4A A +=,即21cos cos 04A A -+=. 所以21(cos )02A -=,1cos 2A =.由于0A <<π,故3A π=.(2)由正弦定理及已知条件可得sin sin B C A -.由(1)知23B C π+=,所以2sin sin()33B B ππ--.即11sin 22B B =,1sin()32B π-=.由于03B 2π<<,故2B π=.从而ABC △是直角三角形.3.解:(1)由正弦定理和已知条件得222BC AC AB AC AB --=⋅,①由余弦定理得2222cos BC AC AB AC AB A =+-⋅,② 由①,②得1cos 2A =. 因为0πA <<,所以2π3A =.(2)由正弦定理及(1)得sin sin sin AC AB BCB C A===从而AC B =,π)3cos AB A B B B =--=-.故π33cos 3)3BC AC AB B B B ++=++=++.又π03B <<,所以当π6B =时,ABC △周长取得最大值3+4.解:方案一:选条件①.由6C π=和余弦定理得2222a b c ab +-=.由sin A B =及正弦定理得a =.222=b c =.由①ac =1a b c ==.因此,选条件①时问题中的三角形存在,此时1c =. 方案二:选条件②.由6C π=和余弦定理得2222a b c ab +-=.由sin A B =及正弦定理得a =.222=b c =,6B C π==,23A π=.由②sin 3c A =,所以6c b a ===.因此,选条件②时问题中的三角形存在,此时c =方案三:选条件③.由6C π=和余弦定理得2222a b c ab +-=.由sin A B =及正弦定理得a =.222=b c =.由③c =,与b c =矛盾.因此,选条件③时问题中的三角形不存在.5.(Ⅰ)解:在ABC △中,由余弦定理及5,a b c ===222cos 22a b c C ab +-==.又因为(0,π)C ∈,所以π4C =.(Ⅱ)解:在ABC △中,由正弦定理及π,4C a c ===,可得sin sin 13a C A c ==.(Ⅲ)解:由a c <及sin A =cos A == 进而2125sin 22sin cos ,cos 22cos 113A A A A A ===-=.所以,πππ125sin(2)sin 2cos cos 2sin 44413213226A A A +=+=⨯+⨯=.6.(Ⅰ)由正弦定理得2sin sin B A A ,故sin B =, 由题意得π3B =. (Ⅱ)由πA B C ++=得2π3C A =-, 由ABC △是锐角三角形得ππ(,)62A ∈.由2π1cos cos()cos 32C A A A =-=-得11π13cos cos cos cos sin()]22622A B C A A A ++++=++∈.故cos cos cos A B C ++的取值范围是3]2.7.解:(1)在ABC △中,因为3,45a c B ===︒,由余弦定理2222cos b a c ac B =+-,得292235b =+-⨯︒=,所以b =在ABC △中,由正弦定理sin sin b cB C=,,所以sin C =(2)在ADC △中,因为4cos 5ADC ∠=-,所以ADC ∠为钝角,而180ADC C CAD ∠+∠+∠=︒,所以C ∠为锐角.故cos C =则sin 1tan cos 2C C C ==. 因为4cos 5ADC ∠=-,所以3sin 5ADC ∠==,sin 3tan cos 4ADC ADC ADC ∠∠==-∠.从而31tan()242tan tan(180)tan()===311tan tan 111()42ADC C ADC ADC C ADC C ADC C -+∠+∠∠=︒-∠-∠=-∠+∠---∠⨯∠--⨯8.解:(1)()cos (sin sin 2)sin (sin sin 2)f x x x x x x x ''=+22sin cos sin 22sin cos2x x x x x =+ 2sin sin3x x =.当(0,)(,)33x π2π∈π时,()0f x '>;当(,)33x π2π∈时,()0f x '<. 所以()f x 在区间(0,),(,)33π2ππ单调递增,在区间(,)33π2π单调递减.(2)因为(0)()0f f =π=,由(1)知,()f x 在区间[0,]π的最大值为()3fπ=,最小值为()3f 2π=.而()f x 是周期为π的周期函数,故|()|f x ≤. (3)由于32222(sin sin 2sin 2)nx xx333|sin sin 2sin 2|n x xx =23312|sin ||sin sin 2sin 2sin 2||sin 2|n n n x x x x x x -= 12|sin ||()(2)(2)||sin 2|n n x f x f x f x x -=1|()(2)(2)|n f x f x f x -≤,所以22223333sin sin 2sin 2()4n nnn x xx ≤=.9.。
高考三角函数专题(含答案)

高考专题复习三角函数专题模块一——选择题一、选择题: (将正确答案的代号填在题后的括号内. )π5π1.(2021天·津)以下图是函数 y =Asin(ωx+φ)(x∈R)在区间 -6,6上的图象,为了得到这个函数的图象,只要将 y =sinx(x∈R)的图象上所有的点 ( )π1A .向左平移3个单位长度,再把所得各点的横坐标缩短到原来的2,纵坐标不变π2倍,纵坐标不变B .向左平移个单位长度,再把所得各点的横坐标伸长到原来的3π1C .向左平移6个单位长度,再把所得各点的横坐标缩短2,纵坐标不变到原来的π2倍,纵坐标不变D .向左平移个单位长度,再把所得各点的横坐标伸长到原来的6y =Asin(ωx+φ)中A =1,2ππ π解析:观察图象可知,函数 ω=π,故ω=2,ω×-6+φ=0,得φ= 3,所以函数y =sin 2x + ,故只要把y =sinx 的图象向左平移π1即个单位,再把各点的横坐标缩短到原来的2可.答案:A2.(2021全·国Ⅱ)为了得到函数 y =sin2x -π的图象,只需把函数y =sin2x +π的图象()36πB .向右平移A .向左平移个长度单位个长度单位44πD .向右平移C .向左平移2个长度单位2个长度单位解析:由y=sin2x+πx→x+φ=sin2x-πππ――→y=sin2(x+φ),即2x+2φ+=2x-,解得φ=-6634π即向右平移4个长度单位.应选B. 答案:B3.(2021重·庆)函数y=sin(ωx +φ)ω>0,|φ|<π的局部图象如下图,那么()2πB.ω=1,φ=-πππA.ω=1,φ=66C.ω=2,φ=6D.ω=2,φ=-6解析:依题意得T=2π7ππππ2πππω=412-3=π,ω=2,sin2×3+φ=1.又|φ|<2,所以3+φ=2,φ=-6,选D.答案:D4.函数 y=2sin(ωx+φ)(ω>0)在区间[0,2π]上的图象如下图,那么ω=( )11A.1B.2 C.2D.32π解析:由函数的图象可知该函数的周期为π,所以 ω=π,解得ω=2.答案:Bπ()5.函数y =sinx -12cosx -12,那么以下判断正确的选项是A .此函数的最小正周期为2π,其图象的一个对称中心是π,012B .此函数的最小正周期为 π,其图象的一个对称中心是π,012C .此函数的最小正周期为 2π,其图象的一个对称中心是π,6D .此函数的最小正周期为 π,其图象的一个对称中心是π,6ππ1π解析:∵y=sinx -12·cosx-12=2sin2x -6,∴T=2ππ2=π,且当x =12时,y=0.答案:Bπa 的值为()6.如果函数y =sin2x +acos2x 的图象关于直线对称,那么实数 x =-8A.2B .-2C.1D.-1π分析:函数f(x)在x =- 时取得最值;或考虑有8ππf-+x=f--x对一切x∈R恒成立.88解析:解法一:设f(x)=sin2x+acos2x,因为函数的图象关于直线x=-πππ8对称,所以f-8+x=f-8-x对一切实数x都成立,即sin2ππ-+x+acos2-+x=sin2ππ--x+acos2--xππsin-4+2x+sin4+2xππ=acos4+2x-cos-4+2x,ππ∴2sin2x·cos4=-2asin2x·sin4,即(a+1)sin2x·=0对一切实数x恒成立,而sin2x不能恒为,∴a+1=0,即a=-1,应选D.π解法二:∵f(x)=sin2x+acos2x关于直线x=-8对称.ππ∴有f-+x=f--x对一切x∈R恒成立.88π特别,对于x=8应该成立.π将x=8代入上式,得f(0)=f-,ππ∴sin0+acos0=sin-2+acos-2∴0+a=-1+a×0.∴a=-1.应选D.解法三:y=sin2x+acos2x=1+a2sin(2x+φ),其中角φ的终边经过点(1,a).其图象的对称轴方程π2x+φ=kπ+2(k∈Z),kππφx=2+4-2(k∈Z).kππφπ令2+4-2=-8(k∈Z).3π得φ=kπ+4(k∈Z).π但角φ的终边经过点(1,a),故k为奇数,角φ的终边与-2角的终边相同,∴a=-1.解法四:y=sin2x+acos2x=21+asin(2x+φ),其中角φ满足tanφ=a.因为f(x)的对称轴为πy=-8,π∴当x=-8时函数y=f(x)有最大值或最小值,所以1+a2=fπ-8或-1+a2=fπ-8,即1+a2=sinπ-4+acosπ-4,或-1+a2=sinπ-4+acosπ-4.解之得a=-1.应选D.答案:D评析:此题给出了四种不同的解法,充分利用函数图象的对称性的特征来解题.解法一是运用了方程思想或恒等式思想求解.解法二是利用了数形结合的思想求解,抓住f(m+x)=f(m-x)的图象关于直线=m对称的性质,取特殊值来求出待定系数a的值.解法三利用函数y=Asin(ωx+φ)的对称轴是方程xωxππkπ+2-φπ+φ=kπ+2(k∈Z)的解x=ω(k∈Z),然后将x=-8代入求出相的φ,再求a的.解法四利ππ用称的特殊性,在此函数f(x)取最大或最小.于是有f-8=[f(x)]max或f-8=[f(x)]min.从而化解方程,体了方程思想.由此可,本体了丰富的数学思想方法,要从多种解法中悟出其西.模块二——填空题二、填空:(把正确答案填在后的横上.)π7.(2021福·建)函数f(x)=3sinωx-6(ω>0)和g(x)=2cos(2x+φ)+1的象的称完全相同.假设π,f(x)的取范是________.x∈0,2解析:∵f(x)与g(x)的象的称完全相同,∴f(x)与g(x)的最小正周期相等,∵ω>0,∴ω=2,∴f(x)ππππ5π13≤3,即f(x)=3sin2x-6,∵≤2x-≤≤sin2x-61,∴-≤3sin2x-6 0≤x≤2,∴-666,∴-22的取范,3.答案:-3,318.函数y=cos2πx的象位于y 右所有的称中心从左依次A1,A2,⋯,An,⋯.A50的坐是________.解析:称中心横坐x=2k+1,k≥0且k∈N,令k=49即可得.答案:(99,0)9.把函数y=cosx+π的象向左平移m个位(m>0),所得象关于y称,m的最小是3________.解析:由y=cos(x+πππ3+m)的象关于y称,所以3+m=kπ,k∈Z,m=kπ-3,当k=1,m最2小3π.答案:2π310.定义集合A,B的积A×B={(x,y)|x∈A,y∈B}.集合M={x|0≤x≤2π},N={y|cosx≤y≤1},那么M×N所对应的图形的面积为________.解析:如下图阴影面积可分割补形为ABCD的面积即BC×CD=π·2=2π.答案:2π模块三——解答题三、解答题:(写出证明过程或推演步骤.) 11.假设方程3sinx+cosx=a在[0,2π]上有两个不同的实数解x1、x2,求a的取值范围,并求x1+x2的值.分析:设函数y1=3sinx+cosx,y2=a,在同一平面直角坐标系中作出这两个函数的图象,应用数形结合解答即可.解:设f(x)=π3 sinx +cosx =2sin x+6,x∈[0,2.π]π令x+6=t,那么f(t)=2sint,且t∈π6,13π6 .在同一平面直角坐标系中作出y=2sint及y=a的图象,从图中可以看出当1<a<2和-2<a<1时,两图象有两个交点,即方程3sinx+cosx=a在[0,2上π]有两个不同的实数解.当1<a<2时,t1+t2=π,ππ即x1+6+x2+6=π,2π∴x1+x2=3;当-2<a<1时,t1+t2=3π,ππ即x1+6+x2+6=3π,8πx1+x2=3.综上可得,a的取值范围是(1,2)∪(-2,1).2π当a∈(1,2)时,x1+x2=3;8πa∈(-2,1)时,x1+x2=3.评析:此题从方程的角度考查了三角函数的图象和对称性,运用的主要思想方法有:函数与方程的思想、数形结合的思想及换元法.解答此题常见的错误是在换元时忽略新变量t的取值范围,仍把t当成在[0,2 π]中处理,从而出错.11πφ<π),其图象过点π1+φ(0<,12.(2021山·东)函数f(x)=2sin2xsinφ+cosxcosφ-2sin262.(1)求φ的值;(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的1,纵坐标不变,得到函数y=g(x)的图象,求函2π数g(x)在0,4上的最大值和最小值.11π解:(1)因为f(x)=sin2xsinφ+cos2xcosφ-sin+φ(0<φ<π),2211+cos2x1所以f(x)=2sin2xsinφ+2cosφ-2cosφ1 12sin2xsinφ+2cos2xcosφ12(sin2xsinφ+cos2xcosφ)1π2cos(2x-φ),π1又函数图象过点6,2,11ππ所以2=2cos2×6-φ,即cos3-φ=1,π又0<φ<π,所以φ=3.1π1(2)由(1)知f(x)=2cos2x-3,将函数y=f(x)的图象上各点的横坐标缩短到原来的2,纵坐标不变,得1 2 3 4 56π到函数y =g(x)的象,可知g(x)=f(2x)=2cos4x -3,π4x∈[0,π],因x∈0,4 ,所以ππ2π1因此4x - 3∈-3,3 ,故- 2≤cos4x -3≤1. 所以y =g(x)在0,π114上的最大和最小分 2和-4.13.〔2021天津卷理〕在⊿ ABC 中,BC=5,AC=3,sinC=2sinA求AB 的: (II) 求sin 2A 的4本小主要考正弦定理、余弦定理、同角三角函数的根本关系、二倍角的正弦与余弦、两角差的正弦等基知,考根本运算能力。
三角函数高三计算题解析

三角函数高三计算题解析一、单选题1.(2024·湖北·二模)若ππcos ,,tan 223sin αααα⎛⎫∈-= ⎪-⎝⎭,则πsin 23α⎛⎫-= ⎪⎝⎭()A .718-B .718-C .18-D .182.(23-24高三下·重庆·阶段练习)若,π2α⎛⎫∈ ⎪⎝⎭,且cos 13αα=,则sin 212α⎛⎫- ⎪⎝⎭的值为()A B .338C .D .3.(2024·全国·模拟预测)已知角θ的顶点为坐标原点,始边与x轴的正半轴重合,点2023π2023πsin,cos46P⎛⎫⎪⎝⎭在角θ的终边上,则sin21cos2θθ=+()AB.C D.4.(2024·陕西咸阳·二模)当函数3sin4cosy x x=+取得最小值时,sin6x⎛⎫+=⎪⎝⎭()A.4+-B.310+-C.310+D.410+5.(2024·安徽·模拟预测)已知()tan 4αβ-=,()()sin 3cos αβαβ-=+,则tan tan αβ-=()A .12B .35C .65D .536.(2024·山东泰安·一模)若2πcos 24sin 22αα⎛⎫+-=- ⎪⎝⎭,则tan2α=()A .2-B .12-C .2D .127.(2024·贵州毕节·模拟预测)已知sin 125α⎛⎫+= ⎪⎝⎭,0,2α⎛⎫∈ ⎪⎝⎭,则cos 3α⎛⎫+= ⎪⎝⎭()A .10-B .5-C .4D .34-8.(2024·福建泉州·模拟预测)若0,2α⎛⎫∈ ⎪⎝⎭,3sin 2cos 2sin cos 20αααα+=,则tan α=()A .4B .2C .12D .149.(2024·河北·模拟预测)已知1tan 22θ=-,则3cos sin cos θθθ=+()A .925-B .925C .2725-D .272510.(2024·江苏盐城·模拟预测)在ABC 中,已知tan tan tan tan 1A B A B ++=,则cos 2sin C C +的值为()A .2B .2C D .11.(2024·辽宁·一模)已知,αβ满足πππ2π,44αβ≤≤-≤≤,且553π32cos 5,962sin252ααββ⎛⎫-+=+=- ⎪⎝⎭,则24πsin 994αβ⎛⎫+-=⎪⎝⎭()A B C D12.(23-24高三下·内蒙古锡林郭勒盟·开学考试)若cos 20501)a -=,则=a ()A .12B .1C .32D .213.(23-24高三下·江苏扬州·阶段练习)已知()cos(),cos 35αβαβ+=-=,则2log (tan tan )αβ-=()A .12B .12-C .2D .2-【答案】D根据余弦的和差角公式求得tan tan αβ,再求结果即可.【详解】因为()11cos(),cos35αβαβ+=-=,14.(2024高三·全国·专题练习)已知sin 1523α︒⎛⎫-= ⎪⎝⎭,则()cos 30α︒-=()A .13B .13-C .23D .23-【答案】A 【详解】因为sin (15°-)=,所以cos (30°-α)=cos 2(15°-)=1-2sin2(15°-)=1-2×=.15.(2024·吉林白山·二模)若πcos 43πcos 4αα⎛⎫+ ⎪⎝⎭=⎛⎫- ⎪⎝⎭,则πtan 24α⎛⎫-= ⎪⎝⎭()A .7-B .7C .17-D .17【详解】因为πcos cos sin 1tan 43πcos sin 1tan cos 4αααααααα⎛⎫+ ⎪--⎝⎭===++⎛⎫- ⎪⎝⎭,故1tan 2α=-,则22122tan 42tan21tan 3112ααα⎛⎫⨯- ⎪⎝⎭===--⎛⎫-- ⎪⎝⎭,故4π1tan2tanπ34tan 27π441tan2tan 143ααα---⎛⎫-== ⎪⎝⎭+⋅-.故选:B.16.(23-24高三下·江西·开学考试)已知α为锐角,且πtan tan 14αα⎛⎫++= ⎪⎝⎭,则sin 21cos 2αα+=()A .12B .3-C .2-D .13【答案】C 【分析】根据已知条件结合两角和的正切公式可得出关于tan α的方程,由已知可得出tan 0α>,可得出关于tan α的方程,求出tan α的值,利用二倍角的正弦和余弦公式可求得所求代数式的值.【详解】因为α为锐角,则tan 0α>,则πtantan π4tan tan tan π41tan tan 4ααααα+⎛⎫++=+⎪⎝⎭-1tan tan 11tan ααα+=+=-,整理可得2tan 3tan 0αα-=,解得tan 3α=,所以,()()()22222cos sin sin 21cos 2sin cos sin cos 2cos sin cos sin cos sin αααααααααααααα++++==--+cos sin 1tan 132cos sin 1tan 13αααααα+++====----.故选:C.17.(2023·全国·高考真题)已知()11sin ,cos sin 36αβαβ-==,则()cos 22αβ+=().A .79B .19C .19-D .79-18.(2021·全国·高考真题)若tan 2θ=-,则sin 1sin 2sin cos θθ+=+()A .65-B .25-C .25D .6519.(2021·全国·高考真题)若0,,tan 222sin παααα⎛⎫∈= ⎪-⎝⎭,则tan α=()A .15B C D20.(1995·全国·高考真题)已知θ是第三象限的角,且44sin cos 9+=θθ,那么sin 2θ的值为A B .C .23D .23-。
高考数学解答题(新高考)三角函数的图象与性质(五点法作图)(典型例题+题型归类练)(解析版)
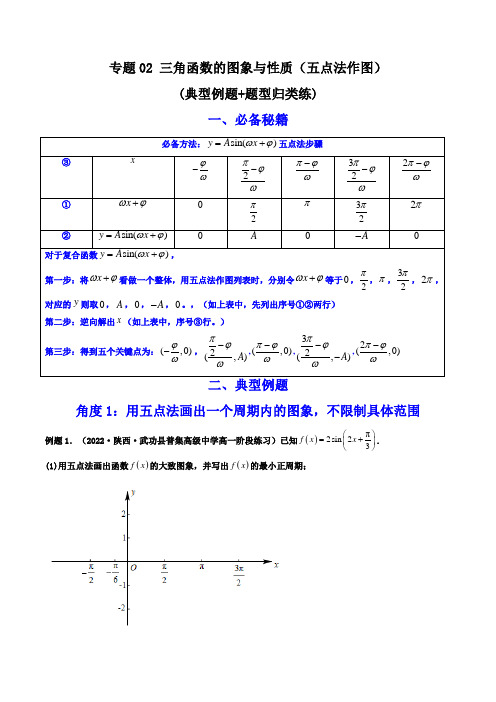
专题02 三角函数的图象与性质(五点法作图)(典型例题+题型归类练)一、必备秘籍角度1:用五点法画出一个周期内的图象,不限制具体范围例题1.(2022·陕西·武功县普集高级中学高一阶段练习)已知()π2sin23f x x⎛⎫=+⎪⎝⎭.(1)用五点法画出函数()f x的大致图象,并写出()f x的最小正周期;【答案】(1)图象见解析,T=π令ππ3π2=0π2π322x +,,,,,得到对应的,()x f x 值如下表所示: π23x +π2π3π2 2πxπ6-π12 π37π125π6 ()f x22-所以()f x 过πππ7π5π(,0),(,2),(,0),(,2),(,0)6123126--,图象如图所示思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3) (1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象周期为T=π例题2.(2022·宁夏吴忠区青铜峡市教育局高一开学考试)已知函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭.请用“五点法”列表并画出函数()f x 在一个周期上的图象;思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3)(1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象【答案】(1)答案见解析列表如下:函数f x在一个周期上的图象如下:角度2:用五点法画出具体某个范围内的图象例题1.(2022·全国·高一课时练习)用五点法画出π2sin23y x⎛⎫=+⎪⎝⎭在π5π,66⎡⎤-⎢⎥⎣⎦内的图象时,应取的五个点为 ______;【答案】π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭由题意可知,令π23X x =+,则123x X π⎛⎫=- ⎪⎝⎭,π5π,66x ⎡⎤∈-⎢⎥⎣⎦,列表,描点.xπ6-π12π3 7π12 5π6X0 π2π3π22π思路点拨:由题意知,目标要求写出五点法画在内的图象时对应的五个关键点解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到由列表可得,应取的五个点为 π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭,故答案为:π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭.例题2.(2022·黑龙江·大庆外国语学校高一期末)已知函数()()3sin 2f x x πϕϕ=+∈-,(,2π)函数关于4x π=对称.(1)求()f x ϕ的值及的解析式;(2)用五点法在下列直角坐标系中画出()f x 在744ππ⎡⎤-⎢⎥⎣⎦,上的图象;【答案】(1)4πϕ=,()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)详见解析(1)因为函数关于直线4x π=对称,所以,42k k Z ππϕπ+=+∈,,4k k Z πϕπ=+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以4πϕ=, 所以()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)首先根据“五点法”,列表如下:第一问略;第(2)问思路点拨:由题意知,目标要求用五点法画在内的图象解答过程: 先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到三、题型归类练1.(2021·全国·高一专题练习)用“五点法”作y =2sin2x 的图象,首先描出的五个点的横坐标是( ) A .30,,,,222ππππ B . 30,,,,424ππππ C . 0,,2,3,4ππππ D .20,,,,6323ππππ【答案】B由“五点法”作图知:令2x =0,2π,π,32π,2π,解得x =0,4π,2π,34π,π,即为五个关键点的横坐标, 故选:B.2.(2022·北京东城·高一期末)某同学用“五点法”画函数()sin()(0,0)f x A x A ωϕω=+>>在一个周期内的简图时,列表如下:则()f x 的解析式为( )A .()2sin 12f x x π⎛⎫=- ⎪⎝⎭ B .()2sin 312⎛⎫=+ ⎪⎝⎭f x x πC .()sin 212f x x π⎛⎫=- ⎪⎝⎭D .n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭【答案】D由表中数据知:2A =且721243T πππ=-=,则23T π=, ∴223ππω=,即3ω=,又342ππϕ⨯+=,可得4πϕ=-. ∴n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭.故选:D.3.(2021·广东揭阳·高一期末)某同学用“五点法”画函数()()πsin 0,2f x A x ωϕωϕ⎛⎫=+>< ⎪⎝⎭在某一个周期内的图象时,列表并填入了部分数据,如下表:根据表格中的数据,函数f x 的解析式可以是( ) A .()π5sin 26f x x ⎛⎫=- ⎪⎝⎭B .()π5sin 26f x x ⎛⎫=+ ⎪⎝⎭C .()π5sin 23f x x ⎛⎫=- ⎪⎝⎭D .()π5sin 23f x x ⎛⎫=+ ⎪⎝⎭【答案】A由题意得最大值为5,最小值为-5,所以A =5,52632T πππ=-=,解得2T ππω==,解得2ω=,又232ππϕ⨯+=,解得6πϕ=-,所以()f x 的解析式可以是()π5sin 26f x x ⎛⎫=- ⎪⎝⎭故选:A4.(2022·北京·高一阶段练习)某同学用“五点法”画函数sin()(0,)2y A x ϖϕϖϕπ=+><在某一个周期内的图像时,列表并填入了部分数据,如下表.【答案】3sin(2)3y x π=+由表格知:3A =且12231227πϕπϕϖπϖπ⎧+=⎪⎪⎨⎪+=⎪⎩,可得23ϖπϕ=⎧⎪⎨=⎪⎩,所以3sin(2)3y xπ=+.故答案为:3sin(2)3y x π=+.5.(2022·河南省嵩县第一高级中学高一阶段练习)已知函数π()2sin 23f x x ⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面的表格,并画出()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象;【答案】(1)答案见解析 完成表格如下:()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象如图所示:6.(2022·辽宁省康平县高级中学高一阶段练习)已知函数()sin 23πf x x ⎛⎫=- ⎪⎝⎭.(1)请用“五点法”画出函数()f x 在一个周期7,66ππ⎡⎤⎢⎥⎣⎦上的简图;【答案】(1)答案见解析 因为()sin 23πf x x ⎛⎫=- ⎪⎝⎭取值列表:7.(2022·广西·钦州一中高一期中)已知函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.(1)请用“五点法”画出函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭在一个周期上的图象;【答案】(1)作图见解析由图横坐标的范围,函数()f x 的周期为π,画出函数()f x 在11,1212ππ⎡⎤-⎢⎥⎣⎦上的图象.列表如下,8.(2022·江西·上饶中学高一阶段练习)已知函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面表格,并画出函数()f x 在区间9,88ππ⎡⎤⎢⎥⎣⎦上的图象.由正弦函数的性质,9,88ππ⎡⎤⎢⎥⎣⎦上的五点如下表:9.(2022·云南玉溪·高一期末)已知函数21()sin cos cos 22f x x x x x =+-.(2)填上面表格并用“五点法”画出()f x 在一个周期内的图象.【答案】(1)T π=,它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈(2)答案见解析.(1)21()sin cos cos 22f x x x x x =+-12cos 2sin 226x x x π⎛⎫+=+ ⎪⎝⎭ ∴函数()f x 的最小正周期22T ππ==;令26x k ππ+=,k Z ∈,解得212k x ππ=-,k Z ∈,可得它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈.。
高考三角函数经典解答题及答案

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值.解:(1) 由余弦定理:conB=14sin 22A B++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a 2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号) 故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,因此.31cos =B(II )解:由2cos ,2==⋅B a BC BA 可得,所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3, 其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
解:(1) m =()B B cos 1,sin -,且与向量n = (2,0)所成角为3π, 又 π<<B 0(2)由(1)知,32π=B ,∴A+C= 3π ∴C A sin sin +=)3sin(sin A A -+π=A A cos 23sin 21+=)3sin(A +π30π<<A ,∴)3sin(A +π⎥⎦⎤ ⎝⎛∈1,23,∴ C A sin sin +⎥⎦⎤⎝⎛∈1,23 4已知向量(1,2sin )m A =,(sin ,1cos ),//,3.n A A m n b c a =++=满足 (I )求A 的大小;(II )求)sin(6π+B 的值.解:(1)由m//n 得0cos 1sin 22=--A A ……2分 即01cos cos 22=-+A A 1cos 21cos -==∴A A 或1cos ,-=∆A ABC A 的内角是 舍去 3π=∴A(2)a c b 3=+由正弦定理,23sin 3sin sin ==+A C Bπ32=+C B23)32sin(sin =-+∴B B π5在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,C =2A ,43cos =A , (1)求BC cos ,cos 的值;(2)若227=⋅,求边AC 的长。
高三数学三角函数试题答案及解析

高三数学三角函数试题答案及解析1.在中,已知,若分别是角所对的边,则的最大值为.【答案】【解析】由正余弦定理得:,化简得因此即最大值为.【考点】正余弦定理,基本不等式2. sin7°cos37°﹣sin83°cos53°的值为()A.﹣B.C.D.﹣【答案】A【解析】sin7°cos37°﹣sin83°cos53°=cos83°cos37°﹣sin83°sin37°=cos(83°+37°)=cos120°=﹣,故选A.3.三角形ABC是锐角三角形,若角θ终边上一点P的坐标为(sin A-cos B,cos A-sin C),则的值是( )A.1B.-1C.3D.4【答案】B【解析】因为三角形ABC是锐角三角形,所以A+B>90°,即A>90°-B,则sin A>sin(90°-B)=cos B,sin A-cos B>0,同理cos A-sin C<0,所以点P在第四象限,=-1+1-1=-1,故选B.4.已知函数则=【答案】【解析】因为函数由需要求的x都是整数,所以当x为奇数时的解析式为,当x为偶数时的解析式为.所以.所以.【考点】1.分段函数的性质.2.归纳推理的思想.3.三角函数的运算.4.等差数列的求和公式.5.若方程有实根,则实数的取值范围为【答案】【解析】由方程得,,即,因为,所以,若方程有实根,则,解得.【考点】方程的根.6.设,将函数在区间内的全部极值点按从小到大的顺序排成数列.(1)求数列的通项公式;(2)设,数列的前项和为,求.【答案】(1);(2).【解析】(1)先根据三角函数的恒等变换化简,得,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列的通项公式;(2)先根据(1)中的结果写出的通项公式,然后写出的解析式,在构造出,利用错位相减法求,计算量比较大,要细心.试题解析:(1),其极值点为, 2分它在内的全部极值点构成以为首项,为公差的等差数列, 4分所以; 6分(2), 8分所以,,相减,得,所以. 12分【考点】1、三角函数的恒等变换及化简;2、三角函数的性质的应用;3、等差数列的通项公式;4、错位相减法求数列的前项和;5、等比数列的前项和.7.已知函数d的最大值为2,是集合中的任意两个元素,且的最小值为.(1)求函数的解析式及其对称轴;(2)若,求的值.【答案】(1),;(2).【解析】本题主要考查两角和与差的正弦公式、二倍角的余弦公式、诱导公式、三角函数的最小正周期、单调性等基础知识,考查运算能力.第一问,利用倍角公式化简表达式,先利用周期求出,再求最值,通过解方程求出,确定了解析式后求正弦函数的对称轴;第二问,通过角之间的关系转化角,考查诱导公式和倍角公式.试题解析:(1),由题意知:的周期为,由,知 2分由最大值为2,故,又, 4分∴ 5分令,解得的对称轴为 7分(2)由知,即, 8分∴ 10分12分【考点】1.倍角公式;2.两角和与差的三角函数;3.函数的周期;4.函数的对称轴.8.是偶函数,,则 .【答案】【解析】,,所以,因为为偶函数,所以对任意的,都有即成立,又,所以.【考点】三角函数的恒等变换,偶函数.9.已知方程在上有两个不同的解、,则下列结论正确的是()A.B.C.D.【答案】C【解析】由于方程在上有两个不同的解、,即方程在上有两个不同的解、,也就是说,直线与函数在轴右侧的图象有且仅有两个交点,由图象可知,当时,直线与曲线相切,且切点的横坐标为,当时,,则,故,在切点处有,即,,两边同时乘以得,,故选C.【考点】1.函数的零点;2.函数的图象;3.利用导数求切线的斜率10.将函数图像上各点的横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位,那么所得图像的一条对称轴方程为()A.B.C.D.【答案】B【解析】将函数的图像按题中要求变换后得到函数的图像,令,则,当时,.【考点】1.三角函数的变换;2.三角函数图象的对称轴.11.函数f(x)=sin+ACos(>0)的图像关于M(,0)对称,且在处函数有最小值,则的一个可能取值是( )A.0B.3C.6D.9【答案】D【解析】根据题意:相邻对称点与最小值之间可以相差也可以是不妨设为:=,可以为9,故选D.【考点】三角函数的最值;正弦函数的对称性.12.已知函数,(1)求的值;(2)若,且,求.【答案】(1);(2).【解析】(1)直接将代入计算即可;(2)用二倍角的正弦、余弦公式化简,再将正弦、余弦合为同一个的三角函数;根据已知条件,求出的值.试题解析:(1)(2)因为,且,所以,所以【考点】1、三角恒等变换;2、三角函数的基本运算.13.已知函数的最小正周期为.(Ⅰ)求的值;(Ⅱ)讨论在区间上的单调性.【答案】(Ⅰ)(Ⅱ)当,即时,单调递增;当,即,单调递减.【解析】(1)由题意,所以由(1)知若,则当,即时,单调递增;当,即,单调递减.第(1)题根据三角函数的和差化简,二倍角公式以及辅助角公式,最后化成的形式,利用确定的值;第(2)题用整体法的思想确定的单调性,再反求出在指定范围内的单调性.本题属简单题.【考点】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.14.已知函数若方程有三个不同的实根,且从小到大依次成等比数列,则m的值为 .【答案】【解析】设三个根由小到大依次为,结合余弦函数图像可知关于直线对称,关于直线对称,代入计算得【考点】三角函数图像及性质点评:题目中主要结合三角函数图像的轴对称性找到三根之间的联系15.已知,则的值为()A.B.C.D.【答案】B【解析】因为,,即,,所以,=,故选B。
(完整版)高考三角函数经典解答题及答案

(完整版)高考三角函数经典解答题及答案1. 在△ABC 中,角 A、B、C 所对的边分别是 a、b、c,且 a²+c²-b²=(1) 求 sin²(2A+C)+cos²B 的值;(2) 若 b=2,求△ABC 面积的最大值。
解:(1) 由余弦定理:cosB=(a²+ c²- b²)/(2ac)=4/√115,得sinB=√(1-cos²B)=3√(23)/23。
由正弦定理sin²(2A+C)+cos²B=4sin²B+cos²B=13/23。
2. 在△ABC 中,角 A、B、C 的对边分别为 a、b、c,且bcosC=3acosB-ccosB。
(I) 求 cosB 的值;(II) 若 BA·BC=2,且b=√2,求 a 和 c·b 的值。
解:(I) 由正弦定理得 a=2RsinA,b=2RsinB,c=2RsinC,则 2RsinBcosC=6RsinAcosB-2RsinCcosB,故sinBcosC=3sinAcosB-sinCcosB,可得sinBcosC+sinCcosB=3sinAcosB,即 sin(B+C)=3sinAcosB,可得 sinA=3sinAcosB/sinB。
又sinA≠0,因此 cosB=1/3。
3. 已知向量 m=(sinB,1-cosB),向量 n=(2,k),且 m 与 n 所成角为π/3,其中 A、B、C 是△ABC 的内角。
(1) 求角 B 的大小;(2) 求 sinA+sinC 的取值范围。
解:(1) ∠m与∠n所成角为π/3,且 m·n=2sinB+ k(1-cosB)=2√3/2cosB+k√(1-cos²B),又 m·n=2cosB+k(1-cosB),解得 k=4/3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值. 解:(1) 由余弦定理:conB=14sin 22A B++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a 2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号) 故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,因此.31cos =B(II )解:由2cos ,2==⋅B a 可得,所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3,其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
解:(1)Θ m =()B B cos 1,sin -,且与向量n = (2,0)所成角为3π,又Θπ<<B 0(2)由(1)知,32π=B ,∴A+C= 3π ∴C A sin sin +=)3sin(sin A A -+π=A A cos 23sin 21+=)3sin(A +πΘ30π<<A ,∴)3sin(A +π⎥⎦⎤ ⎝⎛∈1,23,∴ C A sin sin +⎥⎦⎤⎝⎛∈1,23 4已知向量(1,2sin )m A =u r,(sin ,1cos ),//,.n A A m n b c =++=r u r r满足 (I )求A 的大小;(II )求)sin(6π+B 的值.解:(1)由m//n 得0cos 1sin 22=--A A ……2分 即01cos cos 22=-+A A 1cos 21cos -==∴A A 或1cos ,-=∆A ABC A 的内角是Θ舍去3π=∴A(2)a c b 3=+Θ由正弦定理,23sin 3sin sin ==+A C Bπ32=+C B Θ 23)32sin(sin =-+∴B B π5在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,C =2A ,43cos =A ,(1)求B C cos ,cos 的值;(2)若227=⋅BC BA ,求边AC 的长。
解:(1)81116921cos 22cos cos 2=-⨯=-==A A C(2)24,227cos ,227=∴=∴=⋅ac B ac ①又a A a c A C C c A a 23cos 2,2,sin sin ==∴== ②由①②解得a=4,c=65=∴b ,即AC 边的长为5.6已知A B 、是△ABC的两个内角,向量, sin 22A B A Ba +-=r ),若||a =r . (Ⅰ)试问B A tan tan ⋅是否为定值?若为定值,请求出;否则请说明理由; (Ⅱ)求C tan 的最大值,并判断此时三角形的形状.解:(Ⅰ)由条件223||2a ==r ∴1cos()cos()2A B A B +=-∴3sin sin cos cos A B A B = ∴1tan tan 3A B ⋅=为定值.(Ⅱ)tan tan tan tan()1tan tan A BC A B A B +=-+=--由(Ⅰ)知1tan tan 3A B ⋅=,∴tan ,tan 0A B >从而3tan (tan tan )2C A B =-+≤322-⋅=∴取等号条件是tan tan A B ==, 即6A B π== 取得最大值, 7在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.已知a+b=5,c =7,且.272cos 2sin 42=-+C B A (1) 求角C 的大小; (2)求△ABC 的面积. 解:(1) ∵A+B+C=180°由272cos 2cos 4272cos 2sin 422=-=-+C C C B A 得 ∴27)1cos 2(2cos 142=--+⋅C C整理,得01cos 4cos 42=+-C C解 得:21cos =C ……5分 ∵︒<<︒1800C ∴C=60°(2)解:由余弦定理得:c 2=a 2+b 2-2abcosC ,即7=a 2+b 2-ab∴ab b a 3)(72-+=由条件a+b=5得 7=25-3abab=6……10分∴23323621sin 21=⨯⨯==∆C ab S ABC8已知角C B A ,,为ABC ∆的三个内角,其对边分别为c b a ,,,若)2sin ,2cos (A A-=m ,)2sin ,2(cos A A =n ,32=a ,且21=⋅n m .(1)若ABC ∆的面积3=S ,求c b +的值. (2)求c b +的取值范围.解:(1))2sin ,2cos (A A m -=,)2sin ,2(cos A A n =,且21=⋅n m .212sin 2cos 22=+-∴A A ,即21cos =-A ,又),0(π∈A ,32π=∴A ………..2分 又由3sin 21=⋅=∆A bc S ABC ,4=∴bc由余弦定理得:bc c b bc c b a ++=⋅-+=2222232cos 2π2)(16c b +=∴,故4=+c b(2)由正弦定理得:432sin 32sin sin sin ====πA a C c B b ,又3ππ=-=+A C B ,30π<<B Θ,则3233πππ<+<B .则1)3sin(23≤+<πB ,即c b +的取值范围是].4,32(…10分9在锐角△ABC 中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,且(tanA -tanB)=1+tanA ·tanB .(1)若a 2-ab =c 2-b 2,求A 、B 、C 的大小;(2)已知向量m =(sinA ,cosA),n =(cosB ,sinB),求|3m -2n |的取值范围. 10在ABC ∆中,角A B C 、、的对边分别为a b c 、、,(2,)b c a =-m ,(cos ,cos )A C =-n ,且⊥m n 。
⑴求角A 的大小;⑵当22sin sin(2)6y B B π=++取最大值时,求角B 的大小解:⑴由⊥m n ,得0=g m n ,从而(2)cos cos 0b c A a C --= 由正弦定理得2sin cos sin cos sin cos 0B A C A A C --=Q ,(0,)A B π∈,∴1sin 0,cos 2B A ≠=,∴3A π= (6分)⑵22sin sin(2)(1cos 2)sin 2cos cos 2sin 666y B B B B B πππ=++=-++由(1)得,270,2,366662B B ππππππ<<-<-<=∴2B -时,即3B π=时,y 取最大值211在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos cos B C ba c=-+2. (I )求角B 的大小;(II )若b a c =+=134,,求△ABC 的面积. 解:(I )解法一:由正弦定理a A b B cCR sin sin sin ===2得 将上式代入已知cos cos cos cos sin sin sin B C b a c B C BA C=-+=-+22得 即20sin cos sin cos cos sin A B C B C B ++= 即20sin cos sin()A B B C ++=∵A B C B C A A B A ++=+=+=π,∴,∴sin()sin sin cos sin 20 ∵sin cos A B ≠,∴,012=- ∵B 为三角形的内角,∴B =23π.解法二:由余弦定理得cos cos B a c b ac C a b c ab =+-=+-22222222,将上式代入cos cos B C b a c a c b ac ab a b cba c =-++-+-=-+2222222222得× 整理得a c b ac 222+-=-∴cos B a c b ac ac ac =+-=-=-2222212∵B 为三角形内角,∴B =23π(II )将b a c B =+==13423,,π代入余弦定理b a c ac B 2222=+-cos 得 b a c ac ac B 2222=+--()cos , ∴131621123=--=ac ac (),∴∴S ac B ABC △==12343sin . 12ABC ∆中,a 、b 、c 是三个内角A 、B 、C 的对边,关于x 的不等式2cos 4sin 60x C x C ++<的解集是空集.(1)求角C 的最大值;(2)若72c =,ABC ∆的面积S =C 取最大值时a b +的值. 解析:(1)显然0cos =C 不合题意, 则有cos 00C >⎧⎨∆≤⎩,即2cos 016sin 24cos 0C C C >⎧⎨-≤⎩, 即cos 01cos 2cos 2C C C >⎧⎪⎨≤-≥⎪⎩或, 故1cos 2C ≥,∴角C 的最大值为60︒。
…………………6分(2)当C =60︒时,1sin 2ABC S ab C ∆===6ab =,由余弦定理得22222cos ()22cos c a b ab C a b ab ab C =+-=+--,∴22121()34a b c ab +=+=,∴112a b +=。
13在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足(2a -c )cosB=bcosC. (Ⅰ)求角B 的大小;(Ⅱ)设()()()2411m sin A,cos A ,n k,k ,m n ==>⋅u r r u r r且的最大值是5,求k 的值.解:(I )∵(2a -c)cosB=bcosC ,∴(2sinA -sinC )cosB=sinBcosC.……………………………………………2分 即2sinAcosB=sinBcosC+sinCcosB =sin(B+C)∵A+B+C=π,∴2sinAcosB=sinA.…………………………………………4分 ∵0<A<π,∴sinA ≠0.∴cosB=21.…………………………………………………………………5分∵0<B<π,∴B=3π.…………………………………………………………6分(II )m n ⋅u r r=4ksinA+cos2A.…………………………………………………………7分=-2sin 2A+4ksinA+1,A ∈(0,322)……………………………………10分 设sinA=t ,则t ∈]1,0(.则m n ⋅u r r=-2t 2+4kt+1=-2(t -k)2+1+2k 2,t ∈]1,0(.…………………………12分 ∵k>1,∴t=1时,m n ⋅u r r取最大值.依题意得,-2+4k+1=5,∴k=23.14已知锐角△ABC 三个内角为A 、B 、C ,向量()22sin ,cos sin p A A A =-+u v与向量()sin cos ,1sin q A A A =-+v是共线向量.(Ⅰ)求角A. (Ⅱ)求函数232sin cos2C By B -=+的最大值. 解:(Ⅰ) ,p q u r rQ 共线()()()()22sin 1sin cos sin cos sin A A A A A A ∴-+=+-……2分23sin 4A ⇒=…………4分又A为锐角,所以sin 2A =3A π⇒=………6分(Ⅱ)232sin cos 2C B y B -=+2332sin cos 2B B B ππ⎛⎫--- ⎪⎝⎭=+12cos 2122B B =-+sin(2)16B π=-+……………9分 50,2,2666B B ππππ⎛⎫⎛⎫∈⇒-∈- ⎪ ⎪⎝⎭⎝⎭Q …………10分2623B B πππ∴-=⇒=时,max 2y =…………12分15在三角形ABC 中,m =(cos 2C ,sin 2C ), n =(cos 2C ,-sin )2C且n m ,的夹角为3π(1)求C ;(2)已知c=27,三角形的面积S=233,求a+b (a 、b 、c 分别∠A 、∠B 、∠C 所对的边) 解:(1) C CC n m cos 2sin 2cos 22=-=• cosC=21 C=3π(2) c 2=a 2+b 2-2abcosC c=27449=a 2+b 2-ab=(a+b)2-3ab. S=21absinC=21absin 3π=43ab=233Ab=6 (a+b)2=449+3ab=449+18=4121 a+b=21116已知ABC ∆中,角A ,B ,C ,所对的边分别是,,a b c ,且()22223a b c ab +-=; (1)求2sin 2A B +(2)若2c =,求ABC ∆面积的最大值。
