高中数学限时训练8(必修2)
2023-2024学年河北省衡水市高中数学人教A版 必修二第八章 立体几何强化训练-2-含解析

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年河北省衡水市高中数学人教A 版 必修二第八章 立体几何强化训练(2)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟 满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分),是平行直线 ,是异面直线,是共面直线 , 是不相交直线1. 已知平面 平面,,,则下列结论一定正确的是()A.B. C. D. 平面 平面 平面 平面2. 已知如图,六棱锥 的底面是正六边形, 平面.则下列结论不正确的是( )A. B. C. D. 若 , 则若则若l 与的所成角相等,则若l 上有两个点到α的距离相等,则3. 若是三个互不重合的平面,l 是一条直线,则下列命题中正确的是( )A. B. C. D. 4. 如图所示,正方形 的边长为 ,它是水平放置的一个平面图形的直观图,则原图形的周长是( )A. B. C. D.5. 圆锥内接一个正方体,现有一个平面截这个几何体,则截面图形不可能是( )A. B.C. D.充分不必要条件必要不充分条件充要条件既不充分也不必要条件6. 设平面与平面的交线为,则“ 内存在直线”是“ ”的( )A. B. C. D. 若,,则若,则存在,使得若,,,则若,,则7. 已知平面,,和直线,下列命题中错误的是( )A. B. C. D. 01238. 已知两条不同的直线,和两个不同的平面,,有如下命题:①若,,,,则;②若,,,则;③若,,则.其中正确的命题个数为A. B. C. D. 9. 如图,在棱长为的正方体中,为的中点,点在线段上,则点到直线的距离的最小值为().A. B. C. D.224810.如图所示,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰为2的等腰三角形,那么原平面图形的面积是( )A. B. C. D.一条直线与两个平行平面中的一个相交,则必与另一个平面相交平行于同一平面的两个不同平面平行如果平面α不垂直平面β,那么平面α内一定不存在直线垂直于平面β若直线l 不平行平面α,则在平面α内不存在与l 平行的直线11. 下列命题中,错误的是( )A. B. C. D. 4无法确定12. 已知四棱柱ABCD ﹣A 1B 1C 1D 1的外接球体积为,底面ABCD 是边长为1的正方形,则四棱柱ABCD ﹣A 1B 1C 1D 1的侧面积为( )A. B. C. D. 13. 三棱锥中, ⊥平面 , , , ,则三棱锥 的外接球的表面积为 .14. 如图,在棱长为1的正方体, 点 , 分别是棱 , 的中点,是侧面内一点(含边界),若平面 , 点的轨迹长度为 ,三棱锥的体积为 .15. 已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为 .16. 如图,正方体 的棱长为1,P 为BC 的中点,Q 为线段 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). ①当 时,S 为四边形;②当时,S 为等腰梯形;③当时,S 与 的交点R 满足 ;④当时,S 为六边形;⑤当 时,S 的面积为 .17. 如图,在底面是菱形的四棱锥中, 平面,,点分别为的中点,设直线与平面交于点 .(1) 已知平面平面,求证: .(2) 求直线与平面所成角的正弦值.18. 如图,三棱柱,底面,且为正三角形,,为中点.(1) 求三棱锥的体积;(2) 求证:平面平面;(3) 求证:直线平面19. 如图,已知五面体中,为正方形,且平面平面, .(1) 证明:为等腰梯形;(2) 若,求二面角的余弦值.20. 如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.(1) 证明:B1C1⊥平面BDE;(2) 求二面角D﹣BE﹣C1的大小.21. 现需要设计一个仓库,它的上部是底面圆半径为5米的圆锥,下部是底面圆半径为5米的圆柱,且该仓库的总高度为5米.经过预算,制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为4百元/米2、1百元/米2.(1) 记仓库的侧面总造价为y百元,①设圆柱的高为x米,试将y表示为关于x的函数y=f(x);②设圆锥母线与其轴所在直线所成角为θ,试将y表示为关于θ的函数y=g(θ);(2) 问当圆柱的高度为多少米时,该仓库的侧面总造价(单位:百元)最少?答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)18.(1)(2)(3)19.(1)(2)(1)(2)(1)(2)。
2020新教材人教A版必修第二册第八章 8.2 课后课时精练

解 四边形 ABCD 的真实图形如图所示,
∵A′C′在水平位置,A′B′C′D′为正方形, ∴∠D′A′C′=∠A′C′B′=45°,
答案
∴在原四边形 ABCD 中, DA⊥AC,AC⊥BC, ∵DA=2D′A′=2,AC=A′C′= 2, ∴S 四边形 ABCD=AC·AD=2 2.
答案
10.用斜二测画法画出下列图形的直观图(不写画法).
答案
2 2
答案
解析 点 B′到 x′轴的距离等于点 A′到 x′轴的距离 d,而 O′A′=
12OA=1,∠C′O′A′=45°,∴d=
22O′A′=
2 2.
解析
7.如图是水平放置的△ABC 在坐标系中的直观图,其中 D′是 A′C′ 的中点,且∠ACB≠30°,则原图形中与线段 BD 的长相等的线段有________ 条.
后,a′=a,h′=12hsin45°=
42h,S′=12a′h′=12a×
42h=
42×12ah=
2 4
S.
答案
答案 2
答案
解析 △ABC 为直角三角形,因为 D 为 AC 的中点,所以 BD=AD=CD, 所以与 BD 的长相等的线段有两条.
解析
8.如图,四边形 OABC 是上底为 2,下底为 6,底角为 45°的等腰梯形, 用斜二测画法,画出这个梯形的直观图 O′A′B′C′,在直观图中梯形的 高为________.
解析
2.(1)已知△ABC 的直观图△A′B′C′是边长为 a 的正三角形.求原 △ABC 的面积;
(2)如图,△A′B′C′是水平放置的△ABC 斜二测画法的直观图,能否 判断△ABC 的形状;
(3)若(2)中△A′B′C′的 A′C′=6,B′C′=4,则 AB 边的实际长 度是多少?
2023-2024学年江西省高中数学人教A版 必修二第八章 立体几何强化训练-15-含解析

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年江西省高中数学人教A 版 必修二第八章 立体几何强化训练(15)姓名:____________ 班级:____________ 学号:____________考试时间:120分钟满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)1. 如图,点P,Q ,R ,S 分别在正方体的四条棱上,且是所在棱的中点,则直线PQ 与RS 不是共面直线的图是( )A. B.C. D.242. 将一个棱长为 的正四面体放入一个正方体形的玻璃容器,若要求该正四面体能在正方体形容器中自由旋转,则该正方体容器的棱长的最小值为( )A. B.C.D. 3. 如图P 为平行四边形ABCD 所在平面外一点,Q 为PA 的中点,O 为AC 与BD 的交点,下面说法错误的是( )OQ ∥平面PCD PC ∥平面BDQ AQ ∥平面PCD CD ∥平面PABA. B. C. D. ①②②④②③4.设 ,, 是互不重合的平面,m ,n 是互不重合的直线,给出下面四个命题:①若 ,, 则;②若 ,, 则;③若 ,, 则;④若 ,,, 则 .其中所有正确命题的序号是( )A. B. C. D. 存在一条直线a ,a ∥α,a ∥β存在一条直线a ,a ⊂α,a ∥β存在两条平行直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α存在两条异面直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α5. 平面α∥平面β的一个充分条件是( )A. B. C. D.6. 已知球是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)的外接球,,,点在线段上,且,过点作球的截面,则所得截面圆面积的取值范围是( )A.B.C.D.若l ∥α,α∩β=m ,则l ∥m 若l ∥α,m ∥α,则l ∥m 若l ⊥α,l ∥β,则α⊥β若l ∥α,l ⊥m ,则m ⊥α7. 关于直线l ,m 及平面α,β,下列命题中正确的是( )A. B. C. D. 12348. 已知正方形的边长是4,将沿对角线折到的位置,连接.在翻折过程中,给出以下结论:①平面恒成立;②三棱锥的外接球的表面积始终是;③当二面角为时,;④三棱锥体积的最大值是.其中结论正确的个数是( )A. B. C. D. 9. 已知三棱锥的底面是正三角形,,,,,,则三棱锥的外接球的表面积为( )A.B.C.D.若,则若,则若,且,则若,则10. 关于直线以及平面,下列命题中正确的是( )A. B. C. D. 平行于同一平面的两条直线平行平行于同一直线的两平面平行垂直于同一平面的两条直线平行垂直于同一直线的两条直线平行11. 下列命题为真命题的是( )A. B. C. D. 12. 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )23A. B. C. D.13. 在等腰直角三角形中,,D为的中点,将沿翻折,使点A与点B间的距离为,此时四面体的外接球的体积为 .14. 《九章算术》中记载了我国古代数学家祖暅在计算球的体积时使用的一个原理:“幂势既同,则积不容异”,此即祖暅原理,其含义为:两个同高的几何体,如在等高处的截面的面积恒相等,则它们的体积相等.已知双曲线的右焦点到渐近线的距离记为,双曲线的两条渐近线与直线,以及双曲线的右支围成的图形(如图中阴影部分所示)绕轴旋转一周所得几何体的体积为(其中),则双曲线的离心率为 .15. 已知平面,,直线,若,,则直线与平面的位置关系为 .16. 如图,一个水平放置的平面图形的斜二测直观图是直角梯形,且,,,则该平面图形的高为.阅卷人三、解答得分17. 在直平行六面体ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1=1.(1) 求证:OC1∥平面AB1D1(2) 求证:平面AB1D1⊥平面ACC1A1(3) 求三棱锥A1﹣AB1D1的体积.18. 如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.PA=AD=PD=2,且平面PAD⊥平面ABCD,(1) 求证:AB∥EF;(2) 证明:AF⊥平面PCD;(3) 求三棱锥P﹣ACD的体积.19. 如图,在四棱锥中,底面,底面是边长为2的正方形,, F,G分别是,的中点.(1) 求证:平面;(2) 求平面与平面的夹角的大小.20. 如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1, E、F分别是CC1, BC的中点.(1) 求证:平面AB1F⊥平面AEF;(2) 求二面角B1﹣AE﹣F的余弦值.21. 如图,已知是平行四边形所在平面外一点,、分别是、的中点.(1) 求证:平面;(2) 若,,求异面直线与所成的角.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)(3)18.(1)(2)(3)19.(1)(2)20.(1)(2)21.(1)(2)。
人教版高中数学必修第二册8.1——8.3同步测试滚动训练(含答案)
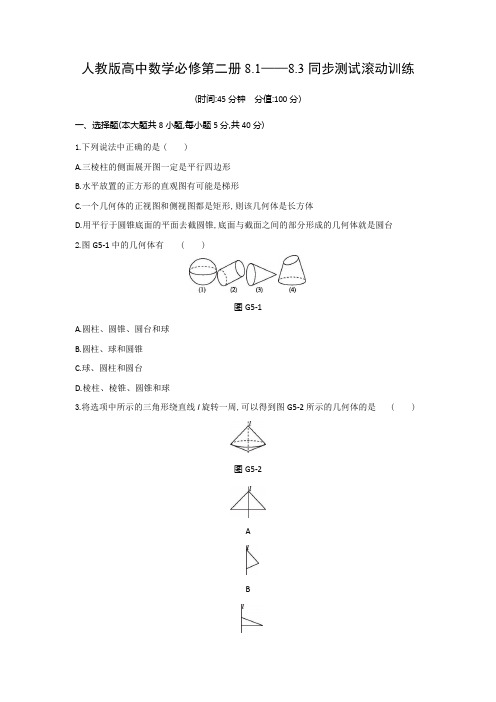
人教版高中数学必修第二册8.1——8.3同步测试滚动训练(时间:45分钟分值:100分)一、选择题(本大题共8小题,每小题5分,共40分)1.下列说法中正确的是()A.三棱柱的侧面展开图一定是平行四边形B.水平放置的正方形的直观图有可能是梯形C.一个几何体的正视图和侧视图都是矩形,则该几何体是长方体D.用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分形成的几何体就是圆台2.图G5-1中的几何体有()图G5-1A.圆柱、圆锥、圆台和球B.圆柱、球和圆锥C.球、圆柱和圆台D.棱柱、棱锥、圆锥和球3.将选项中所示的三角形绕直线l旋转一周,可以得到图G5-2所示的几何体的是()图G5-2ABCD图G5-34.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为()A.1∶3B.1∶9C.1∶33D.1∶(33-1)5.某柱体的正视图与侧视图是全等的正方形,俯视图是圆,记该柱体的表面积为S1,其内切球的表面积为S2,且S1=λS2,则λ=()A.1B.23C.43D.326.在如图G5-4所示的多面体ABCDB1C1D1中,四边形ABCD,四边形BCC1B1,四边形CDD1C1都是边长为6的正方形,则该多面体的体积为()图G5-4A.72B.144C.180D.2167.将一个体积为36π的金属球切割加工成一个底面积为8π的圆柱,则当圆柱的体积最大时,其侧面积为()A.82πB.83πC.62πD.93π8.若圆锥的体积与球的体积相等,且圆锥的底面半径与球的直径相等,则圆锥的侧面积与球的表面积之比为()A.5∶2B.5∶4C.1∶2D.3∶4二、填空题(本大题共4小题,每小题5分,共20分)9.将一个等腰直角三角形绕其斜边所在直线旋转一周所得几何体的体积为V1,绕其一直角边所在直线旋转一周所得几何体的体积为V2,则 1 2=.10.关于斜二测画法,有如下说法:①在画直观图时,由于选轴的不同,所得的直观图可能不同;②等腰三角形的直观图仍然是等腰三角形;③梯形的直观图仍然是梯形;④正三角形的直观图一定为等腰三角形.其中正确说法的序号是.11.在正四棱锥V-ABCD中,底面ABCD的面积为16,一条侧棱的长为211,则该棱锥的高为.12.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且 1 2=94,则 1 2的值是.三、解答题(本大题共3小题,共40分)13.(10分)如图G5-5,该几何体上半部分是母线长为5,底面半径为3的圆锥,下半部分是下底面半径为2,母线长为2的圆台,计算该几何体的表面积和体积.图G5-514.(15分)已知一个圆锥的底面半径为2,母线长为4.(1)求圆锥的侧面展开图的扇形的圆心角;(2)若圆锥中内接一个高为3的圆柱,求圆柱的表面积.15.(15分)如图G5-6,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,且AB=BC=2,A1A=2.(1)求该直三棱柱的表面积;(2)若把两个这样的直三棱柱拼成一个大棱柱,求大棱柱表面积的最小值.图G5-6参考答案与解析1.D[解析]对于选项A,三棱柱的每个侧面都是平行四边形,但是全部展开以后,那些平行四边形未必可以构成一个“大”平行四边形,故A错误.对于选项B,水平放置的正方形的直观图是平行四边形,不可能是梯形,故B错误.对于选项C,一个几何体的正视图和侧视图都是矩形,则该几何体不一定是长方体,也可能是圆柱,故C错误.对于选项D,根据圆台的定义可知D正确.故选D.2.B[解析]由图可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆台,故选B.3.B4.D[解析]由题意得,截得的小锥体与原来大锥体的体积之比为1∶33,故锥体被截面所分成的两部分的体积之比为1∶(33-1),故选D.5.D[解析]由已知可得,该柱体为底面直径与高相等的圆柱,设底面圆的半径为r,则高为2r,则S1=2πr2+2πr·(2r)=6πr2.易知该圆柱内切球的半径为r,则S2=4πr2,则λ= 1 2=6π 24π 2=32,故选D.6.C[解析]如图,把该多面体补成正方体ABCD-A1B1C1D1,则该多面体的体积V=正方体 쪨 - 1쪨11 1- 三棱锥 - 1쪨1 1=63-13×12×63=180.故选C.7.A[解析]设球的半径为R,则由题意知43πR3=36π,解得R=3.当圆柱的体积最大时,圆柱轴截面对角线的长等于球的直径.设圆柱的底面半径为r,则πr2=8π,解得r=22,所以圆柱的高h=2 2- 2=29−8=2,所以圆柱的侧面积S=2πr·h=2π×22×2=82π,故选A.8.A[解析]设圆锥的底面半径为r,圆锥的高为h,则球的半径为 2,由题知13πr2h=43π· 23,解得h= 2,∴圆锥的母线长为 2+ 2=,∴圆锥的侧面积S1=12×2πr2,又球的表面积S2=4π 22=πr2,∴ 1 2=A.9[解析]设等腰直角三角形的斜边长为2,则直角边长为2,则V1=2π3,V21 2=10.①③[解析]由斜二测画法规则可知,正三角形、等腰三角形的直观图不一定是等腰三角形,故②④错误,易知①③正确.11.6[解析]如图,取正方形ABCD的中心O,连接VO,AO,则VO就是正四棱锥V-ABCD的高.∵底面ABCD的面积为16,∴AO=22,又VA=211,∴VO= 2- 2=44−8=6,∴正四棱锥V-ABCD的高为6.12.32[解析]由题意可得甲、乙两个圆柱的底面半径分别为r1r2的高分别为h1= 1 1,h2= 2 2,因为它们的侧面积相等,所以2πr1h1=2πr2h2· 1 1=· 2 2,整理得 1 2==32.13.解:圆锥的侧面积S1=π×3×5=15π,圆台的侧面积S2=π×(3+2)×2=10π,π×22=4π,圆台的下底面面积S底=所以该几何体的表面积S=S1+S2+S底=15π+10π+4π=29π.根据题意得,圆锥的高为4,圆台的高为3,则圆锥的体积V1=13×π×32×4=12π,圆台的体积V2=13×π×3×(32+2×3+22),所以该几何体的体积V=V1+V2=12π.14.解:(1)所求圆心角为2×π×24=4π4=π.(2)由题可知,圆锥的高为23,因为圆柱的高为3,所以圆柱的底面半径为1,则圆柱的表面积S=2×π×12+2×π×1×3=(2+23)π.15.解:(1)该直三棱柱底面的面积为12×2×2=1,侧面积为2×(2+2+2)=42+4,故其表面积S=6+42.(2)设两个这样的直三棱柱拼成一个大棱柱时重合的面的面积为S1,则大棱柱的表面积为2S-2S1,所以当重合的面的面积最大时,大棱柱的表面积最小.因为侧面AA1C1C的面积最大,所以大棱柱表面积的最小值为2S-2四边形 11=4+82.。
高中数学必修2课后限时训练28 圆的一般方程

高中数学必修2课后限时训练28 圆的一般方程一、选择题1.两圆x 2+y 2-4x +6y =0和x 2+y 2-6x =0的圆心连线方程为( )A .x +y +3=0B .2x -y -5=0C .3x -y -9=0D .4x -3y +7=0答案:C解析:两圆的圆心分别为(2,-3)、(3,0),直线方程为y =0+33-2(x -3)即3x -y -9=0,故选C. 2.圆C :x 2+y 2+x -6y +3=0上有两个点P 和Q 关于直线kx -y +4=0对称,则k =( )A .2B .-32C .±32D .不存在 答案:A解析:由题意得直线kx -y =4=0经过圆心C (-12,3),所以-k 2-3+4=0,解得k =2.故选A. 3.当a 取不同的实数时,由方程x 2+y 2+2ax +2ay -1=0可以得到不同的圆,则( )A .这些圆的圆心都在直线y =x 上B .这些圆的圆心都在直线y =-x 上C .这些圆的圆心都在直线y =x 或y =-x 上D .这些圆的圆心不在同一条直线上答案:A解析:圆的方程可化为(x +a )2+(y +a )2=2a 2+1,圆心为(-a ,-a ),在直线y =x 上.4.若圆x 2+y 2-2ax +3by =0的圆心位于第三象限,那么直线x +ay +b =0一定不经过( )A .第一象限B .第二象限C .第三象限D .第四象限答案:D解析:圆x 2+y 2-2ax +3by =0的圆心为(a ,-32b ), 则a <0,b >0.直线y =-1a x -b a ,其斜率k =-1a >0,在y 轴上的截距为-b a>0,所以直线不经过第四象限,故选D.5.在圆x 2+y 2-2x -6y =0内,过点E (0,1)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面只为( )A .5 2B .102C .15 2D .202答案:B解析:圆x 2+y 2-2x -6y =0化成标准方程为(x -1)2+(y -3)2=10,则圆心坐标为M (1,3),半径长为10.由圆的几何性质可知:过点E 的最长弦AC 为点E 所在的直径,则|AC |=210.BD 是过点E 的最短弦,则点E 为线段BD 的中点,且AC ⊥BD ,E 为AC 与BD 的交点,则由垂径定理可是|BD |=2|BM |2-|ME |2=210-[(1-0)2+(3-1)2]=2 5.从而四边形ABCD 的面积为12|AC ||BD |=12×210×25=10 2. 6.已知两定点A (-2,0),B (1,0),如果动点P 满足|P A |=2|PB |,则点P 的轨迹所包围的图形的面积等于( )A .πB .4πC .8πD .9π答案:B解析:设点P 的坐标为(x ,y ),则(x +2)2+y 2=4[(x -1)2+y 2],即(x -2)2+y 2=4,所以点P 的轨迹是以(2,0)为圆心,2为半径长的圆,故面积为π×22=4π.二、填空题7.圆心是(-3,4),经过点M (5,1)的圆的一般方程为________.答案:x 2+y 2+6x -8y -48=0解析:只要求出圆的半径即得圆的标准方程,再展开化为一般式方程.8.设圆x 2+y 2-4x +2y -11=0的圆心为A ,点P 在圆上,则P A 的中点M 的轨迹方程是________. 答案:x 2+y 2-4x +2y +1=0解析:设M (x ,y ),A (2,-1),则P (2x -2,2y +1),将P 代入圆方程得:(2x -2)2+(2y +1)2-4(2x -2)+2(2y +1)-11=0,即为:x 2+y 2-4x +2y +1=0.9.已知圆C :x 2+y 2+2x +ay -3=0(a 为实数)上任意一点关于直线l :x -y +2=0的对称点都在圆C 上,则a =________.答案:-2解析:由题意可知直线l :x -y +2=0过圆心,∴-1+a 2+2=0,∴a =-2. 三、解答题10.判断方程x 2+y 2-4mx +2my +20m -20=0能否表示圆,若能表示圆,求出圆心和半径.解析:解法一:由方程x 2+y 2-4mx +2my +20m -20=0,可知D =-4m ,E =2m ,F =20m -20,∴D 2+E 2-4F =16m 2+4m 2-80m +80=20(m -2)2,因此,当m =2时,D 2+E 2-4F =0,它表示一个点,当m ≠2时,D 2+E 2-4F >0,原方程表示圆的方程,此时,圆的圆心为(2m ,-m ),半径为r =12D 2+E 2-4F =5|m -2|.解法二:原方程可化为(x -2m )2+(y +m )2=5(m -2)2,因此,当m =2时,它表示一个点,当m ≠2时,原方程表示圆的方程.此时,圆的圆心为(2m ,-m ),半径为r =5|m -2|.[点评] (1)形如x 2+y 2+Dx +Ey +F =0的二元二次方程,判定其是否表示圆时有如下两种方法:①由圆的一般方程的定义判断D 2+E 2-4F 是否为正.若D 2+E 2-F >0,则方程表示圆,否则不表示圆.②将方程配方变形成“标准”形式后,根据圆的标准方程的特征,观察是否可以表示圆.(2)在书写本题结果时,易出现r =5(m -2)的错误结果,导致这种错误的原因是没有理解对一个数开偶次方根的结果为非负数.11.自A (4,0)引圆x 2+y 2=4的割线ABC ,求弦BC 中点P 的轨迹方程.解析:方法1:(直接法)设P (x ,y ),连接OP ,则OP ⊥BC ,当x ≠0时,k OP ·k AP =-1,即y x ·y x -4=-1, 即x 2+y 2-4x =0. ①当x =0时,P 点坐标(0,0)是方程①的解,∴BC 中点P 的轨迹方程为x 2+y 2-4x =0(在已知圆内的部分).方法2:(定义法)由方法1知OP ⊥AP ,取OA 中点M ,则M (2,0),|PM |=12|OA |=2, 由圆的定义知,P 的轨迹方程是(x -2)2+y 2=4(在已知圆内的部分).12.已知圆经过点(4,2)和(-2,-6),该圆与两坐标轴的四个截距之和为-2,求圆的方程.解析:设圆的一般方程为x 2+y 2+Dx +Ey +F =0.∵圆经过点(4,2)和(-2,-6),代入圆的一般方程,得⎩⎪⎨⎪⎧4D +2E +F +20=0, ①2D +6E -F -40=0. ②设圆在x 轴上的截距为x 1、x 2,它们是方程x 2+Dx +F =0的两个根,得x 1+x 2=-D .设圆在y 轴上的截距为y 1、y 2,它们是方程y 2+Ey +F =0的两个根,得y 1+y 2=-E .由已知,得-D +(-E )=-2,即D +E -2=0. ③由①②③联立解得D =-2,E =4,F =-20.∴所求圆的方程为x 2+y 2-2x +4y -20=0.。
人教版高中数学必修第二册8.4——8.5同步测试滚动训练(含答案)

人教版高中数学必修第二册8.4——8.5同步测试滚动训练(时间:45分钟分值:100分)一、选择题(本大题共8小题,每小题5分,共40分)1.空间中,如果两个角的两条边分别对应平行,那么这两个角()A.相等B.互补C.相等或互补D.不能确定2.下列条件中能推出平面α与平面β平行的是()A.平面α内有无数条直线与β平行B.平面α内的任意一条直线都与β平行C.直线m∥α,m∥β,且直线m不在α内,也不在β内D.直线m⊂α,直线l⊂β,且m∥β,l∥α3.给出下列四个条件:①空间中的三个点;②一条直线和一个点;③两条平行的直线;④两条垂直的直线.其中能确定一个平面的是()A.①②③④B.①③C.③④D.③4.已知m,n,l1,l2表示直线,α,β表示平面,若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是()A.m∥β且l1∥αB.m∥β且n∥βC.m∥β且n∥l2D.m∥l1且n∥l25.如图G6-1所示,P,Q,R,S分别是所在棱的中点,则这四个点不共面的是()ABCD图G6-16.如图G6-2所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,则下列结论中正确的是()图G6-2A.MN∥APB.MN∥BD1C.MN∥平面BB1D1DD.MN∥平面BDP7.如图G6-3,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P 长度的取值范围是()图G6-3A.[3,17]B.[4,5]C.[3,5]D.[17,5]8.在三棱台ABC-A1B1C1中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且平面BDM∥平面A1C1CA,则动点M的轨迹是()A.平面B.直线C.线段,但只含1个端点D.圆二、填空题(本大题共4小题,每小题5分,共20分)9.空间三个平面之间的交线条数为n,则n的可能值为.10.过平面外一点作与该平面平行的平面有个;过平面外一点作该平面的平行直线有条.11.如图G6-4,在正方体ABCD-A1B1C1D1中,M,N,P,Q,R,S分别是AB,BC,C1D1,C1C,A1B1,BB1的中点,给出下列说法:①PQ与RS共面;②MN与RS共面;③PQ与MN共面.其中正确说法的序号是.图G6-412.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是DD1和AB的中点,若平面B1EF交AD 于点P,则PE=.三、解答题(本大题共3小题,共40分)13.(10分)正方体ABCD-A1B1C1D1如图G6-5所示.(1)若E,F分别为AA1,CC1的中点,画出过点D1,E,F的截面;(2)若M,N,P分别为A1B1,BB1,B1C1上的点(均不与B1重合),求证:△MNP是锐角三角形.图G6-514.(15分)如图G6-6所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AB∥CD,CD=2AB,P,Q分别是CC1,C1D1的中点,求证:平面AD1C∥平面BPQ.图G6-615.(15分)如图G6-7所示,四边形EFGH为四面体ABCD的一个截面,且该截面为平行四边形.(1)求证:AB∥平面EFGH;(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.图G6-7参考答案与解析1.C[解析]由等角定理知选C.2.B[解析]平面α内有无数条直线与β平行,则α与β相交或平行,故A不满足题意;平面α内的任意一条直线都与β平行,则平面α内一定有两条相交直线与平面β平行,则由面面平行的判定定理得α∥β,故B满足题意;直线m∥α,m∥β,且直线m不在α内,也不在β内,则α与β相交或平行,故C不满足题意;直线m⊂α,直线l⊂β,且m∥β,l∥α,则α与β相交或平行,故D不满足题意.故选B.3.D[解析]对于①,当这三个点共线时,经过这三个点的平面有无数个,故①不满足题意.对于②,当此点在此直线上时,有无数个平面经过这条直线和这个点,故②不满足题意.对于③,根据推论3可知两条平行直线唯一确定一个平面,故③满足题意.对于④,当这两条直线是异面直线时,这两条直线不同在任何一个平面内,不能确定一个平面,故④不满足题意.故选D.4.D[解析]由题意得,m,n是平面α内的两条直线,l1,l2是平面β内的两条相交直线,要使α∥β,一个平面内有两条相交直线和另一个平面平行即可,故选D.5.D[解析]对于选项A,连接PS,QR,易证PS∥QR,∴P,S,R,Q四点共面;对于选项B,过P,S,R,Q可作一个正六边形,∴P,S,R,Q四点共面;对于选项C,连接PQ,RS,易证PQ∥RS,∴P,Q,R,S四点共面.故选D.6.C[解析]易知MN与AP是异面直线,故A中结论不正确.易知MN与BD1是异面直线,故B中结论不正确.连接AC,与BD交于点O,则O为BD的中点,连接OD1,ON.在正方体ABCD-A1B1C1D1中,∵M,N分别是C1D1,BC的中点,∴ON∥CD∥D1M,ON=12CD=D1M,∴四边形MNOD1为平行四边形,∴MN∥OD1.∵MN⊄平面BB1D1D,OD1⊂平面BB1D1D,∴MN∥平面BB1D1D,故C中结论正确.由选项C知MN∥平面BB1D1D,而平面BB1D1D和平面BDP相交,∴MN与平面BDP不平行,故D中结论不正确.故选C.7.D[解析]取A1D1的中点E,在DD1上取点F,使D1F=2DF,连接EF,C1E,C1F,则易知平面CMN ∥平面C1EF.∵P是侧面ADD1A1内一动点(含边界),C1P∥平面CMN,∴P∈线段EF,∵C1E= 1 12+ 1 2=5,C1F= 1 12+ 1 2=5,∴当P与EF的中点重合时,线段C1P的长度取得最小值,当P与点E或点F重合时,线段C1P的长度取得最大值.取EF的中点O,连接C1O,则由题意知EF=42,C1O= 1 2- 2=25−(22)2=17,∴线段C1P长度的取值范围是[17,5].故选D .8.C [解析]如图所示,在平面A 1B 1C 1内,过D 作DN ∥A 1C 1,交B 1C 1于点N ,连接BN.∵AA 1∥BD ,AA 1⊂平面A 1C 1CA ,BD ⊄平面A 1C 1CA ,∴BD ∥平面A 1C 1CA.∵DN ∥A 1C 1,DN ⊄平面A 1C 1CA ,A 1C 1⊂平面A 1C 1CA ,∴DN ∥平面A 1C 1CA.∵BD ∩DN=D ,∴平面BDN ∥平面A 1C 1CA.∵点M 是△A 1B 1C 1内(含边界)的一个动点,且平面BDM ∥平面A 1C 1CA ,∴M 的轨迹是线段DN ,且M 与D 不重合,即动点M 的轨迹是线段,但只含1个端点.故选C .9.0,1,2,3[解析]三个平面可以互相平行,可以交于同一条直线,可以两个平面平行且被第三个平面所截,也可以两两相交,故答案为0,1,2,3.10.1无数[解析]过平面外一点作与该平面平行的平面,这样的平面有且只有1个.在符合题意的平面上过这个点的直线有无数条,这些直线都与原平面平行.11.①③[解析]连接PR ,QS ,因为P ,Q ,R ,S 分别是C 1D 1,C 1C ,A 1B 1,B 1B 的中点,所以PR B 1C 1,QS B 1C 1,所以PRQS ,所以四边形PRSQ 是平行四边形,故①正确;连接QN ,C 1B ,PM ,则由题意得QN 12C 1B PM ,所以PQ 与MN 共面,故③正确;因为MN 与RS 既不平行也不相交,故②错误.12[解析]过点C 1作C 1G ∥B 1F ,交CD 于点G ,过点E 作HQ ∥C 1G ,交CD 的延长线于点H ,交C 1D 1于点Q ,连接B 1Q ,HF 交AD 于点P ,则HQ ∥B 1F ,所以Q ,H ,F ,B 1四点共面.由正方体的棱长为1,易知CG=BF=12.设D 1Q=x ,由题知HD=D 1Q ,因为C 1Q ∥HG ,HQ ∥C 1G ,所以四边形HQC 1G 为平行四边形,所以HG=QC 1,即x+12=1-x ,解得x=1.由题可知△PDH ∽△PAF ,所以= =2,则PD=13.在Rt △PED 中,可得PE= 2+ 2=13.解:(1)过点D 1,E ,F 的截面如图所示.(2)证明:设MB 1=a ,NB 1=b ,PB 1=c ,则MN 2=a 2+b 2,NP 2=b 2+c 2,MP 2=c 2+a 2,所以在△MNP 中,cos M= 2+ 2- 22 · =2 22 · >0.同理可得cos N>0,cos P>0.故△MNP的三个内角均为锐角,即△MNP是锐角三角形.14.证明:在直四棱柱ABCD-A1B1C1D1中,易知C1D1∥CD,C1D1=CD.∵AB∥CD,∴AB∥C1D1,即D1Q∥AB.∵Q为C1D1的中点,∴D1Q=12C1D1=12CD=AB,∴四边形D1QBA为平行四边形,∴AD1∥BQ,又AD1⊂平面AD1C,BQ⊄平面AD1C,∴BQ∥平面AD1C.∵P,Q分别为CC1,C1D1的中点,∴PQ∥CD1,又PQ⊄平面AD1C,CD1⊂平面AD1C,∴PQ∥平面AD1C.∵BQ∩PQ=Q,∴平面AD1C∥平面BPQ.15.解:(1)证明:∵四边形EFGH为平行四边形,∴EF∥HG,又HG⊂平面ABD,EF⊄平面ABD,∴EF∥平面ABD.∵EF⊂平面ABC,平面ABD∩平面ABC=AB,∴EF∥AB,又AB⊄平面EFGH,EF⊂平面EFGH,∴AB∥平面EFGH.(2)设EF=x(0<x<4),∵四边形EFGH为平行四边形,∴ = 4,则 6= = - =1- 4,∴FG=6-32x,∴四边形EFGH的周长l=2x+6-32x=12-x,又0<x<4,∴8<l<12,即四边形EFGH周长的取值范围是(8,12).。
2022一轮浙江通用技术选考练习:必修2 第1单元 结构与设计 课后限时训练8 Word版含答案

课后限时训练(八)一、选择题1.如图所示的健身器材,使用者可双手握住扶手,双脚站在踏板上,进行闲逛动作。
当使用者站在踏板上不运动时,连杆的主要受力形式为()A.受拉、受弯曲B.受压、受弯曲C.受扭转、受弯曲D.受压、受扭转A[本题考查构件的受力基本形式。
连杆承受使用者的重力荷载,受力方向沿杆向下,使杆伸长,因此连杆肯定受拉的作用,A项正确,B、C、D项错误。
]2.如图所示,电风扇旋转过程中,倾斜的扇叶将风向前推,扇叶的主要受力形式是()A.受拉、受剪切B.受弯曲、受拉C.受扭转、受剪切D.受压、受剪切B[本题考查构件的基本受力形式。
扇叶一端与转轴固定,一端悬空,受空气的反作用力而弯曲,因此B项正确]3.如图所示的结构中,不属于...壳体结构的是()A.平安帽B.电饭煲C.窗台护栏D.天文台穹顶C[本题考查结构的类型。
壳体结构是指层状的结构,而窗台护栏是有瘦长杆件组成,不具有层状特征,应属于框架结构,因此C项符合题意。
]4.在下列操作过程中,主要受力形式为既受压又受扭转的工具是()A.锯条B.钻头C.锉刀D.剪刀B[本题考查构件的受力形式。
锯条和锉刀受压,剪刀受压,钻头受压和扭转,因此B项正确。
]5.如图所示为某支架的试验方案,支架在同一竖直平面内对称放置。
立柱和转臂的主要受力形式是()A.立柱受压、转臂受弯B.立柱受压、转臂受扭转C.立柱受扭转、转臂受弯D.立柱受弯、转臂受压A[本题主要考查结构中各构件的主要受力形式。
构件的基本受力形式有受拉、受压、受剪切、受扭转和受弯曲等,构件的受力形式,主要依据受力后构件的形变趋势来进行推断。
依据题意,该支架在对称静止放置的时候,装置最左、右两端分别受到重物供应的一个向下的拉力,使得转臂发生弯曲变形的趋势,表现为受弯曲;由于整个装置未发生旋转,因此立柱没有受扭转,而主要承受转臂对它的压力,仅表现为受压。
]6.如图所示是一款创意三轮车葡萄酒瓶架。
若要提高它的稳定性,有效的改进措施是()A.增加瓶筐材料的直径B.缩短前后轮的距离C.增大两后轮的直径D.增大两后轮的间距D[本题考查影响结构稳定性的因素。
高一数学江苏省新课标数学限时训练8(必修2)

第8练 班级 姓名 1.经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是
.
2.一个点到圆的最小距离为6cm ,最大距离为9cm ,则该圆的半径是 .
3.圆O 的弦AB 垂直平分半径OC ,则四边形OACB 是 形.
4.过直线x+y -2=0和直线x-2y+1=0的交点,且垂直于第二直线的直线方程为 .
5.已知半径为1的动圆与圆(x -5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是 .
6.方程(x-2)2+(y+1)2=1表示的图形关于点T (-3,2)的对称图形方程是 .
7.已知圆x 2+y 2=r 2在曲线|x|+|y|=4的内部,则半径r 的范围是 .[来源:Z 。
xx 。
]
8.若实数x 、y 满足等式 3)2(22=+-y x ,那么
x
y 的最大值为 .
9.求经过点P(6,-4),且被圆x 2+y 2=20截得的弦长为62的直线方程.
10.已知圆x2+y2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b对称,(1)求k、b的值;(2)若这时两圆的交点为A、B,求∠AOB的度数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8练 班级 姓名 1.经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是
.
2.一个点到圆的最小距离为6cm ,最大距离为9cm ,则该圆的半径是 .
3.圆O 的弦AB 垂直平分半径OC ,则四边形OACB 是 形.
4.过直线x+y -2=0和直线x-2y+1=0的交点,且垂直于第二直线的直线方程为 .
5.已知半径为1的动圆与圆(x -5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是
.
6.方程(x-2)2+(y+1)
2=1表示的图形关于点T (-3,2)的对称图形方程是
.
8.若实数x 、y 满足等式 3)2(22=+-y x ,那么
x
y 的最大值为 . 9.求经过点P(6,-4),且被圆x 2+y 2
=20截得的弦长为62的直线方程.
10.已知圆x 2+y 2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b 对称,
(1)求k、b的值;(2)若这时两圆的交点为A、B,求∠AOB的度数.。
