框架—侧移计算例题
框架结构内力位移计算算例
结构力学课程大作业——多层多跨框架结构内力及位移计算班级学号姓名华中科技大学土木工程与力学学院年月日结构力学课程大作业——多层多跨框架结构内力与位移计算一、任务1、计算多层多跨框架结构在荷载作用下的弯矩和结点位移。
2、计算方法要求：（1）用迭代法、D 值法、反弯点法及求解器计算框架结构在水平荷载作用下的弯矩，并用迭代法的结果计算其结点位移。
（2）用迭代法、分层法、二次力矩分配法及求解器计算框架结构在竖向荷载作用下的弯矩，并用迭代法的结果计算其结点位移。
3、分析近似法产生误差的原因。
二、计算简图及基本数据本组计算的结构其计算简图如图1所示，基本数据如下。
混凝土弹性模量：723.010/h E kN m =⨯构件尺寸：柱：底 层：23040b h cm ⨯=⨯其它层：23030b h cm ⨯=⨯ 梁：边 梁：22560b h cm ⨯=⨯中间梁：22530b h cm ⨯=⨯ 水平荷载：'15P F kN ＝，30P F kN ＝（见图2）竖向均布恒载：17/q kN m 顶＝ 21/q kN m 其它＝（见图8） 图1各构件的线刚度：EIi L =，其中312b h I ⨯=边 梁：33410.250.6 4.51012I m -⨯==⨯F 7311 3.010 4.510225006EI i kN m L -⨯⨯⨯===⋅ 中间梁： 34420.250.3 5.6251012I m -⨯==⨯ 7422 3.010 5.6251067502.5EI i kN m L -⨯⨯⨯===⋅ 底层柱： 33440.30.4 1.61012I m -⨯==⨯ 7344 3.010 1.61096005EI i kN m L -⨯⨯⨯===⋅ 其它层柱：34430.30.3 6.751012I m -⨯==⨯ 7433 3.010 6.75106136.43.3EI i kN m L -⨯⨯⨯===⋅ 三、水平荷载作用下的计算 （一）用迭代法计算1、计算各杆的转角分配系数ikμ' 转角分配系数计算公式：()2ikikiki i i μ'=-∑结点“1”：12225000.3932(6136.422500)μ'=-=-⨯+156136.40.1072(6136.422500)μ'=-=-⨯+结点“2”：21225000.3182(67506136.422500)μ'=-=-⨯++图2232(67506136.422500)⨯++266136.40.0872(67506136.422500)μ'=-=-⨯++由于该结构是对称结构，因此结点“3”的分配系数应该等于结点“2”的，结点“4”的分配系数应该与结点“1”的相等，所以本题只需计算1、2、5、6、9、10、13、14、17、18结点的分配系数。
框架施工图—内力分析及侧移计算(建筑构造)
（2） 侧移刚度d的确定 侧移刚度d表示柱上下两端有单位侧移时在柱中产生的 剪力。根据假定（1），梁柱线刚度之比无穷大，则各 柱端转角为零，由结构力学的两端无转角但有单位水平 位移时杆件的杆端剪力方程，柱的侧移刚度d可写成：
V 12 i
d= =
c
D
h2
EI
i=
c
h
内力分析及侧移计算
（3）同层各柱剪力的确定
（5
柱端弯矩确定以后，根据节点平衡条件可确定梁的弯矩。
对于边柱节点（图(a)），有Mb=Mc1+Mc2 对于中柱节点（图1(b))
Mb1=ib1/(ib1+ib2)(Mc1+Mc2 Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
内力分析及侧移计算
如图所示，从框架中任取一柱AB，根据转角位移方
内力分析及侧移计算
分层法
认为某层框架梁上的荷载只给本层梁及与本层梁相连的框架产 生剪力和弯矩
进行弯矩分配后叠加，叠加后的不平衡弯矩再分配但不传递
内力分析及侧移计算
2 框架在水平荷载作用下内力的近似计算——反弯点法和D值法
A 反弯点法 反弯点法基本假定: （1） 在进行各柱间的剪力分配时，假定梁与柱的线
（2） 在确定各柱的反弯点位置时，假定除底层柱以
多层多跨框架所受水平荷载主要是风荷载及水平 地震作用。一般可简化为作用在框架节点上的集中 荷载，其弯矩图如图(a)所示。它的特点是，各杆的 弯矩图都是直线形，每杆都有一个零弯矩点，称为 反弯点。框架在水平荷载作用下的变形情况如图(b) 所示
内力分析及侧移计算
程，柱两端剪力为：
V
=
12ic h2
6ic h
框架侧移刚度计算
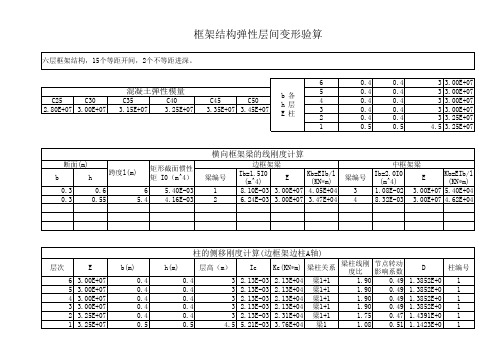
梁柱线刚 节点转动 度比 影响系数 1.90 0.49 1.90 0.49 1.90 0.49 1.90 0.49 1.75 0.47 1.08 0.51
D
1.3852E+0 1.3852E+0 1.3852E+0 1.3852E+0 1.4391E+0 1.1423E+0
柱编号
1 1 1 1 1 1
层次
E
6 3.00E+07
5 3.00E+07
4 3.00E+07
3 3.00E+07
2 3.25E+07 1 3.25E+07
b(m) 0.4 0.4 0.4 0.4 0.4 0.5
层次
E
6 3.00E+07 5 3.00E+07 4 3.00E+07 3 3.00E+07 2 3.25E+07 1 3.25E+07
横向框架顶点位移计算
Gi（KN） ∑Gi(KN）
Di
7200
7200
798315
7200
14400
798315
7200
21600
798315
7200
28800
798315
7200
36000
836720
7200
43200
627006
△(m) 0.0090 0.0180 0.0271 0.0361 0.0430 0.0689
层次
6 5 4 3 2 1
弹性层间变形验算
层间剪力 Vi(KN)
层间刚度Di
层间侧移△ （m）
层间相对 层高hi(m) 弹性转角
地震作用下框架内力和侧移计算
6 地震作用下框架内力和侧移计算6.1刚度比计算刚度比是指结构竖向不同楼层的侧向刚度的比值。
为限制结构竖向布置的不规则性，避免结构刚度沿竖向突变，形成薄弱层。
根据《建筑抗震设计规范》（GB50011-2010）第3.4.2条规定：抗侧力构件的平面布置宜规则对称、侧向刚度沿竖向宜均匀变化、竖向抗侧力构件的截面尺寸和材料强度宜自下而上逐渐减小、避免侧向刚度和承载力突变。
根据《高层建筑混凝土结构技术规程》（JGJ3-2010）第3.5.2条规定：对框架结构，楼层与其相邻上层的侧向刚度比计的比值不宜小于0.7，且与相邻上部三层刚度平均值的比值不宜小于0.8。
计算刚度比时，要假设楼板在平面内刚度无限大，即刚性楼板假定。
7.0939.0/1136076/1066908211>===∑∑mmN mmN DDγ，满足规范要求；()8.0939.0/113607611360761136076/10669083343212>=++⨯=++=∑∑∑∑mmN mmN DD D D γ，满足规范要求。
依据上述计算结果可知：刚度比满足要求，所以无竖向突变，无薄弱层，结构竖向规则，故可不考虑竖向地震作用。
将上述不同情况下同层框架柱侧移刚度相加，框架各层层间侧移刚度∑iD ，见表6-4。
6.2水平地震作用下的侧移计算根据《高层建筑混凝土结构技术规程》（JGJ3-2010）附录C 中第C.0.2条可知：对于质量和刚度沿高度分布比较均匀的框架结构、框架剪力墙结构和剪力墙结构，其基本周期可按公式6-1计算。
T T T μψ7.11= (6-1)式中:1T ——框架的基本自振周期；T μ——计算结构基本自振周期的结构顶点假想位移，单位为m ； T ψ——基本自振周期考虑非承重砖墙影响的折减系数。
根据《高层建筑混凝土结构技术规程》（JGJ3-2010）第4.3.17条规定：1、框架结构可取0.6～0.7；2、框架-剪力墙结构可取0.7～0.8；3、框架-核心筒结构可取0.8～0.9；4、剪力墙结构可取0.8～1.0。
《分层法》例题详解
例:如图1所示一个二层框架,忽略其在竖向荷载作用下的框架侧移,用分层法计算框架的弯矩图,括号内的数字,表示各梁、柱杆件的线刚度值(EIil)。
图1解:1、图1所示的二层框架,可简化为两个如图2、图3所示的,只带一层横梁的框架进行分析。
图2 二层计算简图图3 底层计算简图2、计算修正后的梁、柱线刚度与弯矩传递系数采用分层法计算时,假定上、下柱的远端为固定,则与实际情况有出入。
因此,除底层外,其余各层柱的线刚度应乘以0.9的修正系数。
底层柱的弯矩传递系数为12,其余各层柱的弯矩传递系数为13。
各层梁的弯矩传递系数,均为12。
图4 修正后的梁柱线刚度图5 各梁柱弯矩传递系数3、计算各节点处的力矩分配系数计算各节点处的力矩分配系数时,梁、柱的线刚度值均采用修正后的结果进行计算,如:G节点处:7.630.6687.63 3.79GH GHGHGH GDGjGi ii iiμ====++∑GD3.790.3327.63 3.79GD GDGH GDGjGi ii iiμ====++∑H节点处:7.630.3537.63 3.7910.21HG HGHGHG HE HIHjHi ii i iiμ====++++∑3.790.1757.63 3.7910.21HI HIHIHG HE HIHjHi ii i iiμ====++++∑10.210.4727.63 3.7910.21HE HEHEHG HE HIHjHi ii i iiμ====++++∑同理,可计算其余各节点的力矩分配系数,计算结果见图6、图7。
图6 二层节点处力矩分配系数图7 底层节点处力矩分配系数4、采用力矩分配法计算各梁、柱杆端弯矩(1)第二层:①计算各梁杆端弯矩。
先在G、H、I节点上加上约束,详见图8图8 二层计算简图计算由荷载产生的、各梁的固端弯矩(顺时针转向为正号),写在各梁杆端下方,见图9:213.13kN m 12F GHql M =-=-⋅213.13kN m 12F HGql M ==⋅ 27.32kN m 12F HI ql M=-=-⋅27.32kN m 12F IHql M==⋅ 在节点G 处,各梁杆端弯矩总与为:13.13kN m FG GH M M ==-⋅在节点H 处,各梁杆端弯矩总与为:13.137.32 5.81kN m F F H HG HI M M M =+=-=⋅在节点I 处,各梁杆端弯矩总与为:7.32kN m F I IH M M ==⋅②各梁端节点进行弯矩分配,各两次,详见图9 第一次弯矩分配过程:放松节点G,即节点G 处施加力矩13.13kN m ⋅,乘以相应分配系数0、668与0、332,得到梁端+8.76kN m ⋅与柱端+4.37kN m ⋅,+8.76kN m ⋅按12传到GH 梁H 端;放松节点I,即在节点I 处施加力矩7.32kN m -⋅,乘以相应分配系数0、935与0、065,得到梁端 6.32kN m -⋅与柱端+1.00kN m ⋅, 6.32kN m -⋅按12传到IH 梁H 端;放松节点H,相应的在节点H 处新加一个外力偶矩,其中包括GH 梁右端弯矩、IH 梁左端弯矩、GH 梁与IH 梁传来的弯矩。
框架—侧移计算例题上课讲义
侧移验算——剪切型变形计算
对第i层柱，其层间相 对侧移为：
uiM
Vi
m
Dij
j 1
i
对第i层柱顶的侧移为：uiM uk k 1
n
顶层柱顶的侧移为： unM uk k 1
侧移验算——弯曲型变形计算
建筑高度越大，宽度越小，则在水平荷载作用下由 轴向变形引起的侧移越大。对于高度不大于50m或高宽 比小于4的钢筋混凝土框架结构，柱轴向变形引起的顶 点位移在框架梁柱弯曲变形引起的顶点侧移的5%以内， 可以忽略不计。
(0.6)
(0.9)
3.3m
74kN
C
(1.7) G
(1.0)
K
(0.7)
(0.9)
B
80.7kN
(2.4) F
(0.6)
(0.8)
A
E
2.7m
(1.2)
8.1m
(0.9) 3.3m
J
(0.8) 3.9m
I
解：由于框架同层各柱 h 相等，可直接用杆件线刚度的相对值计算各柱的
分配系数。
DH
M
（1）求各柱剪力分配系数：
侧移验算—— 侧移值要求
高度不大于150m的框架结构在正常使用条件下的变 形验算要求各层的层间侧移值与该层层高之比不宜超过 1/550的限值，即:
ui hi 1 550
详情请参阅《高规》。
用反弯点法求下图框架的弯矩图。图中括号内的数值为该杆
的线刚度比值。
37kN D
H
(1.5)
M (0.8)
(0.7)
)
1.0 1.7 1.0
30.56kN
M GC
(M GH
水平作用下框架结构侧移计算
一、横向水平地震作用下框架结构侧移验算1.横向框架梁的线刚度在框架结构中，现浇楼面可以作为梁的有效翼缘，增大梁的有效线刚度，减小框架侧移。
为考虑这一有利作用， ，在计算梁的截面惯性矩时，对现浇楼面的边框架梁取 I b1.5I 0 〔 I 0 为梁的截面惯性矩〕；对中框架梁取 I b2.0I 0 ，计算结果如下表所示：边框架梁中框架梁梁截面尺寸矩形截面惯性矩 混 凝E c〔 b/mm ×跨度 l/m土 强i b EI b / li b EI b / l /I 0 / ×103 m4I b1.5I 0I b 2.0I 0h/mm 〕度 等/ KN m2/×104KN m×104KN m级3 4/×103 4/×10mmAB 跨 300×600C3030×106横梁BC 跨 300×600C3030×106横梁AC 跨 300×600C30 30×106横梁CD 跨 300×450C3030×106横梁DE 跨 300×600C3030×106横梁2.柱的侧移刚度〔 D 值法〕柱线刚度计算结果如下表：混凝土强 截面尺寸2截面惯性矩线刚度 i c EI c / h柱号度等级〔a/mm × b/mm 〕柱高 h/mEc/KN mIc / ×103 m 4/ ×104 KN mZ 1C30 700×70030×106Z 2C30 ×6550 55030×10：楼层横向框架柱侧移刚度〔 D 值〕计算如下表所示：Ki b K(一般层 )(一般层 )2i c K12柱类型Dic h 2根数i b/ 104KN / mK K(底层 )2(底层 )i c K一层其他层边框架边柱边框架中柱中框架边柱中框架中柱D边框架边柱边框架中柱中框架边柱中框架中柱DA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6653520KN/mA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6794540KN/m3.横向框架自振周期结构自振周期按顶点位移法计算，将各楼层面处的重力荷载代表值G i作为水平荷载作用在各楼层标高处，按弹性方法求得结构顶点的假想侧移，并考虑填充墙对框架的影响取折减系数r，计算结果如下表结构顶点的假想侧移G/KN nG i/KND i / KN m 1i / mm i / mm楼层V Gii 16999099907945405114582144879454041145832906794540311458443647945402114585582279454011241563237653520T1T T4.横向水平地震作用及楼层地震剪力计算本结构重量和刚度沿高度方向分布比拟均匀，高度不超过40m，变形以剪切变形为主，故水平地震作用采用底部剪力法计算。
侧移刚度计算
框架侧移刚度计算在框架结构中，现浇楼面可以作为梁的有效翼缘，增大梁的有效刚度、减少侧移，对于现浇楼面，考虑到这一有利作用，在设计梁的截面的惯性矩时，对现浇板的b 0b 02.0 1.5I I I I ==中框架梁，边框架梁。
本设计中框架柱采用C35混凝土，梁、板采用C30混凝土，海南三亚地区防震烈度7度，基本地震加速度0.1g 。
C30混凝土 E c =3.0×104N/mm 2框架柱1-5层均采用C35混凝土 E c =3.15×104N/m m 2横梁线刚度计算横梁线刚度i b 计算注：0I 为横梁的截面惯性矩 柱线刚度计算柱的侧移刚度D 值法计算 （1） 计算方法柱的侧移刚度按下式计算。
根据梁柱线刚度比K 的不同，结构平面布置图，可分为中框架中柱、边柱，边框架中柱、边柱和楼梯柱，其中楼梯柱的计算在楼梯配筋计算。
柱的侧移刚度D 值计算hiccD 212α=c α:柱侧移刚度修正系数，对不同情况按下式计算，K 表示墙柱线刚度比。
修正系数c α值计算公式（2）框架侧移刚度值计算底层：框架中柱（B1、C1、B2、C2、B 3、C3、B4、C4、B5、C5、B6、C6点处的柱12根）K =ici i 21+=1025.3104.11108.4101010⨯⨯⨯+=4.9825.0++=K Kc α=0.785 hiccD 212α==33001025.321012785.0⨯⨯=28112.95 N/mm Di=∑D=12D=12×28112.95=337355.37 N/mm框架边柱纵向（A1、D1、A2、D2、A3、D 3、A4、D4、A5、D5、A6、D6、共12根）ici K 2==1025.3108.41010⨯⨯=1.4825.0++=K Kc α=0.57 hiccD 212α==33001025.32101257.0⨯⨯=20413.22 N/mmDi=∑D=12Di=12×20413.22=244958.68 N /mm框架边柱横向（A 、B 、C 、D 、A7、B7、C7、D7共8根）ici K 2==1025.3104.111010⨯⨯=3.5125.0++=K Kc α=0.73 hiccD 212α==33001025.32101273.0⨯⨯=26143.25 N/mm Di=∑D=8Di=8×26143.25=209146.01 N/m m2～5层：框架中柱（B1、C1、B2、C2、B3、C3、B 4、C4、B5、C5、B6、C6点处的柱12根）K =12342ci i i ii +++=()1025.32104.11108.41010102⨯⨯⨯⨯⨯+=4.98c α=2KK+=0.71h ic c D 212α==33001025.32101271.0⨯⨯=25427.00 N/mm Di=∑D=12D=12×25427.00=305124.00 N/mm框架边柱纵向（A1、D1、A2、D2、A3、D 3、A4、D4、A5、D5、A6、D6、共12根）ici i K 242+==1025.32108.421010⨯⨯⨯⨯=1.48c α=2KK+=0.43 h icc D 212α==33001025.32101243.0⨯⨯=15399.45 N/mm Di=∑D=12Di=12×15399.45=184793.39 N /mm框架边柱横向（A 、B 、C 、D 、A7、B7、C7、D7共8根）ici i K 242+==1025.32104.1121010⨯⨯⨯⨯=3.51c α=2KK+=0.64 hiccD 212α==33001025.32101264.0⨯⨯=22920.11 N/mmDi=∑D=8Di=8×22920.11=183360.88 N/m m 4）各楼层框架柱总的侧移刚度框架侧移刚度D 值（N/mm ）将上述不同情况下同层框架侧移刚度相同，即得框架柱各层层间侧移刚度∑D i各层层间侧移刚度（N/mm）∑D1/∑D2=791460.06/673278.27=1.18>0.7，故该框架为规则框架。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M DH 19.42kN
M DC 19.42kN
MGH 16.67kN
D
H
(1.5)
G
M GC ? MGC 52.04kN
M GK ?
C
MGK 30.56kN
B
M GF 65.93KN
A
1.0
MGK (MGH MGF ) 1.7 1.0 30.56kN
G (1.7)
F (2.4)
E
M GC
(M GH
M GF
) 1.7 1.7 1.0
52.04kN
M (0.8)
K (1.0)
J (1.2)
I
例5-2：要求用Ｄ值法分析图5-8所示框架结构的内力， 剖面图中给出了水平力及各杆件的线刚度的相对值。
10
解:(1)各杆件的Ｄ值、各层所有柱Ｄ之和，以及每根柱分配到的 剪力见表5-2。每层有5根中柱与10根边柱。
侧移验算
多层框架结构中，由柱轴向变形引起的整体弯曲型 变形所占比例很小，只须计算由框架杆件弯曲变形引起 的整体剪切型变形；当框架高度较大（大于50m）或较 柔(高宽比大于4)时，柱的轴力较大，轴力引起的水平变 形（二阶效应）不可忽略。
侧移验算——剪切型变形计算
对第i层柱，其层间相 对侧移为：
uiM
(0.6)
(0.9)
3.3m
74kN
C
(1.7) G
(1.0)
K
(0.7)
(0.9)
80.7kN B
(2.4) F
(0.6)
(0.8)
A
E
2.7m
6
(1.2)
8.1m
(0.9) 3.3m
J
(0.8) 3.9m
I
解：由于框架同层各柱 h 相等，可直接用杆件线刚度的相对值计算各柱的
分配系数。
D
H
M
（1）求各柱剪力分配系数：
GF
KJ
0.9 0.7 0.9 0.9
0.360
底层：
BA
0.6
0.6 0.8
0.8
0.272
FE
JI
0.8 0.6 0.8 0.8
0.364
D
H
M
（2）求各柱在反弯点处的剪力：
37kN
VDC DC 37 11.77kN
CG
K
74kN
VCB CB (37 74) 31.08kN
BF
J
VBA
BA
(37
74
80.7)
52.14kN
80.7kN
A
E
I
（3）求各柱柱端弯矩：3.3
M DC M CD VDC 2 19.42kN m
M BC
M CB
VBC
3.3 2
51.28kN m
M
AB
2M
BA
VBA
2 3.9 3
135.56k N
m
（4）求梁端弯矩：梁端弯矩按梁线刚度分配 D
Vi
m
Dij
j 1
i
对第i层柱顶的侧移为：uiM uk k 1
n
顶层柱顶的侧移为： unM uk k 1
侧移验算——弯曲型变形计算
建筑高度越大，宽度越小，则在水平荷载作用下由 轴向变形引起的侧移越大。对于高度不大于50m或高宽 比小于4的钢筋混凝土框架结构，柱轴向变形引起的顶 点位移在框架梁柱弯曲变形引起的顶点侧移的5%以内， 可以忽略不计。
D
c
Kc
12 h2
11
12
(2)各柱的反弯点位置
13
(2)各柱的反弯点位置
14
（３）弯矩图：
15
作业：用D值法计算下图框架各杆件的弯矩，并绘出弯矩图。 圆括号内的数字为杆件的相对线刚度，各层框架节点处的作用 力为风荷载的简化力。
16
解：１.计算各层柱的Ｄ值及每根柱分配的剪力
17
１.计算各层柱的Ｄ值及每根柱分配的剪力
侧移验算—— 侧移值要求
高度不大于150m的框架结构在正常使用条件下的变 形验算要求各层的层间侧移值与该层层高之比不宜超过 1/550的限值，即:
ui hi 1 550
详情请参阅《高规》。
用反弯点法求下图框架的弯矩图。图中括号内的数值为该杆
的线刚度比值。
37kN D
H
(1.5)
M (0.8)
(0.7)
18
２.计算反弯点高度比
19
３.计算各柱
４.计算各梁端弯矩
22
４.计算各梁端弯矩
23
５. 弯矩图
24
(0.7)
(0.6)
(0.9)
C
G
K
顶层：
DC
0.7
0.7 0.6
0.9
0.318
(0.7) B
(0.9) F
(0.9) J
HG
0.7
0.6 0.6
0.9
0.273
(0.6) A
(0.8) E
(0.8) I
MK
0.9 0.7 0.6 0.9
0.409
二层：
CB
0.7
0.280
0.7 0.9 0.9