第3章 力矩和平面力偶系
工程力学(静力学与材料力学)第三章力偶系详解

FB
r M2 0 ∑ M = 0 , FA sin
M 2 2r FA
M2 = 4M1 = 8kNm
2M 1 FO FB FA 8kN r
• 作业3-1,3-4,3-8
考虑CB部分为二力构件,得:
FC FA FB FC
例3-4
图示机构自重不记。圆轮上的销子 A 放在 摇杆 BC上的光滑导槽内。M 1 = 2kNm,OA = r = 0.5m 。图示位置OA⊥OB,α = 30°,且系统平衡。 求作用于摇杆 BC 上力偶的矩 M 2 及 O、B 支座的反 力。 解:受力分析
M1
R
F1
M
F2
2
M1 + M2 = rBA×F1 + rBA×F2 = rBA×( F1 + F2 ) = rBA×R = M
如有n个力偶,按上法依次合成, 最后得一力偶,合力偶矩矢为 M = M1 +M2 + … +Mn = ∑M I
B
rBA
A
F2
F1
任意个力偶可以合成为一个 合力偶,这个合力偶矩矢等于各 分力偶矩矢的矢量和。 M = M 1+ M 2+ … + M n = ∑M i
性质三
证:
力偶没有合力
仍用反证法,即假定力偶有合力,那么总可 找到一个与此力大小相等,方向相反而作用线 共线的力与此力平衡,即力与力偶相平衡。与 性质二矛盾。
性质一、二和三告诉我们力偶只能与力偶等 效而不能与单个力等效。
•力偶只能与力偶相平衡 力偶只能与力偶相平衡
§3-4 力偶系的合成
设有两个力偶,由性质一,将 力偶中两力分别移到两力偶作用面 交线上的两点 A 和 B,可得到两个 汇交力系,其合力分别为R 、 R ’ 。
工程力学I-第3章 力矩与平面力偶系

D
x
§3-2 关于力偶的概念
力偶:一对等值、反向而不共线的平行力,用 符号(F ,F′)表示。
力偶臂:两个力作用
线之间的垂直距离d。
F’
F
力偶的作用面:两个 力作用线所决定的平 面
§3-2 关于力偶的概念
F F
d
d
F
d
F
F
F
转动游戏方向盘
拧水龙头
扳手拧螺母
§3-2 关于力偶的概念
Q AABD AABC 显然, 并注意到力偶矩的转向也相同, 则有M ( F , F ) M ( P, P) P
M (P 1, P 1 ) M ( P, P ) 显然, 1, P 1) 从而有M ,( F , F ) M ( P
P1
力偶等效
M ( F , F ) M ( P 1, P 1)
(1)力对点之矩,不仅取决于力的大小,还与矩心的位置有关。
(2)力对任一点之矩,不因该力的作用点沿其作用线移动而改变。 *(3)力的大小等于零或其作用线通过矩心时,力矩等于零。 (4)互成平衡的两个力对同一点之矩的代数和为零。
Mo(F)=±Fd
§3-1 关于力矩的概念及其计算
合力矩定理:
y Fy
(3)将力P和P’沿各自的作用 线移至任意点A’,B’,根 据力的可传性原理,有 (P,P’) =(P1,P1’) 。
§3-2 关于力偶的概念
(4) A′
P1′ b F′ A A F B Q′ D P′ B′ C
M (F , F ) AB BD 2 AABD ,
M(P, P') AB BC 2 AABC
第三章 力偶与平面力偶理论)

M 0 F F h
力对点之矩(力矩)是一个代数量,它的绝 对值等于力的大小与力臂的乘积;
它的正负:力使物体绕矩心逆时针转向时为正,反之为负。 常用单位为 N· m 或 kN· m。 注意:力矩在下列几种情况下等于零 (1)力的大小等于零;
(2)力的作用线通过矩心,即力臂等于零;
(3) 互成平衡的二力对同一点之矩为零。
78.93N m
按合力矩定理 M O F M O Ft M O Fr
F cos θ r 78.93N m
例3-2 已知:q,l; 求: 合力及合力作用线位置. 解: 取微元如图
x q q l l x 1 P q dx ql 0 l 2
M Mi Mi
i 1 n
平面力偶系平衡的充要条件 M = 0,有如下平衡方程
Mi
0
平面力偶系平衡的必要和充分条件是:所有各力 偶矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO
F F h F r cos θ
M1 F1 d M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
=
=
FR F1 F2 Fn
F1 F2 Fn FR
=
=
=
M FRd F1d F2d Fnd M1 M 2 M n
定理:同平面内的两个力偶,如果力偶矩相等,则两力偶 彼此等效。 推论: 任一力偶可在它的作用面内任意转移,而不改变它对刚体 的作用。因此力偶对刚体的作用与力偶在其作用面内的位置无 关。 只要保持力偶矩不变,可以同时改变力偶中力的大小与 力偶臂的长短,对刚体的作用效果不变.
工程力学 第3章 力偶系
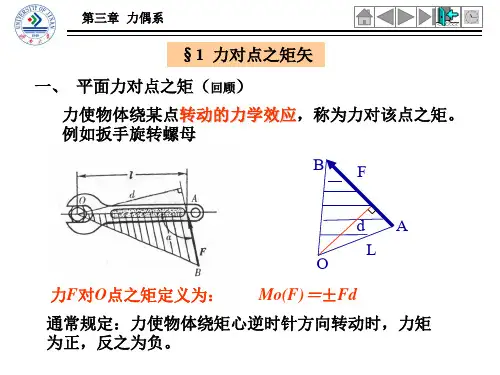
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
第三章-力矩和平面力偶系-第四章-平面任意力系
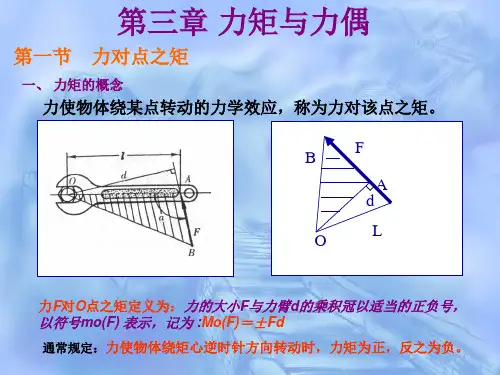
例3-1 试计算力对A点之矩。
解 本题有两种解法。 方法一: 按力矩的定义计算 由图中几何关系有:
d=ADsinα =(AB-DB)sinα =(AB- BCctgα)sinα =(a- bctgα)sinα =asinα-bcosα
所以
mA(F)=F•d =F(asinα-bcosα)
方法二:
解:
图(a):
MA = - 8×2 = -16 kN ·m
MB = 8×2 = 16 kN ·m
图(b): MA = - 4×2×1 = -8 kN · m
MB = 4×2×1 = 8 kN ·m
第二节 力偶
▪ 一、力偶 力偶矩
▪
在日常生活和工程实际中经常见到物体受动两个大小相等、方向相反,
但不在同一直线上的两个平行力作用的情况。例如
2.力偶矩:
▪ 作为力偶对物体转动效应的量度,称为力偶矩,
用m或m( F ,F′)表示。在平面问题中,将力偶中
的一个力的大小和力偶臂的乘积冠以正负号,如图:
即m(F)=F•d=±2ΔABC
通常规定:力偶使物体逆时针方 向转动时,力偶矩为正,反之为 负。
在国际单位制中,力矩的单位 是牛顿•米(N•m)或千牛顿•米 (kN•m)。
▪
在同一平面内的两个力偶,只要两力偶的
力偶矩的代数值相等,则这两个力偶相等。这
就是平面力偶的等效条件。
▪ 根据力偶的等效性,可得出下面两个推论:
▪ 推论1 力偶可在其作用面内任意移动和转动, 而不会改变它对物体的效应。
▪ 推论2 只要保持力偶矩不变,可同时改变力 偶中力的大小和力偶臂的长度,而不会改变它 对物体的作用效应。
主矩: Mo=m1+m2+···+mn
第三章_力对点的矩_平面力偶系

4
平面力偶系的合成和平衡条件
平面力偶系的合成
平面力偶系:作用在同一平面内的一群力偶。 平面力偶系:作用在同一平面内的一群力偶。
=
FR = F1 + F2 + Fn
=
=
′ FR = F1′ + F2′ + Fn′
平面力偶系合成的结果是一个合力偶, 平面力偶系合成的结果是一个合力偶,合力 偶矩等于力偶系中各力偶矩的代数和 中各力偶矩的代数和。 偶矩等于力偶系中各力偶矩的代数和。
力对点的矩
F
h
O
M 0 ( F ) = ± Fh
力对点的矩是一个代数量,它的绝对值 绝对值等于力的大小 力对点的矩是一个代数量,它的绝对值等于力的大小 与力臂的乘积,它的正负可按下法确定, 正负可按下法确定 与力臂的乘积,它的正负可按下法确定,力使物体绕 矩心逆时针转向时为正,反之为负。 矩心逆时针转向时为正,反之为负。 力矩表示力使物体绕某点旋转的量度。 力矩表示力使物体绕某点旋转的量度。 量度
A α M1
OBBiblioteka M2DB 解: 因为杆AB为二力杆,故其反力F 和F 只 因为杆AB为二力杆 故其反力FAB 为二力杆, BA A
α
M1 M2
D
能沿A 能沿A,B的连线方向。 的连线方向。 分别取杆OA和DB为研究对象 分别取杆OA和DB为研究对象。因为力偶只能 为研究对象。 与力偶平衡,所以支座O 与力偶平衡,所以支座O和D的约束力FO 和FD 只 的约束力F ∴ 能分别平行于F 能分别平行于FAB 和FBA ,且与其方向相反。 且与其方向相反。 B 写出杆OA和DB的平衡方程 写出杆OA和DB的平衡方程: ∑M = 0 的平衡方程:
力对点的矩
工程力学第三章力矩与平面力偶系_图文
例题讲解
【解】作 AB 梁的受力图,如图( b )所示。AB梁上作用 有二个力偶组成的平面力偶系,在 A 、B 处的约束
反力也必须组成一个同平面的力偶 ( , ) 与之平衡。 由平衡方程
() RA 、RB为正值,说明图中所示RA 、RB 的指向正确。
力臂d
=
1m
×
sinα
=
1m
×
。 sin45 =
m
MB(F)=+F×d= +15kN×0.5 m = +7.5 kN ·m
注意:负号必须标注,正号可标也可不标。一般不标注。
§3-1力矩的概念和计算
(二)合力矩定理
表达式: 证明: 由图得
而 则
Fy
F
A
Fx
()
§3-1力矩的概念和计算
()
若作用在 A 点上的是一个汇交力系( 、 、 ),则可将每个力对 o 点之矩相加,有
2. 力偶的三要素 (2)力偶的方向; (3)力偶的作用面。
3. 力偶的性质 (1)力偶在任何坐标轴上的投影等于零;
(2)力偶不能合成为一力,或者说力 偶没有合 力,即它不能与一个力等效, y
因而也不能被一个力平衡;
(3)力偶对物体不产生移动效应,只 产生转动 效应,既它可以也只能改变物
体的转动状 态。
例题讲解
【例题5】在一钻床上水平放置工件,在工件上同时钻四个等 直径的孔,每个钻头的力偶矩为 求工件的总切削力偶矩和A 、B端水平反力?
解: 各力偶的合力偶距为
根据平面力偶系平衡方程有:
由力偶只能与力偶平衡的性质 ,力NA与力NB组成一力偶。
例题讲解
理论力学第三章力矩与平面力偶理论(H)
理论⼒学第三章⼒矩与平⾯⼒偶理论(H)第3章⼒矩与平⾯⼒偶理论※平⾯⼒对点之矩的概念及计算※⼒偶及其性质※平⾯⼒偶系的合成与平衡※结论与讨论§3-1 平⾯⼒对点之矩的概念及计算1.⼒对点之矩AFBhhF M O ?±=)(F h ——⼒臂O ——矩⼼OABM O Δ±=2)(F M O (F ) ——代数量(标量)“+”——使物体逆时针转时⼒矩为正;“-”——使物体顺时针转时⼒矩为负。
2. 合⼒之矩定理平⾯汇交⼒系合⼒对于平⾯内⼀点之矩等于所有各分⼒对于该点之矩的代数和。
3. ⼒矩与合⼒矩的解析表达式xA FF xF yOαyx yx y y O x O O yF xF M M M ?=+=)()()(F F F )()()()()(21i O n O O O R O M M M M M F F F F F ∑=+++=")()(ix i iy i R O F y F x M ?∑=FF nαOrF rF 已知:F n ,α,r求:⼒F n 块对轮⼼O 的⼒矩。
h解:(1)直接计算αcos )(r F h F M n n n O ==F (2)利⽤合⼒之矩定理计算αcos )()()()(r F M M M M n O O r O n O ==+=F F F F 例题1§3-2 ⼒偶及其性质1.⼒偶与⼒偶矩⼒偶——两个⼤⼩相等、⽅向相反且不共线的平⾏⼒组成的⼒系。
⼒偶臂——⼒偶的两⼒之间的垂直⼒偶的作⽤⾯——⼒偶所在的平⾯。
(1)⼒偶不能合成为⼀个⼒,也不能⽤⼀个⼒来平衡。
⼒和⼒偶是静⼒学的两个基本要素。
(2)⼒偶矩是度量⼒偶对刚体的转动效果;它有两个要素:⼒偶矩的⼤⼩和⼒偶矩的转向。
F′FABOdx FdFxxdFMMMOOO=+′=′+=′)()()(),(FFFF⼒偶矩±=FdM2.平⾯⼒偶的等效定理1F ′F ′2F ′0F ′F 00F ′F 0ABDCdF F 1F 2★在同平⾯内的两个⼒偶,如果⼒偶矩相等,则两⼒偶彼此等效。
第三章 力对点之矩与平面力偶
第三章力对点之矩与平面力偶一、判断题1、力偶是物体间相互的机械作用,这种作用的效果是使物体的运动状态发生改变。
力偶没合力,不能用一个力来等效代换,也不能用一个力来与之平衡。
(√)2、力偶使物体转动的效果完全由力偶矩来确定,而与矩心位置无关。
只要力偶矩相同,不管其在作用面内任意位置,其对刚体的作用效果都相同。
(√)3、01=∑=n i i M是平面力偶系平衡的充要条件。
(√)4、半径为R 的圆轮可绕通过轮心轴O 转动,轮上作用一个力偶矩为M 的力偶和一与轮缘相切的力F,使轮处于平衡状态。
这说明力偶可用一力与之平衡。
(×)5.刚体的某平面内作用一力和一力偶,由于力与力偶不能等效,所以不能将它们等效变换为一个力。
(×)解析:一个力和一个力偶可以简化为一个力。
6、物体受同一平面内四个力的作用,这四个力组成两个力偶(F1,F1′)和(F2,F2′),其组成的力多边形自行封闭,该物体处于平衡。
(×)7、力偶不是基本力学量,因为构成力偶的两力为基本量。
(×)解析:(1)力学中的基本物理量是长度、质量、时间。
(2)国际单位制中的基本单位:长度,米(m);质量,千克(kg);时间,秒(s);电流,安(A);热力学温度,开(K);物质的量,摩(mol);发光强度,坎(cd)。
8、自由刚体受到力偶作用时总绕力偶臂中点转动。
(×)解析:动力学可以证明,静止的自由刚体受力偶作用时,总是绕着刚体的质量中心转动(与质量分布有关,与作用位置无关)。
9、力偶的合力等于零。
(×)解析:力偶是一对大小相等方向相反但不在同一条直线上的两个力,这与力的平衡定理作用在同一直线上的两个力大小相等方向相反则两力平衡是相悖的.力偶对平面内任意点的力矩不为零.10、力偶的合成符合矢量加法法则。
(×)解析:三角形法则,平行四边形法则。
三角形法则是:如果是两个矢量的相加将这两个矢量的首尾相接,从一个矢量的开头指向另一个矢量的末尾就是它们的和向量。
第三章力矩和平面力偶系第四章平面任意力系
解:
图(a):
MA = - 8×2 = -16 kN ·m
MB = 8×2 = 16 kN ·m
图(b): MA = - 4×2×1 = -8 kN · m
MB = 4×2×1 = 8 kN ·m
第二节 力偶
▪ 一、力偶 力偶矩
▪
在日常生活和工程实际中经常见到物体受动两个大小相等、方向相反,
但不在同一直线上的两个平行力作用的情况。例如
第三节 平面力偶系的合成与平衡
一、平面力偶系的合成
作用在物体同一平面内的各力偶组成平面力偶系。
m1=F1•d1,m2=F2•d2, m3=-F3•d3,
P1•d=F 1•d1 ,P2•d=F2•d2 , -P3•d =-F3•d3
FR=P1+P2-p3
FR′=P1′+P2′-P3′
M=FR d=(P1+P2-P3)d
二、力偶的性质
▪ 力和力偶是静力学中两个基本要素。力 偶与力具有不同的性质:
▪ (1)力偶不能简化为一个力,即力偶不 能用一个力等效替代。因此力偶不能与 一个力平衡,力偶只能与力偶平衡。
▪ (2)无合力,故不能与一个力等效;
▪ (3)力偶对其作在平面内任一点的矩恒 等于力偶矩,与矩心位置无关。
结论:
第三章 力矩与力偶
第一节 力对点之矩
一、 力矩的概念
力使物体绕某点转动的力学效应,称为力对该点之矩。
B
F
A d
O
L
力F对O点之矩定义为:力的大小F与力臂d的乘积冠以适当的正负号, 以符号mo(F) 表示,记为 :Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩为正,反之为负。
▪ 力 F 对O 点之矩的大小,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
F d m O (F )
B A
d F'
由于O点是任取的
x
O
m F d
+
—
性质3:力偶不能简化为一个力,即力偶不能用一个力等效替
代。因此力偶不能与一个力平衡,力偶只能与力偶平衡。
力偶的作用效果取决于三个因素:构成力偶的力、 力偶臂的大小、力偶的转向。 故在平面问题中用一带箭头的弧线来表示如图所求, 其中箭头表示力偶的转向,m表示力偶矩的大小 m表 示。
即:
mi 0
i 1
n
例:三铰拱 AC 的部分上作用有力偶,其力偶矩为 M 。已知 两个半拱的直角边成正比,即 a : b = c : a ,不计三铰拱自重,求 A、B 两点的约束力。
解:各杆受力图如图,由几何关系可得FA 、FC 垂直于AC 。建立平衡方程
M
解得:
FA
0:
M FA
+
-
说明:
①
M O ( F )是代数量。
② 影响转动的独立因素。 M 当F=0或d=0时, O ( F ) =0。
④单位Nm。 ⑤
M O (F )
=2⊿AOB=Fd ,2倍⊿形面积。
在平面问题中,力对点之矩只取决于力矩的大小及其旋 转方向(力矩的正负),因此可以视为代数值。
通常规定:力偶使物体逆时针方向转动时,力偶矩为正,反 之为负(与力矩符号的规定相同)。在国际单位制中,力矩 的单位是牛顿•米(N•m)或千牛•米(kN•m)。
说明:
①力偶矩m是代数量,有+、-;
②F、 d 都不独立,只有力偶矩
③m的值:m=±2⊿ABC ; ④单位:N• m
m F d 是独立量;
解:以杆O1B 为研究对象,受力图如图,建立平衡方程
M
0:
M 2 F A O1 A 0
M
0:
M 2 F A O1 A 0
以曲柄OA 和套筒为研究对象,对于曲柄和套筒力偶只能 与力偶平衡,故力FA 、FO 必构成力偶。受力图如图,建立平 衡方程
由于
a b 0
2 2
M a b
2 2
F B F C F C F A
M a b
2 2
例:图示机构,套筒A 穿过摆杆 O1B ,用销子连接在曲柄OA 上,已知长为 a ,其上作用有力偶 M1 。在图示位置β=30o ,机 械能维持平衡。不计各杆自重及摩擦,试求在摆杆 O1B 上所加力 偶的力偶矩 M2 。
平面力系 ①平面汇交力系 ②平面平行力系(平面力偶系是其中的特殊情况 ) ③平面一般力系(平面任意力系)
平面汇交力系、平面力偶系和平面平行力系:平面特殊力系 力对物体可以产生 移动效应--取决于力的大小、方向; 转动效应--取决于力矩的大小、方向。
§3-1 力矩的概念
一、平面中力对点之矩
力使刚体产生绕点转动效应的度量称为力对点之矩。 例如:扳手旋转螺母,开门、关门。
二、合力矩定理
定理:平面汇交力系的合力对平面内任一点的矩,等于所有各
分力对同一点的矩的代数和。
M O ( F R ) M O ( F1 ) M O ( F 2 ) M O ( F n )
M
O
(F )
[证] 由合力投影定理有:
od=ob+oc
M o ( F 2 ) 2 oAC oA oc M o ( R ) 2 oAD oA od
3、力偶的性质
(1)力偶无合力,不能与一个力等效,力偶不能与一个力平衡。 (2)力偶对其所在平面内任一点的矩恒等于力偶矩,而与矩心的 位置无关,因此力偶对刚体的效应用力偶矩度量。 (3)力偶不能简化为一个力,即力偶不能用一个力等效替代。因此 力偶不能与一个力平衡,力偶只能与力偶平衡。
四、平面力偶等效条件
由右图知,力 F 使物体绕O点转动的 效应,不仅与力的大小有关,而且与O点
到力的作用线的垂直距离d 有关,故用乘 积F· 来度量力的转动效应。 d
力的大小F与力臂d的乘积冠以适当的正负号,以 符号Mo(F) 表示,记为:
M O ( F ) F d 2 AO B
通常规定:力使物体绕矩 心逆时针方向转动时为正,反 之为负。
§3-2 力偶的概念
一、力偶和力偶矩
作用于刚体上等值、反向、平行而不共线的 两个力组成的力系,记作(F,F’)
两个力作用线之间的垂直距离称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
1、力偶:
力偶作用面、力偶臂d
方向盘
(图a)司机转动驾驶汽车时两手作用在方向盘上的力;
(图b)工人用丝锥攻螺纹时两手加在扳手上的力;
M R A d ( P1 P2 ) d P1 d P2 d m1 m 2
结论:
M m1 m 2 m n m i
i 1 n
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩 的代数和。 平面力偶系平衡的充要条件是:所有各力偶矩的代数和
等于零。
力偶在同一刚体内是一自由矢量
§3-3
平面力偶系的合成与平衡
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
d
d
m 1 F1 d 1 ;
又 m 1 P1 d
m 2 P2d
'
R A P1 P2'
R B P1' P2
'
m 2 F2 d 2
合力矩
M 0:
M 1 F A O A sin 30 0
o
FA FA
O A O 1 A sin 30
o
解得:
M 2 4M1
第三章
一、力对点之矩
M O ( F ) F h 2 O A B
力矩与平面力偶系
正负规定:力使刚体绕点逆时针转为正,顺时针转为负。
二、合力矩定理
M O ( F R ) M O ( F1 ) M O ( F 2 ) M O ( F n )
M
O
(F )
⑴ 平面力系合力对平面内任一点之矩等于各分力对同一点之矩的 代数和。 ⑵ 合力对任一轴之矩等于各分力对同一轴之矩的代数和。
三、力偶和力偶矩
作用于刚体上等值、反向、平行而不共线的两个力组成的力系 1、力 偶 2、力偶矩 力偶对物体转动效应的量度
• 由此可得力矩的性质: (1)力对点之矩,不仅取决于力的大小, 还与矩心的位置有关。力矩随矩心的位置 变化而变化。 (2)力对任一点之矩,不会因该力的作用 点沿其作用线移动而改变,再次说明力是 滑移矢量(这也符合力的可传性)。 (3)力的大小等于零或其作用线通过矩心 时,力矩等于零。互成平衡的两个力对同 一点之矩的代数和为零。
(图c)以及用两个手指拧动水龙头所加的力等等。
力偶只能使物体产生转动,不能使物体产生移动。
力偶不能与一个力等效,力和力偶是静力学中两个基本元素。
2、力偶矩:
作为力偶对物体转动效应的量度, 称为力偶矩。用M 或M(F ,F′)表示。 在平面问题中,将力偶中的一个力 的大小和力偶臂的乘积冠以正负号,即 M(F)=F•d=±2ΔABC
C F
B A d
F'
3、力偶的性质
性质1:力偶既没有合力,本身又不平衡,是一个基本力学量。
它在任一轴上投影的代数和均为零——故不能与一个力等效。
F
R=F'-F=0
d F'
力偶 无合力
性质2:力偶对其所在平面内任一点的矩恒等于力偶矩,而
与矩心的位置无关,因此力偶对刚体的效应用力偶矩度量。
M O ( F ) M O ( F ') F ( x d ) F ' x
i 1
n
平衡的充要条件是:所有各力偶矩的代数和等于零。
mi 0
i 1
n
二、平面力偶等效定理
作用在同一平面内的两个力偶,只要它的力偶矩的大小 相等,转向相同,则该两个力偶彼此等效。
例如:双手操作方向盘
M ( F , F ) M ( F 1 , F 1)
可得下列两个推论:
⑴力偶可以在其作用面内任意移动,而不影响它对 刚体的作用效应。
⑵ 保持力偶矩矢量的大小和方向不变,可改变力 偶中的力和力偶臂,不改变对刚体的作用效应。
工程力学
Engineering Mechanics
华东交通大学
Department of Mechanics of School of Civil Engineering and Architecture of East China Jiaotong University
第三章 力矩和平面力偶系
引 言
力偶矩矢等效条件是两个力偶矩矢相等。
推论:
(1)力偶可以在其作用面内任意移动,而不影响它对刚体的作用效应。
(2)保持力偶矩矢量的大小和方向不变,可改变力偶中的力和力偶臂,不 改变对刚体的作用效应。
五、平面力偶系的合成与平衡
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的代数和。
M m1 m 2 m n m i
又∵ M o ( F1 ) 2 oAB oA ob
现 M o ( R ) M o ( F1 ) M o ( F2 ) 证 毕
例:求图所示力F 对A 点之矩。
解:将力F 分解两垂直的力Fx 、Fy ,由合力矩定理可得
M A ( F ) M A ( F x ) M A ( F y ) F cos b F sin a
