(完整版)北京版小学六年级数学知识点汇总剖析,推荐文档
(完整版)北师大版小学数学六年级上册知识点整理+各单元练习,推荐文档

4.小数与百分数互化的规则:
把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号;
把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
5.百分数与分数互化的规则:
把分数化成百分数,通常先把分数化成小数(除不尽的保留三位小数),再把小
15.在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
16.在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
17.一个环形,外圆的半径是 R,内圆的半径是 r,它的面积是 S= R²- r² 或 S= (R²-r²)。
(其中 R=r+环的宽度.)
19.半圆的周长等于圆的周长的一半加直径。半圆的周长与圆周长的一半的区别在于,
4.利率:利息与本金的比值叫做利率。
5.银行存款税后利息的计算公式:税后利息=利息×(1-20%)
6.国债利息的计算公式:利息=本金×利率×时间 7.本息:本金与利息的总和叫做本息。 8.应纳税额:缴纳的税款叫应纳税额。
9.税率:应纳税额与各种收入的比率叫做税率。
10.应纳税额的计算:应纳税额=各种收入×税率 例如:李老师把 2000 元钱存入银行,整存整取五年,年利率按 4.14%计算,到期时, 李老师的本金和利息共有多少元? 解题思路:要求“本金和利息共有多少元”应该用本金的 2000 元加上利息的。 解题步骤:第一步:根据“利息=本金×利率×时间”算利息
24.在同一圆中,圆心角占圆周角的几分之几,它所在扇形面积就占圆面积的几分之
几;所对的弧就占圆周长的几分之几.
25.当长方形,正方形,圆的周长相等时,圆的面积最大,长方形的面积最小
26.扇形弧长公式: 扇形的面积公式: S= n r²
(完整版)北京版小学六年级数学知识点汇总剖析,推荐文档

一、常用的数量关系式1、速度×时间=路程路程÷速度=时间路程÷时间=速度2、单价×数量=总价总价÷单价=数量总价÷数量=单价3、加数+加数=和和-一个加数=另一个加数4、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率5、被减数-减数=差被减数-差=减数差+减数=被减数6、因数×因数=积积÷一个因数=另一个因数7、被除数÷除数=商被除数÷商=除数商×除数=被除数8、利润与折扣问题 利润=售出价格-成本利息=本金×利率×时间二、基本概念第一章:数与代数1. 数的认识正整数整数 0数负整数② 计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是 10。
这样的计数法叫做十进制计数法。
③ 大小比较【熟读即可】A 比较整数大小:位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
B 比较小数的大小:先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……C 比较分数的大小:分母相同的分数,分子大的分数比较大;分子相同的数,分母小的分数大。
分数的分母和分子都不相同的,先通分,再比较两个数的大小。
④ 数的改写一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
1.准确数:把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
例如把 1254300000 改写成以万做单位的数是 125430 万;改写成以亿做单位的数 12.543 亿。
(完整版)新北师大版小学数学六年级上册知识点整理与归纳

六年级数学上册知识点整理一、圆1、圆有无数条半径,有无数条直径。
圆心决定圆的位置,半径决定圆的大小。
2、在同一个圆中,所有的半径都相等,所有的直径都相等。
在同一个圆中,直径是半径的2倍,半径是直径的12。
3、圆内最长的线段是直径,圆规两脚之间的距离是半径。
4、在一个正方形里画一个最大的圆,圆的直径就是正方形的边长。
在一个长方形里画一个最大的圆,圆的直径就是长方形的宽。
5、常见的轴对称图形:等腰三角形(1条)、等边三角形(3条)、等腰梯形(1条)、长方形(2条)、正方形(4条)、圆(无数条)、半圆(1条)。
6、圆的周长=圆周率×直径即 C 圆=πd =2πr 。
7(理解)、圆所占平面的大小叫圆的面积。
把圆等分的份数越多,拼成的图形就越接近平行四边形或长方形。
拼成的平行四边形的底相当于圆周长的一半,高相当于圆的半径;长方形的长相当于圆周长的一半,宽相当于圆的半径。
8、如果用S 表示圆的面积,r 表示圆的半径,那么圆的面积公式:S 圆=πr 2。
9(特别注意)半圆的周长不是圆的周长的一半,而是圆的周长的一半再加上一条直径长,即πr+2r ;2半圆的面积是圆的面积的一半,即πr 2。
10、周长相等时,圆的面积最大;面积相等时,圆的周长最小。
考试一般正方形、长方形和圆:①它们周长相等时,圆的面积最大,正方形面积居中,长方形的面积最小;②它们面积相等时,长方形周长最大,正方形周长居中,圆的周长最小。
11、一个圆的半径扩大(缩小)几倍,直径就扩大(缩小)几倍,周长也扩大(缩小)几倍,面积就扩大(缩小)几的平方倍,但圆周率永远不变。
如:r 扩大3倍,d 扩大3倍,C 扩大3倍,S 扩大9倍.12、几个公式:C =πd =2πr d =C 圆πd = 2r S Cd 圆=πr r =2πr =213、永远记住要带单位,周长是(cm),面积是平方(cm 2),体积是立方(cm 3)。
14、背诵:3.14×1=3.14 3.14×2=6.283.14×3=9.42 3.14×4=12.563.14×5=15.7 3.14×6=18.843.14×7=21.98 3.14×8=25.123.14×9=28.26 3.14×10=31.415、圆的面积:3.14×12=3.14 3.14×22=12.563.14×32=28.26 3.14×42=50.243.14×52=78.5 3.14×62=113.04二、分数混合运算1(计算题,一定注意运算顺序)分数混合运算的运算顺序与整数混合运算的运算顺序完全相同,都是先算乘除,再算加减,有括号的先算括号里的。
最新-北师大版小学数学六年级(全册)知识点归纳 精品

北师大版小学数学六年级(全册)知识点第一单元圆1、使学生认识圆的特征:圆的半径、直径、圆心。
认识在同圆内半径和直径的关系。
知道圆是轴对称图形,有无数条对称轴,而这些对称轴都过圆心。
知道生活中有了圆才使我们的生活更美好。
2、认识同心圆、等圆。
知道圆的位置由圆心决定,圆的大小由半径或直径决定。
等圆的半径相等,位置不同;而同心圆的半径不同,位置相同。
3、使学生知道圆的周长和圆周率的含义,掌握圆的周长的计算公式,能够正确地计算圆的周长.介绍祖冲之在圆周率研究上的成就,渗透爱国主义教育。
在运用上,要能根据圆的周长算直径或半径,会算半圆的周长:圆的周长×1/2+直径。
会求组合图形的周长。
4、了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式。
5、能正确运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题。
会灵活运用圆的面积公式。
已知圆的周长会算圆的面积,会求组合图形的面积。
会算圆环的面积,并且知道在周长相等的情况下,正方形、长方形、圆三种图形中,圆的面积最大。
6、在估一估和探究圆面积公式的活动中,体会“化曲为直”的思想,初步感受极限思想。
第二单元百分数的应用本单元重点讲解百分数在生活中的应用,知识点为:1、知道百分数的意义:表示一个数是另一个数的百分之几的数,叫做百分数。
百分数也叫做百分率或百分比。
百分数通常不写成分数形式,而用百分号“%”表示;百分数有时也定义为分母是100的分数,但百分数与分数是有区别的:分数既可表示具体的量,又可表示两个数量间的倍比关系;然而百分数只能表示两个数量间的倍比关系;所以是不名数,也就是不能带单位的数。
2、在具体情景中理解“增加百分之几”或“减少百分之几”的意义,加深对百分数意义的理解。
3、能解决有关“增加百分之几”或“减少百分之几”的实际问题,提高运用数学解决实际问题的能力,体会百分数与现实生活的密切联系。
4、知道出勤率、出粉率、成活率等百分数的意义及在实际生活中的应用,会计算这种百分数。
完整版)新北师大版小学六年级数学总复习知识点归纳

完整版)新北师大版小学六年级数学总复习知识点归纳小学六年级数学知识点总结一、常用数量关系式1.每份数×份数=总数,总数÷每份数=份数,总数÷份数=每份数2.速度×时间=路程,路程÷速度=时间,路程÷时间=速度3.单价×数量=总价,总价÷单价=数量,总价÷数量=单价4.工作效率×工作时间=工作总量,工作总量÷工作效率=工作时间,工作总量÷工作时间=工作效率5.加数+加数=和,和-一个加数=另一个加数6.被减数-减数=差,被减数-差=减数,差+减数=被减数7.因数×因数=积,积÷一个因数=另一个因数8.被除数÷除数=商,被除数÷商=除数,商×除数=被除数二、小学数学图形计算公式1.正方形(C:周长,S:面积,a:边长)周长=边长×4,C=4a面积=边长×边长,S=a×a正方体(V:体积,a:棱长)表面积=棱长×棱长×6,S表=a×a×6体积=棱长×棱长×棱长,V=a×a×a2.长方形(C:周长,S:面积,a:长,b:宽)周长=(长+宽)×2,C=2(a+b)面积=长×宽,S=ab长方体(V:体积,S:面积,a:长,b:宽,h:高)表面积=(长×宽+长×高+宽×高)×2,S=2(ab+ah+bh) 体积=长×宽×高,V=abh3.三角形(S:面积,a:底,h:高)面积=底×高÷2,S=ah÷2三角形高=面积×2÷底,三角形底=面积×2÷高4.平行四边形(S:面积,a:底,h:高)面积=底×高,S=ah5.梯形(S:面积,a:上底,b:下底,h:高)面积=(上底+下底)×高÷2,S=(a+b)×h÷26.圆形(S:面积,C:周长,d:直径,r:半径)周长=直径×π=2×π×半径,C=πd=2πr面积=半径×半径×π7.圆柱体8.圆锥体9.总数÷总份数=平均数10.相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间11.利润与折扣问题三、常用单位换算1.长度单位换算1千米=1000米,1米=10分米,1分米=10厘米,1厘米=10毫米,1米=100厘米2.面积单位换算1平方千米=100公顷,1公顷=平方米,1平方米=100平方分米,1平方分米=100平方厘米,1平方厘米=100平方毫米3.体(容)积单位换算1立方米=1000立方分米,1立方分米=1000立方厘米,1立方分米=1升,1立方厘米=1毫升,1立方米=1000升4.重量单位换算1吨等于1000千克,1千克等于1000克,1千克等于1公斤。
最新北京版小学数学六年级下册单元知识总结全册
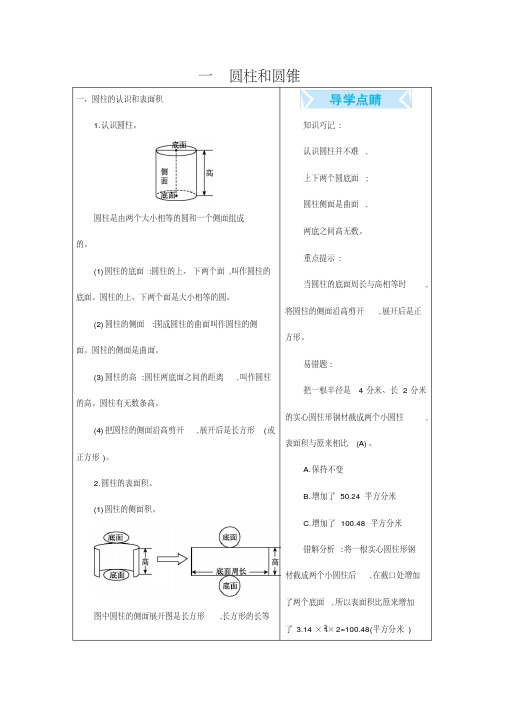
一圆柱和圆锥一、圆柱的认识和表面积1.认识圆柱。
圆柱是由两个大小相等的圆和一个侧面组成的。
(1)圆柱的底面:圆柱的上、下两个面,叫作圆柱的底面。
圆柱的上、下两个面是大小相等的圆。
(2)圆柱的侧面:围成圆柱的曲面叫作圆柱的侧面。
圆柱的侧面是曲面。
(3)圆柱的高:圆柱两底面之间的距离,叫作圆柱的高。
圆柱有无数条高。
(4)把圆柱的侧面沿高剪开,展开后是长方形(或正方形)。
2.圆柱的表面积。
(1)圆柱的侧面积。
图中圆柱的侧面展开图是长方形,长方形的长等知识巧记:认识圆柱并不难,上下两个圆底面;圆柱侧面是曲面,两底之间高无数。
重点提示:当圆柱的底面周长与高相等时,将圆柱的侧面沿高剪开,展开后是正方形。
易错题:把一根半径是4分米、长2分米的实心圆柱形钢材截成两个小圆柱,表面积与原来相比(A)。
A.保持不变B.增加了50.24平方分米C.增加了100.48平方分米错解分析:将一根实心圆柱形钢材截成两个小圆柱后,在截口处增加了两个底面,所以表面积比原来增加了3.14×42×2=100.48(平方分米)于圆柱的底面周长,宽等于圆柱的高。
长方形的面积=长×宽↓↓↓圆柱的侧面积=底面周长×高如果用C表示圆柱的底面周长,用d表示圆柱的底面直径,用r表示圆柱的底面半径,用h表示圆柱的高,用S表示圆柱的侧面积,那么S=Ch或S=πdh或S=2πrh。
(2)圆柱的表面积。
圆柱的表面积是指圆柱的侧面积与两个底面的面积之和,即圆柱的表面积=圆柱的侧面积+两个底面的面积。
如果用S侧表示圆柱的侧面积,用S表表示圆柱的表面积,用S底表示圆柱的底面积,那么S表=S侧+2S底。
(3)特殊圆柱表面积的计算方法。
在实际生活中会遇到特殊的圆柱形物体,如:①圆柱形烟囱(通风管),两头都没有底面,所以烟囱(通风管)的表面积就是烟囱(通风管)的侧面积,等于底面周长×高;②无盖的圆柱形水桶(鱼缸),只有一个底面,因此它的表面积包括两部分,即侧面积和一个底面积,S表正确答案:C。
(完整word版)新北师大版小学六年级数学总复习知识点归纳.docx

或 位的数。 改写后的数是原数的准确数。
例如把1254300000改写成以万做
2、分数的分
1。
位的数是125430万;改写成 以 做 位 的数12.543
。
真分数:分子比分母小的分数叫做真分数。真分数小于
2.近似数:根据 需要,我 可以把一个 大的数,省略某一位后面的尾3.求几个数的最小公倍数的方法是:先用 几个数(或其中的部分数)的公
把整数1平均分成10份、100份、1000份⋯⋯ 得到的十分之几、百分之几、
千分之几 ⋯⋯ 可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几⋯⋯
一个小数由整数部分、 小数部分和小数点部分 成。 数中的 点叫做小数点, 小
假分数:分子比分母大或者分子和分母相等的分数, 叫做假分数。 假分数大于或
4数位
把一个合数用 因数相乘的形式表示出来,叫做分解 因数。
数 位按照一定的 序排列起来,它 所占的位置叫做数位。
例如把28分解 因数
5数的整除
几个数公有的 数, 叫做 几个数的公 数。 其中最大的一个, 叫做 几个数的
整数a除以整数b(b≠0),除得的商是整数而没有余数,我 就
a能被b整
最大公 数,例如12的 数有1、2、3、4、6、12;18的 数有1、2、3、6、9、
一个 大的多位数, 了 写方便,常常把它改写成用
“万”或“ ”作 位的数。
在分数里,中 的横 叫做分数 ; 分数 下面的数, 叫做分母,表示把 位“1”有 可以根据需要,省略 个数某一位后面的数,写成近似数。
平均分成多少份;分数 下面的数叫做分子,表示有 的多少份。
北京版小学六年级数学知识点汇总剖析

小学数学总复习资料·六<1>班·赵一、常用的数量关系式、速度×时间=路程、被减数-减数=差51 被减数-差=减数路程÷速度=时间差+减数=被减数路程÷时间=速度6 、因数×因数=积2、单价×数量=总价积÷一个因数=另一个因数总价÷单价=数量总价÷数量=单价7 、被除数÷除数=商 3、加数+加数=和被除数÷商=除数和-一个加数=另一个加数商×除数=被除数、利润与折扣问题4、工作效率×工作时间=工作总量 8 利润=售出价格-成本工作总量÷工作效率=工作时间利息=本金×利率×时间工作总量÷工作时间=工作效率二、基本概念第一章:数与代数数的认识1.正整数自然数 0 整数负整数数小数。
·在小数里,每相邻两个计数单位之间的进率都是101班·赵小学数学总复习资料·六<1>②计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法大小比较【熟读即可】③大小:位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,整数A比较那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
的大小:先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,小数B比较十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……的大小:分母相同的分数,分子大的分数比较大;分子相同的数,分母小的C比较分数分数大。
分数的分母和分子都不相同的,先通分,再比较两个数的大小。
数的改写④一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、常用的数量关系式1、速度×时间=路程路程÷速度=时间路程÷时间=速度2、单价×数量=总价总价÷单价=数量总价÷数量=单价3、加数+加数=和和-一个加数=另一个加数4、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率5、被减数-减数=差被减数-差=减数差+减数=被减数6、因数×因数=积积÷一个因数=另一个因数7、被除数÷除数=商被除数÷商=除数商×除数=被除数8、利润与折扣问题 利润=售出价格-成本利息=本金×利率×时间二、基本概念第一章:数与代数1. 数的认识正整数整数 0数负整数② 计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是 10。
这样的计数法叫做十进制计数法。
③ 大小比较【熟读即可】A 比较整数大小:位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
B 比较小数的大小:先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……C 比较分数的大小:分母相同的分数,分子大的分数比较大;分子相同的数,分母小的分数大。
分数的分母和分子都不相同的,先通分,再比较两个数的大小。
④ 数的改写一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
1.准确数:把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
例如把 1254300000 改写成以万做单位的数是 125430 万;改写成以亿做单位的数 12.543 亿。
2.近似数:把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。
例如:1302490015 省略亿后面的尾数是 13 亿。
3.四舍五入法:要省略的尾数的最高位上的数是 4 或者比 4 小,就把尾数去掉;如果尾数的最高位上的数是 5 或者比 5 大,就把尾数舍去,并向它的前一位进 1。
例如:省略345900 万后面的尾数约是 35 万。
省略 4725097420 亿后面的尾数约是 47 亿。
·P56因数公因数最大公因数⑤倍数和因数倍数和因数是相互依存的。
例:18÷2=9 我们就说 18 能被 2 整除,18 是 2 的倍数,2 是 18 的因数。
⑥ 特殊倍数:⑥整除:被除数、除数和商都是自然数,并且没有余数。
大数能被小数整除时,大数是小数的倍数,小数是大数的因数。
例: 8 和 2⑦ 自然数按能不能被 2 整除来分:奇数、偶数。
【0 也是偶数。
】奇数:不能被 2 整除的数。
偶数:能被 2 整除的数。
⑧ 自然数(0 除外)按一个数的因数的个数分:质数、合数、1质数:一个数只有 1 和它本身两个因数,这个数叫做质数(也叫做素数)。
合数:一个数除了 1 和它本身,还有别的因数,这个数叫做合数。
1:只有 1 个因数。
1 既不是质数,也不是合数。
·最小的质数是 2,最小的合数是 4。
·20 以内的质数:有 8 个(2、3、5、7、11、13、17、19)注意:用质数作除数, 除到商是质数为止。
注意:除到互质为止, 把所有的除数连乘起来。
59、 61、67、71、73、79、83、89、97二 三 五 七 和 十一, 十三 后面是 十七, 还有 十九 别忘记,二十三,二十九,三十一,三十七, 四一,四三,四十七, 五三九,六一七, 七一,七三,七十九, 八三,八九,九十七。
⑨ 分解质因数把一个合数用质因数(既是质数又是因数)相乘的形式表示出来,叫做分解质因数。
即: 用短除法分解质因数,一个合数写成几个质数相乘的形式。
短除法分解质因数:22⑩ 公因数、最大公因数324=2×2×2×3几个数公有的因数叫他们的公因数。
其中最大的那个就叫它们的最大公因数。
用短除法求 12 和 18 的最大公因数:223(12,18)⑪ 互质:如果两个数的最大公因数是 1,就说这两个数互质。
用短除法求两个数或三个数的最大公因数 (除到互质为止,把所有的除数连乘起来) 几个数的公因数只有 1,就说这几个数互质。
两数互质的特殊情况:⑴ 1 和任何自然数互质; ⑵ 相邻两个自然数互质; ⑶ 两个质数一定互质; ⑷ 2 和所有奇数互质; ⑸ 质数与比它小的合数互质;如果两数是倍数关系时,那么较小的数就是它们的最大公因数。
例:8 和 224 12 2 612 18 3 6 9如果两数互质时,那么 1 就是它们的最大公因数。
例:3 和 7 ⑫ 公倍数、最小公倍数·几个数公有的倍数叫这些数的公倍数。
其中最小的那个就叫它们的最小公倍数。
·用短除法求两个数的最小公倍数(除到互质为止,把所有的除数和商连乘起来)2[12,18]=2×3×2×3=36·用短除法求三个数的最小公倍数(除到两两互质为止,把所有的除数和商连乘起来)如果两数是倍数关系时,那么较大的数就是它们的最小公倍数。
如果两数互质时,那么它们的积就是它们的最小公倍数。
求 4、6、8 的最小公倍数[4,8]=8 [8,6]=24 [4,6,8]=24注意:除到互质为止,把所有的除数和商连乘起来。
12 183 69a 小数点向右移动一位,原来的数就扩大 10 倍;小数点向右移动两位,原来的数就扩大 100 倍;b 小数点向左移动一位,原来的数就缩小 10 倍,也就是缩小到原来的 1/10;小数点向左移动两位,原来的数就缩小 100 倍,也就是缩小到原来的 1/100;依此类推……c 小数点向左移或者向右移位数不够时,要用“0"补足位。
(二)小数1. 小数的认识:①小数的意义把整数“1”平均分成 10 份、100 份、1000 份…… 得到的十分之几、百分之几、千分之几…… 可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几…… ②小数点位置的移动引起小数大小的变化:③小数的分类有限小数 小数无限小数循环小数无限不循环小数2. 小数的一些规律:①小数的性质:在小数的末尾添上零或去掉零,小数的大小不变。
②小数大小比较:先看整数部分,整数部分大的那个数就大; 整数部分相同,十分位上数大的那个数就大;十分位上的数也相同,百分位上的数大的那个数就大……一个循环小数的小数部分,依次不断重复出现的数字叫做这个循环小数的循环节。
例如: 3.99……的循环节是“9”, 0.5454……的循环节是“54”(三)分数:把单位 1 平均分成几份,表示其中的一份或几份:分子(被除数),分母(除数),分数值(商)真分数:真分数都小于 1假分数:假分数大于 1 或等于 1.带分数:(包括整数部分和真分数)用分子和分母的公约数(1 除外)去除分子、分母;通常要除到得出最简分数为止。
小数化分数:小数化成分母是 10、100、1000 的分数再化简2 和 5,这个分数一定能化成有限小数。
同分母分数加、减法(分母不变,分子相加减)异分母分数加、减法(通分后再加减)分数加减混合运算法则与整数运算法则相同(四)百分数表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常用"%"来表示。
①成数成数:“成”表示十分之一,几成就是十分之几,或百分之几。
如:五成就是十分之五或百分之五十。
②折扣几折就是十分之几,或百分之几。
如:八折就是按原价的十分之八出售,也就是 80%出售。
(五)性质和规律1.商不变的规律在除法里,被除数和除数同时扩大或者同时缩小相同的倍,商不变。
2.小数的性质在小数的末尾添上零或者去掉零小数的大小不变。
3.分数的基本性质分数的分子和分母都乘以或者除以相同的数(零除外),分数的大小不变。
4.分数与除法的关系①被除数相当于分子,除数相当于分母,被除数÷除数= 被除数/除数②因为零不能作除数,所以分数的分母不能为零。
5.分数、小数、百分数的互化:2.数的计算*运算定律3.方程·用字母表示数的写法·数字和字母、字母和字母相乘时,乘号可以记作“.”,或者省略不写。
·数字要写在字母的前面。
·当“1”与任何字母相乘时,“1”省略不写。
解方程并检验:3X - 6 = 6.63X = 6.6 + 63X = 12.6X = 12.6 ÷ 3X = 4.2检验:把 X=4.2 带入原方程,左边=3×4.2-6=6.6,右边=6.6,左边=右边,所以 X=4.2 是原方程的解。
·列方程解决实际问题:(1)用方程解简单的问题:特点:列方程解应用题,就是用字母代替应用题中的未知的量,根据数量间的相等关系列方程、解方程进而求出未知量。
列方程解答应用题的步骤:①弄清题意,找出未知量并用 X 表示;②找出题中数量之间的相等关系③列方程,解方程④检查或验算,写出答案。
(2)列方程解应用题的方法*综合法:先把应用题中已知数(量)和所设未知数(量)列成有关的代数式,再找出它们之间的等量关系,进而列出方程。
这是从部分到整体的一种思维过程,其思考方向是从已知到未知。
*分析法:先找出等量关系,再根据具体建立等量关系的需要,把应用题中已知数(量)和所设的未知数(量)列成有关的代数式进而列出方程。
这是从整体到部分的一种思维过程,其思考方向是从未知到已知。
(3)一般应用题;(4)几何形体的周长、面积、体积计算;(5)分数、百分数应用题;(6)比和比例应用题。
(7)和倍、差倍问题特点:已知两个数的和以及它们之间的倍数关系,求两个数各是多少。
方法:找标准量(1 倍量),一般题中说是“谁”的几倍,就把谁定位标准量。
一般把标准量设为 X,另一个量用含有“X”的式子表示。
关系式:标准量+标准量×倍数=两数和(8)相遇问题特征:求总路程的相遇问题可以用算术法解答,如果求的是速度或相遇的时间,则用方程法解决比较方便。
方法:设速度或时间为 X,根据关系式“速度和×时间=路程”列方程。
4.常见的量【单位换算】高级单位×进率低级单位(3)求比值和化简比求比值:用比的前项除以后项,它的结果是一个数值可以是整数,也可以是小数或分数。
根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、 后项是互质的数。
