七年级有理数的加减乘除乘方计算训练(80小题)-有解析
初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.科学发现:植物的花瓣、萼片、果实的数目以及其他方面的特征,都非常吻合于一个奇特的数列——著名的裴波那契数列:1,1,2,3,5,8,13,21,34,55,……仔细观察以上数列,则它的第11个数应该是 .【答案】89.【解析】观察发现:从第三个数开始,后边的一个数总是前边两个数的和,则第11个数是34+55=89.试题解析:第11个数是34+55=89.【考点】规律型:数字的变化类.2.将正整数依次按下表规律排成4列,根据表中的排列规律,数2014应在( )A.第672行第1列B.第672行第4列C.第671行第1列D.第671行第4列【答案】B.【解析】每行有3列,奇数开始的从左边开始排列,偶数开始的从右边开始排列.每行的最后都是3的倍数.2014÷3=671……1,所以数2014应在第672行第4列.故选B.【考点】规律型:数字的变化类.3.已知在0摄氏度及一个标准大气压下1cm3空气的质量是0.001293克,数0.001293用科学计数法表示为__________ .【答案】.【解析】用科学记数法表示绝对值小于的数,只要将小数定向右移到第一个不为零的数后,若共移动位,则最后乘以即可,如本题中向右移了位,变为,在后乘以,最后.【考点】科学记数法.4.计算:= 。
【答案】.【解析】【考点】同底数幂的乘法.5.在一次水灾中,大约有个人无家可归,假如一顶帐篷占地100米,可以放置40个床位(一人一床位),为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多少地方?若某广场面积为5000米2。
要安置这些人,大约需要多少个这样的广场?(所有结果用科学计数法表示)【答案】(1);(2);(3).【解析】根据帐篷的数量=总人数÷每一个帐篷所容纳的人数;所占面积=帐篷数×一顶帐篷所占的面积,计算即可.试题解析:根据题意得2.5×107÷40=625000=顶帐篷,625000×100=6.25×107米2,6.25×107÷5000=个.考点: 整式的除法.6.明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是()A.90分B.75分C.91分D.81分【答案】C【解析】小明第四次测验的成绩是故选C.7.下列各组的两个数中,运算后的结果相等的是()A.和B.和C.和D.和【答案】B【解析】A.,,故本选项错误;B.,,故本选项正确;C.,,故本选项错误;D.,,故本选项错误.故选B.8.若规定“!”是一种数学运算符号,且则的值为()A.B.99!C.9 900D.2!【答案】C【解析】根据题意可得:100!=100×99×98×97×...×1,98!=98×97× (1)∴=100×99="9" 900,故选C.9.若规定,则的值为 .【答案】【解析】.10.李强靠勤工俭学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):星期一二三四五六日(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?【答案】(1)到这个周末,李强有14元节余.(2)照这个情况估计,李强一个月(按30天计算)能有60元节余.(3)按以上的支出水平,李强一个月(按30天计算)至少有360元收入才能维持正常开支.【解析】分析:(1)七天的收入总和减去支出总和即可;(2)首先计算出平均一天的节余,然后乘30即可;(3)计算出这7天支出的平均数,即可作为一个月中每天的支出,乘30即可求得.解:(1)由题意可得:(元).(2)由题意得:14÷7×30=60(元).(3)根据题意得:10+14+13+8+10+14+15=84,84÷7×30=360(元).答:(1)到这个周末,李强有14元节余.(2)照这个情况估计,李强一个月(按30天计算)能有60元节余.(3)按以上的支出水平,李强一个月(按30天计算)至少有360元收入才能维持正常开支.11.有理数0.0050400的有效数字的个数是().A.3个B.4个C.5个D.6个【答案】C【解析】有效数字是从左边第一个不是0的数字起,后面所有的数字都是有效数字.解:有理数0.0050400的有效数字有5、0、4、0、0这5个,故选C.【考点】近似数和有效数字点评:本题是基础应用题,只需学生熟练掌握有效数字的定义,即可完成.12.计算:;【答案】-5【解析】先根据有理数的乘方法则计算,再根据有理数的乘法法则计算,最后算加减即可.解:原式.【考点】有理数的混合运算点评:计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.13.观察下列各式:31=3,32=9,33=27,34=81, 35=243,36=729…你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回答:3的个位数字是。
初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.小华利用计算器计算0.0000001295×0.0000001295时,发现计算器的显示屏上显示如下图的结果,对这个结果表示正确的解释应该是().A.1.677025×10—14B.1.677025×1014C.(1.677025×10)—14D.1.677025×10×(—14)【答案】A.【解析】0.0000001295×0.0000001295,=0.00000000000001677025,=1.677025×10-14.故选A.【考点】计算器—有理数.2.计算:【答案】41.【解析】针对有理数的乘方、绝对值分别进行计算,然后根据实数的运算法则求得计算结果.原式=.【考点】1.有理数的乘方;2..绝对值;3.实数的运算法则.3.人一根头发的直径大约为0.00072分米,用科学记数法表示正确的是()A.B.C.D.【答案】D.【解析】根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值。
在确定n的值时,看该数是大于或等于1还是小于1.当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0).0.00072第一个有效数字前有4个0(含小数点前的1个0),从而.故选D.【考点】科学记数法.4.中学数学中,我们知道加减运算是互逆运算,乘除运算也是互逆运算;其实乘方运算也有逆运算,如式子可写成,式子也可写成;已知式子表示为,则用表示时,=()A.6B.C.D.【答案】B.【解析】根据观察式子23=8可以变形为3=log28,2=log525也可以变形为52=25,可发现规律,根据同底数幂的乘法,可得答案.由y=log318,得3y=183x=2,32=932×3x=32+x=183y=18=32+x所以y=2+x.故选B.【考点】有理数的乘方.5.计算(1)[(x+y)2-(x-y)2]÷(2xy)(2)(3)【答案】(1)2;(2)-0.1;(3)-4.【解析】(1)原式中括号中利用完全平方公式展开,再利用多项式除以单项式法则计算即可得到结果.(2)先算积的乘方,再进行除法运算即可;(3)根据乘方、零次幂、负整数指数幂的意义进行计算即可求出答案.试题解析:(1)原式=(x2+2xy+y2-x2+2xy-y2)÷(2xy)=4xy÷(2xy)=2;(2) 原式====-0.1;(3)原式=-4+4×1-4=-4+4-4=-4【考点】1.完全平方公式;2.整式的除法;3.实数的混合运算.6.用小数表示2.014×10-3是 .【答案】0.002014.【解析】把数据2.014×10-3中2.014的小数点向左移动3位就可以得到.试题解析:2.014×10-3=0.002014.考点: 科学记数法—原数.7.已知,则=_______.【答案】-3.【解析】把变形为3-3,即可求出m的值.试题解析:∵∴m=-3.考点: 负整数指数幂.8.根据下图所示的程序计算代数式的值,若输入n的值为5,则输出的结果为()A.16B.2.5C.18.5D.13.5【答案】A【解析】由程序图可知输出的结果为3.9.明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是()A.90分B.75分C.91分D.81分【答案】C【解析】小明第四次测验的成绩是故选C.10.小彬从家里步行到学校需100步,他到学校的距离可能是()A.250 m B.200 m C.150 m D.50 m【答案】D【解析】0.5×100=50(m).故选D.11.计算(-2.5)×0.37×1.25×(-4)×(-8)=_________.【答案】-37【解析】原式=[(-2.5)×(-4)]×[1.25×(-8)]×0.37=10×(-10)×0.37=-37.12.比较下列各对数的大小.(1)与;(2)与;(3)与.【答案】(1)<(2)<(3)<【解析】解:(1)因为|-4+5|=1,|-4|+|5|=9,所以|-4+5|<|-4|+|5|.(2)因为,所以.(3)因为,,所以.13.务川电视台天气预报,12月20日的气温是﹣2℃~7℃,则这一天的温差是℃【答案】9【解析】用最高气温减去最低气温,然后根据减去一个数等于加上这个数的相反数进行计算即可得解.7﹣(﹣2)=7+2=9℃.故答案为:9.【考点】有理数的减法.14.)计算:(1)(2);(3);(4).【答案】(1)-2.5;(2);(3)-15;(4)1.【解析】(1)原式==0.5+(-3)=-2.5.(2)原式==(-1)×=.(3)原式=-25+=-25+12+16-18=-15(4)原式==1【考点】有理数的运算.15.一振子从点A开始左右振动8次,如果规定向右为正,向左为负,这8次振动记录为(单位:毫米):+10,-9,+8,-6,+7.5,-6,+8,-7.(1)求振子停止时所在位置距A点有多远?(2)如果每毫米需时0.22秒,则共用时多少秒?【答案】(1)5.5;(2)13.53.【解析】(1)将8次的记录相加,得到的数就是停止时所在位置距A点的距离,如果是“正”则在A点右边,如果是“负”则在A点左边;(2)将8次记录的绝对值相加就是它振运8次的距离,再乘以0.22,即可得到共用时间.试题解析:(1)+10-9+8-6+7.5-6+8-7=5.5;答:振子停止时位于A点右边5.5毫米处.(2)10+9+8+6+7.5+6+8+7=61.5,61.5×0.22=13.53(秒)答:振子共用时13.53秒.【考点】正数和负数.16.温家宝总理在十届全国人大四次会议上谈到解决“三农”问题时说,2006年中央财政用于“三农”的支出将达到33970000万元,这个数据用科学记数法可表示为万元.【答案】3.397×107【解析】科学记数法的表示方法:科学记数法的表示形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解:.【考点】科学记数法的表示方法点评:本题属于基础应用题,只需学生熟练掌握科学记数法的表示方法,即可完成.17. (-2)4表示A.(-2)×4B.(-2)×(-2)×(-2)×(-2)C.-4×4D.(-2)+(-2)+(-2)+(-2)【答案】B【解析】有理数的乘方的定义:几个相同因数的积叫做有理数的乘方.(-2)×(-2)×(-2)×(-2),故选B.【考点】有理数的乘方点评:本题属于基础应用题,只需学生熟练掌握有理数的乘方的定义,即可完成.18.按四舍五入法则取近似值:2.096≈(精确到百分位).-0.03445≈(精确到0.001).【答案】2.10,-0.034【解析】精确到百分位即是对千分位四舍五入,精确到0.001即是对0.0001位四舍五入.按四舍五入法则取近似值:2.096≈2.10(精确到百分位).-0.03445≈-0.034(精确到0.001).【考点】近似数和有效数字点评:本题属于基础应用题,只需学生熟练掌握取近似数的方法,即可完成.19.下表是小明记录的10月份某一周内每天中午12时的气温的变化情况(气温比前一天上升记为正数,下降记为负数)星期一二三四五六日(2)本周的最高气温与最低气温相差多少摄氏度?【答案】(1)由题意得【解析】(1)根据气温比前一天上升记为正数,下降记为负数即可依次计算出各天的实际气温;(2)根据(1)中得到的结果即可计算出本周的最高气温与最低气温的差.(1)由题意得13111614131716【考点】有理数的减法法则的应用点评:解题的关键是读懂气温比前一天上升记为正数,下降记为负数,分别计算出各天的实际气温.20.研究下列算式,你会发现什么规律?……问题探究(1)请你找出规律并计算=_____________=( ).(2)用含有的式子表示上面的规律:_____________________________.问题解决(3)用找到的规律解决下面的问题:计算: =_______________.写出运算过程:【答案】(1)8(2)(3)【解析】1)=64=8(2)n(n+2)+1=(3)解:原式==【考点】找规律-数字的变化点评:解答本题的关键是仔细分析题意得到规律,再把这个规律应用于解题.21. 2008年全国人民共向四川地震灾区捐款约43681000000元,这笔款额用科学记数法表示(保留三个有效数字)正确的是()A.0.437×1011B.4.4×1010C.4.37×1010D.43.7×109【答案】C【解析】科学记数法的表示形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.43681000000,故选C.【考点】科学记数法的表示方法,近似数与有效数字点评:解题的关键是熟练掌握从左边第一个不为0的数开始到末尾数字为止,所有的数字都是这个数的有效数字,注意有效数字的个数与乘方的次数无关.22.钓鱼岛自古以来是中国的领土,岛屿周围的海域面积约170 000平方公里,相当于五个台湾本岛面积. 这里的“170 000”用科学记数法表示为 .【答案】【解析】科学记数法的表示形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【考点】本题考查的是科学记数法的表示方法点评:本题属于基础应用题,只需学生熟练掌握科学记数法的表示方法,即可完成.23.有理数3.645精确到百分位的近似数为A.3.6B.3.64C.3.7D.3.65【答案】D【解析】由题意精确到百分位就是对千分位四舍五入取近似值.有理数3.645精确到百分位的近似数为3.65,故选D.【考点】近似数和有效数字点评:本题属于基础应用题,只需学生熟练掌握四舍五入取近似值的方法,即可完成.24.计算:(1)(2)(3)(4)【答案】(1)0;(2)-1;(3)7;(4)6【解析】有理数的混合运算的顺序:先算乘方,再算乘除,最后算加减,同级运算按从左向右的顺序依次计算;有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.(1)原式=-3+3=0;(2)原式==;(3)原式==;(4)原式==.【考点】有理数的混合运算点评:本题属于基础应用题,只需学生熟练掌握有理数的混合运算的顺序,即可完成.25.若a、b互为相反数,c、d互为倒数,∣m∣=2,求+m2-3cd的值.【答案】-2【解析】由题意可得,,,再整体代入求值即可.由题意得,,则【考点】代数式求值点评:解题的关键是熟记相反数之和为0,倒数之积为1,相反数的两个数的绝对值相等.26.计算:(1)4―-3×;(2)【答案】(1)-1;(2)【解析】有理数的混合运算的顺序:先算乘方,再算乘除,最后算加减,同级运算按从左向右的顺序依次计算;有括号的先算括号里的.同时注意运算过程中可以运用运算律计算的要运用运算律简化计算.(1)原式=4-6+1=-1;(2) 原式=-1-=.【考点】有理数的混合运算点评:本题属于基础应用题,只需学生熟练掌握有理数的混合运算,即可完成.27.的个位数字是()A.2B.4C.6D.8【答案】C【解析】∵一个数的乘方的个位数字=这个数的个位数字的乘方的个位数字。
有理数的加减乘除乘方混合运算专题训练(带答案)

1.先乘方,再乘除,最后加减;之青柳念文创作2.同级运算,从左到右停止;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次停止.1357911、—22—(—2)2—23+(—2)3 12、13、15、-10 + 8÷(-2 )2-(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(17、-14 + ( 1-0.5 )[2×(-3)2] 18、(-2)2-2×[(-2-319212325、6-(-12、(-48)÷ 8 -(-527、420.25 2829、(-5)×6+(-125) ÷(-5)3311、【基础题】计算:(1(2(3(4(1(2(3(4(1(34(5(6(7(8;(9)10(1)11+(-22)-3×(-11); (2(34;(5(6(7)-+2×+(-6)÷;(8)(1(2(34(5(6)-10+84×3;(7(81-0.5(1)(-8)×5-40;(2)()÷(-(-2);(3)-20÷5×(-3)÷15;(4)-3[-5+-2)];(5)-23÷2÷(2;(6×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-2016、23 17、2 18、24 19、-28 20、9/1621、1 22、10 23、-1/12 24、104/3 25、9 26、1427、-3128、-81又1/81 29、-9 30、-2931、-1/5 32、91、【答案】(1)17;(2(3)31;(4)-112、【答案】(1)-10;(2)22;(3)-16;(43、【答案】(1)1;(2)0;(3)42;(4(5)18;(6)0;(7)-4.64;(8(9)8;(104、【答案】(1)22;(2)0;(3)-17;(4(5)(6)-95;(7)-85;(8)6 .5、【答案】(1)3;(2)1;(3)-54;(4)0;(5(6)-20;(7)-2;(86、【答案】(1)-80;(2)5.6;(3)-2;(4)16;(5)-复习有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分)1.3×(-2)=________,(-6=________.2.(-3)2的底数是________,成果是;-32的底数是________,成果是________.3=________=________;(+8)÷(-=________.4.233=________2=________.5________=1________=-162.4=________.7.-32×(-5)23=________.83600________.9.________;________10①23________222________3③32________22)3________)2二、断定题(每小题1分,共5分)11.零除以任何数都得零()12.互为相反数的两个数的积为负数()13.如果ab>0,则a>0且b>0()14.1除以一个非零数的商叫做这个数的倒数()15.(-3)5暗示5个-3相乘()三、选择题(每小题3分,共21分)16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A.1个B.2个C.3个D.4个17.下列各对数:①1与1;②-1与1;③a-b与b-a;④-1与-1;⑤-5与|6|,其中互为倒数的是A.①②③B.①③⑤C.①③④D.①④18.下列各题中两个式子的值相等的是A.-23与(-2)3 B.32与23C.(-2)2与-22 D.|-2|与-|-2|19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a,b互为倒数,则-ab=-1.A.4 B.3C.2 D.120.下列各式中成果大于0的是A.1-910×3 B.(1-910)×3C.1-(9×3)10 D.(1-9)10×3 21.下列说法中正确的是A.一个数的平方必为正数B.一个数的平方必小于这个数的相对值C.一个数的平方必大于这个数D.一个数的平方不成能为负数22.用迷信记数法暗示的数2.89×104,原来是A.2890 B.2890000 C.28900 D.289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+1224.(3分)-6÷(+3)÷(-4)×(+2)25.(3分)-5-626.(3分)(-81)÷16)27.(3分)-22×(-328.(3分)(-1)2000200120021)200329.(3分)(-2)×(-20011-200230.(331.(332.(3分)(-2.53)33.(5分)30五、解答题(934.已知A=a+a2+a3+……+a2000(1)若a=1,求A的值.(2)若a=-1,求A的值.一、1.-6 2 2.-3 9 3 -9 3-3245103平方公里9.>>><13.×14.√15.√三、16.A 17.D 18.A 19.B 21.D 22.C四、23.-90 24.1 25.-3 2627.15 28.1 29.-200230.1 31.30 3233.-4五、34.(1)2000 (2)0。
7年级有理数的加减乘除混合运算

七年级有理数的加减乘除混合运算题题目一:(-3)×2 + 5解析:先算乘法,(-3)×2 = -6,再算加法,-6 + 5 = -1。
题目二:4 - 2×(-3)解析:先算乘法,2×(-3) = -6,再算减法,4 - (-6) = 4 + 6 = 10。
题目三:(-2)×3÷(-6)解析:先算乘法,(-2)×3 = -6,再算除法,-6÷(-6) = 1。
题目四:5 + (-3)×4解析:先算乘法,(-3)×4 = -12,再算加法,5 + (-12) = -7。
题目五:(-4)÷2 + 3解析:先算除法,(-4)÷2 = -2,再算加法,-2 + 3 = 1。
题目六:2×(-3) - 4解析:先算乘法,2×(-3) = -6,再算减法,-6 - 4 = -10。
题目七:(-5)×2÷(-10)解析:先算乘法,(-5)×2 = -10,再算除法,-10÷(-10) = 1。
题目八:3 + (-2)×(-4)解析:先算乘法,(-2)×(-4) = 8,再算加法,3 + 8 = 11。
题目九:(-6)÷3 + 2解析:先算除法,(-6)÷3 = -2,再算加法,-2 + 2 = 0。
题目十:4×(-2) + 6解析:先算乘法,4×(-2) = -8,再算加法,-8 + 6 = -2。
题目十一:(-3)×(-3) - 5解析:先算乘法,(-3)×(-3) = 9,再算减法,9 - 5 = 4。
题目十二:5÷(-5) + 4解析:先算除法,5÷(-5) = -1,再算加法,-1 + 4 = 3。
题目十三:(-2)×4÷(-8)解析:先算乘法,(-2)×4 = -8,再算除法,-8÷(-8) = 1。
有理数的加减乘除乘方混合运算专题训练(带答案)

1. 先乘方,再乘除,最后加减;之袁州冬雪创作2. 同级运算,从左到右停止;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次停止.1、12411 ()()()23523+-++-+- 2、4(81)( 2.25)()169-÷-⨯-÷ 3、11(22)3(11)+--⨯- 4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、33102(4)8-÷--7、)]21)21[(122--÷8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯--10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯-13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、-10 + 8÷(-2 )2-(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯20、0)132()43(2⨯+-+-21、6)12()4365127(÷-⨯+-22、22)4()5(25.0)4()85(-⨯-⨯--⨯- 23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯- 25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(- 27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯-30、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+- 1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ]. (1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32; (3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯.(1)36×23121)-(; (2)12.7÷)(-1980⨯; (3)6342+)(-⨯;(4))(-43×)-+(-31328;(5)1323-)(-÷)(-21; (6)320-÷34)(-81-; (7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[2322-)(- ]; (9)[ 2253)-(-)(- ]÷)(-2;(10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-; (3)2332-)(-;(4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯. (1))-(-258÷)(-5; (2)-33121)(--⨯;(3)223232)-(-)(-⨯⨯;(4)0132432⨯⨯)+(-)(-; (5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4) 参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-2016、23 17、2 18、24 19、-28 20、9/1621、1 22、10 23、-1/12 24、104/3 25、9 26、1427、-3128、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 (1)17; (2)511; (3)31; (4)-112、【答案】 (1)-10; (2)22; (3)-16; (4)-253、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64;(8)37; (9)8; (10)-25.4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71;(6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20; (7)-2; (8)-67.6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,成果是________;-32的底数是________,成果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________. 4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用迷信记数法暗示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22②(21)2________(21)3 ③32________22④(-2)3________(-2)2二、断定题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( ) 15.(-3)5暗示5个-3相乘( ) 三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④ 18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中成果大于0的是 A .1-910×3 B .(1-910)×3 C .1-(9×3)10 D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的相对值C .一个数的平方必大于这个数D .一个数的平方不成能为负数22.用迷信记数法暗示的数2.89×104,原来是 A .2890 B .2890000 C .28900 D .289000 四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16) 27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-2002 30.(3分)-)45()45(5222-÷-⨯⨯ 31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3) 33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a2+a3+……+a2000 (1)若a=1,求A 的值. (2)若a=-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91913-32 4.-81 -161 5.-2323 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -14110.> > > <二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C 四、23.-90 24.1 25.-3 26.4127.15 28.1 29.-2002 30.1 31.30 32.-4933.-4 五、34.(1)2000 (2)0。
有理数的加减乘除乘方混合运算专题训练(带答案)
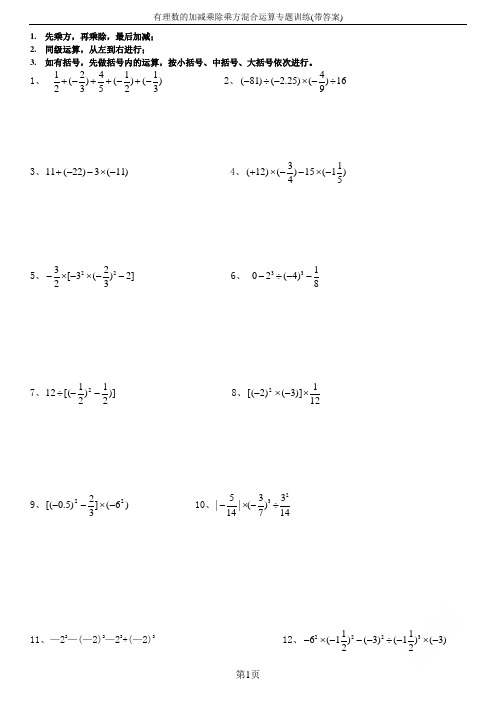
1. 先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷223 3 222113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、-10 + 8÷(-2 )2 -(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ].(1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32;(3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯.(1)36×23121)-(; (2)12.7÷)(-1980⨯;(3)6342+)(-⨯; (4))(-43×)-+(-31328;(5)1323-)(-÷)(-21; (6)320-÷34)(-81-;(7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[ 2322-)(- ];(9)[ 2253)-(-)(- ]÷)(-2; (10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-;(3)2332-)(-; (4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯.(1))-(-258÷)(-5; (2)-33121)(--⨯;(3)223232)-(-)(-⨯⨯; (4)0132432⨯⨯)+(-)(-;(5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 (1)17; (2)511; (3)31; (4)-112、【答案】 (1)-10; (2)22; (3)-16; (4)-253、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64;(8)37; (9)8; (10)-25.4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71; (6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20; (7)-2; (8)-67. 6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516; (6)-2.9复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________.4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用科学记数法表示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22②(21)2________(21)3③32________22④(-2)3________(-2)2二、判断题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( )15.(-3)5表示5个-3相乘( )三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④ 18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中结果大于0的是A .1-910×3B .(1-910)×3C .1-(9×3)10D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不可能为负数22.用科学记数法表示的数2.89×104,原来是A .2890B .2890000C .28900D .289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16)27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-200230.(3分)-)45()45(5222-÷-⨯⨯31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3)33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a 2+a 3+……+a 2000(1)若a =1,求A 的值.(2)若a =-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91 913 -32 4.-81 -161 5.-23 23 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -141 10.> > > < 二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C四、23.-90 24.1 25.-3 26.41 27.15 28.1 29.-2002 30.1 31.30 32.-49 33.-4 五、34.(1)2000 (2)0。
有理数的加减乘除乘方混合运算专题训练(带答案)【通用】.doc

1. 先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷223 3 22231113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、-10 + 8÷(-2 )2 -(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(-5)×6+(-125) ÷(-5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ].(1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32;(3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯.(1)36×23121)-(; (2)12.7÷)(-1980⨯;(3)6342+)(-⨯; (4))(-43×)-+(-31328;(5)1323-)(-÷)(-21; (6)320-÷34)(-81-;(7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[ 2322-)(- ];(9)[ 2253)-(-)(- ]÷)(-2; (10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-;(3)2332-)(-; (4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯.(1))-(-258÷)(-5; (2)-33121)(--⨯;(3)223232)-(-)(-⨯⨯; (4)0132432⨯⨯)+(-)(-;(5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)];(5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 (1)17; (2)511; (3)31; (4)-112、【答案】 (1)-10; (2)22; (3)-16; (4)-253、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64;(8)37; (9)8; (10)-25.4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71; (6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20; (7)-2; (8)-67. 6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516; (6)-2.9复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________.4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用科学记数法表示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22②(21)2________(21)3③32________22④(-2)3________(-2)2二、判断题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( )15.(-3)5表示5个-3相乘( )三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④ 18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中结果大于0的是A .1-910×3B .(1-910)×3C .1-(9×3)10D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不可能为负数22.用科学记数法表示的数2.89×104,原来是A .2890B .2890000C .28900D .289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16)27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-200230.(3分)-)45()45(5222-÷-⨯⨯31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3)33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a 2+a 3+……+a 2000(1)若a =1,求A 的值.(2)若a =-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91 913 -32 4.-81 -161 5.-23 23 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -141 10.> > > < 二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C四、23.-90 24.1 25.-3 26.41 27.15 28.1 29.-2002 30.1 31.30 32.-49 33.-4 五、34.(1)2000 (2)0。
有理数的加减乘除乘方混合运算专题训练(带答案)

1. 先乘方,再乘除,最后加减;之蔡仲巾千创作2. 同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1、12411 ()()()23523+-++-+- 2、4(81)( 2.25)()169-÷-⨯-÷ 3、11(22)3(11)+--⨯- 4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、33102(4)8-÷--7、)]21)21[(122--÷8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯--10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯- 13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+ 15、-10 + 8÷(-2 )2-(-4 )×(-3 ) 16、-49 + 2×(-3 )2 + (-6 )÷(-91)17、-14 + ( 1-0.5 )×31×[2×(-3)2] 18、(-2)2-2×[(-21)2-3×43]÷51.19、)8()4()6(52-÷---⨯20、0)132()43(2⨯+-+- 21、6)12()4365127(÷-⨯+-22、22)4()5(25.0)4()85(-⨯-⨯--⨯- 23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6-(-12)÷2)2(- 26、(-48)÷ 8 -(-5)÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯-30、(-5)×6+(-125) ÷(-5)3 31、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算:(1)618-÷)(-)(-312⨯; (2))(-+51232⨯;(3))(-)(-49⨯+)(-60÷12; (4)23)(-×[ )+(--9532 ]. (1))(-)+(-2382⨯; (2)100÷22)(--)(-2÷)(-32; (3))(-4÷)(-)(-343⨯; (4))(-31÷231)(--3214)(-⨯. (1)36×23121)-(; (2)12.7÷)(-1980⨯; (3)6342+)(-⨯;(4))(-43×)-+(-31328; (5)1323-)(-÷)(-21; (6)320-÷34)(-81-; (7)236.15.02)-(-)(-⨯÷22)(-; (8))(-23×[2322-)(- ]; (9)[ 2253)-(-)(- ]÷)(-2;(10)16÷)(-)-(-)(-48123⨯.(1)11+(-22)-3×(-11); (2)0313243⨯⨯)-(-)(-; (3)2332-)(-;(4)23÷[ )-(-)(-423];(5))-(8743÷)(-87; (6))+()(-654360⨯;(7)-27+2×()23-+(-6)÷()231-; (8))(-)-+-(-4151275420361⨯⨯.(1))-(-258÷)(-5; (2)-33121)(--⨯; (3)223232)-(-)(-⨯⨯;(4)0132432⨯⨯)+(-)(-; (5))(-+51262⨯; (6)-10+8÷()22--4×3;(7)-51-()()[]55.24.0-⨯-; (8)()251--(1-0.5)×31;(1)(-8)×5-40; (2)(-1.2)÷(-13)-(-2);(3)-20÷5×14+5×(-3)÷15; (4)-3[-5+(1-0.2÷35)÷(-2)]; (5)-23÷153×(-131)2÷(132)2; (6)-52+(1276185+-)×(-2.4) 参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、1427、-3128、-81又1/81 29、-9 30、-29 31、-1/5 32、9 1、【答案】 (1)17; (2)511; (3)31; (4)-11 2、【答案】 (1)-10; (2)22; (3)-16; (4)-25 3、【答案】 (1)1; (2)0; (3)42; (4)423; (5)18; (6)0; (7)-4.64;(8)37; (9)8; (10)-25.4、【答案】 (1)22; (2)0; (3)-17; (4)-423; (5)71; (6)-95; (7)-85;(8)6 .5、【答案】 (1)3; (2)1; (3)-54; (4)0; (5)526; (6)-20;(7)-2; (8)-67.6、【答案】(1)-80; (2)5.6; (3)-2; (4)16; (5)-516; (6)-2.9复习 有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分) 1.3×(-2)=________,(-6)×(-31)=________. 2.(-3)2的底数是________,结果是________;-32的底数是________,结果是________.3.(-61)÷(+23)=________;-493÷(-176)=________;(+8)÷(-41)=________. 4.23×(-41)3=________;(-91)÷(+34)2=________.5.(-32)×________=1;(-32)×________=-16.-65×(-2.4)×(-53)=________.7.-32×(-5)2÷(-21)3=________.8.我国台湾省的面积约为3600平方公里,用科学记数法暗示为________. 9.+121的倒数是________;________的倒数是-54. 10.用“>”“<”填空: ①23________22②(21)2________(21)3 ③32________22④(-2)3________(-2)2二、判断题(每小题1分,共5分) 11.零除以任何数都得零( )12.互为相反数的两个数的积为负数( ) 13.如果ab >0,则a >0且b >0( )14.1除以一个非零数的商叫做这个数的倒数( ) 15.(-3)5暗示5个-3相乘( ) 三、选择题(每小题3分,共21分) 16.下列说法,其中错误的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A .1个B .2个C .3个D .4个17.下列各对数:①1与1;②-1与1;③a -b 与b -a ;④-1与-1;⑤-5与|6|,其中互为倒数的是A .①②③B .①③⑤C .①③④D .①④ 18.下列各题中两个式子的值相等的是A .-23与(-2)3B .32与23C .(-2)2与 -22D .|-2|与-|-2| 19.下列结论中,其中正确的个数为①0的倒数是0;②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数等于自身的数是±1;④若a ,b 互为倒数,则-ab=-1.A .4B .3C .2D .1 20.下列各式中结果大于0的是 A .1-910×3 B .(1-910)×3 C .1-(9×3)10 D .(1-9)10×3 21.下列说法中正确的是 A .一个数的平方必为正数B .一个数的平方必小于这个数的绝对值C .一个数的平方必大于这个数D .一个数的平方不成能为负数22.用科学记数法暗示的数2.89×104,原来是 A .2890 B .2890000 C .28900 D .289000 四、计算题(共35分)23.(3分)(-3)×(-5)×(+12)×(-21) 24.(3分)-6÷(+3)÷(-4)×(+2) 25.(3分)-5-6÷(-3)26.(3分)(-81)÷241×91÷(-16) 27.(3分)-22×(-3)÷5428.(3分)(-1)2000×(-1)2001×(-1)2002÷(-1)200329.(3分)(-2)×(-2001)×[-21-(-21)]×1-2002 30.(3分)-)45()45(5222-÷-⨯⨯ 31.(3分)(-5)2÷5×632.(3分)(-2.5)÷(-310)×(-3) 33.(5分)30×(21-31+53-109)五、解答题(9分)34.已知A=a+a2+a3+……+a2000 (1)若a=1,求A 的值. (2)若a=-1,求A 的值.参考答案一、1.-6 2 2.-3 9 3 -9 3.-91913-32 4.-81 -161 5.-2323 6.-1.2 7.1800 8.3.6×103平方公里 9.32 -14110.> > > <二、11.× 12.× 13.× 14.√ 15.√三、16.A 17.D 18.A 19.B 20.D 21.D 22.C 四、23.-90 24.1 25.-3 26.4127.15 28.1 29.-2002 30.1 31.30 32.-4933.-4 五、34.(1)2000 (2)0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)原式=
0
+
16 3
+
11 2
=
32 6
ห้องสมุดไป่ตู้
+
33 6
=
65 6
=
10
5;
6
(3)原式= (4.25 + 2.75) + (5.18 − 2.18) = 7 + 3 = 10;
(4)原式=
(4
3
−
1)
3
−
2
+
(8
7
−
1)
7
=
1
−
2
+
1
=
0.
【解析】此题考查有理数的加减混合运算,熟练掌握有理数的加减混合运算法则和运算
2. 计算:(1) − 7 + 3 − 5 + 20;
(2)2 2 + (−2 2) + 5 1 − (−5 1);
3
3
3
2
(3)4.25 + (−2.18) − (−2.75) + 5.18;
(4) 4 − (− 8) − 2 − 1 − 1
3
7
37
【答案】解:(1)原式= −12 + 23 = 11;
= 9 −1−4+1
4433
=2−1
= 1;
7
1
1
1
(11)(−4 8) − (−5 2) + (−4 4) − (+3 8)
4
5
4
5
7 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
= (13 + 23) − (13 + 42)
44
55
= 9 − 11
= −2;
(9)23 − (+17) + 6 − (+3)
= 23 − 17 + 6 − 3
= 23 − 3 − 17 + 6
=3+6
= 9;
1
1
1
(10)2 4 − (+1 3) − (+0.25) + 3
= 8 − 32 − 16 + 28
= 36 − 48
= −12;
(2)0.36 + (−7.4) + 0.3 + (−0.6) + 0.64
= (0.36 + 0.64) + (−7.4 − 0.6) + 0.3
= 1 − 8 + 0.3
= −6.7;
4
3
7
7
(3)(−3.5) + (− 3) + (− 4) + (+ 2) + 0.75 + (− 3)
号:是同号还是异号,是否有 0,从而确定用那一条法则.在应用过程中,要牢记“先
符号,后绝对值”.
(1)先化简,再算加减法即可求解;
(2)根据减法交换律和结合律即可求解;
6 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
(3)、(4)先算同分母分数,再算加减法即可求解; (5)两个一组计算即可求解.
34
3
= 2;
(3)原式=
(−
1)
32
÷
(14
8
−
5 8
+
4)
8
= (− 1 ) ÷ 13
32
8
=− 1 × 8
32 13
=− 1;
52
3 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
(4)原式=
−3
×
4 7
×
3 4
×
7 3
×
1 9
= − 1.
3
【解析】本题主要考查的是有理数的乘法,有理数的混合运算的有关知识.
律是解题关键.
(1)根据结合律和交换律先同号相加,再异号相加即可求解;
(2)根据结合律和相反数的定义算2
2 3
+
(−2
2)并将5
3
1和5
3
1化成假分数,然后通分后算加
2
1 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
法得出结果再化成带分数即可;
(3)根据结合律和交换律先算4.25 − (−2.75)和(−2.18) + 5.18,再算加法即可求解;
9. (1) (−0.9) + 1.51
(2) 1 + (− 2)
3
5
(3)(−2 1) + (−1 1)
3
6
(4)3 1 – (– 1 3)
4
4
(5)0– (– 7)
(6)(– 8)– (– 8)
(7)(– 1.76) + (– 19.15) + (– 8.24)
(8)(+ 3 1) + (– 2 3) + 5 3 + (– 8 2)
4
4
44 4
(5)0– (– 7) = 0 + 7 = 7;
(6)(– 8)– (– 8) = −8 + 8 = 0;
(7)(– 1.76) + (– 19.15) + (– 8.24)
= −(1.76 + 8.24) −19.15
= −10 − 19.15
= −29.15;
(8)(+ 3 1) + (– 2 3) + 5 3 + (– 8 2)
3 4 5 15
2 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
【答案】解:(1)原式= (−13) × (2 + 1) + 0.34 × (− 1 − 5)
33
77
= −13 × 1 + 0.34 × (−1)
= −13 − 0.34
= −13.34;
(2)原式=
−
1 3
×
(−60)
3
5
6
(4)(+17 4) + (−9 11) + (−2.25) + (−17.5) + (−10 11)
(5)1 + (−2) + 3 + (−4) … + 2009 + (−2010) + 2011 + (−2012)
【答案】解:(1) − (−8) + (−32) + (−| − 16|) + (+28)
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
有理数的加减乘除乘方计算(80 小题)
1. 计算: (1)(−37) − (−47); (2)(−53) − 16; (3)(−210) − 87; (4)1.3 − (−2.7).
【答案】解:(1)(−37) − (−47) = −37 + 47 = 10; (2)(−53) − 16 = −69; (3)(−210) − 87 = −297; (4)1.3 − (−2.7) = 1.3 + 2.7 = 4. 【解析】此题主要考查有理数的减法,解题关键是掌握有理数的减法法则,据此求解即 可. (1)根据有理数的减法法则计算即可; (2)根据有理数的减法法则计算即可; (3)根据有理数的减法法则计算即可; (4)根据有理数的减法法则计算即可.
7
+
9
7 15
=
16
7;
15
(2)原式= 4.85 − 3.25 = 1.6;
(3)原式= −(6.9 − 3.1) = −3.8;
(4)原式=
1 5
−
6
4 5
=
−6
3;
5
(5)原式= −3.125 + 3.125 = 0.
【解析】本题考查有理数的加法,以及绝对值,掌握运算法则是解题关键.
(1)先化简绝对值,再计算加法即可;
−
1 4
×
(−60)
+
1 5
×
(−60)
−
7 15
×
(−60)
= 20 + 15 − 12 + 28
= 51
【解析】本题主要考查了有理数的混合运算,关键是熟练掌握乘法运算律.
(1)运用乘法分配律进行计算可得结果;
(2)利用乘法分配律进行计算,最后计算加减可得结果.
5. 计算:
(1)(−8) × 9 × (−1.25) × (− 1);
= −2 − 20
= −22;
(5)1 + (−2) + 3 + (−4) … + 2009 + (−2010) + 2011 + (−2012)
= (1 − 2) + (3 − 4) … + (2009 − 2010) + (2011 − 2012)
= −1 × 1006
= −1006.
【解析】本题考查了有理数的加法,在进行有理数加法运算时,首先判断两个加数的符
【解析】此题主要考查有理数的加法,根据同号两数相加,取相同的符号,并把绝对值 相加,异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值 求解 (1)根据同号两数相加,取相同的符号,并把绝对值相加求解 (2)根据异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对 值求解 (3)先同号相加,再异号相加求解较简便 (4)先求个数的绝对值,再相加 (5)先求个数的绝对值,再相加
