第九章 电磁感应 电磁场理论
第九章电磁感应电磁场理论
返回 退出
结论 当穿过闭合回路的磁通量发生变化时,不管
这种变化是由什么原因的,回路中有电流产生。 称为电磁感应现象。
电磁感应现象中产生的电流称为感应电流, 相应的电动势称为感应电动势。
返回 退出
二、楞次定律 楞次定律: 感应电动势产生的感应电流方向,总 是使感应电流的磁场通过回路的磁通量阻碍原磁通 量的变化。
求:感应电动势和感应电流以及最大感应电动势和
最大感应电流。
解: 2 n 120 s-1
60
Φ B S BS cos
B r2 cos t
2
a
r
b
i
dΦ dt
B r2
2
sin t
返回 退出
i
dΦ dt
B r2
2
sin t
i max
1 2
B
r2
2.96(V)
Ii
i
R
B r2
2R
sin t
L 0
d
i
0I 2 cos
L
a
cos
ln
a
L cos
a
返回 退出
二、在磁场中转动的线圈内的感应电动势 矩形线圈为N 匝,面积
S,在匀强磁场中绕固定 的轴线OO' 转动,磁感应 强度与轴垂直。
当 t = 0 时, = 0。
任一位置时:
Φ BScos
i
N
dΦ dt
NBS sin
d
dt
返回 退出
(2)非闭合回路
∂B
a.
Ei dl
L
cS
∂t
dS
εi Ei dl
大学物理第九章

动生电动势
由于导体运动而产生的感应电动势。
dΦ B dS Bldx
i
dΦ dt
Bl
dx dt
Bl
d a
B
l
c b
dx
负号表示电动势的方向。
在磁场中运动的导线内的感应电动势
导线内每个自由电子受到的
洛仑F兹力e
B
非静E电k 场 强Fe
B
a
电场。
解:由场的对称性,变化磁场所激发的感生电场
线在管内、外都是与螺线管同轴的同心圆。
取任一电场线(半径为r)作
为闭合回 路, 则
L L
E E
E
ddll21LrESdSlBtBt2ddSrSE
ER
r
B
感生电场
1)
当r
S
<RB时 dS t
S
B t
dS
r 2 dB
dt
E
1
2r
S
§9-1 电磁感应定律
法拉第(1791-1867英国)
1831年,发现电磁感应现象。 1833年,发现电解定律。 1837年,发现电解质对电容的影响, 引入电容率概念。 1845年,发现磁光效应,顺磁质、抗 磁质等。
§9-1 电磁感应定律
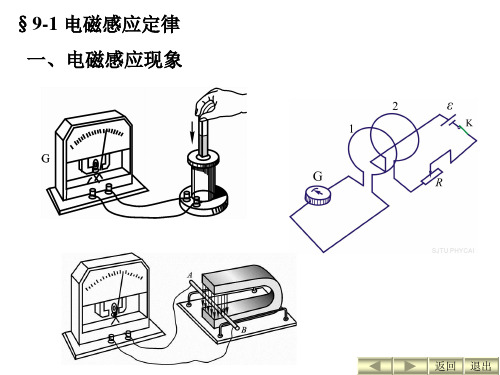
1. 电磁感应现象
N
S
现象1
条形磁铁N极(或S极)插入线圈时,线圈中就有电 流通过,这种电流称为感应电流。 实验表明:磁铁与线圈有相对运动时,线圈中就有感 应电流,相对速度越大,感应电流也越大。
(a)Φ 0, dΦ
B
dt en
0, i
0
i
(b)Φ 0, dΦ
B
dt en
第九章电磁感应电磁场理论b
解:由安培环路定理可得磁场分布:
B0
B 0I 2 r
r R2, r R1 R1 r R2
在筒内距轴心 r 处的磁能密度为:
r dr
I
R1
R2
l
I
1 B2
wm 2 0
0I 2 8 2r 2
取图示体积元,则: dV 2rl dr
此体积元的磁能为: dWm wmdV
例如:汽车和煤气炉的点火器、电警棍等都是感应圈的应用。
9—5 磁场的能量
R
L
一、载流自感线圈的磁能:
i
。。k
在开关合上后的一段时间内,电路中的电流 i 增长:0→I ,
在线圈上产生自感电动势:
L
L
di dt
由全电路欧姆定律有: L i R
iRL
iR Ld i dt
(电源的元功)
线圈的磁能元 (dt时间消耗在负载R上的焦耳热)
0t i dt 0t i2Rdt 0ILi di
(电源的电能) (负载上的焦耳热) (线圈的磁能)
即:线圈提供的电能一部分转化为负载的焦耳热, 另一部分作为磁能储存于线圈。
载流线圈的磁能为:
Wm 0ILi di
原因
L
H
dl
I 0
( S2面) ( S1面)
矛盾
电流的连续性在两极板间遭到破坏,即: j ds 0 s
2. 麦氏位移电流假设:
I
q0
S +++++++++
D
第九章电磁场理论的基本概念(电磁感应部分)精品PPT课件

设单位正电荷所受到的非
静电力为
Ek
I
则电源的电动势为:
i Ekdl
对如图的情况为: i Ek dl
+ + + + + + + Ek f非
+
-
E f静
---------
§ 9-1 法拉第电磁感应定律 一、电磁感应现象
1、 G
A
K
磁场发 生变化
K闭合和打开瞬间,电流计指针偏转。
a
2、
G
v
B
b
ab左右滑动时,电流计指针偏转。
切割磁 感应线
几个典型实验:
(1)
A (2)
B
v
i
B
x
(4) B
(3)
SN
(5)
A
当穿过一个闭合导体回路所包围的面积内的
第 九 章
电 磁 场 理 论 的 基 本 概 念
第九章 电磁场理论的基本概念
(电磁感应部分)
§ 9-1 法拉第电磁感应定律 § 9-2 动生电动势和感生电动势 § 9-3 自感现象和互感现象 § 9-4 磁场的能量
教学要求:
1. 掌握用法拉第定律和楞次定律计算感生电动 势及方向;
2. 理解感生电动势和动生电动势的产生原因; 3. 了解自感与互感,能计算简单回路的L,M; 4. 能计算简单磁场的Wm。
解:通过abcda的磁通量为
Φ=BS=BLx
b
aA
感应电动势为
i
dΦBd LxBv L=
dt
dt
-0.01
c
εi 的方向如图。
i
v
B
dB x
第九章 电磁感应 电磁场理论(完全版)要点

按楞次定律,要想维持回 路中电流,必须有外力不断作 功。这符合能量守恒定律。
如果把楞次定律中的“阻碍”改为“助长”, 则不需 外力作功,导线便会自动运动下去,从而不断获得电 能。这显然违背能量守恒定律。
6
对闭合导体回路而言, 感应电动势的方向和感 应电流的方向是相同的。
I
i
因而回路中感应电动势的方向 ,也用楞次定律来 判断。 应当指出,只要一个回路中的磁通量发生变化, 这个回路中便一定有感应电动势存在,这和回路由 什么材料组成无关。是否有感应电流,那就要看回 路是否闭合。 7
dm i N =Bab sin( t + ) 2 dt
=Bab cos t
m=Babcos ( t + ) 2
a b
图9-4
B
15
(2)一导线弯成角形(bcd=60º , bc=cd=a),在匀强 磁场B中绕oo´轴转动,转速每分钟n转, t=0时如图135所示,求导线bcd中的i。 c 我们连接bd组成一个三 B 角形回路bcd。由于bd段不 产生电动势,所以回路( o b d o´ bcd)中的电动势就是导线 bcd中电动势的。 图9-5 m=BScos ( t+o)
d m i dt
(9-1)
m Bds cos
s
d m (ii)求导: i dt
9
d m i dt
可用如下符号法则判定感应电动势的方向:
若i >0, 则i 的方向与原磁场的正方向组成右手螺 旋关系; 若i <0, 则i 的方向与原磁场的负方向组成右手螺 旋关系。
1
t2
2
1
1 dm R
(9-4)
大学物理-第九章 电磁感应 电磁场理论

2.电场强度沿任意闭合曲线的线积分等于以该曲线
为边界的任意曲面的磁通量的变化率的负值。 3.通过任意闭合曲面的磁通量恒等于零。
4.磁场强度沿任意闭合曲线的线积分等于穿过以该 曲线为边界的曲面的全电流。
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
麦克斯韦方程组(物理含义)
(1) SDdSq (2)
例1 有一圆形平板电容器 R , 现对其充电,使电路上
的传导电流为 I ,若略去边缘效应, 求两极板间离开轴
线的距离为 r(r R) 的区域的(1)位移电流;
(2)磁感应强度 .
解 如图作一半径
Q Q
为 r平行于极板的圆形
回路,通过此圆面积的
电位移通量为
I
R P*r
I
ห้องสมุดไป่ตู้
D D(πr2)
D
Edl BdS
L
s t
(3) SBdS0
(4) LHdl IsD t dS
1.电荷是产生电场的源。
2.变化的磁场也是产生电场的源。
3.自然界没有单一的“磁荷”存在。
4.电流是产生磁场的源,变化的电场也是产生磁场的源。
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
解:∵
B只分布在R 1
r
R 2
区
域内且
wm
B2 2
8
I2 2r 2
B I 2 r
第第九十章一电章磁真感空应中的电恒磁定场磁理场论
RR11 RR22
⊙⊙BB II
rr ⊕⊕BB
r dr
所以取体积元为 dVl2rdr
W m VwmdVR R1 28μπ2Ir22l2πrdr
第9 章 《电磁感应 电磁场理论》复习思考题

第9章 《电磁感应 电磁场理论》复习思考题一、填空题:1.飞机以1s m 200-⋅=v 的速度水平飞行,机翼两端相距离m 30=l ,两端这间可当作连续导体。
已知飞机所在处地磁场的磁感应强度B 在竖直方向上的分量T 1025-⨯。
机翼两端电势差U 为0.12V 。
2.当穿过一个闭合导体回路所包围的面积内的 磁通量 发生变化时,在导体回路中就会产生电流,这种现象称为电磁感应现象。
3.用导线制造成一半径为m 10.0=r 的闭合圆形线圈,其电阻Ω=10R ,均匀磁场B 垂直于线圈平面。
欲使电路有一稳定的感应电流A 01.0=I ,B 的变化率应为__3.18T/s_____________。
4.楞次定律:感生电流的磁场所产生的磁通量总是 阻碍引起感应电流的磁通量的变化。
5.如果导体不是闭合的,即使导体在磁场里做切割磁力线运动也不会产生感应电流,但在导体的两端产生_感应电动势____。
6.楞次定律是 能量守恒和转换 _定律在电磁现象领域中的表现。
二、单选题1.感生电场是 。
(A )由电荷激发,是无源场; (B )由电荷激发,是有源场;(C )由变化的磁场激发,是无源场; (D )由变化的磁场激发,是有源场。
2.关于感应电动势的正确说法是: 。
(A )导体回路中的感应电动势的大小与穿过回路的磁感应通量成正比;(B )当导体回路所构成的平面与磁场垂直时,平移导体回路不会产生感应电动势;(C )只要导体回路所在处的磁场发生变化,回路中一定产生感应电动势;(D )将导体回路改为绝缘体环,通过环的磁通量发生变化时,环中有可能产生感应电动势。
3.交流发电机是根据 原理制成的。
(A )电磁感应; B )通电线圈在磁场中受力转动;(C )奥斯特实验; (D )磁极之间的相互作用。
4.将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则不计自感时, 。
(A )铜环中有感应电动势,木环中无感应电动势(B )铜环中感应电动势大,木环中感应电动势小(C )铜环中感应电动势小,木环中感应电动势大(D )两环中感应电动势相等。
第九章-电磁感应-电磁场理论PPT

在长直导线旁平行放置一矩形线圈,线圈平面与直导线
在同一平面内。已知线圈长为 ,宽为l ,线圈b近长直
导线的一边离直导线距离为 。求任a 一 处的
a
b
磁感应强度为 B 0I
I
2πx
l
选顺时针方向为矩形线圈的绕行
电动势 I
Ek
+-
Ek : 非静电力场强.
E Ek dl
闭合电路的总电动势
E l Ek dl
动生电动势的本质: 当MN速度v向右运动时,导线内每 个自由电子受的洛伦兹力为:
Fm ev B
+ B
+
+ +
Fe++M++++
+ +
++
+ +
v + + + - + + + +
+
+Fm+
vB
v
en
a
O
(2)当 sin 2ntπ, 1
即当 90、 等 2位70置 时电动势 最大 i
i NBl 2 2πn 1.32V
(3)当t=1s时,
i NBl 2 2πn sin 2πn 0
本题也可以将线圈看作由四段长为l的导线在磁场
中运动产生动生电动势之和。显然只有ab和cd两边
O轴转动,角速率ω=100 rπad/s, 求铜棒中的动生电
动势大小及方向。如果是半径为50cm的铜盘以上述 角速度转动,求盘中心和边缘之间的电势差。
解:在铜棒上距O点为 l处取
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
× × × × G × × × × × × × × × a× × × × × × × × ×
× b×
发现检流计的指针偏转,说明回路中有电流。
线圈不动, 线圈不动,磁场变 不动
N
G
G A
K
发现检流计的指针偏转,说明回路中有电流。
解
设回路的绕行方 法一: 法一: ×c × × b × ×b'× × 向为顺时针方向 × × r× × × × × r
ab = l ad = x r r Φ = B ⋅ S = + Blx
× × × × × × × ×d × × a × ×a'× ×
B
v
dΦ dx = − Blv E=− = − Bl i dt dt
B
v
如图,在两无限长载流导线组成的平面内, 例题 9-2 如图,在两无限长载流导线组成的平面内, 有一固定不动的矩形导体回路,两电流方向相反, 有一固定不动的矩形导体回路,两电流方向相反,若电流 I=(2t +1)A,求线圈中 E 的大小和方向。 ( P277 9 - 10) 的大小和方向。 , i 解 ①求通过回路的磁通量Φ 设回路的绕行方向 为顺时针方向, 为顺时针方向,取面元 如图。 如图。 I I d1 d2 l dr r h
4.动生电动势的计算 动生电动势的计算 方法 • 一段直导体在磁场中运动时,用动生电动势的表 一段直导体在磁场中运动时, 达式求解。 达式求解。
r r r E = ∫ (v× B)⋅ dl i
b a
• 在磁场中平动和转动的闭合导体回路,用法拉第 在磁场中平动和转动的闭合导体回路, 平动和转动的闭合导体回路 电磁感应定律求解。 电磁感应定律求解。
磁铁向下运动,判断螺线管的N、S极? 磁铁向下运动,判断螺线管的 、 极 Ii N
r r 结论: 结论:Φm ↑, Ii的B与原 B 反向。 反向。 G r r 同向。 同向 Φm ↓, Ii的B与原 B 。
S
2. 法拉第电磁感应定律 回路中产生的感 应电动势与通过回路 的磁通量对时间的变 化率成正比。 化率成正比。
r en
L
绕行方向
> 的方向与L的绕行向相 。 若 E 0,则 E i< , i的方向与 的绕行向相 反
同
的方向相同。 回路中感应电流的方向与E 的方向相同。 i 如果闭合回路的电阻为R, 如果闭合回路的电阻为 ,则感应电流为
E 1 dΦ i Ii = = − R R dt
从 t1-t2 时间内通过回路任一截面的感应电量为
解 ⑴求动生电动势 用表达式求解 取线元dl 取线元 如图
r × r × × l × v×B × B A × × O × rdl × × ω v
× × × × × × × × × ×
×
× ×
×
× r
r r r dEi = (v × B ) ⋅ dl = ωlBdl
A L
1 2 Ei = ∫ dEi = ∫ ωBldl = BωL O→A 0 O 2 r r 的方向 直导体的动生电动势方向: 直导体的动磁场不变,因导体在磁场中运动而产生 称为动生电动势。 的 E 称为动生电动势。 i × × b × r× v × ra × F × ×
Ei
r r r F = ( −e )v × B
感应电流方向
abcda 方向
电动势 把单位正电荷经电源内部由负极移到正极时 非静电力所作的功。 非静电力所作的功。
b a
r 的方向为积分的方向, → dl 的方向为积分的方向,即a→b
在均匀磁场中运动的一段直导体ab=L 在均匀磁场中运动的一段直导体 r r a • 当 v ⊥ B ⊥ L时
b
E = ±∫ vBdl = ±vBL i
a
b
r B⊗r ⊙v
r r r r r • 若 v与B 间夹角为θ 1,(v × B )与L夹角为θ 2
Eiacb = − Ei ba = − vB ⋅ ba
整个圆弧导线上的动生电动势 整个圆弧 方向
×c × × o × r × ×R ×
B
× ×
Eiacb = − 2vBR
b→c→a
的长直导线旁有一长为l 例题 9-5 在通有电流 I 的长直导线旁有一长为 的金 r 属棒, 平行于导线运动。 棒一端距离导线为a 属棒,以速度 v平行于导线运动。 棒一端距离导线为 , 求棒中的感应电动势。 求棒中的感应电动势。 r 解 取 x 轴如图, 取线元 如图, 该处的 B 为 如图, 轴如图, 取线元dx如图 r r B v µ0 I B= ⊗ r r v× B 2πx x a I O M r r dx N r dEi = (v × B ) ⋅ dl = − vBdx x
①有可以移动的电荷,导体要形成回路。 有可以移动的电荷,导体要形成回路。 有迫使电荷作定向运动的电场或回路中有电动势。 ②有迫使电荷作定向运动的电场或回路中有电动势。
二. 电磁感应定律 1. 楞次定律 闭合回路中感应电流的磁场总是要反抗 引起感应电流的磁通量的变化。 引起感应电流的磁通量的变化。
S N
E 的方向为逆时针方向 i
法二: 法二:设回路的绕行方向为逆时针方向
r r Φ = B ⋅ S = − Blx
dΦ dx E=− = Bl i dt dt
= Blv
E 的方向为逆时针方向 i
×c × × b × ×b'× × × × r× × × × × r × × × × × × × ×d × × a × ×a'× ×
dΦ E = −k i dt 线圈为N匝时 线圈为 匝时 Φ = Nϕ
在 [SI] 中, k =1
dΦ E= − i dt
法拉第在做实验
3. 说明
dΦ 是计算感应电动势的普适公式。 是计算感应电动势的普适公式。 E=− i dt
法拉第电磁感应定律判定 E 的方向: i 的方向:
的方向可用楞次定律或法拉第电磁感应定律来判定。 E的方向可用楞次定律或法拉第电磁感应定律来判定。 i • 先设定回路 的绕行方向 先设定回路L的绕行方向 r r • 求通过 的磁通量 Φ = B⋅ dS 求通过L的磁通量 ∫S dΦ • 据E = − 确定 E的方向 i i dt
第 九 章 电 磁 场 理 论 的 基 本 概 念 电 磁 感 应
法 拉 第 正 在 讲 演
§9-1 法拉第电磁感应定律 - §9-2 动生电动势和感生电动势 - §9-3 自感现象和互感现象 - §9-4 磁场的能量 - §9-5 位移电流 - 全电流定理
§9-6 麦克斯韦方程组的积分形式 -
§9-1 法拉第电磁感应定律
2. 电磁感应现象 当通过闭合 回路的磁通量发 生变化时, 生变化时,在回 路中出现电流的 现象称为电磁感 现象称为电磁感 应现象。 应现象。所产生 的电流称为感应 的电流称为感应 电流。 电流。
电磁感应
3.说明 说明
r r r 的变化, ①无论是磁场 B的变化,还是 B的方向与面元 dS 法向 间的夹角发生变化,还是回路面积的变化, 间的夹角发生变化,还是回路面积的变化,都会产 生电磁感应现象。 生电磁感应现象。
r dS :
dS= hdr 大小 方向
⊗
r r dS 处的 B:
1 1 µ0 I B= ( ) − 2π r + d1 r + d 2 ⊙
I
I d1 d2
I=2t+1 dr r r µ 0 I 1 1 ( ) × hdr cos π − dΦ = B ⋅ dS = 2π r + d 1 r + d 2 r h 1 µ 0 Ih 1 ( )dr =− − 2π r + d 1 r + d 2 l l µ Ih 1 1 0 ( )dr − Φ = ∫ S dΦ = − 2π r + d1 r + d 2 0
∫
µ 0 Ih l + d1 l + d2 (ln ) =− − ln 2π d1 d2
②求 E i
dΦ µ 0 h d 2 ( d 1 + l ) ln = 大小: 大小: Ei = − >0 π d1 (d 2 + l ) dt
方向: 方向: 顺时针方向
§9-2 动生电动势和感生电动势
一.动生电动势 动生电动势 1.动生电动势 动生电动势 2.表达式 2.表达式 洛仑兹力 导体棒内的自由电子 r 在磁场中受到洛仑兹力F × × × × c d × × × × × × × ×
解 用动生电动势公式求 在导线上取弧元dl如图 在导线上取弧元 如图 r r r dEi = (v × B ) ⋅ dl
r ( × × v× B) × × ×
× dl× × ×c ×
θ
= vBR cos θdθ
× r × ×R ×
dθ O
×
θ
B
× ×
× × 45o ×o r× 45 v × × b × ×
a
Ei = ⌒dEi = acb
方向
∫
∫
7π 4
π 4
vBR cos θdθ = − 2vBR
b→c →a
用电磁感应定律求 × 连接ab成闭合回路如图 连接 成闭合回路如图 × × × × × × a × × × 45o ×o r × 45 v × × b × ×
Ei = Eiacb + Ei ba = 0
1 2 UOA = − BωL 2
r 中有一个半径为R的圆弧形导线 例题 9-4 均匀磁场 B 中有一个半径为 的圆弧形导线 r acb以速度 v 沿∠aob的分角线水平向右运动,acb是3/4圆 的分角线水平向右运动, 是 圆 以速度 的分角线水平向右运动 试求导线上的动生电动势。 周。试求导线上的动生电动势。 r
