课程设计一:随机数的产生及统计特性分析-实验报告
实验报告随机数

一、实验目的1. 理解随机数生成的原理和过程。
2. 掌握常见随机数生成算法。
3. 分析随机数生成的性能和特点。
二、实验原理随机数在计算机科学、密码学、统计学等领域有着广泛的应用。
随机数生成算法是指从某种随机过程中产生一系列看似随机数的算法。
本实验主要研究以下几种随机数生成算法:1. 线性同余法(Linear Congruential Generator,LCG)2. Xorshift算法3. Mersenne Twister算法三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 实验工具:Jupyter Notebook四、实验步骤1. 线性同余法(LCG)实验(1)编写LCG算法函数```pythondef lcg(seed, a, c, m, n):random_numbers = []x = seedfor _ in range(n):x = (a x + c) % mreturn random_numbers```(2)设定参数并生成随机数```pythonseed = 12345a = 1103515245c = 12345m = 231n = 1000random_numbers = lcg(seed, a, c, m, n) print(random_numbers)```2. Xorshift算法实验(1)编写Xorshift算法函数```pythondef xorshift(seed, n):random_numbers = []x = seedfor _ in range(n):x ^= (x << 13)x ^= (x >> 17)x ^= (x << 5)return random_numbers```(2)设定参数并生成随机数```pythonseed = 12345n = 1000random_numbers = xorshift(seed, n)print(random_numbers)```3. Mersenne Twister算法实验(1)安装Mersenne Twister算法库```shellpip install numpy```(2)编写Mersenne Twister算法函数```pythonimport numpy as npdef mt19937(seed):random_numbers = np.random.RandomState(seed) return random_numbers.rand(n)n = 1000random_numbers = mt19937(12345)print(random_numbers)```五、实验结果与分析1. 线性同余法(LCG)生成的随机数序列具有较好的随机性,但存在周期性,当n足够大时,周期将变得非常明显。
统计模拟实验 实验报告

统计模拟实验实验报告实验名称:统计模拟实验实验目的:通过模拟统计实验,掌握统计方法及应用。
实验内容:1. 随机数生成:使用Python中的random库生成随机数。
2. 正态分布模拟:使用正态分布模拟实验,掌握正态分布的概念、性质及应用方法。
3. 置信区间估计:使用抽样模拟实验,掌握置信区间估计的方法及应用。
实验步骤:1. 随机数生成利用Python中的random库生成随机数。
根据需要生成随机数的个数及生成的随机数的范围,生成随机数。
2. 正态分布模拟使用Python中的numpy库中的random.normal()函数,生成指定均值和标准差的正态分布随机数序列。
3. 置信区间估计随机抽样,计算样本平均值,并计算样本均值的标准差。
利用中心极限定理,计算样本均值分布的置信区间。
实验结果分析:1. 随机数生成生成了10个[0,1)之间的随机数:0.82, 0.24, 0.77, 0.30, 0.34, 0.43, 0.78, 0.45, 0.57, 0.862. 正态分布模拟生成了一个均值为0,标准差为1的正态分布随机数序列,其中包含了100个随机数:[-0.024, 0.234, -0.933, -0.157, 0.040, 1.759, -1.296, -0.006, 0.768, 0.576, -0.543, -0.402, -1.161, -0.347, -0.046, -0.753, 0.703, 0.551, -1.627, 0.492, -0.957, 0.209, -0.411, -1.473, -0.029, 0.396, -0.710, -1.555, -1.193, 1.236, -0.546, 1.063, 1.976, 0.138, -0.576, -0.602,0.767, -1.394, -0.119, -1.356, 1.195, 0.183, 1.211, 0.899, 0.271,1.137, -1.637, 0.227, 0.819, -1.882, 0.662, -0.428, -0.039, -0.025,0.589, -0.344, 0.110, 1.176, 1.052, 0.047, 1.641, 0.201, -1.167, -1.102, 0.931, -0.659, -0.827, -0.050, 0.728, -0.827, 0.869, 0.192,0.072, -0.988, -0.866, -1.238, 0.011, -1.732, 1.482, 1.256, -0.771,1.284, 0.550, -0.161, -0.213, -0.694,2.114, 0.137, -0.825, 1.218, 0.037, 0.666, 1.260, -1.298, 0.989, -2.163, -1.918, 0.772, 0.269, 0.872, 0.809, -1.046, 0.903, -1.183, 0.854]3. 置信区间估计利用抽样模拟实验,得到了10个样本的样本平均值及标准差,以及样本平均值分布的置信区间:样本数据:[84, 74, 66, 73, 78, 89, 92, 80, 77, 85],样本平均值:79.8,样本标准差:6.68,95%置信区间:(74.47, 85.13)实验结论:通过本次实验,我们掌握了通过随机数生成模拟实验、正态分布随机数生成模拟实验、置信区间估计的模拟实验方法及应用,对统计学方法及实际应用有了更深入的了解。
随机信号分析实验报告(基于MATLAB语言)

随机信号分析实验报告——基于MATLAB语言姓名:_班级:_学号:专业:目录实验一随机序列的产生及数字特征估计 (2)实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试 (18)实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。
2.实现随机序列的数字特征估计。
实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列(样本值序列)。
进行随机信号仿真分析时,需要模拟产生各种分布的随机数。
在计算机仿真时,通常利用数学方法产生随机数,这种随机数称为伪随机数。
伪随机数是按照一定的计算公式产生的,这个公式称为随机数发生器。
伪随机数本质上不是随机的,而且存在周期性,但是如果计算公式选择适当,所产生的数据看似随机的,与真正的随机数具有相近的统计特性,可以作为随机数使用。
(0,1)均匀分布随机数是最最基本、最简单的随机数。
(0,1)均匀分布指的是在[0,1]区间上的均匀分布, U(0,1)。
即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数,通常采用的方法为线性同余法,公式如下:,序列为产生的(0,1)均匀分布随机数。
定理1.1若随机变量X 具有连续分布函数,而R 为(0,1)均匀分布随机变量,则有2.MATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数:rand用法:x = rand(m,n)功能:产生m×n 的均匀分布随机数矩阵。
(2)正态分布的随机序列函数:randn用法:x = randn(m,n)功能:产生m×n 的标准正态分布随机数矩阵。
随机数的产生教学设计

随机数的产生教学设计教学设计:随机数的产生一、教学目标:1.理解随机数的概念和作用;2.了解随机数的产生方法;3.掌握在不同编程语言中生成随机数的方法。
二、教学内容:1.什么是随机数?随机数是一种在一定范围内没有确定规律的数。
在计算机编程中,随机数常常被用于模拟随机事件或生成随机数据。
2.随机数的产生方法:a.物理随机数产生器:利用物理或化学现象(如放射性衰变和电子噪声)产生随机数。
b.伪随机数产生器:利用数学算法根据最初的种子数产生似乎是随机的数列。
三、教学过程:1.引入随机数的概念(10分钟):通过提问和讨论的方式引导学生理解随机数的概念和作用,例如“你们知道什么是随机数吗?在什么情况下我们需要使用随机数呢?”2.介绍随机数的产生方法(15分钟):简要介绍物理随机数产生器和伪随机数产生器的原理,并讨论它们的优缺点和适用范围。
3.物理随机数产生器的实验演示(20分钟):准备一个物理随机数产生器,并进行实验演示。
通过观察随机数产生器的输出结果,学生可以更直观地了解物理随机数产生器的工作原理。
4.编写代码生成伪随机数(30分钟):选择一种编程语言,如Python或Java,向学生展示如何使用该语言生成伪随机数。
教师可以给出示例代码,然后让学生跟着操作,并观察不同种子产生的随机数序列。
5.伪随机数产生器的编程实践(40分钟):让学生按照教师给出的指导,自行编写代码来生成伪随机数。
可以提供几个具体的应用场景,要求学生根据这些场景编写相应的代码,并观察运行结果。
6.比较不同编程语言生成随机数的方法(20分钟):介绍不同编程语言中生成随机数的方法,并比较它们的异同点。
可以通过举例说明来帮助学生更好地理解不同方法的使用。
7.总结回顾(15分钟):准备一些问题和练习题,让学生回顾所学的知识,并发表自己的观点和感想。
四、教学评价:1.观察学生的课堂互动和合作情况,评价学生的参与度和理解程度;2.对学生提交的编程作业进行评价,检查其代码的正确性和创新性;3.布置一份综合性的作业,要求学生考察随机数在实际应用中的作用,并编写相应的代码实现。
随机信号分析实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y实验报告课程名称:随机信号分析院系:电子与信息工程学院班级:姓名:学号:指导教师:实验时间:实验一、各种分布随机数的产生(一)实验原理1.均匀分布随机数的产生原理产生伪随机数的一种实用方法是同余法,它利用同余运算递推产生伪随机数序列。
最简单的方法是加同余法)(mod 1M c y y n n +=+My x n n 11++= 为了保证产生的伪随机数能在[0,1]内均匀分布,需要M 为正整数,此外常数c 和初值y0亦为正整数。
加同余法虽然简单,但产生的伪随机数效果不好。
另一种同余法为乘同余法,它需要两次乘法才能产生一个[0,1]上均匀分布的随机数)(mod 1M ay y n n =+ My x n n 11++= 式中,a 为正整数。
用加法和乘法完成递推运算的称为混合同余法,即)(mod 1M c ay y n n +=+ My x n n 11++= 用混合同余法产生的伪随机数具有较好的特性,一些程序库中都有成熟的程序供选择。
常用的计算语言如Basic 、C 和Matlab 都有产生均匀分布随机数的函数可以调用,只是用各种编程语言对应的函数产生的均匀分布随机数的范围不同,有的函数可能还需要提供种子或初始化。
Matlab 提供的函数rand()可以产生一个在[0,1]区间分布的随机数,rand(2,4)则可以产生一个在[0,1]区间分布的随机数矩阵,矩阵为2行4列。
Matlab 提供的另一个产生随机数的函数是random('unif',a,b,N,M),unif 表示均匀分布,a 和b 是均匀分布区间的上下界,N 和M 分别是矩阵的行和列。
2.随机变量的仿真根据随机变量函数变换的原理,如果能将两个分布之间的函数关系用显式表达,那么就可以利用一种分布的随机变量通过变换得到另一种分布的随机变量。
概率论与数理统计实验

整理课件
3、指数分布随机数
1) R = exprnd(λ):产生一个指数分布随机数 2)R = exprnd(λ,m,n)产生m行n列的指数分布随机数
例3、产生E(0.1)上的一个随机数,20个随机数, 2行6列的随机数。
整理课件
在Matlab命令行中输入以下命令: binomoni(0.5,1000)
整理课件
在Matlab命令行中输入以下命令: binomoni(0.5,10000)
整理课件
在Matlab命令行中输入以下命令: binomoni(0.3,1000)
整理课件
二、常用统计量
1、表示位置的统计量—平均值和中位数
概率论与数理统计实验
实验2 随机数的产生
数据的统计描述
整理课件
实验目的
学习随机数的产生方法 直观了解统计描述的基本内容。
实验内容
1、随机数的产生 2、统计的基本概念。 3、计算统计描述的命令。 4、计算实例。
整理课件
一、随机数的产生 定义:设随机变量X~F(x),则称随机变量X的 抽样序列{Xi}为分布F(x)的随机数 10常用分布随机数的产生
整理课件
例6 生成单位圆上均匀分布的1行10000列随机数,并 画经验分布函数曲线。
Randnum=unifrnd(0,2*pi,1,10000); %(0,2pi)上均匀分布随机数 xRandnum=cos(Randnum);%横坐标 yRandnum=sin(Randnum);%丛坐标 plot(xRandnum,yRandnum);
例9:产生5组指数分布随机数,每组100个, 计算样本偏度和峰度。
随机数的产生及统计特性分析-实验报告

电子科技大学通信与信息工程学院标准实验报告实验名称:随机数的产生及统计特性分析电子科技大学教务处制表电子科技大学实验报告学生姓名:吴子文学号:2902111011 指导教师:周宁实验室名称:通信系统实验室实验项目名称:随机数的产生及统计特性分析实验学时:6(课外)【实验目的】随机数的产生与测量:分别产生正态分布、均匀分布、二项分布和泊松分布或感兴趣分布的随机数,测量它们的均值、方差、相关函数,分析其直方图、概率密度函数及分布函数。
通过本实验进一步理解随机信号的一、二阶矩特性及概率特性。
编写MATLAB程序,产生服从N(m, sigma2)的正态分布随机数,完成以下工作:(1)、测量该序列的均值,方差,并与理论值进行比较,测量其误差大小,改变序列长度观察结果变化;(2)、分析其直方图、概率密度函数及分布函数;(3)、计算其相关函数,检验是否满足Rx(0)=mu^2+sigma2,观察均值mu 为0和不为0时的图形变化;(4)、用变换法产生正态分布随机数,重新观察图形变化,与matlab函数产生的正态分布随机数的结果进行比较。
【实验原理】1、产生服从N(m, sigma2)的正态分布随机数,在本实验中用matlab中的函数normrnd()产生服从正态分布的随机数。
(1)R = normrnd(mu,sigma) 产生服从均值为mu,标准差为sigma的随机数,mu和sigma可以为向量、矩阵、或多维数组。
(2)R = normrnd(mu,sigma,v) 产生服从均值为mu 标准差为sigma的随机数,v是一个行向量。
如果v是一个1×2的向量,则R为一个1行2列的矩阵。
如果v 是1×n 的,那么R 是一个n 维数组。
(3)R = normrnd(mu,sigma,m,n) 产生服从均值为mu 标准差为sigma 的随机数,标量m 和n 是R 的行数和列数。
2、测量该序列的均值、方差,并与理论值进行比较,测量其误差大小,改变序列长度观察结果变化。
随机数的产生和特性曲线
《概率论与随机信号分析》实验报告一、实验目的与任务1.了解随机数的产生方法;2.了解常用随机数的概率分布函数、分布律和概率密度函数。
二、实验原理随机数的产生有好多方法,可以利用乘积法和同余法产生【0,1】之间的均匀分布,然后利用函数变换法产生所需不同分布的随机数。
可以按照所产生的随机数,对落在不同区间的数据进行统计,从而画出所产生的随机数的统计特性。
所有这些工作我们可以自己动手用matlab,VC或VB等语言进行编程实现。
在现代系统仿真中,大量地使用matlab工具,而且它也提供了非常丰富的函数来产生经常使用的分布的随机数,比如rand,randn就是用来产生均匀分布随机数和高斯分布随机数的。
本实验充分利用matlab提供的工具来产生随机数,验证和观察其统计特性。
1.disttool:分布函数和密度函数的可视化工具分布函数和密度函数的工具能够产生22种常用分布的概率分布曲线和概率密度曲线,并通过图形方式显示。
我们还可以通过修改参数产生同一种分布不同参数的概率分布曲线和概率密度曲线。
2.randtool:随机变量模拟工具随机变量模拟工具能够模拟产生22种常用分布的随机数,并可以通过修改它们的参数产生同一种分布不同参数的随机数,并通过图形方式显示它们的概率密度统计。
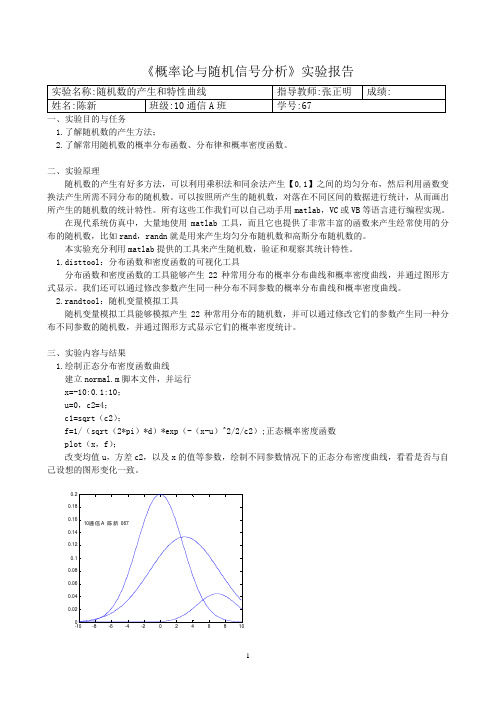
三、实验内容与结果1.绘制正态分布密度函数曲线建立normal.m脚本文件,并运行x=-10:0.1:10;u=0,c2=4;c1=sqrt(c2);f=1/(sqrt(2*pi)*d)*exp(-(x-u)^2/2/c2);正态概率密度函数plot(x,f);改变均值u,方差c2,以及x的值等参数,绘制不同参数情况下的正态分布密度曲线,看看是否与自己设想的图形变化一致。
2.利用disttool产生不同分布、不同参数的分布函数和分布函数密度曲线,观察各种分布曲线的特点,并记录二项分布、正态分布、指数分布、瑞利分布曲线。
正态:二项分布:指数分布:瑞利分布:3.利用randtool工具,产生不同分布、不同参数的随机数并进行统计,绘制密度函数曲线,并观察和记录不同样本数时统计特性的差别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标准实验报告
实验名称:随机数的产生及统计特性分析
实验报告
学生姓名:学号:
指导教师:
实验室名称:通信系统实验室
实验项目名称:随机数的产生及统计特性分析
实验学时:6(课外)
【实验目的】
随机数的产生与测量:产生瑞利分布随机数,测量它们的均值、方差、相关函数,分析其直方图、概率密度函数及分布函数。
通过本实验进一步理解随机信号的一、二阶矩特性及概率特性。
【实验原理】
瑞利分布密度函数为:
)0
(
,0
,
)
(
2
2
2
2
>
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
≥
=
-
σ
σ
σ
x
x
e
x
x
f
x
均值与方差:EX =
σ
π
2,V ar(X)=
2
)
2
2(σ
π
-
相关函数:
⎰+∞
∞
-
-
=
+
=)
(
*)
(
)
(
)
(
)
(t
x
t
x
dt
t
x
t
x
r
x
τ
τ
均值各态历经定义:E[X(t)]以概率1等于A[X(t)],则称X(t)均值各态历经。
物理含义为:只要观测的时间足够长,每个样本函数都将经历信号的所有状态,因此,从任一样本函数中可以计算出其均值。
——“各态历经性”、“遍历”。
于是,实验只需在其任何一个样本函数上进行就可以了,问题得到极大简化。
【实验记录】
程序执行结果:
rayl_mean =
3.7523 err_mean = 0.7523 rayl_var = 3.8303 err_var = 0.8303
【实验分析】
可以看到,统计均值、统计方差与理论值都很接近。
当序列长度为1000时
候,均值误差为5.63%,方差误差为12.19%;当序列长度为10000时,均值误差为0.79%,方差误差为1.04%,可以看到随着序列长度增大,样本的统计均值与统计方差与理论值得误差明显减小,当序列长度足够大的时候,样本的统计均值与统计方差会趋近与理论均值与理论方差,可以用统计均值、统计方差来计算理论均值与方差。
通过比较样本的直方图,与理论的瑞利分布概率密度函数图,发现样本出现的频率分布趋近于理论概率值,可见,当样本足够大的时候,随机变量取值的频率趋近于其概率,可以用频率分布近似概率分布。
由matlab 产生N 个随机数的原理可知,这N 个随机数可以看做一条样本函数,且这个随机序列是广义各态历经的,因此,可以利用样本的时间相关函数来计算统计相关函数。
由图可知,当均值为0的时候,样本相关函数为零。
当均值不为0的时候,样本的相互函数为三角函数。
当均值为0的时候,由图知Rx(0)=0,与理论值2
2
μσ+=相等。
当均值不
为0的时候,由图,得Rx(0)= 15.60,与理论值91
.1722
=+σμ的误差为12.8%。
可见,Rx(0)的计算是正确的。
【思考题】
1、 为什么当均值mu 不为0时,()X R τ的图形是三角形?
在求自相关函数的时候,我们利用的是matlab 自带的卷积公式,即移位相乘再相加,对于我们计算的有限长度的序列,在用此方法进行多次移位之后,之前的序列后续填零,再进行相同的工作。
均值不为0时,当τ=0时,自相关函数最大,τ>0时,序列向后移,该序
列和填零后的新序列相作用,又因为计算是线性的,因此是线性递减。
τ<0与τ>0关于τ=0对称,因此()
X R τ的图形是三角形。
2、 实验中的样本数都设定为1000,试简述样本数对于结果的影响?
答:样本数决定着实验的精度,样本数越大,实验结果越接近于理论值。
样本数过小时容易与理论值产生很大偏差。
由均值误差、方差误差与理论值随样本数目的增大的曲线图很容易得出这样的结论。
【总结及心得体会】
通过本次试验,我对瑞利分布的概率密度和分布函数的形状和大致变化趋势有了更深刻的了解,并通过对由matlab 产生的服从瑞利分布的随机数的相关数字特征和相关函数进行计算,验证了瑞利分布的均值、方差表达式的正确性。
并通过改变实验中样本数观察实际结果与理论值的误差的变化领悟了样本数对于实验的重要性。
【对本实验过程及方法、手段的改进建议】
可以设定多组实验,分别采用不同的样本数,并且各组的样本数差别较大,这样能更明显的显示样本数对实验结果的影响。
Matlab程序:
sigma=3;
N=10000;
X=raylrnd(sigma,1,N);
average=sigma; %理论均值
variable=sigma; %理论方差
A VERAGE=mean(X) %随机数的均值
ERR_A VERAGE=(A VERAGE-average)/average %均值误差
V ARIABLE=var(X) %随机数的方差
ERR_V ARIABLE=(V ARIABLE-variable)/variable %方差误差
f_x=0:1:10;
cdf_f=raylcdf(f_x,sigma); %分布
pdf_f=raylpdf(f_x,sigma); %概率密度
figure(1),stairs(f_x,cdf_f);
figure(2),stem(f_x,pdf_f);
figure(3),hist(X);
max1=max(X);
[b,a]=hist(X,max1+1);
b=b/1000;
t=0:max1;
figure(4),stairs(t,b),hold on;stem(f_x+0.5,pdf_f,'r');
%相关函数
sigma=0;
X1=raylrnd(sigma,1,1000);
[RXX1,LAGS1]=xcorr(X1);
figure(5),plot(LAGS1/1000,RXX1/1000);
sigma=3;
X2=raylrnd(sigma,1,1000);
[RXX2,LAGS2]=xcorr(X2);
figure(6),plot(LAGS2/1000,RXX2/1000);
clear
clc
%误差曲线的绘制
mean1 = 3;
rayl_rnd = raylrnd(mean1 , 1 , 100000) ;
rayl_mean = mean(rayl_rnd)
err_mean = rayl_mean - mean1
rayl_var = var(rayl_rnd)
err_var = rayl_var - mean1
rayl_mean=[]; cha_mean=[];i=1;
for long = 1:100:10000
rayl_rnd = raylrnd(mean1 , 1 , long) ;
rayl_mean(i) = mean(rayl_rnd) ;
err_mean(i) = rayl_mean(i) - mean1 ;
rayl_var(i) = var(rayl_rnd) ;
err_var(i) = rayl_var(i) - mean1 ;
i=i+1;
end
t = 1:100:10000;
figure(1)
plot(t,rayl_mean); title('均值随序列长度变化曲线');grid xlabel('n');ylabel('mean')
figure(2)
plot(t,err_mean); title('均值误差随序列长度变化曲线');grid xlabel('n');ylabel('mean__err')
figure(3)
plot(t,rayl_var);title('方差随序列长度变化曲线'); grid xlabel('n');ylabel('var')
figure(4)
plot(t,err_var) ;title('方差误差随序列长度变化曲线');grid xlabel('n');ylabel('var__err')。
