蜗杆传动基本几何尺寸计算公式表格
蜗杆传动计算公式

q=d1/m=z1/tanγ
d1=q*m=z1*m/tanγ
d1`=(q+2*x2)*m=2a`-m*z2
tanγ =z1/q=z1*m/d
tanγ `=z1/(q+2*x2)
蜗杆类型: ZA 蜗杆——阿基米德圆柱蜗杆; ZN 蜗杆——法向直廓圆柱蜗杆; ZI 蜗杆——渐开线圆柱蜗杆; ZK 蜗杆——锥面包络圆柱蜗杆γຫໍສະໝຸດ 蜗杆节圆圆柱导程角γ`
公式及数据 a=0.5(d1+d2)=0.5(q+z2)*m a`=a+x2*m=0.5(q+z2+2*x2)*m u=z2/z1;z1 蜗杆头数,z2 涡轮齿数 x2=a`/m-0.5(q+z2)=(a`-a)/m
m 取标准值
mn=m*cosγ ,mn 不取标准值 px1=π *m
名称 非变位传动中心距 变位传动啮合中心距
齿数比 涡轮变位系数 蜗杆轴向模数(涡轮端 面模数)
法向模数 蜗杆轴向齿距 蜗杆螺旋线导程
蜗杆轴向齿形角
代号 a a` u x2
m
mn px1 pz1 ax
蜗杆法向齿形角
An
蜗杆直径系数
q
蜗杆分度圆(中圆)直
d1
径
蜗杆节圆直径
d1`
蜗杆分度圆(中圆柱)
导程角
蜗杆计算公式
d2'=d2
b1
见表11-4
由设计确定
蜗轮分度圆直径
d2
d2=mz2=2a-d1-2x2.m
?
蜗轮喉圆直径
da2
da2=d2+2ha2
?
蜗轮齿根圆直径
df2
df2=d2-2ha2
?
蜗轮齿顶高
ha2
ha2=1/2(da2-d2)=m(ha*+x2)
?
蜗轮齿根高
hf2
?
蜗轮齿高
h2
h2=ha2+hf2=1/2(da2-df2)
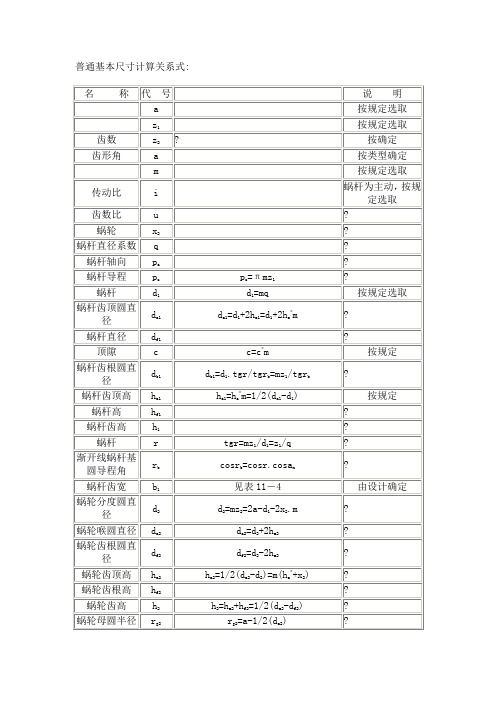
普通基本尺寸计算关系式:
名 称
代 号
说 明
a
按规定选取
z1
按规定选取
齿数
z2
?
按确定
齿形角
a
按类型确定
m
按规定选取
传动比
i
蜗杆为主动,按规定选取
齿数比
u
?
蜗轮
x2
?
蜗杆直径系数
q
?
蜗杆轴向
pa
?
蜗杆导程
pz
pz=πmz1
?
蜗杆
d1
d1=mq
按规定选取
蜗杆齿顶圆直径
da1
da1=d1+2ha1=d1+2ha*m
?
蜗杆直径
df1
?
顶隙
c
c=c*m
按规定
蜗杆齿根圆直径
db1
db1=d1.tgr/tgrb=mz1/tgrb
?
蜗杆齿顶高
ha1
ha1=ha*m=1/2(da1-d1)
按规定
蜗杆高
蜗轮蜗杆常见普通的规格及尺寸

常见普通蜗轮蜗杆的规格及尺寸例:蜗杆传动,已知模数m=4.蜗杆头数z1=1,蜗轮齿数z2=50,特性系数q=10。
求传动中心距a=?变位系数0时:中心距a=(蜗杆分度圆+蜗轮分度圆)/2=(特性系数q*模数m+蜗轮齿数Z2*模数m)/2=(10*4+50*4)/2=120特性系数:蜗杆的分度圆直径与模数的比值称为蜗杆特性系数。
加工蜗轮时,因为是直径和形状与蜗杆相同的滚刀来切制,由上式可看出,在同一模数下由于Z1和λ0的变化,将有很多不同的蜗杆直径,也就是说需要配备很多加工蜗轮的滚刀。
为了减少滚刀的数目,便于刀具标准化,不但要规定标准模数,同时还必须规定对应于一定模数的Z1/tgλ0值,这个值用q表示,称之为蜗杆特性系数。
圆柱蜗轮、蜗杆设计参数选择蜗轮和蜗杆通常用于垂直交叉的两轴之间的传动(图1)。
蜗轮和蜗杆的齿向是螺旋形的,蜗轮的轮齿顶面常制成环面。
在蜗轮蜗杆传动中,蜗杆是主动件,蜗轮是从动件。
蜗杆轴向剖面类是梯形螺纹的轴向剖面,有单头和多头之分。
若为单头,则蜗杆转一圈蜗轮只转一个齿,因此可以得到较高速比。
计算速比(i)的公式如下:i=蜗杆转速n1蜗轮转速n2=蜗轮齿数z2蜗杆头数z11、蜗轮蜗杆主要参数与尺寸计算主要参数有:模数(m)、蜗杆分度圆直径(d1)、导程角(r)、中心距(a)、蜗杆头数(或线数z1)、蜗轮齿数(z2)等,根据上述参数可决定蜗杆与蜗轮的基本尺寸,其中z1、z2由传动要求选定。
(1)模数m 为设计和加工方便,规定以蜗杆轴项目数mx和蜗轮的断面模数mt为标准模数。
对啮合的蜗轮蜗杆,其模数应相等,及标准模数m=mx=mt。
标准模数可有表A查的,需要注意的是,蜗轮蜗杆的标准模数值与齿轮的标准模数值并不相同。
表A图1图2(2)蜗杆分度圆直径d1 再制造蜗轮时,最理想的是用尺寸、形状与蜗杆完全相同的蜗轮滚刀来进行切削加工。
但由于同一模数蜗杆,其直径可以各不相同,这就要求每一种模数对应有相当数量直径不同的滚刀,才能满足蜗轮加工需求。
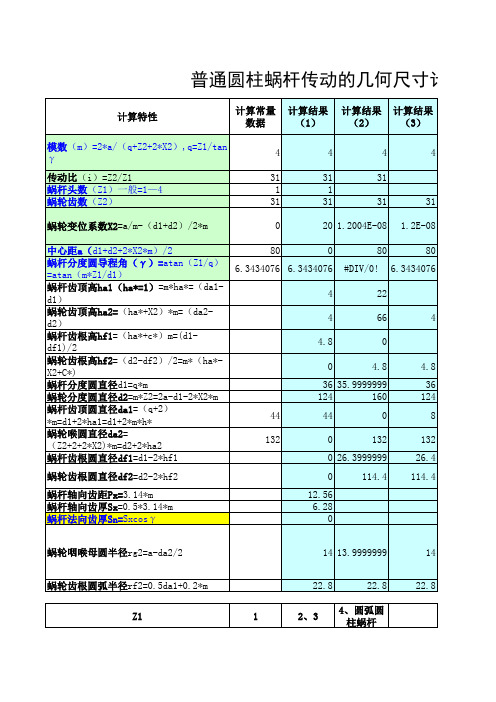
蜗轮蜗杆计算公式(简洁版)
0
20 1.2004E-08 1.2E-08
中心距a(d1+d2+2*X2*m)/2 蜗杆分度圆导程角(γ)=atan(Z1/q) =atan(m*Z1/d1) 蜗杆齿顶高ha1(ha*=1)=m*ha*=(da1d1) 蜗轮齿顶高ha2=(ha*+X2)*m=(da2d2) 蜗杆齿根高hf1=(ha*+c*)m=(d1df1)/2 蜗轮齿根高hf2=(d2-df2)/2=m*(ha*X2+C*) 蜗杆分度圆直径d1=q*m 蜗轮分度圆直径d2=m*Z2=2a-d1-2*X2*m 蜗杆齿顶圆直径da1=(q+2) *m=d1+2*ha1=d1+2*m*h* 蜗轮喉圆直径da2= (Z2+2+2*X2)*m=d2+2*ha2 蜗杆齿根圆直径df1=d1-2*hf1
Z1大、 29.48
Z1小
Z1大、
33 29.48
普通圆柱螺杆L≥ X -1 -0.5 0 0.5 1
Z1=1~2 46
39.44 51.44 56.4 60.4
蜗杆螺纹部分长度L
圆弧圆柱蜗杆
Z1=3~4
X2
Z1
46
<1
1~2
49.16
1~1.5
1~2
61.16
<1
3~4
62.4
1~1.5
3~4
64.4
80
0
80
80
6.3434076 6.3434076 #DIV/0! 6.3434076
4
22
4
66
4
4.8
0
0
4.8
4.8
36 35.9999999
普通圆柱蜗杆传动的基本参数及几何尺寸计算

普通圆柱蜗杆传动的基本参数及几何尺寸计算1.基本参数:(1)模数m和压力角α:在中间平面中,为保证蜗杆蜗轮传动的正确啮合,蜗杆的轴向模数m a1和压力角αa1应分别相等于蜗轮的法面模数m t2和压力角αt2,即m a1=m t2=mαa1=αt2蜗杆轴向压力角与法向压力角的关系为:tgαa=tgαn/cosγ式中:γ-导程角。
(2)蜗杆的分度圆直径d1和直径系数q为了保证蜗杆与蜗轮的正确啮合,要用与蜗杆尺寸相同的蜗杆滚刀来加工蜗轮。
由于相同的模数,可以有许多不同的蜗杆直径,这样就造成要配备很多的蜗轮滚刀,以适应不同的蜗杆直径。
显然,这样很不经济。
为了减少蜗轮滚刀的个数和便于滚刀的标准化,就对每一标准的模数规定了一定数量的蜗杆分度圆直径d1,而把及分度圆直径和模数的比称为蜗杆直径系数q,即:q=d1/m常用的标准模数m和蜗杆分度圆直径d1及直径系数q,见匹配表。
(3)蜗杆头数z1和蜗轮齿数z2蜗杆头数可根据要求的传动比和效率来选择,一般取z1=1-10,推荐z1=1,2,4,6。
选择的原则是:当要求传动比较大,或要求传递大的转矩时,则z1取小值;要求传动自锁时取z1=1;要求具有高的传动效率,或高速传动时,则z1取较大值。
蜗轮齿数的多少,影响运转的平稳性,并受到两个限制:最少齿数应避免发生根切与干涉,理论上应使z2min≥17,但z2<26时,啮合区显著减小,影响平稳性,而在z2≥30时,则可始终保持有两对齿以上啮合,因之通常规定z2>28。
另一方面z2也不能过多,当z2>80时(对于动力传动),蜗轮直径将增大过多,在结构上相应就须增大蜗杆两支承点间的跨距,影响蜗杆轴的刚度和啮合精度;对一定直径的蜗轮,如z2取得过多,模数m就减小甚多,将影响轮齿的弯曲强度;故对于动力传动,常用的范围为z2≈28-70。
对于传递运动的传动,z2可达200、300,甚至可到1000。
z1和z2的推荐值见下表(4)导程角γ蜗杆的形成原理与螺旋相同,所以蜗杆轴向齿距p a与蜗杆导程p z的关系为p z=z1p a,由下图可知:tanγ=p z/πd1=z1p a/πd1=z1m/d1=z1/q导程角γ的范围为3.5°一33°。
普通圆柱蜗杆传动基本几何尺寸计算关系式
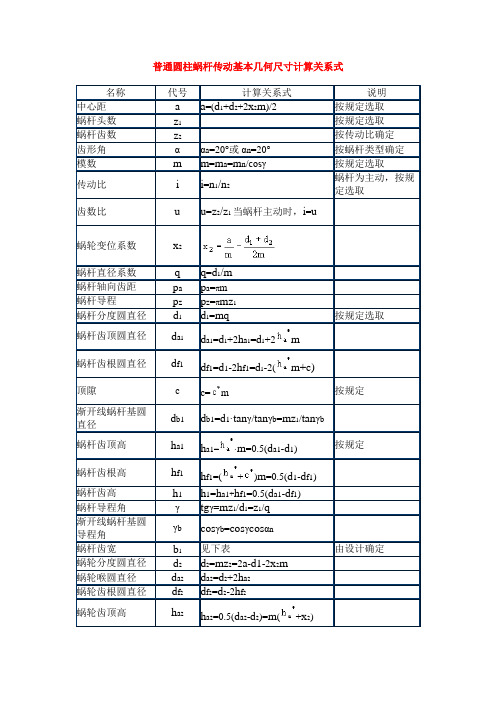
名称
代号
计算关系式
说明
中心距
a
a=(d1+d2+2x2m)/2
按规定选取
蜗杆头数
z1
按规定选取
蜗杆齿数
z2
按传动比确定
齿形角
α
αa=20°或αn=20°
按蜗杆类型确定
模数
m
m=ma=mn/cosγ
按规定选取
传动比
i
i=n1/n2
蜗杆为主动,按规定选取
齿数比
u
u=z2/z1当蜗杆主动时,i=u
经磨削的蜗杆,按左式所求的长度应再增加下列值:
当m<10mm时,增加25mm;
当m=10~16mm时,增加35~40mm;
当m>16mm时,增加50mm;
2
≤da2+1.5m
4
≤0.67da1
≤da2+m
0
-0.5
-1.0
0.5
1.0
≥(12.5+0.09z2)m
≥(9.5+0.09z2)m
≥(10.5+z1)m
蜗轮咽喉母圆半径
rg2
rg2=a-0.5da2
蜗轮齿宽
b2
由设计确定
蜗轮齿宽角
θ
θ=2arcsin(b2/d1)
蜗杆轴向齿厚
sa
sa=0.5πm
蜗杆法向齿厚
sn
sn=sa·cosγ
蜗轮齿厚
st
按蜗杆节圆处轴向齿槽宽ea'确定
蜗杆节圆直径
d1'
d1'=d1+2x2m=m(q+2x2)
蜗杆传动主要参数及几何尺寸.

为了限制 滚刀数目
d1=mq
4. 蜗杆的导程角γ 轴面齿距 pa1=πm 导程 s=z1pa1=z1πm
tan z1 pa1 z1πm z1m z1
πd1 πd1 mq q
二. 蜗杆传动的几何尺 寸
三、蜗杆蜗轮啮合传动 1. 正确啮合条件
中间平面:蜗杆传动似齿轮齿条传动
ma1=mt2=m αa1=αt2=α γ=β (旋向相同)
中间平面:
在阿基米德蜗杆传动中,通过蜗杆轴线垂直蜗 轮轴线的平面
在中间平面内,阿基米德蜗杆传动 相当于齿轮于齿条传动。因此,蜗杆传 动的设计计算以中间平面的参数和几何 几何关系为准。
一、蜗杆传动的主要参数
1. 模数m、压力角a、齿顶高系数h*a和顶隙系数c*
蜗杆的参数
蜗轮的参数
①轴面模数ma1=m ②轴面压力角αa1= α ③齿顶高系数h*a=1 ④顶隙系数c*=0.2
2. 标准中心距
a
1 2
(d1
d2)
m 2
(q
z2 )
传动比i 5~6
z1
6
z2 30~36
7~13 4
28~52
14~27 2
28~54
28~40 2、1 28~80
>40 1
>40
3. 蜗杆的分度圆直径d1 蜗轮配对加工法
①采用与蜗杆参数相同的滚刀;
②滚刀的安装位置同蜗杆传动的 工作位置;直径系数
有多少d1就有多少滚刀
①端面模数mt2=m ②端面压力角αt2=α ③齿顶高系数h*a =1 ④顶隙系数c*=0.2
2. 传动比i、蜗杆头数z1和蜗轮齿数z2
i 1 z2 2 z1
z1少,传动比大,效率低; z1多, 加工难,常取1、2、 4、6。
圆柱蜗杆传动几何尺寸计算公式(很实用)

tanαn=tanαcosγ;阿基米德圆柱蜗杆:α=20°
蜗杆(轮)法向齿形角αn
蜗杆分度圆柱导程角γ
tanγ=mz1/d1=z1/q
蜗杆节圆柱导程角γ'
tanγ'=z1/(q+2x2)
蜗杆导程pz
pz=πmz1
顶隙c
c=c*m;一般顶隙系数c*=0.2,ZC1蜗杆c*=0.16
蜗杆、蜗轮齿顶高ha1、ha2
蜗轮齿宽角θ
θ=2arcsin(b2/d1)
蜗轮咽喉母圆半径rg2
rg2=a-0.5da2
蜗轮齿根圆弧半径rf2
rf2=0.5da1+0.2m
中心距a
a=0.5(d1+d2+2x2m)
蜗杆分度圆直径d1
d1=qm
蜗轮分度圆直径d2
d2=mz2=2a-d1-2x2m
蜗杆齿顶圆直径da1
da1=(q+2)m=d1+2ha*m
蜗轮喉圆直径da2
da2=d2+2m(ha*+x2)
蜗杆齿根圆直径df1
df1=d1-2m(ha*+c*)
蜗轮齿根圆直Leabharlann df2df2=d2-2m(ha*-x2+c*)
蝇杆法向齿厚sn1
sn1=sx1cosγ
蜗轮分度圆齿厚s2
s2=(0.5π+2x2tanα)m
蜗杆齿宽b1
普通圆柱蜗杆:
z1=1、2时b1≥(12+0.1z2)m;z1=3、4时b1≥(13+0.1z2)m
蜗轮齿宽b2
b2≥0.65da1;一般b2=(0.67~0.75)da1;z1大取小值,z1小取大值
ha1=ha*m=(da1-d1)/2;ha2=m(ha*+x2)=(da2-d2)/2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算项目中心距
模数
轴截面齿形角
传动比
变位系数
径向间隙头数
Z1特性系数
q 齿顶高
h di 齿根高
hg 分度圆直径
D fe1节圆直径
D je1齿顶圆直径
D di1齿根圆直径
D g1分度圆螺旋导角
λ法向模数
m f 轴截面齿距P
螺旋导程
P Z 螺牙沿分度圆柱上的轴向齿厚
S z1螺牙沿分度圆柱上的法向齿厚
S f1齿厚测量高度
h~齿数
Z 2分度圆直径
D fe2节圆直径
D je2齿根圆直径
D g2齿顶圆直径
D di2最大外圆直径
Dw 2轮缘宽度
b 齿顶圆弧半径R 1代 号A M du α螺旋长度L☆蜗 轮
圆柱蜗杆传动基本几
i ξc
蜗
杆
齿根圆弧半径
R 2
轮
基本几何尺寸计算公式
公 式计算结果备注A=0.5M du(Z2+q+2ξ)175.00
Mdu=2A/(Z2+q+2ξ) 3.15
α=20°20.00
i=Z2/Z1=n1/n297.00
ξ=(A/Mdu)-0.5(q+z2) 2.06
C=0.25Mdu0.79
Z1=1,2,4 1.00
q=Dfe1/Mdu10.00
hdi=Mdu 3.15
hg=1.25Mdu 3.94
Dfe1=qMdu31.50
Dje1=Dfe1+2Mduξ=Mdu(q+2ξ)44.45
Ddi1=Mdu(q+2)37.80
Dg1=Mdu(q-2.5)23.63
λ=arctgZ1/q0.10
mf=Mducosλ 3.13
L=(12+0.1z2)Mdu68.36Z1=1,2 L=(13+0.1z2)Mdu71.51Z1=4 P=πMdu9.90
PZ=πMduZ19.90
Sz1=0.45πMdu97.00
Sf1=Sz1cosλ96.52
h~=Mdu 3.15
Z2=iZ197.00
Dfe2=MduZ2305.55
Dje2=Dfe2=MduZ2305.55
Dg2=2(A-0.5Ddi1-0.25Mdu)310.63
Ddi2=2(A-0.5Dfe1+Mdu)324.80
Dw2=Ddi2+Mdu327.95
b=0.65Ddi124.57
R1=0.5Dfe1-Mdu12.60
R1=0.5Ddi1+0.25Mdu19.69。
