工程力学静力学和材料力学范钦珊主编答案全集
理论力学课后答案(范钦珊)

(a-2)(a-3)(a) 第1篇工程静力学基础第1章受力分析概述1-1图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1 解:((b1-2a 和b 两种情形下各物体的受力图,并进行比较。
习题1-2图a-1)与图(b-1)不同,因两者之F 1-试画出图示各物体的受力图。
习题1-31-4图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为HG 与ABC 为不同的刚体。
(a-1)(b-1)或(b-2)(d-1)(e-1)(f-1)(e-3)(f-2)F A(d-2)(c-1)(b-1)(b-2)(b-3)(c-2)(d-1)(b) (c) 习题1-5图(a-3)(a-2)(b-2)(b-1)(a-1)1-6试画出图示连续梁中的AC 和CD 梁的受力图。
习题1-6图1-7画出下列每个标注字符的物体的受力图,各题的整体受力图未画重力的物体的自重均不计,所有接触面均为光滑面接触。
1-7d 1-7e 1-7f 1-7g 1-7h 1-7i 1-7j2-(b )l F M O ⋅=αsin )(F(c ))(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF(d )2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2-2图示正方体的边长a =0.5m ,其上作用的力F =100N ,求力F 对O 点的矩及对x 轴的力矩。
工程力学(静力学和材料力学)范钦珊主编答案全集 (3)

习题 3-6 图
FD
D
A
45D
D BM
FRA
FRC
M
C
FRC
FRA
A
FD'
B
D
习题 3-6a 解图
习题 3-6b 解 1 图
习题 3-6b 解 2 图
解:对于图(a)中的结构,CD 为二力杆,ADB 受力如习题 3-6a 解图所示,根据力偶 系平衡的要求,由
ΣMi = 0,
FRA = FRC =
M 2
解得,
FT=50.99kN,
FN= 10kN
即 连 杆 AB作 用 于 曲 柄 上 的 推 力 大 小 为 5 0.99 k N,方 向 与 FT相 反 ,十 字 头 A 对 导 轨 的压力
大小为10kN,方向与FN方向相反。
3-13 异步电机轴的受力如图所示,其中G=4kN为转子铁心绕组与轴的总重量,Pδ =31.8kN为磁拉力,FP=12kN为胶带拉力。试求轴承A、B处的约束力。
10
由几何关系得 cosα = 4500 = 0.9 , 5000
列平衡方程
sin α = 0.436
∑ MO (F ) = 0 : 2FA × 4500 −F Wcosα × 5000 +F Wsinα ×1250 = 0
解得 FA = 27.25 kN
∑ Fx = 0 : FOx = FW sin α = 27.03kN ∑ Fy = 0 : FOy = FW cosα − 2FA = 1.3kN
FP
FP
FA
FB
习题 3-13 图
解:分析轴承受力为一组平行力系,由平衡方程:
习题 3-13 解图
∑ M B (F ) = 0 : − FP ×1380 − FA ×1020 + (G + Pδ ) × 640 = 0
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
(完整版)工程力学习题答案范钦珊蔡新着工程静力学与材料力学第二版

比较:图(a-1)与图(b-1)不同,因两者之1 - 3试画出图示各物体的受力图。
1 - 1图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方 F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a),图(c ):分力: 投影:=90 ° 时, (d ): F cos i 1 FX 1F y1 F sin F y1 F sinj l讨论:(b ),图F X 1 F cos投影与分力的模相等;分力是矢量, X 2投影是代数量。
F sinsin分力: j2BD(b)D(b-1)(a-3)投影: 工90°时, F X 2 F cos , 投影与分量的模不等。
讨论:1 -2试画出图a 、b 两情形下各物体的受力图,并进行比较。
F y2 F cos(F X 2 (F cos F sin tan )i 2 F y2(a)l F AyF A X1F RD 值大小也不同。
a5A■dFBFF CABB(a-1)(b-1)BC DBCBCWDAy或(b-2)(c-1)(d-1)DCABCDFt D或(d-2)(e-2)(e-1)CO iOyBFA(f-3)(e-3)IV2[fW(f-1)(c)习题1—3图F BF BF AxF AF DB FF cW(f-2)AOAF A力 F i 作用在,并加以讨论。
----------------- :B 铰上。
杆AB 不计自重,杆BD 杆自重为 W 。
试画出图1 —4图a 所示为三角架结构 b 、c 、d 所示的隔离体的受力图 A zz ” X Xzr 'i/A1rC[------------DF AxAB虾F 或(a_2)1 — 6图示刚性构件 ABC 由销钉A 和拉杆GH 支撑,在构件的点C 作用有一水平力F 。
试问如果将力 F 沿其作用线移至点 D 或点E (如图示),是否会改变销钉 A 的受力状况。
工程力学(静力学和材料力学)范钦珊主编答案全集 (7)

第7章 弯曲强度7-1 直径为d 的圆截面梁,两端在对称面内承受力偶矩为M 的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E 。
根据d 、ρ、E 可以求得梁所承受的力偶矩M 。
现在有4种答案,请判断哪一种是正确的。
(A) ρ64π4dE M =(B) 4π64d E M ρ=(C) ρ32π3d E M =(D) 3π32d E M ρ=正确答案是 A 。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q 作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
正确答案是d 。
7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm 。
求:梁的1-1截面上A 、习题7-1图习题7-3图5lB 两点的正应力。
解:1. 计算梁的1-1截面上的弯矩:31m 110N 1m+600N/m 1m 1300N m 2M ⎛⎞=−××××=−⋅⎜⎟⎝⎠2. 确定梁的1-1截面上A 、B 两点的正应力: A 点:()3363-3-315010m 1300N m 2010m 210Pa MPa ()10010m 15010m12z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠==×=××× 2.54拉应力 B 点:())1.62MPa(Pa 1062.1120.15m 0.1m m 04.020.150m m N 130063压应力=×=×⎟⎠⎞⎜⎝⎛−×⋅==z z B I y M σ7-5 简支梁如图所示。
理论力学课后答案范钦珊

(a-2)(a-3)(b-1)(a-1)(a)第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ):分力:22)cot sin cos (i F ϕααF F x -= ,22sinsin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b 两种情形下各物体的受力图,并进行比较。
习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
习题1-3图1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
习题1-6图1-7 画出下列每个标注字符的物体的受力图,各题的整体受力图未画重力的物体的自重均不计,所有接触面均为光滑面接触。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .
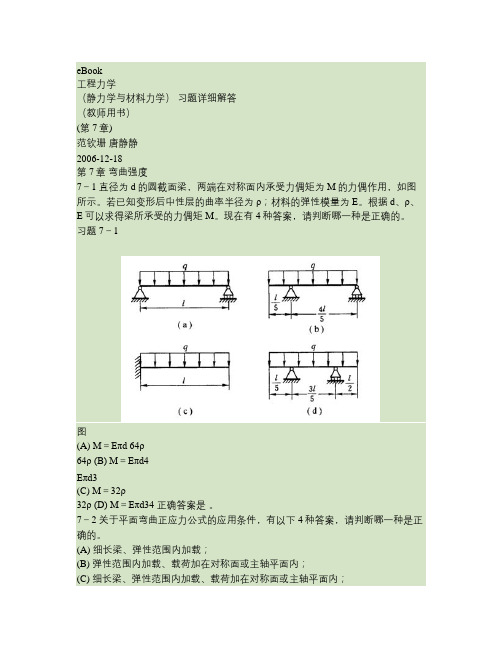
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第6章 圆轴扭转

习题 6-6 图
τ 套 max =
Mx Wp 2
T2 ≤ 60 × 10 6 ×
∴
Tmax ≤ T2 = 2883 N·m = 2.88 ×10 3 N·m
4
6-7 由同一材料制成的实心和空心圆轴,二者长度和质量均相等。设实心轴半径为 R0,空心圆轴的内、外半径分别为 R1 和 R2,且 R1/R2 =n;二者所承受的外加扭转力偶矩分 别为 Mes 和 Meh。若二者横截面上的最大剪应力相等,试证明:
该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6-5 图
解:1. τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2. M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3. τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
eBook
工程力学
(静力学与材料力学)
习题详细解答
(教师用书) (第 6 章) 范钦珊 唐静静
2006-12-18
1
第 6 章 圆轴扭转
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
习题 9-11 图
τ
ε 45D
σ2 = 0
习题 9-11 解图
σ1
D
45
D
45
σ3
解:空心轴表面各力为纯剪应力状态,易求得
σ 45D = τ , σ135D = −τ
应用广义胡克定律:
ε 45D
= σ 45D E
−ν
σ 135D E
= 1+ν τ E
利用 G = E 2(1 +ν )
100 2
+
4τ
2 xy
< 160
解得 | τ xy | <152MPa
(2)
习题 9-5 图
由(1)、(2)知,显然不存在。
2.当 r<OC
1 2
(240
−140) 2
+
4τ
2 xy
>
240 +140 2
即 | τ xy | <183.3MPa 时
⎪⎧σ ⎨
1
=
240 +140 2
+
1 2
⎪⎩σ 3 = 0
FQ
习题 9-10 图
解:第一点:
σx
=−M W
= − 6×10 ×103 60 ×1002 ×109
= −100MPa
τ xy = σ y = 0
σ 1 = σ 2 = 0,σ3 = −100MPa;
τ max = 50MPa
第二点:
σx =σy =0,
τ xy
=
3FQ 2A
=
3×120 ×10−3 2 × 60 ×100 ×10−6
∴ σ 1 = 45 MPa, σ 2 = 0, σ 3 = −45 MPa
σ r3 = 90 MPa
σ r4 =
1 2
(45 2
+ 452
+ 90 2 )
=
77.9
MPa( σ r4
=
3τ xy = 77.9 MPa)
9-10 已知矩形截面梁的某个截面上的剪力 FQ=120kN,弯矩 M=10kN·m,截面尺寸 如图所示。试求 1、2、3、4 点的主应力与最大剪应力。
垂直于木纹方向的正应力:
σθ = −(−1.25)sin(2× (−15°)) = −0.625 MPa
15 D
x
1.25MPa -15D σ τ x' y' x'
x'
(b-1)
9-2 层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。 若已知胶层剪应力不得超过 1MPa。试分析是否满足这一要求。
= 45.63 MPa
σy
=
pD 2δ
=
5× (300 − 8) 2×8
= 91.25 MPa
σθ
=
45.63 + 91.25 2
+
45.63 − 91.25 cos(2 × 20°) 2
= 50.97 MPa
τθ
=
45.63 − 91.25 sin(2× 20°) 2
=
−14.66 MPa
3. 图 a、图 b 叠加: σ x = 45.63 − 34.07 = 11.56 MPa
τθ
=
−4 − (−1.6) sin(2× (−15°)) + 0 ⋅ cos(2× (−15°)) 2
=
0.6 MPa
垂直于木纹方向的正应力:
σθ
=
−4 + (−1.6) 2
+
−4 − (−1.6) cos(2× (−15°)) + 0 = 2
−3.84 MPa
(b)题
平行于木纹方向的切应力:
τθ = −1.25cos(2× (−15°)) = −1.08 MPa
解:
习题 9-2 图
τ x'y'
30D 2MPa
0.5MPa
σ x'
-60D
x'
(a)
τθ
=
−2 − (−1) sin(2× (−60°)) + 0.5⋅ cos(2× (−60°)) 2
=
−1.55 MPa
|τθ |= 1.55 MPa > 1 MPa,不满足。
2
9-3 从构件中取出的微元受力如图所示,其中 AC 为自由表面(无外力作用)。试求 σ x
6
力准则和形状改变比能准则分别计算此几种情形下的计算应力。
1. σ x = 40MPa, σ y = 40 MPa, τ xy = 60 MPa; 2. σ x = 60MPa, σ y = −80 MPa, τ xy = −40 MPa; 3. σ x = −40 MPa, σ y = 50 MPa, τ xy = 0;
= 30MPa
σ1
=
1 2
4×302 = 30MPa
σ 2 = 0,
σ3
=
−
1 2
4 × 302 = −30MPa
τ max
=
σ1
−σ3 2
= 30MPa
8
σx 1
τ xy 2
第三点:
3
σx
=
Mz Iy
=
12
×10 ×10−3 60 ×1003
× 25×10 ×10−12
−3
= 50MPa
τ xy
σ x = 20MPa, σ y = -25MPa, σ z = 30MPa, τ xy = 0, [σ ] = 30MPa。 解:
1. σ r3 = σ 1 − σ 3 = 135MPa < [σ ] 强度满足。 2. σ r1 = σ 1 = 30MPa = [σ ] 强度满足。
9-9 对于图示平面应力状态,各应力分量的可能组合有以下几种情形,试按最大剪应
=
FQ S y bI y
= 120 ×10−3 × 60 × 25× (12.5 + 25) ×10−9 60 × 60 ×1003 ×10−15
= 22.5MPa
12
τ xy σx
σ1
=
50 2
+
1 2
502 + 4× 22.52 = 58.6MPa
σ 2 = 0,
σ3
=
50 2
−
1 2
502 + 4× 22.52 = −8.6MPa
σ r4 =
1 (1002 + 202 +1202 ) = 111.4 MPa 2
2. σ = σ x + σ y ± 2
σ (
x
+σ 2
y
)2
+τ
2 xy
= −10 ±
702 + 402
σ 1 = 70.6 MPa, σ 2 = 0, σ 3 = −90.6 MPa
σ r3 = σ 1 −σ 3 = 161.2 MPa
σx
(a)
(b)
σx
= FP πDδ
=
250 ×10 3 π× (300 − 8)
×
8
=
34.07
MPa(压)
σθ
=
−34.07 2
+
−34.07 cos(2× 20°) 2
=
−30.09 MPa
τθ
=
−34.07 sin(2× 20°) 2
= −10.95 MPa
2. 图 b:
σx
=
pD 4δ
= 5× (300 − 8) 4×8
5
习题 9-7 图
解:
σm
=
3.5× (254× 2 + 4× 7.6
7.6)
=
59.36
MPa
σt
=
3.5× (254× 2 + 2× 7.6
7.6)
= 118.72
MPa
εt
=
2π(r
+ Δr) − 2πr 2πr
=
Δr r
Δr
=
εt
⋅r
=
1 E
[σ t
−νσm ]
=
1 75 ×103
(118.72
= 0.94
(σ x + 92 +14) −14 + (−14) − (σ x + 92 +14) −14 (−0.342) = 92
2
2
解得 σ x = 37.97 MPa
3
τ yx
=
(−14) − (37.97 + 92 +14) × 0.94 = −74.25 MPa 2
9-5 对于图示的应力状态,若要求其中的最大剪应力 τ max <160MPa,试求 τ xy 取何值。
习题 9-9 图
4. σ x = 0, σ y = 0, τ xy = 45 MPa。
解:
1.
σ = σ x +σ y 2
±
σ (
x
−σ 2
y
)2
+τ
2 xy
= 40 ± 60
σ 1 = 100 MPa, σ 2 = 0, σ 3 = −20 MPa
σ r3 = σ 1 −σ 3 = 120 MPa
1.只承受轴向载荷 FP = 250 kN; 2.只承受内压 p = 5.0MPa(两端封闭) *3.同时承受轴向载荷 FP = 250kN 和内压 p = 5.0MPa(两端封闭)
4
x x'
20D σ x σ x'
x'
