投资组合久期计算
金融工程学-第六章久期与凸度

三、久期值的计算方法
1.列表法,这便是上文所有计算久期的方法。 2.封闭式久期计算法 3.有效久期计算法 计算公式
四、久期的性质及应用
1.久期的性质 久期的性质或特点有如下几条: (1)久期值与债券期限长度成正比。具体又有: ①债券期限越长,麦考莱久期和修正久期就越长; ②附息债券的麦考莱久期和修正久期均小于其到期时间,三者的关系是: D修<D麦<n ③零息债券的麦考莱久期等于债券本身的期限,修正久期小于债券期限。
四、资产组合的凸度
在利用凸度进行风险管理时,首先遇到的是计算资产组合的凸度,资产 组合的凸度定义为:资产组合的凸度等于资产组合中的各个证券凸度的 加权平均,权重是各个证券的价值。有时还用到资产的价值凸度,价值 凸度的定义为: 价值凸度=价格×凸度 资产组合的价值凸度定义为: 资产组合的价值凸度=资产组合的价格×资产组合的凸度
一、久期概述
(3)久期的一般表达式 由上所述,可得久期的一般表达式为:
一、久期概述
(4)久期概念的用途:久期可用来表示不可提前赎回债券面临的利率风 险。它考察债券价格对利率变动的敏感性的衡量指标,具体说,久期是 债券价格变化与债券到期收益率变化的比例系数。
一、久期概述
3.修正(Modified)久期 这是实际应用中经常使用的一种久期形式。它是由麦考莱久期衍生出来 的, 修正久期的定义为:
四、久期的性质及应用
(3)预测利率上涨,买入久期较短息票利率较高的债券,因为债券价格 下跌较少(因为快要到期时,价格向价值回归,没有下跌空间)。 (4)一个债券组合的久期为组合中各个债券久期的加权平均值,具体含 义看下一个内容。
五、资产组合的久期
1.一个资产组合的久期的标准定义是:资产组合的久期等于组成资产组合 的各个资产的久期的加权平均(这里的久期是指修正久期),权重是各 个资产的现值。与资产组合久期的定义相对应的是资产组合的收益率, 资产组合的收益率定义为:资产组合的收益率是资产组合的现金流的到 期收益率。
组合久期的计算公式

组合久期的计算公式
答:久期=时间加权现值/总现值=[∑年份×现值]/[∑现值]
={1×[(票面利率*票面额)/(1+到期收益率%)^1]+2×[(票面利率*票面额)/(1+到期收益率)^2]……期限×[(票面利率*票面额)/(1+票面收益率)^期限]+3×[票面额/(1+票面收益率)^期限]}/{[(票面利率*票面额)/(1+到期收益率%)^1]+[(票面利率*票面额)/(1+到期收益率)^2]……+[(票面利率*票面额)/(1+票面收益率)^期限+票面额(1+票面收益率)^期限
^为1次方,2为2次方,^期限为期限次方
(1)期限。
较长期限的价格变动幅度大于较短期限价格的变动幅度。
(2)息票收入及其再投资收益率。
息票额较多的价格变动幅度低于息票额较低的价格变动幅度。
也就是说,价格的易变性与期限长短成正比,与息票额高低成反比。
投资学 实验六 债券久期的计算
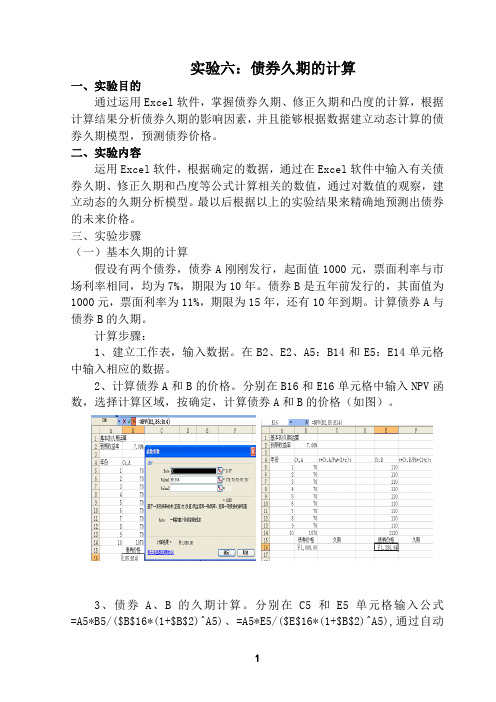
实验六:债券久期的计算一、实验目的通过运用Excel软件,掌握债券久期、修正久期和凸度的计算,根据计算结果分析债券久期的影响因素,并且能够根据数据建立动态计算的债券久期模型,预测债券价格。
二、实验内容运用Excel软件,根据确定的数据,通过在Excel软件中输入有关债券久期、修正久期和凸度等公式计算相关的数值,通过对数值的观察,建立动态的久期分析模型。
最以后根据以上的实验结果来精确地预测出债券的未来价格。
三、实验步骤(一)基本久期的计算假设有两个债券,债券A刚刚发行,起面值1000元,票面利率与市场利率相同,均为7%,期限为10年。
债券B是五年前发行的,其面值为1000元,票面利率为11%,期限为15年,还有10年到期。
计算债券A与债券B的久期。
计算步骤:1、建立工作表,输入数据。
在B2、E2、A5:B14和E5:E14单元格中输入相应的数据。
2、计算债券A和B的价格。
分别在B16和E16单元格中输入NPV函数,选择计算区域,按确定,计算债券A和B的价格(如图)。
3、债券A、B的久期计算。
分别在C5和E5单元格输入公式=A5*B5/($B$16*(1+$B$2)^A5)、=A5*E5/($E$16*(1+$B$2)^A5),通过自动填充单元格命令格式求出C5和F5单元区域的数据(如图)。
分别在C16和F16单元格输公式=SUM(C5:C14)和=SUM(F5:F14),按回车键,分别算出债券A和B的久期(如图)。
从计算结果来看,虽然债券A与债券B的到期期限都是10年,但债券A的久期大于债券B的久期。
(二)久期作为债券价格相对利率的弹性的计算。
已知债券A刚刚发行,其面值为1000元,票面利率为7%,期限为10年;债券B是5年前发行的,其面值为1000元,票面利率为11%,期限为15年,还有10年到期。
假设市场利率(贴现率)从当前的7%增加到7.02%。
请计算:(1)计算债券A与债券B的市场价格变化率;(2)作为债券价格相对市场利率的弹性来估计债券A、B的久期。
债券久期计算-计算债券久期例题

债券久期计算-计算债券久期例题例:假设债券A刚发行,其面值为1000元,市场利率(贴现率8%),票面利率为8%,期限为十年。
债券B是5年前发行的,其面值为1000元,票面利率12%,期限为15年,还有10年到期。
计算:1债券A与债券B的价格2计算债券A和B的久期三种方法1)运用久期的定义:久期作为现金流支付时间的加权平均(2)将久期看作债券价格对贴现率的弹性3)运用久期函数3计算债券A,B的修正久期4如果市场利率上升10%,即从8%上升到8.8%,求债券A与债券B的价格的变化久期(n)一、久期(n)的概念久期的概念最早是XXX(Macaulay)在1938年提出来的,所以又称马考勒久期(简记为D)。
马考勒久期是使用加权平均数的形式计算债券的平均到期时间。
它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。
具体的计算将每次债券现金流的现值除以债券价格得到每一期现金支付的权重,并将每一次现金流的时间同对应的权重相乘,最终合计出整个债券的久期。
XXX、XXX和XXX在随后的若干年独立地发现了久期这一理论范畴,特别是XXX和XXX将久期用于衡量资产/负债的利率敏感性的研究,使得久期具有了第二种含义,即:资产针对利率变化的价格变化率。
久期--的第二个含义是债券投资管理中的一个极其重要的战略----“免疫战略”的理论基础,根据该战略,当交易主体债券组合的久期与债务的持有期相等的时候,该交易主体短期内就实现了“免疫”的目标,即短期内的总财产不受利率波动的影响。
但是应用这一战略的前提则是,现有久期观点能否正确地衡量未来任何利率变动情形下债券代价的变动情况。
二、马考勒久期的计算公式公式1)其中,D是马考勒久期,B是债券当前的市场价格,PV (Ct)是债券未来第t期可现金流(利息或资本)的现值,T是债券的到期时间。
需要指出的是在债券发行时以及发行后,都可以计算马考勒久期。
计算发行时的马考勒久期,T(到期时间)等于债券的期限;计算发行后的马考勒久期,T(到期时间)小于债券的期限。
久期的计算公式范文

久期的计算公式范文久期是衡量固定收益证券价格波动性和利率变动对证券价格的影响程度的重要概念。
通过计算久期,投资者可以更好地评估和管理自己的投资风险。
下面是一个关于久期计算公式的详细范文,供参考。
第一部分:引言引言部分简要介绍了久期的背景和重要性。
久期作为衡量固定收益证券价格波动性的一个重要指标,对投资者来说具有重要的意义。
在久期的计算中,考虑到固定收益证券的现金流量、到期期限和市场利率的变化。
第二部分:久期的定义和相关概念本部分详细介绍了久期的定义和相关概念,包括久期的基本概念、久期和到期期限的关系,以及久期与市场利率的关系。
第三部分:久期的计算公式本部分详细描述了久期的计算公式,包括久期的基本计算公式和修正久期的计算公式。
久期计算的基本公式是通过对固定收益证券的现金流量进行加权平均来计算的。
修正久期的计算公式在基本公式的基础上加上了修正因子,以考虑到市场利率的变化对久期的影响。
第四部分:久期的应用本部分介绍了久期的主要应用领域,包括固定收益证券的投资决策、资产负债管理和风险管理。
久期作为一个衡量固定收益证券价格波动性的指标,可以用于评估不同投资组合的风险和收益,以及选择合适的固定收益证券。
第五部分:久期计算的实例分析本部分通过一个实例分析来详细说明久期的计算方法和应用。
通过给定一个固定收益证券的现金流量、到期期限和市场利率,计算该固定收益证券的久期,并分析不同市场利率变动对久期的影响。
第六部分:结论在结论部分,对久期的定义、计算公式和应用进行总结,并强调久期在评估和管理固定收益证券的风险中的重要性。
这是一个关于久期计算公式的1200字以上的范文,其中详细介绍了久期的定义、计算公式、应用和实例分析。
通过阅读该范文,读者可以更好地理解久期的概念和应用,并掌握久期的计算方法。
计算久期的方法

久期是一个重要的金融概念,它可以帮助投资者更好地理解债券的价值和风险。
久期是指债券的期限,它可以帮助投资者了解债券的价值变化,以及债券的价值变化如何影响投资者的收益。
久期的计算方法是把债券的期限分成几个部分,每个部分的期限都是一样的,然后把每个部分的期限乘以它的票面利率,最后把所有部分的乘积相加,得到的结果就是久期。
久期的计算方法可以帮助投资者更好地理解债券的价值变化,以及债券的价值变化如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的风险,以及债券的风险如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的市场价值,以及债券的市场价值如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的价格波动,以及债券的价格波动如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的收益率,以及债券的收益率如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的风险收益比,以及债券的风险收益比如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的投资组合,以及债券的投资组合如何影响投资者的收益。
久期的计算方法也可以帮助投资者更好地了解债券的投资策略,以及债券的投资策略如何影响投资者的收益。
总之,久期的计算方法可以帮助投资者更好地了解债券的价值、风险、市场价值、价格波动、收益率、风险收益比、投资组合和投资策略,以及这些因素如何影响投资者的收益。
因此,久期的计算方法对于投资者来说是非常重要的,可以帮助投资者更好地理解债券的价值和风险,从而更好地管理自己的投资。
利用EXCEL计算终值现值年金期限收益率与久期

在 Excel 中,我们可以使用各种公式和函数来计算终值、现值、年金、期限、收益率和久期。
下面将详细介绍如何使用 Excel 来进行这些计算。
1. 终值:终值是指一笔投资在指定期限后的价值。
要计算终值,可以使用 Excel 的 FV 函数。
该函数的语法如下:FV(rate, nper, pmt, pv, type),其中:- rate:每个期间的利率。
- nper:期间的总数。
- pmt:每个期间的付款金额(如果有年金)。
- pv:现值(如果有)。
- type:付款类型(1:期末付款,0:期初付款)。
例如,假设您要计算在每个月存入 1000 元、持续 5 年、年化利率为 5% 的情况下,到期后的终值。
Excel 公式如下:=FV(5%/12, 5*12, -1000, 0, 0)。
这将得到一个负数,表示未来的价值。
2. 现值:现值是指一笔未来金额的当前价值。
要计算现值,可以使用 Excel 的 PV 函数。
该函数的语法如下:PV(rate, nper, pmt, fv, type),其中的参数与 FV 函数相同。
例如,假设您要计算每个月存入 1000 元、持续 5 年、年化利率为5% 的情况下,现在的现值。
Excel 公式如下:=PV(5%/12, 5*12, -1000, 0, 0)。
3. 年金:年金是指一系列定期支付的金额。
要计算年金,可以使用Excel 的 PMT 函数。
该函数的语法如下:PMT(rate, nper, pv, fv,type),其中的参数与 FV 函数相同,只是 pmt 参数表示每个期间的支付金额。
例如,假设您要计算每个月存入 1000 元、持续 5 年,年化利率为5% 的情况下的每期支付金额。
Excel 公式如下:=PMT(5%/12, 5*12, 0, 0, 0)。
4. 期限:期限是指一笔投资或贷款的持续时间。
要计算期限,可以使用 Excel 的 NPER 函数。
该函数的语法如下:NPER(rate, pmt, pv, fv, type),其中的参数与 FV 函数相同。
久期——精选推荐

久期(Duration)的概念久期的概念最早是马考勒(Macaulay)在1938年提出来的,所以又称马考勒久期(简记为D)。
马考勒久期是使用加权平均数的形式计算债券的平均到期时间。
它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。
具体的计算将每次债券现金流的现值除以债券价格得到每一期现金支付的权重,并将每一次现金流的时间同对应的权重相乘,最终合计出整个债券的久期。
马考勒久期的计算公式(公式1)其中,D是马考勒久期,B是债券当前的市场价格,PV(Ct)是债券未来第t期现金流(利息或资本)的现值,T是债券的到期时间。
需要指出的是在债券发行时以及发行后,都可以计算马考勒久期。
计算发行时的马考勒久期,T(到期时间)等于债券的期限;计算发行后的马考勒久期,T(到期时间)小于债券的期限。
任一金融工具的久期公式一般可以表示为[1]:(公式2)其中:D为久期;t为该金融工具现金流量所发生的时间;C t为第t期的现金流;F为该金融工具的面值或到期日价值;n为到期期限;i是当前的市场利率。
实际上,公式(公式3)的分母正是该金融工具的市场价值,因此,久期公式又可表示为:(公式3)其中:P表示该金融工具的市场价值或价格。
[编辑]久期的计算过程举例[1]下面试举一例来说明久期的计算过程。
假设面额为1000元的3年期变通债券,每年支付一次息票,年息票率为10%,此时市场利率为12%,则该种债券的久期为:(年)如果其他条件不变,市场利率下跌至5%,此时该种债券的久期为:(年)同理,如果其他条件不变,市场利率上升至20%,此时久期为:(年)再者,如果其他条件不变,债券息票率为0,那么:(年)从上面的计算结果可以发现,久期随着市场利率的下降而上升,随着市场利率的上升而下降,这说明两者存在反比关系。
此外,在持有期间不支付利息的金融工具,其久期等于到期期限或偿还期限。
那些分期付息的金融工具,其久期总是短于偿还期限,是由于同等数量的现金流量,早兑付的比晚兑付的现值要高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结算日2011-10-14
到期日2016-9-30duration 4.591957
息票率 3.75%modified duration 4.559358
到期收益率 1.43%
面值100净价clean price=
计息频率2
发行日2011-9-30
结算日之后下一次计息日2012-3-31 =COUPNCD(B1,B2,2,1)
结算日之前上一次计息日2011-9-30 =COUPPCD(B1,B2,2,1)
应计利息天数14 =COUPDAYBS(B1,B2,2,1)
两个计息日之间天数182 =COUPDAYS(B1,B2,2,1)
NCD-LCD183
到期期限t计息日现金流距离付息日时间现金流现值
0.4615384622012-3-31 1.8750.9231 1.8627
0.9615384622012-9-30 1.875 1.9231 1.8495
1.4615384622013-3-31 1.875
2.9231 1.8364
1.9615384622013-9-30 1.875 3.9231 1.8233
2.4615384622014-3-31 1.875 4.9231 1.8104
2.9615384622014-9-30 1.875 5.9231 1.7975
3.4615384622015-3-31 1.875 6.9231 1.7848
3.9615384622015-9-30 1.8757.9231 1.7721
4.4615384622016-3-31 1.8758.9231 1.7595
4.9615384622016-9-30101.8759.923194.9214
总和111.21751455
传统久期
修正久期
基数为1是实际天数/实际天数
111.0737389应计利息0.143442623全价111.21718148
D(B1,B2,2,1)
D(B1,B2,2,1)
YBS(B1,B2,2,1)
YS(B1,B2,2,1)
注意此处两种方法算出来的间隔天数不一样,是因为这里具体月份不一样。
此处距离付息日时间采用182,算出来的和excel函数有轻微差异。
后一张表就采用183天,算出来的没有差异。
时间加权现值(第1种方
法)
0.8597
1.7784
2.6839
3.5765
4.4563
5.3234
6.1780
7.0202
7.8501
470.9561
510.68266803
4.591747
4.559149
来的没有差异。
