信号与线性系统一二章自测题及参考答案
信号与系统自测题(3套)
信号与系统自测题（一）一、选择题1.积分⎰+--00)()2(dt t t δ等于（ ）A.)(2t δ-B.2-C. )2(-t εD. )2(2-t δ2．计算ε(3-t)ε(t)=（ ） A ．ε(t)-ε(t-3) B ．ε(t) C ．ε(t)-ε(3-t) D ．ε(3-t)3．已知f (t )，为求f (t 0-at )则下列运算正确的是（其中t 0，a 为正数）（）A ．f (-at )左移t 0B ．f (-at )右移atC ．f (at )左移t 0D ．f (at )右移a t4．已知f (t )=δ′(t )，则其频谱F （j ω）=（）A ．ωj 1B ．)(1ωπδω+jC ．ωjD ．)(21ωπδω+j 5．信号f (t )的带宽为Δω，则信号f (2t -1)的带宽为（ ） A ．2ΔωB ．Δω-1 C ．Δω/2D ．（Δω-1）/26．已知周期电流i (t )=1+t t 2cos 22cos 22+，则该电流信号的平均功率P 为（ ） A ．17W B ．9W C ．4WD ．10W7．如题7图所示的信号，其单边拉普拉斯变换分别为F 1(s ), F 2(s ), F 3(s ),则（ ）A ．F 1(s )= F 2(s )≠F 3(s )B ．F 1(s )≠F 2(s )≠F 3(s )C ．F 1(s )≠F 2(s )= F 3(s )D ．F 1(s ) = F 2(s )= F 3(s )8．某系统的系统函数为H （s ），若同时存在频响函数H （j ω），则该系统必须满足条件（ ）A ．时不变系统B ．因果系统C ．稳定系统D ．线性系统 9．已知f (t )的拉普拉斯变换为F （s ），则dt t df )(的拉普拉斯变换为（ ）A ．sF (s )B ．sF (s )-f (0-)C ．sF (s )+f (0-)D ．⎰-∞-+0)(1)(ττd f ss sF10．已知某离散序列，其它 ⎩⎨⎧=≤=n N n n f ,0||,1)(该序列还可以表述为（ ）A ．)()()(N n N n n f --+=εεB ．)()()(N n N n n f ---+-=εεC ．)1()()(---+=N n N n n f εεD ．)1()()(----+-=N n N n n f εε11．已知某离散系统的系统模拟框图如题11图所示，则该系统的差分方程为（ ） A ．)()1(31)(n f n y n y =-+ B ．)()1(31)(n f n y n y =--C ．)()(31)1(n f n y n y =-+ D ．)()(31)1(n f n y n y =++ 12．若f (n )的z 变换为F (z )，则)(n f a n 的z 变换为（ ） A ．)(az F B ．)(z aF C ．)(1z F aD ．⎪⎭⎫ ⎝⎛a z F二、填空题13．矩形脉冲信号ε(t)-ε(t-1)经过一线性时不变系统的零状态响应为g(t)-g(t-1)，则该系统的单位冲激响应h(t)为________。
信号与系统试卷及参考答案
试卷及答案信号与系统试卷（1）（满分：100分，所有答案一律写在答题纸上）考试班级学号姓名成绩考试日期：年月日，阅卷教师：考试时间120分钟，试卷题共2页一一线性非时变离散系统，具有一初始状态x(0)，当激励为时f(k)，响应为y(k)=((1/2)k+1)u(k)；若初始状态不变，当激励为-f(k)时，响应y(k)=((-1/2)k-1)u(k)为；试求当初始状态2x(0)为，激励为4f(k)时，系统的响应？（10分）二绘出下列函数的图形（1）.已知一连续时间信号x(t)如图所示，试概略画出信号y(t)=x(2-t/3)的波形图。
（8分）t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
（8分）三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt （4分） (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) （8分）(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) （8分） （4） 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 （8分） （5）y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? （8分） （6）. y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? （8分）四 一线性非时变因果系统，当激励为u(t)时，响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ，求当激励f(t)=δ(t)时的响应)(t h 。
（10分）五 某一子系统，当输入f(t)=e -t u(t)时，零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时，总系统的冲激响应。
信号与线性系统一二章自测题及参考答案
第一、二章自测题1、判断题（1）若x (t )是一连续时间周期信号，则y (t )=x (2t )也是周期信号。
（2）两个周期信号之和一定是周期信号。
（3）所有非周期信号都是能量信号。
（4）两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
（5）若)()()(t h t x t y *=，则)1()2()1(+*-=-t h t x t y 。
（6）一个系统的自由响应就等于它的零输入响应。
（7）一个系统的零状态响应就等于它的自由响应。
（8）零状态响应是指系统没有激励时的响应。
（9）系统的单位冲激响应是指系统在冲激信号作用下的全响应。
（10）两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号？ （1）3cos(15)0()0t t f t t π≥⎧=⎨<⎩ （2）50()0te tf t t -⎧≥=⎨<⎩（3）()6sin 23cos3f t t t =+ （4）|2|()20sin 2t f t e t -=3、填空题（1）已知)()4()(2t t t f ε+=，则)(''t f =__________________。
（2）=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
（3）=-⎰∞∞-dt t ）（92δ_________________________ 。
（4）=-⎰∞∞-dt t t e t j ）（0δω_________________________ 。
（5）信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε （2）)]4()([3cos )(2--=t t t t f εεπ （3）][sin )(3t t f πε=5、已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形图。
信号与系统(杨晓非)1,2,3章习题答案
2
4s
6s 3 T ' mT1 12 s T 5 12 60 s f (t )为周期信号，周期为60s.
(3) f (t ) 3e t sin(3t ) 3e t Im[e j (3t ) ] 3e t cos(3t ) 2 (4) f (t ) je( j100t 2) e 2 e( j100t 2) e 2e Re[ f (t )] e 2 cos(100t ) 2
信号与系统习题解答
1.1
(1) f(t)=(t) 解 P lim
1 2
| f (t ) | dt
2
lim
1 1 dt 2 0 2
E总 lim | f (t ) |2 dt lim dt
0
f (t ) (t )为功率信号。
t [ f
t 0
3
t (4) (t 2 t 1) ( )dt (t 2 t 1) | 2 | (t )dt 2 2
(5) (t 2 2) (t 5)dt 0
0
3
(6) (t 2 2) (t 5)dt (52 2) (t 5)dt 27
e (e e lim (2 j ) 2 0
j 2t
2 t
j 2t
)
1 dt ( ) lim e2t (e j 4t e j 4t 2)dt 4 0
1 ( ) lim [e (2 j 4)t e (2 j 4)t ]dt 4 0
信号与线性系统 白恩健书答案
第1章基本概念K第1章习题k1.1解：（1）x(t)为周期信号，周期为T=10。
（2）x(t)为非周期信号。
（3）x[n]为非周期信号。
（4）x[n]为周期信号，周期为N=2。
（5）x(t)为非周期信号。
（6）x[n]为周期信号，周期为N=2。
1.2解：（1）x(t)为功率信号。
（2）x(t)既不是能量信号也不是功率信号。
（3）x[n]为能量信号。
（4）x(t)为能量信号。
（5）x(t)为能量信号。
（6）x[n]为能量信号。
1.3略。
1.4略。
1.5（原题有误）一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统，即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解：提示：可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解：（1）因果、无记忆、非线性、时不变、BIBO稳定系统。
（2）因果、无记忆、线性、时变和BIBO稳定系统。
（3）因果、无记忆、线性、时变和非稳定系统。
（4）因果、记忆、线性、时不变和BIBO稳定系统。
（5）因果、无记忆、线性、时变和BIBO稳定系统。
（6）因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念（7）因果、无记忆、线性、时不变和BIBO稳定系统。
（8）非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解：（1）x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
（2）x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
（3）x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示：根据微积分的极限定义证明。
1.10解：（1）x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
（2）x(t)的响应为[2(t+e−t)−2]u(t)。
信号与线性系统_习题答案(有错版)
2.1 (1) 已知连续时间信号 x(t ) 如图 P2.1(a)所示。试画出下列各信号的波形图，并加以标 注。 (a) x(t − 2) (b) x(1 − t ) (c) x(2t + 2) (2) 根据图 P2.1(b)所示的信号 h(t ) ，试画出下列各信号的波形图，并加以标注。 (a) h(t + 3) (b) h( − 2) (c) h(1 − 2t ) (3) 根据图 P2.1(a)和(b)所示的 x(t ) 和 h(t ) ，画出下列各信号的波形图，并加以标注。 (a) x(t )h(−t ) (b) x(1 − t )h(t − 1) (c) x(2 − ) h(t + 4)
其基波周期 T0 是 T1 , T2 的最小公倍数。 (b) x(n) 和 y ( n) 是周期的， x(n + = N1 ) x(n), y (n + N = y ( n) 2) 令 f= (n) x(n) + y (n) ，欲使 f (n) 是周期的，必须有
= N 0 kN = mN 2 1
πn
4
，对所有 n ，
7
1 n , n奇 显然 x(n) 是非周期的，但 y1 (n) 是周期的。 h(n) = 3 0, n偶
(c) 正确。若 x(n) 的周期为 N ，则 y2 (n) 的周期为 2 N 。 (d) 正确。若 y2 (n) 的周期为 N ，则 N 只能是偶数。 x(n) 的周期为 N / 2 。 2.7 判断下列各信号是否是周期信号，如果是周期信号，求出它的基波周期。 (a) = x(t ) 2 cos(3t + π / 4) (c) x(t ) = e (e) = x ( n)
1
信号与线性系统分析试卷
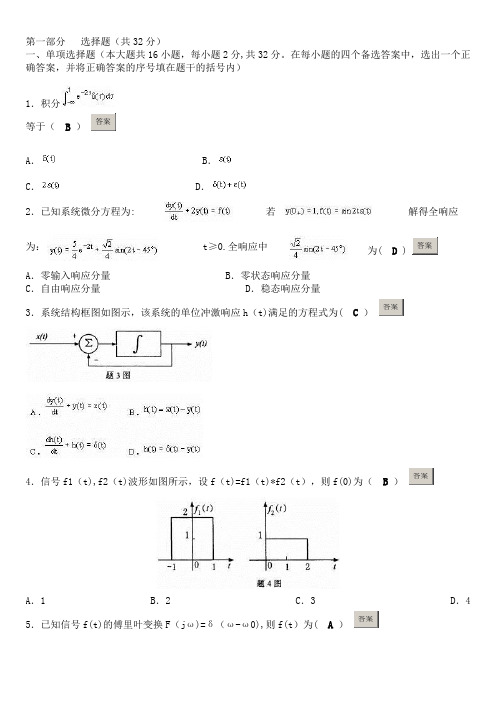
第一部分选择题（共32分）一、单项选择题（本大题共16小题，每小题2分,共32分。
在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内）1．积分等于（B）答案A． B．C． D．2．已知系统微分方程为: 若解得全响应为：t≥0.全响应中为( D ) 答案A．零输入响应分量 B．零状态响应分量C．自由响应分量 D．稳态响应分量3．系统结构框图如图示，该系统的单位冲激响应h（t)满足的方程式为( C）答案4．信号f1（t),f2（t)波形如图所示，设f（t)=f1（t)*f2（t），则f(0)为（B）答案A．1 B．2 C．3 D．4 5．已知信号f(t)的傅里叶变换F（jω)=δ（ω-ω0),则f(t）为( A）答案6．已知信号f（t）如图所示，则其傅里叶变换为（C）答案7．f（t）=ε(t）-ε(t—1)的拉氏变换为（A）答案8. 的拉氏反变换为（D）答案9．图（a）中ab段电路是某复杂电路的一部分，其中电感L和电容C都含有初始状态，请在图(b）中选出该电路的复频域模型。
（B ) 答案10．离散信号f(n)是指（B）答案A．n的取值是连续的，而f（n)的取值是任意的信号B．n的取值是离散的，而f(n)的取值是任意的信号C．n的取值是连续的，而f(n)的取值是连续的信号D．n的取值是连续的,而f（n）的取值是离散的信号11．若序列f（n）的图形如图(a)所示,那么f（—n+1）的图形为图(b)中的( D）答案12．差分方程的齐次解为，特解为，那么系统的稳态响应为( B ) 答案13．已知离散系统的单位序列响应和系统输入如图所示，f（n)作用于系统引起的零状态响应为,那么序列不为零的点数为（C）答案A．3个 B．4个C．5个 D．6个第二部分非选题（共68分）二、填空题(本大题共9小题，每小题2分，共18分）14．=（)。
答案15．GLC并联电路发生谐振时，电容上电流的幅值是电流源幅值的（Q）倍。
信号与系统第一、二、三章自测题解答
第一章自测题答案1．已知)()4()(2t u t t f +=，则)(''t f =(t)4δ2u(t)'+ 2．2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
3．=-⎰∞∞-dt t t e tj ）（0δωoj ωet 。
4．试画出下列各函数式表示的信号图形： （1）0 ),()(001>-=t t t u t f（2）)]4()([3cos )(2--=t u t u t t f π在0到4区间内的6个周期的余弦波，余弦波的周期为2/3。
（3）][sin )(3t u t f π=5．已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形。
答：函数表达式：f(2-t) = [u(t)-u(t-1)]+2[u(t-1)-u(t-2)] f(6-2t)=[u(t-2)-u(t-2.5)]+2[u(t-2.5)-u(t-3)]6．信号f (5-3t )的波形如图1.2所示，试画出f (t )的波形。
答：f(5-3t)左移5/3得到f(-3t)，然后再扩展3倍得到f(-t)，最后反褶可得到f(t)7．对于下述的系统，输入为e (t ), 输出为r (t )，T [e (t )]表示系统对e (t )的响应，试判定下述系统是否为： （1） 线性系统；（2）非时变系统；（3）因果系统；（4）稳定系统：(a) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统9. 一线性非时变系统，当输入为单位阶跃信号u (t )时，输出r (t )为 )1()()(t u t u e t r t --+=-，试求该系统对图1.3所示输入e (t )的响应。
《信号与系统》第一章作业题答案
第一章 绪 论1．试判断系统()()r t e t =-是否是时不变系统？（给出检验步骤）解：由()()r t e t =-，得到输入为()e t 时，对应的输出为()r t ：()()r t e t =-再由()()r t e t =-，得到输入为()e t τ-时，对应的输出为()e t τ--。
假设()()r t e t =-是一个时不变系统，则对应的()()r t e t ττ-=-+显然()()()r t e t e t τττ-=-+≠--假设不成立，这是一个时变系统。
2．已知信号1(/2)f t 和2()f t 的波形如图所示，画出11()(1)()y t f t u t =+-和22()(53)y t f t =-的波形。
图1解：根据一展二反三平移的步骤来做，对于第一个图，第一步将1(/2)f t 展成1()f t第二步将1()f t 平移成1(1)f t +第三步将1(1)f t +乘上()u t -得到11()(1)()y t f t u t =+-对于第二个图，先写出其表达式2()9(1)f t t δ=+则22()(53)9(531)y t f t t δ=-=-+9(63)9(36)3(2)t t t δδδ=-=-=-于是得到2()y t 的图形为3．系统如图2所示，画出1()f t ，2()f t 和3()f t 的图形，并注明坐标刻度。
图2解：由系统图可以得到1()()()f t t t T δδ=--它的图形为（设T>0）21()()[()()]ttf t f t dt t t T dt δδ-∞-∞==--⎰⎰它的图形为（设T>0）32()(2)()f t t T f t δ=-+它的图形为（设T>0）4．确定下列系统是因果还是非因果的，时变还是非时变的，并证明你的结论。
1()(5)cos ()y t t x t ⎛⎫=+ ⎪⎝⎭解：令0t =，则1(0)5cos (0)y x ⎛⎫= ⎪⎝⎭，故是因果系统。
信号与系统自测题(第1章 参考答案)
、 f (−at ) 左移 t B、 f ( at ) 右移 t t t C、 f ( at ) 左移 D、 f ( −at ) 右移 a a 注： f (t − at ) = f [−a(t − ta )] 20、 f ( −t + 2) 是下面哪一种运算的结果（ B ） 。 B、 f ( −t ) 向右移 2 个单位 A、 f (t ) 向左移 2 个单位 C、 f ( −2t ) 向右移 1 个单位 D、 f (t ) 向右移 2 个单位 注： f (−t + 2) = f [−(t − 2)] 21、 f (2t ) 是下面哪一种运算的结果（ C ） 。 A、 f (t ) 向左移 2 个单位 B、 f ( −t ) 向右移 2 个单位 C、 f (t ) 压缩 1 倍 D、 f (t ) 扩展 1 倍 22、已知信号的波形如下图所示，则 f (t ) 的表达式为（ C ） 。
A
0 0 0 0 0 0
f (t )
t
、 f (t ) = tu(t ) B、 f (t ) = (t − 1)u (t − 1) C、 f (t ) = tu (t − 1) D、 f (t ) = 2(t − 1)u (t − 1) 注： 23、已知信号 f (t ) 的波形如下图所示，则 f (5 − 2t ) 的波形为（ C ） 。
∞ 2 −∞
t
D 2δ (2t ) =
、
1 δ (t ) 2
、 ∫ (t + t )δ (t − 1)dt = 3 D、 tδ ′(t ) = tδ (t ) 6、积分 ∫ (τ − 2)δ (τ )dτ 等于（ B ） 。 A、−2δ (t ) B、−2u (t ) C、u (t − 2) 注： ∫ (τ − 2)δ (τ )dτ = (0 − 2)∫ δ (τ )dτ = −2u(t )
信号与系统课后习题参考答案
信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。
题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。
⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。
1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。
题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。
试做出当输⼊为时,响应得波形图。
题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。
题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。
⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。
第⼆章习题2-1试计算下列各对信号得卷积积分:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。
已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。
2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。
信号与线性系统分析试题及答案(10套)
标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。
3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。
4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。
5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。
《信号与线性系统》试题与答案2
一、选择题（3分/每题，共21 分,单选题） 1、下列哪个系统不属于因果系统（ A ）A ]1[][][+-=n x n x n yB 累加器 ∑-∞==nk k x n y ][][C 一LTI 系统，其)()(2t u e t h t-= D LTI 系统的)(s H 为有理表达式，ROC ：1->σ 2、信号45[]cos()2jn x n n eππ=+，其基波周期为（A ）A 20B 10C 30D 5 3、设]3[]1[2][][---+=n n n n x δδδ和]1[2]1[2][-++=n n n h δδ，][*][][n h n x n y =，求=]0[y （ B ）A 0B 4C ][n δD ∞4、已知一离散LTI 系统的脉冲响应h[n]= δ[n]+2δ[n-1]-3δ[n-2]，则该系统的单位阶跃响应S[n]等于（B ）A δ[n ]+δ[n-1]-5δ[n-2]+ 3δ[n-3]B δ[n]+3δ[n-1]C δ[n]D δ[n]+ δ[n-1]-2δ[n-2]5、信号)}2()2({-+--t u t u dt d的傅立叶变换是（ C ）A ω2sin 2jB )(2ωπδC -2j ω2sinD 6、己知)(t x 的频谱函数⎩⎨⎧>=<==2rad/s ||0,2rad/s,||1,)X(j ωωω 设t t x t f 2cos )()(=，对信号)(t f 进行均匀采样的奈奎斯特率为（ C ）A 4 rad/sB 2 rad/sC 8 rad/sD 3 rad/s7、下列说法不正确的是（D ）A 当系统的频率响应具有增益为1和线性相位时，系统所产生的输出就是输入信号的时移；B 取样示波器和频闪效应是欠采样的应用；C 对离散时间信号最大可能的减采样就是使其频谱在一个周期内的非零部分扩 展到将π-到π的整个频带填满；D 听觉系统对声音信号的相位失真敏感。
信号与线性系统分析吴大正习题答案
专业课习题解析课程西安电子科技大学844信号与系统精选专业课习题解析课程第2讲第一章信号与系统（二）精选精选1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fε=t)(sin(t（5）)tf=r(t)(sin精选（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1()1[精选精选1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε精选精选（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε精选1-3 写出图1-3所示各波形的表达式。
精选1-4 写出图1-4所示各序列的闭合形式表达式。
＜信号与系统学习指导＞第二章自测题(参考答案)
y13 [n] = y1[n + 1]
2.6 试判定以下系统的因果性和稳定性。
−6 t
（1） h(t ) = e （3） h(t ) = e
⋅ u (3 − t ) ； ⋅ u (t − 2) ；
（2）
h(t ) = e −2t ⋅ u (t + 50)
−4 t
1 （4） h[n] = n( ) n ⋅ u[n] 2
2.5 假设一个离散线性系统对输入信号 x1[n]、x2[n]和 x3[n]分别产生 y1[n]、y2[n]和 y3[n]的 响应，如图 2.29 所示，如激励 x[n]如图所示， 试问 y[n]是什么？第一个系统对 x2[n]和 x3[n] 的响应是什么？
x1[n] 1 n y1[n] 1 n 2 y2[n] 0 0 x3[n] n 1 y3[n] n -1 0 x [n] 2 1 1 -1 0 0 -2 n 1 2 3 4 n 0 1 1 2 3 -1 1 n
（3）当 -2<t≤-1 时， y (t ) = x(t ) * h(t ) = t + 3 当-1<t≤0 时， y (t ) = x(t ) * h(t ) = t + 4 当 0<t≤1 时， y (t ) = x(t ) * h(t ) = 2 − 2t 其余, y (t ) = x(t ) * h(t ) = 0
n n
1 2
又
n = −∞
∑ h[n] 发散，不稳定.
1 h[n] = ( ) n u[n] 2
∞
2.7 考虑一离散时间系统，其单位样值（脉冲）响应为 （1）求 A 以满足
h[n] − Ah[n − 1] = δ [n]
（2）利用（1）的结果，求系统的逆系统的单位样值（脉冲）响应。 （3）利用（2）的结果，求一信号 x[n]使之满足 x[n] * h[n] = 2 n (u[n] − u[n − 4]) . 解： （1） h[ n] − Ah[n − 1] = δ [ n] ，其中 h[ n] = ( ) u[n] ，
大学科目《信号与系统》各章节习题答案
第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。
信号与线性系统第一二章习题
32下信号与线性系统第一、二章练习题一．选择题：1.*()t A e t ε的卷积积分为( A ) A.不存在 B.()t Ae t ε- C.()t Ae t εD.()At e t ε2．若连续LTI 系统的初始状态不为零，当激励信号增大一倍时，其零状态响应( A ) A.增大一倍B.保持不变C.增大，但不能确定增大倍数D.增大两倍3．式0(2)sin (3)t t dt δω∞--⎰的值是( B )A.cos ω-B.sin ω-C.cos ωD.sin ω4．已知 f (t )的傅里叶变换为()F j ω，则函数()()()y t f t t a δ=-的傅里叶变换()Y j ω为( B ) A.()ja F j e ωω- B.()ja f a e ω- C.()ja F j e ωωD.()ja f a e ω5．已知信号f （t ）如题7图所示，则其傅里叶变换F （j ω）为( B )A.1cos 2ωτ B.2cos ωτ C.1sin 2ωτ D.2sin ωτ6．下列各表达式正确的是（ B ） A ．(t -1)δ(t )=δ(t ) B ．(1-t )δ(1-t )=0 C ．⎰∞∞-=+)()()1(t dt t t δδD ．⎰∞∞-=++1)1()1(dt t t δ7．信号f (-2t +4)是下列哪种运算的结果（ ） A ．f (-2t )右移2 B ．f (-2t )左移2 C ．f (-2t )右移4D ．f (-2t )左移218．设某线性电路的单位冲激响应为h (t )，f (t )为输入，则⎰-=t d h t f t y 0)()()(τττ是系统的（ ） A ．自由响应 B ．零输入响应 C ．完全响应D ．零状态响应9．信号)(2t e t j δ'的傅里叶变换为（ ）A ．j (ω-2)B ．j (ω+2)C ．2+j ωD ．-2+j ω10．已知f (t )的傅里叶变换为)(ωj F ，则f (1-t )的傅里叶变换为（ ） A ．ωωj e j F )(-- B ．ωωj e j F -)( C ．ωωj e j F --)(D ．ωωj e j F )(-11．若周期信号f (t )为对称于原点的奇函数，则其傅里叶级数展开式的结构特点是（ ） A ．只有正弦项 B ．只有余弦项 C ．有直流分量 D ．只含偶次谐波 12.设f (t )为系统输入，y (t )为系统输出，则下列关系式中为线性时不变系统的是( ) A.y (t )=x (t )f (t ) B.y (t )=tf (t ) C.)()()()(22t f t f dt d t y t y dtd +=+D.y (t )=f (2t )13.式⎰∞∞-⎪⎭⎫⎝⎛-+6)sin (πδt t t dt 的值是( )A.6πB.6π-1 C.6π-21 D.6π+21 14.已知f （t ）的傅里叶变换为F （j ω），y (t )=f ⎪⎭⎫⎝⎛+b a t ，其中a 、b 为常数，则Y （j ω）为( )A.|a |F (j ω)ωjab eB.|a |F (ja ω)ωjab e -C.||1a F (j aω)ωa b j e D.||1a F ⎪⎭⎫ ⎝⎛a j ωωa bj e - 15.已知信号f (t )如题7图所示，其傅里叶变换为F （j ω），则F (0)为( ) A.2 B.π C.π21 D.416.积分f （t ）=⎰-11（2t 2+1）δ（t -2）dt 的结果为（ ）A.1B.3C.9D.017.设激励为f 1（t ）、f 2（t ）时系统产生的响应分别为y l （t ）、y 2（t ），并设a 、b 为任意实常数，若系统具有如下性质：af 1（t ）+bf 2（t ）↔ay l （t ）+by 2（t ），则系统为（ ）A.线性系统B.因果系统C.非线性系统D.时不变系统18.周期信号的频谱特点是（ ） A.周期连续谱 B.周期离散谱 C.非周期连续谱D.非周期离散谱19.卷积积分f （t -t 1）*δ（t -t 2）的结果为（ ） A.f （t -t 1-t 2） B. δ（t -t 1-t 2） C.f （t +t 1+t 2）D. δ（t +t l +t 2）20.信号f （t ）的带宽为20KHz ，则信号f （2t ）的带宽为（ ） A.20KHz B.40KHzC.10KHzD.30KHz21.已知信号f （t ）的傅里叶变换为F （ j ω），则t dt t df )(的傅里叶变换为（ ）A.ωωωωd j dF j F )(-)( B.ωωωωd j dF j F )()(+- C.ωωωωd j dF j F )(-)(- D.ωωωωd j dF j F )()(+ 22.已知信号f(t)的波形如题3图所示，则=dt )t (df （ ） A.0B.)2t ()t (-δ-δC.)2t (2)t (2-δ+δD.)2t (2)t (2-δ-δ23.离散信号f(n+i),(i ≥0)，表示（ ） A.信号f (n)的左移序i B.信号f (n)的右移序i C.信号f (n)的折叠 D.信号f (n)的折叠再移序i24.下列表达式中错误的是（ ） A.)t ()t (-δ=δ B.)t t ()t t (00-δ=-δ C.)t ()t (δ-=δD.)t (21)t 2(δ=-δ 25.信号f 1(t)、f 2(t)的波形如题6图所示，则f(t)=f 1(t)*f 2(t)的表达式为（ ） A.)1t ()1t (-ε-+ε B.)2t ()2t (-ε-+ε C.)1t ()1t (+ε--ε D.)2t ()2t (+ε--ε 26．周期信号f(t)=-f(t 2T±),(T —周期)，则其傅里叶级数展开式的结构特点是（ ） A.只有正弦项B.只有余弦项C.只含偶次谐波D.只含奇次谐波 27.已知f(t)↔F(j ω)，则f(2t+4)的傅里叶变换为（ ）A.ωω2j e )2j (F 21 B.2j e )2j (F 21ωω C.ωω2j e )2j (F 2D.2j e )j (F 2ωω二、填空题：1．连续信号是指________的信号，通常表示为f （t ）。
《信号与线性系统》试题与答案
C． D。
97．离散时间单位延迟器D的单位序列响应为（）
A． B。 C。 D。1
98． 周期信号的傅立叶变换为（）
A． B。2 C。 D。0.5
99． 可写成以下正确的表达式是（）
A． B。
C． D。
100． （）
A． B。 C。 D。
二、填空题
1． ________________。
2．从信号频谱的连续性和离散性来考虑，周期信号的频谱是_______________。
A．S／2 B。S／3 C。S／4 D。S
34． …是（）
A．周期信号B。非周期信号C。不能表示信号D。以上都不对
35．线性系统具有（）
A．分解特性B。零状态线性C。零输入线性D。ABC
36．设系统零状态响应与激励的关系是： ，则以下表述不对的是（）
A．系统是线性的B。系统是时不变的C。系统是因果的D。系统是稳定的
A、f(－t+1)B、f(t+1)
C、f(－2t+1)D、f(－t/2+1)
18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（）
19。信号 与冲激函数 之积为（）
A、2B、2 C、3 D、5
A、因果不稳定系统B、非因果稳定系统
C、因果稳定系统D、非因果不稳定系统
21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（）
A、常数B、实数C、复数D、实数+复数
22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（）
A、阶跃信号B、正弦信号C、冲激信号D、斜升信号
23.积分 的结果为()
A B C. D.
24.卷积 的结果为()
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一、二章自测题1、判断题（1）若x (t )是一连续时间周期信号，则y (t )=x (2t )也是周期信号。
（2）两个周期信号之和一定是周期信号。
（3）所有非周期信号都是能量信号。
（4）两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
（5）若)()()(t h t x t y *=，则)1()2()1(+*-=-t h t x t y 。
（6）一个系统的自由响应就等于它的零输入响应。
（7）一个系统的零状态响应就等于它的自由响应。
（8）零状态响应是指系统没有激励时的响应。
（9）系统的单位冲激响应是指系统在冲激信号作用下的全响应。
（10）两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号？ （1）3cos(15)0()0t t f t t π≥⎧=⎨<⎩ （2）50()0te tf t t -⎧≥=⎨<⎩（3）()6sin 23cos3f t t t =+ （4）|2|()20sin 2t f t e t -= 3、填空题（1）已知)()4()(2t t t f ε+=，则)(''t f =__________________。
（2）=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
（3）=-⎰∞∞-dt t ）（92δ_________________________ 。
（4）=-⎰∞∞-dt t t e t j ）（0δω_________________________ 。
（5）信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε （2）)]4()([3cos )(2--=t t t t f εεπ （3）][sin )(3t t f πε=5、已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形图。
6、 对于下述系统，输入为e (t ), 输出为r (t )，T [e (t )]表示系统对e (t )的响应，试判定下述系统是否为：（1） 线性系统；（2）非时变系统；（3）因果系统；（4）稳定系统。
(a) r (t )=T [e (t )]=e (t -2) (b) r (t )=T [e (t )]=e (-t ) (c) r (t )=T [e (t )]=e (t )cos t (d) r (t )=T [e (t )]=a e (t )7、 一线性非时变系统，当输入为单位阶跃信号ε(t )时，输出r (t )为： )1()()(t t e t r t --+=-εε，试求该系统对图1.2所示输入e (t )的响应。
8、一线性时不变系统，当激励)()(1t t e ε=时，响应)()(1t et r atε-=，试求当激励)()(2t t e δ=时，响应)(2t r 的表示式。
（假定起始时刻系统无储能。
） 9、若描述某线性非时变系统的微分方程为)(2)()(2)(3)(22t e t e dt dt r t r dt d t r dtd +=++ 1)0(',1)0(==--r r 试求该系统的零输入响应。
10、线性系统由图1-3的子系统组合而成。
设子系统的冲激响应分别为)3()()(),1()(21--=-=t t t h t t h εεδ。
试求组合系统的冲激响应。
11、一线性时不变系统，在相同初始条件下，当激励为)(t f 时，其全响应为)()2sin 2()(31t t e t y t ε+=-；当激励为2)(t f 时，其全响应为)()2s i n 2()(32t t e t y t ε+=-。
求：（1） 初始条件不变，当激励为)(0t t f -时的全响应)(3t y ，t 0为大于零的实常数。
（2） 初始条件增大1倍，当激励为0.5)(t f 时的全响应。
12、计算以下信号的卷积积分)()(21t f t f * （1）)()(),()(21t e t f t t f at εε-== （2）)45cos()(),()(21 +==t t f t t f ωδ13、已知某连续时间系统的单位冲激响应h (t )与激励信号f (t )的波形如图1-4，试求该系统的零状态响应y (t )，画出y (t )的波形。
第一、 二章自测题参考答案1、判断题（1）正确 （2） 不一定，当它们的周期之比是有理数时，是正确的。
（3）错误，如y=t 不是周期信号，也不是能量信号。
（4）正确 （5）正确 （6） 错误 （7）错误 （8） 错误 （9） 错误 （10）错误 2、（1）功率信号；（2）能量信号；（3）功率信号；（4）能量信号. 3、 填空题(1) 已知)()4()(2t u t t f +=，则)(''t f =(t)4δ2u(t)'+ (2) 2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
(3)=-⎰∞∞-dt t ）（92δ 2 。
(4)00t j t j e dt t t e ωωδ=-⎰∞∞-）（(5)215π 4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε（2）)]4()([3cos )(2--=t t t t f εεπ在0到4区间内的6个周期的余弦波，余弦波的周期为2/3。
（3）][sin )(3t t f πε=5、函数表达式：f(2-t) = [ε(t)-ε(t-1)]+2[ε(t-1)-ε(t-2)] f(6-2t)=[ε(t-2)-ε(t-2.5)]+2[ε(t-2.5)-ε(t-3)]6、 对于下述的系统，输入为e (t ), 输出为r (t )，T [e (t )]表示系统对e (t )的响应，试判定下述系统是否为： （1）线性系统；（2）非时变系统；（3）因果系统；（4）稳定系统：(b) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统7、)2()1()(---=t t t e εε因为是线性时不变系统，输入)2()1(--t t εε和输出分别为)()1())1(1()1()1()(1)1(1t t e t t e t r t r t t -+-=---+-=-=+---εεεε)1()2())2(1()2()2()(2)2(2+-+-=---+-=-=+---t t e t t e t r t r t t εεεε所以 )]1()([)2()1()()()(221----+-⋅=-=--t t t e e t e e t r t r t r t t εεεε8、根据线性时不变系统的微分特性因为dt t d t )()(εδ=，所以)()()()()()(12t ae t t e t ae dtt dr t r at at at εδδε----=+-== 9、零输入响应：零输入响应的形式为齐次解，设为＋0)(221≥+=--t e B e B t r tt zi将初始状态：1)0()0(1)0()0(''====-+-r r r r ＋代入齐次解，得B 1 + B 2 = 1；- B 1 – 2B 2 = 1 所以：B 1 = 3 B 2 = -2因而零输入响应：＋－023)(2≥=--t e e t r tt zi10、)](*)()([*)()()(211t h t h t h t e t e t r ++=)(*)()()()()(2111t h t h t h t h t t h +++=δ)]3()([*)1()1()(---+-+=t t t t t εεδδδ)]4()1([)1()(---+-+=t t t εεδδ11、设系统的零输入响应为)(t r zi ，激励为)(t f 时的零状态响应为)(t r zs ，则有 )()()()2sin 2()(31t r t r t t e t y zs zi t +=+=-ε （1）)(2)()()2sin 2()(32t r t r t t e t y zs zi t +=+=-ε （2）（2）-（1）得)()2sin ()(3t t e t r t zs ε+-=-)(3)(3t e t r t zi ε-=所以初始条件不变时，激励)(0t t f -的全响应：)()](2sin [)(3)()()(00)(33030t t t t e t e t t r t r t y t t t zs zi --+-+=-+=---εε初始条件增大1倍，当激励为0.5)(t f 时的全响应： )()2sin (5.0)(6)(5.0)(2)(334t t e t e t r t r t y t t zs zi εε+-+=+=--)()2s i n 5.5(3t t e t ε+=-12．计算以下卷积积分)()(21t f t f * （1）)()(),()(21t e t f t u t f at ε-== （2）)45cos()(),()(21 +==t t f t t f ωδ答：（1）⎰---=*tat a t e ad et f t f 021)()1(1)()(εττ＝ 或用卷积的微积分性质⎰∞-=t d f dtt df t f t f ])([*)()(*)(2121ττ)()]1(1[*)(t e a t at εδ--=)()1(1t e aat ε--=(2) )45cos()45cos(*)()()(21+=+*at at t t f t f δ＝13、零状态响应)(*)()(t h t f t y =当0<t 时，0)(=t y当10<≤t 时，⎰=⋅=tt d t y 0422)(τ当21<≤t 时，⎰⎰+=-+=⋅+⋅=10122)1(241222)(t t d d t y tττ当32<≤t 时，⎰⎰--=-+--=⋅⋅=1221414)12(2)]2(1[41222)(t t t d d t y ττ＋当43≤≤t 时，⎰--=--=⋅=2228)]2(2[212)(t t t d t y τ当4>t 时， 0)(=t y所以⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤-<≤-<≤+<≤=其它，，，0432********,2210,4)(t t t t t t t t t y。