第7章 排序 习题参考答案
C语言程序设计教程 第七章 课后习题参考答案

{
for(j=0;j<N;j++)
{
printf("%4d",a[i][j]);
}
printf("\n");
}
for(i=0;i<M;iபைடு நூலகம்+)
{
for(j=0;j<N;j++)
{
if(i==j)
m+=a[i][j];
}
}
printf("主对角线元素之和为:%d\n",m);
批注本地保存成功开通会员云端永久保存去开通
P198 3求主、副对角线元素之和
#include<stdio.h>
#define M 4
#define N 4
int main()
{
int a[M][N]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
int i,j,m=0,n=0;
{
if(a[j]>a[j+1])
{
tmp=a[j];
a[j]=a[j+1];
a[j+1]=tmp;
}
}
}
printf("\n");
printf("排序后的数组为:\n");
for(i=0;i<N;i++)
{
printf("%4d",a[i]);
}
}
P76 3成绩
#include<stdio.h>
void input(int cla[50][3],int n);
编译原理(第三版)第7章课后练习及参考答案中石大版

第7章练习P165作业布置:P1651、21.已知文法A→aAd | aAb |ε,判断该文法是否是SLR(1)文法,若是构造相应分析表,并对输入串ab#给出分析过程。
解:拓广文法为G',增加产生式S'→A若产生式排序为:0 S'→A 1 A→aAd 2 A→aAb 3 A→ε由产生式知:从在I0、I2中:A→•aAd和A→•aAb为移进项目,A→•为归约项目,存在移进-归约冲突,因此所给文法不是LR(0)文法。
在I0、I2中:Follow(A)∩{a}= {d, b, #}∩{a}=φ所以在I0状态下面临输入符号为a时移进,为{d, b, #}时归约,为其他时报错。
因此在I0、I2中的移进-归约冲突可以由Follow集解决,所以G是SLR(1)文法。
下面是文法的2、若有定义二进制数的文法如下:S→L.L|LL→LB|BB→0|1(1)试为该文法构造LR分析表,并说明属哪类LR分析表。
(2)给出输入串101.110的分析过程。
答:(1)拓广文法为G′,增加产生式S′→S,若产生式排序为:0 S' →S 1 S →L.L 2 S →L 3 L →LB4 L →B5 B →06 B →1从S'→状态项目集经过符号到达的状态0 S'→•S S 1 S→•L.L L 2 S→•L L 2 L→•LB L 2 L→•B B 3 B→•0 0 4 B→•1 1 51 S'→S•2 S→L•.L . 6 S→L•L→L•B B 7 B→•0 0 4 B→•1 1 53 L→B•4 B→0•5 B→1•6 S→L.•L L 8 L→•LB L 8 L→•B B 3 B→•0 0 4 B→•1 1 57 L→LB•8 S→L.L•L→L•B B 7 B→•0 0 4 B→•1 1 5在I2中:B→•0和B→•1为移进项目,S→L•为归约项目,存在移进-归约冲突,因此所给文法不是LR(0)文法。
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
python核心编程第二版第7章习题答案

7-1.字典方法。
哪个字典方法可以用来把两个字典合并到一起。
答案:dict.update(dict2)将字典dict2的键-值对添加到字典dict中7-2.字典的键。
我们知道字典的值可以是任意的Python对象,那字典的键又如何呢?请试着将除数字和字符串意外的其他不同类型的对象作为字典的键,看看哪些类型可以,哪些不行。
对那些不能作为字典的键的对象类型,你认为是什么原因呢?答案:键必须是可哈希的。
所有不可变的类型都是可哈希的,因此他们都可以作为字典的键。
一个要说明的问题是:值相等的数字表示相同的键。
换句话说,整型数字1和浮点型1.0的哈希值是相同的,即它们是相同的键。
同时,也有一些可变对象(很少)是可哈希的,它们可以作为字典的键,但很少见。
用元组做有效的键,必须要加限制:元组中只包括像数字和字符串这样的不可变参数,才可以作为字典中有效的键。
内建函数hash()可以判断某个对象是否可以做一个字典的键,如果非可哈希类型作为参数传递给hash()方法,会产生TypeError错误,否则会产生hash值,整数。
>>> hash(1)1>>> hash('a')-468864544>>> hash([1,2])Traceback (most recent call last):File "<pyshell#2>", line 1, in <module>hash([1,2])TypeError: unhashable type: 'list'>>> hash({1:2,})Traceback (most recent call last):File "<pyshell#3>", line 1, in <module>hash({1:2,})TypeError: unhashable type: 'dict'>>> hash(set('abc'))Traceback (most recent call last):File "<pyshell#4>", line 1, in <module>hash(set('abc'))TypeError: unhashable type: 'set'>>> hash(('abc'))-1600925533>>> hash(1.0)1>>> hash(frozenset('abc'))-114069471>>> hash(((1,3,9)))1140186820>>> hash(((1,3,9),(1,2)))340745663>>> hash(((1,3,'9'),(1,2)))1944127872>>> hash(((1,3,'9'),[1,2],(1,2)))Traceback (most recent call last):File "<pyshell#11>", line 1, in <module>hash(((1,3,'9'),[1,2],(1,2)))TypeError: unhashable type: 'list'>>>7-3.字典和列表的方法。
数据结构课后习题答案第七章
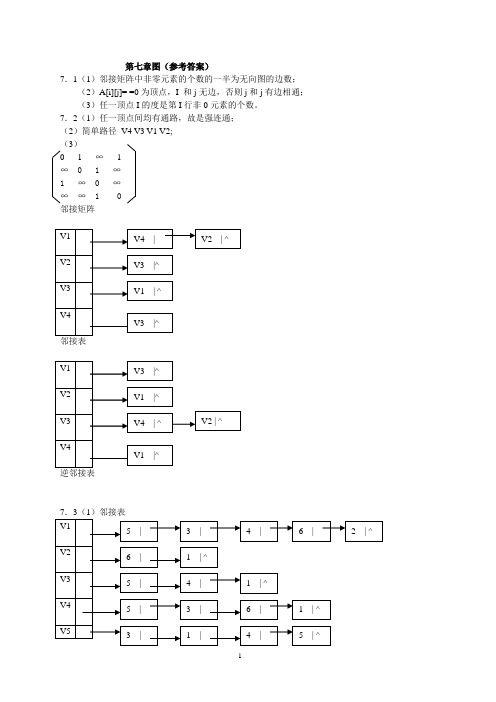
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第七章 练习题参考答案

V1 V3 V6
7. 对下图所示的有向图
(1) 画出它的邻接表 (2) 根据邻接表写出其拓扑排序序列
解:(1)邻接表为
0
2
5∧
2
3
4∧
2 3∧
4∧
1
2
3
6∧
1
4∧
(2)由邻接表可得拓朴排序序列:
1 5 2 3 64
8.已知n个顶点的有向图用邻接矩阵表示,编 写函数,计算每对顶点之间的最短路径。
4 18 ∧
2
1 12
32
5 22 ∧
3
1 16
22
44∧
4
1 18
34
5 10 ∧
5
2 22
4 10 ∧
解:(1) V1
12 V2
16 2
18
4 V3 22
V4
10 V5
(2)深度优先遍历的结点序列:v1,v2,v3,v4,v5
广度优先搜索的结点序列:v1,v2,v3,v4,v5
(3)最小生成树
CD CA CAB
CD CA CAB
CD CA CABΒιβλιοθήκη CD3DB
DB
DB DBC
DBCA DB DBC
DBCA DB DBC
10.对于如图所示的AOE网,求出各活动可能 的最早开始时间和允许的最晚开始时间, 哪些是关键活动?
a1=4
v2
v1
a3=2
a2=3
v3
a5=6 v4
a4=4
解:
顶点 Ve Vl V1 0 0 V2 4 4 V3 6 6 v4 10 10
if(length[i][k]+length[k][j]<length[i][j]) { length[i][j]=length[i][k]+length[k][j];
数据结构-第7章图答案
7.3 图的遍历 从图中某个顶点出发游历图,访遍图中其余顶点, 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发,访问此顶点,然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图,直至图中所有和V0有路径相通的顶点都被访 问到,若此时图中尚有顶点未被访问,则另选图中 一个未曾被访问的顶点作起始点,重复上述过程, 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
林子雨大数据技术原理及应用第七章课后题答案
《大数据技术第七章课后题答案黎狸1.试述MapReduce和Hadoop的关系。
谷歌公司最先提出了分布式并行编程模型MapReduce, Hadoop MapReduce是它的开源实现。
谷歌的MapReduce运行在分布式文件系统GFS 上,与谷歌类似,HadoopMapReduce运行在分布式文件系统HDFS上。
相对而言,HadoopMapReduce 要比谷歌MapReduce 的使用门槛低很多,程序员即使没有任何分布式程序开发经验,也可以很轻松地开发出分布式程序并部署到计算机集群中。
2.MapReduce 是处理大数据的有力工具,但不是每个任务都可以使用MapReduce来进行处理。
试述适合用MapReduce来处理的任务或者数据集需满足怎样的要求。
适合用MapReduce来处理的数据集,需要满足一个前提条件: 待处理的数据集可以分解成许多小的数据集,而且每一个小数据集都可以完全并行地进行处理。
3.MapReduce 模型采用Master(JobTracker)-Slave(TaskTracker)结构,试描述JobTracker 和TaskTracker的功能。
MapReduce 框架采用了Master/Slave 架构,包括一个Master 和若干个Slave。
Master 上运行JobTracker,Slave 上运行TaskTrackero 用户提交的每个计算作业,会被划分成若千个任务。
JobTracker 负责作业和任务的调度,监控它们的执行,并重新调度已经失败的任务。
TaskTracker负责执行由JobTracker指派的任务。
4.;5.TaskTracker 出现故障会有什么影响该故障是如何处理的6.MapReduce计算模型的核心是Map函数和Reduce函数,试述这两个函数各自的输人、输出以及处理过程。
Map函数的输人是来自于分布式文件系统的文件块,这些文件块的格式是任意的,可以是文档,也可以是二进制格式。
第7章图习题及参考答案
第7章-图习题及参考答案第7章习题一、单项选择题1.在无向图中定义顶点的度为与它相关联的()的数目。
A. 顶点B. 边C. 权D. 权值2.在无向图中定义顶点v i与v j之间的路径为从v i到达v j的一个()。
A. 顶点序列B. 边序列C. 权值总和D.边的条数3.图的简单路径是指()不重复的路径。
A. 权值B. 顶点C. 边D. 边与顶点均4.设无向图的顶点个数为n,则该图最多有()条边。
A. n-1B. n(n-1)/2C. n(n+1)/2D.n(n-1)5.n个顶点的连通图至少有()条边。
A. n-1B. nC. n+1D. 06.在一个无向图中,所有顶点的度数之和等于所有边数的( ) 倍。
A. 3B. 2C. 1D. 1/27.若采用邻接矩阵法存储一个n个顶点的无向图,则该邻接矩阵是一个( )。
A. 上三角矩阵B. 稀疏矩阵C. 对角矩阵D. 对称矩阵8.图的深度优先搜索类似于树的()次序遍历。
A. 先根B. 中根C. 后根D. 层次9.图的广度优先搜索类似于树的()次序遍历。
A. 先根B. 中根C. 后根D. 层次10.在用Kruskal算法求解带权连通图的最小(代价)生成树时,选择权值最小的边的原则是该边不能在图中构成()。
A. 重边B. 有向环C. 回路D. 权值重复的边11.在用Dijkstra算法求解带权有向图的最短路径问题时,要求图中每条边所带的权值必须是()。
A. 非零B. 非整C. 非负D. 非正12.设G1 = (V1, E1) 和G2 = (V2, E2) 为两个图,如果V1 ⊆ V2,E1 ⊆ E2,则称()。
A. G1是G2的子图B. G2是G1的子图C. G1是G2的连通分量D. G2是G1的连通分量13.有向图的一个顶点的度为该顶点的()。
A. 入度B. 出度C. 入度与出度之和D. (入度﹢出度))/214.一个连通图的生成树是包含图中所有顶点的一个()子图。
第七章C语言谭浩强答案
7.1用筛法求100之内的素数。
解:所谓“筛法”指的是“Eratosthenes筛法”。
Eratosthenes是古希腊的著名数学家。
他采用的方法是:在一张纸上写下1~1000之间的全部整数,然后逐个判断它们是否素数,找出一个非素数就把它挖掉,最后剩下的就是素数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 …具体做法如下:先将1挖掉(因为1不是素数)。
用2去除它后面的各个数,把能被2整除的数(如4,6,8…)挖掉,即把2的倍数挖掉。
用3去除它后面各数,把3的倍数挖掉。
分别用4,5…各数作为除数去除这些数以后的各数。
这个过程一直进行到在除数后面的数已全被挖掉为止。
例如在上表中1~50范围内的素数,要一直进行到除数为47为止。
事实上,这一过程可以简化。
如果需要找1~n数)即可。
例如对1~50,只需进行到将7上面的算法可表示为:挖去1;用刚才被挖去的数的下一个数p去除p后面的各数,把p的倍数挖掉;检查p n=1000,则检查p<31否),如果是,则返回(2)继续执行,否则就结束;纸上剩下的就是素数。
解题的基本思路有了,但要变成计算机的操作,还要作进一步的分析。
如怎样判断一个数是否已被“挖掉”,怎样找出某一个数p的倍数,怎样打印出未被挖掉的数。
可以设一个数组a,a[1]到a[100]的值分别是1,2,3,…100。
然后用上述方法将非素数“挖去”。
如果一个数被认为是非素数,就将它的值变为零,最后将不为零的数组元素输出,就是所求的素数表。
程序如下:#include <math.h>main ( ){int i,j,n,a[101];for (i=1;i<=100;i++)a[i] =i;for (i=2;i<sqrt(100);i++)for (j=i+1;j<=100;j++){if (a[i]!=0 && a[j]!=0)if (a[j]%a[i]==0)a[j]=0; } /*非素数,赋值为0,“挖掉”*/printf(“\n”);for (i=2,n=0;i<=100;i++){ if (a[i]!=0){printf(“%5d”,a[i]);n++; }if (n==10) /*此处if 语句的作用是在输出10个数后换行*/{ printf (“\n”);n=0; }}}运行结果:2 3 5 7 11 13 17 19 23 29 31 37 41 4347 53 59 61 67 71 73 79 83 89 977.2用选择法对10个整数排序(从小到大)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题七参考答案一、选择题1.内部排序算法的稳定性是指( D )。
A.该排序算法不允许有相同的关键字记录B.该排序算法允许有相同的关键字记录C.平均时间为0(n log n)的排序方法D.以上都不对2.下面给出的四种排序算法中,( B )是不稳定的排序。
A.插入排序B.堆排序C.二路归并排序D.冒泡排序3. 在下列排序算法中,哪一种算法的时间复杂度与初始排序序列无关(D )。
A.直接插入排序B.冒泡排序C.快速排序D.直接选择排序4.关键字序列(8,9,10,4,5,6,20,1,2)只能是下列排序算法中( C )的两趟排序后的结果。
A.选择排序 B.冒泡排序 C.插入排序 D.堆排序5.下列排序方法中,( D )所需的辅助空间最大。
A.选择排序B.希尔排序C.快速排序D.归并排序6.一组记录的关键字为(46,79,56,38,40,84),则利用快速排序的方法,以第一个记录为支点得到的一次划分结果为(C )。
A.(38,40,46,56,79,84) B.(40,38,46,79,56,84)C.(40,38,46,56,79,84) D.(40,38,46,84,56,79)7.在对一组关键字序列{70,55,100,15,33,65,50,40,95},进行直接插入排序时,把65插入,需要比较( A )次。
A. 2B. 4C. 6D. 88.从待排序的序列中选出关键字值最大的记录放到有序序列中,该排序方法称为( B )。
A. 希尔排序B. 直接选择排序C. 冒泡排序D. 快速排序9.当待排序序列基本有序时,以下排序方法中,( B )最不利于其优势的发挥。
A. 直接选择排序B. 快速排序C.冒泡排序D.直接插入排序10.在待排序序列局部有序时,效率最高的排序算法是( B )。
A. 直接选择排序B. 直接插入排序C. 快速排序D.归并排序二、填空题1.执行排序操作时,根据使用的存储器可将排序算法分为内排序和外排序。
2.在对一组记录序列{50,40,95,20,15,70,60,45,80}进行直接插入排序时,当把第7个记录60插入到有序表中时,为寻找插入位置需比较 3 次。
3.在直接插入排序和直接选择排序中,若初始记录序列基本有序,则选用直接插入排序。
4.在对一组记录序列{50,40,95,20,15,70,60,45,80}进行直接选择排序时,第4次交换和选择后,未排序记录为{50,70,60,95,80}。
5.n个记录的冒泡排序算法所需的最大移动次数为3n(n-1)/2 ,最小移动次数为0 。
6.对n个结点进行快速排序,最大的比较次数是n(n-1)/2 。
7.对于堆排序和快速排序,若待排序记录基本有序,则选用堆排序。
8.在归并排序中,若待排序记录的个数为20,则共需要进行5 趟归并。
9.若不考虑基数排序,则在排序过程中,主要进行的两种基本操作是关键字的比较和数据元素的移动。
10.在插入排序、希尔排序、选择排序、快速排序、堆排序、归并排序和基数排序中,平均比较次数最少的是快速排序,需要内存容量最多的是基数排序。
三、算法设计题1.试设计算法,用插入排序方法对单链表进行排序。
参考答案:public static void insertSort(LinkList L) {Node p, q, r, u;p = L.getHead().getNext();L.getHead().setNext(null);//置空表,然后将原链表结点逐个插入到有序表中while (p != null) { //当链表尚未到尾,p为工作指针r = L.getHead();q = L.getHead().getNext();while (q != null && (Integer.parseInt((String) q.getData())) <=(Integer.parseInt((String) p.getData()))) {//查P结点在链表中的插入位置,这时q是工作指针r = q;q = q.getNext();}u = p.getNext();p.setNext(r.getNext());r.setNext(p);p = u;//将P结点链入链表中,r是q的前驱,u是下一个待插入结点的指针}}2.试设计算法,用选择排序方法对单链表进行排序。
参考答案://单链表选择排序算法public static void selectSort(LinkList L) {//p为当前最小,r为此过程中最小,q为当前扫描接点Node p, r, q;Node newNode = new Node();newNode.setNext(L.getHead());L.setHead(newNode);//制造一个最前面的节点newNode,解决第一个节点的没有前续节点需要单独语句的问题。
p = L.getHead();while (p.getNext().getNext() != null) {r = p.getNext();q = p.getNext().getNext();while (q.getNext() != null) {if (Integer.parseInt((String) q.getNext().getData()) <=(Integer.parseInt((String) r.getNext().getData()))) {r = q;}q = q.getNext();}if (r != p) { //交换p与rNode swap = r.getNext();r.setNext(r.getNext().getNext()); //r的next指向其后继的后继swap.setNext(p.getNext());p.setNext(swap); //p的后继为swap}p = p.getNext();}//whilep.setNext(null);}3.试设计算法,实现双向冒泡排序(即相邻两遍向相反方向冒泡)。
参考答案://产生随机数方法public static int[] random(int n) {if (n > 0) {int table[] = new int[n];for (int i = 0; i < n; i++) {table[i] = (int) (Math.random() * 100);//产生一个0~100之间的随机数}return table;}return null;}//输出数组元素方法public static void print(int[] table){if (table.length > 0) {for (int i = 0; i < table.length; i++) {System.out.print(table[i] + " ");}System.out.println();}}//双向冒泡排序方法public static void dbubblesort(int[] table) {int high = table.length;int left = 1;int right = high - 1;int t = 0;do {//正向部分for (int i = right; i >= left; i--) {if (table[i] < table[i - 1]) {int temp = table[i];table[i] = table[i - 1];table[i - 1] = temp;t = i;}}left = t + 1;//反向部分for (int i = left; i < right + 1; i++) {if (table[i] < table[i - 1]) {int temp = table[i];table[i] = table[i - 1];table[i - 1] = temp;t = i;}}right = t - 1;} while (left <= right);}4.试设计算法,使用非递归方法实现快速排序。
参考答案:public static void NonrecursiveQuickSort(int[] ary) { if (ary.length < 2) {return;}//数组栈:记录着高位和低位的值int[][] stack = new int[2][ary.length];//栈顶部位置int top = 0;//低位,高位,循环变量,基准点//将数组的高位和低位位置入栈stack[1][top] = ary.length - 1;stack[0][top] = 0;top++;//要是栈顶不空,那么继续while (top != 0) {//将高位和低位出栈//低位:排序开始的位置top--;int low = stack[0][top];//高位:排序结束的位置int high = stack[1][top]; //将高位作为基准位置 //基准位置int pivot = high;int i = low;for (int j = low; j < high; j++) {if (ary[j] <= ary[pivot]) {int temp = ary[j];ary[j] = ary[i];ary[i] = temp;i++;}}//如果i不是基准位,那么基准位选的就不是最大值//而i的前面放的都是比基准位小的值,那么基准位//的值应该放到i所在的位置上if (i != pivot) {int temp = ary[i];ary[i] = ary[pivot];ary[pivot] = temp;}if (i - low > 1) {//此时不排i的原因是i位置上的元素已经确定了,i前面的都是比i小的,i后面的都是比i大的stack[1][top] = i - 1;stack[0][top] = low;top++;}//当high-i小于等于1的时候,就不往栈中放了,这就是外层while循环能结束的原因//如果从i到高位之间的元素个数多于一个,那么需要再次排序if (high - i > 1) {//此时不排i的原因是i位置上的元素已经确定了,i前面的都是比i小的,i后面的都是比i大的stack[1][top] = high;stack[0][top] = i + 1;top++;}}}5.试设计算法,判断完全二叉树是否为大顶堆。
