工程制图答案孙兰凤第3章习题答案解析
合集下载
工程制图答案孙兰凤第3章习题答案

17
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
2019/9/27
18
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
(1)
19
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
线,建立V/H1,将平面
变成铅垂面求得倾角β
。 注意点在新旧投影
面体系的投影变换规律 。
47
2019/9/27
3-39 已知△ABC是处于正垂面位置的等边三角形,用换面法求作△ABC的 水平投影。
本题是已知一正垂 面的等边三角形的正面 投影和a′。要求用换 面法求正垂面的水平投 影。
建立新投影面体系 V/H1,将平面变换成投影 面的平行面,求得等边 三角形的实形后,返回 V/H投影面体系求得b、 c。
(2)
20
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α 、β 、γ 表示之。
(3)
21
2019/9/27
3-17 在投影图上用字符标出平面A、B、C、D的三面投影,并判别其相对投 影面的位置。
A面是
面
B面是
面
C面是
面
D面是
面
22
2019/9/27
4
3-3 已知各点的两面投影,求作其第三投影。
2019/9/27
5
2019/9/27
3-4 已知点A距离投影面W、V、H分别为20、15、25;点B在A之左10, A之前5,A之下15;点C在A之右5,A之后10,A之上5(单位:mm)。
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
2019/9/27
18
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
(1)
19
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
线,建立V/H1,将平面
变成铅垂面求得倾角β
。 注意点在新旧投影
面体系的投影变换规律 。
47
2019/9/27
3-39 已知△ABC是处于正垂面位置的等边三角形,用换面法求作△ABC的 水平投影。
本题是已知一正垂 面的等边三角形的正面 投影和a′。要求用换 面法求正垂面的水平投 影。
建立新投影面体系 V/H1,将平面变换成投影 面的平行面,求得等边 三角形的实形后,返回 V/H投影面体系求得b、 c。
(2)
20
2019/9/27
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α 、β 、γ 表示之。
(3)
21
2019/9/27
3-17 在投影图上用字符标出平面A、B、C、D的三面投影,并判别其相对投 影面的位置。
A面是
面
B面是
面
C面是
面
D面是
面
22
2019/9/27
4
3-3 已知各点的两面投影,求作其第三投影。
2019/9/27
5
2019/9/27
3-4 已知点A距离投影面W、V、H分别为20、15、25;点B在A之左10, A之前5,A之下15;点C在A之右5,A之后10,A之上5(单位:mm)。
工程制图答案孙兰凤第3章习题答案_图文

44
*
3-36 已知两平行线AB、CD的间距等于16mm,用换面法求直线AB的正面投影。
本题是两水平平 行面,已知其水平 投影、两线间距为 16mm和CD的正面投 影。要求用换面法 求AB的a′b′。
建立新投影面体 系H/V1,将两水平面 变换成正垂线,用 实长求a1′b1′;返 回原投影面体系求 得a ′ b′;
15
*
3-13 作图判别直线AB与CD在空间的相对位置。
16
*
3-14 过点A作直线AB,使平行于直线DE;作直线AC使与直线DE相交,其交点距 V面为15mm。
17
*
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
18
*
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α、β、γ 表示之。
42
*
3-34 求作平面与平面的交线,并判别平面的可见性。
(3)
本题是两个侧垂 面相交。根据交线 的共有性和正垂面 投影特点,两侧垂 面的正面投影交点 m″n″就是交线的 侧面投影。利用点 线从属性可直接求 m′、n′,其连线 即为交线的正面投 影。
注意投影重叠 部分的可见性的判 别。
43
*
3-35 已知直线AB的实长为30mm,用换面法求作Aபைடு நூலகம்的正面投影及α和β角。
本题已知直线AB 的水平投影、实长 30mm和点A的水平投 影,要求用换面法求 b′和α、β角。
先换V面建立新投 影面体系H/V1,将一般 位置直线AB变成正平 线,用实长求b1′和 α角;返回原投影面 体系求得a ′ b′;再 建立新投影面体系 H1/V求得β角。
注意点在新旧投 影面体系的投影变换 规律。
*
3-36 已知两平行线AB、CD的间距等于16mm,用换面法求直线AB的正面投影。
本题是两水平平 行面,已知其水平 投影、两线间距为 16mm和CD的正面投 影。要求用换面法 求AB的a′b′。
建立新投影面体 系H/V1,将两水平面 变换成正垂线,用 实长求a1′b1′;返 回原投影面体系求 得a ′ b′;
15
*
3-13 作图判别直线AB与CD在空间的相对位置。
16
*
3-14 过点A作直线AB,使平行于直线DE;作直线AC使与直线DE相交,其交点距 V面为15mm。
17
*
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
18
*
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α、β、γ 表示之。
42
*
3-34 求作平面与平面的交线,并判别平面的可见性。
(3)
本题是两个侧垂 面相交。根据交线 的共有性和正垂面 投影特点,两侧垂 面的正面投影交点 m″n″就是交线的 侧面投影。利用点 线从属性可直接求 m′、n′,其连线 即为交线的正面投 影。
注意投影重叠 部分的可见性的判 别。
43
*
3-35 已知直线AB的实长为30mm,用换面法求作Aபைடு நூலகம்的正面投影及α和β角。
本题已知直线AB 的水平投影、实长 30mm和点A的水平投 影,要求用换面法求 b′和α、β角。
先换V面建立新投 影面体系H/V1,将一般 位置直线AB变成正平 线,用实长求b1′和 α角;返回原投影面 体系求得a ′ b′;再 建立新投影面体系 H1/V求得β角。
注意点在新旧投 影面体系的投影变换 规律。
工程制图答案孙兰凤第3章习题答案ppt课件

02.06.2020
1
02.06.2020
2
02.06.2020
3-1 已知各点的空间位置,试作其投影图,并写出各点的坐标值。仿照点A填写在括号内)
点A( 5 ,20 ,25) 点B( 10, 1, 5)0 点15C(15 , 0, ) 点D( ,25, )0 0
3
02.06.2020
3-2 试作下列点的三面投影图和直观图。 点A的坐标为(10,10,10),点B的坐标为(20,15,0 ), 点C的坐标为(15,0 ,20),点D的坐标为( 0, 0,15)。
(1)
19
02.06.2020
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α、β、γ 表示之。 (2)
20
02.06.2020
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α、β、γ 表示之。
(3)
21
02.06.2020
为正垂线,故可作出短边 AB的两面投影。 (2)因矩形ABCD的短边AB为 正垂线,故可知矩形BCD 为正垂面,又因矩形的相 邻两边互相垂直故可知 AD和BC为正平线。
注:本题有四解,可向左面画,也可向23 右面画,或向下画。
02.06.2020
3-19 已知等边三角形EFG是正平面,其上方顶点为E,下方的边FG为侧垂线, 边长为30 mm,补全该等边三角形EFG的两面投影。
25
02.06.2020
3-21 已知平面上点和直线的一个投影,求作另一个投影。
(1)
(2)
26
3-22 过点A作属于平面△ABC的正平线和水平线。
02.06.2020
1
02.06.2020
2
02.06.2020
3-1 已知各点的空间位置,试作其投影图,并写出各点的坐标值。仿照点A填写在括号内)
点A( 5 ,20 ,25) 点B( 10, 1, 5)0 点15C(15 , 0, ) 点D( ,25, )0 0
3
02.06.2020
3-2 试作下列点的三面投影图和直观图。 点A的坐标为(10,10,10),点B的坐标为(20,15,0 ), 点C的坐标为(15,0 ,20),点D的坐标为( 0, 0,15)。
(1)
19
02.06.2020
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α、β、γ 表示之。 (2)
20
02.06.2020
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α、β、γ 表示之。
(3)
21
02.06.2020
为正垂线,故可作出短边 AB的两面投影。 (2)因矩形ABCD的短边AB为 正垂线,故可知矩形BCD 为正垂面,又因矩形的相 邻两边互相垂直故可知 AD和BC为正平线。
注:本题有四解,可向左面画,也可向23 右面画,或向下画。
02.06.2020
3-19 已知等边三角形EFG是正平面,其上方顶点为E,下方的边FG为侧垂线, 边长为30 mm,补全该等边三角形EFG的两面投影。
25
02.06.2020
3-21 已知平面上点和直线的一个投影,求作另一个投影。
(1)
(2)
26
3-22 过点A作属于平面△ABC的正平线和水平线。
02.06.2020
工程制图基础习题集第三章答案(高等教育出版社)

3-7(6) 分析曲面立体的相贯线,并补画其所缺的投影。 CAD 立体 返回
3-7(7) 分析曲面立体的相贯线,并补画其所缺的投影。 答案 立体 返回
3-7(7) 分析曲面立体的相贯线,并补画其所缺的投影。 CAD 立体 返回
3-7(8) 分析曲面立体的相贯线,并补画其所缺的投影。 答案 立体 返回
3-7(8) 分析曲面立体的相贯线,并补画其所缺的投影。 CAD 立体 返回
3-8 分析圆柱面与球面的相贯线,完成它们的投影。 答案 立体 返回
3-8 分析圆柱面与球面的相贯线,完成它们的投影。 CAD 立体 返回
3-9 参照轴测图,分析组合体的表面交线,补画左视图及 、 两 点的投影。
′
答案 立体 返回
答案 立体 返回
3-15(4) 根据组合体的视图,画出正等轴测图(尺寸按1∶1量取; 用尺规或计算机或徒手绘图均可)。
CAD 立体 返回
3-16(1) 根据组合体的视图,画出其正等轴测图(尺寸按1:1量取; 用尺规或计算机绘图均可
答案 立体 返回
3-16(1) 根据组合体的视图,画出其正等轴测图(尺寸按1:1量取; 用尺规或计算机绘图均可
3-1(1) 参照轴测图,补画组合体主、左视图中所缺的图线;并判断 其表面之间的关系。
CAD 立体 返回
3-1(2) 参照轴测图,补画组合体主、左视图中所缺的图线;并判断 其表面之间的关系。
答案 立体 返回
3-1(2) 参照轴测图,补画组合体主、左视图中所缺的图线;并判断 其表面之间的关系。
CAD 立体 返回
第三章 习 题
3-1(1) 3-4(1) 3-5(3)
3-1(2) 3-2(1) 3-2(2) 3-3(1) 3-4(2) 3-4(3) 3-4(4) 3-5(1) 3-6(1) 3-6(2) 3-6(3) 3-7(1)
工程制图答案解析孙兰凤知识题

8-12 已知俯视图和A向视图,画出半剖的主视图和全剖的左视图,并标注尺寸(尺寸数值从图中量取整数)。
用形体分析 法标注尺寸
作图步骤 1.画半剖的主视图 2. 全剖的左视图 3.标注尺寸
17
2020年8月11日星期 二1时44分20秒
8-13 已知主视图和俯视图,画出半剖的左视图,并标注尺寸(尺寸数值从图中量取整数)。
2020年8月11日星期 二1时44分20秒
主视方向
3
8-2 按照箭头所指的方向,在适当位置画出相应的向视图。
C
D
2020年8月11日星期 二1时44分20秒
E
F
请单击视图名称看答案
4
主视方向
8-3 作A向斜视图(倾斜和转正)和B向局部视图。
A
或
2020年8月11日星期 二1时44分20秒
请单击视图名称看答案
(1) 题是用视图表示半个物 体。
(2) 题是用半剖视图表示完 整物体。 半个物体与完整物体
形状、大小相同,投影也 相同,但表示方法不同。
8-9 补全视图中所缺的图线。
(1)
(2)
D1 D2
2020年8月11日星期 二1时44分20秒
此两题有何内在的联 系?请认真分析与思考。
(1) (2)
题是用视图表示半个物体。 题是用半剖视图表示完整物体。 半个物体与完整物体形状、大小相
想看立体模型?请单击这里
18
作图步骤 1.画半剖的左视图
2.标注尺寸 用形体分析 法标注尺寸
8-14 补全剖视图中所缺的图线。
2020年8月11日星期 二1时44分20秒
想看立体模型?请单击这里
19
8-15 已知主视图和俯视图,求全剖的左视图。 D1D2
用形体分析 法标注尺寸
作图步骤 1.画半剖的主视图 2. 全剖的左视图 3.标注尺寸
17
2020年8月11日星期 二1时44分20秒
8-13 已知主视图和俯视图,画出半剖的左视图,并标注尺寸(尺寸数值从图中量取整数)。
2020年8月11日星期 二1时44分20秒
主视方向
3
8-2 按照箭头所指的方向,在适当位置画出相应的向视图。
C
D
2020年8月11日星期 二1时44分20秒
E
F
请单击视图名称看答案
4
主视方向
8-3 作A向斜视图(倾斜和转正)和B向局部视图。
A
或
2020年8月11日星期 二1时44分20秒
请单击视图名称看答案
(1) 题是用视图表示半个物 体。
(2) 题是用半剖视图表示完 整物体。 半个物体与完整物体
形状、大小相同,投影也 相同,但表示方法不同。
8-9 补全视图中所缺的图线。
(1)
(2)
D1 D2
2020年8月11日星期 二1时44分20秒
此两题有何内在的联 系?请认真分析与思考。
(1) (2)
题是用视图表示半个物体。 题是用半剖视图表示完整物体。 半个物体与完整物体形状、大小相
想看立体模型?请单击这里
18
作图步骤 1.画半剖的左视图
2.标注尺寸 用形体分析 法标注尺寸
8-14 补全剖视图中所缺的图线。
2020年8月11日星期 二1时44分20秒
想看立体模型?请单击这里
19
8-15 已知主视图和俯视图,求全剖的左视图。 D1D2
工程制图第三章答案

第39页/共52页
3-2.4、在直线EF上取一点p,使P点与H面、V面距离之比为3:2
第40页/共52页
3-3.
第41页/共52页
3-3.
第页
3-3.
第44页/共52页
三角形是 面
水平
侧垂
平面图形是 面
第45页/共52页
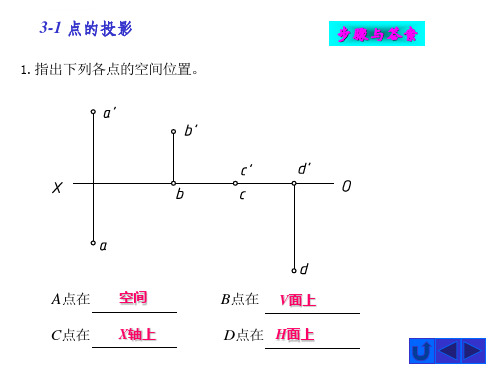
3-1.1、指出下列各点的空间位置
第1页/共52页
答案
第2页/共52页
答案
第3页/共52页
答案
第4页/共52页
答案
第5页/共52页
答案
3-1.
第6页/共52页
3-2 .1、画出下列直线段的第三投影,并判别其相对投影面的位置
正平线
侧平线
第7页/共52页
侧垂线
水平线
第8页/共52页
正垂线
答案
水平
侧垂
平面图形是 面
第24页/共52页
答案
3-4.3、已知矩形ABCD⊥H面,β=45°,完成其水平投影。
第25页/共52页
答案
3-5.
第26页/共52页
答案
3-5.
第27页/共52页
答案
3-5.
第28页/共52页
答案
3-5.
第29页/共52页
答案
3-5.5、求平面上点K与点N的另一投影。
第30页/共52页
第31页/共52页
第32页/共52页
第33页/共52页
第34页/共52页
3-1.
第35页/共52页
3-2.2、作出下列直线的三面投影
第36页/共52页
第37页/共52页
3-2.3、在直线AB上取一点K,使AK:KB=3:2;
3-2.4、在直线EF上取一点p,使P点与H面、V面距离之比为3:2
第40页/共52页
3-3.
第41页/共52页
3-3.
第页
3-3.
第44页/共52页
三角形是 面
水平
侧垂
平面图形是 面
第45页/共52页
3-1.1、指出下列各点的空间位置
第1页/共52页
答案
第2页/共52页
答案
第3页/共52页
答案
第4页/共52页
答案
第5页/共52页
答案
3-1.
第6页/共52页
3-2 .1、画出下列直线段的第三投影,并判别其相对投影面的位置
正平线
侧平线
第7页/共52页
侧垂线
水平线
第8页/共52页
正垂线
答案
水平
侧垂
平面图形是 面
第24页/共52页
答案
3-4.3、已知矩形ABCD⊥H面,β=45°,完成其水平投影。
第25页/共52页
答案
3-5.
第26页/共52页
答案
3-5.
第27页/共52页
答案
3-5.
第28页/共52页
答案
3-5.
第29页/共52页
答案
3-5.5、求平面上点K与点N的另一投影。
第30页/共52页
第31页/共52页
第32页/共52页
第33页/共52页
第34页/共52页
3-1.
第35页/共52页
3-2.2、作出下列直线的三面投影
第36页/共52页
第37页/共52页
3-2.3、在直线AB上取一点K,使AK:KB=3:2;
工程制图第3章答案ppt课件
3.已知矩形ABCD⊥H面,β=45°,完成其水平投影。
3 . 已 知 矩 形 A B C D ⊥ H 面 , ¦ Β= 4 5 ° , 完 成 其 水 平 投 影 。
步骤与答案
β=45°
d(c)
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
下方15mm,前方10mm;点C在点A的正前方15mm;点D距离投影
面W、V、H分别为15mm,20mm,12mm;求各点的三面投 影。
步骤与答案
c′(a′)
d′ b′
10 12
a d b
c 15
a″ c″
d″ b″
20
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1.判别直线AB和CD的相对位置(平行、相交、交叉)。
步骤与答案
平行
交叉
k′
交叉
相交
K C
k 作Cd=c′d′ 交叉 取dK=d′k′
作Kk∥Cc
相交
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
步骤与答案
4.已知A点的侧面投影 ,并已知A点距w面的距离为25mm,
求作 ,
25
a′
a
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
3 . 已 知 矩 形 A B C D ⊥ H 面 , ¦ Β= 4 5 ° , 完 成 其 水 平 投 影 。
步骤与答案
β=45°
d(c)
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
下方15mm,前方10mm;点C在点A的正前方15mm;点D距离投影
面W、V、H分别为15mm,20mm,12mm;求各点的三面投 影。
步骤与答案
c′(a′)
d′ b′
10 12
a d b
c 15
a″ c″
d″ b″
20
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1.判别直线AB和CD的相对位置(平行、相交、交叉)。
步骤与答案
平行
交叉
k′
交叉
相交
K C
k 作Cd=c′d′ 交叉 取dK=d′k′
作Kk∥Cc
相交
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
步骤与答案
4.已知A点的侧面投影 ,并已知A点距w面的距离为25mm,
求作 ,
25
a′
a
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
工程制图第3章答案

3.两直线交叉
交叉两直线各组同面投影不会都平行,特殊情况下可能有一两组 平行;其各组同面投影交点的连线与相应的投影轴不垂直,即不符合 点的投影规律。
重影点 反之,如果两直线的投影既不符合平行两直线的投影特性,也不 符合相交两直线的投影特性,则该两直线空间为交叉两直线。
4.两直线垂直
一般情况下,在投影图中不能确定空间两直线是否垂直, 但当直线处于特殊位置时可以直接从投影图中判断:
三、正投影的基本性质
1. 实形性
2.积聚性
∟
三、正投影的基本性质
3.类似性
4.平行性
三、正投影的基本性质
5.定比性
6.从属性
3-2 三视图的形成及其投影关系
一、 三视图的形成
1. 三投影面体系的建立
物体的一个投影不能确定空间物体的形状。
怎吗办?
建立三面投影体系
2.三视图的形成
主视图
左 视图
[例3-4] 已知点A(15,10,12),求作点A的三面投影图。
作图步骤如下:
1.自原点O沿OX轴向左量取x=15,得点 ax 2.过ax作OX轴的垂线,在垂线上自ax向下量取y=10,得点A的水平投影a 向上量取z=12,得点A的正面投影a
3.根据点的投影规律,可由点的两个投影作出第三投影 a 。
★ 我们只讨论直线与平面中至少有一个处于特殊位置的情况。
[例3-11] 求一般位置直线MN与铅垂面ABC的交点 分析: 作图:
判可见性:
[例3-12] 求铅垂线MN与一般位置平面△ABC的交点 分析: 作图:
判可见性:
⒉ 两平面相交
两平面相交其交线为直线,交线是两平面的共 有线,同时交线上的点都是两平面的共有点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年9月16日星 期一9时10分11秒
1
2019年9月16日星 期一9时10分11秒
2
2019年9月16日星 期一9时10分11秒
3-1 已知各点的空间位置,试作其投影图,并写出各点的坐标值。仿照点A填写在括号内)
点A( 5 ,20 ,25) 点C(15 ,15 , 0)
点B( 10 ,15 , 0 ) 点D( 25 , 0 , 0 )
mm。 mm。 mm。该两点均在
投影面上。
7
2019年9月16日星 期一9时10分11秒
3-6 已知点B距离点A为10 mm;点C与点A是对H面的重影点;点D在点A的正 右方15 mm。补全诸点的三面投影,并标明可见性。
8
2019年9月16日星 期一9时10分11秒
3-7 求直线的第三投影,并判别其相对于投影面的位置,在投影图上反映 倾角实形处用α 、β 、γ 表示之。
注:本题有四解,可向左面画,也可向23 右面画,或向下画。
2019年9月16日星 期一9时10分11秒
3-19 已知等边三角形EFG是正平面,其上方顶点为E,下方的边FG为侧垂线, 边长为30 mm,补全该等边三角形EFG的两面投影。
分析 此题等边三角形为正平面,故 可知其V面投影反映实形,H面投 影积聚为一条直线,且FG边为侧垂 线。
作图步骤 1.在H投影面上过e点作fg线平行于
OX轴,使e=eg=15mm。 2.在V投影面上由e‘点作半径为
30mm的圆弧与f点和g点的投影 连线相交,所得交点即为f‘点和 g'点。
24
2019年9月16日星 期一9时10分11秒
3-20 已知铅垂面ABCD的一条对角线AC的两面投影,并且ABCD是正方形, 求该正方形的两面投影及该平面的倾角。
2019年9月16日星 期一9时10分11秒
11
3-9 由点A作直线AB与CD相交,交点B距离H面15 mm。
(1)
(2)
2019年9月16日星 期一9时10分11秒
12
3-10 已知直线上点K的H投影k,求k′。 (1)D (2)D
(1) (1)
(2) (2)
2019年9月16日星 期一9时10分11秒
3
2019年9月16日星 期一9时10分11秒
3-2 试作下列点的三面投影图和直观图。 点A的坐标为(10,10,10),点B的坐标为(20,15,0 ), 点C的坐标为(15,0 ,20),点D的坐标为( 0, 0,15)。
4
3-3 已知各点的两面投影,求作其第三投影。
2019年9月16日星 期一9时10分11秒
2019年9月16日星 期一9时10分11秒
16
2019年9月16日星 期一9时10分11秒
3-14 过点A作直线AB,使平行于直线DE;作直线AC使与直线DE相交,其交点距 V面为15mm。
17
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
2019年9月16日星 期一9时10分11秒
(1)
直线AB为
线
直线CD为
线
9
2019年9月16日星 期一9时10分11秒
3-7 求直线的第三投影,并判别其相对于投影面的位置,在投影图上反 映倾角实形处用α 、β 、γ 表示之。
(2)
直线EF为Leabharlann 线直线GH为线
10
3-8 求作下列直线的三面投影: (1)水平线AB从点A向右、向后,β =30°,长15 mm。 (2)正垂线CD从点C向前,长20 mm。
18
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
(1)
19
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。 (2)
作图步骤 1.过b′点任作一直线1=ba,在其上量取b′2=bk。
2.连接a′1,作2k′//a′1。
作图步骤 1.过d′点任作一直线d′3=dc,在其上 量取d′4=dk。
2.连接c′3,作4k′//3c′。
13
2019年9月16日星 期一9时10分11秒
3-11 已知直线AB的投影,试定出属于AB线段的点C的投影,使AC:CB=3:2, 并求AB和点C的W投影。
分析 (1)由已知条件知AC为水
平线,其水平投影ac反 映AC实长。 (2)正方形的对角线互相垂 直平分且相等,则其对 角线BD一定为铅垂线, 且其水平投影积聚为一 点位于ac的中点处,其V 面投影b'd'=ac。
5
2019年9月16日星 期一9时10分11秒
3-4 已知点A距离投影面W、V、H分别为20、15、25;点B在A之左10, A之前5,A之下15;点C在A之右5,A之后10,A之上5(单位:mm)。
6
3-5 判别下列各对重影点的相对位置并填空。
2019年9月16日星 期一9时10分11秒
1.点A在点B的 方 2.点D在点C的 方 3.点F在点E的 方
A面是
面
B面是
面
C面是
面
D面是
面
22
2019年9月16日星 期一9时10分11秒
3-18 过点A作矩形ABCD,短边AB=20mm且垂直于V面,长边BC=40mm,α =30°, 求作矩形ABCD的投影(求一解)。
分析: (1)由已知条件可知短边AB
为正垂线,故可作出短边 AB的两面投影。 (2)因矩形ABCD的短边AB为 正垂线,故可知矩形BCD 为正垂面,又因矩形的相 邻两边互相垂直故可知 AD和BC为正平线。
20
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α 、β 、γ 表示之。
(3)
21
2019年9月16日星 期一9时10分11秒
3-17 在投影图上用字符标出平面A、B、C、D的三面投影,并判别其相对投 影面的位置。
作图步骤: 1.任作一直线a′N,量取五单
位长,使 a′M:MN=3:2。 2.连接Nb′,作Mc′//Nb′ ,
得c′。 3.按点的投影规律作出c和
c′点,以及投影a"b"。
14
3-12 判断两直线的相对位置。
(1)
(2)
(3)
2019年9月16日星 期一9时10分11秒
(4)
15
3-13 作图判别直线AB与CD在空间的相对位置。
1
2019年9月16日星 期一9时10分11秒
2
2019年9月16日星 期一9时10分11秒
3-1 已知各点的空间位置,试作其投影图,并写出各点的坐标值。仿照点A填写在括号内)
点A( 5 ,20 ,25) 点C(15 ,15 , 0)
点B( 10 ,15 , 0 ) 点D( 25 , 0 , 0 )
mm。 mm。 mm。该两点均在
投影面上。
7
2019年9月16日星 期一9时10分11秒
3-6 已知点B距离点A为10 mm;点C与点A是对H面的重影点;点D在点A的正 右方15 mm。补全诸点的三面投影,并标明可见性。
8
2019年9月16日星 期一9时10分11秒
3-7 求直线的第三投影,并判别其相对于投影面的位置,在投影图上反映 倾角实形处用α 、β 、γ 表示之。
注:本题有四解,可向左面画,也可向23 右面画,或向下画。
2019年9月16日星 期一9时10分11秒
3-19 已知等边三角形EFG是正平面,其上方顶点为E,下方的边FG为侧垂线, 边长为30 mm,补全该等边三角形EFG的两面投影。
分析 此题等边三角形为正平面,故 可知其V面投影反映实形,H面投 影积聚为一条直线,且FG边为侧垂 线。
作图步骤 1.在H投影面上过e点作fg线平行于
OX轴,使e=eg=15mm。 2.在V投影面上由e‘点作半径为
30mm的圆弧与f点和g点的投影 连线相交,所得交点即为f‘点和 g'点。
24
2019年9月16日星 期一9时10分11秒
3-20 已知铅垂面ABCD的一条对角线AC的两面投影,并且ABCD是正方形, 求该正方形的两面投影及该平面的倾角。
2019年9月16日星 期一9时10分11秒
11
3-9 由点A作直线AB与CD相交,交点B距离H面15 mm。
(1)
(2)
2019年9月16日星 期一9时10分11秒
12
3-10 已知直线上点K的H投影k,求k′。 (1)D (2)D
(1) (1)
(2) (2)
2019年9月16日星 期一9时10分11秒
3
2019年9月16日星 期一9时10分11秒
3-2 试作下列点的三面投影图和直观图。 点A的坐标为(10,10,10),点B的坐标为(20,15,0 ), 点C的坐标为(15,0 ,20),点D的坐标为( 0, 0,15)。
4
3-3 已知各点的两面投影,求作其第三投影。
2019年9月16日星 期一9时10分11秒
2019年9月16日星 期一9时10分11秒
16
2019年9月16日星 期一9时10分11秒
3-14 过点A作直线AB,使平行于直线DE;作直线AC使与直线DE相交,其交点距 V面为15mm。
17
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
2019年9月16日星 期一9时10分11秒
(1)
直线AB为
线
直线CD为
线
9
2019年9月16日星 期一9时10分11秒
3-7 求直线的第三投影,并判别其相对于投影面的位置,在投影图上反 映倾角实形处用α 、β 、γ 表示之。
(2)
直线EF为Leabharlann 线直线GH为线
10
3-8 求作下列直线的三面投影: (1)水平线AB从点A向右、向后,β =30°,长15 mm。 (2)正垂线CD从点C向前,长20 mm。
18
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。
(1)
19
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上反映倾角 实形处用 α 、β 、γ 表示之。 (2)
作图步骤 1.过b′点任作一直线1=ba,在其上量取b′2=bk。
2.连接a′1,作2k′//a′1。
作图步骤 1.过d′点任作一直线d′3=dc,在其上 量取d′4=dk。
2.连接c′3,作4k′//3c′。
13
2019年9月16日星 期一9时10分11秒
3-11 已知直线AB的投影,试定出属于AB线段的点C的投影,使AC:CB=3:2, 并求AB和点C的W投影。
分析 (1)由已知条件知AC为水
平线,其水平投影ac反 映AC实长。 (2)正方形的对角线互相垂 直平分且相等,则其对 角线BD一定为铅垂线, 且其水平投影积聚为一 点位于ac的中点处,其V 面投影b'd'=ac。
5
2019年9月16日星 期一9时10分11秒
3-4 已知点A距离投影面W、V、H分别为20、15、25;点B在A之左10, A之前5,A之下15;点C在A之右5,A之后10,A之上5(单位:mm)。
6
3-5 判别下列各对重影点的相对位置并填空。
2019年9月16日星 期一9时10分11秒
1.点A在点B的 方 2.点D在点C的 方 3.点F在点E的 方
A面是
面
B面是
面
C面是
面
D面是
面
22
2019年9月16日星 期一9时10分11秒
3-18 过点A作矩形ABCD,短边AB=20mm且垂直于V面,长边BC=40mm,α =30°, 求作矩形ABCD的投影(求一解)。
分析: (1)由已知条件可知短边AB
为正垂线,故可作出短边 AB的两面投影。 (2)因矩形ABCD的短边AB为 正垂线,故可知矩形BCD 为正垂面,又因矩形的相 邻两边互相垂直故可知 AD和BC为正平线。
20
2019年9月16日星 期一9时10分11秒
3-16 求平面的第三投影,并判别其相对投影面的位置,在投影图上 反映倾角实形处用 α 、β 、γ 表示之。
(3)
21
2019年9月16日星 期一9时10分11秒
3-17 在投影图上用字符标出平面A、B、C、D的三面投影,并判别其相对投 影面的位置。
作图步骤: 1.任作一直线a′N,量取五单
位长,使 a′M:MN=3:2。 2.连接Nb′,作Mc′//Nb′ ,
得c′。 3.按点的投影规律作出c和
c′点,以及投影a"b"。
14
3-12 判断两直线的相对位置。
(1)
(2)
(3)
2019年9月16日星 期一9时10分11秒
(4)
15
3-13 作图判别直线AB与CD在空间的相对位置。
