弧长、弦长与扇形面积、弓形面积案例教学设计
九年级数学上册《弧长和扇形面积》教案、教学设计

九年级的学生已经具备了一定的数学基础和逻辑思维能力,能够理解并运用基本的几何概念和公式。在《弧长和扇形面积》这一章节中,学生将通过之前的学习,对圆的相关性质有了一定的了解,这为学习弧长和扇形面积打下了基础。然而,由于弧长和扇形面积的计算涉及圆心角、半径等多个变量,学生可能在综合运用这些知识解决实际问题时遇到困难。因此,在教学过程中,教师应关注以下几点:
3.能够通过实际操作,如使用量角器、圆规等工具,测量并计算出具体物体的弧长和扇形面积。
4.掌握弧长和扇形面积单位换算,能够灵活地在不同场景下应用。
(二)过程与方法
在教学过程中,教师将采用以下方法,帮助学生达成学习目标:
1.引导学生通过观察、探索、实践等活动,发现弧长和扇形面积的规律,培养学生的观察能力和探究精神。
-创设问题情境,鼓励学生提出问题、分析问题、解决问题,培养学生的批判性思维和创新意识。
-实施分层教学,为不同水平的学生提供不同难度的任务,确保每个学生都能在自身基础上得到提升。
-引入项目式学习,让学生在完成具体项目任务的过程中,将所学知识综合运用,提高解决实际问题的能力。
3.教学评价的设想:
-采用多元化的评价方式,包括课堂问答、小组讨论表现、课后作业、项目报告等,全面评估学生的学习效果。
-设计一些简单的实际应用题,如计算某段弧的长度、给定半径和圆心角的扇形面积,让学生运用公式进行解答。
2.提高拓展题:
-布置一些综合性的题目,如计算由多个扇形或不规则图形组成的总面积,要求学生结合所学知识,分析问题并给出解题步骤。
-鼓励学生尝试运用弧长和扇形面积的知识解决生活中的实际问题,如园林设计、建筑布局等。
-探究阶段:组织学生进行小组合作,利用教具和信息技术工具,探索圆心角、半径与弧长、扇形面积的关系,引导学生发现并理解计算公式。
《弧长和扇形面积》教学设计方案

《弧长和扇形面积》教学设计方案《《弧长和扇形面积》教学设计方案》这是优秀的教学设计文章,希望可以对您的学习工作中带来帮助!学习主题介绍学习主题名称:《弧长和扇形面积》主题内容简介:《弧长和扇形面积》是人教版九年级上册第二十四章24.4的内容,在此之前,学生已经学习了“圆的认识”、“与圆有关的位置关系”、“圆内接正多边形”等基础知识,让学生具备推导出弧长和扇形面积的计算公式的奠定了基础。
,这为过渡到本节课的学习起着铺垫作用。
本节内容是本章《圆》的重点计算方面内容,是本章的一个教学难点。
它可以强化学生对前面所学知识的理解,使学生对研究圆的性质的基本方法有一个初步的认识与了解,为后面计算扇形面积、圆锥侧面积表面积等有关问题奠定基础。
学习目标分析知识与技能:1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力。
2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题,训练学生的数学应用能力。
过程与方法:1.经历探索的课堂活动模式,富有情趣的体验知识的形成过程,在体验中感受数学。
2.使学生了解公式的同时,体验公式的变式,使学生在合作与竞争中形成良好的数学品质。
情感、态度与价值观:引导学生体验数学与人类生活的密切联系,激发学生学习数学的兴趣,体验学习乐趣,培养良好的学习品质。
学情分析前需知识掌握情况:1、学生的知识技能基础:学生从孩提时代的感觉圆形,到小学的认识圆形,学习过圆周长和面积公式,而这个课题学生在前阶段学完了“圆的认识”、“与圆有关的位置关系”、“圆内接正多边形”的基础上进行的,让学生具备推导出弧长和扇形面积的计算公式的奠定了基础。
2、学生活动经验基础:在相关知识的学习过程中,学生已经经历参与研究探索的情感体验, 自主探索的能力;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
对微课的认识:对于农村的中学生而言,微课对大家来讲比较陌生的,之前还没接触过微课。
九年级数学上册(人教版)24.4弧长与扇形面积(第一课时)优秀教学案例

4.多元化的教学评价:我采用了多元化评价方式,关注学生的学习过程和能力发展。这种评价方式,使评价更加公平、合理,能够更好地激发学生的学习兴趣和动力。
2.小组展示:各小组将解决问题的过程和结果进行展示,其他小组进行评价和补充,促进学生之间的互动和交流。
(四)反思与评价
1.学生自我评价:学生在课后进行自我反思,总结自己在课堂上的学习情况和收获,提高自我认识和自我调节能力。
2.同伴评价:学生之间进行相互评价,给出建设性的意见和建议,促进彼此的学习和进步。
(三)学生小组讨论
1.分组讨论:我将学生分成若干小组,让学生针对具体实例,讨论如何运用弧长和扇形面积的计算公式解决问题。
2.分享讨论成果:各小组将讨论的成果进行分享,其他小组进行评价和补充,促进学生之间的互动和交流。
(四)总结归纳
1.公式总结:引导学生总结弧长和扇形面积的计算公式,加深学生对知识点的记忆和理解。
五、案例亮点
1.生活情境的创设:通过展示地球仪、体育场的跑道等生活中常见的弧形物体,我成功吸引了学生的注意力,让他们感受到弧形在现实生活中的广泛应用。这种生活情境的创设,使学生能够更好地理解弧长和扇形面积的概念,并激发他们学习数学的兴趣。
2.问题导向的教学策略:我设计了一系列具有启发性的问题,引导学生独立思考和探究,激发他们的学习欲望。这种问题导向的教学策略,使学生在解决问题的过程中,能够更好地理解和掌握弧长和扇形面积的计算公式。
在教学过程中,我注重启发式教学,引导学生从实际问题中抽象出数学模型,培养学生运用数学知识解决实际问题的能力。同时,我还结合多媒体教学手段,利用动画、图片等直观展示弧长和扇形面积的计算过程,降低学生的学习难度,提高学习效果。
弧长与扇形的面积教案

弧长与扇形的面积教案一、教学目标1. 理解弧长的概念和计算方法。
2. 掌握扇形面积的计算方法。
3. 能够应用弧长和扇形面积的知识解决实际问题。
二、教学内容1. 弧长的概念和计算方法。
2. 扇形面积的计算方法。
3. 弧长和扇形面积的应用。
三、教学过程1. 导入老师通过引入一道实际问题,如一个半径为10cm的圆的一条弧长为15cm,问这条弧长对应的圆心角是多少度,让学生思考并尝试解答。
2. 弧长的概念和计算方法(1)引导学生观察圆的弧形和其中一个弧长,进一步培养学生对弧的直观感受。
(2)让学生尝试用圆的半径和圆心角来计算弧长,通过实际测量验证计算结果的准确性。
(3)总结弧长的计算方法(弧长 = 半径×圆心角 / 360°),并让学生进行练习。
3. 扇形面积的计算方法(1)引导学生观察一个扇形和其对应的圆,进一步培养学生对扇形的直观感受。
(2)让学生尝试用圆的半径和圆心角来计算扇形的面积,通过实际测量验证计算结果的准确性。
(3)总结扇形面积的计算方法(扇形面积 = 1/2 ×半径×半径×圆心角 / 360°),并让学生进行练习。
4. 弧长和扇形面积的应用(1)导入一个实际问题:一个圆形花坛的周长为30米,花坛中心的喷泉水按每秒60毫升的速度喷出,问这个喷泉每分钟喷水多少升?(2)引导学生分析问题,并利用已学知识解答问题。
(3)通过解答问题,让学生认识到弧长和扇形面积在解决实际问题中的应用价值。
五、教学总结1. 弧长是圆的一部分长度,可以用圆的半径和圆心角来计算。
2. 扇形是圆的一部分面积,可以用圆的半径和圆心角来计算。
3. 弧长和扇形面积的计算方法是由圆的半径和圆心角决定的。
4. 弧长和扇形面积的知识在解决实际问题中有很大的应用价值。
六、教学延伸1. 可以引导学生查找更多弧长和扇形面积的实际应用例子,并进行讨论和分享。
2. 可以设计更多扩展题目和实践任务,让学生更加熟练运用弧长和扇形面积的知识。
弧长及扇形的面积教学设计及反思

弧长及扇形的面积教学设计及反思教学目标(一)教学知识点1.经历探索弧长计算公式及扇形面积计算公式的过程;2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题.(二)能力训练要求1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.2.了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.(三)情感与价值观要求1.经历探索弧长及扇形面积计算公式,让学生体验教学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性.2.通过用弧长及扇形面积公式解决实际问题,让学生体验数学与人类生活的密切联系,激发学生学习数学的兴趣,提高他们的学习积极性,同时提高大家的运用能力.教学重点1.经历探索弧长及扇形面积计算公式的过程.2.了解弧长及扇形面积计算公式.3.会用公式解决问题.教学难点1.探索弧长及扇形面积计算公式.2.用公式解决实际问题.教学方法学生互相交流探索法教具准备:圆规,三角尺,圆锥教学过程Ⅰ.创设问题情境,引入新课[师]在小学我们已经学习过有关圆的周长和面积公式,弧是圆周的一部分,扇形是圆的一部分,那么弧长与扇形面积应怎样计算?它们与圆的周长、圆的面积之间有怎样的关系呢?本节课我们将进行探索.Ⅱ.新课讲解一、复习1.圆的周长如何计算?2.圆的面积如何计算?3.圆的圆心角是多少度?[生]若圆的半径为r,则周长l=2πr,面积S=πr2,圆的圆心角是360°.二、探索弧长的计算公式活动一如图,某传送带的一个转动轮的半径为10cm.(1)转动轮转一周,传送带上的物品A被传送多少厘米?(2)转动轮转1°,传送带上的物品A被传送多少厘米?(3)转动轮转n°,传送带上的物品A被传送多少厘米?[师]分析:转动轮转一周,传送带上的物品应被传送一个圆的周长;因为圆的周长对应360°的圆心角,所以转动轮转1°,传送带上的物品A被传送圆周长的;转动轮转n°,传送带上的物品A被传送转1°时传送距离的n倍.[生]解:(1)转动轮转一周,传送带上的物品A被传送2π×10=20πcm;(2)转动轮转1°,传送带上的物品A被传送 cm;(3)转动轮转n°,传送带上的物品A被传送n×=cm.[师]根据上面的计算,你能猜想出在半径为R的圆中,n°的圆心角所对的弧长的计算公式吗?请大家互相交流.[生]根据刚才的讨论可知,360°的圆心角对应圆周长2πR,那么1°的圆心角对应的弧长为,n°的圆心角对应的弧长应为1°的圆心角对应的弧长的n倍,即n×.[师]表述得非常棒.在半径为R的圆中,n°的圆心角所对的弧长(arclength)的计算公式为:l=.下面我们看弧长公式的运用.三、例题讲解制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即的长(结果精确到0.1mm).分析:要求管道的展直长度,即求的长,根根弧长公式l=可求得的长,其中n为圆心角,R为半径.解:R=40mm,n=110.∴的长=πR=×40π≈76.8mm.因此,管道的展直长度约为76.8mm.四、想一想活动1在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.(1)这只狗的最大活动区域有多大?(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?[师]请大家互相交流.[生](1)如图(1),这只狗的最大活动区域是圆的面积,即9π;(2)如图(2),狗的活动区域是扇形,扇形是圆的一部分,360°的圆心角对应的圆面积,1°的圆心角对应圆面积的,即×9π=,n°的圆心角对应的圆面积为n×=.[师]请大家根据刚才的例题归纳总结扇形的面积公式.[生]如果圆的半径为R,则圆的面积为πR2,1°的圆心角对应的扇形面积为,n°的圆心角对应的扇形面积为n·.因此扇形面积的计算公式为S扇形=πR2,其中R为扇形的半径,n为圆心角.五、弧长与扇形面积的关系[师]我们探讨了弧长和扇形面积的公式,在半径为R的圆中,n°的圆心角所对的弧长的计算公式为l=πR,n°的圆心角的扇形面积公式为S扇形=πR2,在这两个公式中,弧长和扇形面积都和圆心角n.半径R有关系,因此l和S之间也有一定的关系,你能猜得出吗?请大家互相交流.[生]∵l=πR,S扇形=πR2,∴πR2=R·πR.∴S扇形=lR.六、扇形面积的应用活动3扇形AOB的半径为12cm,∠AOB=120°,求的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2)分析:要求弧长和扇形面积,根据公式需要知道半径R和圆心角n即可,本题中这些条件已经告诉了,因此这个问题就解决了.解:的长=π×12≈25.1cm.S扇形=π×122≈150.7cm2.因此,的长约为25.1cm,扇形AOB的面积约为150.7cm2.Ⅲ.课堂练习随堂练习Ⅳ.课时小结本节课学习了如下内容:1.探索弧长的计算公式l=πR,并运用公式进行计算;2.探索扇形的面积公式S=πR2,并运用公式进行计算;3.探索弧长l及扇形的面积S之间的关系,并能已知一方求另一方.Ⅴ.课后作业习题3.10教学反思:本节课充分准备比较,教师学生都能做好各种准备工作,因此课堂效果较好。
弧长和扇形面积(教案)

教案:弧长和扇形面积教学目标:1. 理解弧长的概念及计算方法。
2. 掌握扇形面积的计算公式。
3. 能够运用弧长和扇形面积的知识解决实际问题。
教学重点:1. 弧长的计算。
2. 扇形面积的计算。
教学难点:1. 弧长的计算公式的应用。
2. 扇形面积的计算公式的应用。
教学准备:1. 课件或黑板。
2. 教学卡片。
3. 练习题。
教学过程:一、导入(5分钟)1. 引导学生回顾圆的周长公式:C = 2πr。
2. 提问:如果我们知道圆的半径,如何计算圆的周长呢?二、新课:弧长(10分钟)1. 引入弧长的概念:在圆上,弧长是指连接圆上两点之间的部分的长度。
2. 解释弧长的计算方法:弧长= 圆心角/ 360°×2πr。
3. 示例:给定一个半径为5cm的圆,圆心角为90°,计算弧长。
三、练习:弧长的计算(10分钟)1. 学生独立完成练习题,老师巡回指导。
2. 选取部分学生的作业进行讲解和点评。
四、导入扇形面积的概念(5分钟)1. 引入扇形面积的概念:扇形面积是指圆心角所对应的圆弧与半径所围成的区域的面积。
2. 提问:扇形面积与圆的面积有何关系?五、新课:扇形面积的计算(10分钟)1. 解释扇形面积的计算公式:扇形面积= (圆心角/ 360°) ×πr²。
2. 示例:给定一个半径为5cm的圆,圆心角为90°,计算扇形面积。
3. 强调扇形面积与圆心角的关系:圆心角越大,扇形面积越大。
教学反思:本节课通过引入弧长和扇形面积的概念,让学生掌握了弧长和扇形面积的计算方法。
在教学过程中,通过示例和练习题的讲解,帮助学生理解和应用知识点。
在今后的教学中,可以结合实际问题,让学生更好地运用弧长和扇形面积的知识。
六、练习:弧长和扇形面积的综合应用(10分钟)1. 学生独立完成综合练习题,老师巡回指导。
2. 选取部分学生的作业进行讲解和点评。
七、课堂小结(5分钟)1. 回顾本节课所学内容:弧长的计算方法和扇形面积的计算方法。
《弧长和扇形面积(第一课时)》教案
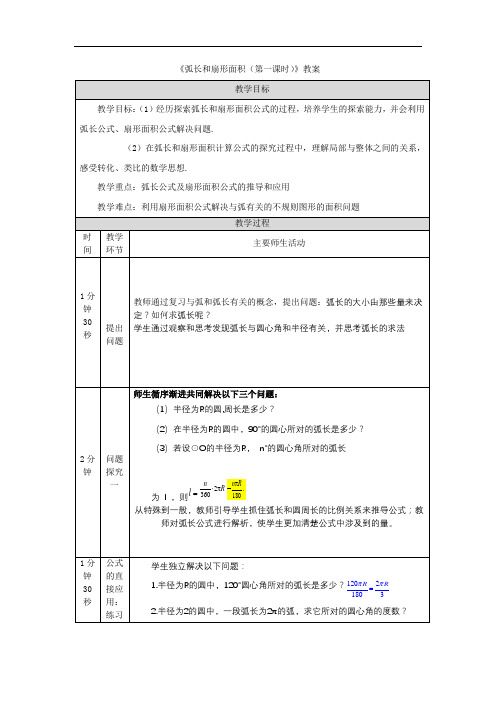
《弧长和扇形面积(第一课时)》教案1.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度教师引导同学们先观察思考一下:要这个弯形管道的展直长度包括哪些部分?进而求弧AB 长公式求解。
例2. 圆心, OA 教师引导学生观察共同总结出扇形的几何定义;(1)扇形的面积由哪些量决定?(2)如何求扇形的面积呢?学生通过前面弧长公式的学习,类比思考扇形面积的求法180n R l π=R 100°AOn °OB学生尝试独立解决以下问题:(1)半径为R的圆,面积是多少?(2)若设⊙O的半径为R,圆心角为n°的扇形面积为类比弧长公式的推导过程,得到扇形面积公式;教师对扇形面积公式进行解析,使学生更加清楚公式中涉及到的量。
例3. 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。
(精确到0.01m2)。
教师引导学生通过读题和识图,需要把文字语言和图形语言对应起来,排水管道的截面就是图中的圆.把已知条件转化成几何元素标在图上,进而分析出所求面积= S扇形OAB-S△OAB进而分别去求扇形和三角形的面积.教师引导学生求扇形和三角形时需要的量,如何得到?最终解决问题。
知能演练提升一、能力提升1.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )A.πB.1C.2D.2π32.如图,在扇形OAB 中,已知∠AOB=90°,OA=√2,过AB ⏜的中点C 作CD ⊥OA ,CE ⊥OB ,垂足分别为D ,E ,则图中阴影部分的面积为( )A.π-1B.π2-1C.π-12D.π2−12⏜上一点,CD⊥OA,CE⊥3.如图,半径为10的扇形AOB中,∠AOB=90°,C为ABOB,垂足分别为D,E.若∠CDE为36°,则图中阴影部分的面积为()A.10πB.9πC.8πD.6π4.如图,水平地面上有一面积为30π cm2的扇形OAB,半径OA=6 cm,且OA与地面垂直.在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O 移动的距离为()A.20 cmB.24 cmC.10π cmD.30π cm5.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在以五边形各顶点为圆心,2 m长为半径的扇形区域(阴影部分)内种上花草,那么种上花草的扇形区域总面积是()A.6π m2B.5π m2C.4π m2D.3π m26.如图,△ABC是正三角形,曲线CDE……叫做“正三角形的渐开线”,其中CD⏜,DE⏜,EF⏜……的圆心依次按A,B,C循环,它们依次相连接,若AB=1,则曲线CDEF 的长是.7.如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长⏜的长为半径画弧,分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则EF为.(结果保留π)⏜是一段圆弧,AC,BD是线段,8.图中的粗线CD表示某条公路的一段,其中AmB⏜相切于点A,B,线段AB=180 m,∠ABD=150°.且AC,BD分别与圆弧AmB⏜的圆心O;(1)画出圆弧AmB(2)求A到B这段弧形公路的长.★9.如图,AB为☉O的直径,CD⊥AB,OF⊥AC,垂足分别为E,F.(1)请写出三条与BC有关的正确结论;(2)当∠D=30°,BC=1时,求圆中阴影部分的面积.二、创新应用★10.图①是某学校存放学生自行车的车棚的示意图(尺寸如图),车棚顶部⏜所在是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部截面的示意图,AB圆的圆心为O.车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)知能演练·提升 一、能力提升1.C 使用扇形的面积公式S=12lR 可求出其面积,即S=12×2×2=2. 2.B 3.A4.C 点O 移动的距离即扇形OAB 所对应的弧长,先运用扇形的面积公式S 扇形=nπR 2360求出扇形的圆心角n=300°,再由弧长公式l=nπR180,得l=10π cm .5.A6.4π 关键是确定圆心角和半径.因为△ABC 是边长为1的正三角形,所以CD⏜,DE ⏜,EF ⏜的圆心角都为120°,对应的半径分别为1,2,3. 因此CD ⏜=2π3,DE ⏜=4π3,EF ⏜=6π3=2π.所以曲线CDEF 的长是2π3+4π3+2π=4π. 7.π28.解 (1)如图,过点A 作AO ⊥AC ,过点B 作BO ⊥BD ,AO 与BO 相交于点O ,O 即为圆心.(2)因为AO ,BO 都是圆弧AmB ⏜ 的半径,O 是其所在圆的圆心, 所以∠OBA=∠OAB=150°-90°=60°. 所以△AOB 为等边三角形, 即AO=BO=AB=180 m . 所以AB⏜=60×π×180180=60π(m),即A 到B 这段弧形公路的长为60π m .9.解 (1)答案不唯一,只要合理均可.例如: ①BC=BD ;②OF ∥BC ; ③∠BCD=∠A ; ④BC 2=CE 2+BE 2; ⑤△ABC 是直角三角形;⑥△BCD 是等腰三角形.(2)连接OC (图略),则OC=OA=OB.∵∠D=30°,∴∠A=∠D=30°. ∴∠AOC=120°. ∵AB 为☉O 的直径, ∴∠ACB=90°.在Rt △ABC 中,BC=1,∴AB=2,AC=√3. ∵OF ⊥AC ,∴AF=CF. ∵OA=OB ,∴OF 是△ABC 的中位线. ∴OF=12BC=12.∴S △AOC =12AC ·OF=12×√3×12=√34,S 扇形AOC =13π·OA 2=π3.∴S 阴影=S 扇形AOC -S △AOC =π3−√34.二、创新应用10.分析 车棚的顶棚的展开图是矩形,顶棚的横截面是弓形,求出弓形的弧长,即得到了展开图的宽.解 连接OB ,过点O 作OE ⊥AB ,垂足为点E ,并延长交AB⏜于点F ,如图.由垂径定理,知E 是AB 的中点,F 是AB ⏜的中点,从而EF 是弓形的高. 故AE=12AB=2√3 m,EF=2 m . 设半径为R m, 则OE=(R-2)m .在Rt △AOE 中,由勾股定理, 得R 2=(R-2)2+(2√3)2. 解得R=4(m). 在Rt △AEO 中,AO=2OE ,故∠OAE=30°,∠AOE=60°,∠AOB=120°. 所以AB⏜的长为120×4π180=8π3(m). 即帆布的面积为8π3×60=160π(m 2).。
九年级数学下册《弧长和扇形的面积》教案、教学设计

1.引入环节:
利用生活中的实例,如圆蛋糕、时钟等,引导学生观察并思考其中所包含的扇形元素,从而自然引入本章节的学习内容。
2.新课导入:
(1)通过复习圆的相关知识,如周长、面积等,为新课的学习做好铺垫。
(2)以问题驱动的形式,让学生自主探究扇形的定义、性质,培养学生的探究意识。
3.知识讲解:
鼓励学生发挥想象,设计一道具有创意的扇形相关问题,并尝试运用所学知识进行解答。
作业要求:
1.认真完成作业,注意书写规范,保持卷面整洁。
2.对于实践应用题和拓展提高题,要求学生详细阐述解题思路,展示解题过程。
3.小组合作题需充分发挥团队协作精神,共同完成任务。
4.作业完成后,及时进行自我检查,发现问题并及时改正。
3.拓展提高题:
(1)探究扇形的对称性质,并运用对称性质解决相关问题。
(2)研究扇形与三角形、矩形等图形的面积关系,推导相关公式。
4.小组合作题:
以小组为单位,共同探讨以下问题:
(1)扇形在生活中的应用,以及如何利用扇形优化设计。
(2)比较不同扇形面积与半径、圆心角的关系,总结规律。
5.创新思维题:
3.教师指导:
教师巡回指导,关注各小组的讨论进度,给予适当的提示和指导,引导学生深入思考。
(四)课堂练习
1.教学活动设计:
设计具有层次性和挑战性的练习题,让学生独立完成,巩固所学知识。
2.练习题类型:
(1)基础题:计算给定圆心角和半径的扇形的弧长和面积。
(2)提高题:解决实际问题,如计算河流的弯曲长度、不规则图形的面积等。
4.引导学生认识到数学在生活中的广泛应用,体会数学的价值,培养学生的数学素养。
二、学情分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学案例教学题目:弧长、弦长与扇形面积、弓形面积案例教学设计作者:左春香王瑞霞单位:唐山市丰南区职教中心教学内容分析:下料问题是机械专业每天都要遇到的实际生产问题。
经常要遇到的是长度、周长、弧长、弦长、扇形、弓形面积和各种体积重量的计算等数学知识。
本节数学课紧密地和生产实习的实例相联系,学生经过自己充分地思考和讨论后,能够更深刻地理解和记忆公式,掌握数学知识在专业生产中的应用。
教学目的:(1)通过学习掌握圆周长、弧长、弦长、扇形面积和弓形的面积的计算。
(2)能熟练运用所学的数学知识解决机械专业中气割、钳工、钣金等工种的计算和下料等实际问题。
教学重点:弧长、弦长、扇形面积、弓形面积的计算。
实际生产问题和数学问题的联系。
课时:2课时教学方法:讲练结合、理论联系实际教学用具:投影仪、黑板、硬纸板做成的两个防护罩和一个圆锥形的烟囱帽、胶片7张,如下所示:教学过程:[投影本节课的学习目标][出示胶片1]案例引入:[出示胶片2](并用硬纸板按尺寸或比例做两个模型向学生展示,让学生边观察边回答问题)。
提出问题:[单独提问][师]:左图中有几个侧面?是什么形状?[生甲]:3个,A和B是扇形的一部分,展开后C可能是矩形。
[师]:回答得很正确,如何计算各侧面的面积和全面积?[生乙]:要计算它的侧面积需要掌握扇形的面积公式,全面积当然就是矩形面积和另两个侧面积之和。
[师]:有道理,可是,你知道那个矩形的长是多少吗?如何计算?[生丙]:要计算它的长度还需要掌握弧长公式。
[师]:右图中的前后侧面是什么形状?它的面积如何计算?[生丙]:前后侧面是弓形[师]:用气割方法下料时气割长度各是多少应如何计算?[生丁]:是各面边线长度的总和。
引入数学知识:[师]:要解决这些问题,要用到数学中,弧长、弦长、扇形的面积的计算等。
这次课我们就介绍这些知识,同时,共同探讨一下机械专业中有关的下料问题复习导入:[出示胶片3][生]:气割长度为大圆和小圆的周长之和。
L=π×250+π×1500=1750π=5497.8mm[师]:刚才这个问题中,复习了圆周长计算公式:[板书]:圆的周长:L=πd=2πr(d为直径)[出示胶片4][师]:这个长度还是一个完整的周长吗?[生]:答:不是。
[师]:请同学们看图,在轮缘上和轮毂上两个辐条中心的部分是什么图形?[生]: 是圆弧。
[师]: 弧的长度应如何计算?本节课我们先研究这个问题。
[板书]: 一、弧长[师]:360o 的圆心角所对的弧长就是圆周长L=πd=2πr ,那么1o 的圆心角所对的弧长是 多少? [生]:2π360r = π180r[师]:于是可得半径为r (直径为d )的圆中,αo 的圆心角所对的弧长L n 的计算公式: 是什么? [生]: L n =π180r α=π360dα[板书]: 360o 的圆心角所对的弧长即圆周长 L=πd=2πr ,1o 的圆心角所对的弧长是2π360r = π180r。
半径为r (直径为d )的圆中,αo 的圆心角所对的弧长 L n =π180rα =π360dα[师]: 有了弧长公式,例1中的问题可迎刃而解了。
[经学生讨论后得出结论并找学生板演]例1 解:两根辐条间所夹的圆心角α=12360=30o ,轮缘上两根辐条中心距弧长L α1=1π30360d =π160012⨯=418.88mm 轮毂上相邻辐条中心距弧长 L α2=2π30360d =π35012⨯=91.63mm [师]: 事实上弧与角很难测量,故实际工作中常以弦长为检验尺寸,在一圆周上n 等分,求弦长就是圆的内接正n 边形的边长。
那么弦长如何计算呢? [[师生共同分析]:∵在Rt △BOC 中,∠BOC=2α,BC=2L , ∴ rL2 = r L 2 = sin 2α∴L=2r sin 2α=d sin 2α[板书]:二、弦长公式由 r L2 = r L 2 = sin 2α得αo 的圆心角所对的弦长L=2r sin2α=d sin 2α其中圆心角α=n 360,则L=dsin n180.[师] 那么例1中若求轮缘和轮毂上的中心距弦长如何计算?[找学生板演] [生] 解:设它们分别为l 1和l 2,则l 1=d 1sin 12180=1600×sin15o =414.11mml 2= d 2sin 12180=350×sin15o =90.59mm评注: 如果再求两辐条间间隙距离,只要把上面的值分别减去φ25mm 即可。
[出示胶片6][师] 通过观察,我们看出这块钢板面是什么图形? [生] 大扇形中去掉了一个小扇形。
[师] 那么我们要求钢板的面积,就得知道扇形的面积如何计算,下面我们探讨扇形的面积公式。
同学们知道扇形是什么图形的一部分吗?[生甲] 圆的一部分。
[师] 整个圆的圆心角是多少度? [生] 360o[师] 再接着想一想,在半径为r 的圆中,圆心角为1o 的扇形的面积是多少?[生] 2π360r[师] 那么圆心角为αo 的扇形的面积是多少? [生]2π360r α[板书] 三、扇形面积公式由圆心角为1o的扇形面积 2π360r得圆心角为αo的扇形面积公式为 2π360r S α=扇[师] 弧长公式与扇形面积公式有什么关系? [生] 两公式中都含有π180rα= L n 。
[师] 那么我们又得出了扇形的另一个面积公式为: [生] S =21L n r (教师板书添上此公式) S 扇 = 3602r απ =21L n r[师] 有了这个公式,上面的问题就很简单了(请一位同学板演)。
解:钢板的面积S=2π360rα=)64620(36014.37222-⨯=238952mm2=0.239m2[出示胶片7][师] 上面三个图中阴影部分是什么图形呢?这三个图形都是弓形,它和我们看到的哪件物品有关系?[生] 它和第二个防护罩的侧面是一种图形。
[师] 可见要解决开始提出的问题,我们还得学习弓形的面积公式。
同学们接着观察上面的三个图形中,弓形的面积和扇形的面积有何关系?[生] 把扇形OAmB的面积以及△OAB的面积计算出来,就可以得到弓形的面积,图(1)中,弓形AmB的面积小于半圆的面积,这时S弓形=S扇-S△ABC,图(2)中,弓形AmB的面积大于半圆的面积,这时S弓形=S扇+S△ABC,图(3)中,弓形AmB的面积等于半圆的面积,这时S弓形=21S圆。
[板书] 四、弓形面积公式(1)弓形AmB的面积小于半圆的面积,这时S弓形=S扇-S△ABC,(2)弓形AmB的面积大于半圆的面积,这时S弓形=S扇+S△ABC,(3)弓形AmB的面积等于半圆的面积,这时S弓形=21S圆。
[师] 同学们,通过我们共同探讨和总结得出了哪些结论呢?[生] 弧长公式、弦长公式、扇形面积公式、弓形面积公式。
[师] 我们掌握了这些知识是非常重要的,而且有些公式不可死记,要理解它的推导过程,同时可以促进我们逻辑推理能力的提高。
当然,也可以很容易地解决本次课开始提出的问题了。
[出示胶片2]并展开硬纸片做成的模型(1),把各个面展示给学生,让学生求其全面积,(学生板演)。
解:S侧=2135π480360⨯⨯-2135π85360⨯⨯= 262788.56 mm2S全=2×S侧+120×2135π480360⨯⨯=593401.12 mm2展开模型(2),让学生求其侧面积,学生板演。
解:S侧=2135π400360⨯⨯-21× 2×400sin2135O= 131840mm2[课下思考题][师] [拿出做好的烟囱帽模型],这是一个做好烟囱帽模型,谁能看出它是什么形状?[生] 是圆锥形。
[师] 如果沿一条母线展开这个模型,展开后是什么形状呢?[沿一条母线展开这个模型][生] 是扇形。
[师] 如果已知这个圆锥形的底边周长和母线长,要用铁片做一个烟囱帽,应如何下料?留作课下思考。
本节小结:通过本次课的学习,大家应理解对弧长公式,弦长公式,扇形面积公式,弓形面积公式的推导,识记这些公式,并会灵活的应用到实际生活、生产中。
板书设计:布置作业: 1.要气割一块如图(1)所示的钢板求气割的总长度。
2.型钢横断面如图(2)所示,求其面积。
(1)(2)3.连接件样板如图(3)所示,求样板面积。
4.防护罩如图(4)所示,求其侧面积。
(3)(4)。
