复合材料细观有限元分析专题.
复合材料用有限元分析

复合材料用有限元分析引言复合材料是由不同类型的材料组合而成的,具有优异的力学性能和轻质化的特点,在航空航天、汽车工程、建筑结构等领域得到广泛应用。
有限元分析是一种常用的工程分析方法,可用于预测复合材料结构在受力过程中的应力和变形情况。
本文将介绍复合材料用有限元分析的基本原理、建模过程、分析方法和结果解读。
有限元分析基本原理有限元分析基于有限元法,将复杂的结构分割成许多简单的单元,再利用数学方法求解这些单元的力学行为,最终得出整个结构的应力和变形情况。
复合材料的有限元分析一般采用3D固体单元或板单元,考虑复合材料的各向异性和层合板的分层结构。
有限元分析的基本原理可以总结为以下几个步骤:1.确定有限元模型:–根据复合材料结构的几何形状和材料性质,选择适当的有限元单元类型。
–确定网格划分方案,将结构划分为单元网格。
–确定边界条件和加载方式,包括约束条件和外部加载。
2.确定单元性质:–根据复合材料的材料力学性质,将其转化为有限元单元的材料刚度矩阵。
–考虑各向异性和分层结构,将材料刚度矩阵进行相应的转换。
3.确定单元相互连接关系:–根据结构的几何体系,确定单元之间的连接关系,包括单元之间的约束和边界条件。
4.求解方程组:–根据单元的刚度矩阵和边界条件,建立整个结构的刚度矩阵。
–考虑加载情况,求解结构的位移和应力。
5.结果后处理:–分析结构的应力和变形分布,评估结构的安全性和性能。
–对结果进行解读和优化。
复合材料有限元分析的建模过程复合材料的有限元分析建模过程与传统材料的有限元分析类似,但在材料性质和单元连接方面存在一些特殊性。
下面是复合材料有限元分析的建模过程的简要步骤:1.几何建模:–根据实际结构的几何形状,利用建模软件(如Solidworks或CATIA)进行3D建模。
–根据复合材料的分层结构,将各层材料的几何形状分别绘制。
2.材料定义:–根据复合材料的材料属性,定义合适的材料模型和参数。
–考虑复合材料的各向异性和分层结构,定义材料的力学参数。
复合材料多墙盒段的有限元分析
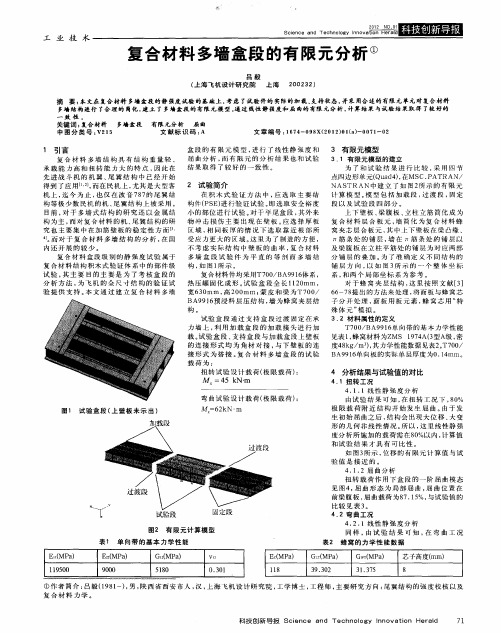
2 试验简 介
在 积 木 式 验 证 方 法 中 , 选 取 主 要 结 应 构 件( S 进 行 验 证 试验 。 P E) 即选 取 安 全 裕 度 小 的 部 位进 行试 验 。 对于 平 尾盒 段 , 外 来 其 物 冲 击 损 伤 主 要 出 现 在 壁 板 。 选 择 厚 板 应 区 域 , 同 板 厚 的 情 况 下 选 取 靠 近 根 部 所 相 受应力更大的区域。 这里 为 了 制造 的 方 便 , 不 考 虑 实 际 结 构 中 壁 板 的 曲 率 , 合 材 料 复 多 墙 盒 段 试 验 件 为 平 直 的 等 剖 面 多 墙 结 构 , 图1 示 。 如 所 复合材 料 件均 采用T7 0 0 /BA9 6 系 , 91 体 热 压 罐 固化 成 形 。 验 盒 段 全 长 1 0 m , 试 1 r 2a 宽6 0 3 mm , 2 0 高 0 mm ; 皮 和 粱 为 T7 0 蒙 0/ B 9 6 浸 料 层 压 结 构 , 为 蜂 窝夹 层 结 A9 1 预 墙
M , 4 k ・ = 5 N m
上 下 壁 板 、 腹 板 、 柱 立 筋 简 化 成 为 梁 立 复 合 材 料 层合 板 元 , 简 化 为 复 合 材料 蜂 墙 窝夹 芯 层合 板 元 , 中 上 下 壁板 在 梁 凸缘 、 其 筋 条 处 的 铺 层 , 在 筋 条 处 的 铺 层 以 墙 及 梁 腹 板 在 立 柱 平 筋 处 的 铺 层 为 对 应 两 部 分 铺 层 的 叠加 。 了 准 确 定 义 不 同 结 构 的 为 铺 层 方 向 , 如 图3所 示 的 一 个 整 体 坐 标 以 系 , 两 个 局 部 坐 标 系 为参 考 。 和 对 于 蜂 窝 夹 层结 构 , 里 按 照文 献 【 】 这 3 6 —7 提 出的 方 法 来处 理 , 面 板 与 蜂窝 芯 6 8 将 子分开处理 , 板用板元 素, 窝芯用 “ 面 蜂 特 殊 体元” 拟 。 模 3 2 材料 属性 的定义 . T7 0 BA9 6 向带 的基 本 力 学 性 能 0/ 9l 单 见表 1 蜂窝材 料 为z 1 7 A(型 A , , MS 9 4 3 级 密 度4 k / )其 力学性 能 数据 见表 2 T7 0 8 g m , 。 0/ B 9 6 向板 的实 际单 层 厚度 为0 1 rm。 A9 1 单 .4 a
聚四氟乙烯复合材料力学性能研究与有限元分析

t h e t e n s i l e p r o p e r t i e s o f P TF E c o mp o s i t e s a r e s e n s i t i v e t o t h e t e mp e r a t u r e c h a n g e a n d n o t t o t h e t e n s i l e r a t e c h a n g e .I n o r d e r t o d e s c r i b e t h e me c h a n i c a l p r o p e r t i e s o f P TF E c o mp o s i t e s q u a n t i t a t i v e l y a n d s u p p l y a ma t e r i a l mo d e l or f F E M s i mu l a t i o n, b a s e d o n t h e e x p e r i me n t a l r e s u l t s ,a u n i a x i a l t e n s i l e c o n s t i t u t i v e mo d e l wa s d e v e l o p e d . Th e c o n s t i ut t i v e mo d e l c a n d e s c r i b e t h e s t r e s s — s t r a i n r e l a t i o n s h i p u n d e r d i f f e r e n t t e mp e r a ur t e s a n d t e n s i l e r a t e s q u a n t i t a t i v e l y . At l a s t , t h e u n i a x i a l c o mp r e s s i o n t e s t o f P T F E c o mp o s i t e
复合材料力学课件第06章 细观力学

§6.1(2)
假 设
初应 力;无缺陷;纤维和基体的性能不变; 无缺陷;纤维和基体的性能不变; 线弹性. 线弹性. 2∘ 增强相(纤维):匀质;各向同性;线弹 增强相(纤维):匀质;各向同性; ):匀质 性; 定向有序排列;连续。 定向有序排列;连续。 3∘ 基体(树脂):匀质;各向同性;线弹性。 基体(树脂):匀质;各向同性;线弹性。 ):匀质 4∘ 界面:粘接完好;变形协调。 界面:粘接完好;变形协调。
§6.1(1)
细观力学(Meso-Mechanics) 细观力学(Meso-Mechanics) 细观力学两种世界观: 细观力学两种世界观 (1) 从实际中抽取模型 用精确方法 从实际中抽取模型—用精确方法 求解模型—问题的解 问题的解; 求解模型 问题的解; (2) 模型力与实际一致 用近似方法 模型力与实际一致—用近似方法 求解模型—问题的解 问题的解。 求解模型 问题的解。
∴ ε 2 = ε f V f + ε mVm σf σm σ2
E2 =Vf Ef + Vm Em
f
∵σ 2 = σ m = σ
V f Vm E f Em 1 ∴ = + ⇒ E2 = E2 E f Em Vm E f + V f E m
3∘
21
的确定
§6.2(3)
ε2 µ 21 = − ε1
γf =
τ
Gf
γm =
τ
Gm
∆ =γB ∆ m = V m Bγ m
∆ f =Vf Bfγ f τ τ τ γ = = Vm γ m + V f γ f = Vm +Vf
G
G12 = Vm G f + V f G m V f G m + G f (1 − V f 1 = 1 − V f + V f Gm / G f Gm G f = Gm G f
--复合材料力学第六章细观力学基础

(二)纵向泊松比
21
RVE的纵向应变关系式:
2 f 2V f m2Vm
两边同时除以 1 ,可得:
21 f V f mVm
(三)纵横(面内)剪切模量
G12
在剪应力作用下,RVE的剪应变有如下 关系:
12 f V f mVm
以
12
12
G12
可在复合圆柱模型上施加不同的均匀应力边界条件,利用 弹性力学方法进行求解而得到有效模量,结果为:
2
2Gm
E
f
rf2
ln(
R rf
)
其中 Gm 为基体剪切模量,rf 为纤维半经,R为纤维间距,
l为纤维长度,R与纤维的排列方式和 V f 有关。
ET(短) ET (长)
2、Halpin-Tsai方程
EL Em
1
2
l d
LV
f
1 LV f
ET
1 2TV f
Em 1 TV f
此时,对L取:
RVE的要求: 1 、 RVE 的 尺 寸 << 整 体 尺 寸 , 则宏观可看成一点;
2、RVE的尺寸>纤维直径;
3、RVE的纤维体积分数=复合材料的纤维体积分数。
纤维体积分数:
Vf
vf v
v f —纤维总体积;
v —复合材料体积
注意:
只有当所讨论问题的最小尺寸远大于代表性体积单元时,
复合材料的应力应变等才有意义。
并可由RVE的解向邻近单元连续拓展到整体时,所得的有效 弹性模量才是严格的理论解。
则只有满足上述条件的复合材料的宏观弹性模量才能通过 体积平均应力、应变进行计算;或按应变能计算。
聚四氟乙烯复合材料力学性能研究与有限元分析

聚四氟乙烯复合材料力学性能研究与有限元分析发布时间:2021-01-21T06:14:00.885Z 来源:《中国科技人才》2021年第2期作者:肖志远[导读] 随着科技的发展,聚四氟乙烯在工程中的应用日益广泛,并已成为尖端科学及现代工业中最重要的材料之一,具有广阔的发展前景。
基于此,本文对聚四氟乙烯复合材料的力学性能及有限元分析进行了论述。
肖志远中航复合材料有限责任公司北京 101300摘要:随着科技的发展,聚四氟乙烯在工程中的应用日益广泛,并已成为尖端科学及现代工业中最重要的材料之一,具有广阔的发展前景。
基于此,本文对聚四氟乙烯复合材料的力学性能及有限元分析进行了论述。
关键词:聚四氟乙烯;力学性能;有限元分析聚四氟乙烯(PTFE)自20世纪50年代投入工业生产以来,以其优异的性能广泛应用于机械、石化、航空航天等领域。
聚四氟乙烯性能稳定,具有较高的耐腐蚀、耐老化、自润滑、无粘性,是工业领域重要的密封材料和耐腐蚀材料。
聚四氟乙烯作为工业设备的一个重要部件,其力学性能对设备的整体运行稳定性有着重要的影响。
因此,研究PTFE的力学性能具有重要意义。
一、PTFE的性质和应用聚四氟乙烯(Poly tetra fluoroethylene,简写为PTFE),俗称“塑料王”,由四氟乙烯单体组成的高结晶聚合物,是一种白色且有蜡状感的热塑性塑料。
其分子式为C2F2,为完全对称无支链的线型高分子,聚乙烯中的氢原子被氟原子取代,由于氟原子半径明显大于氢原子半径,从而使碳-碳链从聚乙烯的平面完全伸展的曲折构象逐渐扭转成螺旋构象。
该螺旋构象正好包围在聚四氟乙烯易受化学侵袭的碳链骨架外,形成一个紧密的“氟化”保护层,PTFE的主链不受任何外界试剂的侵袭,使PTFE具有其他材料无法比拟的耐溶剂性、化学稳定性和低内聚能密度,而且碳-氟键键能远高于碳-氢键及碳-碳键,从而使PTFE具有更好的热稳定性及化学惰性。
另外,氟原子的电负性强,再加上四氟乙烯单体的完美对称性使PTFE的吸引力及表面能较低,从而使PTFE具有优良的摩擦学性能和良好的低温延展性,同时,PTFE的抗蠕变性能较差,易出现冷流现象,而且耐磨性差。
复合材料力学 第六章 细观力学基础
3、 K 23 K m
Vf Vm 1 K f K m K m Gm
(平面应变体积模量)
4、 G12 G m
G f (1 V f ) G mVm G f Vm G m (1 V f )
5、
G23
可由三相模型求得: 利 用 在 r 处 施 加
纯剪均匀应力边界
1 1 * U ij ij dv Cijkl ij kl v 2 v 2
3)有效模量的严格理论解 并可由RVE的解向邻近单元连续拓展到整体时,所得的有效
只有按上述两种均匀边界条件算得的有效弹性模量一致,
弹性模量才是严格的理论解。
则只有满足上述条件的复合材料的宏观弹性模量才能通 过体积平均应力、应变进行计算;或按应变能计算。
* ij
对椭圆形夹杂,Eshelby已经证明
而在夹杂以外为零,且有:
在夹杂内部是均匀的,
S 0 0 c * 0 c Cijkl ( kl kl kl ) Cijkl ( kl kl )
c ij * ijkl kl
其中 Sijkl 为Eshelby张量; kl 为因夹杂的出现而形成的 0 kl 为无限远处的均匀应变。 干扰应变;
4V f Vm (v f v m ) 2 E1 E f V f E mVm Vm V f 1 K f K m Gm
V f Vm (v f v m )(
2、
21 f V f mVm
1 1 ) Km K f
Vm V f 1 K f K m Gm
Mf
其中:
(M表示
E2 , G12或 23 )
*
Mm Mf Mm
碳纤维增强复合材料力学性能的有限元模拟分析
碳纤维增强复合材料力学性能的有限元模拟分析引言:碳纤维增强复合材料是一种重要的结构材料,具有高强度、低密度和优异的耐腐蚀性能。
为了更好地理解和预测这种材料的力学性能,有限元模拟成为一种有效的工具。
本文将探讨碳纤维增强复合材料的力学性能及其有限元模拟分析方法。
1. 碳纤维增强复合材料的力学性能碳纤维增强复合材料由碳纤维和基体材料组成,具有独特的力学性能。
首先,碳纤维的高强度和高模量使得复合材料具有出色的抗拉强度和刚度。
其次,由于碳纤维和基体的界面结合紧密,复合材料还表现出较好的层间剪切性能。
此外,碳纤维增强复合材料的疲劳强度和耐冲击性也远远优于传统金属材料。
2. 有限元模拟在力学性能分析中的应用有限元模拟是一种计算方法,通过将复杂结构离散为数学模型,基于力学原理求解结构的应力和变形分布。
在碳纤维增强复合材料力学性能分析中,有限元模拟被广泛应用。
首先,可以通过有限元模拟研究复合材料在静力载荷下的应力分布和应变响应,从而评估其强度和刚度。
其次,有限元模拟还可以模拟在动力载荷下复合材料的疲劳寿命和冲击行为,并优化复合材料的设计和性能。
3. 有限元模拟参数的选择在进行碳纤维增强复合材料力学性能的有限元模拟时,需要选择合适的模拟参数。
首先,应选择适当的网格划分,以保证模型几何形状和表面质量的准确性。
其次,需要确定材料的力学性能参数,如弹性模量、剪切模量和层间剪切强度等。
对于复合材料的层间剪切强度,通常需要进行微观结构分析以获取准确的数值。
此外,外界加载条件(如温度、湿度等)也需要考虑进来以获得可靠的模拟结果。
4. 有限元模拟分析的挑战和进展尽管有限元模拟在碳纤维增强复合材料力学性能分析中具有重要的应用前景,但仍面临一些挑战。
首先,材料的非线性和各向异性使得模拟计算的复杂度增加。
其次,复合材料的失效机制与金属材料有所不同,需要改进模型和算法以准确地预测结构破坏行为。
此外,对于复合材料的疲劳和寿命预测,还需要开展更多的试验和验证以提高模拟的准确性。
四步法三维编织复合材料力学性能的有限元分析
四步法三维编织复合材料力学性能的有限元分析本文提出了一种新的单胞模型,并采用有限元法分析了三维编织复合材料的力学性能。
本文给出了一种三维编织预制件的纱线编织结构的分析方法,得出了编织纱线的运动规律。
编织纱线由携纱器携带,沿携纱器的运动趋势线方向运动。
采用最小二乘法分段对携纱器的相关运动位置点进行拟合,得到编织过程中纱线的空间运动规律,在此基础上,获得的预制件结构的单胞模型,包含内部单胞,表面单胞和棱角单胞。
单胞的取向平行于预制件的表面。
并建立了编织工艺参数和几何结构参数的关系,通过实验验证,证明了工艺参数和几何结构参数之间关系的正确性。
本文在上述几何模型的基础上,建立了有限元的分析模型并进行数值计算来预报三维编织复合材料的弹性模量。
对于三维编织复合材料来说,其划分的单元内既含有基体材料又含有纤维束材料,而且两种材料间还存在界面。
对于这类单元难以用通常的有限元方法进行分析。
因此本文提出了一种新的离散单元模型,将细观单胞作为离散单元对三维编织复合材料进行宏观网格剖分,然后对细观单元进行分析。
根据结构单胞模型,将长方体单胞理想化为加强筋单元,即由一个各向同性弹性基体材料长方体和不同取向具有单轴刚度的纤维单元叠加而成。
并推导了加强筋单元的刚度矩阵,在给定的边界条件下,得出三维编织复合材料的模量。
通过相应软件的编制,使得只要输入相应的编织工艺参数,便可快速,及时准确的做出预报。
并进行了实验验证,预测结果和实验结果吻合较好,证实了三维编织复合材料弹性模量预报的精确性。
基于有限元计算细观力学的复合材料宏观性能的一体化预测
有 限元法 与细 观力学 和材 料科 学相 结合产 生 了 有 限元 计算 细 观力 学 (ii lme t o uainl f t ee n mp tt a ne c o mi o c ai ,E M)1。 为细 观计 算力学 的最 c meh nc F C [ 作 r s ] 主要 的组成 部分 , 限元 计算 细 观 力 学 的发 展一 直 有
一
吕 毅 ,吕 国 志 赵 庆 兰 , ,熊 璇
(. 1西北工业 大学 航 空学 院 。 陕西 西安 7 07 ;2西 安邮电学 院 , 102 . 陕西 西安 706) 1 0 1
摘 要: 基于有限元计算细观力学理论 , 以MS . A R N 为平台, CP T A 利用 P L实现 了R E的参数 C V 化 自动 建模 , 立 了 R 建 VE库 。并根 据不 同 的细观 力学方 法 , 通过在 后 台对 R VE边 界条 件 的设 置及
其 中并 未集 成相 应 的计算 程 序来实 现一体 化预测 。
本 文 以先进 的前 后 处 理软 件 MS . ATR CP AN—
着 复合材 料 的几 何结 构 越来 越 复 杂 ,E M 已经 成 F C
为 预测复合 材料宏 观 性能 的主要 方法 E 。 2 ] F C 方 法 的关 键 是 建 立 合 适 的 代 表 性 特 征 EM
有限元计 算 , 集成 了相应 的计 算程 序 , 而 实现 了复合材料 宏观 性 能的一 体化 预 测 。 从 最后 , 以单 向复
合 材料 的宏观 弹性模 量 预测 为例 , 示 了一体 化预 测 系统 。 展
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b) simple cube
(SC)
(d) face-centered cube (f) body-face-edge-centered (FC) cube (BFE)
晶体点阵结构
单胞及有限元网格(规则排列)
多颗粒单胞(随机分布、不同形状)
b/a=3/4
L/d=1
基体材料的弹塑性力学性能参数
不同纤维位向角下的拉伸应力-应变曲线
二、循环变形行为的模拟
采用如图所示的代表性体积单元来分析复合材料 的整体行为。
x Matrix D/2 O Fiber d/2 l/2 L/2 z
复合材料代表性体积单元以及有限元分析网格(Vf=15%,l/d=20)
在有限元分析中可采用 2-D轴对称8节点单元进 行分析(如图中所示),边界条件为对称位移 边界条件。 各个尺寸之间满足如下关系: L/2=l/2+2.5d,ld2 /LD2=Vf Al2O3 纤维为弹性材料,弹性模量 Ef=300 GPa , 泊松比f=0.20。
r
1.5 1.0 0.5 0.0 1
2
3
4
5
6
7
8
9
10
Cyclic Number N , cycle
复合材料的r~N模拟结果
§A-2 颗粒增强复合材料力学行为分析
1、颗粒增强复合材料的形貌
Vp=14%
Vp=21%
2、颗粒增强复合材料的力学行为
单调拉伸
应变循环
棘轮行为
3、单颗粒有限元模型
轴对称边界条件
上述模型中的材料参数可以通过单拉实验确 定,对纯Al的值如表1所示。
基体材料的材料参数值
M=10, E=70GPa, v=0.33, Q0=15MPa; ξ(1)=5000, ξ(2)=1250, ξ(3)=800, ξ(4)=400, ξ(5)=200, ξ(6)=100, ξ(7)=50, ξ(8)=33.3, ξ(9)=25, ξ(10)=20; r(1)=4.6, r(2)=3.5, r(3)=4.5, r(4)=2.4, r(5)=5.2, r(6)=5.4, r(7)=2.6, r(8)=2.1, r(9)=2.0, r(10)=12.5 (MPa).
述代表性体积单元。对随机 分布短纤维复合材料的处理
方法与前一致。
斜向纤维等效模型
不同的方法得到的结果不同,见下表。
复合材料 -Al2O3f/Al5.5Mg -Al2O3f/Al5.5Zn -Al2O3f/Al12Si Vf 0 10 15 20 0 10 15 20 0 10 20 混合律 -85 93 102 -85 93 102 -85 102 H-T方程 夹杂理论 -76 80 84 -76 80 84 -76 84 -78 83 88 -78 83 88 -78 88
(单位:GPa)
FEM -81.4 87.7 93.9 -81.4 87.7 93.9 -81.4 93.9
测量 70 78.1~80.2 85.2~89.8 94.2~97.2 70 78.9 87.4~89.2 94.8~95.6 70 73.6~75.0 80.6
二、有效性能分析(拉伸应力-应变曲线)
Different multi-particle unit cell models
0.40
0.40
Ratchetting strain r , %
0.32
Ratchetting strain r , %
0.32
Sphere Ellipsoid Cylinder Cube Mixed
0.24
0.24
只需求出了
p为离散的单元号,n为单元总数。
c
,即可得:
c Ec c
y Fiber y o Matrix l Interface z
c
S
c
x d
L
a) Longitudinal section
S
b) Transverse section
三维代表性体积单元
所有的计算都是基于上
(k ) (k ) 2 p (k ) (k ) b p b ε 3 (k ) k (k ) (k ) p [ H f 1 ]p
r ( k ) (k ) (k )
为材料常数
该模型能够合理描述未增强基体的循环变形 行为。
0.16
Uniform random distribution Normal distribution
0.16
0.08
0
2
4
6
8
10
12
0.08
0
2
4
6
8
Ratcheting Strain , %
=0.0 =0.1 =1.0
r
1
2
3
4
5
6
7
8
9
10
Cyclic Number N , cycle
未增强基体的r~N模拟结果
2.5
Ratcheting Strain , %
2.0
=0.0 =0.1 =1.0
• Al合金基体为弹塑性材料,其循环本构模型描 述如下。 主控方程:
ε ε p εe εe D1 : σ
ε
p
3 sα 2 sα
屈服函数:
F 1.5(s α) : (s α) Q0
背应力演化方程:
α r ( k )b ( k )
k 1
M
(k=1, 2, …, M)
专题 复合材料细观有限元分析
§A-1 短纤维复合材料力学行为分析 一、有效模量分析
1、短纤维复合材料的形貌
面内分布
厚度方向分布
2、有限元分析模型
层板比拟法
c
c c
c
a) aligned fiber model
b) tilted fiber model
单向短纤维复合材料的理想化模型
1 n ij ( ij ) p V p V p 1
Kang GZ, et al: Mater. Sci. Eng. A 426(2006), 66; Mater. Sci. Eng. A 458(2007), 170.
单拉应力-应变曲线
单轴应变循环曲线
棘轮行为
4、多颗粒有限元模型
(a) single particle (c) body-centered cube (e) edge-centered cube
