2011年广州市中考数学真题及答案
2011广东中考数学试卷及答案,推荐文档
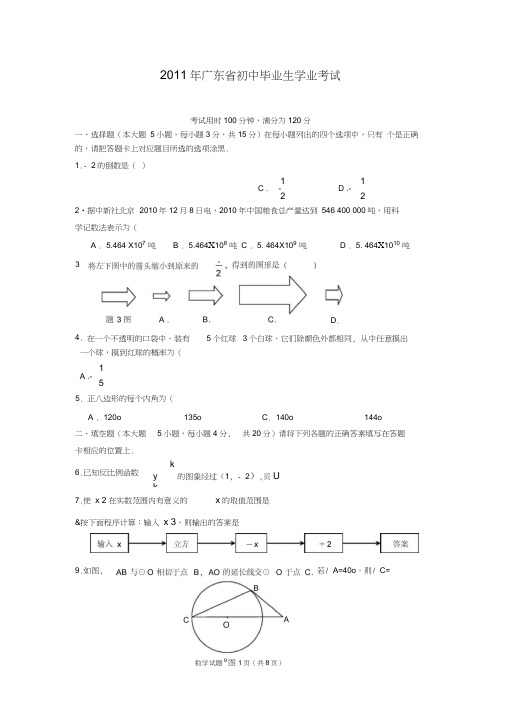
2011年广东省初中毕业生学业考试考试用时100分钟,满分为120分一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有个是正确的,请把答题卡上对应题目所选的选项涂黑.1.- 2的倒数是()1 1C . -D .-2 22010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为(A . 5.464 X107吨B . 5.464X108吨C . 5. 464X109吨D . 5. 464X1010吨一个球,摸到红球的概率为(1A .-5正八边形的每个内角为(2•据中新社北京4. 3个白球,它们除颜色外都相同, 从中任意摸出5.A . 120o 135o C. 140o 144o二、填空题(本大题5小题,每小题4分, 共20分)请将下列各题的正确答案填写在答题卡相应的位置上.6.已知反比例函数ky 的图象经过(1, - 2),贝Uk7.使x 2在实数范围内有意义的x的取值范围是3.在一个不透明的口袋中,装有5个红球D.若/ A=40o,则/ C=&按下面程序计算:输入x 3,则输出的答案是9.如图,910.如图 ⑴,将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ ABC 和厶DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图⑵中阴影部分;取△ A 1B 1C 1和厶D 1E 1F 1各边中点,连接成正六角星形 A 2F 2B 2D 2C 2E 2,如图 ⑶中阴影部分; 如此下去…,则正六角星形 A 4F 4B 4D 4C 4E 4的面积为 _____________________ .(本大题5小题,每小题6分,共30 分)14. 如图,在平面直角坐标系中,点 P 的坐标为(一4, 0), O P 的半径为2,将O P 沿x 轴向右平移4个单位长度得O P 1.(1) 画出O P 1,并直接判断O P 与O P 1的位置关系;(2) 设O P 1与x 轴正半轴,y 轴正半轴的交点分别为 A , B ,求劣弧AB 与弦AB 围成的图 形的面积(结果保留n ). 14、(1 )0 P 与O P i 外切。
2011年广东省中考数学试卷(含答案)

2011年广东省初中毕业生学业考试数学说明:1.全卷共4页,满分为120分,考试用时为100分钟.2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号.用2B 铅笔把对应该号码的标号涂黑.3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用 橡皮擦干净后,再选涂其他答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上; 如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答 的答案无效.5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回.一、选择题(本大题共5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一项是符合题目要求的.1. -2的倒数是 ( )A. 2B. -2C. 12D. -122. 据中新社北京2010年12月8日电,2010年中国粮食总产量达到546400000吨.用科学记数法表示为 ( )A. 5.464×107吨B. 5.464×108吨C. 5.464×109吨D. 5.464×1010吨3. 将图中的箭头缩小到原来的12,得到的图形是 ( )4. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为 ( )A. 15B. 13C. 58D. 385. 正八边形的每个内角为 ( ) A. 120° B. 135° C. 140° D. 144°二、填空题(本大题共5小题,每小题4分,共20分)6. 已知反比例函数y =kx 的图象经过(1,-2),则k = .7. 使x -2在实数范围内有意义的x 的取值范围是 . 8. 按下面程序计算:输入x =3,则输出的答案是__12__.第9题图9. 如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接B C.若∠A =40°,则∠C = . 10. 如图①,将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1,取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图②中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图③中阴影部分;如此下去…,则正六角星形A n F n B n D n C n E n 的面积为 .第10题图三、解答题(一)(本大题共5小题,每小题6分,共30分) 11. 计算:(2011-1)0+18sin 45°-22.12. 解不等式组:⎩⎪⎨⎪⎧2x +1>-38-2x ≤x -1,并把解集在数轴上表示出来.13. 已知,如图,E 、F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B. 求证:AE =CF .第13题图14. 如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系;(2)设⊙P 1与x 轴正半轴、y 轴正半轴的交点分别为A ,B ,求劣弧AB ︵和弦AB 围成的图形的面积(结果保留π).第14题图15. 已知抛物线y =12x 2+x +c 与x 轴没有交点.(1)求c 的取值范围;(2)试确定直线y =cx +1经过的象限,并说明理由.四、解答题(二)(本大题共4小题,每小题7分,共28分)16. 某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,购买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,问该品牌饮料一箱有多少瓶?17. 如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l .AB 是A 到l 的小路,现新修一条路AC 到公路l ,小明测量出∠ACD =30°,∠ABD =45°,BC =50 m .请你帮小明计算他家到公路l 的距离AD 的长度(精确到0.1 m ,参考数据:2≈1.414,3≈1.732).第17题图18. 李老师为了解班里学生的作息时间,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么? (2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?第18题图19. 如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.(1)求∠BDF的度数;(2)求AB的长.第19题图五、解答题(三)(本大题共3小题,每小题9分,共27分)20. 如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.(1)表中第8行的最后一个数是,它是自然数的平方,第8行共有个数;(2)用含n的代数式表示:第n行的第一个数是,最后一个数是,第n行共有个数;(3)求第n行各数之和.21. 如图①,△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF =90°.固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止,现不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图②.(1)问:始终与△AGC相似的三角形有及;(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图②的情形说明理由);(3)问:当x为何值时,△AGH是等腰三角形?第21题图22. 如图,抛物线y =-54x 2+174x +1与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B作BC ⊥x 轴,垂足为点C (3,0).(1)求直线AB 的函数关系式;(2)动点P 在线段OC 上从原点O 出发以每秒一个单位的速度向点C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N ,设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设在(2)的条件下(不考虑点P 与点O 、点C 重合的情况),连接CM 、BN ,当t 为何值时,四边形BCMN 为平行四边形?问对于所求的t 值,平行四边形BCMN 是否为菱形?请说明理由.第22题图2011年广东省中考数学试卷参考答案与试题解析1. D2. B3. A4. C5. B6. -27. x ≥28. 129. 25° 10. 14n11.解:原式=1+32×22-4(3分) =1+3-4=0.(6分) 12.解:⎩⎪⎨⎪⎧2x +1>-38-2x ≤x -1,移项可得⎩⎪⎨⎪⎧2x >-49≤3x ,(2分)解得⎩⎪⎨⎪⎧x >-2x ≥3,∴不等式组的解集为x ≥3.(4分) 用数轴表示如下:第12题解图13.证明:∵AD ∥CB , ∴∠A =∠C.在△ADF 与△CBE 中 ⎩⎪⎨⎪⎧∠D =∠B AD =CB ∠A =∠C,(3分) ∴△ADF ≌△CBE (ASA ), ∴AF =CE ,(5分)∴AF +EF =CE +EF ,即AE =CF .(6分)14.解:(1)如解图所示,∵⊙P 的圆心坐标为(-4,0),∴将⊙P 沿x 轴向右平移4个单位长度得⊙P 1,P 1的坐标为(0,0),即与原点重合,(2分) ∴PP 1=4,即PP 1等于⊙P 与⊙P 1半径之和,所以⊙P 与⊙P 1的位置关系为外切.(3分)(2)由(1)得点A 、B 的坐标分别为(2,0)、(0,2), 则可知∠AOB =90°,∴劣弧AB 与弦AB 围成的图形的面积等于 S 扇形BOA -S Rt △BOA =90πr 2360-12OA ·OB =90π×22360-12×2×2=π-2.(6分)第14题解图15.解:(1)∵抛物线y =12x 2+x +c 与x 轴没有交点 ,∴方程12x 2+x +c =0无解,(2分)即Δ=b 2-4ac =1-2c <0,解得c >12.(3分)(2)∵c >12>0,也就是一次函数k >0,b =1>0,∴直线y =cx +1经过一、二、三象限.(6分) 16.解:设该品牌饮料一箱有x 瓶,依题意,得26x -26x +3=0.6.(4分)化简,得x 2+3x -130=0,解得x 1=-13(不合题意,舍去),x 2=10,(6分)经检验:x =10符合题意.答:该品牌饮料一箱有10瓶.(7分)易错分析解分式方程时不要忘记检验. 17. 解:设AD =x ,∵tan ∠ABD =AD BD ,tan ∠ACD =ADCD ,(2分)∴BD =AD tan ∠ABD =AD tan 45°=AD1=x ,(4分)CD =AD tan ∠ACD =AD tan 30°=AD33=3x ,(5分)∴BC =CD -BD =3x -x =50,(6分)∴x =503-1=25×(3+1)≈68.3(m ).(7分)答:小明家到公路l 的距离AD 的长度约为68.3 m .18.解:(1)此次调查的总体是班里学生的上学路上花费的时间.(2分) (2)如解图:第18题解图(3)路上时间花费在30分钟以上(含30分钟)的人数占全班人数的百分比是4+150×100%=10%.(7分)19.第19题解图解:(1)∵BF =CF , ∴∠1=∠C =30°.(2分) 又∵∠2=∠1=∠C =30°,(4分) ∴∠BDF =180°-3×30°=90°.(2)由(1)知在Rt △BDF 中,∠2=30°, ∴BD =BF ·cos ∠2,∴BD =4 3.(5分) ∵AD ∥BC , ∴∠ABC =90°.在Rt △BAD 中,∠3=90°-∠1-∠2=30°, ∴AB =BD ·cos ∠3=6.(7分) 20.解:(1)64;8;15.(3分)(2)n 2-2n +2;n 2;2n -1.(3分)(3)n 2-2n +2+n 22×(2n -1)=(n 2-n +1)(2n -1).(9分)21.第21题解图解:(1)始终与△AGC 相似的三角形有:△HAB 和△HG A.(3分) (2)由(1)知△AGC ∽△HAB , ∴CG AB =AC HB ,即x 9=9y, ∴y =81x(0<x <92).(5分)(3)由(1)知△AGC ∽△HGA ,∴要使得△AGH 是等腰三角形,只要△AGC 是等腰三角形即可.(6分)22.解:(1)设直线AB 的函数关系式为y =ax +b , 对于抛物线y =-54x 2+174x +1,令x =0,得y =1,即有A (0,1),将A 代入直线AB 的关系式得b =1; 令x =3,得y =52,即有B (3,52),将B 代入直线AB 的关系式得a =12;∴直线AB 的函数关系式为y =12x +1.(2分)(2)显然OP =t ,即P (t ,0).将x =t 代入抛物线可得y =-54t 2+174t +1,即N (t ,-54t 2+174t +1).将x =t 代入直线AB 的关系式可以得到y =12t +1,即M (t ,12t +1).(4分)∴s =MN =-54t 2+174t +1-12t -1,∴s =-54t 2+154t (0≤t ≤3).(5分)(3)显然NM ∥BC ,∴要使得四边形BCMN 为平行四边形,只要MN =BC ,即s =-54t 2+154t =52,解得t =1或t =2.(6分)①当t =1时,M (1,32),∴MP =32,CP =2.在Rt △MPC 中,CM =MP 2+CP 2=52=BC ,∴四边形BCMN 为菱形.(7分)②当t =2时,M (2,2),∴MP =2,CP =1. 在Rt △MPC 中,CM =MP 2+CP 2=5≠B C. ∴四边形BCMN 不是菱形.(9分)。
2011年广东省广州市数学中考试题

2011年广东省广州市数学中考试题一、选择题(每小题3分,共30分)1.四个数-5,-0.1,21,3中为无理数的是()A. -5B. -0.1C.21D. 32.已知□ABCD的周长为32,AB=4,则BC=()A. 4B. 121C. 24D. 283.某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( )A. 4B. 5C. 6D. 104.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A. (0,1)B. (2,-1)C. (4,1)D. (2,3)5.下列函数中,当x>0时,y值随x值增大而减小的是()A.2xy= B. 1-=xy C. xy43= D.xy1=6.若a<c<0<b,则abc与0的大小关系是()A. abc<0B. abc=0C. abc>0D. 无法确定7.下面的计算正确的是()A. 2221243xxx=⋅ B. 1553xxx=⋅ C. 34xxx=÷ D. 725)(xx=8.如图所示,将矩形纸片先沿虚线AB按箭头方向向右..对折,接着对折后的纸片沿虚线CD向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是()9.当实数x的取值使得2-x有意义时,函数y=4x+1中y的取值范围是()A.y≥-7B. y≥9C. y>9D. y≤910.如图,AB切⊙O于点B,OA=23,AB=3,弦BC//OA,则劣弧BC的弧长为()A.π33B. π23C. πD. π23二、填空题:(每小题3分,共18分)11.9的相反数是______12.已知α∠=260,则α∠的补角是______度。
13.方程231+=xx的解是______14.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形EDCBA''''',已知OA=10cm,AO'=20cm,则五边形ABCDE的周长与五边形EDCBA'''''的周长的比值是______15.已知三条不同的直线a、b、c在同一平面内,下列四条命题:(①如果a //b ,a ⊥b ,那么b ⊥c ; ②如果b //a ,c //a ,那么b//c ; ③如果b ⊥a ,c ⊥a ,那么b ⊥c ;④如果b ⊥a ,c ⊥a ,那么b//c. 其中真命题的是_________。
2011年广东省中考数学试卷解析

点关注,每天更新全国各区真题详解版和经典中考题型、考点、知识点2011年广东省中考数学试卷参考答案与试题解析一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.(3分)﹣2的倒数是( ) A . 2 B . ﹣2 C . D.考点: 难度: M112 倒数 容易题. 分析: 这道题需要我们清楚倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.而以上四个选项中,只有﹣2×()=1,所以﹣2的倒数是﹣.其余均选项不符合提议。
故选D 解答: D .点评:本题主要考查倒数的概念及性质,属于中考的一个高频考点,倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数2.(3分)据中新社北京2010年12月8日电,2010年中国粮食总产量达到546400000吨,用科学记数法表示为( )A . 5.464×107吨B . 5.464×108吨C . 5.464×109吨D . 5.464×1010吨考点: 难度: M11C 科学记数法 容易题.分析: 首先我们要知道,什么是科学计数法:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.那么本题中将546400000用科学记数法可表示为5.464×108.故选B解答: B .点评: 本题我们需要注意科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.3.(3分)将下图中的箭头缩小到原来的,得到的图形是( )A .B.C.D .考点:难度:M32I 相似图形的应用 容易题.分析:本题需要我们根据相似图形的定义,并且结合图形,然后对选项一一分析,即可排除错误答案.∵图中的箭头要缩小到原来的,∴箭头的长、宽都要缩小到原来的;选项B箭头大小不变;选项C箭头扩大;选项D的长缩小、而宽没变.故选A解答:A.点评:本题较简单,主要考查了相似图形的定义,注意:即两个图形的形状相同,但大小不一定相同的变换就是相似变换.4.(3分)在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为()A .B.C.D.考点:难度:M222 概率的计算容易题.分析:解决本题,我们需要先求出所有球的个数与红球的个数,然后再根据概率公式便可求出答案.即,共8球在袋中,其中5个红球,故摸到红球的概率为,故选C.解答:C.点评:这道题需要掌握概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,难度适中.5.(3分)正八边形的每个内角为()A .120°B.135°C.140°D.144°考点:难度:M331 多边形的内(外)角和中等题.分析:此题我们要根据正多边形的内角求法,得出每个内角的表示方法,便可求出答案.即:[(n﹣2)×180]÷n=[(8﹣2)×180]÷8=135°,故选B解答:B.点评:本题主要考查了多边形的内(外)角和,属于中考中频考点,注意正n边形的内角ɑ=[(n﹣2)×180]÷n.正确的记忆正多边形的内角求法公式是解决问题的关键.二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上. 6.(4分)已知反比例函数解析式的图象经过(1,﹣2),则k=.考点:难度:M137 用待定系数法求函数关系式容易题.分析:根据待定系数法,将(1﹣2)代入式即可得出k的值.具体解法如下:∵反比例函数解析式的图象经过(1,﹣2),∴k=xy=﹣2,解答: ﹣2.点评:本题比较简单,考查了用待定系数法求反比例函数的解析式,属于中考高频考点,对以此类题型只需要将已知点带入函数即可求出答案。
2011年广东中考数学试卷及答案

数学试题全卷共6页,考试用时100分钟,满分为120分。
一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的, 1.-3的相反数是( ) A .3B .31C .-3D .31-2.如图,已知∠1 = 70º,如果CD ∥BE ,那么∠B 的度数为( ) A .70ºB .100ºC .110ºD .120º3.某学习小组7位同学,为玉树地震灾区捐款,捐款金额分别为5元,10元,6元,6元,7元, 8元,9元,则这组数据的中位数与众数分别为( ) A .6,6B .7,6C .7,8D .6,84.左下图为主视方向的几何体,它的俯视图是( )5.下列式子运算正确的是( ) A .123=-B .248=C .331= D .4321321=-++二、填空题(本大题5小题,每小题4分,共20分)6. 据中新网上海6月1日电:世博会开园一个月来,客流平稳,累计至当晚19时,参观者已超过8000000人次。
试用科学记数法表示8000000=_______________________。
7.化简:11222---+-y x y xy x =_______________________。
8.如图,已知Rt △ABC 中,斜边BC 上的高AD=4,cosB=54,则AC=____________。
9.已知一次函数b x y -=与反比例函数xy 2=的图象,有一个交点的纵坐标是2,则b 的值为________。
10.如图(1),已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1;把正方形A 1B 1C 1D 1边长按原法延长一倍得到正方形A 2B 2C 2D 2(如图(2));以此下去···,则正方形A 4B 4C 4D 4的面积为__________。
2011广州市中考数学真题

秘密★启用前2011年广州市初中毕业生学业考试数 学本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;填写考场试室号、座位号,再用2B 铅笔把对应这两个号码的标号涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图.答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔、圆珠笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回.第一部分 选择题(共30分)一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 四个数5-,0.1-,12* ).(A) -5 (B )0.1- (C )12(D 2. 已知ABCD 的周长为32,AB = 4,则BC =( * ).(A) 4 (B )12 (C )24 (D )283. 某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( * ).(A) 4 (B )5 (C )6 (D )10 4. 将点A (2,1)向.左.平移2个单位长度得到点A ',则点A '的坐标是( * ). (A) (0,1) (B )(2,1-) (C )(4,1) (D )(2,3) 5. 下列函数中,当0x >时y 值随x 值增大而减小的是( * ).(A) 2y x = (B )1y x =- (C) 34y x =(D )1y x =6. 若0a c b <<<,则abc 与0的大小关系是( * ).(A) 0abc < (B )0abc = (C )0abc > (D )无法确定图27. 下面的计算正确的是( * ).(A) 2223412x x x = (B )3515x x x = (C) 43x x x ÷= (D )527()x x = 8. 如图1所示,将矩形纸片先沿虚线AB 按箭头方向向右..对折,接着将对折后的纸片沿虚线CD 向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( * ).9. 当实数x41y x =+中y 的取值范围是( * ).(A) y ≥7- (B )y ≥9 (C )9y > (D )y ≤9 10.如图2,AB 切O 于点B ,OA =3AB =,弦BC ∥OA ,则劣弧 BC 的弧长为( * ).(A)(B(C )π (D )32π第二部分 非选择题(共120分)二、填空题(本大题共6小题,每小题3分,满分18分.)11. 9的相反数是 * .12. 已知26α∠= ,则α∠的补角是 * 度.13. 方程132x x =+的解是 * .14. 如图3,以点O 为位似中心,将五边形ABCDE 放大后得到五边形A B C D E ''''',已知10OA =cm ,20OA '=cm ,则五边形ABCDE 的周长与五边形A B C D E '''''的周长的比值是 * . 15. 已知三条不同的直线a 、b 、c 在同一平面内,下列四个命题:① 如果a ∥b ,a ⊥c ,那么b ⊥c ; ② 如果b ∥a ,c ∥a ,那么b ∥c ; ③ 如果b ⊥a ,c ⊥a ,那么b ⊥c ; ④ 如果b ⊥a ,c ⊥a ,那么b ∥c . 其中真命题是 * .(填写所有真命题的序号)16. 定义新运算“⊗”,规定:143a b a b ⊗=-,则12(1)⊗-= * .(A )(B ) (C )(D )图1ADCDB (A )图3三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分9分)解不等式组13, 210. xx-<⎧⎨+>⎩18.(本小题满分9分)如图4,AC是菱形ABCD的对角线,点E、F分别在AB、AD上,且AE=AF.求证:△ACE≌△ACF.19.(本小题满分10分)分解因式:228(2)(7)x y x x y xy--++.20.(本小题满分10分)5个棱长为1的正方体组成如图5的几何体.(1)该几何体的体积是 * (立方单位),表面积是 * (平方单位);(2)画出该几何体的主视图和左视图.21.(本小题满分12分)某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品一律按商品价格的9.5折优惠.已知小敏不是该商店的会员.(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?(2)请帮小敏算一算,所购买商品的价格在什么范围时,采用方案一更合算?22.(本小题满分12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图(图6),根据图中信息回答下列问题:(1)求a的值;(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少..有1人的上网时间在8~10小时.a频数分布直方图时间/小时频数(学生人数)236251008642图6图4AB CDEF正面图523.(本小题满分12分)已知R t △ABC 的斜边AB 在平面直角坐标系的x 轴上,点C (1,3)在反比例函数ky x=的图象上,且3sin 5BAC ∠=.(1)求k 的值和边AC 的长; (2)求点B 的坐标. 24.(本小题满分14分)已知关于x 的二次函数2(0)y ax bx c a =++>的图象经过点C (0,1),且与x 轴交于不同的两点A 、B ,点A 的坐标是(1,0). (1)求c 的值; (2)求a 的取值范围;(3)该二次函数的图象与直线1y =交于C 、D 两点,设A 、B 、C 、D 四点构成的四边形的对角线相交于点P ,记△PCD 的面积为1S ,△P AB 的面积为2S ,当01a <<时,求证:12S S -为常数,并求出该常数.25.(本小题满分14分)如图7,AB 是O 中直径,C 是O 上一点,45ABC ∠= ,等腰直角三角形DCE 中DCE ∠是直角,点D 在线段AC 上. (1)证明:B 、C 、E 三点共线;(2)M 是线段BE 的中点,N 是线段AD的中点,证明:MN =;(3)当△DCE 绕点C 逆时针旋转α(090α<< )后,记为△11D CE (图8),1M 是线段1BE 的中点,1N 是线段1AD的中点,111M N 是否成立?若是,请证明;若不是,说明理由.E DN MCBA O图7图8E 1CD 1N 1M 1BOA。
2011年广州市中考数学试题答案——分析

24、解:(1)将点 C(0,1)代入 y ax bx c 得 c 1 (2)由(1)知 y ax bx 1 ,将点 A(1,0)代入得
2
a b 1 0 , ∴ b a 1
∴ 二次函数为 y ax a 1 x 1
2
∵二次函数为 y ax a 1 x 1 的图像与 x 轴交于不同的两点
22.(12 分)某中学九年级(3)班 50 名学生参加平均每周上网时间的调查,由 调查结果绘制了频数分布直方图,根据图中信息回答下列问题: (1)求 a 的值; (2)用列举法求以下事件的概率:从上网时间在 6~10 小时的 5 名学生中随机 选取 2 人,其中至少 有 1 人的上网时间在 8~10 小时。 ..
初一、三:直方图和概率相结合,列举法大多数学生少用。中下学生估计会一时 无法完整正确解答。
3
23.(12 分)已知 Rt△ABC 的斜边 AB 在平面直角坐标系的 x 轴上,点 C(1,3)在 k 3 反比例函数 y= 的图象上,且 sin∠BAC= 。 x 5 (1)求 k 的值和边 AC 的长;(2)求点 B 的坐标。 初二、三:反比例函数和锐角三角函数综合。分类讨论,学生容易考虑欠全面。
x
1 2
∴ 不等式组的解集为
1 x4 2
18、证明:∵ AC 是菱形 ABCD 的对角线 ∴ ∠CAE=∠CAF 在△ACE 和△ACF 中 AE=AF,∠CAE=∠CAF,AC=AC ∴ △ACE≌△ACF 19、解: 8 x 2 y
2
2
x 7 x y xy
2 2 2
= 8x 16 y 7 x xy xy
2
= x 16 y = x 4 y x 4 y
2011年广东省中考数学试题及答案

2011年广东省初中毕业生学业考试数 学一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.-2的倒数是( ) A .2 B .-2C .21D .21-2.据中新社北京2010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为( )A .5.464×107吨B .5.464×108吨C .5.464×109吨D .5.464×1010吨 3.将左下图中的箭头缩小到原来的21,得到的图形是( )4.在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出 一个球,摸到红球的概率为( ) A .51 B .31 C .85 D .835.正八边形的每个内角为( )A .120ºB .135ºC .140ºD .144º二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上.6.已知反比例函数xky =的图象经过(1,-2),则=k ____________. 7.使2-x 在实数范围内有意义的x 的取值范围是______ _____. 8.按下面程序计算:输入3=x ,则输出的答案是_______________.9.如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C .若∠A=40º,则∠C=_____.A .B . D .C . 题3图输入x立方-x÷2答案10.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取 △ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1 和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…, 则正六角星形A 4F 4B 4D 4C 4E 4的面积为_________________.三、解答题(一)(本大题5小题,每小题6分,共30分) 11.计算:20245sin 18)12011(-︒+-.12.解不等式组:⎩⎨⎧-≤-->+128,312x x x ,并把解集在数轴上表示出来.13.已知:如图,E ,F 在AC 上,AD//CB 且AD=CB ,∠D=∠B .求证:AE=CF .题13图DAFE题10图(1)A 1BAFBA FB A FEB 1C 1F 1 D 1 E 1 A 1B 1C 1F 1 D 1 E 1 A 2B 2C 2F 2 D 2 E 2 题10图(2)题10图(3)①②14.如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系;(2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A ,B ,求劣弧AB 与弦AB 围成的图形的面积(结果保留π).15.已知抛物线c x x y ++=221与x 轴没有交点. (1)求c 的取值范围;(2)试确定直线1+=cx y 经过的象限,并说明理由. 四、解答题(二)(本大题4小题,每小题7分,共28分)16.某品牌瓶装饮料每箱价格26元.某商店对该瓶装饮料进行“买一送三”促销活动,若整17.如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l ,AB 是A 到l 的小路. 现新修一条路AC 到公路l. 小明测量出∠ACD=30º,∠ABD=45º,BC=50m. 请你帮小明计算他家到公路l 的距离AD 的长度(精确到0.1m ;参考数据:414.12≈,732.13≈).18.李老师为了解班里学生的作息时间表,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?19.如图,直角梯形纸片ABCD中,AD//BC,∠A=90º,∠C=30º.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.(1)求∠BDF的度数;(2)求AB的长.五、解答题(三)(本大题3小题,每小题9分,共27分)20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36…………………………(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;(2)用含n 的代数式表示:第n 行的第一个数是___________________,最后一个数是________________,第n 行共有_______________个数;(3)求第n 行各数之和.21.如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与DE 重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC ,将△DEF 绕点A 顺时针旋转,当DF 边与AB 边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE ,DF(或它们的延长线)分别交BC(或它的延长线) 于G ,H 点,如图(2) (1)问:始终与△AGC 相似的三角形有 及 ;(2)设CG=x ,BH=y ,求y 关于x 的函数关系式(只要求根据图(2)的情形说明理由) (3)问:当x 为何值时,△AGH 是等腰三角形.题21图(1)BHFA (D )GCEC (E )BFA (D )题21图(2)22.如图,抛物线2517144y x x =-++与y 轴交于A点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C(3,0). (1)求直线AB 的函数关系式;(2)动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N. 设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设在(2)的条件下(不考虑点P 与点O ,点C 重合的情况),连接CM ,BN ,当t 为何值时,四边形BCMN 为平行四边形?问对于所求的t 值,平行四边形BCMN 是否菱形?请说明理由.2011年广东省初中毕业生学业考试数 学考试用时100分钟,满分为120分一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.-2的倒数是( ) A .2 B .-2 C .21D .21-【答案】D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
秘密★启用前广州市2011年初中毕业生学业考试数 学本试卷分选择题和非选择题两部分,共三大题25小题,满分150分.考试时间120分钟.注意事项:1.答卷前,考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;填写考场试室号、座位号,再用2B 铅笔把对应这两个号码的标号涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题同的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图.答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔、圆珠笔和涂改 液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回.第一部分 选择题(共30分)一、选择题(每小题3分,共30分)1.四个数-5,-0.1,21,3中为无理数的是( ) A. -5 B. -0.1 C. 21D. 32.已知□ABCD 的周长为32,AB=4,则BC=( ) A. 4 B. 121 C. 24 D. 283.某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( ) A. 4 B. 5 C. 6 D. 104.将点A (2,1)向左平移2个单位长度得到点A ',则点A '的坐标是( ) A. (0,1) B. (2,-1) C. (4,1) D. (2,3)5.下列函数中,当x>0时,y 值随x 值增大而减小的是( ) A.2x y = B. 1-=x y C.x y 43=D. x y 1=6.若a<c<0<b ,则abc 与0的大小关系是( ) A. abc<0 B. abc=0 C. abc>0 D. 无法确定7.下面的计算正确的是( )A. 2221243x x x =⋅B. 1553x x x =⋅C. 34x x x =÷D. 725)(x x =8.如图所示,将矩形纸片先沿虚线AB 按箭头方向向右..对折,接着对折后的纸片沿虚线CD 向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )9.当实数x 的取值使得2-x 有意义时,函数y=4x+1中y 的取值范围是( )A.y ≥-7B. y ≥9C. y>9D. y ≤910.如图,AB 切⊙O 于点B ,OA=23,AB=3,弦BC//OA ,则劣弧BC 的弧长为( )A.π33 B. π23 C. π D. π23 第二部分 非选择题(120分)二、填空题:(每小题3分,共18分) 11.9的相反数是______12.已知α∠=260,则α∠的补角是______度。
13.方程231+=x x 的解是______ 14.如图,以点O 为位似中心,将五边形ABCDE 放大后得到五边 形E D C B A ''''',已知OA=10cm ,A O '=20cm ,则五边形ABCDE 的周长与五边形E D C B A '''''的周长的比值是______15.已知三条不同的直线a 、b 、c 在同一平面内,下列四条命题: ①如果a //b ,a ⊥b ,那么b ⊥c ; ②如果b //a ,c //a ,那么b//c ; ③如果b ⊥a ,c ⊥a ,那么b ⊥c ;④如果b ⊥a ,c ⊥a ,那么b//c. 其中真命题的是_________。
(填写所有真命题的序号) 16.定义新运算“⊗”,b a ba 431-=⊗,则)1(12-⊗=________。
三、解答题(本大题共9大题,满分102分) 17.(9分)解不等式组⎩⎨⎧>+<-01231x x(18. (9分)如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且AE=AF 。
求证:△AC E ≌△ACF19. (10分)分解因式:8(x 2-2y 2)-x(7x+y)+xy20. (10分)5个棱长为1的正方体组成如图的几何体。
(1)该几何体的体积是_________(立方单位) 表面积是_________(平方单位) (2)画出该几何体的主视图和左视图。
21.(12分)某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠。
已知小敏5月1日前不是该商店的会员。
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元? (2)请帮小敏算一算,所购买商品的价格在什么范围时,采用方案一更合算?ADFEBC正面22.(12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: (1)求a 的值;(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少..有1人的上网时间在8~10小时。
23.(12分)已知R t △ABC 的斜边AB 在平面直角坐标系的x 轴上,点C(1,3)在反比例函数y=xk的图象上,且sin ∠BAC=53。
(1)求k 的值和边AC 的长;(2)求点B 的坐标。
24.(14分)已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0)(1)求c的值;(2)求a的取值范围;(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1- S2为常数,并求出该常数。
25.(14分)如图7,⊙O中AB是直径,C是⊙O上一点,∠ABC=450,等腰直角三角形DCE中∠DCE是直角,点D在线段AC上。
(1)证明:B、C、E三点共线;(2)若M是线段BE的中点,N是线段AD的中点,证明:MN=2OM;(3)将△DCE绕点C逆时针旋转α(00<α<900)后,记为△D1CE1(图8),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=2OM1是否成立?若是,请证明:若不是,说明理由。
2011年广州市中考数学试题答案一、选择题1、D2、B3、B4、A5、D6、C7、C8、D9、B 10、A 二、填空题11、﹣9; 12、154; 13、1x =; 14、1︰2; 15、①②④; 16、8。
三、解答题17、解:解不等式①,得4x <解不等式②,得 12x >-∴ 不等式组的解集为142x -<<18、证明:∵ AC 是菱形ABCD 的对角线 ∴ ∠CAE=∠CAF 在△ACE 和△ACF 中AE=AF ,∠CAE=∠CAF ,AC=AC ∴ △ACE ≌△ACF 19、解:()()22827x y x x y xy --++=2228167x y x xy xy ---+=2216x y -=()()44x y x y +-20、解:(1)5,22;(2)21、解:(1)实际应支付:120×0.95=114(元)(2) 设所购商品的价格为x 元,依题意得 168+0.8x <0.95x 解得 x >1120∴ 当所购商品的价格高于1120元时,选方案一更合算。
22、解:(1)506253214a =----=(2)将上网时间在6~8小时的3人记为A 、B 、C ,上网时间在8~10小时的2人记为D 、E ,从中选取2人的所有情况为(A 、B )、(A 、C )、(A 、D )、(A 、E )、(B 、C )、(B 、D )、(B 、E )、(C 、D )、(C 、E )、(D 、E )共10种等可能的结果,其中至少有一人上网时间在在8~10小时的有(A 、D )、(A 、E )、(B 、D )、(B 、E )、(C 、D )、(C 、E )、(D 、E )这7种,所以至少有一人上网时间在在8~10小时的概率为0.7。
23、解:(1)∵点A (1,3)在反比例函数ky x=的图像上 左视图主视图∴ 133k xy ==⨯= 作CD ⊥AB 于点D ,所以CD =3 在Rt △ACD 中,sin ∠BAC=CDAC, ∴335AC=,解得 AC=5 (2) 在Rt △ACD中,4AD ===cos ∠BAC=45AD AC =如图1,在在Rt △ACD 中,cos ∠BAC=ACAB, ∴2554cos 45ACAB BAC===∠ ∴413AO AD OD =-=-=2513344OB AB OA =-=-=∴ 点B 的坐标为13,04⎛⎫ ⎪⎝⎭如图2,∴415AO AD OD =+=+=255544OB AB OA =-=-=∴ 点B 的坐标为5,04⎛⎫-⎪⎝⎭24、解:(1)将点C (0,1)代入2y ax bx c =++得1c =(2)由(1)知21y ax bx =++,将点A (1,0)代入得10a b ++=, ∴ ()1b a =-+∴ 二次函数为()211y ax a x =-++∵二次函数为()211y ax a x =-++的图像与x 轴交于不同的两点∴0∆>,而()()222214214211a a a a a a a a ∆=-+-=++-=-+=-⎡⎤⎣⎦∴ a 的取值范围是 0a >且1a ≠(3)证明: ∵01a <<∴ 对称轴为11122a a x a a--+=-=> ∴ 11212a a AB a a +-⎛⎫=-=⎪⎝⎭把1y =代入()211y ax a x =-++得()210ax a x -+=,解得 1210,ax x a+==∴1aCD a+=∴ 12PCD PAB ACD CAB S S S S S S ∆∆∆∆-=-=-=1122CD OC AB OC ⨯⨯-⨯⨯ =111111222a aa+-⨯⨯-⨯⨯=1∴12S S -为常数,这个常数为1。
25、(1)证明:∵ AB 是⊙O 的直径 ∴ ∠ACB=90° ∵ ∠DCE=90°∴∠ACB +∠DCE=180° ∴ B 、C 、E 三点共线。
