梳状滤波器工作原理
数字梳状滤波器讲解

数字梳状滤波器梳状滤波对于画面质量是非常重要的一个技术,因此我们有必要对其进行详细刨析。
那么具体什么是梳状滤波器呢?这就要从源头(信号源)开始讲起了,一开始,接收视频的Video端子是Composite端子(比如RF射频接口和AV接口),它所能接收的信号叫Composite Video Signal,即混合视频信号(也称复合信号),什么意思呢?因为这个Composite(混合)信号包括了亮度(Luminance,用字母Y表示)和色度/彩度(Chrominace)两方面的信号,视频电路要做的工作就是Y/C进行分离处理,目前的梳状滤波器是在保证图像细节的情况下解决视频信号亮色互窜的唯一方法,其内部有许多按一定频率间隔相同排列的通带和阻带,只让某些特定频率范围的信号通过,因为其特性曲线象梳子一样,故人们称之为梳状滤波器(Comb Filtering)。
梳状滤波器一般由延时、加法器、减法器、带通滤波器组成。
对于静止图像,梳状滤波在帧间进行,即三维梳状滤波。
对活动图像,梳状滤波在帧内进行,即二维梳状滤波。
高档数字电视机采用行延迟的梳状滤波器与带通滤波器级联,构成Y/C分离方案就可获得满意的图像质量。
使用梳状滤波器能使图像质量明显提高。
解决了色串亮及亮串色造成的干扰光点、干扰花纹;消除了色度正交分量U、V色差信号混迭造成的彩色边缘蠕动;消除了亮、色镶边,消除了高频信号的色彩错误和灰度值表示错误。
有一段时期国内很多工厂(为了节省成本)使用模拟的方式实现梳状滤波器,实际上效果很不好,原因有两个,一是延迟器件的带宽很难保证,二是解决行相关性差问题的自适应电路很复杂。
而在数字电路里,只要有足够的存储器,就可以保证足够的延迟时间与信号带宽,且复杂的自适应电路很容易集成在芯片中硬件固化。
梳状滤波器原理及发展历史:梳状滤波器采用频谱间置技术,理论上可以保证亮度和色度的无失真分离。
如果我们好好回顾一下梳状滤波器的发展历程,将对其有个清醒的认识。
梳状滤波器功能

梳状滤波器功能梳状滤波器是一种常见且实用的信号处理工具,广泛应用于音频、视频等领域,具有很多有用的功能。
本文将介绍梳状滤波器的功能及其在不同领域中的应用。
梳状滤波器的基本原理梳状滤波器是一种反馈式的滤波器,其基本原理是延迟输入信号并将延迟后的信号与原始信号进行相减,从而实现频率特性的调整。
通过调整梳状滤波器的延迟时间和反馈系数,可以实现不同的滤波效果,包括陷波、通带等。
梳状滤波器的功能1.频率选择:梳状滤波器可以选择特定频率的信号进行增强或抑制,常用于去除信号中的噪音或强调特定频率成分。
2.时域处理:通过调整梳状滤波器的延迟时间,可以实现时域上的信号平移或延迟,对信号进行时域处理。
3.音频效果:在音频处理中,梳状滤波器常用于实现混响、回声等特效,增强音频效果。
4.频率估计:梳状滤波器可以用于频率估计,通过观察滤波器的输出可以确定信号中的频率成分。
5.波形合成:梳状滤波器也可以用于波形合成,将不同频率的信号进行合成,生成新的波形。
梳状滤波器在不同领域中的应用1.音频处理:梳状滤波器在音频处理中被广泛应用,用于混响、均衡等效果的实现。
2.图像处理:在图像处理中,梳状滤波器可以用于图像增强、边缘检测等任务。
3.通信系统:在通信系统中,梳状滤波器可以用于信号解调、信号滤波等应用。
4.生物医学工程:在生物医学工程领域,梳状滤波器可以用于心电信号处理、脑电信号处理等。
总的来说,梳状滤波器是一种功能强大且多用途的信号处理工具,其在不同领域中都有着重要的应用。
通过合理的参数设置和应用场景选择,梳状滤波器可以发挥出最佳的效果,对信号处理和处理效果的改善具有重要意义。
累积梳状(CIC)滤波器分析与设计
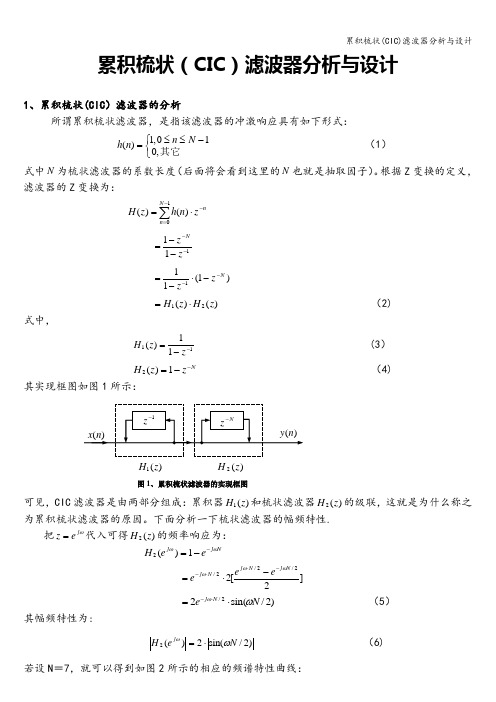
累积梳状(CIC )滤波器分析与设计1、累积梳状(CIC )滤波器的分析所谓累积梳状滤波器,是指该滤波器的冲激响应具有如下形式: ⎩⎨⎧-≤≤=其它,010,1)(N n n h (1)式中N 为梳状滤波器的系数长度(后面将会看到这里的N 也就是抽取因子)。
根据Z 变换的定义,滤波器的Z 变换为:∑-=-⋅=10)()(N n n z n h z H111----=z z N)1(111Nz z---⋅-=)()(21z H z H ⋅= (2) 式中,1111)(--=zz H (3) N z z H --=1)(2 (4) 其实现框图如图1所示:可见,CIC 滤波器是由两部分组成:累积器)(1z H 和梳状滤波器)(2z H 的级联,这就是为什么称之为累积梳状滤波器的原因。
下面分析一下梳状滤波器的幅频特性.把ωj e z =代入可得)(2z H 的频率响应为: N j j e e H ωω--=1)(2 ]2[22/2/2/N j N j N j e e eωωω-⋅⋅--⋅=)2/sin(22/N e N j ωω⋅=⋅- (5) 其幅频特性为:)2/sin(2)(2N e H j ωω⋅= (6) 若设N =7,就可以得到如图2所示的相应的频谱特性曲线:)(2z H)(1z H图1、累积梳状滤波器的实现框图由图2可以清楚地看到:)(2ωj e H 的形状犹如一把梳子,故把其形象地称之为梳状滤波器。
同样可以求得累积器)(1z H的频率响应为:ωj e z H --=11)(112/2/2/]2[2---=ωωωj j j e e e 12/)2(sin 2-⋅=ωωj e (7) 故CIC 滤波器的总频率响应为:)()()(21ωωωj j j e H e H e H ⋅= )2/sin(/)2/sin(ωωN = )2()2(1ωω-⋅⋅=Sa NSa N (8)式中,x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:N e H j =)(0 (9)CIC 滤波器的幅频特性如图3所示:在)~0(π区间上称)/2~0(N π的区间为CIC 滤波器的主瓣,而其它区间称为旁瓣。
(完整版)CIC滤波器的原理与设计
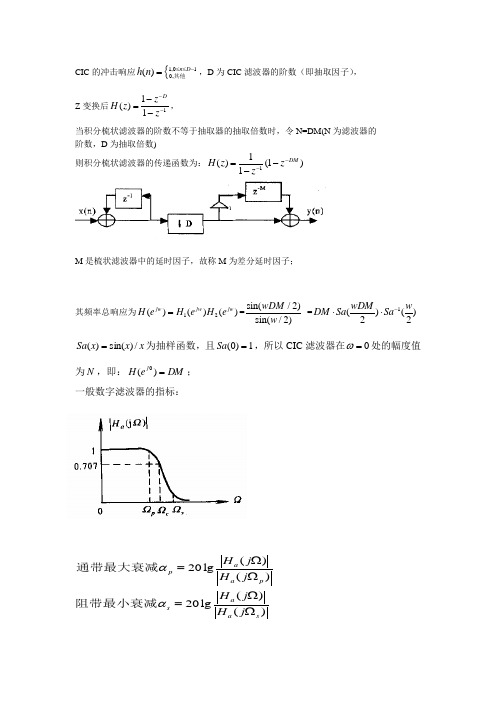
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
matlab设计梳状滤波器

matlab设计梳状滤波器梳状滤波器是一种常用于信号处理领域的数字滤波器,它的设计和实现可以通过MATLAB进行。
本文将介绍梳状滤波器的原理、设计方法及MATLAB实现,并通过实例演示其应用。
一、梳状滤波器原理梳状滤波器是一种基于延迟和加权求和的滤波器,它通过一系列延迟单元和权重系数的组合,对输入信号进行滤波处理。
其基本原理是将输入信号与多个延迟版本的自身进行加权求和,从而实现对特定频率的滤波。
二、梳状滤波器设计方法梳状滤波器的设计方法主要包括确定延迟单元数目和权重系数。
延迟单元数目决定了滤波器的频率响应范围,权重系数决定了滤波器的增益和频率选择性。
确定延迟单元数目的方法有多种,常用的方法是通过信号频率和采样频率的比值计算得到。
例如,对于采样频率为Fs的信号,如果要设计一个梳状滤波器以滤除频率为f的信号成分,则延迟单元数目可以通过计算Fs/f得到。
确定权重系数的方法也有多种,常用的方法是通过设置滤波器的带宽和增益来实现。
带宽越窄,滤波器的频率选择性越高;增益越高,滤波器对信号的抑制效果越明显。
三、MATLAB实现梳状滤波器在MATLAB中,可以使用fir1函数进行梳状滤波器的设计和实现。
该函数可以根据指定的参数自动计算出滤波器的权重系数,并生成滤波器的传递函数。
下面通过一个实例来演示如何使用MATLAB实现梳状滤波器。
我们需要定义信号频率和采样频率,并计算出延迟单元数目。
假设信号频率为f=100Hz,采样频率为Fs=1000Hz,则延迟单元数目为N=Fs/f=10。
接下来,我们可以使用fir1函数设计滤波器,并指定希望滤波器的带宽为0.2。
代码如下:```matlabf = 100; % 信号频率Fs = 1000; % 采样频率N = Fs/f; % 延迟单元数目bw = 0.2; % 滤波器带宽h = fir1(N, bw); % 设计梳状滤波器freqz(h); % 绘制滤波器的频率响应曲线```我们可以使用filter函数对输入信号进行滤波处理。
通信电子领域中的梳状滤波器设计

通信电子领域中的梳状滤波器设计梳状滤波器是一种常用的通信电子领域的滤波器,具有高速、低功耗、小体积等优点,广泛应用于数字信号处理、无线通信、雷达信号处理等领域。
本文将介绍梳状滤波器的原理、分类、设计方法及应用等方面的内容。
一、梳状滤波器的原理传统的滤波器是通过调节电阻、电容、电感等元件的数值来实现对不同频率信号的滤波,但由于这些元件在高频应用中往往会感到非理想效应,导致滤波器性能下降。
而梳状滤波器则是利用时钟信号来在时域上对输入信号进行采样,再根据采样数据进行数字卷积运算,从而实现对特定频谱范围的信号滤波。
具体来说,梳状滤波器采用周期性函数作为滤波器的冲激响应,对输入信号进行卷积计算。
梳状滤波器的输入信号经过时钟采样后,得到采样序列,将采样序列与周期性函数进行卷积运算,最后得到滤波后的输出信号。
由于梳状滤波器的卷积运算是利用移位寄存器实现的,因此具有高速、低功耗、小体积等优点。
二、梳状滤波器的分类梳状滤波器可以分为单倍频梳状滤波器和多倍频梳状滤波器两种。
单倍频梳状滤波器的冲激响应是一个周期性的函数,频率等于采样频率的一半。
多倍频梳状滤波器则是通过修改周期性函数的频率来实现对不同频率信号的滤波,可以实现更高的滤波性能。
此外,梳状滤波器还可以根据其实现方式分为顺序梳状滤波器和并行梳状滤波器。
顺序梳状滤波器逐个计算序列中的每个样本,具有较低的硬件成本,但计算速度较慢;并行梳状滤波器则同时计算序列中的多个样本,具有较高的计算速度,但需要更多的硬件资源支持。
三、梳状滤波器的设计方法梳状滤波器的设计首先需要确定所需要滤波器的频率响应特性,然后根据特定的应用场景选择合适的梳状滤波器类型,最后根据所选型号的特性进行设计与实现。
具体来说,梳状滤波器的设计需要确定采样率、滤波器带宽、阶数等参数。
在确定这些参数的基础上,可以采用从时钟信号导出生成冲激响应、通过FIR散点插值方法进行实现、利用频率变换法将低通滤波器变换成带通或高通滤波器等方法进行设计。
1.2 梳状滤波器.

Interleaver的功能
功能:将一组入射的DWDM信号,按照奇偶波长分成两组 输出。 特点:通带特性好、串扰低。
Interleaver的应用
作为波段滤波器,将DWDM信号的通带 间隔扩展为原来的两倍,降低对后续滤 波器的设计要求。
用作波段滤波器,保留一半波长以备 系统升级。
1.2 梳状滤波器
I1 cos2 ( / 2) 2 I sin ( / 2) 2
2nL f c来自I1, I2f (THz)
单级Interleaver的通带特性不好
冲击响应法分析
为了优化通带特性,将多个玻片叠在一起。 输入一个光脉冲,通过1个玻片之后,在时间序列上得到2个光脉冲输出; 输入一个光脉冲,通过n个玻片之后,在时间序列上得到n+1个光脉冲输出。 光脉冲的叠加为一个有限冲击响应FIR系统:
定向耦合器的传输矩阵:
Aout cos B j sin out j sin Ain cos Bin
PLC型Interleaver的矩阵描述
光学延迟线:
e j / 2 Sd 0
相移器:
0 e j / 2
1.2 梳状滤波器
1.2.1 Interleaver的功能和应用 1.2.2 Interleaver的基本原理 1.2.3 基于双折射晶体的Interleaver 1.2.4 基于PLC技术的Interleaver 1.2.5 基于GTI干涉仪的Interleaver
PLC型Interleaver结构
1.2.1 Interleaver的功能和应用 1.2.2 Interleaver的基本原理 1.2.3 基于双折射晶体的Interleaver 1.2.4 基于PLC技术的Interleaver 1.2.5 基于GTI干涉仪的Interleaver
深入分析梳状滤波器原理Comb-filter

Mode B (2D weighting with bandpass filter)
Normal mode ,Y-C can be separated quite well.
Mode C (2D weighting without bandpass filter)
constant[ monochrome receivers]).
180 degrees
2D comb filter
Important concept…picture information (y , c) is about the same from line to line .
Special case( y - c , y + c ).
( key advantage over the 2D filter ). motion or serious color changes , 3D filter may
perform no better than the 2D filter. has to store two frames of video data.
Comb Filter
Outline
Y-C separation 2D comb filter 3D comb filter 2D adaptive comb filter conclusion
Comb filter (Y-C separator)
Separate the incoming composite video signal into luminance (Y) and chrominance (C).
y y+c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梳状滤波器工作原理
梳状滤波器对于画面质量是非常重要的一个技术。
一开始,接收视频的Video端子是Composite端子(比如RF射频接口和AV接口),它所能接收的信号叫Composite VideoSignal,即混合视频信号(也称复合信号)。
因为这个Composite(混合)信号包括了亮度(Luminance,用字母Y表示)和色度/彩度(Chrominace)两方面的信号,视频电路要做的工作就是Y/C进行分离处理,目前的梳状滤波器是在保证图像细节的情况下解决视频信号亮色互窜的唯一方法,其内部有许多按一定频率间隔相同排列的通带和阻带,只让某些特定频率范围的信号通过,因为其特性曲线象梳子一样,故人们称之为梳状滤波器。
图2-6-1 梳状滤波器框图
梳状滤波器主要由延迟线和相加电路、相减电路构成的,用以分离FU 和±FV。
一个实际的梳状滤波器电路如图2-6-1所示。
其中V1为延时激励放大器,DL为延迟线,T1为裂相变压器、L1为调谐电感,C2为耦合电容。
色度信号F经电容C1耦合加于V1基极,经放大后由集极输出,再经延迟线由A点加至裂相变压器T1上端,取自Rw的直通信号经C2耦合加至T1中点,这样可在输出端分别得到相加和相减输出。
将直通信号和延迟信号分别以un和un-1表示,其输出电压的合成原理图如图4-32等效电路所示。
调节Rw可保证两信号幅度严格相等,输出分离更彻底。
延迟线DL多为超声延迟线,它由输入、输出压电换能器和延迟介质组成。
压电换能器由多晶压电陶瓷薄片制成,当信号加到输入压电换能器两端面的电极上时,输入信号在延迟介质中激起机械振动,形成超声波。
延
迟介质多为熔融石英或玻璃,超声波在玻璃中传播速度较低,再将其制作
成如图4-33形式,经多次反射超声波方到达输出换能器还原为电信号,这
样使可大大地缩小延迟线体积。
为使超声波按规定的路径传播,减少不规
则反射引起的干扰杂波,在延迟线表面涂有若干吸声点,吸声点所涂吸声
材料为橡胶、环氧树脂和钨粉配制而成。
最后用塑料外壳封装,以减小外
界的影响。
2.6.2 PAL 解码器的梳状滤波器
PAL 的特殊电路是梳状滤波器.为使它
能够有效的分离两个色度分量,延时线的
延时时间要有准确的数值. 延时线延迟时
间τd 应选择得既非常接近行周期(64μ
s),以便相加、减时是相邻行相应像素间
的加或减;而又必须为副载波半周期的整
数倍,以保证延时前、后色度信号副载波相位相同(0°)或相反(180°)。
由
fSC=283.75fH+25Hz 的关系,则行周期TH 与副载波TSC 之间的关系为:
τd 可选为副载波半周期TSC/2的567倍或568倍。
通常为567, τd
略小于行周期,若为568则略大于行周期
梳状滤波器:作用是将色度信号分离出两个色差分量FU 、FV ,组成包
括一行延时线、加法器和减法器。
传统的色度延时电路采用64μs 超声波玻璃延时线,其原理是利用输
入、输出换能器实现电—超声波—电信号间的转换。
在梳状滤波器中,延时线的精确延时时间为63.943μs ,延时后的信号
与直通信号在加法器和减法器中运算,完成色度分量的分离任务。
设输入到梳状滤波器的第n 行色度信号为
F(n)=Usin ωSCt+Vcos ωSCt=FU+FV (2―35) 则第n+1行色度信号必然为 SC SC SC T T T T 751.283156252575.283H =+=s T T SC SC d μτ943.6310
43361875.45.2835.28325676≈⨯==⨯=
F n+1=UsinωSCt-VcosωSCt=FU-FV (2―36)
根据τd的选择知,延时前与延时后的副载波相位相反,若以F′n-1、F′n分别表示经延时后的相应行的色度信号,则
F′n-1=-F n-1=-(UsinωSCt-VcosωSCt)=-FU+FV (2―37) F′n=-Fn=-(UsinωSCt+VcosωSCt)=-FU-FV (2―38) 由此可以求得,第n行输入时,相加电路输出为
Fn+F′n-1=(FU+FV)+(-FU+FV)=2FV (2―39) 相减电路的输出为
Fn-F′n-1=(FU+FV)-(-FU+FV)=2FU (2―40) 同理,在第n+1行输入时,相加电路和相减电路分别输出为:
Fn+1+F′n=-2FV (2―41)
F n+1-F′n=2FU (2―42)
依次类推。
由式(2―39)~式(2―42)明显地看出,梳状滤波器有效地分离了两个色度分量FU与±FV。
