第11章电路的频率响应例题
(完整版)电路原理课后习题答案
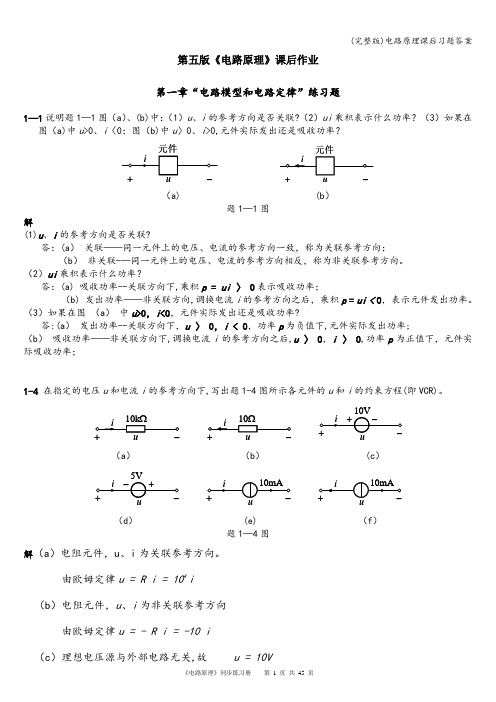
(b)非关联-—同一元件上的电压、电流的参考方向相反,称为非关联参考方向。
(2)ui乘积表示什么功率?
答:(a)吸收功率--关联方向下,乘积p=ui〉 0表示吸收功率;
(b)发出功率——非关联方向,调换电流i的参考方向之后,乘积p=ui<0,表示元件发出功率。
行列式解方程组为
所以
3-11用回路电流法求解题3—11图所示电路中电流I。
题3—11图
解由题已知,
其余两回路方程为
代人整理得
所以
3—12用回路电流法求解题3-12图所示电路中电流 及电压 .
题3—12图
3-15列出题3—15图(a)、(b)所示电路的结点电压方程。
(a)(b)
题3-15图
解:图(a)以④为参考结点,则结点电压方程为:
电压源功率 (发出30W)
(b)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b)
故电阻功率 (吸收45W)
电流源功率 (发出30W)
电压源功率 (发出15W)
(c)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1—5图(c)
故电阻功率 (吸收45W)
电流源功率 (吸收30W)
独立的KVL方程数分别为
(1) (2)
3—7题3—7图所示电路中 , , , , , ,用支路电流法求解电流 。
题3-7图
解由题中知道 , , 独立回路数为 由KCL列方程:
对结点①
对结点②
对结点③
由KVL列方程:
对回路Ⅰ
对回路Ⅱ
对回路Ⅲ
联立求得
3—8用网孔电流法求解题3—7图中电流 。
电路习题册

《电路分析》习题册班级学号姓名中国地质大学(武汉)电子信息工程系注意事项:1. 习题册请用A4纸双面打印,装订成册,填好相关信息;2. 每章习题均来自课本中的课后习题,不清楚的地方可以参看教材。
这里挑选出来整理成册,方便大家使用;3. 后附有两套模拟试题,供考前进行模拟测试;4. 册内带两张空白的课堂测试答题纸,不要损坏。
通知课堂测试的时候再使用。
第一章电路模型与电路定律1-1 求解电路以后,校核所得结果的方法之一是核对电路中所有元件的功率平衡,即一部分元件发出的总功率应等于其他元件吸收的总功率。
试校核图1-1电路所得解答是否正确。
图1-11-2 电路如图1-2所示,试求:(1) 图(a)中,i1与u ab;(2) 图(b)中,u cb。
图1-21-3 对图1-3所示的电路,若:(1) R1、R2、R3不定;(2)R1 = R2 = R3。
在以上两种情况下,尽可能地确定各电阻中的未知电流。
图1-31-4 电路如题1-4图所示,试求每个元件发出和吸收的功率。
图1-41-5 试求图1-5所示电路中控制量I1及电压U o。
图1-5第二章电阻电路的等效变换2-1 电路如题2-1图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压u2和电流i2;(2)若电阻R1增大,对哪些元件的电压、电流有影响?影响如何?图2-1 2-2 求图2-2所示电路中对角线电压U及总电压U ab。
图2-22-3 利用电源的等效变换,求图2-3所示电路的电流i。
图2-32-4 利用电源的等效变换,求图2-4所示电路中电压比u o/u s。
已知R1 = R2 = 2Ω,R3 = R4 = 1Ω。
图2-42-5 试求图2-5(a)和(b)的输入电阻R i。
图2-5第三章电阻电路的一般分析3-1 用网孔电流法求解图3-1所示电路中电流I a及电压U o 。
图3-1 3-2 用网孔电流法求解图3-2所示电路中I x以及CCVS的功率。
2014-2015福建工程学院电路(2)课程补充练习及答案解析(第十一章)电路的频率响应

11-1 图示电路,已知V cos 21.0t u ω=,410=ωrad/s 时电流i 的有效值为最大,量值是1A ,此时V 10=L U 。
(1)求R 、L 、C 及品质因数Q ;(2)求电压C u 。
解: ()()()()0000404U 100.1Q=1000.10.1111Q=10100,10/L=1m ,10(2)10,102cos(1090)L L L C L c jw U jw U V V U jw U V I jw AL L w w rad s R C CLCH C uF U U V u t V =====Ω========∴=-︒(1)品质因数,R=又解得11-2 R =4Ω、L =10mH 、C =100μF 的串联电路,接于U =20V 的正弦电源。
试求:电路发生谐振时的电源频率及此时的电容电压。
解:3000363311/10/,159.2,21010100101 2.5,202cos(10)50,502cos(1090)C L C w w rad s rad s f HZ LC L Q u t V R CU U QU V u t Vπ-=====⨯⨯⨯======∴=-︒设11-3图示RLC 并联电路处于谐振状态,已知A )10cos(21.03t i S =,H 2.0=L ,电容电流有效值A 2=C I 。
求R 和C 的值。
解: R C L -+L u -+u+-Cu i 图 题9.8题11-1 i S题11-3C R L i C300200()112=10rad/s 5,20,0.1LC 1U()4C SC S C S I w A C uF Q w L I A I w RI I R K wC I wC ∴=⇒=======⇒==Ω电路处于谐振状态,w11-4 图示网络电压u =60cos ωt V ,R 1=60Ω,R 2=30Ω,L =0.2H ,C =0.05F 。
高等教育出版社第六版《电路》第011章 电路的频率响应.ppt

sin2 (0t)
( Q 2
1 R2
L) C
CQ2US 2
1 2
CQ
2U
2 Sm
=
常量
1 2
L
I
2
m
10
§11-3 RLC串联电路的频率响应
一、电路的频率响应:
本节讨论
U U
R S
( (
j) j)
、 UU
C S
( (
j) j)
和
U L ( j) US ( j)
j
+ _
U S
I1
j
+ U L _ I2
2Ω I2
2Ω
{ (2 j)I1 2I2 U S 2I1 (4 j)I2 0
I2
(2
2U S
j)(4
j)
4
4
2U S
2
j6
H1
(
j)
I2 U S
2
4 2 j6
0
1 1 2
0
但作为一个放大器,如音频放大器就不好了,会产生严
重的线性失真。 这就要求通频带越宽越好。
15
2、H
C
(
j
)
U C U S
( (
j)、H j)
L
(
j
)
U U
L S
( (
j j
) )
的频率特性 :
H
C
(
j
)
U C U S
( (
j) j)
a c
(整理)第11章电路的频率响应

第11章 电路的频率响应重点:1. 网络函数;2. 串、并联谐振的概念;本章与其它章节的联系:本章的学习内容建立在前面各章理论的基础之上。
预习知识: 电磁感应定律11-1 网络函数当电路中激励源的频率变化时,电路中的感抗、容抗将跟随频率变化,从而导致电路的工作状态亦跟随频率变化。
因此,分析研究电路和系统的频率特性就显得格外重要。
频率特性:电路和系统的工作状态跟随频率而变化的现象,称为电路和系统的频率特性,又称频率响应。
1. 网络函数H (j ω)的定义在线性正弦稳态网络中,当只有一个独立激励源作用时,网络中某一处的响应(电压或电流)与网络输入之比,称为该响应的网络函数。
2. 网络函数H (j ω)的物理意义1)H (j ω)与网络的结构、参数值有关,与输入、输出变量的类型以及端口对的相互位置有关,与输入、输出幅值无关。
因此网络函数是网络性质的一种体现。
2)H (j ω) 是一个复数,它的频率特性分为两个部分: 幅频特性 模与频率的关系相频特性 幅角与频率的关系ωω-|)(j |H ωωϕ-)(j3)网络函数可以用相量法中任一分析求解方法获得。
11-2 RLC 串联电路的谐振谐振是正弦电路在特定条件下所产生的一种特殊物理现象,谐振现象在无线电和电工技术中得到广泛应用,对电路中谐振现象的研究有重要的实际意义。
1. 谐振的定义含有 R 、L 、C 的一端口电路,外施正弦激励,在特定条件下出现端口电压、电流同相位的现象时,称电路发生了谐振。
因此谐振电路的端口电压、电流满足:2. 串联谐振的条件图 11.1 所示的 R 、L 、C 串联电路发生谐振时称串联谐振。
电路的输入阻抗为:根据谐振定义,当时电路发生谐振,由此得 R 、L 、C 串联电路的谐振条件是谐振角频率为:谐振频率为:上式说明R 、L 、C 串联电路的谐振频率仅由电路的参数决定,因此谐振频率又称固有频率。
由谐振条件得串联电路实现谐振或避免谐振的方式为: (1)L 、C 不变,改变 ω 达到谐振。
电路教案第11章_电路的频率响应

重点1. 网络函数2. 串、并联谐振的概念;11.1 网络函数当电路中激励源的频率变化时,电路中的感抗、容抗将跟随频率变化,从而导致电路的工作状态亦跟随频率变化。
因此,分析研究电路和系统的频率特性就显得格外重要。
● 频率特性:电路和系统的工作状态跟随频率而变化的现象,称为电路和系统的频率特性,又称频率响应。
1. 网络函数H (j ω)的定义在线性正弦稳态网络中,当只有一个独立激励源作用时,网络中某一处的响应(电压或电流)与网络输入之比,称为该响应的网络函数。
)()()(ωωωj E j R j H def∙∙=2. 网络函数H (j ω)的物理意义● 驱动点函数(同一点处的电压电流的函数关系) 激励是电流源,响应是电压)j ()j ()j (ωωωI UH = 策动点阻抗激励是电压源,响应是电流)j ()j ()j (ωωωU I H = 策动点导纳● 转移函数(传递函数,不同点处的电流电压关系)a. 激励是电压源)j ()j ()j (12ωωωU I H =(转移导纳) )j ()j ()j (12ωωωUUH = (转移电压比) b. 激励是电流源)j ()j ()j (12ωωωI UH = (转移阻抗) )j ()j ()j (12ωωωI I H =(转移电流比) 注意:1. H(j ω)与网络的结构、参数值有关,与输入、输出变量的类型以及端口对的相互位置有关,与输入、输出幅值无关。
因此网络函数是网络性质的一种体现。
2. H(j ω) 是一个复数,它的频率特性分为两个部分: 幅频特性:模与频率的关系 ωω|~)(j |H 相频特性:幅角与频率的关系 ωωϕ~)(j3. 网络函数可以用相量法中任一分析求解方法获得。
注意:● 以网络函数中j ω的最高次方的次数定义网络函数的阶数。
● 由网络函数能求得网络在任意正弦输入时的端口正弦响应,即有)j ()j ()j (ωωωE R H = → )j ()j ()j (ωωωE H R = 11.2 RLC 串联电路的谐振谐振是正弦电路在特定条件下产生的一种特殊物理现象。
电路分析第11章

11.1 网络函数
一、网络函数 1、网络函数的定义和分类 定义: 动态电路在频率为ω的单一正弦激励下,正弦稳 态响应(输出)相量与激励(输入)相量之比,称为 正弦稳态的网络函数。记为H(jω ),即
输出相量 H( j) 输入相量
1
分类:
若输入和输出属于同一端口,称为驱动点函数。 若输入是电流源,输出是电压时,称为驱动点阻抗。 若输入是电压源,输出是电流时,称为驱动点导纳。 二、网络函数的计算方法 正弦稳态电路的网络函数是以ω为变量的两个多 项式之比,它取决于网络的结构和参数,与输入的量 值无关。计算网络函数的基本方法是“外施电源法”。
当ω 0 L 1 时,电路发生谐振。 0 C
U _
谐振角频率 (resonant angular frequency) 谐振频率 (resonant frequency) 固有 频率
4
T0 1 / f 0 2π LC 谐振周期 (resonant period)
2、使RLC串联电路发生谐振的条件
1 L 1 20 103 Q 1000 12 R C 10 200 10
U L QU 1000 10V 10000V UC
11
11.3 RLC串联电路的频率响应
研究物理量与频率关系的图形(谐振曲线) 可以加深对谐振现象的认识。
一、 H ( j ) U R ( j ) U S ( j ) 的频率响应
H C (C1 ) 1
C3 H C (C3 ) 0
Q
dH C ( ) 0 d
1 C2 1 2 2Q
H C (C2 )
L1
1
C3
1
0
第11章 电路的频率响应汇总

§11-2 RLC串联电路的谐振 §11-4 RLC并联谐振电路
§11-2 RLC串联电路的谐振
谐振现象的研究有重要的实际意义。一方 面谐振现象得到广泛的应用,另一方面在某些 情况下电路中发生谐振会破坏正常工作。
一、RLC串联电路
I
R
j L
1 j C
U
1 Z (j ) R j( L ) C
I
角频率 0
频率 f 0
IS
U
IG
IL
1 j L
IC
jC
G
2 LC
该频率称为电路的固有频率。 五、并联谐振的特征 1、输入导纳最小 或者说输入阻抗最大
1 Y (j0 ) G j(0C ) =G 0 L
Z (j0 ) R
2、端电压达最大值
U (0 ) Z (j0 ) I S RIS
提取信号
R E
L
谐振 滤波器
C
S
E N
接 收 网 络
已知:
( ) ---信号源 E S S ( ) ---噪声源 E N N
在信号源频率下发生串联谐 振,信号即可顺利地到达接 收网络。
f0 f S
1 2 LC
消除噪声 提取信号
E S E N
分析(一):抑制噪声
QL (0 ) QC (0 ) 0
谐振时电路不从外部吸收无功功率 但 QL (0 ), QC (0 ) 分别不等于零。 电路内部的电感与电容之间周期性地进行磁场 能量和电场能量的交换,这一能量的总和为常量。
串联谐振应用举例
收音机接收电路
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
jω + U1 _ jω + UL 2 I
.
第11章 电路的频率响应
_
I2
2 转移导纳
I1
2
解 列网孔方程解电流 I 2
(2 j ) I1 2 I 2 U S
I 2 / US
返 回 上 页 下 页
•
例6 如图R=10的线圈其QL=100,与电容接成并联
谐振电路,如再并联上一个100k的电阻,求 电路的Q. R C 0L 解 Q 100 100k L R L
0 L RQL 1000 R (0 L) 2 10 6 Re 100 k R 10
RQ
返 回
上 页
下 页
•
例4
+ u1 _ + _u2 + u3 _ f (kHz) L
1 ωC
R L
C
北京台 820 1290 -1290 0 UR0=10
一接收器的电路参数为: L=250H, R=20, U1=U2=U3=10V, 当电容调至 C=150pF时谐振 0=5.5106rad/s, f0=820 kHz 中央台 640 1000 –1660 – 660 UR1=0.304 北京经济台 1026 1611 -1034 577 UR2=0.346
-20lg 1+j /2
-20lg 1+ j/10
幅频波特图 幅频波特图 (a)
返 回
上 页
下 页
•
相位(单位度)
90 tan
。 90
1
2
tan
1
10
。 90
。 0 0.1
0.2 - tan-1 2
1
2
10
20
100
200
- tan-110
。 -90
相频波特图
+ _
10
u R
L C
一信号源与R、L、C电路串 联,要求 f0=104Hz, △f=100Hz,R=15,请设 计一个线性电路。
解
ω0 f 0 10 4 Q 100 f 100
100 15 L 39.8mH 4 0 2π 10 1 C 2 6360 pF 0L RQ
(b)
相频波特图
返 回
上 页
下 页
• 例9 一阶RC无源低通滤波器
R
C
传递函数,设:
ui
低通
uo
duC ui Ri uC RC uC dt um sin(t ) uC uo 2 ( RC ) 1
Uo H ( ) Ui 1 ( RC ) 2 1
200j H ( j ) ( j +2)(j +10)
返 回
上 页
下 页
•
因此对数模(单位分贝)
H dB 20 lg10 20 lg j 20 lg 1 j
HdB /dB
2
20 lg 1 j
10
20lg10 20
0 0.1
0.2
1
2
10
20
100
200
20lg j -20
一接收器的电路参数为:U=10V =5103 rad/s, 调C使电路中的 电流最大,Imax=200mA,测得 电容电压为600V,求R 、 L 、 C 及Q。
10 U R 50 3 I 0 200 10
U C 600 U C QU Q 60 U 10
1 50 60 L 60mH C 2 6.67μF 3 0L 0 5 10
R ( j ) H ( j ) E ( j )
R( j ) H ( j ) E ( j )
返 回
上 页
下 页
•
例2 某收音机输入回路 L=0.3mH,R=10,为收到
中央电台560kHz信号,求:(1)调谐电容C值; (2) 如输入电压为1.5V,求谐振电流和此时的 电容电压。
返 回 上 页 下 页
ui um cos(t )
ui
高通
C R
uo
•
u+= u-= uC 例10 有源滤波器 if i-=i+=0 Rf i1= if ii1 R1 _ u u uo u + ui + R1 Rf + + uo u i2 R2 C _ Rf uo (1 )u R1 duC ui uC duC R2C uC ui i2 C dt R2 dt
Rf
uom
uom 2
幅频特性
截至频率
o
o
返 回 上 页 下 页
• 例11 激励 u1(t),包含两个频率1、2分量 (1<2): u1(t) =u11(1)+u12(2)
要求响应u2(t)只含有1频率电压。如何实现?
+ u1(t) _
解
u2(t)
设计下列滤波电路实现:
返 回
上 页
设: ui cos t
uC u 解得:
cos(t 90 0 )
R C
2
2
1
上 页 下 页
返 回
•
R f cos(t 90 0 ) uo (1 ) 2 R1 R2C 1
当 0 uom (1 ) R1 1 Rf uom 1 当 0 uom0 (1 ) R2C R1 2 2 w= 0
返 回 上 页 下 页
X UR=UR/|Z|
•
UR=UR/|Z| (A) UR0=10 UR1=0.304 UR2=0.346
UR(f )
U R1 3.04% UR0
UR2 3.46% UR0
∴收到北京台820kHz的节目。
o
640 820 1200 f (kHz)
返 回
上 页
下 页
• 例5
下 页
•
Hale Waihona Puke 1 L1C2 并联谐振,开路 1 ω1 L1 (C2 C3 ) ω2
串联谐振,短路
C3 + _ u1(t)
L1
C2
R
+ u2(t) _
1 信号短路直接加到负载上。
该电路 2 >1 ,滤去高频,得到低频。
注意 滤波器利用谐振电路的频率特性,只允
许谐振频率邻域内的信号通过
返 回 上 页
U L / US
2 4 2 j6
j2 4 2 j6
2I1 (4 j ) I 2 0
2U S I2 2 4 (j ) j6
转移电压比
上 页 下 页
•
注意 ①以网络函数中jω的最高次方的次数定义网
络函数的阶数。 ②由网络函数能求得网络在任意正弦输入时 的端口正弦响应,即有
等效电路 Re L C
Req 100 // 100 50k
50 10 Q 50 0 L 1000 Req
3
100k
返 回
上 页
下 页
•
如图RS=50k,US=100V,0=106,Q=100, 例7 谐振时线圈获取最大功率,求L、C、R及谐振 i0 时I0、U和P。 + 0L R 50k 解 QL 100 C R + u ( 0 L) 2 L Re RS 50k uS R - -
1 0 LC
R 5 L 0.5mH C 0.002μ F
US 100 I0 1mA 3 2 RS 2 50 10 US U 50V 2 P UI 0 0.05W
返 回 上 页 下 页
• 例8
画出网络函数的波特图。 解
改写网络函数为 10j H ( j ) (1+ j 2)(1+ j 10) 10 j 200j 90 tan 1 ( 2) tan 1 ( 10) H ( j ) 1+ +2)(j +10) ( j j 2 1 j 10
解 (1)
1 C 269 pF 2 (2 f ) L
+
R L C
u
_
U 1.5 (2) I 0 0.15μ A R 10
U C I 0 X C 158.5μ V 1.5μ V
or U C QU
0 L
R
U
返 回 上 页 下 页
•
例3
+ u _ 解
R
L V
C
