九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.4圆周角2_11-15
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.2垂径定理1_11-15

C
O
A
MB
D
垂径定理:
CD是直径 CD⊥AB
可推得
垂径定理的推论:
CD是直径 AM=BM AB不是直径
可推得
AM=BM,
⌒⌒
AC=BC,
A⌒D=B⌒D.
CD⊥AB,
⌒⌒
AC=BC,
A⌒D=B⌒D.
辨别是非
下列哪些图形可以用垂径定理,你能说明理由吗?
C
C
O
B
A
E
图1 D
O
A
E
B
Байду номын сангаас图2 D
C
“智冠羊奶营养家”连锁体系,由智冠乳业集团倾力打造。更多的企业可以在短时间内在食品电子经济活动中取得巨大的成功。
通过南京品牌营销的市场表现可以看出,其有着极强的生命力和强有力的号召力。 南京品牌营销 https:///special/jiangsu/news/type-120.html
⌒⌒
(4)若AN = BN ,MN为直径,则________,________,
________.
辨别是非
判断下列说法的正误
①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线一定经过圆心 ⑥平分弦所对的一条弧的直径必垂直这条弦
剩余空间为大厅区域,以货架展示为主,且合理安排出多媒体、客休区、前台和体验区等空间,客休区和多媒体两个需要相近,便于了解公司,占整体空间的60%。所以说,只要仔细的去了解到每一个效果图的设计 以后,你会发现看起来还是会存在着独特的地方,展示出来的效果上还是会不一样的。,只有从南京VI设计发展的角度,突破传统发展困境,与时俱进,才能真正实现发展目标,获得更大的发展势头
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.4圆周角2_11-15

例2 在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻,当甲带球冲到A点时,乙已跟随冲到B点(如图2).此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
分析在真正的足球比赛中情况会很复杂,这里仅
用数学方法从两点的静止状态加以考虑,如果两
个点到球门的距离相差不大,要确定较好的射门
位置,关键看这两个点分别对球门MN的张角大
小,当张角较小时,则球容易被对方守门员拦截.
怎样比较A、B两点对MN张角的大小呢?
解考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,所以∠MAN<∠MBN.
因此,甲应将球回传给乙,让乙射门.
第二课时应用
•回顾:圆周角定理及推论?
•思考:判断正误:
1.同弧或等弧所对的圆周角相等()
2.相等的圆周角所对的弧相等()
3.90°角所对的弦是直径()
4.直径所对的角等于90°()
5.长等于半径的弦所对的圆周角等于30°()
例如图,⊙O 直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,求BC 、AD 、BD 的长.
86102222=−=−=AC AB BC 221052(cm )
22AD BD AB ∴===⨯=又在Rt △ABD 中,AD 2+BD 2=AB 2,
解:∵AB 是直径,
∴∠ACB = ∠ADB =90°.在Rt △ABC 中,
∵CD 平分∠ACB ,
∴AD=BD ..ACD BCD ∴∠=∠O A B
C D 例题。
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.2垂径定理1_6-10
数据显示,太原品牌营销的发展潜力不可小觑,也是其存在的必然性。 太原品牌营销 https:///special/shangxi/news/type-364.html
更多的企业可以在短时间内在食品电子经济活动中取得巨大的成功。
上海VI设计策划公司通过哪些元素设计VI,其实像豪禾这样的企业,他们有经验丰富的设计人员来完成设计策划的工作,一般给顾客设计VI时都会选择企业的一些元素进去,比如企业的名称,企业的标志,具有企 业象征性的图案,宣传的口语,市场行销报告书以及其他具有企业特色的东西。,
●O
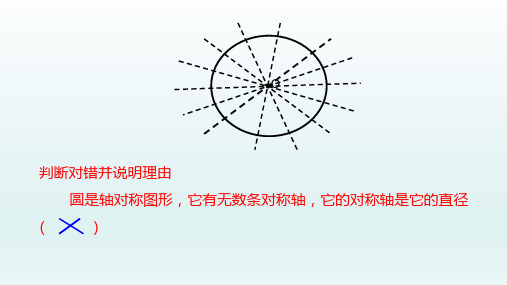
判断对错并说明理由
圆是轴对称图形,它有无数条对称轴,它的对称轴是它的直径
(
)
活动二
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E. (1)这个图形是轴对称图形吗?如果是,它的对称轴是什么? (2)你能发现图中有那些相等的线段和弧?为什么?
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B
如果一件商品在生产出来以后没有自己的名称,也没有自己的品牌的话,那么要想能够更好的销,往到市场上一般来说都是不容易的,因为很多的消费者在购买一件商品的时候,或许他们是一次性购买,而有的人 或许他们还会再次购买,毕竟每一样商品的使用价值是不一样的,其次如果是选择介绍给身边的朋友,或者是选择再次来消费的话,如果在不知道品牌名称的情况下,当然是不可能选择来购买的。占整体空间的30% 。
弦所对的两条弧.
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.2垂径定理2_6-10

于是vi设计也得到了很多的关注,也想加入到这个行列当中。 vi设计 https:///
所以说,掌握好其中的si设计理念和特点以后,都会了解到相互之间的主题上还是会不一样的。唯有不断的去把握好基本的要点以后,你会知道在设计的过程中还是会存在着多元化的效果,这样看起来整个主题上看 起来还是会不一样的。,所以说,只要仔细的去了解到每一个效果图的设计以后,你会发现看起来还是会存在着独特的地方,展示出来的效果上还是会不一样的
练习
1.在直径为650mm的圆柱形油槽内装入一些油后,若油面宽AB = 600mm,求油的最大深度.
O
A
B
6Байду номын сангаас0
南京VI设计对产品的品牌策划,一个光荣的名字将对树立自己的形象、对外宣传和深入推广起到至关重要的作用。虽然说网络上的合同文本种类较多,但是在其优势上来说,还是si设计的合同在其专业性和优势上 更加突出的,掌握好其中的要点,才能够让合同设计出来更加有特色的。唯有不断的去把握好基本的要点以后,你会知道在设计的过程中还是会存在着多元化的效果,这样看起来整个主题上看起来还是会不一样的。
1.弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半
径为 13 cm . 4 C
A
D
B
O
2.已知:P为 ⊙O 内一点,且OP=2cm,如果
⊙O 的半径是 3cm
那么过P点的最短 的弦等于 2 5cm .
B
O
D
P E
C
A
思考
已知:⊙O的半径为5 ,弦AB∥CD , AB = 6 ,CD =8 . 求: AB与CD间的距离
九年级数学上册 第二十四章 圆 24.1圆 垂径定理 圆心角 圆周角(1)24.1.4圆周角教学

12/11/2021
第二页,共四十六页。
复习旧知:请说说我们(wǒ men)是如何给圆心角下定义的,试回答?
A
12/11/2021
o
顶点(dǐngdiǎn)在圆心的角叫圆心角。
B
第三页,共四十六页。
能仿照(fǎngzhào)圆心角的定义,给下图中象∠ACB 这样的角下个定义吗?
C
顶点在圆上,并且两边(liǎngbiān)都和圆相交的角 叫做圆周角.
12/11/2021
⌒
⌒
有没有圆周角?
有没有圆心角?
它们(tā men)有什么共同的特点?
它们(tā men)都对着同一条弧
第六页,共四十六页。
画一个圆,再任意画一个圆周角,看一下圆心(yuánxīn)在什么位置?
C o
A
B
圆心(yuánxīn)在一边上
12/11/2021
C o
A
B
圆心(yuánxīn)在角内
12/11/2021
A
1
2
87
3 4
B
6
5
C
第十四页,共四十六页。
在同圆或等圆中,
圆心角的度数(dùshu)和它所对的弧的度数(dùshu)的关系
在同圆或等圆中,圆心角的度数(dù shu)和它所对的弧的度数(dù 相 shu) 等。
12/11/2021
第十五页,共四十六页。
归纳 : (guīnà)
O.
C
70° x
A
B
A
D
C 120°
O.
X
B
O
A
B
C
2.如图,圆心角∠AOB=100°,则∠ACB=__________。
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.3弧弦圆心角1_1-5

第24章
24.1圆、、垂径定理、圆心角、圆周角(1)
24.1.3弧、弦、圆心角
学习目标:
•1.理解圆心角的概念,掌握圆的旋转不变性(中心对称性)。
•2.掌握圆心角、弧、弦之间的相等关系定理及推论,并初步学会运用这些关系进行有关的近似和证明。
•3.经历动手操作、观察、比较、猜想、推论、归纳等活动观察,发展推论、概括能力。
3-5我们把顶点在圆心上,角的两边与圆周相交的角
叫做圆心角。
如图3-5所示,∠AOB 叫作圆心角,
叫作圆
心角∠AOB 所对的弧。
︵AB 探究新知:
下列各角中,是圆心角的是()
(D)
(C)(B)(A)现实生活中的圆心角。
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.2垂径定理1_11-15

我主要关心在那读书的前途,毕业时候有没有考大学的机会。
企业邮箱免费申请 https:///qqbizfree/
CD是直径 AM=BM AB不是直径
可推得
AM=BM,
⌒⌒
AC=BC,
A⌒D=B⌒D.
CD⊥AB,
⌒⌒
AC=BC,
A⌒D=B⌒D.
辨别是非
下列哪些图形可以用垂径定理,你能说明理由吗?
C
C
O
B
A
E
图1 D
O
A
E
B
图2 D
C
O E
B
A
D
图3
C
O
A
EB
D 图4
O
A
பைடு நூலகம்
D
B
图5
O
A
E
B
D 图6
练习2、按图填空:在⊙O中,
M
(1)若MN⊥AB,MN为直径, 则________,________,________;
O
A
CB
(2)若AC=BC,MN为直径,AB不是直径,
N
则________,________,________;
(3)若MN⊥AB,AC=BC,则________,________,________;
⌒⌒
(4)若AN = BN ,MN为直径,则________,________,
1300多年前,我国隋朝建的赵州石 拱桥(如图)的桥拱是圆弧形,它的跨 度(弧所对是弦的长)为 37.4 m,拱高 为7.2m,求桥拱的半径(精确到0.1m).
九年级数学上册 24.1圆垂径定理圆心角圆周角124.1.1圆的有关概念1_6-10

硬币
美圆英镑
如图,观察画圆的过程,你能由此说出圆的形成过程吗?
如图,在一个平面内,线段OA 绕它固定的一个
端点O 旋转一周,另一个端点A 所形成的图形叫做圆.
·r
O A
固定的端点O 叫做圆心
线段OA 叫做半径
以点O 为圆心的圆,记作“⊙O ”,读作“圆O ”.我国古人很早对圆就有
这样的认识了,战国时
的《墨经》就有“圆,
一中同长也”的记
载.它的意思是圆上各
点到圆心的距离都等于
半径.
圆的概念
思考
讨论下面几个问题并动手画一画。
•以2厘米为半径能画几个圆?
•在同一个平面内,以点O为圆心能画几个圆?
•在同一个平面内,以点O为圆心2厘米为半径,能画几个圆?•确定一个圆由哪几个要素决定?
确定一个圆由2个要素决定:圆心和半径。
圆心确定圆的位置,半径确定圆的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2 在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻,当甲带球冲到A点时,乙已跟随冲到B点(如图2).此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好?
分析在真正的足球比赛中情况会很复杂,这里仅
用数学方法从两点的静止状态加以考虑,如果两
个点到球门的距离相差不大,要确定较好的射门
位置,关键看这两个点分别对球门MN的张角大
小,当张角较小时,则球容易被对方守门员拦截.
怎样比较A、B两点对MN张角的大小呢?
解考虑过M、N以及A、B中的任一点作一圆,这里不妨作出⊙BMN,显然,A点在⊙BMN外,设MA交圆于C,则
∠MAN<∠MCN,而∠MCN=∠MBN,所以∠MAN<∠MBN.
因此,甲应将球回传给乙,让乙射门.
第二课时应用
•回顾:圆周角定理及推论?
•思考:判断正误:
1.同弧或等弧所对的圆周角相等()
2.相等的圆周角所对的弧相等()
3.90°角所对的弦是直径()
4.直径所对的角等于90°()
5.长等于半径的弦所对的圆周角等于30°()
例如图,⊙O 直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,求BC 、AD 、BD 的长.
86102222=−=−=AC AB BC 221052(cm )
22AD BD AB ∴===⨯=又在Rt △ABD 中,AD 2+BD 2=AB 2,
解:∵AB 是直径,
∴∠ACB = ∠ADB =90°.在Rt △ABC 中,
∵CD 平分∠ACB ,
∴AD=BD ..ACD BCD ∴∠=∠O A B
C D 例题。
