统计学习题集5
统计学试题答案(5、6)
统计学试题（5）一、单项选择：1、各变量值与其均值离差之和（）。
A.小于0B.等于0C.大于0D.等于12、某校男生平均体重为60㎏，标准差为5㎏，女生的平均体重为50㎏，标准差为5㎏，数据表明（）。
A.男生的体重差异与女生相等B. 男生的体重差异大于女生相等C.男生的体重差异小于女生相等D. 男生的体重差异与女生体重差异无法比较3、全国人口普查中，所调查的项目性别是（）。
A.指标B.标志C.质量指标D.数量指标4、样本均值是总体均值的（）。
A.有偏估计量B.唯一的估计量C.无偏估计量D.近似估计量5、比例估计量的标准误是A.PB.P(1-P)C.pP-1( D.n PP)1(-6、假设检验的功效为（）。
A.αB.1-αC.βD.1-β7、一元线性回归中的判定系数等于（）。
A.相关系数B.相关系数的平方C.相关系数的倒数D.相关系数的立方8、置信区间的长度越短，估计的精度则（）。
A.越高B.越低C.与长短无关D.无法判定9、假设检验的显著性水平越大。
A.弃真错误越小B.弃真错误越大C.纳伪错误越大D.第一类错误越小10、右侧检验的拒绝域在（）。
A.两侧B.左侧C.中间D.右侧二、多项选择：1、概率抽样的形式有。
A.等距抽样B.整群抽样C.简单随机抽样D.非随机抽样E.分层抽样2、下列属于位置平均数的有（）。
A.均值B.众数C.中位数D.方差E.离散系数3、以下说法正确的有（）。
A.累计增长量等于逐期增长量之和B.环比发展速度的连乘积等于定基发展速度C.增长速度等于发展速度减1D.平均发展速度减1等于平均增长速度E.增长1%的绝对值等于100除以前期水平4、进行假设检验时，原假设正确但却被拒绝的错误是。
A. 弃真错误B. 第一类错误C. 纳伪错误D. 第二类错误E. 功效错误5、如果分析数据中存在极端数值，则这组分析数据的众数（）。
A.受极端数值大小的影响B.不受极端数值大小的影响C.是出现次数最多的数值D.受极端数值位置的影响E. 不受极端数值位置的影响三、名词解释：1、总体单位2、变异指标3、样本4、时间数列5、参数四、 简答题：1、标准差和离散系数的适用场合。
统计学原理试题(5)
《统计学原理》试题（5）一、填空（1分×9=9分）1、统计学自身的发展，沿着两个不同的方向，形成（理论统计）和（应用统计学）两类。
2、全面调查包括（普查）和（全面统计报表）两种。
3、强度相对数的数值大小，如果与现象的发展程度或密度等成正相关，叫做（正指标）；反之，叫做（逆指标）。
4、总体成数P的平均数等于（p），其方差为（p(1-p)）。
5、某班数学平均75分，英语平均80分，则该班两门课总成绩平均（155）分。
6、完全相关即函数关系，其相关系数为（1或-1）。
7、价格上涨后，同样多的人民币少购买商品8%，则物价上涨（8.7%）。
8、时间序列的波动可以分解为趋势变动、（季节变动）、循环变动和随机变动。
9、综合评价的常规方法有总分评定法、指数综合法和最优值距离法、（功效系数）法。
二、单项选择题（1分×10=10分）1、设某地区有60家生产皮鞋的企业，要研究他们的产品情况，总体是（4）。
（1）每一个企业（2）所有60家企业（3）每一双皮鞋（4）所有企业生产的皮鞋2、数量指标和质量指标的根本区别在于（1）。
（1）说明总体现象的内容不同（2）数量大小不同（3）计量单位不同（4）使用领域不同3、某灯泡厂对产品质量进行大检查，应该选择（4）。
（１）统计报表（２）重点调查（３）全面调查（４）抽样调查４、统计分组的关键在于确定（4）。
（１）组中值（２）组距（３）组数（４）分组标志和分组界限５、某商场计划４月份销售利润比３月份提高２％，实际却下降了５％，则销售利润计划完成程度为（3）。
（１）６６.９７％（２）１０５.０３％（３）９３.１４％（４）９２.７８％6、单相关系数和可决系数（3）。
（１）二者的作用完全相同（２）二者数量上没有联系（３）二者数量上有密切联系（４）二者的符号相同７、编制总指数的两种方式是（2）。
（1）数量指标指数和质量指标指数（2）综合指数和平均指数（3）算术平均数指数和调和平均数指数（4）定基指数和环比指数8、时间数列的项数是9，可以计算的环比发展速度有（ 1 ）个。
生物统计学习题集5
生物统计学姓名：班级：学号：第一章概论一、填空1 变量按其性质可以分为_______变量和_______变量。
2 样本统计数是总体_______的估计量。
3 生物统计学是研究生命过程中以样本来推断_______的一门学科。
4 生物统计学的基本内容包括_______、_______两大部分。
5 统计学的发展过程经历了_______、_______、_______3个阶段。
6 生物学研究中，一般将样本容量_______称为大样本。
7 试验误差可以分为_______、_______两类。
二、判断（）1 对于有限总体不必用统计推断方法。
（）2 资料的精确性高，其准确性也一定高。
( ) 3 在试验设计中，随机误差只能减少，而不可能完全消除。
（）4 统计学上的试验误差，通常指随机误差。
三、名词解释样本总体连续变量非连续变量准确性精确性第二章试验资料的整理与特征数的计算一、填空1 资料按生物的性状特征可分为_______变量和_______变量。
2 直方图适合于表示_______资料的次数分布。
3 变量的分布具有两个明显基本特征，即_______和______。
4 反映变量集中性的特征数是_______，反映变量离散性的特征数是_______。
5 样本标准差的计算公式s=_______。
二、判断( ) 1 计数资料也称连续性变量资料，计量资料也称非连续性变量资料。
( ) 2 条形图和多边形图均适合于表示计数资料的次数分布。
（）3 离均差平方和为最小。
（）4 资料中出现最多的那个观测值或最多一组的中点值，称为众数。
（）5 变异系数是样本变量的绝对变异量。
三、名词解释资料数量性状资料质量性状资料计数资料计量资料普查抽样调查全距（极差）组中值算数平均数中位数众数几何平均数方差标准差变异系数四、单项选择（ ）1 下面变量中属于非连续性变量的是_______。
A 身高 B 体重 C 血型 D 血压（ ）2 对某鱼塘不同年龄鱼的尾数进行统计分析时，可做成_______图来表示。
统计学计算题 (5)
3）110%（提高 5%） 收购量不变=106.67% 收购额总指数=110% 117.34%-112%=5.34% 360 5.34%=19.22 亿元 4）43.2=24.02+19.22 从一个标准差为 8 的总体中抽取一个容量为 40 的样本，计算得样本均值为 32，试在 0.05 的显著水平下估计总体均值的 置信区间。 n=40 σ=8
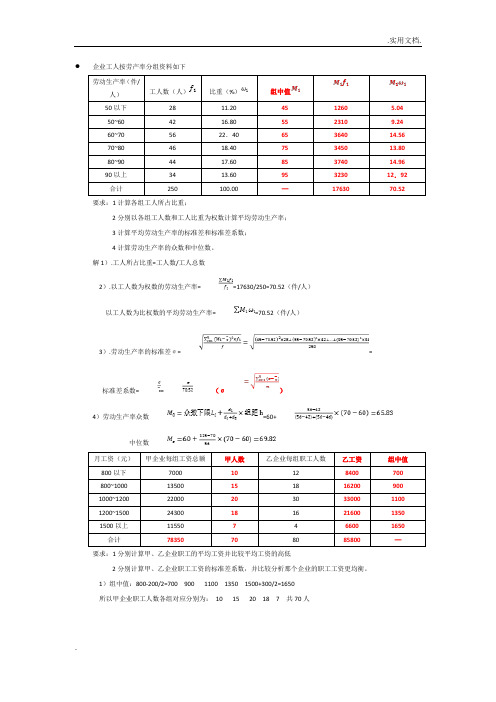
以工人数为比权数的平均劳动生产率=
=70.52（件/人）
.实用文档.
5.04 9.24 14.56 13.80 14.96 12．92 70.52
3）.劳动生产率的标准差σ=
=
标准差系数=
=
（σ
）
4）劳动生产率众数
=60+
中位数
月工资（元） 甲企业每组工资总额
甲人数
乙企业每组职工人数 乙工资
800 以下
使用寿命（小时） 3000 以下 3000~5000 5000~7000 7000 以上 合计 根据以上资料，要求：
产品件数 1 14 15 10 40
组中值 2000 4500 6500 8000
1） 按重复抽样和不重复抽样计算该产品平均寿命的抽样平均误差； 2） 按重复抽样和不重复抽样计算该产品合格率的抽样平均误差； 3） 根据重复抽样计算的抽样平均误差，以 95%的概率保证程度对该产品的平均使用寿命和合格率进行区间估计。
1）组中值：800-200/2=700 900 1100 1350 1500+300/2=1650
所以甲企业职工人数各组对应分别为： 10 15 20 18 7 共 70 人
组中值 700 900 1100 1350 1650 —
.
乙企业工资 12
北师大统计学基础习题答案5
Exercise 51. P201: 4.59.Let 54321Y Y Y Y Y <<<<be the order statistics of a random sample of size n from a distribution with p.d.f. ∞<<=-x e x f x 0,)(,zero elsewhere..Show that 21Y Z =and 242Y Y Z -=are independent. Solution: Since ∞<<=-x e x f x 0,)(, so ∞<<-=-x e x F x 0,1)()()()]()][()()][([!1!1!1!5),(424242424,2y f y f y F y F y F y F y y g -=424422))()(1(120y y y y y y e e e e e e --------= Since 12Z Y =，214Z Z Y +=，11101==J . 22111211212112421)1)(1(120))(1(120),(z z z z z z z z z z z z z e e e e ee eee e z z g ---------------=--=)1(20)()]'([)](1)][([!3!1!5)()(11424322211z z e e y f y F y F y F y g z g ---=-== ⎰⎰∞----∞--==01240121222211)1)(1(120),()(dz e e e e dz z z g z g z z z z222211222205042)1(6)1(201120)|5|4()1(120z z z z z z z z e e e e e e ee----∞-∞----=-⋅=----= Thus, =),(21z z g )()(2211z g z g .So 1Z and 2Z are independent.P274: 6.15. Let X be the mean of a random sample of size n from adistribution that is )9,(μN . Find n such that 90.0)11Pr(=+<<-X X μ, approximately.Solution: Since ~X )9,(n N μ,)1,0(~3)(N X n μ-.90.01)3(2)3|3)(Pr(|)1|Pr(|)11Pr(=-Φ=<-=<-=+<<-nn X n X X X μμμ Thus )3(n Φ=0.95, 645.13=nand 35.24≈n . Because n must be an integer, so n=24 or 25.P275: 6.18. Let 121,,,+n n X X X X be a random sample of size 9 from adistribution that is ),(2σμN .(a) If σis known, find the length of a 95 percent confidence interval for if this interval is based on the random variable.(b) If σis unknown, find the expected value of the length of a 95 percent confidence interval for if this interval is based on the random variable S X /)(8μ-. (c) Compare these two answers. Solution:(a) Since ~991∑==i iXX )9,(2σμN ,thus)1,0(~)(9N X σμ-.Pr(|σμ)(9-X |<1.96)=0.9595.0)96.1)(396.1Pr(=<-<-⇔σμX95.0)396.1396.1Pr(=+<<-⇔σμσX X . The 95 percent confidence interval for μis )396.1,396.1(σσ+-X X and the length of it isσσ31.17598≈ (b) Since σ is unknown, then )8(~)(81/t SX n S X T μμ-=--=975.0)P r (95.01)Pr(295.0))(8Pr(=≤⇒=-≤⇒=<-<-b T b T b S X b μFrom TABLE IV of Appendix B, we know b=2.306, thus95.0)8306.28306.2Pr(=+<<-σμσX X . The 95 percent confidence interval for μ is )8306.2,8306.2(σσ+-X X with the length S L 8612.4=⎰∞-Γ===02342121222)4(183612.4))/9((38612.4)(8612.4)(dx e x x S E S E L E xσσσ)29(22)4(183612.422)4(183612.42)4(183612.429402729402274ΓΓ=Γ=Γ=⎰⎰∞-∞-σσσdy e y dx e x y xThen σ49.1)(≈L E(c) From (a) we know the answer is σ31.1, from (b) we know the answer isσ49.1. The two methods yield results that are in substantial agreement, which shows the length of the confidence interval for μ is almost the same with the parameter σ known or unknown.P279: 6.30.Let two independent random samples, each of size 10, from two normal distributions ),(21σμN and ),(22σμN yield 8.4=x ,64.821=s ,6.5=y ,88.722=s . Find a 95 percent confidence interval for.Solution: Let 1021,,X X X and 1021,,Y Y Y denote, respectively, independent random samples from the two distributions ),(21σμN and),(22σμN , then ~10101∑==i iXX )10,(21σμN and ~10101∑==i iYY )10,(22σμN .)5,(~221σμμ--N Y X .)18(~/)1010(222221χσS S +)18(~9)()()()101101(18)(10)()(222121222121t S S Y X S S Y X T +---=++---=μμμμ.101.295.0)Pr(=⇒=<<-b b T b and95.0))(3)()(3)Pr((2221212221=++-<-<+--S S b Y X S S b Y X μμ So the random intervalis )3101.2)(,3101.2)((22212221S S Y X S S Y X ++-+--. Let 8.4=x ,64.821=s ,6.5=y ,88.722=s , we get a 95 percent confidenceinterval (-3.6,2.0).2. Use Splus or R software to compute the mean, standard deviation, skewness and kurtosis of the following dataset.-0.4292, 0.0064, 0.1181, -0.6282, 2.2010, -1.7623, 0.0921,1.8742, 1.4538, 0.3575, -1.5848, 0.4993, 0.7762, -0.2638, -1.1003, -2.2480, 0.5419, -0.4018, -0.3562, -0.5872. Solution: > x<-c(-0.4292,0.0064,0.1181,-0.6282,2.2010,-1.7623,0.0921,1.8742,1.4538,0.3575,-1.5848,0.4993,0.7762,-0.2638,-1.1003,-2.2480,0.5419,-0.4018,-0.3562,-0.5872) > a=mean(x) > a[1] -0.072065 > b=sd(x) > b[1] 1.143067> c=mean(((x-a)/b)^3) > c[1] 0.1234913> d=mean(((x-a)/b)^4)-3 > d[1] -0.5280221So the mean of the dataset is -0.072065, the standard deviation is 1.143067, the skewness is 0.1234913 and the kurtosis is -0.5280221.3*. P203: 4.73. Let n Y Y Y <<< 21be the order statistics of a random sample of size n from the exponential distribution with p.d.f.∞<<=-x e x f x 0,)(,zero elsewhere..(a) Show that 11nY Z =,))(1(122Y Y n Z --=,))(2(233Y Y n Z --=,…1--=n n n Y Y Z , are independent and that each i Z has the exponential distribution.Solution: Since n y y y n e e e n y y y g ---= 21!),,(21, andn n n Z Z n Zn Z Y n Z n Z Y n Z Y ++-+=-+==-21,,1,12121211 and the Jacobian is!1121111021111011101n n n n n n n n J =---=nn z z z z n z n z n z n z nz n n e e e eee y y y g J z z z g ---++-+--+--=== 2121211)1()1(2121),,(||),,(k z n k k n k k e dz dz dz dz z z z g z g -+-∞∞∞∞==⎰⎰⎰⎰ 11012100),,()(So )()()(),,(221121n n n z g z g z g z z z g = and ∞<<=-k z k k z e z g k 0,)( Which shows that n z z z ,,21are independent and that each i z has the exponential distribution.(b) Demonstrate that all linear functions of n Y Y Y ,,,21 , such as ∑ni i Y a 1, canbe expressed as linear functions of independent random variables. Solution:)())(1())(1(11122112211---++---++--+=+++n n n k k k n n Y Y b Y Y k n b Y Y n b nY b Y a Y a Y a n n Z b Z b Z b +++= 2211. Then ,)2()1(,)1(232121a n b n n b a n b n b =---=-- n n n n n k k k a b a b b a k n b k n b ==-=--+---+)1(,)1()2(,,)()1(,111 . Then n n nk k n n a b k n a a b n a a a b n a a a b =+-++=-++=++=,1,,1,322211So1,11+-+==∑∑==i n a a b Z b Y a ni i ni i i ni i i .Since n Z Z Z ,,,21 are independent, thenn n Z b Z b Z b ,,,2211 are independent. So∑=ni i i Y a 1can be expressed as linearfunctions of independent random variables.P275: 6.19.Let 121,,,+n n X X X X be a random sample of size n+1, n>1, from a distribution that is ),(2σμN . Let n X X ni /1∑= andn X X S ni /)(212-=∑. Find the constant c so that the statisticσ1+-n X X chas a t-distribution. If n=8, determine k suchthat 80.0)Pr(=+<<-kS X kS X μ. The observed interval is ),(ks x ks x +- often called an 80 percent prediction interval for 9X . Solution: )/,(~2n N X σμ，),(~21σμN X n +，),1,0(~21σnn N X X n +-+ ).1(~11)1(1),1(~).1,0(~112212221--⋅+⋅-=-+--+-+++n t SX X n nn n n nS n n X X n nS N nn X X n n n σσχσσTherefore 11+-=n n c . 80.0)9797Pr()Pr()Pr(999=<-=<-=+<<-k S X X k S X X kS X x kS X 60.1,415.197==k k . So k=1.60.。
统计学习题集
XIN BIAN TONG JI XUE XI TI JI 新编统计学习题集汪全勇汤莉编写石河子大学经贸学院SHIHEZI DAXUE JINGMAO XUEYUAN第一章绪论一、填空题1、统计一词有三种涵义，即统计工作、______和______。
2、在统计发展的不同阶段，形成三种主要学派，它们是_________、政治算术学派和________。
3、统计总体特点有三性，即_______、___________和_________。
4、统计工作与统计资料的关系是和的关系。
5、统计工作与统计学的关系是和的关系。
6、从统计方法构成来看，统计学可以分为和。
7、从统计方法研究和统计方法的应用角度来看，统计学可以分为和。
二、简答题1、统计学研究的对象及特点是什么？2、简述统计学的三种涵义之间的关系。
第二章统计资料的搜集的整理一、填空题1、统计资料分为两种类型：一是_______；另一_______。
2、重点调查是对_______进行的调查，抽样调查则是按照________原则在总体中抽取________组成样本加以研究，并以________推算______的一种资料搜集方式。
3、原始资料准确性审查包括_______和_________。
4、变量值按其数值是否连续，有_________变量和_________变量之分。
5、统计指标和统计标志的区别之一，就是统计指标是说明__________特征，而统计标志是说明_________特征。
6、统计指标按其反映的时间特点不同。
可分为_________指标和_____指标；按其反映总体特证的不同，可分为________指标和_________指标。
7、、对调查对象的所有单位都进行调查，这是调查;而重点调查、典型调查、抽样调查都属于调查。
8、若要调查某地区工业企业职工的生活状况，调查对象是，调查单位是，填报单位是。
9、调查单位是的承担者，填报单位是的单位。
10、一个完整的统计调查方案应包括、、、。
统计学第五章练习题
第五章 统计推断一、填空题5.1.1 设样本n X X X ,,,21 来自总体)69.1,(μN ，则检验假设35:=μo H 时，使用的检验量是 。
5.1.2 设n X X X ,,,21 是来自总体X 的一个样本，又设μ=)(X E ，2)(σ=X D ，则总体均值μ的无偏估计为 ；总体方差σ2的无偏估计为 。
5.1.3 若检验统计量的观测值落在拒绝域内，则应 。
5.1.4 设∑==n i i X n X 11为来自正态总体),(2σμN 的样本均值，μ未知，欲检验假设22:σσ=o H ，需要使用的检验统计量为 。
5.1.5 其他条件不变时，置信度越高，则置信区间就越 。
☆5.1.6 检验两个正态总体均值的假设21:μμ=o H ，（已知2221σσ=）时，使用的检验量为 ，拒绝域为 。
二、单项选择题（在每小题的3个备选答案中选出1个正确答案，并将其字母填在题干后面的括号内。
）5.2.1 对总体参数进行抽样估计的首要前提是必须 （ ） A ．事先对总体进行初步分析 B ．按随机原则抽取样本C ．保证调查数据的准确性、及时性5.2.2 若其它条件相同，则下列诸检验的P 值中拒绝原假设理由最充分的是 （ ） A ．2% B ．10% C ．25%5.2.3 某校有学生8000人，随即抽查100人，其中有20人对学生管理有意见，则该校学生中对学校后勤管理有意见的人数的点估计值为 （ ）A ．20%B ．20C ．16005.2.4 如果总体服从正态分布，但总体均值和方差未知，样本量为n ，则用于构造总体方差置信区间的随机变量的分布是 （ ）A ．()0,1NB ．),(2σμN C ．χ2(n-1)5.2.5 其他条件相同时，要使抽样误差减少1/4，样本量必须增加 （ ） A ．1/4 B ．4倍 C ．7/95.2.6 影响区间估计质量的因素不包括 （ ） A. 置信度 B. 总体参数 C. 样本量5.2.7 某企业最近几批产品的优质品率分别为88％，85％，91％，为了对下一批产品的优质品率进行抽样检验，确定必要的抽样数目时，P 应选 （ ）A ．85%B ．87%C ．90%5.2.8 设),(~2σμN X ，（n X X X ,,,21 ）是X 的一个简单随机样本，则未知参数2σ的矩估计量为 （ ）A .nX Xni i∑=-12)( B .∑=-ni iX X12)( C .1)(12--∑=n X Xni i三、多项选择题（在下列4个备选答案中，至少有二个是正确的，请将其全部选出，并把字母填在题干后面的括号内。
统计学第5章 习题
） C.6.50
D.7.50
t=2
9. 从两个总体中分别抽取n1=7，n2=6的两个独立
随机样本。经计算得到下面的方差分析表：
差异源 SS df MS F P-value F crit
组间 组内 总计
7.50 26.19 33.69
A B 12
7.50 2.38
3.15
0.10
4.84
表中 在下面的假定中，哪一个不属于方差分析中的假定 （ ） A. 每个总体都服从正态分布 B. 各总体的方差相等 C. 观测值是独立的 D. 各总体的方差等于0
4.在方差分析中提出的原假设是H0: 1 2 … k ， 备择假设是（ ） A. H1: 1 ≠ 2 ≠ … ≠ k B. H1: 1 > 2 >… > k C. H1: 1 < 2 < … < k D. H1: 1 , 2 , … , k 不全相等
第五章 复习题
选择题
1.方差分析的主要目的是（
）
A. 各总体是否存在方差 B. 各样本数据之间是否有显著差异 C. 分类型自变量对数值型因变量的影响是否显著 D. 分类型因变量对数值型自变量的影响是否显著
2. 在方差分析中，检验统计量F是（ A.组间平方和除以组内平方和 B.组间均方除以组内均方 C.组间平方和除以总平方和 D.组间均方除以总均方 ）
表中“A、B”的结果是（ ） A. 6.50和1.38 B.7.50和2.38 C.8.50和3.38 D.9.50和4.38
t 2, n n1 n2 13, SA SE 7.5 26.19 A 7.5, B 2.38 t 1 1 nt 13 2
11. 从两个总体中分别抽取n1=7，n2=6的两个独
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章统计指数
一、填空题
1.编制综合指数的一般原则是：编制数量指数时，把作为同度量因素的质量指标固定在期。
编制质量指数时，把作为同度量因素的数量指标指标固定在期。
2.由加权算术平均式形式计算数量指数时，其权数是。
3.由加权调和平均式形式计算质量指数时，其权数是。
4.平均指标指数由可变构成指数、指数、指数构成。
5.某企业今年比去年产品产量增长12%，出厂价格平均下降了12%，则产品产值指数为。
6.某地区两年中，每年都用100元购买某商品，而第二年购回的该商品数量却比第一年少了10%，该商品的价格第二年比第一年。
二、判断题
1.某商店今年比去年销售量增长12%，价格下降了12%，则销售额指数为100%。
（）
2.某居民两年中，每年都用100元购买某商品，而第二年购回的该商品数量却比第一年少了20%，该商品的价格第二年比第一年上涨了20%。
（）
3.编制价格指数时，一般用报告期销售量作同度量因素。
（）
4.编制销售量指数时，一般用报告期价格作同度量因素。
（）
5.职工平均工资下降了15%，固定构成指数为115%，则职工人数指数为100%。
（）
6.某居民两年中，每年都用100元购买某商品，而第二年购回的该商品数量却比第一年多了20%，该商品的价格第二年比第一年下降了20%。
（）
7.把构成固定下来，单纯反映各组水平变动的指数是结构影响指数。
（）
8.个体指数是反映个别现象数量变动的相对数。
（）
三、单项选择题
1.按照个体单位成本指数和报告期总成本资料计算的单位成本总指数是
（）。
A.综合指数
B.平均指标指数
C.加权算术平均指数
D.加权调和平均指数 2.下列指数中的质量指标指数是（ ）。
A.劳动生产率指数
B.总产值指数
C.总成本指数
D.产量指数 3.某企业生产多种产品，实际与计划相比，其产品单位成本总指数为98%，则说明平均来说该企业（ ）。
A.未完成成本降低的计划
B.超额完成成本降低的计划
C.产品单位成本上升2%
D.总成本下降2%
4.设q 为产品产量，m 为单位产品原材料消耗量，p 为单位产品原材料价格，则公式110100q m p q m p -∑∑的意义是（ ）。
A.反映费用总额变动的绝对额
B.反映由于单耗的变动使费用总额变动的绝对额
C.反映由于产品产量的变动使费用总额变动的绝对额
D.反映由于单位产品原材料价格的变动使费用总额变动的绝对额
5.设q 为产品产量，m 为单位产品原材料消耗量，p 为单位产品原材料价格，则
公式
11
1
1
10
q m p q m
p ∑∑的意义是（ ）。
A.反映费用总额变动的程度
B.反映产品产量变动的程度
C.反映单耗变动的程度
D.反映单位产品原材料价格变动的程度
6.设q 为产品产量，z 为单位产品成本，则公式1111
1
z
q z
q z
k ∑∑的意义是（ ）。
A.反映总成本变动的程度
B.反映产品产量变动的程度
C.反映单位成本变动的绝对额
D.反映单位产品成本变动的程度 7. 设q 为产品产量，p 为单位产品价格，则公式00
00
q k q p q p -∑∑的意义是
（ ）。
A.反映由于产品产量的变动使费用总产值变动的绝对额
B.反映由于单位产品价格的变动使总产值变动的绝对额
C.反映总产值变动的绝对额
D.反映由于产品产量的变动使费用总产值变动的程度
8.平均单位成本可变构成指数的公式是（ ）。
A.
1110
1
1
q z q z
q q
÷∑∑∑∑ B.
1000
1
q z q z q q
÷∑∑∑∑
C.
1100
1
q z q z q q
÷∑∑∑∑ D.
0100
q z q z q q
÷∑∑∑∑
9.某企业报告期产量比基期增长了15%，生产费用增长了10%，则其产品单位成本降低了（ ）。
A.33.33%
B.95.65%
C.5%
D.4.35% 10.如果产值增长20%，职工人数增长10%，则全员劳动生产率增长（ ）。
A.10%， B.2% C.32% D.132% 四、多项选择题
1.指数的作用有（ ）。
A.综合反映现象总体的变动方向和程度
B.分析现象总体变动中各个因素的影响方向和影响程度
C.利用指数数列分析现象发展变化趋势
D.建立回归方程进行预测
E.利用相关系数测定现象之间相关的程度 2.编制综合指数的一般原则是（ ）。
A.编制数量指数时，把作为同度量因素的质量指标固定在基期。
B.编制质量指数时，把作为同度量因素的数量指标固定在基期。
C.编制数量指数时，把作为同度量因素的质量指标固定在报告期。
D.编制质量指数时，把作为同度量因素的数量指标固定在报告期。
E.数量指数和质量指数都把同度量因素固定在报告期。
3.平均指标指数包括（ ）。
A.可变构成指数
B.固定构成指数
C.加权算术平均式指数
D.结构影响指数
E.加权调和平均式指数
4.作为综合指数变形的平均式指数应用的一般规则是（ ）。
A.计算数量指标指数，应采用以基期总量指标（00p q ）为权数的加权算术平均式指数。
B.计算数量指标指数，应采用以报告期总量指标（11p q ）为权数的加权算术平均式指数。
C.计算质量指标指数，应采用以报告期总量指标（11p q ）为权数的加权调和平均式指数。
D.计算质量指标指数，应采用以报告期总量指标（11p q ）为权数的加权算术平均式指数。
E.计算数量指标指数，应采用以基期总量指标（00p q ）为权数的加权调和平均式指数。
五、计算题 1.某工厂资料如下：
计算三种产品产量总指数以及由于产量增长使企业增加的产值。
三种产品产量总指数为：%64.103550570
000==∑∑=p q p q k k q q
由于产量增长使企业增加的产值为：
205505700000=-=∑-∑p q p q k q （万元）
2.某企业资料如下：
计算三种产品价格总指数以及由于价格变动使销售额变动的绝对额。
三种产品价格总指数为：%85.10263211
11
1==∑∑=p q k k
p
p
由于价格变动使销售额变动的绝对额为： 18632650=-(万元) 3.某工厂资料如下： 从相对数和绝对数两方面对该厂总产值的变动进行因素分析。
（万元）（万元）万元）9
.94.23(3.33%
59
.111%7.137%7.1534.853
.95624.8562
3.95011100010011+=⨯=⨯
=∑∑⨯∑∑=∑∑p q p q p q p q p q p q 计算结果表明：从相对数来说，该工厂产值报告期比基期增长了53.7%，是由于产量增长了37.7%和价格上升了11.59%两个因素共同影响的结果；从绝对数来说，该工厂产值报告期比基期增加了33.3万元，是由于产量增长使产值增加了23.4万元和价格上升使产值增加了9.9万元两个因素共同影响的结果。
4.某企业三种产品的有关资料如下：
从相对数和绝对数两方面对该企业总成本的变动进行因素分析。
）（万元）
（（万元）万元）05.031.0(26.0%24.97%67.120%33.11781
.176
.15.181.15.176.1011
100010011-+=+=⨯
=∑∑⨯
∑∑=∑∑z q z q z q z q z q z q 计算结果表明：从相对数来说，该企业总成本报告期比基期增长了17.33%，是由于产量增长了20.67%和单位成本下降了2.76%两个因素共同影响的结果；从绝对数来说，该企业总成本报告期比基期增加了0.26万元，是由于产量增长使总成本增加了0.31万元和单位成本下降使总成本减少了0.05万元两个因素共同影
响的结果。
5.某企业有关资料如下： 从相对数和绝对数两方面对该企业平均工资的变动进行因素分析。
520
480
480620520620500
260000
1000480000
1000480000100062000050026000010006200000
1
1
1
1
1
1
1
1
1
1
⨯=⨯=∑∑∑∑⨯
∑∑∑∑=
∑∑∑∑f f
x f
f
x f f
x f
f
x f f
x f
f
x
119.23%=129.17%×92.31% 100（元）=140（元）+（-40元）
计算结果表明：从相对数来说，该企业工人总平均工资报告期比基期增长了19.23%，是由于各组工资水平的增长使总平均工资上升了29.17%和工人构成的变化使总平均工资下降了7.69%两个因素共同影响的结果；从绝对数来说，该企业总平均工资报告期比基期增加了100元，是由于各组工资水平的增长使总平均工资增加了140元和工人构成的变化使总平均工资减少了40元两个因素共同影响的结果。