(名师整理)最新数学中考专题冲刺《二次函数动点成特殊三角形问题》压轴真题训练(含答案)

合集下载

(名师整理)最新数学中考专题冲刺《函数》压轴真题训练(含答案)

冲刺中考《函数》压轴真题训练第Ⅰ卷（选择题）一．选择题1．（2019•兴安盟）如图，反比例函数y ＝的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为（）A．1 B．2 C．4 D．82．（2019•恩施州）函数y ＝﹣中，自变量x的取值范围是（）A．x ≤B．x ≥C．x ＜且x≠﹣1 D．x ≤且x≠﹣1 3．（2019•济南）函数y＝﹣ax+a与y ＝（a≠0）在同一坐标系中的图象可能是（）A ．B ．1C ．D ．4．（2019•阜新）如图，在平面直角坐标系中，将△ABO沿x轴向右滚动到△AB1C1的位置，再到△A1B1C2的位置……依次进行下去，若已知点A（4，0），B（0，3），则点C100的坐标为（）A．（1200，）B．（600，0）C．（600，）D．（1200，0）5．（2019•铁岭）如图，在Rt△ABC中，AB＝AC，BC＝4，AG⊥BC于点G，点D为BC边上一动点，DE⊥BC交射线CA于点E，作△DEC关于DE的轴对称图形得到△DEF，设CD的长为x，△DEF与△ABG重合部分的面积为y．下列图象中，能反映点D从点C向点B运动过程中，y与x的函数关系的是（）A ．B ．C ．D ．6．（2019•盘锦）如图，四边形ABCD是矩形，BC＝4，AB＝2，点N在对角线BD上（不与点B，D重合），EF，GH过点N，GH∥BC交AB于点G，交DC于点H，EF∥AB交AD于点E，交BC于点F，AH交EF于点M．设BF＝x，MN＝y，则y关于x的函数图象是（）2A ．B ．C ．D ．7．（2019•恩施州）抛物线y＝ax2+bx+c的对称轴是直线x＝﹣1，且过点（1，0）．顶点位于第二象限，其部分图象如图4所示，给出以下判断：①ab＞0且c＜0；②4a﹣2b+c＞0；③8a+c＞0；④c＝3a﹣3b；⑤直线y＝2x+2与抛物线y＝ax2+bx+c两个交点的横坐标分别为x1，x2，则x1+x2+x1x2＝5．其中正确的个数有（）A．5个B．4个C．3个D．2个38．（2019•朝阳）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，现给出下列结论：①abc＞0；②9a+3b+c＝0；③b2﹣4ac＜8a；④5a+b+c＞0．其中正确结论的个数是（）A．1 B．2 C．3 D．49．（2019•营口）如图，A，B是反比例函数y ＝（k＞0，x＞0）图象上的两点，过点A，B分别作x轴的平行线交y轴于点C，D，直线AB交y轴正半轴于点E．若点B的横坐标为5，CD＝3AC，cos∠BED ＝，则k的值为（）A．5 B．4 C．3 D ．10．（2019•莱芜区）如图，直线l与x轴，y轴分别交于A，B两点，且与反比例函数y ＝（x＞0）的图象交于点C，若S△AOB＝S△BOC＝1，则k＝（）4A．1 B．2 C．3 D．411．（2019•日照）如图，在单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，都是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角三角形，若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，1），A3（0，0），则依图中所示规律，A2019的坐标为（）A．（﹣1008，0）B．（﹣1006，0）C．（2，﹣504）D．（1，505）12．（2019•丹东）如图，二次函数y＝ax2+bx+c（a≠0）的图象过点（﹣2，0），对称轴为直线x＝1．有以下结论：①abc＞0；②8a+c＞0；③若A（x1，m），B（x2，m）是抛物线上的两点，当x＝x1+x2时，y＝c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取5值范围为a≥1；⑤若方程a（x+2）（4﹣x）＝﹣2的两根为x1，x2，且x1＜x2，则﹣2≤x1＜x2＜4．其中结论正确的有（）A．2个B．3个C．4个D．5个6第Ⅱ卷（非选择题）二．填空题13．（2019•无锡）如图，已知A（0，3）、B（4，0），一次函数y ＝﹣x+b的图象为直线l，点O关于直线l的对称点O′恰好落在∠ABO的平分线上，则b的值为．14．（2019•无锡）如图，A为反比例函数y＝（k＜0）的图象上一点，AP⊥y轴，垂足为P．点B在直线AP上，且PB＝3PA，过点B作直线BC∥y轴，交反比例函数的图象于点C，若△PAC的面积为4，则k的值为．15．（2019•兴安盟）若抛物线y＝﹣x2﹣6x+m与x轴没有交点，则m的取值范围是．16．（2019•济南）某市为提倡居民节约用水，自今年1月1日起调整居民用水价格．图中l1、l2分别表示去年、今年水费y（元）与用水量x（m3）之间的关系．小雨家去年用水量为150m3，若今年用水量与去年相同，水费将比去年多元．717．（2019•朝阳）如图，直线y ＝x+1与x轴交于点M，与y轴交于点A，过点A作AB⊥AM，交x轴于点B，以AB为边在AB的右侧作正方形ABCA1，延长A1C交x轴于点B1，以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去，再将每个正方形分割成四个全等的直角三角形和一个小正方形，每个小正方形的每条边都与其中的一条坐标轴平行，正方形ABCA1，A1B1C1A2，…，A n﹣1B n﹣1C n﹣1A n中的阴影部分的面积分别为S1，S2，…，S n，则S n可表示为．18．（2019•营口）如图，在平面直角坐标系中，直线l1：y＝x+与x轴交于点A1，与y轴交于点A2，过点A1作x轴的垂线交直线l2：y＝x于点B1，过点A1作A1B1的垂线交y轴于点B2，此时点B2与原点O重合，连接A2B1交x轴于点C1，得到第1个△C1B1B2；过点A2作y轴的垂线交l2于点B3，过点B3作y轴的平行线交l1于点A3，连接A3B2与A2B3交于点C2，得到第2个△C2B2B3……按照此规律进行下去，则第2019个△C2019B2019B2020的面积是．8三．解答题19．（2019•无锡）已知二次函数y＝ax2﹣4ax+c（a＜0）的图象与它的对称轴相交于点A，与y轴相交于点C（0，﹣2），其对称轴与x轴相交于点B（1）若直线BC与二次函数的图象的另一个交点D在第一象限内，且BD ＝，求这个二次函数的表达式；（2）已知P在y轴上，且△POA为等腰三角形，若符合条件的点P恰好有2个，试直接写出a的值．20．（2019•恩施州）如图，已知∠AOB＝90°，∠OAB＝30°，反比例函数y ＝﹣（x＜0）的图象过点B（﹣3，a），反比例函数y ＝（x＞0）的图象过点A．（1）求a和k的值；（2）过点B作BC∥x轴，与双曲线y ＝交于点C．求△OAC的面积．21．（2019•济南）如图1，点A（0，8）、点B（2，a）在直线y＝﹣2x+b上，反比例函数y ＝（x＞0）9的图象经过点B．（1）求a和k的值；（2）将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E ，求的值；②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三角形，求所有满足条件的m的值．22．（2019•济南）如图1，抛物线C：y＝ax2+bx经过点A（﹣4，0）、B（﹣1，3）两点，G是其顶点，将抛物线C绕点O旋转180°，得到新的抛物线C′．（1）求抛物线C的函数解析式及顶点G的坐标；（2）如图2，直线l：y＝kx ﹣经过点A，D是抛物线C上的一点，设D点的横坐标为m（m＜﹣2），连接DO并延长，交抛物线C′于点E，交直线l于点M，若DE＝2EM，求m的值；（3）如图3，在（2）的条件下，连接AG、AB，在直线DE下方的抛物线C上是否存在点P，使得∠DEP ＝∠GAB？若存在，求出点P的横坐标；若不存在，请说明理由．1023．（2019•恩施州）如图，抛物线y＝ax2﹣2ax+c的图象经过点C（0，﹣2），顶点D的坐标为（1，﹣），与x轴交于A、B两点．（1）求抛物线的解析式．（2）连接AC，E为直线AC上一点，当△AOC∽△AEB时，求点E 的坐标和的值．（3）点F（0，y）是y轴上一动点，当y 为何值时，FC+BF的值最小．并求出这个最小值．（4）点C关于x轴的对称点为H ，当FC+BF取最小值时，在抛物线的对称轴上是否存在点Q，使△QHF是直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．24．（2019•兴安盟）如图，在▱OABC中，A、C两点的坐标分别为（4，0）、（﹣2，3），抛物线W经过O、A、C三点，点D是抛物线W的顶点．11（1）求抛物线W的函数解析式及顶点D的坐标；（2）将抛物线W和▱OABC同时先向右平移4个单位长度，再向下平移m（0＜m＜3）个单位长度，得到抛物线W1和□O1A1B1C1，在向下平移过程中，O1C1与x轴交于点H，▱O1A1B1C1与▱OABC重叠部分的面积记为S，试探究：当m为何值时，S有最大值，并求出S的最大值；（3）在（2）的条件下，当S取最大值时，设此时抛物线W1的顶点为F，若点M是x轴上的动点，点N是抛物线W1上的动点，是否存在这样的点M、N，使以D、F、M、N为顶点的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．25．（2019•抚顺）如图，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是抛物线的顶点．（1）求抛物线的解析式．（2）点N是y轴负半轴上的一点，且ON ＝，点Q在对称轴右侧的抛物线上运动，连接QO，QO与抛物线的对称轴交于点M，连接MN，当MN平分∠OMD时，求点Q的坐标．（3）直线BC交对称轴于点E，P是坐标平面内一点，请直接写出△PCE与△ACD全等时点P的坐标．1226．如图，在平面直角坐标系中，一次函数y＝mx+n（m≠0）的图象与y轴交于点C，与反比例函数y ＝（k≠0）的图象交于A，B两点，点A在第一象限，纵坐标为4，点B在第三象限，BM⊥x轴，垂足为点M，BM＝OM＝2．（1）求反比例函数和一次函数的解析式．（2）连接OB，MC，求四边形MBOC的面积．27．（2019•丹东）如图，在平面直角坐标系中，抛物线y ＝﹣x2+bx+c与x轴交于B，C两点，与y轴交于点A，直线y ＝﹣x+2经过A，C两点，抛物线的对称轴与x轴交于点D，直线MN与对称轴交于点G，与抛物线交于M，N两点（点N在对称轴右侧），且MN∥x轴，MN＝7．（1）求此抛物线的解析式．（2）求点N的坐标．（3）过点A的直线与抛物线交于点F，当tan∠FAC ＝时，求点F的坐标．13（4）过点D作直线AC的垂线，交AC于点H，交y轴于点K，连接CN，△AHK沿射线AC以每秒1个单位长度的速度移动，移动过程中△AHK与四边形DGNC产生重叠，设重叠面积为S，移动时间为t（0≤t ≤），请直接写出S与t的函数关系式．14参考答案一．选择1．解：∵反比例函数y ＝，∴OA•AD＝2．∵D是AB的中点，∴AB＝2AD．∴矩形的面积＝OA•AB＝2AD•OA＝2×2＝4．故选：C．2．解：根据题意得：2﹣3x≥0且x+1≠0，解得：x ≤且x≠﹣1．故选：D．3．解：a＞0时，﹣a＜0，y＝﹣ax+a在一、二、四象限，y ＝在一、三象限，无选项符合．a＜0时，﹣a＞0，y＝﹣ax+a在一、三、四象限，y ＝（a≠0）在二、四象限，只有D符合；故选：D．4．解：根据题意，可知：每滚动3次为一个周期，点C1，C3，C5，…在第一象限，点C2，C4，C6，…在x 轴上．∵A（4，0），B（0，3），∴OA＝4，OB＝3，∴AB ＝＝5，15∴点C2的横坐标为4+5+3＝12＝2×6，同理，可得出：点C4的横坐标为4×6，点C6的横坐标为6×6，…，∴点C2n的横坐标为2n×6（n为正整数），∴点C100的横坐标为100×6＝600，∴点C100的坐标为（600，0）．故选：B．5．解：∵AB＝AC，AG⊥BC，∴BG＝GC ＝，∵△DEC与△DEF关于DE对称，∴FD＝CD＝x．当点F与G重合时，FD＝CD，即2x＝2，∴x＝1，当点F与点B重合时，FC＝BC，即2x ＝4，∴x＝2，如图1，当0≤x≤1时，y＝0，∴B选项错误；如图2，当1＜x≤2时，，∴选项D错误；如图3，当2＜x≤4时，，∴选项C错误．16故选：A．6．解：tan∠DBC ＝＝＝，tan∠DAH ＝＝＝＝﹣x，y＝EF﹣EM﹣NF＝2﹣BF tan∠DBC﹣AE tan∠DAH＝2﹣x ×﹣x （）＝x2﹣x+2，故选：B．7．解：∵抛物线对称轴x＝﹣1，经过（1，0），∴﹣＝﹣1，a+b+c＝0，∴b＝2a，c＝﹣3a，∵a＜0，∴b＜0，c＞0，∴ab＞0且c＞0，故①错误，∵抛物线对称轴x＝﹣1，经过（1，0），∴（﹣2，0）和（0，0）关于对称轴对称，∴x＝﹣2时，y＞0，∴4a﹣2b+c＞0，故②正确，∵抛物线与x轴交于（﹣3，0），∴x＝﹣4时，y＜0，17∵b＝2a，∴16a﹣8a+c＜0，即8a+c＜0，故③错误，∵c＝﹣3a＝3a﹣6a，b＝2a，∴c＝3a﹣3b，故④正确，∵直线y＝2x+2与抛物线y＝ax2+bx+c两个交点的横坐标分别为x1，x2，∴方程ax2+（b﹣2）x+c﹣2＝0的两个根分别为x1，x2，∴x1+x2＝﹣，x1•x2＝，∴x1+x2+x1x2＝﹣+＝﹣+＝﹣5，故⑤错误，故选：D．8．解：①由图象可知：a＞0，c＜0，∴由于对称轴＞0，∴b＜0，∴abc＞0，故①正确；②抛物线过（3，0），∴x＝3，y＝9a+3b+c＝0，故②正确；③顶点坐标为：（，）由图象可知：＜﹣2，∵a＞0，18即b2﹣4ac＞8a，故③错误；④由图象可知：＞1，a＞0，∴2a+b＜0，∵9a+3b+c＝0，∴c＝﹣9a﹣3b，∴5a+b+c＝5a+b﹣9a﹣3b＝﹣4a﹣2b＝﹣2（2a+b）＞0，故④正确；故选：C．9．解：∵BD∥x轴，∴∠EDB＝90°，∵cos∠BED ＝＝，∴设DE＝3a，BE＝5a，∴BD ＝＝＝4a，∵点B的横坐标为5，∴4a＝5，则a ＝，∴DE ＝，设AC＝b，则CD＝3b，∵AC∥BD，∴＝＝＝，19∴EC ＝b，∴ED＝3b +b ＝，∴＝，则b＝1，∴AC＝1，CD＝3，设B点的纵坐标为n，∴OD＝n，则OC＝3+n，∵A（1，3+n），B（5，n），∴A，B是反比例函数y ＝（k＞0，x＞0）图象上的两点，∴k＝1×（3+n）＝5n，解得k ＝，故选：D．10．解：如图，作CD⊥x轴于D，设OB＝a（a＞0）．∵S△AOB＝S△BOC，∴AB＝BC．∵△AOB的面积为1，∴OA•OB＝1，∴OA ＝，∵CD∥OB，AB＝BC，∴OD＝OA ＝，CD＝2OB＝2a，20∴C （，2a），∵反比例函数y ＝（x＞0）的图象经过点C，∴k ＝×2a＝4．故选：D．11．解：观察图形可以看出A1﹣﹣A4；A5﹣﹣﹣A8；…每4个为一组，∵2019÷4＝504 (3)∴A2019在x轴负半轴上，纵坐标为0，∵A3、A7、A11的横坐标分别为0，﹣2，﹣4，∴A2019的横坐标为﹣（2019﹣3）×＝﹣1008．∴A2019的坐标为（﹣1008，0）．故选：A．12．解：①由图象可知：a＞0，c＜0，＞0，∴abc＞0，故①正确；②∵抛物线的对称轴为直线x＝1，抛物线的对称轴为直线x＝1，21∴＝1，∴b＝﹣2a，当x＝﹣2时，y＝4a﹣2b+c＝0，∴4a+4a+c＝0，∴8a+c＝0，故②错误；③∵A（x1，m），B（x2，m）是抛物线上的两点，由抛物线的对称性可知：x1+x2＝1×2＝2，∴当x＝2时，y＝4a+2b+c＝4a﹣4a+c＝c，故③正确；④由题意可知：M，N到对称轴的距离为3，当抛物线的顶点到x轴的距离不小于3时，在x轴下方的抛物线上存在点P，使得PM⊥PN，即≤﹣3，∵8a+c＝0，∴c＝﹣8a，∵b＝﹣2a，∴，解得：a，故④错误；⑤易知抛物线与x轴的另外一个交点坐标为（4，0），∴y＝ax2+bx+c＝a（x+2）（x﹣4）若方程a（x+2）（4﹣x）＝﹣2，22即方程a（x+2）（x﹣4）＝2的两根为x1，x2，则x1、x2为抛物线与直线y＝2的两个交点的横坐标，∵x1＜x2，∴x1＜﹣2＜4＜x2，故⑤错误；故选：A．二．填空题（共6小题）13．解：延长OO'交AB于点C，交l于点E，过点O'作DG⊥x轴交于G，过点E作EF⊥x轴于点F；∵A（0，3）、B（4，0），∴直线AB的解析式为y ＝﹣x+3，∵直线l的解析式为y ＝﹣x+b，∴AB∥l，∵OO'⊥l，∴OC⊥AB，∵OA＝3，OB＝4，由等积法可求，OC ＝，∵∠COB+∠AOC＝∠BAO+∠AOC＝90°，∴∠BOC＝∠BAO，∵BO'是∠ABO的角平分线，∴CO'＝GO'，23∴sin∠BAO ＝＝＝＝，∴OO'＝，∴O'G ＝﹣＝，在Rt△OO'G中，GO ＝，∵E、F是△OO'G的中位线，∴E （，），∵E点在直线l上，∴＝﹣×+b，∴b ＝，故答案为．14．解：当B点在P点右侧，如图，设A（t ，），∵PB＝3PA，24∴B（﹣3t ，），∵BC∥y轴，∴C（﹣3t ，﹣），∵△PAC的面积为4，∴×（﹣t ）×（+）＝4，解得k＝﹣6；当B点在P点左侧，设A（t ，），∵PB＝3PA，∴B（3t ，），∵BC∥y轴，∴C（3t ，），∵△PAC的面积为4，∴×（﹣t ）×（﹣）＝4，解得k＝﹣12；综上所述，k的值为﹣6或﹣12．故答案为﹣6或﹣12．2515．解：∵抛物线y＝﹣x2﹣6x+m与x轴没有交点，∴当y＝0时，0＝﹣x2﹣6x+m，∴△＝（﹣6）2﹣4×（﹣1）×m＜0，解得，m＜﹣9故答案为：m＜﹣9．16．解：设当x＞120时，l2对应的函数解析式为y＝kx+b，，得，即当x＞120时，l2对应的函数解析式为y＝6x﹣240，当x＝150时，y＝6×150﹣240＝660，由图象可知，去年的水价是480÷160＝3（元/m3），故小雨家去年用水量为150m3，需要缴费：150×3＝450（元），660﹣450＝210（元），即小雨家去年用水量为150m3，若今年用水量与去年相同，水费将比去年多210元，故答案为：210．17．解：在直线y ＝x+1中，当x＝0时，y＝1；当y＝0时，x＝﹣3；26∴OA＝1，OM＝3，∴tan∠AMO ＝，∵∠OAB+∠OAM＝90°，∠AMO+∠OAM＝90°，∴∠OAB＝∠AMO，∴tan∠OAB ＝，∴OB ＝．∵，∴，易得tan，∴，∴，∴，同理可得，，…，＝．故答案为：．18．解：∵y ＝x +与x轴交于点A1，与y轴交于点A2，∴，27在y ＝中，当x＝﹣1时，y ＝﹣，∴，设直线A2B1的解析式为：y＝kx+b，可得：，解得：，∴直线A2B1的解析式为：，令y＝0，可得：x ＝﹣，∴C1（﹣，0），∴＝，∵△A1B1B2∽△A2B2B3，∴△C1B1B2∽△C2B2B3，∴，∴，同理可得：…，∴△C2019B2019B2020的面积＝，28故答案为：．三．解答题（共9小题）19．解：（1）过点D作DH⊥x轴于点H，如图1，∵二次函数y＝ax2﹣4ax+c，∴对称轴为x ＝，∴B（2，0），∵C（0，﹣2），∴OB＝OC＝2，∴∠OBC＝∠DBH＝45°，∵BH ＝，∴BH＝DH＝1，∴OH＝OB+BH＝2+1＝3，∴D（3，1），把C（0，﹣2），D（3，1）代入y＝ax2﹣4ax+c中得，，29∴，∴二次函数的解析式为y＝﹣x2+4x﹣2；（2）∵y＝ax2﹣4ax+c过C（0，﹣2），∴c＝﹣2，∴y＝ax2﹣4ax+c＝a（x﹣2）2﹣4a﹣2，∴A（2，﹣4a﹣2），∵P在y轴上，且△POA为等腰三角形，若符合条件的点P恰好有2个，∴①当抛物线的顶点A在x轴上时，∠POA＝90°，则OP＝OA，这样的P点只有2个，正、负半轴各一个，如图2，此时A（﹣2，0），∴﹣4a﹣2＝0，解得a ＝；②当抛物线的顶点A不在x轴上时，∠AOB＝30°时，则△OPA为等边三角形或∠AOP＝120°的等腰三角形，这样的P点也只有两个，如图3，30∴AB＝OB•tan30°＝2×＝，∴|﹣4a﹣2|＝，∴或．综上，a ＝﹣或或．20．解：（1）∵比例函数y ＝﹣（x＜0）的图象过点B（﹣3，a），∴a ＝﹣＝1，∴OE＝3，BE＝1，分别过点A、B作AD⊥x轴于D，BE⊥x轴于E，∴∠BOE+∠OBE＝90°，∵∠AOB＝90°，∠OAB＝30°，∴∠BOE+∠AOD＝90°，tan30°＝＝，∴∠OBE＝∠AOD，∵∠OEB＝∠ADO＝90°，∴△BOE∽△OAD31∴＝＝＝，∴AD ＝•OE ＝＝3，OD ＝•BE ＝＝∴A （，3），∵反比例函数y ＝（x＞0）的图象过点A，∴k ＝×＝9；（2）由（1）可知AD＝3，OD ＝，∵BC∥x轴，B（﹣3，1），∴C点的纵坐标为1，过点C作CF⊥x轴于F，∵点C在双曲线y ＝上，∴1＝，解得x＝9，∴C（9，1），∴CF＝1，∴S△AOC＝S△AOD+S梯形ADFC﹣S△COF＝S梯形ADCF＝（AD+CF）（OF﹣OD）＝（3+1）（9﹣）＝13．3221．解：（1）∵点A（0，8）在直线y＝﹣2x+b上，∴﹣2×0+b＝8，∴b＝8，∴直线AB的解析式为y＝﹣2x+8，将点B（2，a）代入直线AB的解析式y＝﹣2x+8中，得﹣2×2+8＝a，∴a＝4，∴B（2，4），将B（2，4）在反比例函数解析式y ＝（x＞0）中，得k＝xy＝2×4＝8；（2）①由（1）知，B（2，4），k＝8，∴反比例函数解析式为y ＝，当m＝3时，∴将线段AB向右平移3个单位长度，得到对应线段CD，∴D（2+3，4），即：D（5，4），33∵DF⊥x轴于点F，交反比例函数y ＝的图象于点E，∴E（5，），∴DE＝4﹣＝，EF ＝，∴＝＝；②如图，∵将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，∴CD＝AB，AC＝BD＝m，∵A（0，8），B（2，4），∴C（m，8），D（m+2，4），∵△BCD是以BC为腰的等腰三形，∴Ⅰ、当BC＝CD时，∴BC＝AB，∴点B在线段AC的垂直平分线上，∴m＝2×2＝4，Ⅱ、当BC＝BD时，∵B（2，4），C（m，8），∴BC ＝，∴＝m，34∴m＝5，即：△BCD是以BC为腰的等腰三角形，满足条件的m的值为4或5．22．解：（1）将A（﹣4，0）、B（﹣1，3）代入y＝ax2+bx 中，得解得∴抛物线C解析式为：y＝﹣x2﹣4x，配方，得：y＝﹣x2﹣4x＝﹣（x+2）2+4，∴顶点为：G（﹣2，4）；（2）∵抛物线C绕点O旋转180°，得到新的抛物线C′．∴新抛物线C′的顶点为：G′（2，﹣4），二次项系数为：a′＝1∴新抛物线C′的解析式为：y＝（x﹣2）2﹣4＝x2﹣4x将A（﹣4，0）代入y＝kx ﹣中，得0＝﹣4k ﹣，解得k ＝，∴直线l解析式为y ＝x ﹣，设D（m，﹣m2﹣4m），∵D、E关于原点O对称，∴OD＝OE∵DE＝2EM∴OM＝2OD，过点D作DF⊥x轴于F，过M作MR⊥x轴于R，35∴∠OFD＝∠ORM，∵∠DOF＝∠MOR∴△ODF∽△OMR∴＝＝＝2∴OR＝2OF，RM＝2DF∴M（﹣2m，2m2+8m）∴2m2+8m ＝•（﹣2m ）﹣，解得：m1＝﹣3，m2＝，∵m＜﹣2∴m的值为：﹣3；（3）由（2）知：m＝﹣3，∴D（﹣3，3），E（3，﹣3），OE＝3，如图3，连接BG，在△ABG中，∵AB2＝（﹣1+4）2+（3﹣0）2＝18，BG2＝2，AG2＝20∴AB2+BG2＝AG2∴△ABG是直角三角形，∠ABG＝90°，∴tan∠GAB ＝＝＝，∵∠DEP＝∠GAB∴tan∠DEP＝tan∠GAB ＝，在x轴下方过点O作OH⊥OE，在OH上截取OH ＝OE ＝，36过点E作ET⊥y轴于T，连接EH交抛物线C于点P，点P即为所求的点；∵E（3，﹣3），∴∠EOT＝45°∵∠EOH＝90°∴∠HOT＝45°∴H（﹣1，﹣1），设直线EH解析式为y＝px+q，则，解得∴直线EH解析式为y ＝﹣x，解方程组，得，，∴点P 的横坐标为：或．3723．解：（1）由题可列方程组：，解得：∴抛物线解析式为：y ＝x2﹣x﹣2；（2）如图1，∠AOC＝90°，AC ＝，AB＝4，设直线AC的解析式为：y＝kx+b ，则，解得：，∴直线AC的解析式为：y＝﹣2x﹣2；当△AOC∽△AEB时38＝（）2＝（）2＝，∵S△AOC＝1，∴S△AEB ＝，∴AB×|y E|＝，AB＝4，则y E ＝﹣，则点E （﹣，﹣）；由△AOC∽△AEB 得：∴；（3）如图2，连接BF，过点F作FG⊥AC于G，39则FG＝CF sin∠FCG ＝CF，∴CF+BF＝GF+BF≥BE，当折线段BFG与BE重合时，取得最小值，由（2）可知∠ABE＝∠ACO∴BE＝AB cos∠ABE＝AB cos∠ACO＝4×＝，|y|＝OB tan∠ABE＝OB tan∠ACO＝3×＝，∴当y ＝﹣时，即点F（0，﹣），CF+BF 有最小值为；（4）①当点Q为直角顶点时（如图3）：由（3）易得F（0，﹣），40∵C（0，﹣2）∴H（0，2）设Q（1，m），过点Q作QM⊥y轴于点M．则Rt△QHM∽Rt△FQM∴QM2＝HM•FM，∴12＝（2﹣m）（m +），解得：m ＝，则点Q（1，）或（1，）当点H为直角顶点时：点H（0，2），则点Q（1，2）；当点F为直角顶点时：同理可得：点Q（1，﹣）；综上，点Q的坐标为：（1，）或（1，）或Q（1，2）或Q（1，﹣）．24．解：（1）设抛物线W的函数解析式为y＝ax2+bx，图象经过A（4，0），C（﹣2，3）41∴抛物线W 的函数解析式为，顶点D的坐标为（2，﹣1）；（2）根据题意，由O（0，0），C（﹣2，3），得O1（4，﹣m），C1（2，3﹣m）设直线O1C1的函数解析式为y＝kx+b把O1（4，﹣m），C1（2，3﹣m）代入y＝kx+b 得：，直线O1C1与x轴交于点H∴过C1作C1E⊥HA于点E，∵0＜m＜3∴，∴，∵，抛物线开口向下，S 有最大值，最大值为∴当时，；42（3）当时，由D（2，﹣1）得F（6，）∴抛物线W1的函数解析式为，依题意设M（t，0），以D，F，M，N为顶点的四边形是平行四边形，分情况讨论：①以DF为边时∵D（2，﹣1），F点D，F横坐标之差是4，纵坐标之差是，若点M、N的横纵坐标与之有相同规律，则以D，F，M，N为顶点的四边形是平行四边形，∵M（t，0），∴把分别代入得t1＝0，t2＝4，t3＝6，t4＝14∴M1 （0，0），M2（4，0），M3 （6，0），M4 （14，0）②以DF为对角线时，以点D，F，M，N为顶点不能构成平行四边形．综上所述：M1 （0，0），M2（4，0），M3 （6，0），M4 （14，0）．25．解：（1）∵抛物线y＝ax2+bx﹣3经过A（﹣1，0），B（3，0）两点，∴，解得：，∴抛物线的解析式为：y＝x2﹣2x﹣3．43（2）如图1，设对称轴与x轴交于点H，∵MN平分∠OMD，∴∠OMN＝∠DMN，又∵DM∥ON，∴∠DMN＝∠MNO，∴∠MNO＝∠OMN，∴OM＝ON ＝．在Rt△OHM中，∠OHM＝90°，OH＝1．∴，∴M1（1，1）；M2（1，﹣1）．①当M1（1，1）时，直线OM解析式为：y＝x，依题意得：x＝x2﹣2x﹣3．解得：，，∵点Q在对称轴右侧的抛物线上运动，∴Q点纵坐标y ＝．∴，②当M2（1，﹣1）时，直线OM解析式为：y＝﹣x，同理可求：，综上所述：点Q 的坐标为：，，44（3）由题意可知：A（﹣1，0），C（0，﹣3），D（1，﹣4），∴AC ＝，AD ＝，CD ＝，∵直线BC经过B（3，0），C（0，﹣3），∴直线BC解析式为y＝x﹣3，∵抛物线对称轴为x＝1，而直线BC交对称轴于点E，∴E坐标为（1，﹣2）；∴CE ＝，设P点坐标为（x，y），则CP2＝（x﹣0）2+（y+3）2，则EP2＝（x﹣1）2+（y+2）2，∵CE＝CD，若△PCE与△ACD全等，有两种情况，Ⅰ．PC＝AC，PE＝AD，即△PCE≌△ACD（SSS）．∴，解得：，，即P点坐标为P1（﹣3，﹣4），P2（﹣1，﹣6）．45Ⅱ．PC＝AD，PE＝AC，即△PCE≌△ACD（SSS）．∴，解得：，，即P点坐标为P3（2，1），P4（4，﹣1）．故若△PCE与△ACD全等，P点有四个，坐标为P1（﹣3，﹣4），P2（﹣1，﹣6），P3（2，1），P4（4，﹣1）．26．解：（1）∵BM＝OM＝2，∴点B的坐标为（﹣2，﹣2），∵反比例函数y ＝（k≠0）的图象经过点B，则﹣2＝，得k＝4，∴反比例函数的解析式为y ＝，∵点A的纵坐标是4，∴4＝，得x＝1，46∴点A的坐标为（1，4），∵一次函数y＝mx+n（m≠0）的图象过点A（1，4）、点B（﹣2，﹣2），∴，解得，即一次函数的解析式为y＝2x+2；（2）∵y＝2x+2与y轴交于点C，∴点C的坐标为（0，2），∵点B（﹣2，﹣2），点M（﹣2，0），∴OC＝MB＝2，∵BM⊥x轴，∴MB∥OC，∴四边形MBOC是平行四边形，∴四边形MBOC的面积是：OM•OC＝4．27．解：（1）直线y ＝﹣x+2经过A，C两点，则点A、C的坐标分别为（0，2）、（4，0），则c＝2，抛物线表达式为：y ＝﹣x2+bx+2，将点C坐标代入上式并解得：b ＝，故抛物线的表达式为：y ＝﹣x2+x+2…①；（2）抛物线的对称轴为：x ＝，47点N 的横坐标为：+＝5，故点N的坐标为（5，﹣3）；（3）∵tan∠ACO ＝＝tan∠FAC ＝，即∠ACO＝∠FAC，①当点F在直线AC下方时，设直线AF交x轴于点R，∵∠ACO＝∠FAC，则AR＝CR，设点R（r，0），则r2+4＝（r﹣4）2，解得：r ＝，即点R 的坐标为：（，0），将点R、A的坐标代入一次函数表达式：y＝mx+n 得：，解得：，故直线AR的表达式为：y ＝﹣x+2…②，48联立①②并解得：x ＝，故点F （，﹣）；②当点F在直线AC的上方时，∵∠ACO＝∠F′AC，∴AF′∥x轴，则点F′（3，2）；综上，点F的坐标为：（3，2）或（，﹣）；（4）如图2，设∠ACO＝α，则tan α＝＝，则sin α＝，cos α＝；①当0≤t ≤时（左侧图），设△AHK移动到△A′H′K′的位置时，直线H′K′分别交x轴于点T、交抛物线对称轴于点S，则∠DST＝∠ACO＝α，过点T作TL⊥KH，则LT＝HH′＝t，∠LTD＝∠ACO＝α，则DT ＝＝＝＝t，DS ＝，S＝S△DST ＝DT×DS ＝t2；②当＜t ≤时（右侧图），49同理可得：S＝S梯形DGS′T′＝×DG×（GS′+DT ′）＝3+（+﹣）＝t ﹣；③当＜t ≤时，同理可得：S ＝t +；综上，S ＝．50。

(名师整理)最新数学中考专题冲刺《三角形》压轴真题训练(含答案)

冲刺中考《三角形》压轴真题训练1．（2019•鄂州）如图，在四边形ABCD中，∠DAB＝90°，DB＝DC，点E、F分别为DB、BC 的中点，连接AE、EF、AF．（1）求证：AE＝EF；（2）当AF＝AE时，设∠ADB＝α，∠CDB＝β，求α，β之间的数量关系式．2．（2019•江西）在图1，2，3中，已知▱ABCD，∠ABC＝120°，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且∠EAG＝120°．（1）如图1，当点E与点B重合时，∠CEF＝°；（2）如图2，连接AF．①填空：∠FAD∠EAB（填“＞”，“＜“，“＝”）；②求证：点F在∠ABC的平分线上；1（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求的值．3．（2019•扬州）如图，平面内的两条直线l1、l2，点A，B在直线l1上，点C、D在直线l2上，过A、B两点分别作直线l2的垂线，垂足分別为A1，B1，我们把线段A1B1叫做线段AB 在直线l2上的正投影，其长度可记作T（AB，CD）或T，特别地线段AC在直线l2上的正投影就是线段A1C．请依据上述定义解决如下问题：（1）如图1，在锐角△ABC中，AB＝5，T（AC，AB）＝3，则T（BC，AB）＝；（2）如图2，在Rt△ABC中，∠ACB＝90°，T（AC，AB）＝4，T（BC，AB）═9，求△ABC的面积；（3）如图3，在钝角△ABC中，∠A＝60°，点D在AB边上，∠ACD＝90°，T（AD，AC）＝2，T（BC，AB）＝6，求T（BC，CD），24．（2019•枣庄）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN ＝AM．5．（2019•杭州）如图，在△ABC中，AC＜AB＜BC．（1）已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B．（2）以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ．若∠AQC＝3∠B，求∠B的度数．6．（2019•呼和浩特）如图，在△ABC中，内角A、B、C所对的边分别为a、b、c．（1）若a＝6，b＝8，c＝12，请直接写出∠A与∠B的和与∠C的大小关系；（2）求证：△ABC的内角和等于180°；3（3）若＝，求证：△ABC是直角三角形．7．（2019•镇江）如图，四边形ABCD中，AD∥BC，点E、F分别在AD、BC上，AE＝CF，过点A、C分别作EF的垂线，垂足为G、H．（1）求证：△AGE≌△CHF；（2）连接AC，线段GH与AC是否互相平分？请说明理由．8．（2019•北京）已知∠AOB＝30°，H为射线OA上一定点，OH ＝+1，P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON．（1）依题意补全图1；（2）求证：∠OMP＝∠OPN；（3）点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON＝QP，并证明．49．（2019•河北）已知：整式A＝（n2﹣1）2+（2n）2，整式B＞0．尝试化简整式A．发现A＝B2，求整式B．联想由上可知，B2＝（n2﹣1）2+（2n）2，当n＞1时，n2﹣1，2n，B为直角三角形的三边长，如图．填写下表中B的值：直角三角形三边n2﹣1 2n B勾股数组Ⅰ/ 8勾股数组Ⅱ35 /510．（2019•赤峰）【问题】如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC，过点C作直线l平行于AB．∠EDF＝90°，点D在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系．【探究发现】（1）如图2，某数学兴趣小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，通过推理就可以得到DP＝DB，请写出证明过程；【数学思考】（2）如图3，若点P是AC上的任意一点（不含端点A、C），受（1）的启发，这个小组过点D作DG⊥CD交BC于点G，就可以证明DP＝DB，请完成证明过程；【拓展引申】（3）如图4，在（1）的条件下，M是AB边上任意一点（不含端点A、B），N是射线BD 上一点，且AM＝BN，连接MN与BC交于点Q，这个数学兴趣小组经过多次取M点反复进行实验，发现点M在某一位置时BQ的值最大．若AC＝BC＝4，请你直接写出BQ的最大值．611．（2019•长春）教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．例2 如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G ，求证：＝＝证明：连结ED．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在▱ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．（1）如图②，若▱ABCD为正方形，且AB＝6，则OF 的长为．（2）如图③，连结DE交AC于点G，若四边形OFEG的面积为，则▱ABCD的面积为．712．（2019•鸡西）如图，在△ABC中，AB＝BC，AD⊥BC于点D，BE⊥AC于点E，AD与BE交于点F，BH⊥AB于点B，点M是BC的中点，连接FM并延长交BH于点H．（1）如图①所示，若∠ABC＝30°，求证：DF+BH ＝BD；（2）如图②所示，若∠ABC＝45°，如图③所示，若∠ABC＝60°（点M与点D重合），猜想线段DF、BH与BD之间又有怎样的数量关系？请直接写出你的猜想，不需证明．13．（2019•铁岭）如图，△ABC中，AB＝AC，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且∠GEF+∠BAC ＝180°．（1）如图1，当∠B＝45°时，线段AG和CF 的数量关系是．（2）如图2，当∠B＝30°时，猜想线段AG和CF的数量关系，并加以证明．（3）若AB＝6，DG＝1，cos B＝，请直接写出CF的长．814．（2019•阜新）如图，是具有公共边AB的两个直角三角形，其中，AC＝BC，∠ACB＝∠ADB＝90°．（1）如图1，若延长DA到点E，使AE＝BD，连接CD，CE．①求证：CD＝CE，CD⊥CE；②求证：AD+BD ＝CD；（2）若△ABC与△ABD位置如图2所示，请直接写出线段AD，BD，CD的数量关系．15．（2019•锦州）已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF．9（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，求证：①∠CAD＝∠CDF，②BD＝EF；（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由．10参考答案1．（1）证明：点E、F分别为DB、BC的中点，∴EF ＝CD，∵∠DAB＝90°，∴AE ＝BD，∵DB＝DC，∴AE＝EF；（2）解：∵AF＝AE，AE＝EF，∴△AEF是等边三角形，∴∠AEF＝60°，∵∠DAB＝90°，点E、F分别为DB、BC的中点，∴AE＝DE，EF∥CD，∴∠ADE＝∠DAE，∠BEF＝∠BDC＝β，∴∠AEB＝2∠ADE＝2α，∴∠AEF＝∠AEB+∠FEB＝2α+β＝60°，∴α，β之间的数量关系式为2α+β＝60°．2．解：（1）∵四边形AEFG是菱形，∴∠AEF＝180°﹣∠EAG＝60°，∴∠CEF＝∠AEC﹣∠AEF＝60°，11故答案为：60°；（2）①∵四边形ABCD是平行四边形，∴∠DAB＝180°﹣∠ABC＝60°，∵四边形AEFG是菱形，∠EAG＝120°，∴∠FAE＝60°，∴∠FAD＝∠EAB，故答案为：＝；②当BA＜BE时，如图2，作FM⊥BC于M，FN⊥BA交BA的延长线于N，则∠FNB＝∠FMB＝90°，∴∠NFM＝60°，又∠AFE＝60°，∴∠AFN＝∠EFM，∵EF＝EA，∠FAE＝60°，∴△AEF为等边三角形，∴FA＝FE，在△AFN和△EFM中，，∴△AFN≌△EFM（AAS）∴FN＝FM，又FM⊥BC，FN⊥BA，∴点F在∠ABC的平分线上，当BA＝BE时，如图4，12∵BA＝BE，∠ABC＝120°，∴∠BAE＝∠BEA＝30°，∵∠EAG＝120°，四边形AEFG为菱形，∴∠EAF＝60°，又EA＝EF，∴△AEF为等边三角形，∴∠FEA＝60°，FA＝FE，则∠FAB＝∠FEB＝90°，又FA＝FE，∴点F在∠ABC的平分线上，当BA＞BE时，同理可证，点F在∠ABC的平分线上，综上所述，点F在∠ABC的平分线上；（3）∵四边形AEFG是菱形，∠EAG＝120°，∴∠AGF＝60°，∴∠FGE＝∠AGE＝30°，∵四边形AEGH为平行四边形，∴GE∥AH，∴∠GAH＝∠AGE＝30°，∠H＝∠FGE＝30°，∴∠GAN＝90°，又∠AGE＝30°，∴GN＝2AN，∵∠DAB＝60°，∠H＝30°，∴∠ADH＝30°，∴AD＝AH＝GE，13∵四边形ABCD为平行四边形，∴BC＝AD，∴BC＝GE，∵∠HAE＝∠EAB＝30°，∴平行四边形ABEN为菱形，∴AB＝AN＝NE，∴GE＝3AB，∴＝3．3．解：（1）如图1中，作CH⊥AB．14∵T（AC，AB）＝3，∴AH＝3，∵AB＝5，∴BH＝5﹣3＝2，∴T（BC，AB）＝BH＝2，故答案为2．（2）如图2中，作CH⊥AB于H．∵T（AC，AB）＝4，T（BC，AB）═9，∴AH＝4，BH＝9，∵∠ACB＝∠CHA＝∠CHB＝90°，∴∠A+∠ACH＝90°，∠ACH+∠BCH＝90°，∴∠A＝∠BCH，∴△ACH∽△CBH，15∴＝，∴＝，∴CH＝6，∴S△ABC ＝•AB•CH ＝×13×6＝39．（3）如图3中，作CH⊥AD于H，BK⊥CD于K．∵∠ACD＝90°，T（AD，AC）＝2，∴AC＝2，∵∠A＝60°，∴∠ADC＝∠BDK＝30°，∴CD ＝AC＝2，AD＝2AC＝4，AH ＝AC＝1，DH＝AD﹣AH＝3，∵T（BC，AB）＝6，CH⊥AB，∴BH＝6，∴DB＝BH﹣DH＝3，在Rt△BDK中，∵∠K＝90°，BD＝3，∠BDK＝30°，∴DK＝BD•cos30°＝，16∴CK＝CD+DK＝2+＝，∴T（BC，CD）＝CK ＝．4．（1）解：∵∠BAC＝90°，AB＝AC，AD⊥BC，∴AD＝BD＝DC，∠ABC＝∠ACB＝45°，∠BAD＝∠CAD＝45°，∵AB＝2，∴AD＝BD＝DC ＝，∵∠AMN＝30°，∴∠BMD＝180°﹣90°﹣30°＝60°，∴∠MBD＝30°，∴BM＝2DM，由勾股定理得，BM2﹣DM2＝BD2，即（2DM）2﹣DM2＝（）2，解得，DM ＝，∴AM＝AD﹣DM ＝﹣；（2）证明：∵AD⊥BC，∠EDF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（ASA）∴BE＝AF；17（3）证明：过点M作ME∥BC交AB的延长线于E，∴∠AME＝90°，则AE ＝AM，∠E＝45°，∴ME＝MA，∵∠AME＝90°，∠BMN＝90°，∴∠BME＝∠AMN，在△BME和△NMA中，，∴△BME≌△NMA（ASA），∴BE＝AN，∴AB+AN＝AB+BE＝AE ＝AM．5．解：（1）证明：∵线段AB的垂直平分线与BC边交于点P，∴PA＝PB，∴∠B＝∠BAP，∵∠APC＝∠B+∠BAP，∴∠APC＝2∠B；18（2）根据题意可知BA＝BQ，∴∠BAQ＝∠BQA，∵∠AQC＝3∠B，∠AQC＝∠B+∠BAQ，∴∠BQA＝2∠B，∵∠BAQ+∠BQA+∠B＝180°，∴5∠B＝180°，∴∠B＝36°．6．解：（1）∵在△ABC中，a＝6，b＝8，c＝12，∴∠A+∠B＜∠C；（2）如图，过点B作MN∥AC，∵MN∥AC，∴∠MBA＝∠A，∠NBC＝∠C（两直线平行，内错角相等），∵∠MBA+∠ABC+∠NBC＝180°（平角的定义），∴∠A+∠ABC+∠C＝180°（等量代换），即：三角形三个内角的和等于180°；（3）∵＝，∴ac ＝（a+b+c）（a﹣b+c ）＝[（a2+2ac+c2）﹣b2]，∴2ac＝a2+2ac+c2﹣b2，∴a2+c2＝b2，19∴△ABC是直角三角形．7．（1）证明：∵AG⊥EF，CH⊥EF，∴∠G＝∠H＝90°，AG∥CH，∵AD∥BC，∴∠DEF＝∠BFE，∵∠AEG＝∠DEF，∠CFH＝∠BFE，∴∠AEG＝∠CFH，在△AGE和△CHF 中，，∴△AGE≌△CHF（AAS）；（2）解：线段GH与AC互相平分，理由如下：连接AH、CG，如图所示：由（1）得：△AGE≌△CHF，∴AG＝CH，∵AG∥CH，∴四边形AHCG是平行四边形，∴线段GH与AC互相平分．208．解：（1）如图1所示为所求．（2）设∠OPM＝α，∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN＝150°，PM＝PN∴∠OPN＝∠MPN﹣∠OPM＝150°﹣α∵∠AOB＝30°∴∠OMP＝180°﹣∠AOB﹣∠OPM＝180°﹣30°﹣α＝150°﹣α∴∠OMP＝∠OPN（3）OP＝2时，总有ON＝QP，证明如下：过点N作NC⊥OB于点C，过点P作PD⊥OA于点D，如图2∴∠NCP＝∠PDM＝∠PDQ＝90°21∵∠AOB＝30°，OP＝2∴PD ＝OP＝1∴OD ＝∵OH ＝+1∴DH＝OH﹣OD＝1∵∠OMP＝∠OPN∴180°﹣∠OMP＝180°﹣∠OPN即∠PMD＝∠NPC在△PDM与△NCP中∴△PDM≌△NCP（AAS）∴PD＝NC，DM＝CP设DM＝CP＝x，则OC＝OP+PC＝2+x，MH＝MD+DH＝x+1∵点M关于点H的对称点为Q∴HQ＝MH＝x+1∴DQ＝DH+HQ＝1+x+1＝2+x∴OC＝DQ在△OCN与△QDP中22∴△OCN≌△QDP（SAS）∴ON＝QP9．解：A＝（n2﹣1）2+（2n）2＝n4﹣2n2+1+4n2＝n4+2n2+1＝（n2+1）2，∵A＝B2，B＞0，∴B＝n2+1，当2n＝8时，n＝4，∴n2+1＝42+1＝17；当n2﹣1＝35时，n2+1＝37．故答案为：17；3710．证明：【探究发现】（1）∵∠ACB＝90°，AC＝BC∴∠CAB＝∠CBA＝45°∵CD∥AB∴∠CBA＝∠DCB＝45°，且BD⊥CD∴∠DCB＝∠DBC＝45°∴DB＝DC即DB＝DP【数学思考】23（2）∵DG⊥CD，∠DCB＝45°∴∠DCG＝∠DGC＝45°∴DC＝DG，∠DCP＝∠DGB＝135°，∵∠BDP＝∠CDG＝90°∴∠CDP＝∠BDG，且DC＝DG，∠DCP＝∠DGB＝135°，∴△CDP≌△GDB（ASA）∴BD＝DP【拓展引申】（3）如图4，过点M作MH⊥MN交AC于点H，连接CM，HQ，∵MH⊥MN，∴∠AMH+∠NMB＝90°∵CD∥AB，∠CDB＝90°∴∠DBM＝90°∴∠NMB+∠MNB＝90°∴∠HMA＝∠MNB，且AM＝BN，∠CAB＝∠CBN＝45°∴△AMH≌△BNQ（ASA）∴AH＝BQ24∵∠ACB＝90°，AC＝BC＝4，∴AB＝4，AC﹣AH＝BC﹣BQ∴CH＝CQ∴∠CHQ＝∠CQH＝45°＝∠CAB∴HQ∥AB∴∠HQM＝∠QMB∵∠ACB＝∠HMQ＝90°∴点H，点M，点Q，点C四点共圆，∴∠HCM＝∠HQM∴∠HCM＝∠QMB，且∠A＝∠CBA＝45°∴△ACM∽△BMQ∴∴∴BQ ＝∴AM＝2时，BQ有最大值为2．11．教材呈现：证明：如图①，连结ED．∵在△ABC中，D，E分别是边BC，AB的中点，∴DE∥AC，DE ＝AC，25∴△DEG∽△ACG，∴＝＝＝2，∴＝＝3，∴＝＝；结论应用：（1）解：如图②．∵四边形ABCD为正方形，E为边BC的中点，对角线AC、BD交于点O，∴AD∥BC，BE ＝BC ＝AD，BO ＝BD，∴△BEF∽△DAF，∴＝＝，∴BF ＝DF，∴BF ＝BD，∵BO ＝BD，∴OF＝OB﹣BF ＝BD ﹣BD ＝BD，∵正方形ABCD中，AB＝6，∴BD＝6，∴OF ＝．26故答案为；（2）解：如图③，连接OE．由（1）知，BF ＝BD，OF ＝BD，∴＝2．∵△BEF与△OEF的高相同，∴△BEF与△OEF 的面积比＝＝2，同理，△CEG与△OEG的面积比＝2，∴△CEG的面积+△BEF的面积＝2（△OEG的面积+△OEF的面积）＝2×＝1，∴△BOC 的面积＝，∴▱ABCD的面积＝4×＝6．故答案为6．12．（1）证明：连接CF，如图①所示：∵AD⊥BC，BE⊥AC，∴CF⊥AB，27∵BH⊥AB，∴CF∥BH，∴∠CBH＝∠BCF，∵点M是BC的中点，∴BM＝MC，在△BMH和△CMF 中，，∴△BMH≌△CMF（ASA），∴BH＝CF，∵AB＝BC，BE⊥AC，∴BE垂直平分AC，∴AF＝CF，∴BH＝AF，∴AD＝DF+AF＝DF+BH，∵在Rt△ADB中，∠ABC＝30°，∴AD ＝BD，∴DF+BH ＝BD；（2）解：图②猜想结论：DF+BH＝BD；理由如下：同（1）可证：AD＝DF+AF＝DF+BH，∵在Rt△ADB中，∠ABC＝45°，28∴AD＝BD，∴DF+BH＝BD；图③猜想结论：DF+BH ＝BD；理由如下：同（1）可证：AD＝DF+AF＝DF+BH，∵在Rt△ADB中，∠ABC＝60°，∴AD ＝BD，∴DF+BH ＝BD．13．解：（1）相等，理由：如图1，连接AE，∵DE垂直平分AB，∴AE＝BE，∴∠BAE＝∠B＝45°，∴AE⊥BC，∵AB＝AC，∴BE＝EC＝AE，∠BAE＝∠EAC＝∠C＝45°，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝360°﹣180°＝180°，∵∠AFE+∠CFE＝180°，29∴∠AGE＝∠CFE，∵∠GAE＝∠C＝45°，∴△AEG≌△CEF（AAS），∴AG＝CF；故答案为：AG＝CF；（2）AG ＝CF，理由：如图2，连接AE，∵AB＝AC，∴∠B＝∠C＝30°，∴∠BAC＝120°，∵DE垂直平分AB，∴AE＝BE，∴∠BAE＝∠B＝30°，∴∠CAE＝90°，∠BAE＝∠C，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝180°，∵∠CFE+∠AFE＝180°，∴∠AGE＝∠CFE，∴△AGE∽△CFE，30∴，在Rt△ACE中，∵∠C＝30°，∴＝sin C ＝，∴＝，∴AG ＝CF；（3）①当G在DA上时，如图3，连接AE，∵DE垂直平分AB，∴AD＝BD＝3，AE＝BE，∵cos B ＝，∴BE ＝＝＝4，∴AE＝BE＝4，∴∠BAE＝∠B，∵AB＝AC，∴∠B＝∠C，∴∠C＝∠BAE，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝360°﹣180°＝180°，∵∠AFE+∠CFE＝180°，31∴∠CFE＝∠AGE，∴△CFE∽△AGE，∴＝，过A作AH⊥BC于点H，∵cos B ＝，cos45°＝，∵＞，∴∠B＜45°，∴E在H的左侧，∵cos B ＝，∴BH ＝AB ＝×6＝，∵AB＝AC，∴BC＝2BH＝9，∵BE＝4，∴CE＝9﹣4＝5，∵AG＝AD﹣DG＝3﹣1＝2，∴＝，∴CF＝2.5；②当点G在BD上，如图4，同（1）可得，△CFE∽△AGE，∴＝，32∵AG＝AD+DG＝3+1＝4，∴＝，∴CF＝5，综上所述，CF的长为2.5或5．14．（1）证明：①在四边形ADBC中，∠DAC+∠DBC+∠ADB+∠ACB＝360°，∵∠ADB+∠ACB＝180°，∴∠DAC+∠DBC＝180°，∵∠EAC+∠DAC＝180°，∴∠DBC＝∠EAC，∵BD＝AE，BC＝AC，33∴△BCD≌△ACE（SAS），∴CD＝CE，∠BCD＝∠ACE，∵∠BCD+∠DCA＝90°，∴∠ACE+∠DCA＝90°，∴∠DCE＝90°，∴CD⊥CE；②∵CD＝CE，CD⊥CE，∴△CDE是等腰直角三角形，∴DE ＝CD，∵DE＝AD+AE，AE＝BD，∴DE＝AD+BD，∴AD+BD ＝CD；（2）解：AD﹣BD ＝CD；理由：如图2，在AD上截取AE＝BD，连接CE，∵AC＝BC，∠ACB＝90°，∴∠BAC＝∠ABC＝45°，∵∠ADB＝90°，∴∠CBD＝90°﹣∠BAD﹣∠ABC＝90°﹣∠BAD﹣45°＝45°﹣∠BAD，∵∠CAE＝∠BAC﹣∠BAD＝45°﹣∠BAD，∴∠CBD＝∠CAE，∵BD＝AE，BC＝AC，∴△CBD≌△CAE（SAS），34∴CD＝CE，∠BCD＝∠ACE，∵∠ACE+∠BCE＝∠ACB＝90°，∴∠BCD+∠BCE＝90°，即∠DCE＝90°，∴DE ＝＝＝CD，∵DE＝AD﹣AE＝AD﹣BD，∴AD﹣BD ＝CD．15．（1）证明：①∵∠ACB＝90°，∴∠CAD+∠ADC＝90°，∵∠CDF+∠ADC＝90°，∴∠CAD＝∠CDF；②作FH⊥BC交BC的延长线于H，则四边形FECH为矩形，∴CH＝EF，在△ACD和△DHF中，，35∴△ACD≌△DHF（AAS）∴DH＝AC，∵AC＝CB，∴DH＝CB，∴DH﹣CD＝CB﹣CD，即HG＝BD，∴BD＝EF；（2）BD＝EF，理由如下：作FG⊥BC交BC的延长线于G，∵∠CAD＝∠GDF，∠ACD＝∠DGF＝90°，∴△ACD∽△DGF，∴＝＝＝2，即DG＝2AC，GF＝2CD，∵BC＝2AC，CE＝2CD，∴BC＝DG，GF＝CE，∴BD＝CG，∵GF∥CE，GF＝CE，∠G＝90°，∴四边形FECG为矩形，∴CG＝EF，∴BD＝EF．3637。

中考数学总复习《二次函数综合压轴题》专项提升练习(附答案)

中考数学总复习《二次函数综合压轴题》专项提升练习(附答案）学校:___________班级：___________姓名：___________考号：___________1．已知，如图，抛物线y=ax2+bx−8与x轴交于A、B两点，与y轴交于点C，OA=6，OB=43点P为x轴下方的抛物线上一点．(1)求抛物线的函数表达式；(2)连接AP、CP，求四边形AOCP面积的最大值；(3)若点P到AB和AC两边的距离相等，求点P的坐标．2．在平面直角坐标系中，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C．过点D(−52,34)，且顶点P的坐标为(−1,3)．(1)求二次函数的解析式；(2)如图1，若点M是二次函数图象上的点，且在直线CD的上方．连接MC，MD求△MCD面积的最大值；(3)如图2，设点Q是抛物线对称轴上的一点，连接QC，将线段QC绕点Q逆时针旋转90°，点C的对应点为F，连接PF交抛物线于点E，请直接写出点E的坐标．3．在平面直角坐标系中，已知点A(3,3)、B(6,0),AC⊥x轴，垂足为点C，直线y=12x与抛物线y=−14x2+2x相交于点O、D过x轴正半轴上的任意一点P作y轴的平行线PE交射线OA于点E．(1)求点D的坐标；(2)设点P的横坐标为a a≠3求以点A、B、C、E为顶点的四边形的面积S与a的函数关系式；(3)设直线PE交射线OD于点F交抛物线于点Q以FQ为一边在FQ的右边作矩形FQMN若FN=32且矩形FQMN与△AOB重叠部分为轴对称图形求出a的取值范围．4．在平面直角坐标系中设直线l的解析式为：y=kx+m(k、m为常数且．k≠0) 当直线l与一条曲线有且只有一个公共点时我们称直线l与这条曲线“相切” 这个公共点叫做“切点”．(1)求直线l：y=−x+6与双曲线y=9x的切点坐标；(2)已知一次函数y1=2x二次函数y2=x2+1是否存在二次函数y3=ax2+bx+c其图象经过点(−3，2)使得直线y1=2x与y2=x2+1，y3=ax2+bx+c都相切于同一点? 若存在求出y3的解析式；若不存在请说明理由；(3)已知直线l1:y=k1x+m1(k1≠0)直线l2:y2=k2x+m2(k2≠0)是抛物线y=−x2+2x+2的两条切线当l1与l2的交点P的纵坐标为4时试判断k1⋅k2是否为定值并说明理由．5．如图在平面直角坐标系中点O为坐标原点抛物线y=512x2−136x−2与x轴的交点分别为点A B与y轴的交点为点C．(1)求直线BC解析式；(2)点P为第四象限的抛物线上一点连接PB、PC当PB=PC时求点P的坐标；(3)在（2）的条件下连接OP点M在y轴的负半轴上连接MP∠OMP=∠CBP N为OM的中点点Q 在OP上连接MQ、NQ，MQ交抛物线于点R当MQ=2NQ时求R点的横坐标．6．如图在平面直角坐标系中抛物线y=ax2+bx+c(a≠0)若抛物线与x轴交于B(4，0)C(−2，0)两点与y轴交于点A(0，−2)．(1)求该抛物线的函数表达式；(2)如图1 若点E是直线CA下方的抛物线上一点过点E作EF∥AB交x轴于点F且EF=√5求点E的横坐标；(3)如图2 点M在点B的正下方连接CM交抛物线于点N直线BN交对称轴于点P作PQ∥CM交射线BM于点Q求BQ的大小．7．如图在平面直角坐标系xOy中已知直线y=−x−3与x轴交于点A与y轴交于点C过A C两点的抛物线y=ax2+bx+c与x轴交于另一点B(1,0)抛物线对称轴为直线l．(1)求抛物线的解析式；(2)点M为直线AC下方抛物线上一点当△MAC的面积最大时求点M的坐标；(3)点P是抛物线上的点过点P作l的垂线垂足为D E是l上的点．要使得以P D E为顶点的三角形与△BOC全等请求出点P点E的坐标；8．如图抛物线y=−x2+bx+c与x轴相交于A B两点与y轴交于点C抛物线的对称轴交x轴于点D．已知A(−1,0),C(0,3)．(1)求抛物线的解析式；(2)在抛物线的对称轴上有一点P使得|PB−PC|的值最大求此点P的坐标；(3)点M为该抛物线的顶点直线MD⊥x轴于点D在直线MD上是否存在点N使点N到直线MC的距离等于点N到点A的距离？若存在求出点N的坐标；若不存在请说明理由；9．在平面直角坐标系中点O为坐标原点抛物线y=ax2+x+6交x轴负半轴于A交正半轴于B交y 轴于C OB=OC．(1)求抛物线的解析式；(2)如图1 点P是第三象限抛物线上一点连接BP交y轴于点D设点P横坐标为t线段CD长为d求d与t的函数关系；(3)如图2 在（2）的条件下过点C作BP的垂线交x轴于点F垂足为点G E为CF上一点连接BE 若BE=BD∠BEG=2∠PBA求点P坐标．10．如图1 在平面直角坐标系中O为坐标原点AD为等腰直角△ABC底边BC上的高抛物线y=a(x−2)2+4的顶点为点A且经过B C两点B C两点在x轴上．(1)求该抛物线的解析式；(2)如图2 点E为抛物线上位于直线AC上方的一点过点E作EN⊥x轴交直线AC于点N求线段EN的长度最大值及此时点E的坐标；(3)如图2 点M(5，b)是抛物线上的一点点P为对称轴上一动点在(2)的条件下当线段EN的长度最大时求PE+PM的最小值．11．抛物线y=ax2−2ax−3a(a>0)与x轴交于A B两点（点A在点B的左边）与y轴交于点C．(1)求抛物线的对称轴；(2)求证：不论a取何值函数图象必过两个定点；(3)如图若OB=OC点P是直线BC（不与B C重合）上一动点过点P作x轴的垂线交抛物线于M点连接CM将△PCM沿CM对折如果点P的对应点N恰好落在y轴上求此时点P的坐标．12．已知抛物线y=a(x+6)(x−2)经过点(0，2)交x轴于点A和点B（点A在点B的左侧）抛物线的顶点为D对称轴DE交x轴于点E连接EC．(1)直接写出a的值点A的坐标；(2)若点M是抛物线对称轴DE上的点当△MCE是等腰三角形时求点M的坐标；(3)点P是抛物线上的动点连接PC、PE将△PCE沿CE所在的直线对折点P落在坐标平面内的点P′处．直接写出点P′恰好落在直线AD上时点P的横坐标．13．综合与探究如图1 抛物线y=ax2+bx+4与x轴交于A(−4,0)B(3,0)两点与y轴交于点C连接AC BC现将△ABC沿x轴向右平移至△A′B′C′线段A′C′与线段BC交于点E与抛物线交于点F．(1)求出抛物线和直线BC的函数表达式；(2)当线段FE的长度最大时求此时点F的坐标；(3)如图2 连接OC′将△OA′C′沿着A′C′翻折得到△O′A′C′是否存在某一时刻使得点O′恰好在抛物线上若存在请直接写出此时平移的距离；若不存在请说明理由．14．如图1 已知二次函数y=ax2+bx+c（a b c为常数且a≠0）的图像与x轴交于A B两点（A 点在B点左侧）与y轴交于点C(0,3)且其函数表达式可以变形为y=a(x+1)(x−3)的形式．已知点P为该抛物线在第一象限内的一动点设其横坐标为m．(1)求出点A点B的坐标和该二次函数的表达式；(2)连接BC过点P作PQ⊥x轴于点Q交BC于点N直线AP交y轴于点M连接MN．①求出直线AP的函数表达式（用含有m的代数式表示）；②设四边形MNQO的面积为S求S关于m的函数关系式并求S的最大值；(3)如图2 若直线l为该二次函数图像的对称轴交x轴于点H直线AP BP分别交直线l于点E F．在点P运动的过程中HF+HE是否为定值？若是请求出该定值；若不是请说明理由．15．在平面直角坐标系中关于x的二次函数y=ax2+bx+c（a b c为常数且a<0）与x轴交于两个不同的点A(x1,0)B(x2,0)(x1<x2)与y轴交于点C抛物线的顶点为M．(1)如图1 已知a=−1b=2c=3．①求此二次函数图象的顶点M的坐标；②点E是x轴正半轴上的一个动点过点E作直线PE⊥x轴交抛物线于点P交直线BC于点F．当点E在线EF求此时点P的坐标．段OB上运动时（不与点O B重合）恰有线段PF=12(2)如图2 当c=0时点P是抛物线对称轴左侧图像上任意一点过点P作PE⊥x轴于点E连接MP交y轴于点Q连接EQ MB．则EQ MB有怎样的位置关系?说明理由．16．如图抛物线的顶点坐标为(2,−3)与y轴交于点C(0,1)．(1)求抛物线的解析式；(2)求点A B的坐标及线段AB的长；(3)求△ABC的外接圆⊙D的半径；(4)若（3）中的⊙D交抛物线的对称轴于M N两点（点M在点N的上方）在对称轴右边的抛物线上有一动点P连接PM PN PC线段PC交弦MN于点G．若PC把图形PMCN（指圆弧MCN和线段PM PN组成的图形）分成两部分当这两部分面积之差等于4时求出点P的坐标．17．如图在平面直角坐标系中抛物线y=12x2−32x−2与x轴分别交于点A点B与y轴交于点C．(1)如图1 连接AC直接写出sin∠ACO的值；(2)如图2 连接BC．点G(1,a)在抛物线上连接CG、BG若异于点G的点H也在抛物线上且S△BCH= S△BCG求点H的坐标；(3)如图3 若直线y=mx+n与抛物线交于点P Q连接AP交y轴正半轴于点M连接AQ交y轴负半轴于点N若OM⋅ON=32求4m+n的值．18．如图1 已知二次函数图象与y轴交点为C(0,3)其顶点为D(1,2)．(1)求二次函数的表达式；(2)直线CD与x轴交于M现将线段CM上下移动若线段CM与二次函数的图象有交点求CM向上和向下平移的最大距离；(3)若将（1）中二次函数图象平移使其顶点与原点重合然后将其图象绕O点顺时针旋转90°得到抛物线G如图2所示直线y=−x+2与G交于A B两点P为G上位于直线AB左侧一点求ΔABP面积最大值及此时点P的坐标．19．如图在平面直角坐标系中抛物线y=ax2+bx+4(a≠0)经过点(−1,6)与x轴交于点A(−4,0)B 两点与y轴交于点C．(1)求抛物线的解析式；(2)点P是直线AC上方抛物线上一动点过点P作PD∥y轴交AC于点D求PD的最大值及此时点P的坐标；个单位长度得到新抛物线y′新抛物线y′的对称轴交x轴于点M点N是直(3)将该抛物线沿x轴向右平移52线AC上一点在平面内确定一点K使得以C，M，N，K为顶点的四边形是以CN为边的菱形写出所有符合条件的点K的坐标并写出求解点K坐标的其中一种情况的过程．20．如图抛物线y=x2+bx+c与x轴交于A(1,0)B两点与y轴交于点C(0,3)．(1)求该抛物线的解析式；(2)如图（1）点P是线段BC上的一动点过点P作PQ∥y轴交抛物线于点Q连接CQ若CQ平分∠OCB求点P的坐标；(3)如图（2）过A B C三点作⊙I直线y=t(t>3)交⊙I于点M N交抛物线于点E F．若EM+FN=MN求t的值参考答案：1．(1)y =x 2+143x −8 (2)51(3)P (56,−4112)【分析】（1）利用待定系数法求解即可；（2）如图所示连接AC 过点P 作PD ⊥x 轴交AC 于D 先求出直线AC 的解析式设P (t,t 2+143t −8) 则D (t,−43t −8) 则PD =−t 2−6t 求出S △APC 的最大值再由S 四边形AOCP =S △ACP +S △AOC 可知当S △APC最大时 S 四边形AOCP 最大由此即可得到答案；（3）如图所示取点E 使其坐标为(4，0) 连接AC 、CE 取CE 中点F 连接AF 先证明AE =AC 进而得到AF 平分∠CAE 则直线AF 上的点到AC AB 的距离相等由此即可知点P 即为直线AF 与抛物线的交点据此求解即可．【详解】（1）解：∵OA =6∵A (−6,0)∵可设抛物线解析式为y =a (x +6)(x −43)又∵当x =0时 y =−8 即C (0,−8)∵6×(−43)a =−8 ∵a =1∵抛物线解析式为y =(x +6)(x −43)=x 2+143x −8；（2）解：如图所示连接AC 过点P 作PD ⊥x 轴交AC 于D 设直线AC 的解析式为y =kx +b 1∵{−6k +b 1=0b 1=−8∵{k =−43b 1=−8∵直线AC 的解析式为y =−43x −8设P(t,t2+143t−8)则D(t,−43t−8)∵PD=−43t−8−(t2+143t−8)=−t2−6t∵S△APC=S△APD+S△CPD=12PD⋅(x P−x A)+12PD⋅(x C−x P)=12PD⋅(x C−x A)=3PD=−3(t+3)2+27∵−3<0∵当t=−3时S△APC最大最大为27∵S四边形AOCP=S△ACP+S△AOC∵S四边形AOCP=S△ACP+24∵当S△APC最大时S四边形AOCP最大最大为27+24=51；（3）解：如图所示取点E使其坐标为(4，0)连接AC、CE取CE中点F连接AF∵A(−6,0)C(0,−8)∠AOC=90°∵AE=10，AC=√OA2+OC2=10∵AC=AE∵F是CE的中点∵AF平分∠CAE∵直线AF上的点到AC AB的距离相等设直线AF的解析式为y=k1x+b2∵{−6k1+b2=0 2k1+b2=−4∵{k1=−12 b2=−3∵直线AF的解析式为y=−12x−3联立{y=−12x−3y=x2+14x3−8得6x2+31x−30=0解得{x=56y=−4112或{x=−6y=0（舍去）∵点P的坐标为(56,−4112)．【点睛】本题主要考查了二次函数的综合一次函数与几何综合角平分线的性质等腰三角形的性质与判定勾股定理等等正确作出辅助线是解题的关键．2．(1)y=−x2−2x+2(2)12564(3)(−2,2)或(−1,3)【分析】（1）用待定系数法即可求解；（2）由△MCD面积=S△MHD+S△MHC即可求解；（3）①当点Q在点C的下方时证明△QNF≌△CQH(AAS)得到CG=2−t=QN QH=1=FN则点F(t−3,t+1)求出直线PF的表达式进而求解；②当点Q在点C的上方时同理可得：点F′的坐标为(t−3,t−1)进而求解．【详解】（1）解：设抛物线的表达式为：y=a(x−ℎ)2+k则y=a(x+1)2+3将点C的坐标代入上式并得：34=a(−52+1)2+3解得：a=−1故抛物线的表达式为：y =−(x +1)2+3=−x 2−2x +2 即y =−x 2−2x +2；（2）解：由抛物线的表达式知点C (0,2)如图1 过点M 作MH∥y 轴交CD 于点H设直线CD 的表达式为：y =sx +t则{34=−52s +t t =2解得{s =12t =2 故直线CD 的表达式为：y =12x +2 设点M(m,−m 2−2m +2) 点H(m,12m +2) 则△MCD 面积=S △MHD +S △MHC =12MH ×(x C −x D )=12×[(−m 2−2m +2)−(12m +2)]×52 =−54(m 2+52m) ∵ −54<0 故函数由最大值当m =−54时 △MCD 面积的最大值为12564；（3）设点Q(−1,t) 如图2①当点Q 在点C 的下方时过点Q 作x 轴的平行线交y 轴于点H 交过点F 与y 轴的平行线于点N∵∠FQN +∠QFN =90°∴∠QFF =∠CQH∵∠N =∠CHQ =90°∴△QNF ≌△CQH (AAS )∴CH =2−t =QN∴点F(t −3,t +1)设直线FP 的表达式为：y =px +q则{3=−p +q t +1=p(t −3)+q解得{p =1q =4 故直线PF 的表达式为：y =x +4②联立直线PE 与抛物线的：{y =x +4y =−x 2−2x +2解得：{x =−2y =2（不合题意的值已舍去）即点E(−2,2)；②当点Q 在点C 的上方时同理可得：点F′的坐标为(t −3,t +1)由点P F ′的坐标得：直线PF ′的表达式为y =x +4 同情况①故点E(−2,2)；当点F 与点E 重合时也符合题意综上点E 的坐标为(−2,2)或(−1,3)．【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质和旋转的性质；会利用三角形全等的知识解决线段相等的问题；会解一元二次方程；理解坐标与图形性质．3．(1)D(6,3)(2)S ={9−32a (0<a <3)3a −92(a >3)(3)a =3−√3或a =94或3≤a <4【分析】（1）联立两个函数解析式解方程组即可；（2）先求解直线OA 的解析式为y =x 可得点E(a,a) 再分两种情况讨论即可；（3）分情况讨论：①如图当a <3 且FQ =FN 时矩形FQMN 与△AOB 重叠部分为轴对称图形 ②如图当AC 为矩形FQMN 的对称轴时矩形FQMN 与△AOB 重叠部分为轴对称图形 ③如图当PQ 与AC 重合时矩形FQMN 与△AOB 重叠部分为等腰直角三角形是轴对称图形 ④如图当点F 为直线OD 与AB 的交点时可得当3≤a <4时矩形FQMN 与△AOB 重叠部分为等腰直角三角形是轴对称图形从而可得答案．【详解】（1）解：联立y =12x 和y =−14x 2+2x 得{x =0,y =0 或{x =6y =3∵点D(6,3)．（2）设直线OA 的解析式为y =kx∵点A(3,3)∴3k =3 解得k =1∴直线OA 的解析式为y =x ．∵点P 的横坐标为a,PE ∥y 轴且交射线OA 于点E∴点E(a,a)．当0<a <3时如图S =S △OAB −S △OCE =12×6×3−12×3a =9−32a ．当a >3时如图S =S △OBE −S △OAC =12×6a −12×3×3=3a −92．综上 S ={9−32a (0<a <3)3a −92(a >3)；（3）①如图当a <3 且FQ =FN 时矩形FQMN 与△AOB 重叠部分为轴对称图形∵FQ=FN∴−14a2+2a−12a=32解得a=3±√3其中a=3+√3不满足a<3∴a=3−√3．②如图当AC为矩形FQMN的对称轴时矩形FQMN与△AOB重叠部分为轴对称图形此时∴32=2(3−a)解得a=94．③如图当PQ与AC重合时矩形FQMN与△AOB重叠部分为等腰直角三角形是轴对称图形此时a=3．④如图当点F为直线OD与AB的交点时∵点A(3,3),B(6,0)∵AB所在的直线方程为y=−x+6联立y=−x+6和y=12x解得x=4．∴当3≤a<4时矩形FQMN与△AOB重叠部分为等腰直角三角形是轴对称图形综上 a 的取值范围是a =3−√3或a =94或3≤a <4．【点睛】本题考查的是利用二次函数的图象与性质列二次函数关系式矩形的性质轴对称图形的性质一元二次方程的解法清晰的分类讨论熟练的运用数形结合的方法解题是关键．4．(1)切点坐标为(3，3)(2)y 3=12x 2+x +12(3)k 1⋅k 2是定值【分析】（1）联立直线和双曲线解析式得到关于x 的一元二次方程由相切的定义得出x 的值解之可得；（2）联立{y =2x y =x 2+1可得切点为(1，2) 从而得出y 3=ax 2+bx +c 经过点(−3，2) (1，2) 利用待定系数法得出y 3=ax 2+2ax +2−3a 联立{y =ax 2+2ax +2−3a y =2x 得：ax 2+(2a −2)x +2−3a =0 利用Δ=0得出a =12 b =1 c =12 即可得解；（3）由l 1与l 2的交点P 的纵坐标为4 可令P(t ，4) 则直线l 1:y =k 1x −k 1t +4 直线 l 2:y 2=k 2x −k 2t +4 联立{y =k 1x −k 1t +4y =−x 2+2x +2得：x 2+(k 1−2)x −k 1t +2=0 由直线l 1:y =k 1x +m 1(k 1≠0)是抛物线y =−x 2+2x +2的切线可得Δ=k 12+(4t −4)k 1−4=0 同理可得：k 22+(4t −4)k 2−4=0 从而得出k 1，k 2为x 2+(4t −4)x −4=0的两根最后由一元二次方程根与系数的关系即可得出答案．【详解】（1）解：联立{y =−x +6y =9x得：x 2−6x +9=0 解得：x =3∴切点坐标为(3，3)；（2）解：∵直线y 1=2x 与二次函数y 2=x 2+1相切∴联立{y =2x y =x 2+1得：x 2−2x +1=0 解得：x =1∴切点为(1，2)∵ y 1=2x 与y 2=x 2+1，y 3=ax 2+bx +c 都相切于同一点∴ y 3=ax 2+bx +c 经过点(−3，2)∴{a +b +c =29a −3b +c =2解得：{b =2a c =2−3a∴y 3=ax 2+2ax +2−3a联立{y =ax 2+2ax +2−3a y =2x得：ax 2+(2a −2)x +2−3a =0 ∴Δ=(2a −2)2−4×a ×(2−3a )=4a 2−8a +4−8a +12a 2=16a 2−16a +4=(4a −2)2=0 解得：a =12 ∴b =2a =1∴ y 3的解析式为：y 3=12x 2+x +12；（3）解：k 1⋅k 2是定值理由如下：∵ l 1与l 2的交点P 的纵坐标为4∴令P(t ，4)∴直线l 1:y =k 1x +m 1=k 1t +m 1=4 直线 l 2:y 2=k 2x +m 2=k 2t +m 2=4∴m 1=4−k 1t∴直线l 1:y =k 1x −k 1t +4 直线 l 2:y 2=k 2x −k 2t +4联立{y =k 1x −k 1t +4y =−x 2+2x +2得：x 2+(k 1−2)x −k 1t +2=0 ∵直线l 1:y =k 1x +m 1(k 1≠0)是抛物线y =−x 2+2x +2的切线∴Δ=(k 1−2)2−4×1×(2−k 1t )=k 12−4k 1+4−8+4k 1t =k 12+(4t −4)k 1−4=0同理可得：k 22+(4t −4)k 2−4=0∴ k 1，k 2为x 2+(4t −4)x −4=0的两根∴k 1⋅k 2=−4．【点睛】本题是二次函数综合题考查了新定义二次函数的性质一元二次方程的根与系数的关系等知识解题的关键是理解题意学会构建方程组解决问题属于中考压轴题．5．(1)y =13x −2(2)P (4,−4)(3)0或5−√2655【分析】（1）令抛物线y =0 x =0 求出点B C 的坐标设直线BC 的解析式为y =kx +b (k ≠0) 代入点B C 的坐标即可求解；（2）由题意得△PBC 是等腰三角形即点P 在过点B C 的BC 中点且垂直于直线BC 的直线上求出点B C的中点坐标设点P (a,512a 2−136a −2) 利用勾股定理即可求出a 的值求出符合点点P 特征的点即可；（3）过点P 作PF ⊥x 轴垂足为点F 根据（2）的结论结合已知分别证明△PFO,△PBC,△OPM 是等腰直角三角形利用等腰直角三角形的性质求出点M 的坐标进而得到N 点的坐标求出直线OP 的解析式设点Q (b,−b ) 利用两点间距离公式结合MQ =2NQ 求出点Q 的坐标再求出直线MQ 的解析式联立抛物线即可求解．【详解】（1）解：在抛物线y =512x 2−136x −2中令x =0 则y=−2∴C (0,−2)令y =0 则512x 2−136x −2=0 即5x 2−26x −24=0解得：x 1=6,x 2=−45 ∵点B 在x 轴的正半轴∴B (6,0)设直线BC 的解析式为y =kx +b (k ≠0) 代入点B C 的坐标得{−2=b 0=6k +b解得：{b =−2k =13∴直线BC 的解析式为y =13x −2；（2）解：设点P (a,512a 2−136a −2) ∵ PB =PC ∴PB 2=PC 2 即(a −6)2+(512a 2−136a −2)2=a 2+(512a 2−136a −2+2)2整理得：a 2+2a −24=0解得：a =4或a =−6（舍去不符合题意）当a =4时∴P (4,−4)；（3）解：如图过点P 作PF ⊥x 轴垂足为点F由（2）知点P(4,−4)∴PF=OF=4∴△PFO是等腰直角三角形∴∠POF=∠POM=45°∵PC=√(4−0)2+[(−4)−(−2)]2=2√5,BC=√(0−6)2+(−2−0)2=2√10又PC2+PB2=BC2∴△PBC是等腰直角三角形∴∠BPC=90°,∠CBP=∠PCB=45°∵∠OMP=∠CBP∴∠OMP=45°∴△OPM是等腰直角三角形∴OP=MP∴OP=√42+(−4)2=4√2=MP∴OM=√OP2+MP2=8∵点M在y轴的负半轴上∴点M(0,−8)∵N为OM的中点∴N(0,−4)设直线OP的解析式为y=k′x(k′≠0)将P(4,−4)代入得−4=4k′解得k′=−1∴直线OP的解析式为y=−x设Q(b,−b)∵MQ=2NQ∴√b2+(−b+8)2=2√b2+(−b+4)2∴b=0或b=83当b=0时此时点Q与点O重合∴MQ与抛物线交点在y轴上∴点R的横坐标为0当b=83时设直线MQ的解析式为y=sx+t将点Q(83,−83)M(0,−8)代入得{−8=t−83=83s+t解得{s=2t=−8∵直线MQ的解析式为y=2x−8联立直线MQ与抛物线y=512x2−136x−2得{y=2x−8y=512x2−136x−2解得{x=5+√2655y=2√2655+2（舍去不符合题意）或{x=5−√2655y=2−2√2655∵此时MQ交抛物线于点R的横坐标为5−√2655综上点R的横坐标为0或5−√2655．【点睛】本题考查二次函数的图象及性质一次函数解析式熟练掌握二次函数的图象及性质等腰直角三角形的判定及性质直角三角形的性质用待定系数法求函数的解析式是解题的关键．6．(1)y=14x2−12x−2(2)点E的横坐标为1−√5(3)BQ=92【分析】（1）将B(4，0)C(−2，0)A(0，−2)代入抛物线解析式得到{16a+4b+c=04a−2b+c=0c=−2求出a、b、c的值即可得出答案；（2）先利用待定系数法求出直线AB 的解析式为：y =12x −2 设点E 的坐标为(e ，14e 2−12e −2)(−2<e <0) 从而求出直线EF 的解析式为：y =12x +14e 2−e −2 进而得出F (2e +4−12e 2，0) 表示出EF =√[e −(2e +4−12e 2)]2+(14e 2−12e −2)2=√5(14e 2−12e −2)2=√5 解方程即可得出答案；（3）设点M 的坐标为(4，m)(m <0) 待定系数法求出直线CM 的解析式为：y =m6x +m3 联立{y =m6x +m 3y =14x 2−12x −2得出N (12+2m 3，m2+9m9) 再利用待定系数法求出直线BN 的解析式为：y =m+96x −2m+183 从而得出P (1，−m−92) 利用待定系数法求出直线PQ 的解析式为y =m 6x −4m+276从而得出Q (4，−92) 即可得解．【详解】（1）解：∵ 抛物线y =ax 2+bx +c (a ≠0)与x 轴交于B(4，0) C(−2，0)两点与y 轴交于点A(0，−2)∴{16a +4b +c =04a −2b +c =0c =−2解得：{a =14b =−12c =−2∴抛物线的解析式为y =14x 2−12x −2；（2）解：设直线AB 的解析式为：y =k 1x +b 1 将A(0，−2) B(4，0)代入直线得：{0=4k 1+b 1b 1=−2解得：{k 1=12b 1=−2∴直线AB 的解析式为：y =12x −2 ∵点E 是直线CA 下方的抛物线上一点∴设点E 的坐标为(e ，14e 2−12e −2)(−2<e <0)∵EF ∥AB∴设直线EF 的解析式为：y =12x +b 2∴14e 2−12e −2=12e +b 2∴b 2=14e 2−e −2∴直线EF 的解析式为：y =12x +14e 2−e −2令y =0 则12x +14e 2−e −2=0 解得：x =2e +4−12e 2∴F (2e +4−12e 2，0)∴EF =√[e −(2e +4−12e 2)]2+(14e 2−12e −2)2=√(e −2e −4+12e 2)2+(14e 2−12e −2)2=√(12e 2−e −4)2+(14e 2−12e −2)2=√[2(14e 2−12e −2)]2+(14e 2−12e −2)2=√4(14e 2−12e −2)2+(14e 2−12e −2)2=√5(14e 2−12e −2)2∵EF =√5∴√5(14e 2−12e −2)2=√5∴(14e 2−12e −2)2=1 ∴14e 2−12e −2=1或14e 2−12e −2=−1 ∵点E 是直线CA 下方的抛物线上一点∴14e 2−12e −2<0 ∴14e 2−12e −2=−1 ∴e 2−2e −4=0解得：e =1+√5或e =1−√5∵−2<e <0 ∴e =1−√5∴点E 的横坐标为1−√5；（3）解：∵点M 在点B 的正下方 ∴设点M 的坐标为(4，m)(m <0) 设直线CM 的解析式为y =k 2x +b 2将C(−2，0) M(4，m)代入解析式得：{0=−2k 2+b 2m =4k 2+b 2解得：{k 2=m6b 2=m 3∴直线CM 的解析式为：y =m 6x +m3联立{y =m 6x +m 3y =14x 2−12x −2整理得：3x 2−(6+2m )x −(24+4m )=0∴(x +2)(3x −12−2m )=0解得：x 1=−2 ∴点N 的横坐标为12+2m 3纵坐标为y =12+2m36⋅m +m 3=12+2m 18⋅m +m 3=18m+2m 218=m 2+9m9∴N (12+2m 3，m 2+9m 9)设直线BN 的解析式为：y =k 3x +b 3 将B(4，0) N (12+2m 3，m 2+9m9)代入解析式得：{0=4k 3+b 3m 2+9m9=12+2m 3k 3+b 3解得：{k 3=m+96b 3=−2m+183∴直线BN 的解析式为：y =m+96x −2m+183∵抛物线的解析式为y =14x 2−12x −2 ∴对称轴为直线x =−−122×14=1∴点P 的横坐标为1 纵坐标为y =m+96×1−2m+183=−3m−276=−m−92∴P (1，−m −92) ∵PQ ∥CM∴设直线PQ 的解析式为y =m 6x +b 4∴−m −92=m6×1+b 4 解得：b 4=−4m−276∴直线PQ 的解析式为y =m6x −4m+276∵作PQ ∥CM 交射线BM 于点Q ∴点Q 的横坐标为4 纵坐标为y =m 6×4−4m+276=−92∴Q (4，−92)∴BQ =0−(−92)=92．【点睛】本题考查了二次函数综合题待定系数法求二次函数解析式一次函数解析式二次函数综合—线段问题勾股定理求两点之间的距离等知识点熟练掌握以上知识点并灵活运用采用数形结合的思想是解此题的关键． 7．(1)y =x 2+2x −3 (2)M (−32,−154)(3)P 点坐标为(−4,5)或(2,5)或(−2,−3)或(0,−3) E(−1,6)或(−1,4)或(−1,−6)或(−1,0)【分析】（1）先求出A,C 的坐标进而利用待定系数法求出二次函数解析式即可；（2）过点M 作MF 垂直于x 轴交AC 于点F 设M (x,x 2+2x −3) F(x,−x −3) 则MF =(−x −3)−(x 2+2x −3)=−x 2−3x 由S △AMC =12MF ×|x C −x A |即可求解；（3）抛物线对称轴为直线x=−1．∠PDE =∠BOC OB =1 OC =3．设P (x,x 2+2x −3) 则D (−1,x 2+2x −3) 分两种情况当PD =OC DE =OB 时 △PDE ≌△COB 此时|−1−x |=3 当PD =OB DE =OC 时 △EDP ≌△COB 此时|−1−x |=1 求解即可．【详解】（1）解：把x =0代入y =−x −3得y=−3；把y =0代入y =−x −3得x =−3． ∴A(−3,0) C(0,−3)．∵抛物线y =ax 2+bx +c 经过A,C,B 三点∴{9a −3b +c =0a +b +c =0c =−3解得{a =1b =2c =−3．∴抛物线的解析式为y =x 2+2x −3；（2）过点M 作MF 垂直于x 轴交AC 于点F 设M (x,x 2+2x −3) 则F(x,−x −3) 则MF =(−x −3)−(x 2+2x −3)=−x 2−3xS △AMC =12MF ×|x C −x A |= 12(−x 2−3x )×3=−32(x +32)2+278∴当x =−32时 S △AMC 最大此时y =x 2+2x −3=−154． ∴当M 坐标为(−32,−154)时 S △AMC 取得最大值．（3）∵y =x 2+2x −3=(x +1)2−4 ∵抛物线对称轴为直线x=−1． ∵过点P 作l 的垂线垂足为D ∵∠PDE =∠BOC =90° ∵C(0,−3)，A (−3,0) ∵B (1,0)∵OB =1 OC =3．设P (x,x 2+2x −3) 则D (−1,x 2+2x −3) 当PD =OC DE =OB 时此时|−1−x |=3 解得x =−4或x =2． ∵P 点坐标为(−4,5)或(2,5)∵DE =OB =1∴E(−1,6)或(−1,4)．当PD =OB DE =OC 时此时|−1−x |=1 解得x =−2或x =0． ∵P 点坐标为(−2,−3)或(0,−3)∵DE =3∴E(−1,−6)或(−1,0)．综上：P 点坐标为(−4,5)或(2,5)或(−2,−3)或(0,−3) E(−1,6)或(−1,4)或(−1,−6)或(−1,0)．【点睛】本题考查了二次函数求解析式二次函数的性质三角形全等的性质最值问题等熟练掌握各知识点能准确作出辅助线并结合图形列出相应关系式是解题的关键． 8．(1)y =−x 2+2x +3 (2)P (1,6)(3)存在点N 满足要求点N 坐标为(1,−4+2√6)或(1,−4−2√6)【分析】本题考查了待定系数法求二次函数表达式二次函数的图像与性质及二次函数与一次函数综合（1）用待定系数法求二次函数表达式；（2）根据抛物线特征得出当A,C,P 三点共线时 |PA −PC |最大求出直线AC 的解析式为y =3x +3 即可求出结论；（3）设直线MC 与x 轴交于点E 过点N 作NQ ⊥MC 于Q 先求出直线MC 的解析式为y =x +3 证出MQ =NQ =√22MN 设点N (1,n ) 根据NQ 2=AN 2列方程并解方程即可解决．【详解】（1）解：∵抛物线y =−x 2+bx +c 经过A (−1,0),C (0,3)两点∴{−1−b +c =0c =3解得：{b =2c =3∴该抛物线的解析式为y =−x 2+2x +3；（2）解：由抛物线的对称性得点B 关于抛物线对称轴的对称点是点A∴PA =PB∴|PB −PC |=|PA −PC |∴当A,C,P 三点共线时 |PA −PC |最大如图连接AC 并延长AC 交抛物线的对称轴于点P设直线AC 的解析式为y =kx +d 把A (−1,0),C (0,3)代入得：{−k +d =0d =3解得：{k =3d =3∴直线AC 的解析式为y =3x +3 ∵抛物线的对称轴为直线x =−2−2=1当x =1时 ∴点P (1,6)；（3）存在N 满足条件理由如下：∵抛物线y =−x 2+2x +3与x 轴交于A 、B 两点 ∴点A (−1,0)∵y =−x 2+2x +3=−(x −1)2+4∴顶点M 为(1,4) ∵点M 为(1,4) 点C (0,3) ∴直线MC 的解析式为：y =x +3如图设直线MC 与x 轴交于点E 过点N 作NQ ⊥MC 于Q∴点E (−3,0)∴DE =4=MD ∴∠NMQ =45°∵NQ⊥MC∴∠NMQ=∠MNQ=45°∴MQ=NQ∴MQ=NQ=√22MN设点N(1,n)∵点N到直线MC的距离等于点N到点A的距离∴NQ=AN∴NQ2=AN2∴(√22MN)2=AN2即(√22|4−n|)2=4+n2∴n2+8n−8=0∴n=−4±2√6∴存在点N满足要求点N坐标为(1,−4+2√6)或(1,−4−2√6)．9．(1)y=−13x2+x+6(2)d=−2t(3)P(−4,−103)【分析】（1）先令x=0求出点C坐标再根据已知可得点B的坐标运用待定系数法即可求出抛物线解析式；（2）由（1）可得点B的坐标设P(t,−13t2+t+6)运用待定系数法求得直线PB的解析式为y=−13(t+3)x+2(t+3)进而求出D(0,2t+6)即可求得答案；（3）找点F关于原点的对称点F′连接CF′过点F′作F′K⊥GE于K根据已知先证△COF≌△BOD得OF= OD再证∠F′CK=2∠PBA进而证得△CF′K≌△EBG得F′K=BG再证△F′FK≌△BFG可得F′F=BF OB=3OF进而求出点D的坐标运用待定系数法求出直线BD的解析式再求出直线BD与抛物线的交点P的坐标．【详解】（1）解：∵抛物线y=ax2+x+6交y轴于点C∴C(0,6)∴OC=6∵OB=OC∴B(6,0)∵ B (6,0)在抛物线y =ax 2+x +6上∴ 0=36a +6+6∴ a =−13∴ y =−13x 2+x +6．（2）∵点P 是第三象限抛物线上一点∴ P (t,−13t 2+t +6)设直线PB 的解析式为y =kx +b (k ≠0)∴ {6k +b =0kt +b =−13t 2+t +6∴ {k =−13(t +3)b =2(t +3)∴直线PB 的解析式为y =−13(t +3)x +2(t +3)．令x =0 得y =2(t +3)=2t +6∴ D (0,2t +6)∴ CD =6−(2t +6)=−2t∵线段 CD 长为 d∴ d =−2t ；（3）解：找点F 关于原点的对称点F ′ 连接CF ′ 过点F ′作F ′K ⊥GE 于K∵ CG ⊥BP OB ⊥OC∴ ∠COF =∠BOD =90°∵ OC =OB∴ △COF ≌△BOD∴ CF =BD∵点F 关于原点的对称点F ′∴∠FCO=∠F′CO OF=OF′∴∠F′CK=2∠PBA∵∠BEG=2∠PBA∴∠F′CK=∠BEG∵F′K⊥CG∴△CF′K≌△EBG∴F′K=BG∵F′K⊥CG∴∠FKF′=∠FGB=90°∵∠F′FK=∠BFG∴△F′FK≌△BFG∴F′F=BF∴OB=3OF∴OD=OF=13OB=2∴D(0,−2)设直线BD的解析式是y=mx+n∴{−2=0×m+n0=8m+n∴{m=1 3n=−2∴直线BD的解析式是y=13x−2∵点P在直线BD上也在抛物线y=−13x2+x+6上∴{y=13x−2y=−13x2+x+6∴{x=−4y=−103∴P(−4,−103)；【点睛】本题考查了二次函数的综合题熟练掌握二次函数图像上点的坐标特征二次函数的性质中心对称的性质全等三角形的判定和性质等知识添加正确的辅助线是解题的关键．10．(1)y=−14x2+x+3(2)1(3)5√174【分析】（1）先确定点A的坐标为(2，4)再结合等腰直角三角形的性质可得C(6，0)然后运用待定系数法即可解答；（2）先用待定系数法可得AC的函数解析式为y=−x+6设E(t,−14t2+t+3)N（t，−t+6）则EN=−14t2+2t−3然后化成顶点式求最值即可；（3）先确定点M(5,74)过点E作AD的对称点E′(0,3)连接E′M交AD于点P此时PE+PM最短时M(5,74)最后运用勾股定理即可解答．【详解】（1）解：∵AD为等腰直角△ABC底边BC上的高y=a(x−2)2+4的顶点为点A ∵A的坐标为(2，4)∵AD=4∵AD为等腰直角△ABC底边BC上的高∵CD=AD=4∵C(6，0)．把C(6，0)代入y=a(x−2)2+4解得：a=−14∵抛物线的解析式为y=−14(x−2)2+4即y=−14x2+x+3．（2）解：设直线AC的函数解析式为y=kx+b ∵A(2，4)，C(6，0)∵AC的函数解析式为y=−x+6．设E(t,−14t2+t+3)EN=−14t2+t+3−(−t+6)=−14t2+2t−3=−14(t−4)2+1∵当t=4时EN最大为1∵E(4，3)．（3）解：∵M(5，b)在抛物线y =−14(x −2)2+4上∵M (5,74)．∵AD 是此抛物线的对称轴∵过点E 作AD 的对称点E ′(0,3) 连接E ′M 交AD 于点P 此时PE +PM 最短 M (5,74);∵PE +PM 最短=E ′M =√(0−5)2+(3−74)2=5√174．【点睛】本题主要考查了二次函数与几何的综合求函数解析求函数最值等知识点灵活运用相关知识成为解题的关键．11．(1)x =1； (2)(3,0) (−1,0)；(3)点P 的坐标为(3−√2,−√2)或(3+√2,√2)．【分析】（1）本题根据抛物线y =ax 2+bx +c(a ≠0)的对称轴公式为x =−b2a 即可解题．（2）本题根据抛物线公式可整理为y =a (x 2−2x −3)=a (x −3)(x +1) 即可解题．（3）本题由（2）得到点B 的坐标利用OB =OC 求得点C 的坐标推出a 值得到抛物线解析式设直线BC 的解析式为y =kx −3 利用待定系数法求出直线BC 的解析式设点P (m,m −3) 则M (m,m 2−2m −3) 根据过点P 作x 轴的垂线交抛物线于M 点分以下两种情况讨论当P 在M 的上方时当P 在M 的下方时根据这两种情况分析得到PM = CP 并对应的建立等式求解即可解题．【详解】（1）解：∵抛物线解析式为y =ax 2−2ax −3a (a >0)∴抛物线的对称轴为x =−−2a2a =1；（2）解：∵抛物线解析式为y =ax 2−2ax −3a (a >0)整理可得y =a (x 2−2x −3)=a (x −3)(x +1)∴不论a 取何值函数图象必过(3,0) (−1,0)；（3）解：由（2）可知点B 的坐标为(3,0)∴OB =3∵ OB =OC∴OC =3∴点C 的坐标为(0,−3) 且−3a =−3 即a =1∴抛物线解析式为y=x2−2x−3设直线BC的解析式为y=kx−3将(3,0)代入解析式有3k−3=0解得k=1∴直线BC的解析式为y=x−3设点P(m,m−3)则M(m,m2−2m−3)当P在M的上方时则PM=−m2+3m∵△PCM沿CM对折如果点P的对应点N恰好落在y轴上∴∠PCM=∠NCM∵PM∥y轴∴∠NCM=∠PMC∴∠PCM=∠PMC∴PC=PM∴√2m=−m2+3m整理得：m2+(√2−3)m=0解得：m1=0（不合题意舍去）则点P的坐标为(3−√2,−√2)；当P在M的下方时则PM=m2−3m同理可得：√2m=m2−3m整理得：m2−(√2+3)m=0解得：m1=0（不合题意舍去）则点P的坐标为(3+√2,√2)；综上所述点P的坐标为(3−√2,−√2)或(3+√2,√2)．【点睛】本题考查了二次函数与一次函数综合折叠的性质二次函数的图象和性质待定系数法求函数解析式勾股定理表示两点间的距离等腰三角形性质熟练掌握折叠的性质结合分类讨论的数学思想即可解题．12．(1)a =−16(2)(−2，−2)或(−2，4)或(−2，2√2)或(−2，−2√2)(3)−13−√2412或−13+√2412．【分析】本题主要考查了二次函数的应用等腰三角形全等三角形等几何图形等知识点熟练运用数形结合利用几何关系寻找等量关系是解题的关键．（1）将点C 坐标代入抛物线解析式即可解答；（2）分三种情况：当ME =MC 、CE =CM 、EM =CE 时然后利用等腰三角形的性质即可解答；（3）先判断出△PQE≌△P ′Q ′E (AAS )得出PQ =P ′Q ′、EQ =EQ ′ 进而得出P ′Q ′=n ，EQ ′=QE =m +2 确定出点P ′(n −2，2+m) 将点P ′的坐标代入直线AD 的解析式中和点P 代入抛物线解析式中联立方程组求解即可．【详解】（1）解：∵抛物线y =a (x +6)(x −2)过点(0，2)∵2=a (0+6)(0−2) a =−16．（2）解：∵a =−16 ∵抛物线的解析式为y =−16(x +6)(x −2)=−16(x +2)2+83 ∵抛物线的对称轴为直线x =−2；∵E(−2，0)∵C(0，2)∵OC =OE =2∵CE =√2OC =2√2∵△CME 是等腰三角形∵①当ME =MC 时∵∠ECM =∠CED =45°∵∠CME =90°∵M(−2，2)；②当CE =CM 时。

2023年九年级中考数学专题复习：二次函数的特殊三角形问题压轴训练

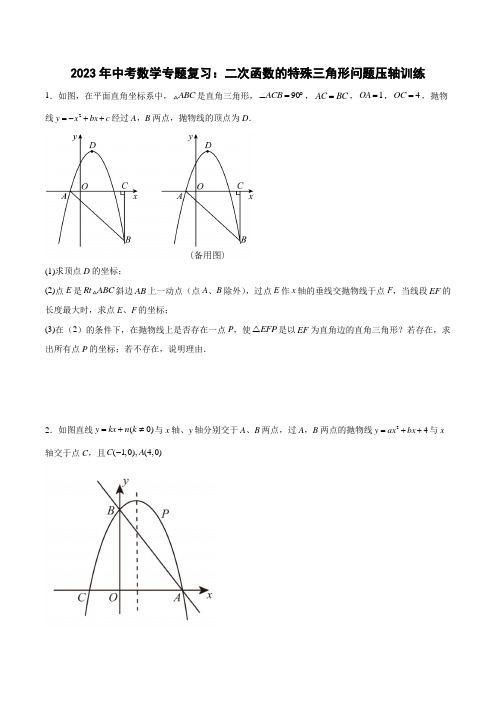
2023年中考数学专题复习：二次函数的特殊三角形问题压轴训练 1．如图，在平面直角坐标系中，ABC 是直角三角形，90ACB ∠=︒，AC BC =，1OA =，4OC =，抛物线2y x bx c =-++经过A ，B 两点，抛物线的顶点为D ．(1)求顶点D 的坐标；(2)点E 是Rt ABC 斜边AB 上一动点（点A 、B 除外），过点E 作x 轴的垂线交抛物线于点F ，当线段EF 的长度最大时，求点E 、F 的坐标；(3)在（2）的条件下，在抛物线上是否存在一点P ，使EFP △是以EF 为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，说明理由．2．如图直线()0y kx n k =+≠与x 轴、y 轴分别交于A 、B 两点，过A ，B 两点的抛物线24y ax bx =++与x 轴交于点C ，且(1,0),(4,0)C A -(1)求抛物线和直线AB 的解析式；(2)若M 点为x 轴上一动点，当MAB △是以AB 为腰的等腰三角形时，求点M 的坐标．(3)若点P 是抛物线上A ，B 两点之间的一个动点（不与A ，B 重合），则是否存在一点P ，使PAB △的面积最大？若存在求出PAB △的最大面积；若不存在，试说明理由．3．综合与实践如图，已知抛物线2y x bx c =-++与x 轴交于A ，B (3，0)，与y 轴交于点C (0，3)，直线l 经过B ，C 两点，抛物线的顶点为D ．(1)求抛物线的解析式；(2)求点D 的坐标及抛物线的对称轴；(3)判断BCD 的形状，并说明理由．4．如图，抛物线()224y x m x =-++的顶点C 在x 轴的正半轴上，直线2y x =+与抛物线交于A ，B 两点，且点A 在点B 的左侧．(1)求m 的值；(2)点P 是抛物线()224y x m x =-++上一点，当PAB △的面积是ABC 面积的2倍时，求点P 的坐标；(3)将直线AB 向下平移(0)k k >个单位长度，平移后的直线与抛物线交于D ，E 两点(点D 在点E 的左侧)，当DEC 为直角三角形时，求k 的值．5．如图，已知抛物线y ＝ax 2＋bx ＋4（a ≠0）与x 轴交于点A 和B （4，0），与y 轴交于点C ，对称轴为直线x ＝52．(1)求抛物线的表达式；(2)如图1，若点P 是线段BC 上的一个动点（不与点B ，C 重合），过点P 作y 轴的平行线交抛物线于点Q ，连接OQ ，当线段PQ 长度最大时，判断四边形OCPQ 的形状并说明理由；(3)如图2，在（2）的条件下，点D 是OC 的中点，过点Q 的直线与抛物线交于点E ，且∠DQE ＝2∠ODQ ．在y 轴上是否存在点F ，使得△BEF 为等腰三角形？若存在，求点F 的坐标；若不存在，请说明理由．6．如图，抛物线234y x bx c =-++交x 轴于(1,0)A -，(4,0)B 两点，交y 轴于点C ，点D 是抛物线上位于直线BC 上方的一个动点．(1)求抛物线的解析式；(2)连接AC ，BD ，若ABD ACB ∠=∠，求点D 的坐标；(3)在（2）的条件下，将抛物线沿着射线AD 平移m 个单位，平移后A 、D 的对应点分别为M 、N ，在x 轴上是否存在点P ，使得PMN 是等腰直角三角形？若存在，请求出m 的值；若不存在，请说明理由．7．如图，在平面直角坐标系中，点O 为坐标原点，二次函数23(0)y ax bx a a =+-<的图像与x 轴交于A 、B（点A 在点B 左侧）两点，与y 轴交于点C ，已知点(30)B ，，P 点为抛物线的顶点，连接PC ，作直线BC ．(1)点A 的坐标为_______；(2)若射线CB 平分PCO ∠，求二次函数的表达式；(3)在（2）的条件下，如果点(0)D m ，是线段AB （含A 、B ）上一个动点，过点D 作x 轴的垂线，分别交直线BC 和抛物线于E 、F 两点，当m 为何值时，CEF ∆为直角三角形？8．如图，已知抛物线2()40y ax bx a =++≠与x 轴交于点A （1，0）和B ，与y 轴交于点C ，对称轴为52x =．(1)求抛物线的解析式；(2)如图1，若点Q 在抛物线上且位于线段BC 下方的一个动点（不与点B ，C 重合），求当△BCQ 面积的最大时，点Q 的坐标；(3)如图2，在（2）的条件下，D 是OC 的中点，过点Q 的直线与抛物线交于点E ，且2DQE ODQ ∠=∠．在y 轴上是否存在点F ，使得△BEF 为等腰三角形？若存在，求点F 的坐标；若不存在，请说明理由．9．如图①，二次函数y ＝﹣x 2+bx +c 的图象与x 轴交于点A （﹣1，0）、B （3，0），与y 轴交于点C ，连接BC ，点P 是抛物线上一动点．(1)求二次函数的表达式．(2)当点P不与点A、B重合时，作直线AP，交直线BC于点Q，若△ABQ的面积是△BPQ面积的4倍，求点P的横坐标．(3)如图②，当点P在第一象限时，连接AP，交线段BC于点M，以AM为斜边向△ABM外作等腰直角三角形AMN，连接BN，△ABN的面积是否变化？如果不变，请求出△ABN的面积；如果变化，请说明理由．10．如图，抛物线y＝ax2+bx+c与x轴交于A(﹣2，0)，B(6，0)两点，与y轴交于点C，直线l与抛物线交于A，D两点，与y轴交于点E，且点D为(4，3)．(1)求抛物线及直线l的函数关系式；(2)点F为抛物线顶点，在抛物线的对称轴上是否存在点G，使AFG为等腰三角形，若存在，求出点G的坐标；(3)若点Q是y轴上一点，且∠ADQ＝45°，请直接写出点Q的坐标．11．如图，已知二次函数()20y ax bx c a =++≠的图象与x 轴交于A ，C 两点（点A 在点C 的左侧），与y 轴交于点B ，且()1,0C ，3OA OB ==．(1)求二次函数的解析式；(2)若点P 是抛物线位于第二象限上的点，过点P 作PQ y ∥轴，交直线AB 于点Q ，交x 轴于点H ，过点P 作PD ⊥AB 于点D ．①求线段PD 的最大值；②若PDQ AHQ △≌△时，请求出此时点P 的坐标．12．如图，在平面直角坐标系中，抛物线M 的表达式为y ＝﹣12x 2+2x ，与x 轴交于O 、A 两点，顶点为点B ．(1)求证：△OAB 为等腰直角三角形：(2)已知点P 在y 轴上，且OP ＝1，点C 在第一象限，△ABC 为等腰直角三角形，将抛物线M 进行平移，使其对称轴经过点C ，请问平移后的抛物线能否经过点P ？如果能，求出平移方式；如果不能，说明理由．13．抛物线223y x x =-++与x 轴交于另一点A ，B 两点．与y 轴交于C ，D 为抛物线的顶点．(1)求A ，B ，C ，D 的坐标；(2)点P 为抛物线上的点，且PAC 是直角三角形，求点P 的坐标．(3)点M 是y 轴上一动点，点Q 为平面内任意一点，当以A ，D ，M ，Q 为顶点的四边形是矩形，直接写出点Q 的坐标．14．如图，抛物线2y x bx c =-++经过(1,0)A ，(3,0)B -两点，交y 轴于点C ，过点A 的直线与y 轴交于点D ，与抛物线交于点M ，且tan ∠BAM ＝1．(1)求该抛物线的解析式．(2)P 为抛物线上一动点，E 为直线AD 上一动点，是否存在点P ，使得以点A ，P ，E 为顶点的三角形为等腰直角三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．(3)点N 为x 轴上一动点，请直接写出当∠DNM 最大时点N 的坐标．15．如图，抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点，与y 轴交于点C ，设抛物线的顶点为D ．(1)求该抛物线的表达式与顶点D 的坐标；(2)试判断BCD △的形状，并说明理由；(3)探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与BCD △相似？若存在，请求出点P 的坐标；若不存在，请说明理由．16．如图，已知抛物线26y ax bx =++与直线2y x =+相交于15,22A ⎛⎫ ⎪⎝⎭和()4,B m 两点，动点P 在线段AB 上，PE y ∥轴与抛物线相交于点E ．(1)求抛物线的表达式及m 的值；(2)求线段PE 长的最大值；(3)求△P AE为直角三角形时点P的坐标．17．如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+2x+3与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，抛物线顶点为点D．(1)求B，C，D三点坐标；(2)如图1，抛物线上有E，F两点，且EF//x轴，当△DEF是等腰直角三角形时，求线段EF的长度；(3)如图2，连接BC，在直线BC上方的抛物线上有一动点P，当△PBC面积最大时，点P坐标．18．如图，已知二次函数y＝ax2＋bx﹣3a经过点A（﹣1，0），C（0，3），与x轴交于另一点B，抛物线的顶点为D．(1)求此二次函数解析式；(2)连接DC、BC、DB，求证：△BCD是直角三角形；(3)在y轴上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．19．已知，如图，在平面直角坐标系中，A (-3，0)、B (1，0)，把点A 绕原点逆时针旋转，使其落在y 轴负半轴点C 处，抛物线y =ax 2+bx +c 过A 、B 、C 三点，连接AC ．(1)求抛物线的解析式；(2)把直线AC 向上平移、平移后的直线DM 交y 轴于点D ，交y 轴右侧的抛物线于点M ，连接AM 、CM 、若=15ACM S △，求点M 的坐标； (3)点N 为直线BC 上一个动点，设点N 的横坐标为n ，若以A 、C 、N 三点组成的三角形为钝角三角形、试求出n 的取值范围．20．如图，抛物线2y x bx c =-++与x 轴交于()1,0A ，()3,0B -两点，与y 轴交于点C ．P 是抛物线上一动点．(1)求抛物线的解析式；(2)当点P在直线BC上方的抛物线上时，求PBC的最大面积，并直接写出此时P点坐标；(3)若点M在抛物线的对称轴上，以B，C，P，M为顶点、BC为边的四边形能否是平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．答案1．(1)(1，4)(2)E (32，52-)，F (32，154)(3)存在，P 点的坐标为(12，154)或52-)或52-)． 2．(1)234y x x =-++，4y x =-+(2)()()()1234,0,4,4,0M M M --(3)存在，83．(1)2y x 2x 3=-++(2)顶点()1,4D ,对称轴1x =(3)BCD △是直角三角形，4．(1)2m = (2)()19P -，或()616P ， (3)2k =或35．(1)y ＝x 2－5x ＋4(2)平行四边形(3)存在，（0，1）或（0，－1）或（0，258）6．(1)239344y x x =-++ (2)D 点坐标为(3,3) (3)203m =，53，567．(1)()1,0-(2)2=y (3)当2m =或1-时，ΔCEF 为直角三角形8．(1)254y x x =-+(2)Q （2，-2）(3)（0，258）或（0，1）或（0，-1）9．(1)y ＝﹣x 2+2x +3．(2)P 352或 (3)△ABN 的面积不变，为4．10．(1)y ＝﹣14x 2+x +3，y ＝12x +1(2)存在，(2,0)或或或(2,-4)(3)(0，﹣9)或(0，133)11．(1)223y x x =--+(2)①PD ②(P + 12．(2)将抛物线M 向右平移34个单位，再向上平移8732个点，得过点C 1和点P 的抛物线；抛物线M 向右平移76个单位，再向上平移28972得出过点C 2和点P 的抛物线；抛物线M 向右平移14个单位。

中考数学压轴题二次函数动点问题专题练习

中考数学压轴题二次函数动点问题专题练习二次函数的动点问题已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B(-2,m)，且与y轴、直线x=2分别交于点D、E。

1) 求m的值及该抛物线对应的函数关系式。

通过点B(-2,m)在直线y=-2x-1上，可以求得m的值以及点B的坐标，进而求得抛物线的解析式。

解析式为y=x^2-x。

2) 求证：①CB=CE；②D是BE的中点。

通过分别求得CB和CE的长度来说明CB=CE。

过点B作BG∥x轴，与y轴交于F、直线x=2交于G，过点E作EH∥x轴，交y轴于H。

由△DFB≌△DHE，证得D是BE的中点。

3) 若P(x,y)是该抛物线上的一个动点，是否存在这样的点P，使得PB=PE？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由。

若存在点P使得PB=PE，则点P必在线段BE的中垂线CD上。

动点P又在抛物线上。

通过解直线CD和抛物线对应的函数关系式所联立的方程组，其解即为所求点的坐标。

符合条件的点P应是直线CD与该抛物线的交点。

1.将点D(0,-1)和C(2,0)代入直线方程组，解得直线CD对应的函数关系式为y=x-1.另外，符合条件的点P的坐标为(3+5/22,1/2)或(3-5/22,-1/2)。

2.(1) 直线BC的解析式为y=-2x+5.2) 由三角形面积公式可得△ABC的面积为6.3) 设点M到点B的距离为x，则点N到点C的距离为2x。

由三角形面积公式可得△MNB的面积为(1/2)x(5-x)。

对该函数求导可得其最大值为5/8，此时x=5/4.因此，当点M运动1.25秒时，△MNB的面积最大，最大面积为1.5625.3.(1) 由平行四边形的性质可得FE∥AB，因此∠XXX∠CEG，且XXX。

因此，ΔBEF∽ΔCEG。

2) 当点E在线段BC上运动时，△BEF和△XXX的周长之间的比值为BE/CE，即x/(x+5)。

最新九年级数学中考复习：二次函数综合压轴题(特殊三角形问题)含答案

2023年九年级数学中考复习：二次函数综合压轴题（特殊三角形问题）1．如图，直线y=﹣23x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣43x2+bx+c经过点A，B，M（m，0）为x轴上一动点，点M在线段OA上运动且不与O，A重合，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．（1）求点B的坐标和抛物线的解析式；（2）在运动过程中，若点P为线段MN的中点，求m的值；（3）在运动过程中，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；2．如图△，已知抛物线y＝ax2﹣4amx+3am2（a、m为参数，且a＞0，m＞0）与x轴交于A、B两点（A在B的左边），与y轴交于点C．（1）求点B的坐标（结果可以含参数m）；（2）连接CA、CB，若C（0，3m），求tan△ACB的值；（3）如图△，在（2）的条件下，抛物线的对称轴为直线l：x＝2，点P是抛物线上的一个动点，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的的等腰直角三角形．若存在，求出所有符合条件的点P的坐标，若不存在，请说明理由．3．如图，已知二次函数的图象经过点A （4，4）、B （5，0）和原点O ．P 为二次函数图象上的一个动点，过点P 作x 轴的垂线，垂足为D （m ，0），并与直线OA 交于点C ．（1）求出二次函数的解析式；（2）当点P 在直线OA 的上方时，求线段PC 的最大值；（3）当m ＞0时，探索是否存在点P ，使得△PCO 为等腰三角形，如果存在，求出P 的坐标；如果不存在，请说明理由．4．已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B .（1）求抛物线的解析式；（2）设C ，D 分别是x 轴、y 轴上的两个动点.△当四边形ABCD 的周长最小时，在图1中作直线CD ，保留作图痕迹.并直接写出直线CD 的解析式；△点()(),0P m n m >是直线y x =上的一个动点，Q 是OP 的中点，以PQ 为斜边按图2所示构造等腰Rt PQR ∆.在△的条件下，记PQR ∆与COD ∆的公共部分的面积为S .求S 关于m 的函数关系式，并求S 的最大值.5．已知抛物线y＝a（x﹣1）（x﹣3）（a＜0）的顶点为A，交y轴交于点C，过C作CB△x 轴交抛物线于点B，过点B作直线l△x轴，连结OA并延长，交l于点D，连结OB．（1）当a＝﹣1时，求线段OB的长．（2）是否存在特定的a值，使得△OBD为等腰三角形？若存在，请写出求a值的计算过程；若不存在，请说明理由．（3）设△OBD的外心M的坐标为（m，n），求m与n的数量关系式．6．如图，抛物线y＝ax2+bx﹣4a（a≠0）经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B，连接AC，BC．（1）求抛物线的解析式；（2）过点C作x轴的平行线交抛物线于另一点D，连接BD，点P为抛物线上一点，且△DBP＝45°，求点P的坐标；（3）在抛物线的对称轴上是否存在点M，使得由点M，A，C构成的△MAC是直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．7．如图，二次函数y=x2+bx+c的图像与x轴交于A，B两点，B点坐标为(4,0)，与y 轴交于点C(0,4).点D为抛物线上一点(1)求抛物线的解析式及A点坐标；(2)若△BCD是以BC为直角边的直角三角形时，求点D的坐标；(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围.8．已知：如图，抛物线y＝ax2+bx﹣3与x轴交于A点，与y轴交于C点，且A（1，0）、B（3，0），点D是抛物线的顶点．（1）求抛物线的解析式（2）在y轴上是否存在M点，使得△MAC是以AC为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．（3）点P为抛物线上的动点，且在对称轴右侧，若△ADP面积为3，求点P的坐标．9．如图，抛物线y＝ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0），与y轴交于点C．（1）求抛物线的解析式；（2）连接BC，若点P为线段BC上的一个动点（不与点B、点C重合），过点P作直线PN△x 轴于点N ，交抛物线于点M ，当△BCM 面积最大时，求△BPN 的周长．（3）在（2）的条件下，当△BCM 面积最大时，在抛物线的对称轴上是否存在点Q ，使△CNQ 为等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．10．如图1，抛物线243y x x =++与x 轴交于,A B 两点（点A 在点B 左侧），与y 轴交于点C ，点D 抛物线的顶点.（1）求直线BD 的解析式；（2）抛物线对称轴交x 轴于点E ，P 为直线BD 上方的抛物线上一动点，过点P 作PF BD ⊥于点F ，当线段PF 的长最大时，连接PE ，过点E 作射线EM ，且EM EP ⊥，点G 为射线EM 上一动点（点G 不与点E 重合），连接PG ，H 为PG 中点，连接AH ，求AH 的最小值；（3）如图2，平移抛物线，使抛物线的顶点D 在射线BD 上移动，点B ，D 平移后的对应点分别为点'B ，'D ，y 轴上有一动点M ，连接'MB ，'MD ，''MB D ∆是否能为等腰直角三角形？若能，请求出所有符合条件的M 点的坐标；若不能，请说明理由.11．如图1，抛物线()230y ax bx a =++≠与x 轴交于()1,0A -、()30B ，两点，与y 轴交于点C ，顶点为点M ．（1）求这条抛物线的解析式及直线BM 的解析式；（2）P 段BM 上一动点（点P 不与点B 、M 重合），过点P 向x 轴引垂线，垂足为Q ，设OQ 的长为t ，四边形PQAC 的面积为S ．求S 与t 之间的函数关系式及自变量t 的取值范围；（3）在线段BM 上是否存在点N ，使NMC ∆为等腰三角形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．12．如图,已知抛物线与x 轴交于A(−1,0)、B(3,0)两点,与y 轴交于点C(0,3).(1)该抛物线的对称轴是直线___________， (2)求抛物线的解析式；(3)设抛物线的顶点为D ，在其对称轴的右侧的抛物线上是否存在点P ，使得△PDC 是等腰三角形?若存在，求出符合条件的点P 的坐标；若不存在，请说明理由：13．在平面直角坐标系中，将二次函数()20y ax a =>的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x 轴交于点A 、B (点A 在点B 的左侧)，1OA =，经过点A 的一次函数()0y kx b k =+≠的图象与y 轴正半轴交于点C ，且与抛物线的另一个交点为D ，ABD ∆的面积为5．(1)求抛物线和一次函数的解析式；(2)抛物线上的动点E 在一次函数的图象下方，求ACE ∆面积的最大值，并求出此时点E 的坐标；(3)若点P 为x 轴上任意一点，在(2)的结论下，求35PE PA +的最小值．14．如图，抛物线2y ax bx c =++与x 轴的交点分别为()6,0A -和点()4,0B ，与y 轴的交点为()0,3C ．（1）求抛物线的解析式；（2）点P 是线段OA 上一动点（不与点A 重合），过P 作平行于y 轴的直线与AC 交于点Q ，点D 、M 在线段AB 上，点N 在线段AC 上．△是否同时存在点D 和点P ，使得APQ ∆和CDO ∆全等，若存在，求点D 的坐标，若不存在，请说明理由；△若DCB CDB ∠=∠，CD 是MN 的垂直平分线，求点M 的坐标．15．如图，抛物线y=ax 2+bx+2交x 轴于点A(-3，0)和点B(1，0)，交y 轴于点C (1)求这个抛物线的函数表达式．(2)点D 的坐标为(-1，0)，点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．(3)点M 为抛物线对称轴上的点，问：在抛物线上是否存在点N ，使△MNO 为等腰直角三角形，且△MNO 为直角？若存在，请直接写出点N 的坐标；若不存在，请说明理由．16．如图，抛物线23y ax bx =+-与x 轴交于(1,0)A -，(3,0)B 两点，与y 轴交于点C ，点D 是抛物线的顶点．（1）求抛物线的解析式．（2）点N 是y 轴负半轴上的一点，且ON =Q 在对称轴右侧的抛物线上运动，连接QO ，QO 与抛物线的对称轴交于点M ，连接MN ，当MN 平分OMD ∠时，求点Q 的坐标．（3）直线BC 交对称轴于点E ，P 是坐标平面内一点，请直接写出PCE ∆与ACD ∆全等时点P 的坐标．17．已知：直线122y x =+与y 轴交于A ，与x 轴交于D ，抛物线y ＝12x 2+bx +c 与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为（1，0）．（1）求抛物线的解析式；（2）点P 是直线AE 上一动点，当△PBC 周长最小时，求点P 坐标；（3）动点Q 在x 轴上移动，当△QAE 是直角三角形时，求点Q 的坐标；（4）在y 轴上是否存在一点M ，使得点M 到C 点的距离与到直线AD 的距离恰好相等？若存在，求出所有符合条件的点M 的坐标；若不存在，请说明理由．18．如图，已知抛物线y ＝x 2+bx +c 与x 轴交于点A ，B ，AB ＝2，与y 轴交于点C ，对称轴为直线x ＝2．（1）求抛物线的函数表达式；（2）设D 为抛物线的顶点，连接DA 、DB ，试判断△ABD 的形状，并说明理由；（3）设P 为对称轴上一动点，要使PC ﹣PB 的值最大，求出P 点的坐标．19．如图，抛物线2y ax bx c =++ 经过点()2,5A -，与x 轴相交于()1,0B -，()3,0C 两点，（1）抛物线的函数表达式；（2）点D 在抛物线的对称轴上，且位于x 轴的上方，将BCD ∆沿沿直线BD 翻折得到BC D '∆，若点D '恰好落在抛物线的对称轴上，求点C '和点D 的坐标；（3）设P 是抛物线上位于对称轴右侧的一点，点Q 在抛物线的对称轴上，当CPQ ∆为等边三角形时，求直线BP 的函数表达式.20．如图，在直角坐标系中有Rt AOB ∆，O 为坐标原点，1,tan 3OB ABO =∠=，将此三角形绕原点O 顺时针旋转90︒，得到Rt COD ∆，二次函数2y x bx c =-++的图象刚好经过,,A B C 三点．（1）求二次函数的解析式及顶点P 的坐标；（2）过定点Q 的直线:3l y kx k =-+与二次函数图象相交于,M N 两点． △若2PMN S ∆=，求k 的值；△证明：无论k 为何值，PMN ∆恒为直角三角形；△当直线l 绕着定点Q 旋转时，PMN ∆外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．参考答案：1．（1）B （0，2），抛物线解析式为y=﹣43x 2+103x+2；（2）m 的值为12；（3）当以B ，P ，N 为顶点的三角形与△APM 相似时，点M 的坐标为（2.5.0）或（118，0）． 2．（1）B （3m ，0）；（2）tan△ACB ＝12；（3）点P 的坐标是：）或）． 3．（1）y ＝﹣x 2+5x ；（2）当点P 在直线OA 的上方时，线段PC 的最大值是4；（3）存在，P 的坐标是（4，2﹣）或（6，﹣6）或（5，0）． 4．（1）()21154y x =--+；（2）；4y x =-+；△S 27448x x =-+-；S 的最大值为47.5．（1）5；（2）a ＝﹣1（3）m ＝3n 2+2 6．（1）y ＝﹣x 2+3x +4；（2）P （﹣25，6625）；（3）点M 的坐标为（32，298）或（32，﹣58）或（32，52）或（32，32）．7．(1)y=x 2-5x+4, A(1,0)；(2)(6,10)或(2,-2)；m ＜6或 3m ＜28．（1）y ＝﹣x 2+4x ﹣3；（2）在y 轴上存在点M ，点M 的坐标为(0,3)，(0,3-或(0,3-，（3）P （4，﹣3）．9．（1）y ＝﹣x 2+2x+3 （2）310．（1）43y x =-+（2（3）(0,,,.11．（1）2y x 2x 3=-++，26y x =-+；（2）四边形ACPQ S 29322t t =-++，t 的取值范围是13t <<；（3）716,55N ⎛⎫⎪⎝⎭或14N ⎛ ⎝⎭或()2,2N 12．（1）1x = （2）2y x 2x 3=-++；（3）存在，⎝⎭或（2.3）13．(1)21322y x x =--；1122y x =+；(2)ACE ∆的面积最大值是2516，此时E 点坐标为315,28⎛⎫- ⎪⎝⎭；(3)35PE PA +的最小值是3.14．（1）211384y x x =--+；（2）△存在点D ，使得APQ ∆和CDO ∆全等，3,02D ⎛⎫⎪⎝⎭，理由见解析；△点3,02M ⎛⎫⎪⎝⎭15．(1)y=-23x 2-43x+2；(2)S 的最大值为174；(3)存在，点N或)或)或)．16．（1）223y x x =--；（2）点Q 的坐标为：1Q ，2Q ；（3）若PCE ∆与ACD ∆全等，P 点有四个，坐标为1(3,4)P --，2(1,6)P --，3(2,1)P ，4(4,1)P -． 17．（1）215222y x x =-+；（2）P （1213，3213）；（3）Q 点坐标为（1，0）或（172，0）；（4）存在；M 点坐标为M （0，﹣8）.18．（1）抛物线的函数表达式为y ＝x 2﹣4x +3；（2）△ADB 是等腰直角三角形；理由见解析；（3）P （2，﹣3）．19．（1）223y x x =--；（2）点'C 坐标为(点D 的坐标为⎛ ⎝⎭；（3）直线BP 的函数表达式为y =y x =20．（1）2y x 2x 3=-++,()1,4P ;（2）△k =±△2241y x x =-++．。

中考数学压轴题：二次函数的动点问题压轴题专题练习(含答案)

⎪二次函数的动点问题压轴题专题练习1.如图①，正方形 ABCD 的顶点 A ，B 的坐标分别为(0，10)，(8，4)，顶点 C ，D 在第一象限．点 P 从点 A 出发，沿正方形按逆时针方向匀速运动，同时，点Q 从点 E (4，0)出发，沿 x 轴正方向以相同速度运动．当点 P 到达点C 时， P ，Q 两点同时停止运动，设运动的时间为t 秒．（1）求正方形 ABCD 的边长．（2）当点 P 在 AB 边上运动时， △OPQ 的面积 S （平方单位）与时间t （秒）之间的函数图象为抛物线的一部分（如图②所示），求 P ，Q 两点的运动速度．（3）求（2）中面积 S （平方单位）与时间t （秒）的函数关系式及面积 S 取最大值时点 P 的坐标．（4）若点 P ，Q 保持（2）中的速度不变，则点 P 沿着 AB 边运动时，∠OPQ 的大小随着时间t 的增大而增大；沿着 BC 边运动时，∠OPQ 的大小随着时间t 的增大而减小．当点 P 沿着这两边运动时，使∠OPQ = 90的点 P 有个．2⎛ - b 4ac - b 2 ⎫（抛物线 y = ax + bx + c (a ≠ 0)的顶点坐标是，． 2a 4a⎝ ⎭图①[解] （1）作 BF ⊥ y 轴于 F ． A (0，10)，B (8，4)，∴ FB = 8，FA = 6．∴ AB = 10．（2）由图②可知，点 P 从点 A 运动到点 B 用了 10 秒．又 AB = 10，10 ÷10 = 1．∴ P ，Q 两点的运动速度均为每秒 1 个单位．（3）方法一：作 PG ⊥ y 轴于G ，则 PG ∥ BF ．∴GA = AP ，即 GA = t． FA AB 6 10∴GA = 3 t ．∴OG = 10 - 3 t ． OQ = 4 + t ，∴ S = 1 ⨯ OQ ⨯ OG = 1 (t + 4)⎛10 - 3 t ⎫5 5 2 2 5 ⎪．19即 S = - 3 t 2 + 19 t + 20． - b = -5 ⎝ ⎭= 19，且0 ≤ 19 ≤10， 10 5 2a 2 ⨯ ⎛ - 3 ⎫ 3 310 ⎪ ⎝ ⎭∴当t = 19时， S 有最大值．此时GP = 4 t = 76 ，OG = 10 - 3 t = 31，3 点 P 的坐标为⎛ 76 31 ⎫．5 15 5 5， ⎪ ⎝ 15 5 ⎭方法二：当 t = 5时， OG = 7，OQ = 9，S = 1 OG OQ =63．设所求函数关系式为2263 ⎧100a +10b + 20 = 28 S = at 2 + bt + 20．抛物线过点 (10，28)，⎛ 5， ⎫， ∴ ⎪ 63 2 ⎪⎨25a + 5b + 20 = .⎝⎭⎪⎩2⎧a = - 3 ， ⎪ ⎨ ⎪b = ⎩10 19 .5 ∴ S = - 3 t 2 + 19 t +20． 105 19- b= - 5 = 19，且0 ≤ 19 ≤10，∴当t = 19时， S 有最大值． 2a 2 ⨯ ⎛ - 3 ⎫ 3 3 3 10 ⎪ ⎝ ⎭此时GP = 76 ，OG = 31，∴点 P 的坐标为⎛ 76 31 ⎫．15 5， ⎪ ⎝ 15 5 ⎭（4） 2．2.如图①， Rt △ABC 中， ∠B = 90， ∠CAB = 30．它的顶点 A 的坐标为(10，0)，顶点B 的坐标为(5，5 3)， AB = 10，点 P 从点 A 出发，沿 A → B →C 的方向匀速运动，同时点Q 从点 D (0，2)出发，沿 y 轴正方向以相同速度运动，当点 P 到达点C 时，两点同时停止运动，设运动的时间为t 秒．（1）求∠BAO 的度数．∴（2）当点P在AB上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数S 3010O 52 2 ，图象为抛物线的一部分，（如图②），求点 P 的运动速度．（3）求（2）中面积 S 与时间t 之间的函数关系式及面积 S 取最大值时点 P 的坐标．（4）如果点 P ，Q 保持（2）中的速度不变，那么点 P 沿 AB 边运动时， ∠OPQ 的大小随着时间t 的增大而增大；沿着 BC 边运动时， ∠OPQ 的大小随着时间t 的增大而减小，当点 P 沿这两边运动时，使∠OPQ = 90的点 P 有几个？请说明理由． yCBQPDO A xt （第 29 题图（第 29 题图②）解: （1）∠BAO = 60．（2）点 P 的运动速度为 2 个单位/秒．1 ⎛ 9 ⎫2121 （3） P (10 - t ，3t )（ 0 ≤ t ≤ 5） S = (2t + 2)(10 - t ) = - t - ⎪ +．⎝ ⎭ 4∴当t = 9时， S 有最大值为121，此时 P ⎛ 11 9 3 ⎫．2 4 2 ， 2 ⎪ ⎝ ⎭（4）当点 P 沿这两边运动时，∠OPQ = 90的点 P 有 2 个．①当点 P 与点 A 重合时，∠OPQ < 90，当点 P 运动到与点 B 重合时， OQ 的长是 12 单位长度，作∠OPM = 90交 y 轴于点 M ，作 PH ⊥ y 轴于点 H ，由△OPH ∽△OPM 得： OM =20 3= 11.5，所以OQ > OM ，从而∠OPQ > 90 ． 3所以当点 P 在 AB 边上运动时，∠OPQ = 90的点 P 有 1 个．②同理当点 P 在 BC 边上运动时，可算得OQ = 12 + 3= 17.8．而构成直角时交 y 轴于⎛ 0 35 3 ⎫， 35 3= 20.2 > 17.8， 3 ⎪ 3 ⎝ ⎭所以∠OCQ < 90，从而∠OPQ = 90的点 P 也有 1 个．第 29 题图①10 3 yQM H CB(P ) DO A x⎨0 = a - b + 4．所以当点 P 沿这两边运动时，∠OPQ = 90的点 P 有 2 个．3.如图12，直线 y = - 4x + 4与 x 轴交于点 A ，与 y 轴交于点 C ，已知二次函数的图象经3过点 A 、C 和点 B ( - 1 , 0 ).（1）求该二次函数的关系式；（2）设该二次函数的图象的顶点为 M ，求四边形 AOCM 的面积；（3）有两动点 D 、 E 同时从点 O 出发，其中点 D 3以每秒 2个单位长度的速度沿折线OAC 按O → A → C 的路线运动，点 E 以每秒4个单位长度的速度沿折线OCA 按O → C → A 的路线运动，当 D 、 E 两点相遇时，它们都停止运动.设 D 、 E 同时从点 O 出发 t 秒时， ∆ODE 的面积为 S .①请问 D 、 E 两点在运动过程中，是否存在 DE ∥ OC ，若存在，请求出此时t 的值；若不存在，请说明理由；②请求出 S 关于t 的函数关系式，并写出自变量t 的取值范围； ③设 S 0是②中函数 S 的最大值，那么 S 0=.解：（1）令 x = 0，则 y = 4；令 y = 0则 x = 3．∴ A (3，0)． C (0 ，4) ∵二次函数的图象过点C (0 ，4)，∴可设二次函数的关系式为 y = ax 2 + bx + 4又 ∵ 该函数图象过点 A (3，0)． B (-1，0)∴ ⎧0 = 9a + 3b + 4⎩解之，得 a = - 4，3 b = 8． 3∴所求二次函数的关系式为 y = - 4x 2+ 8x + 43 3（2）∵ y = - 4x 2+ 8x + 43 3y 4 3 ⎪ = = -4(x - 1)2 + 1633∴顶点 M 的坐标为⎛1 16 ⎫ ， ⎪⎝ 3 ⎭过点 M 作 MF ⊥ x 轴于 F ∴ S 四边形AOCM = S △ AFM + S 梯形FOCM= 1 ⨯ (3 - 1)⨯ 16 + 2 3 1 ⨯ ⎛ 4 + 2 ⎝16 ⎫⨯1 = 10∴四边形 AOCM 的面积为⎭ （3）①不存在 DE ∥OC∵若 DE ∥OC ，则点 D ，E 应分别在线段 OA ，CA 上，此时1 < t < 2，在Rt △AOC 中， AC = 5．设点 E 的坐标为(x ，y )∴ = 4t - 4，∴ x = 12t - 12∵ DE ∥OC ， 1 1 3 5 1 5∴ 12t - 12 = 3 t ∴ t = 8∵ t = 8>2，不满足1 < t < 2．∴不存在 DE ∥OC ．5 2 3 3②根据题意得 D ，E 两点相遇的时间为3 +4 +5 = 24（秒）现分情况讨论如下：3 +4 11 2ⅰ）当0 < t ≤1时， S = 1 ⨯ 3 t 4t = 3t 2；2 2ⅱ）当1 < t ≤ 2时，设点 E 的坐标为(x 2，y 2 )5 - (4t - 4) ∴ 4 5，∴ y 2 =36 - 16t 5 ∴ S = 1 ⨯ 3 t ⨯36 - 16t = - 12 t 2 + 27 t2 2 5 5 5ⅲ）当 2 < t <24时，设点 E 的坐标为(x ，y )，类似ⅱ可得 y = 36 - 16t 11设点 D 的坐标为(x 4 , y 4 )3t - 33 3 35 ∴ = 2， 4 5∴ y 4 =6t - 125∴ S = S △ AOE - S △ AODx 1y 22 2 2 2 2= 1 ⨯ 3 ⨯ 36 - 16t - 1 ⨯ 3 ⨯ 6t - 12= - 33 t + 72 2 ③ S 0 5 2 =243805 5 547.关于 x 的二次函数 y = -x 2+ (k 2- 4)x + 2k - 2以 y 轴为对称轴，且与 y 轴的交点在 x 轴上方．（1）求此抛物线的解析式，并在下面的直角坐标系中画出函数的草图；（2）设 A 是 y 轴右侧抛物线上的一个动点，过点 A 作 AB 垂直于 x 轴于点 B ，再过点 A 作 x 轴的平行线交抛物线于点 D ，过点 D 作 DC 垂直于 x 轴于点 C ，得到矩形 ABCD ．设矩形 ABCD 的周长为l ，点 A 的横坐标为 x ，试求l 关于 x 的函数关系式；（3）当点 A 在 y 轴右侧的抛物线上运动时，矩形 ABCD 能否成为正方形．若能，请求出此时正方形的周长；若不能，请说明理由．参考资料：抛物线 y = ax 2+ bx + c (a ≠ 0)的顶点坐标是⎛ - b 4ac - b 2 ⎫， ⎪，对称轴是直线x = - b ．2a⎝ 2a 4a ⎭ 解：（1）据题意得： k 2- 4 = 0，∴ k = ±2．当 k = 2时， 2k - 2 = 2 >0．当 k = -2时， 2k - 2 = -6 < 0．又抛物线与 y 轴的交点在 x 轴上方，∴ k = 2．∴抛物线的解析式为： y = -x 2 + 2．函数的草图如图所示．（只要与坐标轴的三个交点的位置及图象大致形状正确即可）（2）解：令-x 2+ 2 = 0，得 x = ±．不0 < x <时，A 1D 1 = 2x ， A 1B 1 = -x 2 + 2，∴l = 2( A B + A D ) = -2x 2 + 4x + 4．1 11 1当 x >时，A 2 D 2 = 2x ，A 2B 2 = -(-x + 2) = x - 2． 2 2∴l = 2( A D + A B ) = 2x 2+ 4x - 4．2 22 2∴l 关于 x 的函数关系是：（第 26 题）当 0 < x <时，l = -2x 2 + 4x + 4；当 x >时， y4 3D 12 A 1C 2 1-4 -3 -2 -1C 1B 11 B2 23 4 x D 2-1 -2-3-4-5 -6 -7A 22 3 3 3 2 3 3 3 3 3 3 3 3 2 33 2 33 3 3 3 3 3 3 3 3 3 3 3 3 3 l = 2x 2 + 4x - 4．（3）解法一：当0 < x <时，令 A B = A D ，得 x 2+ 2x - 2 = 0．1 11 1解得 x = -1-（舍），或 x = -1+．将 x = -1+代入l = -2x 2+ 4x + 4，得l = 8 - 8．当 x >时，令 A B = A D ，得 x 2- 2x - 2 = 0．2 22 2解得 x = 1-（舍），或x = 1+．将 x = 1+代入 l = 2x 2 + 4x - 4，得l = 8 + 8．综上，矩形 ABCD 能成为正方形，且当 x = -1时正方形的周长为 8 - 8；当x = +1时，正方形的周长为8 + 8．解法二：当0 < x <时，同“解法一”可得 x = -1+．∴正方形的周长l = 4 A 1D 1 = 8x = 8 - 8．当 x >时，同“解法一”可得 x = 1+．∴正方形的周长l = 4 A 2 D 2 = 8x = 8 + 8．综上，矩形 ABCD 能成为正方形，且当 x = -1时正方形的周长为 8 - 8；当x = +1时，正方形的周长为8 + 8．解法三：点 A 在 y 轴右侧的抛物线上，∴ x > 0，且点 A 的坐标为(x ，- x 2+ 2)．令AB = AD ，则 -x 2 + 2 = 2x ．∴ -x 2 + 2 = 2x ， ①或-x 2 + 2 = -2x ②由①解得 x = -1-（舍），或 x = -1+；由②解得 x = 1-（舍），或 x = 1+ ．又l = 8x ，∴当 x = -1+时l = 8- 8；当 x = 1+时l = 8 + 8．综上，矩形 ABCD 能成为正方形，且当 x = -1时正方形的周长为 8 - 8；当x = +1时，正方形的周长为8 + 8．5.已知抛物线 y ＝ax 2＋bx ＋c 与 x 轴交于 A 、B 两点，与 y 轴交于点 C ，其中点 B 在 x 轴的正半轴上，点 C 在 y 轴的正半轴上，线段 OB 、OC 的长（OB <OC ）是方程 x 2－10x ＋16＝ 0 的两个根，且抛物线的对称轴是直线 x ＝－2．3 33 3（1）求A、B、C 三点的坐标；（2）求此抛物线的表达式；（3）连接AC、BC，若点E 是线段AB上的一个动点（与点A、点B不重合），过点E 作EF∥AC 交BC 于点F，连接CE，设AE 的长为m，△CEF 的面积为S，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（4）在（3）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．第26 题图解：（1）解方程x2－10x＋16＝0 得x1＝2，x2＝8∵点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，且OB＜OC∴点B的坐标为（2，0），点C的坐标为（0，8）又∵抛物线y＝ax2＋bx＋c 的对称轴是直线x＝－2∴由抛物线的对称性可得点A 的坐标为（－6，0）（2）∵点C（0，8）在抛物线y＝ax2＋bx＋c 的图象上∴c＝8，将A（－6，0）、B（2，0）代入表达式，得x － x 5 5 4第 26 题图(批卷教师用图)Error! 解得Error!∴所求抛物线的表达式为 y ＝－2 2 8＋83 3 （3）依题意，AE ＝m ，则 BE ＝8－m ， ∵OA ＝6，OC ＝8，∴AC ＝10∵EF ∥AC ∴△BEF ∽△BAC ∴EF ＝BE EF 8－m AC ∴EF AB 40－5m即10 ＝ 8 ＝ 4过点 F 作 FG ⊥AB ，垂足为 G ，则 sin∠FEG ＝sin∠CAB 4FG 4＝ 54 40－5m ∴EF ＝ ∴FG ＝ · ＝8－m ∴S ＝S △BCE －S △BFE ＝1（8－m ）×8－1（8－m ）（8－m ）2 21 1 12 ＝（8－m ）（8－8＋m ）＝（8－m ）m ＝－ m ＋4m 2 2 2 自变量 m 的取值范围是 0＜m ＜8 （4）存在．理由：∵S1 2＋4m 1 m －4）2＋8 1＝－ m2 ＝－（ 2且－＜0，2∴当 m ＝4 时，S 有最大值，S 最大值＝8 ∵m ＝4，∴点 E 的坐标为（－2，0） ∴△BCE 为等腰三角形．6.（14 分）如图：抛物线经过 A （-3，0）、B （0，4）、C （4，0）三点. （1）求抛物线的解析式. （2）已知 AD = AB （D 在线段 AC 上），有一动点 P 从点 A 沿线段 AC 以每秒 1 个单AO 2+BO232 + 42 ⎨ ⎨ 1 位长度的速度移动；同时另一个动点 Q 以某一速度从点 B 沿线段 BC 移动，经过 t 秒的移动，线段 PQ 被 BD 垂直平分，求 t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点 M ，使 MQ+MC 的值最小？若存在，请求出点 M 的坐标；若不存在，请说明理由。

中考数学总复习《二次函数与特殊三角形问题综合》专题训练(附答案)

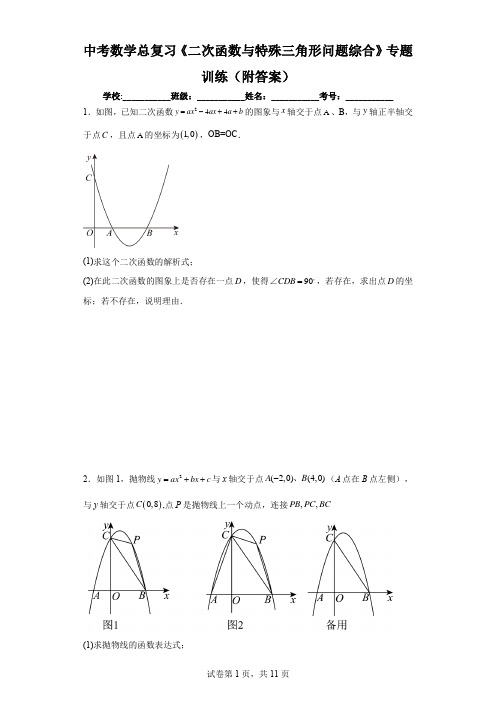
中考数学总复习《二次函数与特殊三角形问题综合》专题训练（附答案）学校:___________班级：___________姓名：___________考号：___________ 1．如图，已知二次函数244y ax ax a b =-++的图象与x 轴交于点A 、B ，与y 轴正半轴交于点C ，且点A 的坐标为()1,0，OB=OC ．(1)求这个二次函数的解析式；(2)在此二次函数的图象上是否存在一点D ，使得90CDB =∠，若存在，求出点D 的坐标；若不存在，说明理由．2．如图1，抛物线2y ax bx c =++与x 轴交于点(2,0)(4,0)-、A B （A 点在B 点左侧），与y 轴交于点()0,8C ,点P 是抛物线上一个动点，连接,,PB PC BC(1)求抛物线的函数表达式；(2)若点P 的横坐标为2，求BPC △的面积；(3)如图2所示，当点P 在直线BC 上方运动时，连接AC ,求四边形ABPC 面积的最大值，并写出此时P 点坐标．(4)若点M 是x 轴上的一个动点，P 的横坐标为3．试判断是否存在这样的点M ,使得以点,,B M P 为顶点的三角形是直角三角形，若存在，请直接写出点M 的坐标；若不存在，请说明理由．3．综合与探究：如图，抛物线23834333y x x =-+-与x 轴交于A ，B 两点（点A 在点B 的左侧）．抛物线上另有一点C 在第一象限，且满足90ACB ∠=︒ OCA OBC ∠=∠．(1)求A ，B 两点的坐标，并直接写出抛物线的对称轴； (2)求线段BC 的长；(3)探究在对称轴上是否存在点P ，使BCP 为直角三角形？若存在，请直接写出点P 的坐标；若不存在．请说明理由．4．如图，已知二次函数2y ax bx c =++的图象与x 轴相交于()()1,0,3,0A B -两点，与y 轴相交于点()0,3C -．(1)求这个二次函数的表达式；(2)若P 是第四象限内这个二次函数的图象上任意一点，PH x ⊥轴于点H ，与线段BC 交于点M ，连接PC ．当PCM △是以PM 为一腰的等腰三角形时，求点P 的坐标．5．如图，已知抛物线2y ax bx c =++与x 轴交于(3,0)A -和(1,0)B 两点，与y 轴交于点C ．(1)求抛物线的解析式；(2)设抛物线的顶点为M ，试判断△ACM 的形状；(3)在x 轴上方的抛物线上是否存在一点P ，使△P AB 的面积为8，若存在，直接写出点P 的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，抛物线2142y x x =--+与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C ．连接AC 、BC ．(1)求ABC 的面积；(2)点P 是直线AC 上方抛物线上一点，过点P 作PE x ⊥轴于点E ，交AC 于点D ，求22PD AD -的最大值及此时点P 的坐标； (3)在（2）的条件下，将抛物线向右平移4个单位，向下平移4.5个单位，点M 为点P 的对应点，平移后的抛物线与y 轴交于点N ，点Q 为平移后的抛物线对称轴上任意一点．写出所有使得以QM 为腰的QMN 是等腰三角形的点Q 的坐标，并把求其中一个点Q 的坐标的过程写出来．7．综合与探究如图，抛物线24y ax bx =+-与x 轴交于(10)(30)A B -，，，两点，与y 轴交于点C ，D 是x 轴上的一个动点（不与点A ，O ，B 重合），过点D 作DP y ∥轴，分别交抛物线，直线BC 于点P ，E ．设点D 的横坐标为m ．(1)求抛物线的函数解析式及点C 的坐标，并直接写出直线BC 的函数解析式． (2)当点D 在线段OB 上运动，且E 为PD 的中点时，求m 的值．(3)连接CD ，是否存在点D ，使CDE 是等腰三角形？若存在，请直接写出点D 的坐标；若不存在，请说明理由．8．如图1，抛物线2()30y ax bx a =++≠与x 轴交于(3,0)A -和(1,0)B 两点，与y 轴交于点C ．(1)求该抛物线的函数表达式；(2)P 是抛物线上，位于直线AC 上方的一个动点，过点P 作PD AC ⊥于点D ，求P 坐标为何值时PD 最大，并求出最大值；(3)如图△，将原抛物线向左平移2个单位长度得到抛物线,y y ''与原抛物线相交于点M ，点N 为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点H ，使以点A ，M ，N ，H 为顶点的四边形为矩形，若存在，请直接写出点H 的坐标；若不存在，请说明理由．9．如图，在平面直角坐标系中，抛物线2y x bx c =++（b ，c 是常数）经过点()10A ，，点()03B ，点P 在此抛物线上，其横坐标为m ．(1)求此抛物线的解析式．(2)当点P 在x 轴上方时，结合图象，直接写出m 的取值范围．(3)若此抛物线在点P 左侧部分（包括点P ）的最低点的纵坐标为2m -． △求m 的值．△以PA 为边作等腰直角三角形PAQ ，当点Q 在此抛物线的对称轴上时，直接写出点Q 的坐标．10．已知抛物线2114y x =+（如图所示）．(1)填空：抛物线的顶点坐标是（，），对称轴是；(2)已知y 轴上一点02A （，），点P 在抛物线上，过点P 作PB x ⊥轴，垂足为B ．若PAB 是等边三角形，求点P 的坐标；(3)在（2）的条件下，点M 在直线AP 上．在平面内是否存在点N ，使四边形OAMN 为菱形？直接写出所有满足条件的点N 的坐标；若不存在请说明理由11．在平面直角坐标系中，二次函数()20y ax bx c a =++≠的图象与x 轴的交点为()30A -,，()10B ,两点，与y 轴交于点()0,3C -，顶点为D ，其对称轴与x 轴交于点E ．(1)求二次函数解析式及顶点D坐标；(2)点P为第三象限内抛物线上一点，APC△的面积记为S，求S的最大值及此时点P 的坐标；(3)在线段AC上，是否存在点F，使AEF△为等腰三角形？若存在，求出点F的坐标；若不存在，请说明理由．12．如图，一次函数122y x=-＋分别交y轴，x轴于A，B两点，抛物线2y x bx c=-++过A，B两点，点M为直线AB上一个动点，过点M作x轴垂线交抛物线与点N．(1)求这个抛物线的解析式．(2)当M在线段AB上时，求MN的最大值．(3)若AMN为等腰三角形，求点M的坐标．13．如图，二次函数211y x mx =++的图像与y 轴相交于点A ，与反比例函数23(0)y x x=-<的图像相交于点(),1B a ．(1)求出a 的值及二次函数的表达式；(2)当1y 随x 的减少而增大且12y y <时，直接写出x 的取值范围； (3)在抛物线上是否存在一点E ，使ABE 的面积等于158，若存在请求出E 点坐标，不存在请说明理由；(4)在x 轴上确定一点P 使APB △为直角三角形，请直接写出P 点的坐标．14．如图，抛物线23y ax bx =+-经过()1,0A -，()3,0B 两点，与y 轴交于点C ，P 为第四象限内抛物线上一点，过点P 作PM △x 轴于点M ，连接AC ，AP ，AP 与y 轴交于点D ．(1)求抛物线的函数表达式．(2)当△MP A ＝2△P AC 时，求直线AP 的函数表达式．(3)在（2）的条件下，在抛物线的对称轴上是否存在点E ，使以E ，M ，C 为顶点的三角形是直角三角形？若存在，请直接写出点E 的坐标；若不存在，请说明理由．15．如图△，抛物线与x 轴交于点()2,0A -和()6,0B ，与y 轴交于点C ，且OC ＝6，连接BC ．(1)求抛物线的解析式；(2)点M 是直线BC 下方抛物线上一点，过点M 作MN △BC 于点N ，若线段528MN OA =，求点M 的坐标；(3)如图△，若点P是对称轴右侧抛物线上一点，点Q是x轴下方对称轴上一点，是否存在点P、Q，使得△CPQ为等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．参考答案： 1．(1)243y x x =-+；(2)存在，5515,22⎛⎫++ ⎪ ⎪⎝⎭或5515,22⎛⎫-- ⎪ ⎪⎝⎭．2．(1)228y x x =-++(2)8(3)()2,8P(4)存在，()22,0M -或()3,0M3．(1)()2,0A ()6,0B ，对称轴4x =(2)23(3)()4,23或()4,23-4．(1)2=23y x x --(2)()2,3-或()32,242--．5．(1)223y x x =--+(2)直角三角形(3)(1,4)-6．(1)12ABC S=； (2)22PD AD -最大值为12，点P 的坐标为53,2⎛⎫- ⎪⎝⎭； (3)点Q 的坐标为133,22⎛⎫-+ ⎪ ⎪⎝⎭或133,22⎛⎫-- ⎪ ⎪⎝⎭或173,4⎛⎫- ⎪⎝⎭．7．(1)抛物线的函数解析式为248433y x x -=- (0,4)C -；直线BC 的函数解析式为443y x =- (2)m 的值为1(3)存在，点D 的坐标为(3,0)-或96,07⎛⎫ ⎪⎝⎭或(12,0)-或4,03⎛⎫ ⎪⎝⎭8．(1)223y x x =--+(2)当P 点运动到315,24⎛⎫- ⎪⎝⎭时，PD 最大值为928(3)H 点的坐标为12,3⎛⎫-- ⎪⎝⎭或70,3⎛⎫ ⎪⎝⎭或()4,2-或()4,1-9．(1)243y x x =-+(2)1m <或3m >(3)△352或3；△()2,1或2,1或()2,510．(1)0，1；直线0x =（或y 轴）(2)()()1223,4,23,4P P -(3)存在()13,1N ()2,31N -- ()33,1N - ()431,N -使得四边形OAMN 是菱形11．(1)223y x x =+- ()1,4D --(2)S 的最大值是278，点P 的坐标是315,24⎛⎫-- ⎪⎝⎭ (3)存在，点F 的坐标为(1,2)--或()32,2-+-或(2,1)--12．(1)2722y x x =-++ (2)4(3)554,24M ⎛⎫+- ⎪ ⎪⎝⎭或554,24⎛⎫- ⎪ ⎪⎝⎭或7515,24⎛⎫+- ⎪ ⎪⎝⎭或7515,24⎛⎫-+ ⎪ ⎪⎝⎭或151,48⎛⎫ ⎪⎝⎭13．(1)3a =-，二次函数的表达式为2131y x x =++(2)332x -<≤-(3)E 点坐标为3149,24⎛⎫-+ ⎪ ⎪⎝⎭或3149,24⎛⎫-- ⎪ ⎪⎝⎭或11,24⎛⎫-- ⎪⎝⎭或51,24⎛⎫-- ⎪⎝⎭ (4)P 点的坐标为35,02⎛⎫-+ ⎪ ⎪⎝⎭或35,02⎛⎫-- ⎪ ⎪⎝⎭或()0,0或()3,0-14．(1)2=23y x x --；(2)4433y x =--； (3)存在，点E 的坐标为321,9⎛⎫- ⎪⎝⎭或101,27⎛⎫ ⎪⎝⎭或31051,26⎛⎫-+ ⎪⎝⎭或31051,26⎛⎫-- ⎪⎝⎭15．(1)21262y x x =-- (2)151,2M -⎛⎫ ⎪⎝⎭或75,2⎛⎫- ⎪⎝⎭ (3)存在，()4,6P -或()222,4P +-或()15,55P +--。

中考数学总复习《二次函数与三角函数综合压轴题》专项训练题(附有答案)

中考数学总复习《二次函数与三角函数综合压轴题》专项训练题(附有答案)学校:___________班级：___________姓名：___________考号：___________1．如图1，抛物线y＝ax2+bx+c的顶点坐标为A（1，2），与x轴交于点B（﹣1，0），C两点，点P是抛物线上的动点．（1）求这条抛物线的函数表达式；（2）如图2，连接CD，点E在CD上，且∠PEC＝90°，求线段PE长度的最大值；（3）如图3，连接AB、AC，已知∠ACB+∠PCB＝α，使得tanα＝2？若存在，求出点P 的横坐标，请说明理由．2．抛物线y＝ax2+bx+c（a＞0）的对称轴是y轴，与x轴交于A、B两点且A点坐标是（﹣2，0），且OB＝2OC．（1）如图1，求抛物线的解析式；（2）如图2，若M（﹣4，m），N是抛物线上的两点．求N点坐标；（3）如图3，D是B点右侧抛物线上的一动点，D、E两点关于y轴对称．直线DB、EB 分别交直线x＝﹣1于G、Q两点，请问PG﹣PQ是定值吗？若是请直接写出此定值．3．如图，在平面直角坐标系中，点O为坐标原点2+x+8交x轴于点A（﹣4，0）、B，交y 轴于点C．（1）求点B的坐标；（2）点D是第一象限抛物线上的一点，连接AD交y轴于点E，设点D的横坐标为t，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，当4＜t＜8时，且横坐标为﹣t，连接BF交y轴于点G，点H 为线段BG的中点，连接AG，若AG＝EH，求tan∠CMD的值．4．二次函数y＝ax2+bx﹣3的图象交x轴于点A（﹣1，0），点B（3，0），交y轴于点C （1）求二次函数的解析式；（2）如图1，点P是抛物线上的一点，设点P的横坐标为m（m＞3），且AQ⊥PQ，若AQ＝2PQ；（3）如图2，将抛物线绕x轴正半轴上一点R旋转180°得到新抛物线C1交x轴于D、E两点，点A的对应点为点E，点B的对应点为点D．若sin∠BME＝5．如图，已知抛物线过平面直角坐标系中A（1，0）、B（3，0）（0，3）三个点．（1）求抛物线的表达式及顶点D的坐标．（2）如图②连接BC、BD、CD，求△BCD的面积．（3）点P是抛物线上的一点，已知，求满足条件的P点的坐标．6．在平面直角坐标系中，将二次函数y＝ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线（点A在点B的左侧），OA＝1，经过点A的一次函数y＝kx+b（k≠0），且与抛物线的另一个交点为D，△ABD的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E在一次函数的图象下方，当△ACE面积的最大值时，求出此时点E的坐标；（3）点Q是直线上的一动点，连接OQ，设△OQF外接圆的圆心为M，当sin∠OQF 最大时（直接写答案）．7．在平面直角坐标系中，已知抛物线与x轴交于点A（1，0），与y轴交于点C（0，﹣4）．（1）求这条抛物线的函数解析式；（2）P是抛物线上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D①如图，若点P在第三象限，且tan∠CPD＝2；②直线PD交直线BC于点E，当点E关于直线PC的对称点E′落在y轴上时，请直接写出四边形PECE'的周长．8．如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+1交y轴于点A，直线y＝﹣x+2交抛物线于B（点B在点C的左侧），交y轴于点D，交x轴于点E．（1）求点D，E，C的坐标；（2）F是线段OE上一点（OF＜EF），连接AF，DF，且AF2+EF2＝21．①求证：△DFC是直角三角形；②∠DFC的平分线FK交线段DC于点K，P是直线BC上方抛物线上一动点，当3tan∠PFK＝1时9．已知抛物线y＝ax2+bx+4与x轴相交于点A（1，0），B（4，0），与y轴相交于点C．（1）求抛物线的表达式；（2）如图1，点P是抛物线的对称轴l上的一个动点，当△P AC的周长最小时，求；（3）如图2，取线段OC的中点D，在抛物线上是否存在点Q？若存在，求出点Q的坐标，请说明理由．10．在平面直角坐标系xOy中，抛物线y＝ax2+x+c与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）（﹣，0），tan∠ACO＝．（1）求抛物线的解析式；（2）线段OB上有一动点P，连接CP，当CP+，请直接写出此时点P的坐标和CP+ PB的最小值．（3）如图2，点D为直线BC上方抛物线上一点，连接AD、BC交于点E，记△BDE的面积为S1，△ABE的面积为S2，求的最大值．11．如图，已知一次函数y1＝kx+m的图象经过A（﹣1，﹣5），B（0，﹣4）两点，且与x 轴交于点C2＝ax2+bx+4的图象经过点A，C，连接OA．（1）求一次函数和二次函数的解析式．（2）求∠OAB的正弦值．（3）在点C右侧的x轴上是否存在一点D，使得△BCD与△OAB相似？若存在，求出点D的坐标，请说明理由．12．如图，边长为4的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，过点P作PE⊥OA于点E，点Q的坐标为（0，3）（1）求抛物线的解析式；（2）①当PQ∥EQ时，PQ+PE＝；②某班数学科代表经过一番探究后发现：对于A、C间的任意一点P，PQ与PE之和为定值，你是否同意他的观点？请说明理由；（3）延长EP交BC于点F，当∠FPQ为锐角，且时，求点P的坐标．13．如图，已知二次函数y＝﹣x2+2x+3的图象交x轴分别于A，D两点，交y轴于B点（1）求抛物线的对称轴；（2）求tan∠BAC；（3）在y轴上是否存在一点P，使得以P，B，D三点为顶点的三角形与△ABC相似？如果存在；如果不存在，请说明理由．14．抛物线y＝﹣x2+bx+c与x轴交于点A（3，0）、B（﹣1，0），与y轴交于点C．（1）求抛物线解析式；（2）如图，连接AC，点P在线段AC上，与抛物线交于点Q．以线段PQ为边构造矩形PQMN，边MN在y轴上．①当矩形PQMN周长最大时，求点P坐标．②在①的条件下，点T在第四象限内，作射线AT，求tan∠TAO的值．15．如图，在平面直角坐标系中，O为原点，OQ＝18，点P是x轴正半轴上一点，连接PQ，⊙A经过点O且与QP相切于点P（1）若圆心A在x轴上，求⊙A的半径；（2）若圆心A在x轴的上方，且圆心A到x轴的距离为2，求⊙A的半径；（3）在（2）的条件下，若OP＜10，D，P的抛物线上的一个动点，点F为x轴上的一个动点的点M共有4个，求点F的横坐标的取值范围．参考答案1．解：（1）由题可设抛物线解析式为y＝a（x﹣1）2+6代入点B，得4a+2＝2∴a＝∴抛物线解析式为：；（2）如图1，过P作PF⊥x轴于F∵PE⊥CD∴∠PEH＝∠PFC＝90°∴∠PHE+∠EPH＝∠CHF+DCB＝90°∵∠PHE＝∠CHF∴∠EPH＝∠DCB令x＝6，则y＝＝∴D（0，）令y＝0，则解得x＝﹣2或3∴C（3，5）∴DO＝，CO＝7∴∴cos∠EPH＝cos∠DCB＝设直线CD为y＝kx+代入点C，得k＝∴直线CD为设P（），则H（）∴∵cos∠EPH＝∴PE＝＝∵P在第一象限∴0＜m＜6∴时，PE最大值为；（3）①如图2，当P在x轴下方时延长AB交CP延长线于K，过A作x轴平行线，两线交于点Q 过C作CR⊥AQ于R∵A（7，2），0），5）∴AB＝同理，AC＝∴AB2+AC2＝BC6，AB＝AC∴∠BAC＝90°∵∠AKQ+∠QAK＝∠QAK+∠RAC＝90°∴∠AKQ＝∠RAC又∠AQK＝∠CRA＝90°∴△AQK∽△CRA∴又tan∠ACK＝∴又AR＝CR＝8∴QK＝AQ＝4∴K（﹣3，﹣2）设直线CK为y＝k1（x﹣3），代入点K解得∴直线CK为联立∴3x3﹣4x﹣15＝0解得x＝或3∴P的横坐标为②如图3，当P在x轴上方时，则K′（﹣2，2）连接CK′交抛物线于点P可设直线CK′为y＝k2（x﹣5），代入点K′解得∴直线CK′为y＝联立∴6x2+4x﹣6＝0∴x＝或3∴P的横坐标为综上，P的横坐标为或．2．解：（1）∵抛物线y＝ax2+bx+c（a＞0）的对称轴是y轴∴b＝3∵A点坐标是（﹣2，0）∴B点坐标是（2，0）∴OB＝2∵OB＝5OC∴OC＝1∴C（0，﹣4）∴c＝﹣1把A（﹣2，5）代入y＝ax2﹣1，得5a﹣1＝0解得：a＝∴该抛物线的解析式为y＝x2﹣1；（2）当x＝﹣5时，y＝4﹣1＝3∴M（﹣8，3）过点M作MG⊥x轴于点G则MG＝3，OG＝5在Rt△OMG中，OM＝＝过点O作FK⊥OM，使OF＝OK＝，如图，过点K作KL⊥x轴于点L连接MF交抛物线于点N，连接MK交抛物线于点N′则∠MGO＝∠FHO＝∠KLO＝∠MOF＝∠MOK＝90°，tan∠OMN＝＝＝∵∠MOG+∠FOH＝90°，∠OFH+∠FOH＝90°∴∠OFH＝∠MOG∴△FOH∽△OMG∴＝＝，即＝＝∴OH＝1，FH＝∴F（1，）设直线MF的解析式为y＝kx+n，则解得：∴直线MF的解析式为y＝﹣x+与抛物线y＝x2﹣1联立，得：x2﹣6＝﹣x+解得：x1＝﹣8（舍去），x2＝当x＝时，y＝﹣×+＝∴N（，）；同理可得K（﹣2，﹣），直线MK的解析式为y＝﹣与抛物线y＝x2﹣1联立，得：x2﹣8＝﹣x﹣解得：x6＝﹣4（舍去），x2＝﹣当x＝﹣时，y＝﹣）﹣∴N′（﹣，﹣）；综上所述，N点坐标为（，，﹣）；（3）由（1）知：A（﹣2，7），0）∵D、E两点关于y轴对称设D（m，m2﹣1），则E（﹣m，m2﹣6）设直线BD的解析式为y＝k1x+b1则解得：∴直线BD的解析式为y＝x﹣当x＝﹣1时，y＝﹣﹣∴G（﹣1，﹣）同理可得：直线BE的解析式为y＝x+当x＝﹣8时，y＝∴Q（﹣1，）∵P（﹣1，4）∴PG＝0﹣（﹣）＝∴PG﹣PQ＝﹣＝3故PG﹣PQ的值为5．3．解：（1）∵抛物线y＝ax2+x+8交x轴于点A（﹣5，0）∴0＝（﹣4）2+（﹣4）+8解得a＝﹣∴y＝﹣x2+x+2当y＝0时，0＝﹣x2+x+4解得x1＝﹣4，x6＝8∴B（8，5）；（2）如图1，过D作DP⊥x轴于P∵点D的横坐标为t，点D是第一象限抛物线上的一点∴D（t，﹣x2+x+8）∴PD＝﹣x2+x+7，AP＝t+4在Rt△P AD中，tan∠P AD＝＝（t﹣8）在Rt△AOE中，tan∠OAE＝∴OE＝8﹣t在y＝﹣x2+x+8中，令x＝2∴C（0，8）∴OC＝3∴d＝CE＝OC﹣OE＝8﹣（8﹣t）＝t；（3）如图7，连接BC，FT⊥y轴于T在Rt△ABC中，∵OB＝OC＝8∴∠OBC＝∠OCB，BC＝∵∠OBC+∠OCB＝90°∴∠OBC＝∠OCB＝45°∵点F的横坐标为﹣t，点F在抛物线上∴F（﹣t，﹣t2﹣t+4）∴t6+t﹣8，BR﹣8+t在Rt△BFR中，tan∠FBR＝＝在Rt△BOG中，tan∠OBG＝∴OG＝2t﹣8∴EG＝OE+OG＝6﹣t+2t﹣8＝t＝CE．∵点H为线段BG的中点∴EH∥BC，EH＝∴AG＝EH＝6在Rt△OAG中，OG＝∴∠OAG＝∠OGA∵∠OAG+∠OGA＝90°∴∠OAG＝∠OGA＝45°＝∠OBC∴AE∥GH∴∠CMD＝∠CFB∵OG＝7t﹣8＝4∴t＝4∴﹣t5﹣t+8＝﹣7，CE＝3t＝12∴F（﹣6，﹣7）∴FT＝7，GT＝OT﹣OG＝7﹣4＝6在Rt△FGT中，FG＝＝在Rt△BOG中，BG＝在Rt△CGN中，sin∠CGN＝∴CN＝∴GN＝∴FN＝FG+GN＝3+在Rt△CFN中，tan∠CFN＝＝∴tan∠CMD＝tan∠CFN＝．4．解：（1）将A（﹣1，0），7）解得：∴这个二次函数的表达式是y＝x6﹣2x﹣3；（2）过点Q作x轴的平行线交过点P与y轴的平行线与点N，交过点A与y轴的平行线于点M∵∠NQP+∠MQA＝90°，∠MQA+∠QAM＝90°∴∠NQP＝∠QAM∵∠AMQ＝∠QNP＝90°∴△AMQ∽△QNP∴设点Q的坐标为（1，t），m2﹣6m﹣3）则AM＝t，QN＝m﹣1，NP＝t﹣m8+2m+3即解得m＝6（舍去）或4故m＝4；（3）过点E作EH⊥MB交MB的延长线于点H由抛物线的表达式知，点M（4，BM＝2则tan∠OBM＝＝3＝tan∠HBE∵sin∠BME＝，故tan∠BME＝故设BH＝x，则HE＝2x在Rt△HEM中，tan∠BME＝则tan∠BME＝＝＝，解得x＝在Rt△BHE中，BE＝＝故点E的坐标为（9，0）由旋转的定义知，点R是点A则x R＝（9﹣3）＝4故点R的坐标为（4，8）．5．解：（1）设抛物线的表达式为y＝ax2+bx+c 把A（1，2），0），3）代入得解方程组得：∴y＝x2﹣6x+3配方得：y＝（x﹣2）2﹣1顶点D的坐标为（2，﹣2）；（2）设直线CD的表达式为y＝kx+m把C（0，3），﹣6）代入得解方程组得：∴y＝﹣7x+3如图（2），设直线y＝﹣2x+8交x轴于点E当y＝0时，﹣2x+7＝0∴点E坐标为：（，2）∴BE＝3﹣过D作DF⊥x轴于点F∴；（3）∵BC5＝32+62＝18，BD2＝72+18＝2，CD2＝72+42＝20∴BC2+BD2＝CD7∴△BCD为直角三角形，∠CBD＝90°又∵tan∠BCP＝，即点D为满足条件的点P7（2，﹣1）如图（3），延长DB至点H，得H（2连接CH交抛物线于点P，所得的∠PCB＝∠BCD设直线CH的表达式为y＝k1x+n把C（0，7），1）代入得解得则直线CH的表达式为：由题意得：解得x＝0或当时，∴点满足条件的P点的坐标有P1（2，﹣3），．6．解：（1）将二次函数y＝ax2（a＞0）的图象向右平移4个单位，再向下平移2个单位2﹣2∵OA＝1∴点A的坐标为（﹣1，3），4a﹣2＝2∴∴抛物线的解析式为，即．令y＝0，则解得：x1＝﹣5，x2＝3∴B（5，0）；∴AB＝OA+OB＝4∵△ABD的面积为4∴∴∴解得：x1＝﹣2，x8＝4∴．设直线AD的解析式为y＝kx+b，则有解得：∴直线AD的解析式为．（2）如图，过点E作EM∥y轴交AD于M设，则∴∴S△ACE＝S△AME﹣S△CME＝＝＝＝．∴当此时E点坐标为．（3）如图，H是OF的中点上运动∴∠OQF＝∠OMH∴∴当OM取得最小值时，sin∠OQF的值最大∵MO＝MQ∴当MQ取得最小值时，sin∠OQF的值最大∵当MQ垂直直线时，MQ取得最小值∴此时M、Q在二次函数的对称轴直线x＝7上∴根据对称性，存在故：或．7．解：（1）∵抛物线与x轴交于点A（1，与y轴交于点C（4∴解得∴抛物线的解析式为．答：抛物线的解析式为．（2）①设P（x，），如图∴∠PEC＝∠CED＝90°∵C（0，﹣2）∴OC＝4∵PD⊥x轴∴∠PDO＝90°∵∠DOC＝90°∴四边形DOCE是矩形∴DE＝OC＝4，OD＝CE＝﹣x∴＝∵∴∴（舍去）∴＝∴P（﹣．②设P（m，）对于，当y＝4时，解得x1＝7，x2＝﹣3∴B（﹣5，0）∵OC＝4∴当点P在第三象限时，如图则四边形DEFO是矩形∴EF＝OD＝﹣m∵点E与点E′关于PC对称∴∠ECP＝∠E′CP，CE＝CE′∵PE∥y轴∴∠EPC＝∠PCE′∴PE＝CE∴PE＝CE′∴四边形PECE′是菱形∵EF∥OA∴△CEF∽△CBO∴∴∴设直线BC的解析式为y＝kx+b∴解得∴直线BC的解析式为y＝﹣x﹣2∴∴＝∵，PE＝CE∴解得（舍去）∴∴四边形PECE′的周长C＝4CE＝4×＝当点P在第二象限时，如图同理可得解得（舍去）∴∴四边形PECE′的周长C＝4CE＝3×＝综上，四边形PECE′的周长为或．8．（1）解：∵直线y＝﹣x+8交y轴于点D 当x＝0时，y＝2∴D（4，2）当y＝0时，x＝5∴E（6，0）∵直线y＝﹣x+2交抛物线于B∴﹣x7+3x+1＝﹣x+2∴7x2﹣10x+3＝8解得∵点B在点C的左侧∴点C的横坐标为6，当x＝3时∴C（3，3）答：C（3，1），8），0）．（2）如图①证明：∵抛物线y＝﹣x2+5x+1交y轴于点A 当x＝0时，y＝4∴A（0，1）∴OA＝6在Rt△AOF中，∠AOF＝90°∴AF2＝OA2+OF3设F（m，0）∴OF＝m∴AF2＝5+m2∵E（6，2）∴OE＝6∴EF＝OE﹣OF＝6﹣m∵AF5+EF2＝21∴1+m8+（6﹣m）2＝21∴m2＝2，m2＝7∵OF＜EF∴m＝2∴OF＝2∴F（4，0）∵D（0，4）∴OD＝2∴OD＝OF∴△DOF是等腰直角三角形∴∠OFD＝45°过点C作CG⊥x轴于G∵C（3，6）∴CG＝1，OG＝3∵GF＝OG﹣OF＝3∴CG＝GF∴△CGF是等腰直角三角形∴∠GFC＝45°∴∠DFC＝90°∴△DFC是直角三角形．②解：∵FK平分∠DFC，∠DFC＝90°∴∠DEK＝∠CFK＝45°∴∠OFK＝∠OFD+∠DFK＝90°∴FK∥y轴∵3tan∠PFK＝1∴设点P的坐标为（t，﹣t2+5t+1），根据题意得．（i）当点P在直线KF的左侧抛物线上时，．过点P1作P6H⊥x轴于H∴P1H∥KF∴∠HP1F＝∠P8FK∴∵HF＝OF﹣OH∴HF＝2﹣t在Rt△P1HF中，∵∴P1H＝3HF∵∴﹣t2+3t+6＝3（2﹣t）∴t3﹣6t+5＝3∴t1＝1，t5＝5（舍去）当t＝1时，﹣t7+3t+1＝2∴P1（1，7）．（ii）当点P在直线KF的右侧抛物线上时，过点P7作P2M⊥x轴于M∴P2M∥KF∴∠MP8F＝∠P2FK∴∴P3M＝3MF∵∴﹣t7+3t+1＝6（t﹣2）∴（舍去）当t＝时，∴．∴点P的坐标为（3，3）或（）．9．解：（1）∵抛物线y＝ax2+bx+4与x轴相交于点A（7，0），0）解得：∴抛物线的表达式为y＝x2﹣5x+2；（2）由（1）知y＝x2﹣5x+2，当x＝0时∴C（0，3）∵△P AC的周长等于P A+PC+AC，AC为定长∴当P A+PC的值最小时，△P AC的周长最小∵A，B关于抛物线的对称轴对称∴P A+PC＝PB+PC≥BC，当P，B，P A+PC的值最小，此时点P为直线BC与对称轴的交点设直线BC的解析式为：y＝mx+n则：解得：∴直线BC的解析式为y＝﹣x+4当时，∴∵A（1，8），4）∴P A＝＝，PC＝＝∴；（3）存在∵D为OC的中点∴D（5，2）∴OD＝2∵B（3，0）∴OB＝4在Rt△BOD中，∴∠QDB＝∠OBD；①当Q点在D点上方时：过点D作DQ∥OB，交抛物线于点Q，此时Q点纵坐标为2设Q点横坐标为t，则：t2﹣5t+4＝2，解得：∴Q（，2）或（；②当点Q在D点下方时：设DQ与x轴交于点E则：DE＝BE设E（p，0）2＝OE4+OD2＝p2+7，BE2＝（4﹣p）6∴p2+4＝（6﹣p）2解得：∴设DE的解析式为：y＝kx+q则：解得：∴联立解得：或∴Q（3，﹣2）或；综上所述，或（，﹣2）或．10．解：（1）∵A（﹣，0）∴OA＝∵tan∠ACO＝∴OC＝4∴C（0，3）将A，C的坐标代入y＝ax3+x+c得，∴∴抛物线的解析式为：y＝﹣x2+x+3；（2）令y＝4，则y＝﹣x3+x+3＝0解得x＝﹣或x＝3∴B（8，0）∴OC＝6，OB＝3∴tan∠OBC＝＝∴∠OBC＝30°，∠OCB＝60°；如图1，作点C关于x轴的对称点C′，C′H与x轴的交点即为所求点P∴PH＝PB∴CP+PB＝CP+PH＝C′P+PH＝C′H∵OC＝OC′＝3∴CC′＝6∴C′H＝6；连接CP∴C′P＝CP，∠PCC′＝∠PC′C＝30°∴OP＝综上，当P（，CP+；（3）如图2，过点D作DG⊥x轴于点G，过点A作AK⊥x轴交BC的延长线于点K ∴△DEF∽△AEK∴＝∵C（0，3），0）∴直线BC的解析式为：y＝﹣x+3；设点D的横坐标为t∴D（t，﹣t2+t+3）∴F（t，﹣t+3），4）∴AF＝4，DF＝﹣t2+t+4﹣（﹣t2+t；∴＝＝﹣t2+t＝﹣）2+∴当t＝时，的最大值为．11．解：（1）将A（﹣1，﹣5），﹣3）代入y1＝kx+m ∴解得∴y＝x﹣5令y＝0，则x＝4∴C（6，0）将A（﹣1，﹣2），0）代入y2＝ax2+bx+4∴解得∴y＝﹣2x2+7x+7；（2）过点O作OH⊥AC交于H∵B（0，﹣4），2）∴∠OCB＝45°∵OC＝4∴OH＝CH＝2∵AC＝5∴AH＝8∴AO＝∴sin∠AOB＝＝；（3）存在点D，使得△BCD与△OAB相似∵D点在C点右侧∴∠BCD＝135°∵∠ABO＝135°∴∠CBD＝∠OAB或∠CDB＝∠OAB当∠OAB＝∠CBD时，△OAB∽△DBC∴＝∵OB＝4，BC＝2∴CD＝16∴D（20，6）；当∠OAB＝∠BCD时，△OAB∽△BDC∴＝∴CD＝2∴D（6，6）；综上所述：D点坐标为（20，0）或（6．12．解：（1）∵边长为4的正方形OABC的两边在坐标轴上∴点C坐标为（0，8），0）根据抛物线的点C为顶点，设该抛物线的解析式为：y＝ax2+6将点A（﹣4，0）代入可得16a+3＝0解得a＝﹣∴此抛物线关系式为：y＝﹣x3+4；（2）①当点P与点A重合时，PQ+PE＝AQ＝当点P与点C重合时，PQ+PE＝CQ+CO＝2+4＝5故答案为：2；②对于A，C间的任意一点P理由如下：过点P作PD⊥y轴于点D设点P的坐标为（m，﹣m7+4）∵点P是抛物线上点A，C间的一个动点∴PD＝﹣m，QD＝|﹣m2+4﹣4|∴PQ＝＝m2+1∴PQ+PE＝m2+6+（﹣m3+4）＝5；（3）由（2）得PQ+PE＝6设点P的坐标为（x，y）∴PE＝y，PQ＝5﹣y∵∠FPQ为锐角，则y＜3∴QD＝8﹣y∵cos∠FPQ＝而∠FPQ＝∠DQP∴＝解得：y＝1把y＝1代入抛物线解析式得y＝﹣x2+5＝1解得x＝±2∵点P在AC段上∴x＝﹣2∴点P坐标为（﹣6，1）．13．解（1）∵二次函数y＝﹣x2+2x+3∴抛物线的对称轴x＝﹣＝﹣∴抛物线的对称轴为直线x＝1；（2）∵二次函数y＝﹣x3+2x+3＝﹣（x﹣6）2+4∴C（7，4），3）把y＝3代入y＝﹣x2+2x+8解得：x1＝﹣1，x7＝3∴D（﹣1，5），0）过点C作CE⊥y轴，垂足为点E则BE＝4﹣3＝1，CE＝1∴BC＝，∠EBC＝∠ECB＝45°又∵OB＝OA＝3∴AB＝3，∠OBA＝∠OAB＝45°∴∠CBA＝180°﹣45°﹣45°＝90°又∵BC＝，AB＝3∴tan∠BAC＝＝；（3）存在，P（6，（0，﹣）当点P在原点时，∠BPD＝90°，∴，∠BPD＝∠ABC则△BPD∽△ABC；在Rt△ABC中，BC＝∴AC＝2在Rt△BOD中，OD＝1∴BD＝当PD⊥BD时，设点P的坐标为（0若△BDP∽△ABC，则，即＝解得y＝﹣∴点P的坐标为（0，﹣）∴当P的坐标为（0，0）或（3，﹣，以P、B．14．解：（1）由题意得，抛物线的表达式为：y＝﹣（x﹣3）（x+1）＝﹣（x6﹣2x﹣3）＝﹣x2+2x+3；（2）①由点A、C的坐标得设点P（x，﹣x+3），﹣x2+2x+6）则PQ＝（﹣x2+2x+5）﹣（﹣x+3）＝﹣x2+3x则矩形PQMN的周长＝2（PQ+PN）＝2（﹣x6+3x+x）＝﹣2（x8﹣4x）∵﹣2＜7，故矩形PQMN的周长有最大值即点P（2，1）；②由①知，点P的坐标为（7，则NP＝2当x＝2时，PQ＝﹣x2+3x＝2故PQ＝PQ＝5＝PN故矩形PQMN为正方形，如图连接AQ、AN，设CP交AQ于点M由正方形轴对称性知，AQ＝AN∵∠TAQ＝3∠P AN∴∠TAN＝∠P AN设AT交y轴于点H，即∠HAN＝∠P AN在等腰Rt△MNP中，PN＝2由点P、A的坐标得则tan∠P AN＝＝＝＝tan∠NAH过点H作HK⊥AN于点K在Rt△ONA中，tan∠ONA＝设HK＝3t，则NK＝t在Rt△AHK中，tan∠NAH＝则AK＝6t则AN＝NK+AK＝t+6t＝＝则t＝则HN＝t＝则OH＝HN﹣ON＝﹣1＝则tan∠TAO＝＝＝．15．解：（1）∵圆心A在x轴上，⊙A经过点O且与QP相切于点P ∴PQ⊥x轴，OP为直径∵tan∠POC＝1，∴PQ＝OP∵在Rt△OPQ中，．∴OP＝18．∴⊙A的半径为9；（2）如图所示，过点A作AM⊥x轴于点M，连接AP∵PQ是⊙A的切线∴AP⊥PQ，则∠APQ＝90°∵AM⊥x轴，QB⊥x轴∴∠AMP＝∠PBC＝90°∴∠P AM＝90°﹣∠APM＝∠QPB∴△APM∽△PBQ∴∵tan∠POC＝1，QB＝18∴OB＝QB＝18∵AM＝2，设MP＝MO＝x∴PB＝18﹣2x∴解得x＝3或x＝6∴MO＝3或MO＝x∴A（3，3）或A（6∴AP＝＝或AP＝．∴半径为或2．（3）∵OP＜10∴BO＝3，P（8∴A（3，2）∵tan∠POC＝6，设D（a∵∴（3﹣a）2+（7﹣a）2＝13解得：a＝0或a＝5∴D（5，5）设抛物线解析式为y＝ax7+bx将点P（6，0），2）代入得，解得：∴y＝﹣x2+6x∵点F可能在点O的左边或点P的右边，则|K FM|＝设直线MF：或联立，得或当或解得：或∴直线MF：或令y＝0，解得：或∴或．。

中考数学总复习《二次函数与特殊三角形问题压轴题》专项提升练习(附答案)

中考数学总复习《二次函数与特殊三角形问题压轴题》专项提升练习(附答案）学校:___________班级：___________姓名：___________考号：___________1．如图①，二次函数245y x x =--与x 轴交于点A 、C ，且点A 在点C 的右侧，与y 轴交于点B ，连接AB ．(1)求抛物线的对称轴；(2)求直线AB 的解析式；(3)如图①，点P 是x 轴下方、抛物线对称轴右侧图象上的一动点，连接PB ，过点P 作PQ AB ∥，与抛物线的另一个交点为Q ，M 、N 为AB 上的两点，且PM y ∥轴，QN y ∥轴．①当BPM △为直角三角形时，求点P 的坐标；①是否存在点P ，使得PB 与QN 互相平分，若存在，直接写出点P 的坐标，若不存在，说明理由．2．如图①，抛物线2y ax bx c =++与x 轴相交于O 、A 两点，直线3y x =-+与y 轴交于B 点，与该抛物线交于A ，D 两点，已知点D 横坐标为1-．(1)求这条抛物线的解析式；(2)如图①，在线段OA 上有一动点H （不与O 、A 重合），过H 作x 轴的垂线分别交AB 于P 点，交抛物线于Q 点，若x 轴把POQ △分成两部分的面积之比为1:2，求H 点的坐标；(3)如图①，在抛物线上是否存在点C ，使ABC 为直角三角形？若存在，直接写出点C 的坐标；若不存在，请说明理由．3．如图，抛物线2y x bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ．已知点B 的坐标为()1,0，经过点B 的直线与抛物线另一个交点D 的坐标为()2,3--．(1)求抛物线解析式并直接写出顶点坐标；(2)连接BC ，若点Q 为抛物线上一动点①求直线BC 的解析式；①当COQ OCB ∠=∠时，求点Q 的坐标；(3)是否存在点M 在抛物线上，点N 在直线BD 上，使得DMN 为等腰直角三角形？若存在，直接写出点N 的坐标；若不存在，请说明理由．4．如图，在平面直角坐标系中，直线123y x =-+交x 轴于点P ，交y 轴于点A ．抛物线212y x bx c =-++的图象过点()10E -，，并与直线相交于A 、B 两点．(1)求抛物线的解析式（关系式）；(2)过点A 作AC AB ⊥交x 轴于点C ，求点C 的坐标；(3)除点C 外，在坐标轴上是否存在点M ，使得MAB 是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．5．已知抛物线()20y ax bx c a =++≠与x 轴交于()20A -，，()60B ，两点，与y 轴交于点()03C -，．(1)求抛物线的表达式；(2)点P 在直线BC 下方的抛物线上，连接AP 交BC 于点M ，当PM AM最大时，求点P 的坐标； (3)在（2）的条件下，过点P 作x 轴的垂线l ，在l 上是否存在点D ，使BCD △是直角三角形若存在，请求出点D 的坐标；若不存在，请说明理由．6．如图所示，在平面直角坐标系中，抛物线24y ax bx =++的对称轴是直线1x =，拋物线与x 轴分别交于点A 、B ，与y 轴交于点C ，点A 的坐标是(2,0)-．(1)求抛物线的解析式；(2)如图1所示，P 是第一象限抛物线上的一个动点，点D 是抛物线对称轴与x 轴的交点，连接CD 、CP 、PB ．求四边形PCDB 的面积的最大值，并求出此时点P 的坐标；(3)如图2所示，在（2）的条件下，点M 是直线BC 上一点，当POM 是以OP 为腰的等腰三角形时，请直接写出点M 的坐标．7．如图，抛物线22y ax bx =++交x 轴于点()()3,0,1,0A C -两点，交y 轴于点B ．(1)求二次函数表达式和点B 的坐标．(2)在直线AB 上方的抛物线上有一动点E ，作EG x ⊥轴交x 轴于点G ，交AB 于点M ，作EF AB ⊥于点F ，若点M 的横坐标为m ，求线段EF 的最大值．(3)抛物线对称轴上是否存在点P 使得ABP 为直角三角形，若存在，请直接写出点P 的坐标，若不存在，说明理由．8．如图，已知抛物线2y ax bx c =++过点()30A -,，()2,3B -和()0,3C ，其顶点为D ．(1)求抛物线的解析式；(2)若P 是抛物线上的一个点，是否存在点P ，使得PA PC =，若存在，求出点P 坐标；若不存在，请说明理由；(3)若抛物线的对称轴与直线AC 相交于点N ，E 为直线AC 上任意一点，过点E 作EF ND ∥交抛物线于点F ，以N ，D ，E ，F 为顶点的四边形能否为平行四边形？若能，求点E 的坐标；若不能，请说明理由．9．如图，已知抛物线2y ax bx c =++与x 轴交于()3,0A ，()10B ,两点，与y 轴交于点C ．且有OA OC =．(1)求抛物线解析式；(2)点P 在抛物线的对称轴上，使得ACP △是以AC 为底的等腰三角形，求出点P 的坐标；(3)在（2）的条件下，若点Q 在抛物线的对称轴上，并且有12AQC APC ∠=∠，直接写出点Q 的坐标．10．如图，抛物线2y ax bx =+过点()4,0A 、()1,3B 两点，点C 、B 关于抛物线的对称轴对称，过点B 作直线BH x ⊥轴，交x 轴于点H ．(1)求抛物线的表达式；(2)直接写出点C 的坐标，并求出ABC 的面积；(3)点P 是抛物线上一动点，且位于第四象限，当ABP 的面积为6时，求出点P 的坐标；(4)已知点M 在直线BH 上运动，点N 在x 轴上运动，若CMN 是以点M 为直角顶点的等腰直角三角形，请直接写出此时CMN 的面积．11．如图1，在平面直角坐标系中，抛物线2y x bx c =-++与x 轴分别交于A 、B 两点，与y 轴交于点C ，连接AC BC 、，其中()2,0A -和()0,6C ．(1)求抛物线的解析式：(2)点P 是直线BC 上方抛物线上一点，过点P 作PE y 轴交BC 于点E ，作PE x ∥轴交BC 于点F ，求CF BE+的最小值，及此时点P 的坐标；(3)如图2，x 轴上有一点()1,0Q -，将抛物线向x 轴正方向平移，使得抛物线恰好经过点Q ，得到新抛物线y 1，点D 是新抛物线1y 与原抛物线的交点，点E 是直线BC 上一动点，连接DQ ，当DQE 是以DQ 为腰的等腰三角形时，直接写出所有符合条件的点E 的坐标．12．如图所示，抛物线()240y ax bx a =++≠经过点()1,0A -，点()4,0B ，与y 轴交于点C ，连接AC ，BC ．点M 是线段OB 上不与点O 、B 重合的点，过点M 作DM x ⊥轴，交抛物线于点D ，交BC 于点E ．(1)求抛物线的表达式；(2)过点D 作DF BC ⊥，垂足为点F ．设M 点的坐标为(),0M m ，请用含m 的代数式表示线段DF 的长，并求出当m 为何值时DF 有最大值，最大值是多少？(3)试探究是否存在这样的点E ，使得以A ，C ，E 为顶点的三角形是等腰三角形．若存在，请求出此时点E 的坐标；若不存在，请说明理由．13．已知：如图，抛物线2y x bx c =-++经过原点O ，它的对称轴为直线2x =，动点P 从抛物线的顶点A 出发，在对称轴上以每秒1个单位的速度向下运动，设动点P 运动的时间为t 秒，连接OP 并延长交抛物线于点B ，连接OA ，AB ．(1)求抛物线解析式及顶点坐标；(2)当三点A ，O ，B 构成以为OB 为斜边的直角三角形时，求t 的值；(3)将PAB 沿直线PB 折叠后，那么点A 的对称点1A 能否恰好落在坐标轴上？若能，请直接写出所有满足条件的t 的值；若不能，请说明理由．14．如图1，直线y kx b =+与抛物线2y ax x c =-+交于(20)A -，，(02)C ，两点，抛物线与x 轴的另一个交点为B ，顶点为D ．(1)求直线及抛物线的解析式．(2)M 是第二象限内抛物线上的一个动点，过点M 作MN AC ⊥于N ，当MN 最大时，求点M 的坐标．(3)如图2，将抛物线沿射线AC 2个单位的速度平移，平移后抛物线的顶点为D ，设平移时间为t 秒，当CDD '△为等腰三角形时，求t 的值．15．如图1，在平面直角坐标系中，抛物线2143y x bx =-++经过()13A -,，与y 轴交于点C ，经过点C 的直线与抛物线交于另一点()6,E m ，点M 为抛物线的顶点，抛物线的对称轴与x 轴交于点D ．(1)求直线CE 的解析式；(2)如图2，点P 为直线CE 上方抛物线上一动点，连接PC ，PE ，当PCE 的面积最大时，求点P 的坐标以及PCE 面积的最大值；(3)如图3，将点D 右移一个单位到点N ，连接AN ，将（1）中抛物线沿射线NA 平移得到新抛物线y '，y '经过点N ，y '的顶点为点G ，在新抛物线y '的对称轴上是否存在点H ，使得MGH 是等腰三角形？若存在，请直接写出点H 的坐标：若不存在，请说明理由．参考答案：1．(1)直线2x =(2)5y x =-(3)①()4,5-或()3,8-①存在 1065,39P ⎛⎫- ⎪⎝⎭2．(1)23y x x =- (2)102，⎛⎫ ⎪⎝⎭或()20， (3)()12-，或(277++，或(277，或()00，或3172⎫+⎪⎝⎭或3172⎫-⎪⎝⎭3．(1)223y x x =+- ()1,4E --(2)①33y x =- ①1133313⎫--⎝⎭或53715337-+-⎝⎭(3)存在，点N 的坐标为()0,1-或()1,2--或()3,4--4．(1)213222y x x =-++ (2)203C ⎛⎫- ⎪⎝⎭， (3)存在，点M 的坐标分别为92027⎛⎫ ⎪⎝⎭， 1165116500⎫⎫+-⎪⎪⎪⎪⎝⎭⎝⎭， 709⎛⎫ ⎪⎝⎭， 9209⎛⎫- ⎪⎝⎭，5．(1)2134y x x =-- (2)153,4P ⎛⎫- ⎪⎝⎭(3)存在，()3,6或()3,9-或3533,22⎛⎫-- ⎪ ⎪⎝⎭或3533,22⎛⎫- ⎪ ⎪⎝⎭6．(1)2142y x x =-++ (2)P 点的坐标是(2,4)(3)1(4,0)M 2(2,6)M - 3(26,26)M 4(26,26)M7．(1)224233y x x =-++ ()0,2B 913(3)存在，点P 的坐标为()1,3-或71,2⎛⎫ ⎪⎝⎭或(1,13或(1,138．(1)223y x x =--+(2)存在，点P 的坐标为13113-+-⎝⎭或13113--+⎝⎭(3)能，点E 的坐标为()2,1-或3173172-++⎝⎭或317317---⎝⎭9．(1)243y x x =-+(2)()2,2P(3)Q 点坐标为2,1或(2,2510．(1)24y x x =-+；(2)3ABC S =△；(3)点P 坐标为()5,5-； (4)52或292．11．(1)2+6y x x =-+(2)155，点321,24P ⎛⎫ ⎪⎝⎭； (3)(3,0)或1356(,)55-或112348434(+-或112348434()-+．12．(1)234y x x =-++ (2)222)22DF m =-+2m =时，DF 有最大值为22(3)存在，点E 的坐标为34834-⎝⎭或()3,1或177,66⎛⎫ ⎪⎝⎭13．(1)24y x x =-+；(2,4)(2)1秒(3)能，(5-5)秒或25(5+5)秒14．(1)抛物线的解析式为22y x x =--+，直线的解析式为2y x =+；(2)当MN 最大时，点M 的坐标为()12-，； (3)当14t =秒或5810秒时，CDD '△为等腰三角形．15．(1)443y x =-+ (2)()3,3P ，PCE 面积的最大值为9 (3)11,3⎛⎫- ⎪⎝⎭或25233,⎛- ⎝-或254233,⎛- ⎝+或133,3⎛⎫- ⎪⎝⎭。

中考数学总复习《二次函数压轴题(特殊三角形问题)》专项提升练习(附答案)

(2)作射线，将射线绕点A顺时针旋转交抛物线于另一点D，在射线上是否存在一点H，使的周长最小，若存在，求出点H的坐标；若不存在，请说明理由；
(3)在（2）的条件下，点Q为抛物线的动点，过Q点作x轴的垂线交射线与P点，点Q从A点出发，P点随之运动，当是以为腰的等腰三角形时，直接写出Q点的坐标．
（1）求直线BC的函数表达式；
（2）求出P，D两点的纵坐标（用含t的代数式表示，结果需化简）；
（3）试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值：若不存在，请说明理由．
5．如图，抛物线与x轴交于点和，与y轴交于点C．
(1)求抛物线的表达式；
13．已知在平面直角坐标系xOy中，二次函数y=2x2−(1+2c)x+c（c> ，c是常数）的图像与x轴分别交于点A，点B（点B在点A右侧），与y轴交于点C，连接BC．
(1)证明：△BOC是等腰直角三角形；
(2)抛物线顶点为D，BC与抛物线对称轴交于点E，当四边形AEBD为正方形时，求c的值．
14．如图，抛物线y＝ax2＋bx＋c与坐标轴交于点A（0，﹣3）、B（﹣1，0）、E（3，0），点P为抛物线上动点，设点P的横坐标为t．
(1)若点C与点A关于抛物线的对称轴对称，求C点的坐标及抛物线的解析式；
(2)若点P在第四象限，连接PA、PE及AE，当t为何值时，△PAE的面积最大？最大面积是多少？
(3)是否存在点P，使△PAE为以AE为直角边的直角三角形，若存在，直接写出点P的坐标；若不存在，请说明理由．
15．如图，已知抛物线于x轴交于A（－1,0）、B（3,0）两点，与y轴交于点C（0,3）．
(2)过点P作，垂足为点N．求线段的最大值；

2023年九年级数学中考专题：二次函数综合压轴题(特殊三角形问题)(含简单答案)

10．如图，在平面直角坐标系中，点O为坐标原点，二次函数的图象与x轴交于A、B（点A在点B左侧）两点，与y轴交于点C，已知点，P点为抛物线的顶点，连接PC，作直线．
(1)点A的坐标为；
(2)若射线平分，求二次函数的表达式；
(3)在（2）的条件下，如果点是线段（含A、B）上一个动点，过点D作x轴的垂线，分别交直线和抛物线于E、F两点，当m为何值时，为直角三角形？
②在①的条件下，点N在抛物线对称轴上，当∠MNC＝45°时，求出满足条件的所有点N的坐标．
14．如图1，抛物线y＝ax2＋bx＋3过点A（﹣1，0），点B（3，0），与y轴交于点C．M是抛物线任意一点，过点M作直线l⊥x轴，交x轴于点E，设M的横坐标为m（0＜m＜3）．
(1)求抛物线的解析式及tan∠OBC的值；
(2)当m＝1时，P是直线l上的点且在第一象限内，若△ACP是直角三角形时，求点P的坐标；
(3)如图2，连接BC，连接AM交y轴于点N，交BC于点D，连接BM，设△BDM的面积为S1，△CDN的面积为S2，求S1﹣S2的最大值．
15．如图，抛物线与轴交于，两点，与轴交于点，已知抛物线的对称轴是直线，．为抛物线上的一个动点，过点作轴于点，交直线于点．
(3)将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求直线的解析式．
6．已知抛物线经过、两点，O为坐标原点，抛物线交正方形的边于点E，点M为射线上一动点，连接，交于点F．
(1)求b和c的值及点C的坐标；
(2)求证∶
(3)是否存在点M，使为等腰三角形？若不存在，请说明理由；若存在，求ME的长．
(1)求，的长（结果均用含的代数式表示）．

2023年九年级数学中考专题：二次函数综合压轴题(特殊三角形问题)(含简略答案)

9．在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，对称轴与轴交于点，点在抛物线上．
（1）求直线的解析式；
（2）如图1，点是直线下方抛物线上的一点，连接，当的面积最大时，连接，设分别是线段上的点，且，求四边形的面积；
（3）如图2，点是线段的中点，将抛物线沿轴正方向平移得到新抛物线，经过点，的顶点为，在新抛物线的对称轴上，是否存在点，使得为等腰三角形？若存在，写出点的坐标；若不存在，请说明理由．
（3）若点Q是上述抛物线上一点，且满足∠ABQ=2∠ABC，求满足条件的点Q的坐标．
11．如图，在平面直角坐标系中，已知抛物线与直线相交于，两点，其中，．
（1）求该抛物线的函数表达式；
（2）点为直线下方抛物线上的任意一点，连接，，求面积的最大值；
（3）在抛物线对称轴上找一点，使点，，三点构成的图形是直角三角形，求点的坐标．
（2）当△PBC的面积最大时，求P点的坐标．
（3）在X轴上是否存在点N，使△NBC是等腰三角形，若存在直接写出所有符合条件的点N的坐标，若不存在说明理由
8．如图，直线交轴于点，交轴于点B，抛物线的顶点为，且经过点．
（1）求该抛物线所对应的函数表达式；
（2）点是抛物线上的点，是以为直角边的直角三角形，请直接写出点的坐标．
13．如图，抛物线经过，两点，且与轴交于点，点是抛物线的顶点，抛物线的对称轴交轴于点，连接．
（1）求经过三点的抛物线的函数表达式；
（2）点在该抛物线的对称轴上，若是以为直角边的直角三角形，求点的坐标；
（3）若为的中点，过点作轴于点，为抛物线上一动点，为轴上一动点，为直线上一动点，当以、、、为顶点的四边形是正方形时，请求出点的坐标．

中考数学专题复习《二次函数与相似三角形综合压轴题》测试卷(附答案)

中考数学专题复习《二次函数与相似三角形综合压轴题》测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________1．如图，在平面直角坐标系xOy中，已知抛物线y=x2+bx经过点A（2，0）和点B(−1,m)，顶点为点D．(1)求直线AB的表达式；(2)求tan∠ABD的值；(3)设线段BD与x轴交于点P如果点C在x轴上且△ABC与△ABP相似求点C的坐标．2．如图在平面直角坐标系中点A(1,2)B(5,0)抛物线y=ax2−2ax(a>0)交x轴正半轴于点C连结AO AB．(1)求点C的坐标和直线AB的表达式(2)设抛物线y=ax2−2ax(a>0)分别交边BA BA延长线于点D E．①若△CDB与△BOA相似求抛物线表达式②若△OAE是等腰三角形则a的值为______（请直接写出答案即可）．3．如图拋物线经过A(4,0),B(1,0),C(0,−2)三点．(1)求出抛物线的解析式(2)若在直线AC上方的抛物线上有一点D使得△DCA的面积最大求出点D的坐标(3)若P是抛物线上一动点过P作PM⊥x轴垂足为M使得以A,P,M为顶点的三角形与△OCA相似请直接写出符合条件的点P的坐标．x2+bx+c与x轴交于A B(4,0)两点与y轴交于点C(0,2)连4．如图抛物线y=−12接BC交抛物线的对称轴于点D连接AC．(1)求抛物线的表达式(2)若点E在对称轴上①当AE+CE的值最小时求点E的坐标②以C D E为顶点的三角形与△ABC相似时求点E的坐标．5．如图已知A(−2,0)B(4,0)抛物线y=ax2+bx+c经过A B两点交y轴于点C(0,4)．点P是第一象限内抛物线上的一点连接AC BC．M为OB上的动点过点M作PM⊥x轴交抛物线于点P交BC于点Q．(1)求抛物线的函数表达式(2)过点P作PN⊥BC垂足为点N设点M的坐标为(m,0)请用含m的代数式表示线段PN的长并求出当m为何值时PN有最大值最大值是多少？(3)试探究M在运动过程中是否存在这样的点Q使得以O M Q为顶点的三角形与△AOC相似．若存在请求出此时点Q的坐标若不存在请说明理由．6．在平面直角坐标系xOy中已知抛物线y=ax2+bx+c（a≠0）的图像经过点B(4,0) D(5,3)设它与x轴的另一个交点为A（点A在点B的左侧）且△ABD的面积是3．（1）求该抛物线的表达式和顶点坐标（2）求∠DAB的度数（3）若抛物线与y轴相交于点C直线CD交x轴于点E点P在线段AD上当△APE与△ABD相似时求AP的长．7．如图抛物线y=−12x2+32x+2与x轴交于A B两点（点A在点B的左边）与y轴交于点C连接BC．(1)求点A B C的坐标(2)设x轴上的一个动点P的横坐标为t过点P作直线PN⊥x轴交抛物线于点N交直线BC于点M．①当点P在线段AB上时设MN的长度为s求s与t的函数关系式②当点P在线段OB上时是否存在点P使得以O P N三点为顶点的三角形与△COB相似？若存在请求出点P的坐标若不存在请说明理由．8．如图在同一直角坐标系中抛物线L1：y=ax2+bx+8与x轴交于A(−8,0)和点C 且经过点B(−2,12)若抛物线L1与抛物线L2关于y轴对称点A的对应点为A′点B的对应点为B′．（1）求抛物线L2的表达式（2）现将抛物线L2向下平移后得到抛物线L3抛物线L3的顶点为M 抛物线L3的对称轴与x轴交于点N 试问：在x轴的下方是否存在一点M 使△MNA′与△ACB′相似？若存在请求出抛物线的L3表达式若不存在说明理由．9．抛物线y=−x2+bx+3与x轴交于A(−3,0),B(1,0)两点与y轴交于点C点D为抛物线的顶点．（1）求抛物线的表达式及顶点D的坐标S△ACD求点P的坐标（2）在直线AC上方的抛物线上找一点P使S△ACP=12（3）在坐标轴上找一点M使以点B C M为顶点的三角形与△ACD相似直接写出点M 的坐标．(x+2)(ax+b)的图象过点A(−4，3)，B(4，4)．10．如图已知二次函数y=148(1)求二次函数的解析式(2)请你判断△ACB是什么三角形并说明理由．(3)若点P在第二象限且是抛物线上的一动点过点P作PH垂直x轴于点H试探究是否存在以P H D为顶点的三角形与△ABC相似？若存在求出P点的坐标．若不存在请说明理由．11．如图直线y=−x+4与x轴交于点A与y轴交于B抛物线y=−x2+bx+c经过A B两点与x轴负半轴交于点C连接BC抛物线对称轴与x轴交于点F P为y轴右侧抛物线上的动点直线BP交对称轴于点D．(1)求抛物线的解析式(2)当BD=3PD时求点P的坐标(3)作PQ⊥AB垂足为Q当△BPQ与△BCO相似时直接写出点Q的坐标．12．在平面直角坐标系中二次函数y=ax2+bx+2的图象与x轴交于A（－3 0）B （1 0）两点与y轴交于点C．(1)求这个二次函数的解析式(2)点Q是线段AC上方的抛物线上一动点过点Q作QE垂直于x轴垂足为E．是否存在点Q使以点B Q E为顶点的三角形与△AOC相似？若存在求出点Q的坐标若不存在说明理由(3)点M为抛物线上一动点在x轴上是否存在点Q使以A C M Q为顶点的四边形是平行四边形？若存在直接写出点Q的坐标若不存在说明理由．13．如图① 抛物线y=ax2+bx+c(a≠0)经过点A(−4,0)点B(2,0)和点C(0,−4)它的对称轴为直线l顶点为D．（1）求该抛物线的表达式（2）如图② 点P是直线AC下方该抛物线上的一个动点连接AP CP AC当△APC的面积取得最大值时求点P的坐标（3）如图③ 点E是直线AD下方该抛物线上的一个动点过E点作EF⊥直线l于F连接DE当以D E F为顶点的三角形与△BOC相似时求点E的坐标．14．已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣3 0）B（1 0）两点与y轴交于点C（0 ﹣3m）（m＞0）顶点为D．(1)如图1 当m＝1时①求该二次函数的解析式②点P为第三象限内的抛物线上的一个动点连接AC OP相交于点Q求PQ的最大值OQ(2)如图2 当m取何值时以A D C为顶点的三角形与∠BOC相似．15．如图1 在平面直角坐标系中抛物线y=ax2+bx+c经过A(−2,0)B(8,0)C(0,4)三点．(1)求抛物线y=ax2+bx+c的表达式(2)如图2 设点P是抛物线上在第一象限内的动点（不与B C重合）过点P作PD⊥BC 垂足为点D点P在运动的过程中以P D C为顶点的三角形与△AOC相似时求点P 的坐标(3)在y轴负半轴上是否存在点N使点A绕点N顺时针旋转后恰好落在第四象限抛物线上的点M处且使∠ANM+∠ACM=180°若存在请求N点坐标若不存在请说明理由．（请在备用图中自己画图）16．抛物线y=−x2+2mx−m2+2m(m>0)交x轴于A B两点（A在B的左边）C是抛物线的顶点．(1)当m=2时直接写出A B两点的坐标：(2)点D是对称轴右侧抛物线上一点∠COB=∠OCD①如图（1）求线段CD长度②如图（2）当m>2T(t,0)(t>0)P为线段OC上一点．若△PCD与△POT相似并且符合条件的点P有2个求t和m之间的数量关系．17．如图1 抛物线y=−x2+bx+c经过A(0,3)和B(72,−94)两点直线AB与x轴相交于点C P是直线AB上方的抛物线上的一个动点PD⊥x轴交AB于点D抛物线与x轴的交点为F G．(1)求该抛物线的表达式．(2)当点P的坐标为(2，3)时求四边形APGO的面积．(3)如图2 若PE∥x轴交AB于点E且点P在直线AB上方求PD+PE的最大值．(4)若以A P D为顶点的三角形与△AOC相似请直接写出所有满足条件的点P的坐标．18．如图1 抛物线y=ax2+23x+c(a≠0)与x轴交于A(−2，0)B两点与y轴交于点C(0，4)．(1)求抛物线的解析式(2)若点D是第一象限内抛物线上的一点AD与BC交于点E且AE=5DE求点D的坐标(3)如图2 已知点M(0，1)抛物线上是否存在点P使锐角∠MBP满足tan∠MBP=1若2存在求出点P的坐标若不存在说明理由．19．如图1 平面直角坐标系xOy中抛物线y=ax2+bx+c过点A(−1,0)B(2,0)和C(0,2)连接BC点P(m,n)(m>0)为抛物线上一动点过点P作PN⊥x轴交直线BC于点M交x 轴于点N．(1)直接写出抛物线和直线BC的解析式(2)如图2 连接OM当△OCM为等腰三角形时求m的值(3)当P点在运动过程中在y轴上是否存在点Q使得以O P Q为顶点的三角形与以B C N为顶点的三角形相似（其中点P与点C相对应）若存在直接写出点P和点Q的坐标若不存在请说明理由．20．如图（1）在平面直角坐标系中抛物线y=ax2+bx−4(a≠0)与x轴交于A B两点(点A在点B的左侧)与y轴交于点C点A的坐标为(−1,0)且OC=OB点D和点C关于抛物线的对称轴对称．(1)分别求出a b的值和直线AD的解析式(2)直线AD下方的抛物线上有一点P过点P作PH⊥AD于点H作PM平行于y轴交直线AD 于点M交x轴于点E求△PHM的周长的最大值(3)在（2）的条件下如图2 在直线EP 的右侧 x 轴下方的抛物线上是否存在点N 过点N 作NG ⊥x 轴交x 轴于点G 使得以点E N G 为顶点的三角形与△AOC 相似？如果存在请直接写出点G 的坐标如果不存在请说明理由．参考答案1．（1）解：∠抛物线y =x 2+bx 经过点A （2 0） ∠22+2b =0 解得：b =−2 ∠抛物线解析式为y =x 2−2x 当x =−1 时 y =3 ∠点B 的坐标为B (−1,3)设直线AB 的解析式为y =kx +m (k ≠0) 把A （2 0） B (−1,3) 代入得： {2k +m =0−k +m =3 解得：{k =−1m =2 ∠直线AB 的解析式为y =−x +2 （2）如图连接BD AD∠y =x 2−2x =(x −1)2−1 ∠点D 的坐标为D (1,−1) ∠A （2 0） B (−1,3)∠AB 2=(−1−2)2+32=18,AD 2=(2−1)2+(−1)2=2,BD 2=(−1−1)2+(−1−3)2=20∠AB 2+AD 2=BD 2 ∠∠ABD 为直角三角形 ∠tan∠ABD =ADAB =√2√18=13（3）设直线BD 的解析式为y =k 1x +b 1(k 1≠0) 把点D (1,−1) B (−1,3)代入得：{k 1+b 1=−1−k 1+b 1=3 解得：{k 1=−2b 1=1∠直线BD 的解析式为y =−2x +1当y =0 时 x =12 ∠点P 的坐标为P (12,0) 当∠ABP ∠∠ABC 时 ∠ABC =∠APB如图过点B 作BQ ∠x 轴于点Q 则BQ =3 OQ =1∠∠ABP ∠∠ABC∠∠ABD =∠BCQ由（2）知tan∠ABD =13∠tan∠BCQ =13 ∠BQ CQ =13∠CQ =9∠OC =OQ +CQ =10∠点C 的坐标为C (−10,0)当∠ABP ∠∠ABC 时 ∠APB =∠ACB 此时点C 与点P 重合∠点C 的坐标为C (12,0)综上所述点C 的坐标为C (−10,0)或(12,0)．2．（1）解：∠x =−b 2a =1∠O C 两点关于直线x =1对称∠C (2,0)设直线AB ：y =kx +b (k ≠0)把A (1,2) B (5,0) 代入得{k +b=25k +b=0解得{k =−12b =52则y =−12x +52 （2）①设D 的坐标为(p,q ) 则BD AB =q 2 若△CDB 与△BOA 相似则BD AB =BC BO∠q 2=BC BO =35∠q =65 ∠D (p,q )在直线AB 上∠D (135,65) 代入抛物线解析式可得a =1013∠抛物线解析式为y =1013x 2−2013x ．②∠A (1,2) B (5,0) O (0,0)∠OA =√5 OB =5 AB =2√5∠OA 2+AB 2=OB 2∠∠OAB=90°∠∠OAE=90° 设E 的坐标为(m,n )∠△OAE 是等腰三角形∠AE =AO =√5∠BE =3√5∠S △BEO =12BE ⋅OA =12BO ⋅n ∠12×3√5×√5=12×5n∠n =3∠E (m,n )在直线AB 上∠3=−12m +52 ∠m =−1又∠E (−1,3)在抛物线上∠3=a +2a故答案为：1．3．解：（1）设抛物线的解析式为y =a (x −4)(x −1)∵点C (0,−2)在抛物线上∴−4×(−1)a =−2∴a =−12∴抛物线的解析式为y =−12(x −4)(x −1)=−12x 2+52x −2（2）如图当点D 在抛物线上且使△DCA 的面积最大必有平行于直线AC 的直线DE且和抛物线只有一个交点设直线AC 解析式为y =kx +m∵A (4,0) C (0,−2)∠{4k +m =0m =−2解得{k =12m =−2∴直线AC 解析式为y =12x −2设直线DE 解析式为y =12x +b ①∵抛物线的解析式为y =−12x 2+52x −2②联立①②化简得 x 2−4x +4+2b =0∴ Δ=16−4(4+2b )=0∴b =0∴x 2−4x +4=0∴x =2∴D (2,1)过点P 作PM ⊥OAA (4,0) C (0,−2)∴OA =4 OC =2∴ OA OC =2设点P (p,ℎ)∴AM =|4−p|．PM =|ℎ| ℎ=−12p 2+52p −2③∵∠APM =∠AOB =90°∵以A P M 为顶点的三角形与△OAC 相似∴ PM AM=OA OC =2 ① ∴ |ℎ||4−p|=2④联立③④解得{p =4ℎ=0 （舍)或{p =5ℎ=−2或{p =−3ℎ=−14 ∴P (−3,−14)或(5,−2)②PM AM=OC OA =12 ∴ |ℎ||4−p|=12⑤联立③⑤解得 {p =2ℎ=1 或{p =4ℎ=0 （舍)或{p =0ℎ=−2∴P (2,1)或(0,−2)综上得到点P (−3,−14)或(5,−2)或(2,1)或(0,−2)．4．（1）解：将点B C 的坐标代入抛物线表达式得：{c =2−12×16+4b +c =0解得：{b =32c =2故抛物线的表达式为：y =−12x 2+32x +2（2）解：①∵B 是点A 关于抛物线对称轴的对称点连接BC 交抛物线对称轴于点E 则点E 为所求点则点D E 重合设BC 的解析式为y =kx +b将B(4,0) C(0,2)代入解析式可得{0=4k +b b =2解得{k =−12b =2∴直线CB 的表达式为：y =−12x +2 由y =−12x 2+32x +2知点D 的横坐标为−b 2a =32把x =32代入y =−12x +2 可得y =54∴E (32,54)②令y =−12x 2+32x +2=0 解得：x =−1或4 则点A(−1,0)由点A B C 的坐标得 AB =5 AC =√5 BC =√20∵AB 2=AC 2+BC 2∴△ABC 为直角三角形且∠ACD =90°∵以C D E 为顶点的三角形与△ABC 相似则△CDE 为直角三角形当∠CE ′D 为直角时如图则点E ′的坐标为E ′(32,2)当∠ECD 为直角时如图∵∠ACB 为直角∴A,C,E 三点共线设AC 的解析式为y =k 1x +b 1把A (−1,0),C (0,2)代入可得{2=b 0=−x +b 解得{k =2b =2∴直线AC 的表达式为：y =2x +2当x =32时 y =2x +2=5即点E(32,5)综上点E的坐标为：(32,2)或(32,5)．5．（1）解：∵A(−2,0)B(4,0)抛物线y=ax2+bx+c经过A B两点交y轴于点C(0,4)∴c=4{4a−2b+4=016a+4b+4=0解得{a=−12 b=1∴抛物线解析式为y=−12x2+x+4（2）解：设直线BC的解析式为y=kx+b1∵点C的坐标为(0,4)B点坐标为(4,0)∴{4k1+b=0b=4∴{k1=−1b=4∴直线BC的解析式为y=−x+4∴点P的坐标为(m,−12m2+m+4)点Q的坐标为(m,−m+4)∴PQ=−12m2+m+4−(−m+4)=−12m2+2m=−12(m−2)2+2∵OC=OB=4∴∠B=45°∠BQM=∠PQN=45°∴PN=√22PQ=−√22m2+√2m=−√22(m−2)2+√2∴当m=2时PN有最大值√2（3）解：存在Q(43,83)或Q(83,43)理由：如图所示OC=4OA=2Q的坐标为(m,−m+4)∠COA=∠OMQ=90°当△OAC∽△MOQ时MQOM =OCOA=2即−m+4m=2解得m=43此时Q的坐标为(43,83)当△OAC∽△MQO时MQOM =OAOC=12即−m+4m=12解得m=83此时Q的坐标为(83,43)综上Q点坐标为(43,83)或(83,43)．6．解：（1）设A(m,0)∵B(4,0),D(5,3)∴AB=4−m AB边上的高为3则由ΔABD的面积是3可得：12(4−m)×3=3解得m=2∴A(2,0)设抛物线解析式为y=a(x−2)(x−4)将D(5,3)代入得：3a=3解得a=1∴y=(x−2)(x−4)=x2−6x+8∵y=x2−6x+8=(x−3)2−1∴顶点坐标为(3,−1)故该抛物线的表达式为y=x2−6x+8顶点坐标为(3,−1)（2）如图过点D作DF⊥x轴于点F∵A(2,0),B(4,0),D(5,3)∴DF =3,AF =5−2=3,AB =4−2=2∴DF =AF∴∠DAB =∠DAF =45°（3）如图∵抛物线的表达式为y =x 2−6x +8令x =0 则y =8∴ C(0,8)设直线CD 解析式为y =kx +b将C(0,8),D(5,3)代入得{b =85k +b =3解得{k =−1b =8直线CD 解析式为：y =-x +8当y =0时 −x +8=0 解得x =8∴E(8,0)∵A(2,0),B(4,0),D(5,3)∴AB =4−2=2 AD =√(5−2)2+32=3√2,BD =√(5−4)2+32=√10 ①若ΔADB ∽ΔAPE 则AP AE =AD AB∴AP =AE⋅AD AB =3√2×62=9√2>AD∵点P 在线段AD 上∴此种情形不存在不合题意②若ΔADB ∽ΔAEP 则AP AB =AE AD∴AP =AE ⋅AB AD =3√2=2√2 综上所述 AP 的长为2√2．7．（1）解：当x =0时 y =2当y =0时即−12x 2+32x +2=0 解得：x 1=−1 x 2=4∠A(−1，0) B(4，0) C(0，2)（2）解：①设直线BC 的解析式为y =kx +b (k ≠0)把B(4，0) C(0，2)代入得{4k +b =0b =2解得：{k =−12b =2∠直线BC 的解析式为y =−12x +2 ∠点P 的横坐标为t∠M (t,−12t +2) N (t,−12t 2+32t +2) 当点P 在y 轴的左侧即−1≤t <0时由题意得：s =−12t +2−(−12t 2+32t +2)=−12t +2+12t 2−32t −2=12t 2−2t 当点P 在y 轴的右侧（包含原点）即0≤t ≤4时由题意得：s =−12t 2+32t +2−(−12t +2)=−12t 2+32t +2+12t −2=−12t 2+2t 综上 s ={12t 2−2t (−1≤t <0)−12t 2+2t (0≤t ≤4)②如图当△OP 1N 1∽△COB 时可得OP 1CO =N 1P 1BO 即t 2=−12t 2+32t+24∠−t 2+3t +4=4t整理得：t 2+t −4=0 解得：t 1=−1+√172 t 2=−1−√172（不合题意舍去）当△OP2N2∽△BOC时可得OP2BO =N2P2CO即t4=−12t2+32t+22∠−2t2+6t+8=2t整理得：t2−2t−4=0解得：t3=1+√5t4=1−√5（不合题意舍去）综上点P的坐标为(−1+√172,0)和(1+√5,0)．8．解：（1）将A(−8,0)B(−2,12)分别代入y=ax2+bx+8中得{a×(−8)2−8b+8=0a×(−2)2−2b+8=12解得{a=−12 b=−3∴抛物线L1的解析式为y=−12x2−3x+8=−12(x+3)2+252则：顶点为(−3,252)∵抛物线L1与抛物线L2关于y轴对称顶点也关于y轴对称开口方向及大小均相同即二次项系数相同∴抛物线L2的顶点为(3,252)∴抛物线L2的解析式为y=−12(x−3)2+252=−12x2+3x+8．故抛物线L2的解析式为y=−12x2+3x+8．（2）如图存在点M 使△MNA′与△ACB′相似．由题意得：A′(8,0) B′(2,12) C (2,0) N (3,0) ∴ AC =10 B′C =12 A′N =5 ∵ ∠A′NM =∠ACB′=90°∴ △A′MN 与△AB′C 相似可以分两种情况： ①当△AB′C ∽△A′MN 时则MNNA′=B′C AC=1210=65∴ MN =6 即点M (3,−6)此时抛物线L 3的表达式为y =−12(x −3)2−6=−12x 2+3x −212．②当△AB′C ∽△MA′N 时同理可得：点M (3,−256)此时抛物线L 3的表达式为y =−12(x −3)2−256=−12x 2+3x −263故：函数L 3的解析式为：y =−12x 2+3x −212或y =−12x 2+3x −263．9．解：（1）将A(−3,0),B(1,0)代入抛物线解析式中得：{9a −3b +3=0a +b +3=0解得：{b =−2c =3∠抛物线解析式为y =−x 2−2x +3=−(x 2+2x)+3 =−(x 2+2x +1−1)+3=−(x +1)2+4 当x =−1时 y =4 ∠顶点D(−1,4)（2）当x =0时 ∠点C 的坐标为(0,3)∠AC =√32+32=3√2,CD =√12+12=√2,AD =√22+42=2√5 ∠AC 2+CD 2=AD 2∠△ACD 为直角三角形 ∠ACD =90°．设直线AC 的解析式为y =kx +b 根据题意得：{−3k +b =0b =3解得：{k =1b =3∠直线AC 的解析式为y =x +3 ∠A(−3,0) D(−1,4)∠线段AD 的中点N 的坐标为(−2,2) 过点N 作NP//AC 交抛物线于点P 设直线NP 的解析式为y =x +c 则−2+c =2 解得：c =4 ∠直线NP 的解析式为y =x +4由y =x +4,y =−x 2−2x +3联立得：−x 2−2x +3=x +4 解得：x 1=−3−√52,x 2=−3+√52∠P (−3−√52,5−√52)或(−3+√52,5+√52)（3）分三种情况： ①△CMB ∽△ACD∴CM CB =ACAD ∴CM √10=3√22√5∴CM =3此时M 恰好为原点 M(0,0) ②△MCB ∽△ACD∴MC AC =CBCD∴3√2=√10√2 ∴CM =3√10设M(x,0)∵OM 2+OC 2=CM 2 ∴x 2+32=(3√10)2∴x 2=81∴x =−9或x =9（舍去）此时M(−9,0) ③△CBM ∽△ACD∴CB AC =CM AD∴√103√2=CM2√5 ∴CM =103设M(x,0)∴|CM −OC |=103−3=13∴x =−13或x =13（舍去）此时M 在y 轴负半轴上 M (0,−13)综上所述点M 的坐标为(0,0)或(−9,0)或(0,−13)．10．（1）解：由题意得函数图象经过点A （﹣4 3） B （4 4）故可得：{3=148（−4+2）（−4a +b ）4=148（4+2）（4a +b ）解得：{a =13b =−20故二次函数关系式为： y =148(x +2)(13x −20)=1348x 2+18x −56．故答案为：y =1348x 2+18x −56．（2）解：△ACB 是直角三角形理由如下：由（1）所求函数关系式y =1348x 2+18x −56当y =0时 0=1348x 2+18x −56解得x 1=−2 x 2=2013∠点C 坐标为（﹣2 0）点D 坐标为（2013 0）又∠点A （﹣4 3） B （4 4） ∠AB =√(4+4)2+（4−3）2=√65 AC =√(−2+4)2+（0−3）2=√13BC =√(4+2)2+（4−0）2=2√13∠满足AB 2=AC 2+BC 2 ∠△ACB 是直角三角形．（3）解：存在点P 的坐标为（−50133513）或（−1221328413）．设点P 坐标为（x 148（x +2）（13x ﹣20））则PH ＝148（x +2）（13x ﹣20） HD ＝﹣x +2013 若∠DHP ∠∠BCA 则PH AC＝DH BC即148(x+2)(13x−20)√13＝−x+20132√13解得：x =−5013或x =2013（因为点P 在第二象限故舍去）代入可得PH =3513即P 1坐标为（−50133513）若∠PHD ∠∠BCA 则PH BC＝HD AC即148(x+2)(13x−20)2√13＝−x+2013√13解得：x =−12213或 x =2013（因为点P 在第二象限故舍去）．代入可得PH =28413即P 2坐标为：（−1221328413）．综上所述满足条件的点P 有两个即P 1（−50133513）或P 2（−1221328413）．11．（1）解：∠直线y =−x +4与x 轴交于点A 与y 轴交于B ∴当x =0时 y =4 当y =0时 ∴A (4,0) B (0,4)又抛物线y =−x 2+bx +c 经过A B 两点把A (4,0) B (0,4)代入得：{−16+4b +c =0c =4解得：{b =3c =4∠抛物线的解析式是y =−x 2+3x +4 （2）解：作PE ⊥AC 垂足为E 如图所示∠∠DFA =∠PEA =∠BOA =90° ∠DF ∥PE ∥BO由（1）得：抛物线的解析式是y =−x 2+3x +4 抛物线对称轴是x =−b2a =−32×(−1)=32 ∠BD =3PD①当P 在对称轴右侧时 OF ∶OE =BD ∶BP =3∶4 点P 的横坐标是2 y =−4+6+4=6 ∠点P 的坐标是(2,6)②当P 在对称轴左侧时 OF ∶OE =BD ∶BP =3∶2 点P 的横坐标是1 y =−1+3+4=6 ∠点P 的坐标是(1,6)∠点P 的坐标是(2,6)或(1,6)（3）解：∠抛物线对称轴与x轴交于点F对称轴是x=−b2a =−32×(−1)=32∠F(32,0)∠点A C关于对称轴对称∠CF=AF=4−32=52∠C(−1,0)∠A(4,0)B(0,4)∠OC=1OA=OB=4∠△ABO是等腰直角三角形∠∠BAO=∠ABO=45°设P(t,−t2+3t+4)过点P作PM∥y轴交直线AB于点M过点M作MN⊥y轴于点N 当点P在AB上方点Q在点B的右侧时如图所示则M(t,−t+4)MN=t∠PM=−t2+3t+4−(−t+4)=−t2+4t∠△BMN是等腰直角三角形∠BM=√2MN=√2t∠∠PMQ=∠ABO=45°∠PQM=90°∠△PMQ是等腰直角三角形∠PQ=MQ=√22PM=√22(−t2+4t)∠BQ=BM−MQ=√2t−√22(−t2+4t)=√22t2−√2t若△BPQ∼△BCO则PQOB =BQOC∠√22(−t 2+4t )4=√22t 2−√2t 1解得：t 1=0（舍） t 2=125当t 2=125时 −t 2+3t+4=−(125)2+3×125+4=13625∠P (125,13625) M (125,85) ∠PM =13625−85=9625过点Q 作QK ⊥PM 轴于点K 则QK =12PM =12×9625=4825∠点Q 的横坐标为125−4825=1225 纵坐标为−1225+4=8825 ∠Q (1225,8825)若△BPQ ∼△CBO 则PQ OC =BQOB ∠√22(−t 2+4t )1=√22t 2−√2t 4解得：t 1=0（舍） t 2=185当t 2=185时 −t 2+3t+4=−(185)2+3×185+4=4625∠P (185,4625) M (185,25) ∠PM =4625−25=3625 同理可得：Q (7225,2825)当点P 在AB 上方点Q 在点B 的左侧时如图所示则M (t,−t+4) MN =t∠PM =−t 2+3t+4−(−t+4)=−t 2+4t同理可得：PQ =MQ =√22PM =√22(−t 2+4t ) BM =√2MN =√2t∠BQ =BM −MQ =−√22t 2+√2t 若△BPQ ∼△CBO 则PQOB =BQOC ∠√22(−t 2+4t )4=−√22t 2+√2t 1解得：t 1=0（舍） t 2=43当t 2=43时 −t 2+3t+4=−(45)2+3×43+4=569∠P (43,569)同理可得：Q (−49,329) 若△BPQ ∼△BCO 则PQ OC=BQ OB∠√22(−t 2+4t )1=−√22t 2+√2t 4解得：t 1=0（舍） t 2=143（舍去）当点P 在AB 下方对称轴左侧的抛物线上时则t <0 如图所示∠PM =−t+4−(−t 2+3t+4)=t 2−4t ME =−t ∠PQ =MQ =√22PM =√22t 2−2√2t BM =√2ME =−√2t∠BQ =MQ −BM =√22t 2−√2t若△BPQ ∼△CBO 则PQOB =BQOC ∠√22t 2−2√2t 4=√22t 2−√2t 1解得：t 1=0（舍） t 2=43（舍）若△BPQ ∼△BCO 则PQOC =BQOB∠√22t 2−2√2t 1=√22t 2−√2t 4解得：t 1=0（舍） t 2=143（舍）当点P 在AB 下方对称轴右侧的抛物线上时则t>4 如图所示∠PM =t 2−4t ME =t ∠PQ =MQ =√22PM =√22t 2−2√2t BM =√2ME =√2t∠BQ =BM+MQ =√22t 2−2√2t+√2t =√22t 2−√2t若△BPQ ∼△CBO 则PQOB=BQ OC∠√22t 2−2√2t 4=√22t 2−√2t 1解得：t 1=0（舍） t 2=43（舍）若△BPQ ∼△BCO 则PQ OC=BQ OB∠√22t 2−2√2t 1=√22t 2−√2t 4解得：t 1=0（舍） t 2=143（舍）当t 2=143时 −t 2+3t+4=−(143)2+3×143+4=−349∠P (143,−349)同理可得：Q (569,−209)综上所述：点Q 的坐标为Q 1(7225,2825),Q 2(1225,8825),Q 3(569,−209),Q 4(−49,409) 12．解：（1）∠抛物线y =ax 2+bx +2过点A （－3 0） B （1 0）∠{9a −3b +2=0a +b +2=0 解得：{a =−23b =−43∠二次函数的关系解析式为y =−23x 2−43x +2．（2）存在点Q （-2 2）或(−34,218)使以点B Q E 为顶点的三角形与△AOC 相似．理由如下：如图①设点E 的横坐标为c 则点Q 的坐标为（c −23c 2−43c +2）∠BE =1-c QE =−23c 2−43c +2①OA 和BE 是对应边时 ∠∠BEQ ∠∠AOC ∠OA BE=OC QE即31−c =2−23c 2−43c+2整理得 c 2+c -2=0 解得c 1=-2 c 2=1（舍去）此时 −23×(−2)2−43×(−2)+2=2点Q （-2 2）②OA 和QE 是对应边时 ∠∠QEB ∠∠AOC ∠OA QE=OC BE 即3−23c 2−43c+2=21−c整理得 4c 2-c -3=0解得c 1=−34 c 2=1（舍去）此时−23×(−34)2−43×(−34)+2=218点Q(−34,21 8)综上所述存在点Q（-2 2）或(−34,218)使以点B Q E为顶点的三角形与∠AOC相似．（3）①如图2当MC//AQ且MC=AQ时M与C关于对称轴x=-1对称∠AQ=MC=2∠Q1（-1 0）Q2（-5 0）②如图3当AC//MQ且AC=MQ时因为平行四边形是中心对称图形并且中心对称点在x轴上所以点M到x轴的距离为2．设M（m23m2−43m+3）∠2 3m2−43m+3=-2∠m2+2m-6=0∠m=-1±√7∠QG=3∠Q 3（2+√7 0） Q 4（2−√7 0）．综上所述满足条件的点Q 的坐标为：Q 1（-5 0） Q 2（-1 0） Q 3（2+√7 0） Q 4（2−√7 0）．13．解：（1）将点A (−4,0) 点B (2,0) 点C (0,−4)代入y =ax 2+bx +c得{c =−416a −4b +c =04a +2b +c =0∠{a =12b =1c =−4∠y =12x 2+x −4（2）如图过P 点作x 轴垂线交AC 于点Q设直线AC 的解析式为y =kx +b∠{−4k +b =0b =−4∠{k =−1b =−4∠y =−x −4设P (t,12t 2+t −4) 则Q (t,−t −4) ∠PQ =−t −4−12t 2−t +4=−12t 2−2t∠S △ACP =12×4×(−12t 2−2t)=−t 2−4t =−(t +2)2+4∠当t =−2时 S △ACP 有最大值∠P (−2,−4)（3）抛物线的对称轴为x =−1 顶点D (−1,−92)设E (m,12m 2+m −4) 则F (−1,12m 2+m −4)∠EF =−1−m DF =12m 2+m −4+92=12m 2+m +12∠点E 是直线AD 下方该抛物线上的一个动点∠−4<m <−1∠B (2,0) C (0,−4)∠OB =2 OC =4∠tan∠OCB =12当∠EDF =∠OCB 时 △EDF ∼△BCO∠EF FD =12∠2(−1−m)=12m 2+m +12解得m =−1（舍）或m =−5（舍）当∠FED =∠OCB 时 △EDF ∼△DBO∠EF FD =2∠2(12m 2+m +12)=−1−m解得m =−1（舍）或m =−2∠E (−2,−4)综上所述：当以D E F 为顶点的三角形与△BOC 相似时 E 点坐标(−2,−4)．14．（1）解：①由m ＝1可知点C （0 ﹣3）∵抛物线与x 轴交点为A(−3,0) B(1,0)∴抛物线解析式为：y =a(x +3)(x −1)将点C(0,−3)代入上式得a ×3×(−1)=−3∴a =1∴抛物线的解析式为：y =(x +3)(x −1)=x 2+2x −3②由①可知抛物线解析式为y =x 2+2x −3 则设P(x,x 2+2x −3) 设直线AC 的解析式为y =kx +b由题意可得{−3k +b =0b =−3解得{k =−1b =−3∴直线AC 的解析式为y =−x −3如图1 过点P 作PN ⊥x 轴交AC 于N 则PN//OC∴点N(x,−x −3)∴PN =(−x −3)−(x 2+2x −3)=−x 2−3x∵PN//OC∴△PQN ∽△OQC∴ PQ OQ =PN OC∴ PQ OQ =−x 2−3x 3=−(x+32)2+943 ∴当x =−32时 PQ OQ 的最大值为34 （2）解：∵y =mx 2+2mx −3m =m(x +1)2−4m∴顶点D 坐标为(−1,−4m)如图2 过点D 作DE ⊥x 轴于点E 则DE =4m OE =1 AE =OA −OE =2 过点D 作DF ⊥y 轴于点F 则DF =1 CF =OF −OC =4m −3m =m由勾股定理得：AC2=OC2+OA2=9m2+9CD2=CF2+DF2=m2+1AD2=DE2+AE2=16m2+4∵ΔACD与ΔBOC相似且ΔBOC为直角三角形∴ΔACD必为直角三角形i)若点A为直角顶点则AC2+AD2=CD2即：(9m2+9)+(16m2+4)=m2+1整理得：m2=−12∴此种情形不存在ii)若点D为直角顶点则AD2+CD2=AC2即：(16m2+4)+(m2+1)=9m2+9整理得：m2=12∵m>0∴m=√2 2此时可求得ΔACD的三边长为：AD=2√3CD=√62AC=3√62ΔBOC的三边长为：OB=1OC=3√22BC=√222两个三角形对应边不成比例不可能相似∴此种情形不存在iii)若点C为直角顶点则AC2+CD2=AD2即：(9m2+9)+(m2+1)=16m2+4整理得：m2=1∵m>0∴m=1此时可求得ΔACD的三边长为：AD=2√5CD=√2AC=3√2ΔBOC的三边长为：OB=1OC=3BC=√10∵ADBC =ACOC=CDOB=√2∴满足两个三角形相似的条件∴m=1．综上所述当m=1时以A D C为顶点的三角形与ΔBOC相似．15．（1）解：将A(−2,0),B(8,0),C(0,4)三点坐标代入y=ax2+bx+c中得{4a−2b+c=0c=464a+8b+c=0解得{a=−14b=32c=4所以抛物线表达式为：y=−14x2+32x+4．（2）解：根据题意得：∵A(−2,0),B(8,0),C(0,4)∠OA=2,OB=8,OC=4∴AOOC=COBO=12又∠AOC=∠COB=90°∴△AOC∽△COB∴∠ACO=∠CBO∴∠ACB=∠ACO+∠BCO=∠CBO+∠BCO=90°当△AOC∽△PDC时∴∠ACO=∠PCD∵∠ACO+∠OCB=90°∴∠PCD+∠OCB=90°∴PC⊥OC∴点P的纵坐标为4当y=4时有−14x2+32x+4=4解得x=6或x=0（舍）∴点P的坐标为(6,4)当△AOC∽△CDP时∠P′CD′=∠CAO作P′G⊥y轴于点G过点P′作P′H∥y轴交BC于点H如图∴∠P′HC=∠BCO∵AOOC=COBO=12,∠AOC=∠BOC=90°∴△AOC∽△COB∴∠OCB=∠OAC∴∠P′CH=∠P′HC∴P′C=P′H设直线BC的解析式为y=k′x+b′把点B(8,0),C(0,4)代入得：{8k ′+b′=0b′=4解得：{k′=−12b′=4∠直线BC的解析式为y=−12x+4设P′(m,−14m2+32m+4)则H(m,−12m+4)∴P′C=P′H=−14m2+32m+4−(−12m+4)=−14m2+2m在Rt△P′GC中由勾股定理得P′C2=P′G2+GC2即(−14m2+2m)2=m2+(−14m2+32m)2解得m=3∴P′(3,254)综上点P的坐标为：(6,4)或(3,254)．（3）解：过N作NF⊥MC交MC于点F过N点作NG⊥AC交CA的延长线于点G则∠G=∠CFN=90°∴∠ACM+∠GNF=180°设CM与x轴交于K由旋转得：AN=MN∵∠ANM+∠ACM=180°∴∠ANM=∠GNF∴∠ANG=∠MNF∵∠G=∠MFN=90°∴△NGA≌△NFM∴NG=NF∴NC平分∠ACM∵CO⊥AB ∴OK=OA=2∴K(2,0)∴CK的解析式为：y=−2x+4∴−2x+4=−14x2+32x+4解得：x1=0,x2=14∴M(14，−24)设N(0,n)∵AN=MN∴(−2)2+n2=142+(−24−n)2解得：n=−16所以点N坐标为(0,−16)．16．解：（1）∠抛物线y=−x2+2mx−m2+2m(m>0)交x轴于A B两点∠当m=2∠y=−x2+4x∠x1=0x2=4∠A(0,0)B(4,0)．（2）①∠y=−x2+2mx−m2+2m∠对称轴x=−b2a=m∠顶点坐标C(m,2m)延长CD交x轴于点E设点E(a,0)a>m∠∠COB=∠OCD∠|OE|=|CE|∠a2=(a−m)2+(2m)2解得：a=52m∠点E的坐标为：(52m,0)设直线CE的解析式为：y=k1x+b1(k≠0)∠{2m=km+b 0=52mk+b解得：{k=−43b=103m∠y=−43x+103m∠−43x+103m=−x2+2mx−m2+2m解得：x1=m（舍）x2=m+43∠点D(m+43,2m−169)∠CD=209．②设直线OC的解析式为：y=k1x(k≠0)∠y=2x∠设点P(b,2b)∠OP=√b+24b2=√5b CP=√(m−b)2+(2m−2b)2=√5(m−b)当△OPT∼△CDP∠OP CD =OTCP∠√5b×920=√5(m−b)整理得：9b2−9mb+4t=0∠Δ>0∠81m2−4×9×4t>0∠9m2−16t>0当△OTP∼△CDP∠OT CD =OPCP∠t×920=√5b√5(m−b)整理得：b =9tm 20+9t∠仅存在一个点P∠不符合题意∠综上 t 和m 之间的数量关系为：9m 2−16t >0．17．（1）解：∵抛物线y =−x 2+bx +c 经过A (0,3)和B (72,−94)两点∴将A (0,3)和B (72,−94)代入y =−x 2+bx +c 得{c =3−(72)2+72b +c =−94 解得{b =2c =3 ∴抛物线的解析式为y =−x 2+2x +3（2）解：在 y =−x 2+2x +3中当y =0时 −x 2+2x +3=0 解得x =3或x =−1 ∠G(3，0)∠OG =3∠A(0，3)，P(2，3)∠OA =3，AP =2，AP ∥x 轴∠S 四边形APGO =AP+OG 2⋅OA =2+32×3=7.5（3）解：设直线AB 的解析式为y =kx +n 把A (0,3)和B (72,−94)代入得{n =372k +n =−94解得{k =−32n =3∴直线AB 的解析式为y =−32x +3 在y =−32x +3 当y =0时 −32x +3=0 解得x =2 ∴C (2,0)联立{y =−x 2+2x +3y =−32x +3 解得x 1=0 x 2=72 ∵PD ⊥x 轴 PE ∥x 轴∴∠ACO =∠DEP∴Rt △DPE ∽Rt △AOC∴ PD PE =OA OC =32 即PE =23PD∴PD +PE =53PD设点P (a,−a 2+2a +3) 0<a <72 则D (a,−32a +3)∴PD =(−a 2+2a +3)−(−32a +3)=−(a −74)2+4916 ∴PD +PE =−53(a −74)2+24548∵−53<0 抛物线开口向下 PD +PE 有最大值 0<a <72 ∴当a =74时 PD +PE 有最大值为24548（4）解：∵PD ⊥x 轴∴PD ∥y 轴即∠OAC =∠PDA根据题意分两种情况：①当△AOC ∽△DPA 时∴∠DPA =∠AOC =90°∵PD ⊥x 轴 ∠DPA =90° A (0,3)∴点P 纵坐标是3 横坐标x >0 即−x 2+2x +3=3 解得x =2∴点D 的坐标为(2,0)∵PD ⊥x 轴∴点P 的横坐标为2∴点P (2,3)②当△AOC ∽△DAP 时∴ ∠APD =∠ACO过点A 作AG ⊥PD 于点G 如图所示：∴△APG ∽△ACO∴ PG AG =OC AO设点P (n,−n 2+2n +3) 则D (n,−32n +3) 则−n 2+2n+3−3n =23 解得n =43 ∠P (43,359)综上所述 P (2,3)或P (43,359)．18．（1）解：把点A(−2，0) C(0，4)代入y =ax 2+23x +c (a ≠0)得：{4a −43+c =0c =4 解得：{a =−23c =4 ∠抛物线的解析式为y =−23x 2+23x +4 （2）解：过点D 作DF∥AB 交BC 于点F当y =0时有−23x 2+23x +4=0 解得x 1=−2,x 2=3∠B (3,0)设直线BC 的解析式为：y =kx +b代入B (3,0) C(0，4)得：{3k +b =0b =4解得{k =−43b =4∠直线BC 的解析式为：y =−43x +4 设点D 的横坐标为t 则D (t ，−23t 2+23t +4) ∠F (12t 2−12t,−23t 2+23t +4) ∠DF =t −(12t 2−12t)=−12t 2+32t∠A(−2，0) B(3，0)∠AB =5∠DF∥AB∠△DEF∽△AEB∠DF AB =DE AE∠−12t 2+32t 5=DE 5DE =15 ∠−12t 2+32t =1解得：t 1=1 t 2=2∠点D 的坐标为(1，4)或(2,83)（3）解：存在点P 使tan∠MBP =12 ①当PB 在MB 上方时过点M 作IM ⊥PB 交PB 于I 过I 作IJ ⊥y 轴于J则tan∠MBI =MI MB =12∠∠JMI +∠JIM =90° ∠JMI +∠OMB =90°∠∠JIM =∠OMB又∠∠IJM =∠MOB =90°∠△MIJ∽△BMO∠IJ MO=JM OB =IM MB ∠IJ 1=JM 3=12 ∠IJ =12 JM =32∠OJ =JM +OM =52∠I (12,52)设直线BI 的解析式为：y =mx +n代入B(3，0) I (12,52)得：{3m +n =012m +n =52 解得：{m =−1n =3∠直线BI 的解析式为：y =−x +3联立{y =−23x 2+23x +4y =−x +3解得：{x =−12y =72或{x =3y =0 （不合题意舍去）∠此时点P 的坐标为(−12,72)②当PB 在MB 下方时过点M 作KM ⊥P ′B 交P ′B 于K 过K 作KL ⊥y 轴于L 同理可得点P 的坐标为(−3114,−7398)综上所述点P 的坐标为(−12,72)或(−3114,−7398)．19．（1）解：∠抛物线y =ax 2+bx +c 过点A (−1,0) B (2,0)∠抛物线的表达式为y =a (x +1)(x −2)将点C (0,2)代入y =a (x +1)(x −2) 得：2=−2a解得：a =−1∠抛物线的表达式为y =−(x +1)(x −2) 即y =−x 2+x +2设直线BC 的表达式为y =kx +t 过点B (2,0) C (0,2)∠{2k +t =0t =2解得：{k =−1t =2∠直线BC 的表达式为y =−x +2（2）∠点M 在直线BC 上且P (m,n )(m >0) PN ⊥x 轴 C (0,2)∠M (m,−m +2) OC =2∠CM 2=(m −0)2+(−m +2−2)2=2m 2 OM 2=m 2+(−m +2)2=2m 2−4m +4 当△OCM 为等腰三角形时①若CM =OM 则CM 2=OM 2即2m 2=2m 2−4m +4解得：m =1②若CM =OC 则CM 2=OC 2即2m2=4解得：m=√2或m=−√2（舍去）③若OM=OC则OM2=OC2即2m2−4m+4=4解得：m=2或m=0（舍去）综上所述m=1或m=√2或m=2（3）∠B(2,0)C(0,2)∠COB=90°∠OC=OB=2∠∠OCB=∠OBC=45°CB=√OC2+OB2=√22+22=2√2∠点P与点C相对应P(m,n)(m>0)∠△POQ∽△CBN或△POQ∽△CNB①若点P在点B的左侧则∠CBN=45°BN=2−m CB=2√2∠CNB=∠CON+∠OCN=90°+∠OCN>90°如图当△POQ∽△CBN即∠POQ=45°时∠P(m,m)此时直线OP的表达式为y=x∠直线OP：y=x与抛物线y=−x2+x+2交于点P(m,m)(m>0)∠−m2+m+2=m解得：m=√2或m=−√2（负值舍去）∠OP=√(√2)2+(√2)2=2∠OP BC =OQBN即2√2=2−√2解得：OQ=√2−1∠P(√2,√2)Q(0,√2−1)如图当△POQ∽△CNB即∠PQO=45°时过点P作PK⊥y轴于K点∠PK=KQ=m KO=PN=−m2+m+2∠PQ=KPsin∠PQO =msin45°=√2m OQ=KQ−KO=m−(−m2+m+2)=m2−2∠PQ CB =OQNB即√2m2√2=m2−22−m解得：m=1+√133或m=1−√133（负值舍去）∠P(1+√133,7+√139)Q(0,4−2√139)②若点P在点B的右侧则∠CBN=135°BN=m−2如图当△POQ∽△CBN即∠POQ=135°时过点P作PK⊥y轴于K点∠P(m,−m)此时直线OP的表达式为y=−x PK=KQ=m KO=−(−m2+m+2)=m2−m−2∠m2−m−2=m解得：m=1+√3或m=1−√3（负值舍去）∠OP=PKsin∠POK =msin45°=√2m=√2(1+√3)=√2+√6∠OP BC =OQBN即√2+√62√2=1+√3−2解得：OQ=1∠P(1+√3,−1−√3)Q(0,1)如图当△POQ∽△CNB即∠PQO=135°时过点P作PK⊥y轴于K点∠PK=KQ=m KO=PN=−(−m2+m+2)=m2−m−2∠PQ=KPsin∠PQK =msin45°=√2m OQ=KO−KQ=m2−m−2−m=m2−2m−2∠PQ CB =OQNB即√2m2√2=m2−2m−2m−2解得：m=1+√5或m=1−√5（负值舍去）∠P(1+√5,−3−√5)Q(0,−2)综上所述P(√2,√2)Q(0，√2−1)或P(1+√133,7+√139)Q(0,4−2√139)或P(1+√3,−1−√3)Q(0,1)或P(1+√5,−3−√5)Q(0,−2)．20．解：（1）∵点A的坐标为(−1,0)∴OA=1．令x=0则y=−4∴C(0,−4)OC=4∵OC=OB∴OB=4∴B(4,0)设抛物线的解析式为y=a(x+1)(x−4)∵将x=0y=−4代入得：−4a=−4解得a=1∴抛物线的解析式为y=x2−3x−4∴a=1b=−3∵抛物线的对称轴为x=−−32×1=32C(0,−4)∵点D和点C关于抛物线的对称轴对称∴D(3,−4)设直线AD的解析式为y=kx+b．∵将A(−1,0)D(3,−4)代入得：{−k+b=03k+b=−4解得k=−1b=−1∴直线AD的解析式y=−x−1（2）∵直线AD的解析式y=−x−1∴直线AD的一次项系数k=−1∴∠BAD=45°．∵PM平行于y轴∴∠AEP=90°∴∠PMH=∠AME=45°．∴△MPH的周长=PM+MH+PH=PM+√22MP+√22PM=(1+√2)PM．设P(a,a2−3a−4)则M(a,−a−1)则PM=−a−1−(a2−3a−4)=−a2+2a+3=−(a−1)2+4．∴当a=1时PM有最大值最大值为4．∴△MPH的周长的最大值=4×(1+√2)=4+4√2（3）在直线EP的右侧x轴下方的抛物线上存在点N过点N作NG⊥x轴交x轴于点G使得以点E N G为顶点的三角形与△AOC相似理由如下：设点G的坐标为(a,0)则N(a,a2−3a−4)①如图2.1若OAOC =EGGN时△AOC∠△EGN．则a−1−a2+3a+4=14整理得：a2+a−8=0．得：a=−1+√332(负值舍去)∴点G为(−1+√332,0)②如图2.2若OAOC =GNEN时△AOC∠△NGE则a−1−a2+3a+4=4整理得：4a2−11a−17=0得：a=11+√3938(负值舍去)∴点G为(11+√3938,0)综上所述点G的坐标为(−1+√332,0)或(11+√3938,0)．。

2023年中考数学专题复习——二次函数的特殊三角形问题压轴训练

2023年中考数学专题复习——二次函数的特殊三角形问题压轴训练1．抛物线22y ax bx =+-与x 轴交于A 、B 两点（点A 在点B 的左侧），且A （﹣1，0），B （4，0），与y 轴交于点C ．连接BC ，以BC 为边，点O 为中心作菱形BDEC ，点P 是x 轴上的一个动点，设点P 的坐标为（m ，0），过点P 作x 轴的垂线交抛物线于点Q ，交BD 于点M ．(1)求该抛物线对应的函数表达式；(2)x 轴上是否存在一点P ，使△PBC 为等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由；(3)当点P 在线段OB 上运动时，试探究：当m 为何值时，四边形CQMD 是平行四边形？请说明理由．2．如图，在平面直角坐标系中，二次函数2y x bx c =-++的图象与x 轴交于A 、B 两点，与y 轴交于()0,3C ，A 点在原点的左侧，B 点的坐标为3,0．点P 是抛物线上一个动点，且在直线BC 的上方．(1)求这个二次函数及直线BC 的表达式．(2)过点P 做PD y ∥轴交直线BC 于点D ，求PD 的最大值．(3)点M 为抛物线对称轴上的点，问在抛物线上是否存在点N ，使MNO 为等腰直角三角形，且NMO ∠为直角，若存在，请直接写出点N的坐标；若不存在，请说明理由．3．如图，抛物线y＝ax2+bx+c经过点A（﹣2，5），与x轴相交于B（﹣1，0），C（3，0）两点．(1)求抛物线的函数表达式；(2)点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC'D，若点C'恰好落在抛物线的对称轴上，求点C'和点D的坐标；(3)设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△CPQ为等边三角形时，求直线BP的函数表达式．4．如图，抛物线y＝x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点（0，3）．(1)求抛物线的解析式；(2)点P是x轴下方的抛物线上的一个动点，过点P的直线y＝x+m与直线BC交于点E，与y轴交于点F，当PE+EF有最大值时，求P点的坐标；(3)在抛物线的对称轴上是否存在一点D使△BCD是以BC为斜边的直角三角形，若存在，请求出点D的坐标；若不存在，请说明理由．5．抛物线y＝ax2−4ax＋3a交x轴于点B、C两点，交y轴于点A，点D为抛物线的顶点，连接AB、AC，已知△ABC的面积为3(1)求抛物线的解析式；(2)点P为抛物线对称轴右侧一点，点P的横坐标为m，过点P作PQ//AC交y轴于点Q，AQ的长度为d，求d与m的函数关系式；(3)在（2）的条件下，当d＝4时，作DN⊥y轴于点N，点G为抛物线上一点，AG交线段PD于点M，连接MN，若△AMN是以MN为底的等腰三角形，求点G的坐标．6．已知一次函数y＝x＋4的图象与二次函数y＝ax（x－2）的图象相交于点A（－1，b）和点B，点P是线段AB上的动点（不与A、B重合），过点P作PC⊥x轴，与二次函数y＝ax（x－2）的图象交于点C．(1)a＝，b＝，B点的坐标为；(2)求线段PC 长的最大值．(3)连接AC ，当△P AC 是以AP 为腰的等腰三角形时，直接写出点P 的坐标．7．如图,在坐标系中△ABC 是等腰直角三角形,∠BAC =90°,A (1, 0),B (0, 2),抛物线2122y x bx =--的图象过点（2，-1）及点C .(1)求该抛物线的解析式；(2)求点C 的坐标(3)点P 是抛物线上一动点，是否存在点P ，使以P ，A ，C ，B 为顶点的四边形是平行四边形？若存在，求出P 点坐标；若不存在，说明理由.8．如图，二次函数2(1)4y x k x =-+-+的图像与y 轴交于点A ，与x 轴的负半轴交于点B ，且AOB 的面积为6．(1)求A ，B 两点的坐标；(2)求该二次函数的表达式；(3)如果点p 在坐标轴上，且ABP △是等腰三角形，直接写出p 点坐标．9．如图，已知二次函数的图象经过点()3,3A 、()4,0B 和原点O ．P 为二次函数图象上的一个动点，过点P 作x 轴的垂线，垂足为(),0D m ，并与直线OA 交于点C ．(1)求出二次函数的解析式；(2)当点P 在直线OA 的上方时，求线段PC 的最大值；(3)当0m >时，探索是否存在点P ，使得PCO △为等腰三角形，如果存在，求出P 的坐标；如果不存在，请说明理由．10．如图，抛物线y ＝ax 2+bx +4与x 轴相交于点A （0），B 0），与y 轴相交于点C ，抛物线的对称轴与x 轴相交于点D ，点P 是x 轴上的一个动点，连接CP ，并把线段CP 绕着点C 按逆时针方向旋转60°，得到CQ ，连接PQ ，OQ ．(1)求抛物线的解析式；(2)当点P 运动到点D 时，求Q 点坐标，并判断点Q 是否在抛物线上；(3)当△OPQ P的坐标．11．如图1，抛物线y=-x2+bx+c交x轴于A，B两点，交y轴于C点，D是抛物线上的动点，已知A的坐标为（-3，0），C的坐标为（0，3）．(1)求该抛物线的函数表达式以及B点的坐标；(2)在第二象限内是否存在点D使得△ACD是直角三角形且∠ADC=90°，若存在请求出D点的坐标，若不存在请说明理由；(3)如图2，连接AC，BC，当∠ACD=∠BCO，求D点的坐标．12．如图：已知关于x的二次函数y=x2+bx+c的图像与x轴交于点A（1，0）和点B，与y轴交于点C（0，3）．(1)求二次函数的解析式；(2)在抛物线的对称轴上是否存在一点P，使△PBC为等腰三角形，若存在，请求出点P的坐标；(3)有一个点M 在线段CB 上运动，作MN ⊥x 轴交抛物线于点N ，问当M 、N 点位于何处时，△BCN 的面积最大，求最大面积.13．如图，抛物线212y x bx c =-++与x 轴交于A ，B 两点，与y 轴交于点C ，点B ，C 的坐标分别为（2，0），（0，3），点D 与点C 关于x 轴对称，P 是直线AC 上方抛物线上一动点，连接PD 、交AC 于点Q ．(1)求抛物线的函数表达式及点A 的坐标；(2)在点P 运动的过程中，求PQ ：DQ 的最大值；(3)在y 轴上是否存在点M ，使∠AMB ＝45°？若存在，请直接写出点M 的坐标；若不存在，请说明理由．14．如图，抛物线2y x bx c =-++与x 轴相交于A ，B 两点（点A 位于点B 的左侧），与y 轴相交于点C ，M 是抛物线的顶点，直线1x =是抛物线的对称轴，且点C 的坐标为(0,3)．(1)求抛物线的解析式；(2)已知P 为线段MB 上一个动点，过点P 作PD x ⊥轴于点D ．若,PD m PCD =△的面积为S ． ①求S 与m 之间的函数关系式，并写出自变量m 的取值范围；②当S 取得最大值时，求点P 的坐标．(3)在（2）的条件下，在线段MB 上是否存在点P ，使PCD 为等腰三角形？如果存在，直接写出满足条件的点P 的坐标；如果不存在，请说明理由．15．如图，直线334y x =+与x 轴交于点A ，与y 轴交于点C ，经过A 、C 两点的抛物线y ＝ax 2＋bx ＋c 与x 轴的另一交点为(1,0)B ．(1)求该抛物线的函数表达式；(2)点P 是该抛物线上的动点，过点P 作PD ⊥x 轴于点D ，交AC 于点E ，设点P 的横坐标为t （－4＜t ＜0）． ①求出四边形P AOC 面积S 与t 的函数表达式，并求S 的最大值；②当△PEC 为等腰三角形时，求所有满足条件的t 的值．16．将抛物线C ：244y x x =-+向下平移6个单位长度得到抛物线1C ，再将抛物线1C 向左平移得到抛物线2C ．抛物线2C 的顶点在y 轴上．(1)分别求抛物线1C 的顶点坐标及抛物线2C 的解析式；(2)点A 在抛物线1C 对称轴右侧的图像上，点B 在抛物线1C 的对称轴上，△OAB 是以OB 为斜边的等腰直角三角形，求点A 的坐标；(3)如图，直线y kx =（0k ≠，k 为常数）与抛物线2C 交于E ，F 两点，M 为线段EF 的中点直线4y x k=-与抛物线2C 交于G ，H 两点，N 为线段GH 的中点，求证：直线MN 经过一个定点．17．如图，抛物线234y x bx c =-++交x 轴于()1,0A -，()4,0B 两点，交y 轴于点C ，点D 是抛物线上位于直线BC 上方的一个动点．(1)求抛物线的解析式；(2)连接AC ，BD ，若90ACO DBA ∠+∠=︒，求点D 的坐标；(3)在（2）的条件下，将抛物线沿着射线AD 平移m 个单位，平移后A 、D 的对应点分别为M 、N ，在x 轴上是否存在点P ，使得PMN 是等腰直角三角形？若存在，请求出m 的值：若不存在，请说明理由．18．如图，四边形ABCD 的顶点坐标分别为(A ，12B ⎛- ⎝⎭，()1,0C ，(D ，抛物线经过A ，B ，D 三点．(1)求证：四边形AOCD 是矩形；(2)求抛物线的解析式；(3)ACD △绕平面内一点M 顺时针旋转90︒得到111AC D ，即点A ，C ，D 的对应点分别为1A ，1C ，1D ，若111AC D 恰好两个顶点落在抛物线上，请直接写出1A 的坐标．19．如图1，以点M （1，4）为顶点的抛物线与直线y ＝kx +b 交于A ，B 两点，且点A 坐标为（4，﹣12），点B 在y 轴上．(1)求直线和抛物线解析式；(2)若点D 是抛物线上位于直线AB 上方的一点（如图2），过点D 作DE ⊥x 轴于点E ，交直线AB 于点F ，求线段DF 长度的最大值；(3)在抛物线的对称轴l 上是否存在点P ，使以点A ，M ，P 为顶点的三角形是直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．20．如图，抛物线2122y x mx =-++与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的对称轴32x =交x 轴于点D ．(1)求m 的值；(2)在抛物线对称轴上找点P ，使PCD 是以CD 为腰的等腰三角形，请求出点P 的坐标；（提醒满足条件的点P 可能不只一个）(3)点E 是线段BC 上一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，与x 轴相交于点H ，连接CF 、BF 、OE ，当四边形CDBF 的面积最大时，请你说明四边形OCFE 的形状．参考答案：1．(1)213222y x x =--；(2)存在，点P 的坐标为（32，0）或（0）或（4﹣0）或（﹣4，0）； (3)当m ＝2时，四边形CQMD 是平行四边形，理由见解析．2．(1)二次函数的表达式为2y x 2x 3=-++，直线BC 的表达式为3y x =-+； (2)94(3)存在，点N 的坐标为或或）或，．3．(1)y ＝x 2﹣2x ﹣3(2)点C ′的坐标为（1，，点D 的坐标为（1(3)33y x =+或y = 4．(1)y ＝x 2﹣4x +3(2)点P 的坐标为（2，﹣1）(3)存在，点D 的坐标为：（22．5．(1)243y x x =-+(2)2|3|(2)d m m m =-> (3)85,39⎛⎫- ⎪⎝⎭G 或(4,3)6．(1)1；3；（4，8） (2)254(3)()2,6或(47．(1)211222y x x =-- (2)（3，1）(3)满足条件的P 点只有一个，为(-2，1)8．(1)()04A ，，()30B -， (2)2543y x x =--+ (3)()30，，()0-1，，()09，，()8,0-，()0-4，，()20,，70,8⎛⎫ ⎪⎝⎭，7,06⎛⎫ ⎪⎝⎭9．(1)y =-x 2+4x (2)94(3)存在，点P 的坐标为(3+或(3-或（5，-5）或（4，0）10．(1)2144y x x =-++(2)Q ，4），点Q 在抛物线上(3)符合条件的点P 0），0），（0），（0）11．(1)y ＝-x 2-2x ＋3，B (1，0)(2)存在，D (－2，3) (3)D (－52，74)或(－4，－5)12．(1)243y x x =-+(2)存在，P （2，2）（2，（2，3，（2（2，(3)当3322M ⎛⎫ ⎪⎝⎭，，3324N ⎛⎫- ⎪⎝⎭，时，△BCN 的面积最大，最大面积为27813．(1)211322y x x =--+；（－3，0） (2)316(3)存在，M （0，6）或M （0，－6）14．(1)2y x 2x 3=-++(2)①213(04)42S m m m =-+<≤；②S 有最大值为94，此时3,32P ⎛⎫ ⎪⎝⎭(3)存在，(6-+-或(42-+15．(1)239344y x x =--+ (2)①23662S t t =--+(40)t -<<，S 的最大值为12；②73-或2-或4718-16．(1)C 1的顶点坐标是（2，-6），C 2：y ＝x 2﹣6；(2)A （4，﹣2）或（5，3）；(3)见解析17．(1)239344y x x =-++ (2)()3,3D(3)存在，203m =或53或56时，PMN 是等腰直角三角形18．(1)平行四边形AOCD 是矩形(2)2y x =(3)1A 点的坐标为112⎛⎫++ ⎪ ⎪⎝⎭或1142⎫⎪⎪⎝⎭19．(1)72y x =-+，21722y x x =-++ (2)2(3)1(1,)2-或5(1,)2-20．(1)32 m=(2)135 , 22P ⎛⎫⎪⎝⎭，235,22P⎛⎫-⎪⎝⎭，33,42P⎛⎫⎪⎝⎭(3)当四边形CDBF的面积最大时，四边形OCFE是平行四边形。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

冲刺中考《二次函数动点成特殊三角形问题》压轴专题1.如图，在平面直角坐标系中，二次函数y＝－13x2＋bx＋c的图象与坐标轴交于A，B，C三点，其中点A的坐标为(－3，0)，点B的坐标为(4，0)，连接AC，BC.动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒．连接PQ.(1)填空：b＝________，c＝________；(2)在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；(3)在x轴下方的二次函数的图象上是否存在点M，使△PQM是以点P为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由．第1题图解：(1)13，4；【解法提示】∵二次函数y＝－13x2＋bx＋c与x轴交于A(－3，0)，B(4，0)，∴b c=b c=--+⎧⎪⎨-++⎪⎩33016403，解得b=c=⎧⎪⎨⎪⎩134，1(2)可能是，理由如下：∵点P在AC上以每秒1个单位的速度运动，∴AP＝t，∵点Q在OB上以每秒1个单位的速度运动，∴OQ＝t，∴AQ＝t＋3，∵∠PAQ<90°，∠PQA<90°，∴若要使△APQ是直角三角形，则∠APQ＝90°，在Rt△AOC中，OA＝3，OC＝4，∴AC＝5，如解图①，设PQ与y轴交于点D，第1题解图①∵∠ODQ＝∠CDP，∠DOQ＝∠DPC＝90°，2∴∠DQO＝∠DCP，∴tan∠DQO＝APPQ＝tan∠DCP＝AOCO＝34，∵AP＝t,∴PQ＝43 t，由勾股定理得：AQ2＝AP2＋PQ2，即(t＋3)2＝t2＋(43t)2，解得t＝92或t＝－98(舍去)，根据题意，点Q在线段OB上，∴0≤t≤4，∴不存在这样的t值满足题意，即△APQ不可能是直角三角形；（3）假设存在点M使得△PMQ是以点P为直角顶点的等腰直角三角形，如解图②，过P作PE⊥x轴于E，过M作MN⊥PE交PE的延长线于点N，34第1题解图②∵∠MPN ＋∠PMN ＝90°， ∠MPN ＋∠QPE ＝90°， ∴∠PMN ＝∠QPE ，在△PMN 和△QPE 中，∠∠⎧⎪∠∠⎨⎪⎩PMN=QPE PNM=PEQ MP=PQ ， ∴△PMN ≌△QPE (AAS)， ∴PN ＝EQ ，MN ＝PE ，∵AP ＝t ，cos∠CAO ＝AO AC ＝35， sin∠CAO ＝OC AC ＝45，5∴AE ＝35t ，PE ＝45t ，∴MN ＝45t ，EN ＝EQ －PE ＝AQ －AE －PE ＝3＋t －35t －45t ＝3－25t ， ∴x M ＝x E －MN ＝35t －3－45t ＝－15t －3，∴点M 的坐标为(－15t －3，25t －3)，在x 轴下方，∵点M 在抛物线上，∴－13(－15t －3)2－13(15t ＋3)＋4＝25t －3，整理得t 2＋65t ＝225，解得t ＝－65＋52052或t ＝－65－52052(舍)，综上，存在满足条件的点M ，此时运动时间t 为－65＋52052秒．2. 如图，已知抛物线y ＝ax 2＋bx ＋c (a ≠0)的对称轴为直线x ＝－1，且经过A (1，0)，C (0，3)两点，与x 轴的另一个交点为B . (1)若直线y ＝mx ＋n 经过B ，C 两点，求抛物线和直线BC 的解析式；(2)在抛物线的对称轴x ＝－1上找一点M ，使点M 到点A 的距离与到点C 的距离之和最6小，求点M 的坐标；(3)设点P 为抛物线的对称轴x ＝－1上的一个动点，求使△BPC 为直角三角形的点P 的坐标．第2题图解：(1)由题意得⎩⎪⎨⎪⎧－b 2a＝－1a ＋b ＋c ＝0c ＝3，解得⎩⎨⎧a ＝－1b ＝－2c ＝3，∴抛物线的解析式为y ＝－x 2－2x ＋3.∵对称轴为直线x ＝－1，抛物线经过A (1，0)， ∴B (－3，0)．设直线BC 的解析式y ＝mx ＋n ，把B (－3，0)，C (0，3)分别代入y ＝mx ＋n 得 ⎩⎨⎧－3m ＋n ＝0n ＝3，解得⎩⎨⎧m ＝1n ＝3， ∴直线BC 的解析式为y ＝x ＋3；7(2)如解图，连接MA ，第2题解图∵MA ＝MB ， ∴MA ＋MC ＝MB ＋MC .∴使MA ＋MC 最小的点M 应为直线BC 与对称轴x ＝－1的交点．设直线BC 与对称轴x ＝－1的交点为M ，把x ＝－1代入直线y ＝x ＋3，得y ＝2.∴M (－1，2);(3)设P (－1，t )，∵B (－3，0)，C (0，3)，∴BC 2＝18，PB 2＝(－1＋3)2＋t 2＝4＋t 2， PC 2＝(－1)2＋(t －3)2＝t 2－6t ＋10.①若B 为直角顶点，则BC 2＋PB 2＝PC 2，即18＋4＋t 2＝t 2－6t ＋10，解得t ＝－2； ②若C 为直角顶点，则BC 2＋PC 2＝PB 2，即18＋t 2－6t ＋10＝4＋t 2，解得t ＝4； ③若P 为直角顶点，则PB 2＋PC 2＝BC 2，即：4＋t 2＋t 2－6t ＋10＝18，解得t 1＝3＋172，t 2＝3－172. 综上所述，满足条件的点P 共有四个，分别为：P 1(－1，－2)，P 2(－1，4)，P 3(－1，3＋172)，P 4(－1，3－172)．83. 如图，在平面直角坐标系中，抛物线y ＝x 2＋bx ＋c 经过点A (0，－6)和点C (6，0)． (1)求抛物线的解析式；(2)若抛物线与x 轴的负半轴交于点B ，试判断△ABC 的形状；(钝角三角形、直角三角形、锐角三角形)(3)在抛物线上是否存在点P ，使得△PAC 是以AC 为底的等腰三角形？若存在，请求出所有点P 的坐标；若不存在，请说明理由．第3题图解：(1)将C 、A 两点坐标代入y ＝x 2＋bx ＋c ，可得⎩⎨⎧36＋6b ＋c ＝0c ＝－6，解得⎩⎨⎧b ＝－5c ＝－6，∴抛物线的解析式为y ＝x 2－5x －6； (2)当y ＝0时，则有：x 2－5x －6＝0，即(x ＋1)(x －6)＝0， ∴解得x 1＝－1，x 2＝6(舍)， ∴B (－1，0)．由两点之间的距离公式可得：BC 2＝2＝49，AC 2＝(6－0)2＋2＝72， AB 2＝(－1－0)2＋2＝37，9∵AB 2＋BC 2>AC 2， ∴△ABC 为锐角三角形．(3)存在满足条件的点P ，使得△PAC 是以AC 为底的等腰三角形理由：如解图，过线段AC 的中点M ，作AC 的垂线交抛物线于点P ，第3题解图直线MP 与抛物线必有两个满足条件的交点P ， ∵A (0，－6)，C (6，0)，∴点M 的坐标为(3，－3)，且OA =OC ， ∴直线MP 过点O ，设直线MP 的解析式为y ＝kx ，将点M (3，－3)代入得，k ＝－1，即直线MP 的解析式为y ＝－x ，联立⎩⎨⎧y ＝－x y ＝x 2－5x －6，解得⎩⎪⎨⎪⎧x 1＝2－10y 1＝10－2或⎩⎪⎨⎪⎧x 2＝2＋10y 2＝－2－10，∴点P 的坐标为(2－10，10－2)或(2＋10，－2－10)．4. 如图，在平面直角坐标系中，直线y ＝－2x ＋10与x 轴，y 轴相交于A ，B 两点，点C 的坐标是(8，4)，连接AC ，BC . (1)求过O ，A ，C 三点的抛物线的解析式，并判断△ABC 的形状；10(2)动点P 从点O 出发，沿OB 以每秒2个单位长度的速度向点B 运动，同时，动点Q 从点B 出发，沿BC 以每秒1个单位长度的速度向点C 运动，规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t 秒．当t 为何值时，PA ＝QA?(3)在抛物线的对称轴上，是否存在点M ，使以A ，B ，M 为顶点的三角形是等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．第4题图解：(1)∵直线y ＝－2x ＋10与x 轴、y 轴相交于A 、B 两点， ∴A (5，0)，B (0，10)，设过O 、A 、C 三点的抛物线的解析式为y ＝ax 2＋bx (a ≠0)，把点A (5，0)和C (8，4)代入可得⎩⎨⎧25a ＋5b ＝064a ＋8b ＝4，解得⎩⎪⎨⎪⎧a ＝16b ＝－56，∴抛物线的解析式为y ＝16x 2－56x ；∵A (5，0)，B (0，10)，C (8，4)， ∴AB 2＝125，AC 2＝25，BC 2＝100， ∵AB 2＝AC 2＋BC 2，11∴△ABC 是直角三角形．(2)如解图，连接AP ，AQ ，当P ，Q 运动t 秒，即OP ＝2t ，CQ ＝10－t ，第4题解图在Rt△AOP 和Rt△ACQ 中， ⎩⎨⎧AC ＝OA PA ＝QA， ∴Rt△AOP ≌Rt△ACQ ， ∴OP ＝CQ ， ∴2t ＝10－t ，∴t ＝103， ∵t <5，∴当运动时间为103秒时，PA ＝QA ；(3)存在．由题可得，抛物线的对称轴直线为x ＝52，设点M的坐标为( 52，b)，利用点的坐标可求得AB2＝102＋52＝125，MB2＝(52)2＋(b－10)2，MA2＝(52)2＋b2，∵△MAB是等腰三角形，∴可分以下三种情况讨论：①当AB＝MA时，即125＝(52)2＋b2，解得b＝±519 2，即点M的坐标为(52，5192)或(52，－5192)；②当AB＝BM时，即125＝(52)2＋(b－10)2，解得b＝10±519 2，即点M的坐标为(52，10＋5192)或(52，10－5192)；12③当MB＝MA时，即(52)2＋(b－10)2＝(52)2＋b2，解得b＝5，此时点A、M、B共线，故这样的点M不存在．综上所述，存在点M，使以点A、B、M为顶点的三角形是等腰三角形，点M的坐标为(52，5192)或(52，－5192)或(52，10＋5192)或(52，10－5192)．5.如图，抛物线y＝x2＋bx＋c与x轴交于A、B两点，B点坐标为(3，0)，与y轴交于点C(0，3)．(1)求抛物线的解析式；(2)点P在x轴下方的抛物线上，过点P的直线y＝x＋m与直线BC交于点E，与y轴交于点F，求PE＋EF的最大值；(3)点D为抛物线对称轴上一点，当△BCD是以BC为直角边的直角三角形时，求点D的坐标．解：(1)由题意得⎩⎨⎧32＋3b＋c＝0c＝3，解得⎩⎨⎧b＝－4c＝3，∴抛物线的解析式为y＝x2－4x＋3；13(2)如解图①，过点P作PG∥CF交CB与点G，第5题解图①由题可知，直线BC的解析式为y＝－x＋3，OC＝OB＝3，∴∠OCB＝45°.同理可知∠OFE＝45°，∴△CEF为等腰直角三角形，∵PG∥CF，∴△GPE为等腰直角三角形，∵F(0，m)，C(0，3)，∴CF＝3－m，∵△CEF∽△GEP∴EF＝22CF＝22(3－m), PE＝22PG，设P(t，t2－4t＋3)(1<t<3), 则G(t，－t＋3)PE＝22PG＝22(－t＋3－t－m)＝22(－m－2t＋3)，∵点P是直线y＝x＋m与抛物线的交点，∴t2－4t＋3＝t＋m，14∴PE＋EF＝22(3－m)＋22(－m－2t＋3)＝22(－2t－2m＋6)＝－2(t＋m－3)＝－2 (t2－4t)＝－2(t－2)2＋42，∴当t＝2时，PE＋EF最大，最大值为42；(3)由(1)知对称轴x＝2，设点D(2，n)，如解图②.第5题解图②当△BCD是以BC为直角边的直角三角形时，分两种情况讨论：(ⅰ)D在C上方D1位置时，由勾股定理得CD21＋BC2＝BD21，即(2－0)2＋(n－3)2＋(32)2＝(3－2)2＋(0－n)2 ，解得n＝5；(ⅱ)D在C下方D2位置时，由勾股定理得BD22＋BC2＝CD22，即(2－3)2＋(n－0)2＋(32)2＝(2－0)2＋(n－3)2 ，解得n＝－1，综上所述，当△BCD是以BC为直角边的直角三角形时，D为(2，5)或(2，－1)．6.如图，抛物线y＝ax2－2ax＋c(a≠0)与y轴交于点C(0，4)，与x轴交于点A、B，点A的坐标为(4，0)．(1)求该抛物线的解析式；15(2)抛物线的顶点为N，在x轴上找一点K，使CK＋KN的值最小，求出此时点K的坐标；(3)若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为(2，0)．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．第6题图解：(1)∵抛物线经过点C(0，4)，A(4，0)，∴c=a a c=⎧⎨-+⎩41680，解得a=c=⎧-⎪⎨⎪⎩124，∴抛物线的解析式为y＝－12x2＋x＋4；(2)由y＝－12x2＋x＋4＝－12(x－1)2＋92可得抛物线的顶点坐标为N(1，92)，如解图①，作点C关于x轴的对称点C′，则C′(0，－4)，连接C′N交x轴于点K，则K点即为所求点，1617第6题解图①设直线C′N 的解析式为y ＝kx ＋b (k ≠0)，把N ，C′两点坐标代入可得：k b=b=⎧+⎪⎨⎪-⎩924，解得k=b=⎧⎪⎨⎪-⎩1724，∴直线C′N 的解析式为y ＝172x －4，令y ＝0，解得x ＝817， ∴点K 的坐标为(817，0)； (3)存在．要使△ODF 是等腰三角形，需分以下三种情况讨论： ①DO ＝DF ，∵A (4，0)，D (2，0)， ∴AD ＝OD ＝DF ＝2，18在Rt △AOC 中，OA ＝OC ＝4， ∴∠OAC ＝45°， ∴∠DFA ＝∠OAC ＝45°， ∴∠ADF ＝90°.此时，点F 的坐标为(2，2)；由－12x2＋x ＋4＝2得，x 1＝1＋5，x 2＝1－ 5.此时，点P 的坐标为(1＋5，2)或(1－5，2)； ②FO ＝FD ，如解图②，过点F 作FM ⊥x 轴于点M .第6题解图②由等腰三角形的性质得：OM ＝12OD ＝1，∴AM ＝3，∴在等腰直角△AMF 中，MF ＝AM ＝3，19∴F (1，3)．由－12x 2＋x ＋4＝3得，x 1＝1＋3，x 2＝1－ 3.此时，点P 的坐标为(1＋3，3)或(1－3，3)； ③OD ＝OF ，∵OA ＝OC ＝4，且∠AOC ＝90°， ∴AC ＝42，∴点O 到AC 的距离为2 2.而OF ＝OD ＝2<22，∴在AC 上不存在点F 使得OF ＝OD ＝2.此时，不存在这样的直线l ，使得△ODF 是等腰三角形．综上所述，存在这样的直线l ，使得△ODF 是等腰三角形，所求点P 的坐标为(1＋5，2)或(1－5，2)或(1＋3，3)或(1－3，3)．7. 如图①，抛物线y ＝－13x 2＋bx ＋8与x 轴交于点A (－6，0)，点B (点A 在点B 左侧)，与y 轴交于点C ，点P 为线段AO 上的一个动点，过点P 作x 轴的垂线l 与抛物线交于点E ，连接AE 、EC .(1)求抛物线的表达式及点C 的坐标；(2)连接AC 交直线l 于点D ，则在点P 运动过程中，当点D 为EP 中点时，求S △ADP ∶S △CDE ；(3)如图②，当EC∥x轴时，点P停止运动，此时，在抛物线上是否存在点G，使△AEG 是以AE为直角边的直角三角形？若存在，请求出点G的坐标；若不存在，说明理由．第7题图解：(1)∵点A(－6，0)在抛物线y＝－13x2＋bx＋8上，∴0＝－13×(－6)2＋(－6b)＋8，解得b＝－2 3，∴抛物线的表达式为y＝－13x2－23x＋8，令x＝0，得y＝8，∴C(0，8);(2)设点E(t，－13t2－23t＋8)，∴P(t，0)，∵点D为EP的中点，2021∴DP ＝DE ，D (t ，－16t 2－13t ＋4)，设直线AC 的解析式为y ＝kx ＋b (k ≠0)，将A (－6，0)，C (0，8)，代入得：k b=b=-+⎧⎨⎩608，解得k=b=⎧⎪⎨⎪⎩438，∴直线AC 的解析式为y ＝43x ＋8，∵点D 在直线AC 上， ∴43t ＋8＝－16t 2－13t ＋4，解得t 1＝－6(舍去)，t 2＝－4， ∴P (－4，0)， ∴AP ＝2，OP ＝4，∴S △ADP S △CDE ＝1212g g DP AP DE OP ＝AP OP ＝12； (3)存在．如解图①，连接EG ，AG ，过点G 作GM ⊥l ，GN ⊥x 轴，垂足分别为M ，N ，第7题解图①∵EC∥x轴，∴EP＝CO＝8，把y＝8代入y＝－13x2－23x＋8，则8＝－13x2－23x＋8，解得x＝0(舍去)或x＝－2，∴P(－2，0)，∴AP＝AO－PO＝4，(ⅰ)如解图①，当∠AEG＝90°时，∵∠MEG＋∠AEP＝90°，∠AEP＋∠EAP＝90°，∴∠MEG＝∠EAP，又∵∠APE＝∠EMG＝90°，∴△EMG∽△APE，22∴EMAP＝MGEP，设点G(m，－13m2－23m＋8)(m＞0)，则GN＝MP＝－13m2－23m＋8，∴EM＝EP－MP＝8－(－13m2－23m＋8)＝13m2＋23m，MG＝PN＝PO＋ON＝2＋m，∴13m2＋23m4＝2＋m8，∴m＝－2(舍去)或m＝3 2，∴G(32，254)；(ⅱ)如解图②，当∠EAG＝90°时，23第7题解图②∵∠NAG＋∠EAP＝90°，∠AEP＋∠EAP＝90°，∴∠NAG＝∠AEP，∵∠APE＝∠GNA＝90°，∴△GNA∽△APE，∴GNAP＝ANEP，设点G(n，－13n2－23n＋8)(n＞4)，∴GN＝13n2＋23n－8，AN＝AO＋ON＝6＋n，∴2128334+-n n＝68+n，∴n＝－6(舍去)或n＝11 2，∴G(112，－234)，综上，符合条件的G点的坐标为(32，254)或(112，－234)．24258. 如图，在平面直角坐标系中，已知抛物线y ＝ax 2＋bx －8与x 轴交于A ，B 两点，与y 轴交于点C ，直线l 经过坐标原点O ，与抛物线的一个交点为D ，与抛物线的对称轴交于点E ，连接CE .已知点A ，D 的坐标分别为(－2，0)，(6，－8)． (1)求抛物线的函数表达式； (2)分别求出点B 和点E 的坐标；(3)若点P 是y 轴负半轴上的一个动点，设其坐标为(0，m )，直线PB 与直线l 交于点Q .试探究：当m 为何值时，△OPQ 是等腰三角形．第8题图解：(1)∵抛物线y ＝ax 2＋bx －8经过点A (－2，0)，D (6，－8)， ∴将A 、D 两点的坐标代入得⎩⎨⎧4a －2b －8＝036a ＋6b －8＝－8，解得⎩⎨⎧a ＝12b ＝－3，∴抛物线的函数表达式为y ＝12x 2－3x －8；(2)∵y ＝12x 2－3x －8＝12(x －3)2－252，∴抛物线的对称轴为直线x＝3，又∵抛物线与x轴交于A，B两点，点A的坐标为(－2，0)，∴点B的坐标为(8，0)．设直线l的函数表达式为y＝kx，∵点D(6，－8)在直线l上，代入得6k＝－8，解得k＝－4 3，∴直线l的函数表达式为y＝－43x，∵点E为直线l和抛物线对称轴的交点，∴点E的横坐标为3，纵坐标为－43×3＝－4，即点E的坐标为(3，－4)；(3)需分两种情况进行讨论：①当OP＝OQ时，△OPQ是等腰三角形，如解图①，第8题解图①∵点E的坐标为(3，－4)，26∴OE＝32＋42＝5，过点E作直线ME∥PB，交y轴于点M，交x轴于点H，则OMOP＝OEOQ，∴OM＝OE＝5，∴点M的坐标为(0，－5)，设直线ME的函数表达式为y＝k1x－5，E（3，-4）在直线ME上，∴3k1－5＝－4，解得k1＝1 3，∴直线ME的函数表达式为y＝13x－5，令y＝0，解得x＝15，∴点H的坐标为(15，0)．又∵MH∥PB，∴OPOM＝OBOH，即－m5＝815，∴m＝－8 3；②当QO＝QP时，△OPQ是等腰三角形，如解图②，27第8题解图②∵当x＝0时，y＝12x2－3x－8＝－8，∴点C的坐标为(0，－8)，∴CE＝32＋（8－4）2＝5，∴OE＝CE，∴∠1＝∠2，又∵QO＝QP，∴∠1＝∠3，∴∠2＝∠3，∴CE∥PB.设直线CE交x轴于点N，其函数表达式为y＝k2x－8，E（3，-4）在直线CE上，∴3k2－8＝－4，解得k2＝43，28∴直线CE的函数表达式为y＝43x－8，令y＝0，得43x－8＝0，∴x＝6，∴点N的坐标为(6，0)．∵CN∥PB.∴OPOC＝OBON，∴－m8＝86，解得m＝－323.综上所述，当m的值为－83或－323时，△OPQ是等腰三角形．9.如图，抛物线y＝13x2＋bx＋c与x轴交于A(3，0)，B(－1，0)两点，过点B作直线BC⊥x轴，交直线y＝－2x于点C.(1)求该抛物线的解析式；(2)求该抛物线的顶点D的坐标，并判断顶点D是否在直线y＝－2x上；(3)点P是抛物线上一动点，是否存在这样的点P(点A除外)，使△PBC是以BC为直角边的直角三角形？若存在，求出所有满足条件的点P的坐标；若不存在，请说明理由．2930第9题图解：(1)∵y ＝13x 2＋bx ＋c 与x 轴交于A (3，0)，B (－1，0)两点，∴⎩⎪⎨⎪⎧13×32＋3b ＋c ＝013×（－1）2－b ＋c ＝0，解得⎩⎨⎧b ＝－23c ＝－1， ∴抛物线的解析式为y ＝13x 2－23x －1；(2)∵a ＝13，b ＝－23，c ＝－1，抛物线的顶点D 的坐标为(－b 2a ，4ac －b 24a)，∴x D ＝－－232×13＝1，y D ＝4×13×（－1）－（－23）24×13＝－43，∴D(1，－43)．把x＝1代入y＝－2x中得y＝－2，∵－43≠－2，∴顶点D不在直线y＝－2x上；(3)存在．理由如下：如解图，过点C作x轴的平行线，与该抛物线交于点P1，P2，连接BP1，BP2.第9题解图∵直线BC⊥x轴，∴△P1BC、△P2BC都是直角三角形．把x＝－1代入y＝－2x中得：y＝－2×(－1)＝2，∴C(－1，2)．31∴把y＝2代入y＝13x2－23x－1中得13x2－23x－1＝2，解得x1＝10＋1，x2＝－10＋1.∴P1(10＋1，2)，P2(－10＋1，2)．10.如图，抛物线y＝－12x2＋bx＋c与x轴交于A(－1，0)、B两点，与y轴交于点C(0，2)，抛物线的对称轴交x轴于点D.(1)求抛物线的解析式；(2)求sin∠ABC的值；(3)在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形，如果存在，直接写出点P的坐标；如果不存在，请说明理由．第10题图解：(1)将点A(－1，0)，C(0，2)代入抛物线y＝－12x2＋bx＋c中得，⎩⎨⎧－12－b＋c＝0c＝2，解得⎩⎨⎧b＝32c＝2，32∴抛物线的解析式为y＝－12x2＋32x＋2；(2)令y＝－12x2＋32x＋2＝0，解得x1＝－1，x2＝4，∴点B的坐标为(4，0)，在Rt△BOC中，BC＝OC2＋OB2＝22＋42＝25，∴sin∠ABC＝OCBC＝225＝55；(3)存在，点P坐标为(32，52)或(32，－52)或(32，4)．【解法提示】由抛物线y＝－12x2＋32x＋2得对称轴为直线x＝32，∴点D的坐标为(32，0)．∴CD＝OC2＋OD2＝22＋（32）2＝52.∵点P在对称轴x＝32上，且△PCD是以CD为腰的等腰三角形，∴当点D为顶点时，有DP＝CD＝52，33此时点P的坐标为(32，52)或(32，－52)；当点C为顶点时，如解图，连接CP，则CP＝CD，过点C作CG⊥DP于点G，则DG＝PG，第10题解图∵DG＝2，∴PG＝2，PD＝4，∴点P的坐标为(32，4)．综上，存在点P使△PCD是以CD为腰的等腰三角形，点P的坐标为(32，52)或(32，－52)或(32，4)．34。